Уравнение для ускорений в плоском движении

Ускорения точек тела при плоском движении

Рассмотрим плоское движение плана этажа как сложное. Это состоит из поступательного перевода, состоящего из относительных вращений вокруг полюсов A и A согласно теореме ускорения точки B. Рисунок 54. Переносимое ускорение переводится с точки А на рисунке, поэтому переносное ускорение. Относительное ускорение aBr точки B от вращения вокруг полюса A обозначается abA. После этого уравнение (9) принимает вид: av = aA + avl, (10).

То есть ускорение точки на виде сверху во время плоского движения равно векторной сумме ускорения на полюсе и ускорения в этой точке от вращательного движения вида сверху вокруг полюса. Как и в случае вращения тела вокруг неподвижной оси, ускорение от относительного вращательного движения вокруг полюса состоит из тангенциальной и нормальной составляющих ABA и ABA. ^ vl- ^ vl + dVA, (11) далее abA = eAB; (12) аВА = о> 2АВ （13） и + («SJ» = V’2 + «‘■ Людмила Фирмаль

Нормальное относительное ускорение a «VA направлено вдоль линии AB от точки B к полюсу A. Наконец, полное относительное ускорение aVA составляет угол a с отрезком AB. tga = я «ow 1/1» ow 1 = e / w2- (15) Из уравнения (15) видно, что угол a одинаков во всех точках на виде сверху. Если φ> 0, угол a от ускорения aVA до сегмента B A должен быть установлен против часовой стрелки. Когда φ B / dz = aB, dvA / dt

aA — ускорение точек B и A относительно фиксированной системы координат. d (b / dz = — плоское угловое ускорение. Поскольку модуль вектора AJ постоянен, производная по времени выражается в виде ^ (ЛВ) = хAB. Объединение полученных результатов дает aV = aL + eX LV + yx (yx AY).

Можно сделать вывод, что ex AB = aBA с аргументами, аналогичными аргументам, выполняемым для скорости vBA. yx (wx AB) = & xiVL = aVL, то есть yy AI и yy (yy AI) — тангенциальное ускорение и вертикальное ускорение от вращения плоской фигуры вокруг точки A соответственно. Таким образом, ai = a0 + a «Mo + a’mo I аналогичная формула для точек N и P. Тангенциальная скорость и стандартная скорость точки M, обусловленные вращением колеса вокруг точки O, составляют a’mo = eOM = £ £; a «oo = / (ao-H 0 = / dt, , = Re, Ячейка О движется линейно, B = | dco / dr |;. aj> = | diio / dr |. Учитывая, что У нас есть , = EOP = tR = ac Так что, если колесо вращается по прямой без скольжения д, = д? o # 0, То есть ускорение в центре скорости в момент, когда скорость равна нулю. Если угловое ускорение не указано, его можно определить по формуле, если нет проскальзывания колеса по прямой я = a0IR.

О есть ускорение точки на виде сверху во время плоского движения равно векторной сумме ускорения на полюсе и ускорения в этой точке от вращательного движения вида сверху вокруг полюса

Уравнение (10), которое определяет зависимость ускорения двух точек на плане этажа, может быть получено путем прямого дифференцирования уравнения вектора скорости. Это всегда верно. Существует vB = + th x AH. Различают обе стороны этого уравнения во времени, принимая во внимание изменение величины вектора относительно фиксированной системы координат (полностью дифференцированной). получить д «, дз дз дз дз » Где di> B / dz = aB, dvA / dt

Так что, если колесо вращается по прямой без скольжения д, = д? o # 0, То есть ускорение в центре скорости в момент, когда скорость равна нулю. Если угловое ускорение не указано, его можно определить по формуле, если нет проскальзывания колеса по прямой я = a0IR.

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Плоское движение твердого тела

Краткое содержание: Плоское движение твердого тела. Уравнения плоского движения. Разложение плоского движения на поступательное и вращательное движения. Угловая скорость и угловое ускорение при плоском движении. Скорости точек тела при плоском движении. Мгновенный центр скоростей. Методы нахождения положения мгновенного центра скоростей.

Плоское движение твердого тела

Плоским движением твердого тела называется такое его движение, при котором каждая его точка все время движется в одной и той же плоскости.

Плоскости, в которых движутся отдельные точки тела, параллельны между собой и параллельны одной и той же неподвижной плоскости. Плоское движение твердого тела часто называют плоскопараллельным. Траектории точек тела при плоском движении являются плоскими кривыми.

Плоское движение твердого тела имеет большое значение в технике. Вращательное движение твердого тела вокруг неподвижной оси является частным случаем движения твердого тела.

При изучении плоского движения, как и любого другого, необходимо рассмотреть способы задания этого движения, а также приемы вычисления скоростей и ускорений точек тела.

Если в теле провести некоторую прямую О₁О₂, перпендикулярную плоскостям, в которых происходит движение точек, то все точки этой прямой будут двигаться по одинаковым траекториям с одинаковыми скоростями и ускорениями; сама прямая будет, естественно, сохранять свою ориентацию в пространстве. Таким образом, при плоском, движении твердого тела достаточно рассмотреть движение одного из сечений тела.

Рекомендуемые материалы

Сечение твердого тела будем называть плоской фигурой. Положение фигуры на ее плоскости полностью определяется положением отрезка прямой линии, жестко скрепленной с этой плоской фигурой.

Уравнения плоского движения твердого тела

Для задания положения плоской фигуры на плоскости относительно системы координат , лежащей в плоскости фигуры, достаточно задать на этой плоскости положение отрезка АВ, скрепленного с фигурой.

Положение отрезка АВ, относительно системы координат определяется заданием координат какой-нибудь точки этого отрезка и его направления. Например, координаты точки А () и направление, заданное углом .

Уравнения движения плоской фигуры относительно системы координат имеют вид: .

Твердое тело при плоском движении имеет три степени свободы.

называются уравнениями плоского движения твердого тела.

Перейдем к изучению движения отдельной точки твердого тела. Положение любой точки М плоской фигуры относительно подвижной системы отсчета , скрепленной с этой движущейся фигурой и лежащей в ее плоскости, полностью определяется заданием координат x и y точки М (Рис.6-3).

Между координатами точки М в различных системах отсчета существует связь:

, (6-1)

где — длина отрезка ОМ, — постоянный угол между ОМ и осью . С учетом выражений и получаем

, (6-2)

Формулы (6-2) являются уравнениями движения точки М плоской фигуры относительно координат . Эти формулы позволяют определить координаты любой точки плоской фигуры по заданным уравнениям движения этой фигуры и координатам этой точки относительно подвижной системы отсчета, скрепленной с движущейся фигурой.

Используя матрично-векторные обозначения уравнения (6-2) можно записать в такой форме:

, (6-3)

где А – матрица поворота на плоскости:

, , , .

Разложение плоского движения на поступательное

и вращательное движения.

Теорема. Любое движение твердого тела, в том числе и движение плоской фигуры в ее плоскости, бесчисленным множеством способов можно разложить на два движения, одно из которых переносное, а другое – относительное.

В частности, движение плоской фигуры в ее плоскости относительно системы , расположенной в той же плоскости, можно разложить на переносное и относительное движения следующим образом. Примем за переносное движение фигуры ее движение вместе с поступательно движущейся системой координат , начало которой скреплено с точкой О фигуры, принятой за полюс. Тогда относительное движение фигуры будет по отношению к подвижной системе координат вращением вокруг подвижной оси, перпендикулярной плоской фигуре и проходящей через выбранный полюс.

Для доказательства этого достаточно показать, что плоскую фигуру в ее плоскости из одного положения в любое другое можно перевести двумя перемещениями – поступательным перемещением в плоскости фигуры вместе с каким –либо полюсом и поворотом в той же плоскости вокруг этого полюса.

Рассмотрим два любых положения плоской фигуры 1 и 2. Выделим отрезок АB в рассматриваемой фигуре. Перевод фигуры из положения 1 в положение 2 можно рассматривать как суперпозицию двух движений: поступательного из 1 в 1′ и вращательного из 1′ в 2 вокруг точки A’, называемой обычно полюсом (рис. 6-4а). Существенно, что в качестве полюса можно выбрать любую точку, принадлежащую фигуре или даже лежащую в плоскости вне фигуры. На рис. 6-4б, к примеру, в качестве полюса выбрана точка В. Обратите внимание: длина пути при поступательном перемещении изменилась (в данном случае увеличилась), но угол поворота остался прежним!

Угловая скорость и угловое ускорение тела при плоском движении.

Для характеристики вращательной части плоского движения твердого тела вокруг подвижной оси, проходящей через выбранный полюс, вводится понятие угловой скорости и углового ускорения .

и , где — единичный вектор, направленный по оси вращения.

Если угол поворота вокруг подвижной оси, проходящей через полюс, обозначить , то , а

Векторы и можно изображать в любых точках подвижной оси вращения, т.е. они являются свободными векторами.

Скорости точек тела при плоском движении

Теорема. Скорость какой-либо точки фигуры при ее плоском движении равна векторной сумме скорости полюса и относительной скорости этой точки от вращения фигуры вокруг полюса.

Применяя к плоскому движению теорему о сложении скоростей для какой-либо точки В фигуры, получаем , где — абсолютная скорость точки В плоской фигуры; — скорость точки В переносного поступательного движения плоской фигуры вместе, например, с точкой А этой фигуры; — скорость точки B в относительном движении, которым является вращение плоской фигуры вокруг точки А с угловой скоростью w.

Так как за переносное движение выбрано поступательное движение вместе с точкой А, то у всех точек плоской фигуры одинаковые переносные скорости, совпадающие с абсолютной скоростью точки А, т.е.

Скорость относительного движения, в случае когда оно является вращательным движением, равна

Скорость расположена в плоскости движущейся фигуры и направлена перпендикулярно отрезку АВ, соединяющему точку В с полюсом А. Эту относительную скорость можно выразить в виде векторного произведения , где угловая скорость считается направленной по подвижной оси вращения, проходящей через точку А и перпендикулярной плоскости фигуры. Относительную скорость обозначим . Это обозначение показывает, что скорость относительного движения точки В получается от вращения плоской фигуры вокруг подвижной оси, проходящей через точку А, или просто вокруг точки А.

, где

Что и требовалось доказать.

Мгновенный центр скоростей

Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.

Теорема. В каждый момент времени при плоском движении фигуры в ее плоскости при (непоступательное движение), имеется один единственный центр скоростей.

Для доказательства достаточно указать способ нахождения мгновенного центра скоростей, если известны скорость какой-либо точки О плоской фигуры и ее угловая скорость в рассматриваемый момент времени.

, , , следовательно

Мгновенный центр скоростей находится на перпендикуляре к скорости , проведенном из точки О, на расстоянии .

Мгновенный центр скоростей это единственная точка плоской фигуры для данного момента времени. В другой момент времени мгновенным центром скоростей будет уже другая точка.

Возьмем точку Р за полюс

Так как , то . Аналогичный результат получается для любой другой точки плоской фигуры.

Скорости точек плоской фигуры определяются в данный момент так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей.

Скорости точек плоской фигуры пропорциональны их расстояниям до мгновенного центра скоростей.

Методы нахождения положения МЦС

1). Известен вектор скорости какой -либо точки A плоской фигуры и ее угловая скорость .

МЦС (точка P) находится на перпендикуляре к вектору , проведенном через точку A. Расстояние и откладывается в сторону, которую указывает вектор после поворота на угол в направлении дуговой стрелки . При этом получается, что скорость

()

2). Известны не параллельные друг другу скорости и двух точек плоской фигуры.

МЦС (точка P) находится в точке пересечения перпендикуляров, проведенных через точки A и B к скоростям этих точек. Угловая скорость плоской фигуры равна . Отметим, что для нахождения только положения МЦС достаточно знать лишь направления скоростей двух точек .

3). Известны параллельные друг другу скорости и точек A и B плоской фигуры, перпендикулярные отрезку AB, направленные в одну сторону и не равные по модулю ().

МЦС (точка P) находится в точке пересечения продолжения отрезка AB и прямой, проведенной через концы векторов и . При заданной длине отрезка AB расстояния от МЦС до точек A и B определяются из пропорции . Угловая скорость фигуры . Случай равенства () см. п. 6.

Методы нахождения положения МЦС

4). Известны параллельные друг другу скорости и точек A и B плоской фигуры, перпендикулярные отрезку AB, направленные в разные стороны.

МЦС (точка P) находится в точке пересечения отрезка AB и прямой, проведенной через концы векторов и . При заданной длине отрезка AB расстояния от МЦС до точек A и B определяются из пропорции: . Угловая скорость фигуры .

5). Плоская фигура катится без скольжения по неподвижной кривой.

МЦС (точка P) находится в точке соприкосновения фигуры с кривой, так как скорости точек фигуры и неподвижной кривой, находящиеся в соприкосновении, равны между собой и, следовательно, равны нулю. Если известна скорость какой-либо точки A фигуры, то угловая скорость .

В лекции «Учет основных средств» также много полезной информации.

6). Известно, что скорости и двух точек плоской фигуры параллельны друг другу и не перпендикулярны отрезку AB.

МЦС в данный момент времени не существует или, другими словами, находится в бесконечности. Угловая скорость плоской фигуры в данный момент равна нулю. Движение фигуры называется мгновенно-поступательным. Скорости всех точек фигуры равны . Аналогичный результат показан в п. 4.

Кинематический анализ плоского механизма – пример решения задачи

Основные законы и формулы, применяемые при решении задач

Использование мгновенного центра скоростей

При плоском движении твердого тела, отличном от поступательного, существует такая точка, скорость которой равна нулю. Такая точка называется мгновенным центром скоростей (МЦС) тела. Точка МЦС может как принадлежать телу, так и находиться за его пределами. Положение мгновенного центра скоростей может как оставаться неизменным, так и меняться в течении времени.

Если положение МЦС остается неизменным, то такое движение называется вращением вокруг неподвижной оси. В этом случае точка мгновенного центра скоростей совпадает с осью вращения, направленной перпендикулярной плоскости движения. Все необходимые для этого случая формулы даны на странице «Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях».

Но даже если положение МЦС меняется со временем, то формулы для определения скоростей точек тела имеют тот же вид, что и при вращении вокруг неподвижной оси, проходящей через мгновенный центр скоростей. Для ускорений такой подход не работает, но скорости точек можно определять по формулам вращательного движения с неподвижной осью.

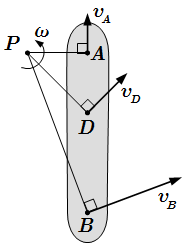
Рис. 1. Мгновенный центр скоростей P.

Для определения положения МЦС мы используем свойство вращательного движения: направление скорости любой точки тела перпендикулярно прямой, проведенной через эту точку и центр вращения. Здесь мы изначально принимаем, что движение является плоским. То есть центр вращения является осью, перпендикулярной плоскости движения. Если мы знаем направления скоростей и двух точек A и B, то мы можем определить положение МЦС. Для этого надо через эти точки провести прямые, перпендикулярные векторам и . Точка P пересечения этих прямых и является мгновенным центром скоростей. Если эти прямые не пересекаются, то это поступательное движение. В этом случае скорости всех точек тела равны. Если же прямые совпадают, то зная только направления скоростей выбранных точек, определить положение МЦС нельзя.

Зная положение МЦС и абсолютное значение скорости хотя бы одной точки тела, мы можем определить угловую скорость ω и скорости всех точек тела в рассматриваемый момент времени. Для этого мы применяем следующую формулу:
.
Здесь |DP| – расстояние между произвольной точкой D и мгновенным центром скоростей P. Вектор скорости направлен перпендикулярно DP.

Применение теоремы о проекции скоростей

Пусть мы знаем направление и абсолютную величину скорости одной точки и направление другой точки тела. Тогда найти абсолютное значение второй точки можно с помощью теоремы о проекции скоростей:
.

Применение теоремы о скоростях точек плоской фигуры

Согласно теореме о скоростях точек плоской фигуры, скорость произвольной точки B определяется по формуле:
(1) .
Здесь – скорость наперед выбранной точки тела, которую, в данном случае, называют полюсом; – скорость точки B относительно A.

Удобство применения этой теоремы состоит в том, что относительное движение является вращением вокруг неподвижной оси, проходящей через полюс A. Тогда относительная скорость определяется по формулам вращательного движения. То есть мы раскладываем движение на поступательное со скоростью и вращательное относительно центра A.

Вектор угловой скорости перпендикулярен плоскости движения. Поэтому он перпендикулярен AB (см. рисунок 3). Тогда относительная скорость направлена перпендикулярно отрезку AB в сторону вращения. Спроектировав векторное равенство (1) на ось AB, получим теорему о проекциях скоростей (см. рис. 2):
(2) .
Спроектировав (1) на ось, перпендикулярную AB, получим уравнение, связывающее скорости точек с угловой скоростью тела:
(3) .
Здесь следует выбрать знак плюс или минус исходя из направления вращения.

Применение теоремы об ускорениях точек плоской фигуры

При вычислении ускорения мы также можем разложить движение на поступательное и вращательное. Согласно теореме об ускорениях точек плоской фигуры, ускорение произвольной точки B фигуры определяется по формуле:
(4)
.
Здесь – ускорение предварительно выбранной точки тела, которую называют полюсом; – ускорение точки B относительно точки A. Относительное движение является вращением вокруг неподвижной оси, проходящей через полюс A. К относительному ускорению применимы формулы вращения вокруг неподвижной оси. Тогда вектор можно разложить на касательное и нормальное ускорение:
.

Касательное относительное ускорение еще называют вращательным или тангенциальным ускорением. Оно определяется аналогично скорости точки, вращающейся вокруг неподвижного центра:
.
Только вместо угловой скорости здесь стоит угловое ускорение . Вектор направлен по касательной к траектории, то есть по касательной к окружности с центром в точке A и радиусом AB.

Нормальное относительное ускорение также называют центростремительным ускорением. Оно всегда направлено к центру вращения (нормально, то есть перпендикулярно траектории):
.

Пример решения задачи

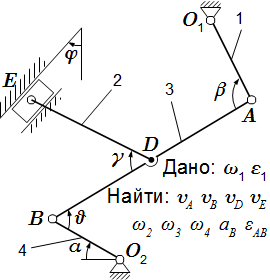
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна Е, соединенных друг с другом и с неподвижными опорами O₁, О₂ шарнирами. Точка D находится в середине стержня АВ. Длины стержней равны соответственно: l₁ = 0,4 м, l₂ = 1,2 м, l₃ = 1,4 м, l₄ = 0,6 м. Взаимное расположение элементов механизма определяется углами: α = 90°, β = 120°, γ = 150°, φ = 0°, θ = 30°. Задана угловая скорость и угловое ускорение звена 1: ω₁ = 5 c –1 , ε₁ = 10 c –2 . Угловая скорость направлена против часовой стрелки; угловое ускорение – в противоположную сторону.

Определить скорости точек A, B, D, E; угловые скорости звеньев 2, 3, 4; ускорение точки B и угловое ускорение звена 3.

Указания. Эта задача – на анализ и исследование кинематики плоского механизма. При ее решении, для определения скоростей точек и угловых скоростей звеньев, следует воспользоваться понятием о мгновенном центре скоростей и теоремой о проекциях скоростей двух точек тела. При определении ускорения точки В звена АВ, применить теорему об ускорении точек плоской фигуры.

Дано:
ω₁ = 5 c –1 , ε₁ = 10 c –2 , l₁ = 0,4 м, l₂ = 1,2 м, l₃ = 1,4 м, l₄ = 0,6 м, α = 90°, β = 120°, γ = 150°, φ = 0°, θ = 30°.

Решение

Определение скоростей с помощью мгновенного центра скоростей

Делаем рисунок механизма при заданных значениях углов.
Точка A вращается вокруг неподвижного центра O₁ с заданной угловой скоростью ω₁ = 5 c –1 против часовой стрелки. Поэтому скорость точки A направлена перпендикулярно вниз, и имеет абсолютную величину
м/с.

Найдем мгновенный центр скоростей (МЦС) звена AB. Для этого воспользуемся свойством, согласно которому, скорость произвольной точки твердого тела перпендикулярна прямой, проведенной через эту точку и мгновенный центр скоростей. Тогда, чтобы найти МЦС, нужно знать направления скоростей двух точек тела.

Нам известно направление скорости точки A. Далее замечаем, что точка B вращается вокруг неподвижного центра O₂. Поэтому скорость этой точки перпендикулярна отрезку O₂B. Изображаем вектор скорости на рисунке. Определяем МЦС. Для этого через точки A и B проводим прямые, перпендикулярные векторам и . Они пересекаются в точке, которую обозначим как P_AB. Эта точка и является мгновенным центром скоростей звена AB.

Из геометрического построения получаем, что треугольник ABP_AB – прямоугольный. Находим длины его сторон:
м;
м.
Используя формулу , находим угловую скорость вращения звена AB:
с –1 .
Находим абсолютную величину скорости точки B:
м/с.

Найдем скорость точки D учитывая, что она принадлежит звену AB, угловую скорость которого и положение мгновенного центра скоростей мы знаем. Соединяем точки D и P_AB отрезком. Из геометрического построения получаем, что треугольник DAP_AB – равносторонний. Тогда
м.
Модуль скорости точки D:
м/с.
Направление скорости перпендикулярно отрезку DP_AB. В нашей задаче получается, что скорость направлена вдоль звена DE.

Теперь рассмотрим звено DE. Направление скорости точки D мы уже знаем. Направление движения точки E задается направляющими, то есть, в нашем случае, вертикально. Через точки D и E проводим прямые, перпендикулярные векторам и . Точка пересечения этих прямых является мгновенным центром скоростей P_DE звена DE.

Из построения находим, что в треугольнике EDP_DE, угол , . Тогда
м;
м.
Угловая скорость звена DE:
с –1 .
Скорость точки E:
м/с.

Точка B вращается вокруг неподвижного центра O₂. Зная скорость этой точки, находим угловую скорость вращения звена 4:
с –1 .

Определение скоростей с помощью теоремы о проекциях скоростей и теоремы о скоростях точек плоской фигуры

Теперь найдем значения скоростей, используя теорему о проекциях скоростей двух точек твердого тела на соединяющих их прямую. и теорему о скоростях точек плоской фигуры. Вычисляем скорость точки A.
м/с.

Применим теорему о проекциях скоростей. Из построения, угол между вектором и осью BA равен 60°. Угол между вектором скорости и той же осью равен 30°. По этой теореме, проекции скоростей двух точек твердого тела на прямую, проведенную через эти точки равны:
.
Отсюда м/с.

Найдем угловую скорость звена AB, применяя теорему о скоростях точек плоской фигуры: .
Направим ось x вдоль AB, ось y – перпендикулярно (см. рисунок 7). Спроектируем это векторное уравнение на ось y:
;
с –1 .

Найдем скорость точки D. Применим теорему о скоростях точек плоской фигуры:
(П1) .
Пусть δ – угол между осью x и вектором скорости . Относительная скорость направлена по оси y и по модулю равна м/с.
Спроектируем векторное уравнение (П1) на оси x и y:
м/с;
м/с.
Отсюда
м/с;
.
Мы нашли . То есть вектор направлен вдоль звена 2.

Применим теорему о проекциях скоростей для звена 2. Векторы скоростей и составляют углы 0° и 60° с прямой DE. Тогда
;
м/с.

Найдем угловую скорость звена DE, применяя теорему о скоростях точек плоской фигуры. В качестве полюса возьмем точку D.
.
Спроектируем это векторное уравнение на ось y₂, перпендикулярную DE (см. рисунок 7):
;
с –1 .

Находим угловую скорость вращения звена 4:
с –1 .

Определение ускорений

Точка A движется по окружности радиуса O₁A = l₁. Найдем ее ускорение учитывая, что движение является вращением вокруг неподвижной оси.
.
Касательное ускорение направлено по касательной к траектории, то есть по касательной к дуге окружности радиуса |O₁A| с центром в точке O₁. Направление задается направлением углового ускорения ε₁. В нашем случае, оно направлено вверх и имеет абсолютную величину
м/с 2 .
Нормальное ускорение направлено к центру вращения и имеет абсолютную величину
м/с 2 .

Применим теорему об ускорениях точек плоской фигуры. В качестве полюса возьмем точку A. Тогда для ускорения точки B имеем:
.
Подставим .
(У1) .
Здесь нормальное ускорение точки B относительно точки A. Относительное движение является вращением вокруг неподвижной оси, проходящей через точку A перпендикулярно плоскости рисунка. Поскольку угловая скорость звена AB известна, то м/с 2 .
Вектор направлен к оси вращения. В нашем случае – от B к A.

– касательное ускорение при движении точки B относительно A. Оно перпендикулярно AB и имеет абсолютную величину
.
Угловое ускорение ε_AB звена AB нам не известно. Выберем его направление произвольным образом. Будем считать, что оно направлено по часовой стрелке. Если оно будет направлено в противоположную сторону, то для ε_AB получим отрицательное значение. Изображаем векторы и на рисунке. Для удобства откладываем их из точки B.

С другой стороны, точка B вращается вокруг неподвижного центра O₂. Для вращения вокруг неподвижной оси имеем:
(У2) .
Здесь – нормальное ускорение. Оно направлено от B к O₂. Зная угловую скорость вращения звена 4, найдем его абсолютную величину.
м/с 2 .

– касательное ускорение точки B при вращении относительно неподвижного центра O₂. Оно направлено по касательной к окружности и по абсолютной величине равно
.
Здесь – угловое ускорение звена 4. Считаем, что оно направлено против часовой стрелки. Изображаем векторы и на рисунке.

Итак, для ускорения точки B мы получили два уравнения.
(У1) .
(У2) .
Отсюда
(У3) .

Проводим оси системы координат. Ось x направим горизонтально, ось y – вертикально. Спроектируем векторное уравнение (У3) на ось y.
;
.
Отсюда
м/с 2 ;
с –2 .
Спроектируем уравнение (У3) на ось x.
;
.
Отсюда

м/с 2 .
Полное ускорение точки B.
м/с 2 .

м/с; м/с; м/с; м/с; с –1 ; с –1 ; с –1 ; с –2 ; м/с 2 .

Автор: Олег Одинцов . Опубликовано: 13-11-2019

источники:

http://studizba.com/lectures/fizika/kinematika/19146-ploskoe-dvizhenie-tverdogo-tela.html

http://1cov-edu.ru/mehanika/kinematika/kinematicheskij-analiz-ploskogo-mehanizma/