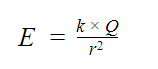Материальное уравнение для векторов электрического поля
Вы будете перенаправлены на Автор24
Теорема Остроградского — Гаусса
Одним из фундаментальных уравнений электростатики является теорема Остроградского — Гаусса:
«Поток вектора электрического смещения ($Ф_D$) (электрической индукции) через замкнутую поверхность равен сумме свободных зарядов ($q_i$), которые находятся внутри этой поверхности)».
Математическая форма записи интегральной форме этой теоремы для электрического поля в диэлектрике выглядит следующим образом (система СИ):
где $D_n$ — нормальная составляющая вектора электрического смещения, $dS$ — элемент поверхности, через которую ищется поток вектора $\overrightarrow
В дифференциальном виде эта же теорема выглядит следующим образом:
где $\rho $ — объемная плотность свободных зарядов. Выражения (1) и (2) справедливы не только в электростатике, они выполняются и для переменных полей. Уравнения (1) и (2) являются составной частью системы фундаментальных уравнений Максвелла для электродинамики.
В вакууме поле можно охарактеризовать одним вектором напряженности уравнения (1) или (2) записываются для него и их достаточно. В таком случае, если к ним добавляется теорема о циркуляции вектора напряженности:
где $\overrightarrow$ — элемент перемещения вдоль контура L. Интеграл в левой части уравнения (3) есть циркуляция вектора напряженности по контуру L. Характерным свойством электростатического поля является то, что циркуляция его вектора напряжённости по любому замкнутому контуру равна нулю.
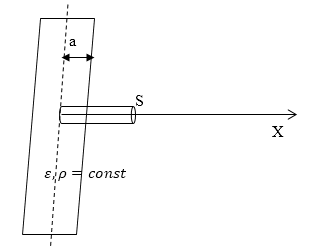
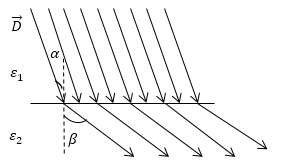
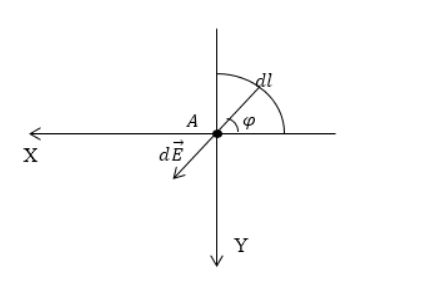
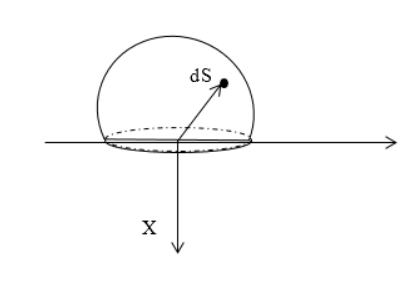
В вакууме уравнения (1 или 2) и (3) образуют полную систему уравнений электростатики. В веществе этих уравнений не достаточно, так как необходимо описать поведение самой среды в электрическом поле. Следовательно, к выше названным уравнениям электростатики добавляют еще одно векторное уравнение, которое называют материальным уравнением. Оно связывает вектор напряженности поля ($\overrightarrow $). В основном, способ получения такого уравнения содержится уже в определении $\overrightarrow $. Так как если нам известна атомная структура вещества, то можно рассчитать, как смещаются электроны и атомные ядра под воздействием электрического поля. Значит, можно вычислить вектор поляризации и таким образом получить нужное нам уравнение. Однако если идти данным путем, то в зависимости от конкретных условий могут получаться весьма разные соотношения, что неудобно. Опыты показали, что для большого класса диэлектриков и широкого круга явлений связь между векторами поляризации ($\overrightarrow $) и напряженности ($\overrightarrow \[\overrightarrow =\varkappa <\varepsilon >_0\overrightarrow где $\varkappa $ — диэлектрическая восприимчивость (безразмерная величина), уравнение записано в системе СИ. Такая связь между векторами $\overrightarrow $ и $\overrightarrow В анизотропных диэлектриках направление вектора напряженности и вектора поляризации не совпадают. И их связь устанавливается в виде: где индексы i,j — нумеруют компоненты по осям декартовой системы координат ($i=x,\ y,z;j=x,\ y,z$), $<\varkappa >_ По определению, вектор $\overrightarrow Следовательно, для изотропного диэлектрика используем (4), запишем: \[\overrightarrow \[\overrightarrow =\varkappa <\varepsilon >_0\overrightarrow называют материальными уравнениями для векторов электрического поля. Эти соотношения, несмотря на их значимость, являются приближенными и не относятся к фундаментальным, так как область применения их ограничена. Существуют вещества, к которым уравнения (8) не применимы. Например, ионные кристаллы могут быть поляризованы в отсутствии внешнего поля. Поведение же, например, электретов (веществ, которые длительное время сохраняют состояние поляризации в отсутствии электрического поля) можно охарактеризовать вектором поляризации, который с вектором напряженности связан уравнением: где $\overrightarrow Задание: Бесконечная пластина из однородного, изотропного диэлектрика с диэлектрической проницаемостью$\ \varepsilon $ заряжена равномерно сторонними зарядами, объемная плотность распределения этого заряда равна $\rho $. Толщина пластины 2а. Найдите поляризованность диэлектрика как функцию х (рис.1). Вне пластины диэлектрическую проницаемость среды считать равной единице. Для бесконечной пластины диэлектрика напряженность поля зависит от одной координаты (в нашем случае — x). Допустим, что ось X направлена перпендикулярно к плоскости пластины и ее начало совпадает с центром слоя диэлектрика. Напряженность бесконечной пластины легко находится из теоремы Остроградского — Гаусса. Выберем в качестве поверхности, поток через которую будем искать прямой цилиндр, ось которого параллельна оси X (рис.1)площадь основания равна $S$. В таком случае поток вектора напряженности для точек внутри пластины ($\ при\ |x| \[Ф_E=E\cdot S=\frac где x — высота цилиндра для внутренности пластины она изменяется от $-a напряженность поля равна: Силовые линии, создаваемые полем пластины, направлены вдоль оси X. Зная, что диэлектрик изотропный, используем связь напряженности и вектора поляризации, учитываем, что вне плоскости связанных зарядов нет: \[\overrightarrow =\varkappa <\varepsilon >_0\overrightarrow Найдем модуль вектора поляризации: где $\varepsilon =1+\varkappa ,\ \to \varkappa =\varepsilon -1$. По направлению вектор поляризации будет совпадать с вектором напряженности. Задание: На рис. 2 изображена картина линий вектора $\overrightarrow Рассмотрим, как ведут себя силовые линии при прохождении через границу раздела двух диэлектриков. В том случае, если на границе нет свободных зарядов, то должны выполняться граничные условия: Для тангенциальной составляющей напряженности поля: и нормальной составляющей: Если использовать функции углов, которые показаны на рис. 1, то получим: \[E_1sin\alpha =E_2sin\beta \ \left(2.3\right).\] \[<<\varepsilon >_1E>_1cos\alpha =<\varepsilon >_2E_2cos\beta \left(2.4\right).\] Зная связь между напряженностью и вектором смещения для изотропного диэлектрика: \[\overrightarrow Разделим (2.6) на (2.7), получим: Из уравнения (2.8) видно, что при переходе через границу из диэлектрика с меньшей диэлектрической проницаемостью в диэлектрик с большей проницаемостью угол увеличивается, то есть силовая линия удаляется от нормали. Значит, для нашего случая $<\varepsilon >_2><\varepsilon >_1$. Получи деньги за свои студенческие работы Курсовые, рефераты или другие работы Автор этой статьи Дата последнего обновления статьи: 04 12 2021 О чем эта статья: 8 класс, 10 класс Долгое время ученые не могли толком объяснить, как именно заряженные тела взаимодействуют друг с другом, не соприкасаясь. Майкл Фарадей первым выяснил, что между ними есть некое промежуточное звено. Его выводы подтвердил Джеймс Максвелл, который установил, что для воздействия одного такого объекта на другой нужно время, а значит, они взаимодействуют через «посредника». В современной физике электрическое поле — это некая материя, которая возникает вокруг заряженных тел и обусловливает их взаимодействие. Если речь идет о неподвижных объектах, поле называют электростатическим. Тела, имеющие одноименные заряды, будут отталкиваться, а разноименные — притягиваться. Для исследования электрического поля используются точечные заряды. Давайте выясним, что это такое. Точечным зарядом называют такой наэлектризованный объект, размерами которого можно пренебречь, поскольку он слишком мал в сравнении с расстоянием, отделяющим этот объект от других заряженных тел. Теперь поговорим непосредственно о напряженности, которая является одной из главных характеристик электрического поля. Это векторная физическая величина. В отличие от скалярных она имеет не только значение, но и направление. Для того, чтобы исследовать электрическую напряженность, нужно в поле заряженного тела q1 поместить еще один точечный заряд q2 (допустим, они оба будут положительными). Со стороны q1 на q2 будет действовать некая сила. Очевидно, что для расчетов нужно иметь в виду как значение данной силы, так и ее направление. Напряженность электрического поля — это показатель, равный отношению силы, действующей на заряд в электрическом поле, к величине этого заряда. Напряженность является силовой характеристикой поля. Она говорит о том, как сильно влияние поля в данной точке не только на другой заряд, но также на живые и неживые заряженные объекты. Из указанного выше определения понятно, как найти напряженность электрического поля в некой точке: E = F / q, где F — действующая на заряд сила, а q — величина заряда, расположенного в данной точке. Если нужно выразить силу через напряженность, мы получим следующую формулу: Направление напряженности электрического поля всегда совпадает с направлением действующей силы. Если взять отрицательный точечный заряд, формулы будут работать аналогично. Поскольку сила измеряется в ньютонах, а величина заряда — в кулонах, единицей измерения напряженности электрического поля является Н/Кл (ньютон на кулон). Допустим, у нас есть несколько зарядов, которые взаимодействуют. Вокруг каждого существует свое электрическое поле. Тогда существует некая точка или область, в которой одновременно существует электрическое поле нескольких зарядов. Чему равна общая напряженность электрического поля, создаваемого этими зарядами? Было установлено, что общая сила воздействия на конкретный заряд, расположенный в поле, является суммой сил, действующих на данный заряд со стороны каждого тела. Из этого следует, что и напряженность поля в любой взятой точке можно вычислить, просуммировав векторно напряженности, создаваемые каждым зарядом в отдельности в той же точке. Это и есть принцип суперпозиции. Это правило корректно для любых полей, за некоторыми исключениями. Принцип суперпозиции не соблюдается в следующих случаях: расстояние между зарядами очень мало — порядка 10 -15 м; речь идет о сверхсильных полях с напряженностью более 10 20 в/м. Но задачи с такими данными выходят за пределы школьного курса физики. У электрического поля, создаваемого точечным зарядом, есть одна особенность — ввиду малой величины самого заряда оно очень слабо влияет на другие наэлектризованные тела. Именно поэтому такие «точки» используют для исследований. Но прежде чем рассказать, от чего зависит напряженность электрического поля точечного заряда, рассмотрим подробнее, как взаимодействуют эти заряды. Предположим, в вакууме есть два точечных заряда, которые статично расположены на некотором расстоянии друг от друга. В зависимости от одноименности или разноименности они могут притягиваться либо отталкиваться. В любом случае на них действуют силы, направленные вдоль соединяющей их прямой. Закон Кулона Модули сил, действующих на точечные заряды в вакууме, пропорциональны произведению данных зарядов и обратно пропорциональны квадрату расстояния между ними. Силу электрического поля в конкретной точке можно найти по формуле: В формуле участвует коэффициент пропорциональности k, который был определен опытным путем и представляет собой постоянную величину. Он обозначает, с какой силой взаимодействуют два тела с зарядом 1 Кл, расположенные на расстоянии 1 м. Учитывая все вышесказанное, напряжение электрического поля точечного заряда в некой точке, удаленной от заряда на расстояние r, можно вычислить по формуле: Итак, мы выяснили, что называется напряженностью электрического поля и от чего зависит эта величина. Теперь посмотрим, как она изображается графическим способом. Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл. Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном. Линии напряженности — это прямые, которые совпадают с силовыми линиями в системе из положительного и отрицательного зарядов. Касательные к ним в каждой точке электрического поля имеют то же направление, что и напряженность этого поля. При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно). В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля. Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними. По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля. Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле: E → = F → q , где F → — сила, действующая со стороны поля на неподвижный (пробный) заряд q . Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд. У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным. Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий. Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках. Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться. Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно: E → = ∑ i = 1 n E → i . Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле: Интегрирование E → = ∫ d E → проводится по области распределения зарядов. Если их распределение идет по линии ( τ = d q d l — линейная плотность распределения заряда), то интегрирование E → = ∫ d E → тоже. Когда распределение зарядов идет по поверхности и поверхностная плоскость обозначается как σ = d q d S , тогда интегрируют по поверхности. Интегрирование по объему выполняется, если имеется объемное распределение заряда: ρ = d q d V , где ρ — объемная плотность распределения заряда. Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные E 0 → и связанные E p → заряды: Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид: E → = E 0 → ε , где ε обозначает относительную диэлектрическую проницаемость среды в рассматриваемой точке поля. Отсюда следует, что по выражению E → = E 0 → ε имеется однородный изотропный диэлектрик с напряженностью электрического поля в ε меньше, чем в вакууме. Напряженность электростатического поля системы точечных зарядов равняется: E → = 1 4 π ε 0 ∑ i = 1 n q i ε r i 3 r i → . В системе СГС напряженность поля точечного заряда в вакууме: Дан равномерно распределенный заряд по четверти окружности радиуса R с линейной плотностью τ . Необходимо найти напряженность поля в точке А , являющейся центром окружности. Решение Произведем выделение на заряженной части окружности элементарного участка d l , который будет создавать элемент поля в точке А . Следует записать выражение для напряженности, то есть для d E → . Тогда формула примет вид: d E → = d q R 3 R → R . Проекция вектора d E → на ось О х составит: d E x = d E cos φ = d q cos φ R 2 . Произведем выражение d q через линейную плотность заряда τ : d q = τ d l = τ · 2 πRdR . Необходимо использовать d q = τ d l = τ · 2 πRdR для преобразования d E x = d E cos φ = d q cos φ R 2 : d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R , где 2 π d R = d φ . Далее перейдем к нахождению полной проекции E x при помощи интегрирования d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R , по d φ с изменением угла 0 ≤ φ ≤ 2 π . E x = ∫ 0 2 π τ cos φ d φ R = τ R ∫ 0 2 π cos φ d φ = τ R sin φ 0 2 π = τ R . Перейдем к проекции вектора напряженности на О у : d E y = d E sin φ = τ R sin φ d φ . Следует проинтегрировать с изменяющимся углом π 2 ≤ φ ≤ 0 : E y ∫ π 2 0 τ R sin φ d φ = τ R ∫ π 2 0 sin φ d φ = — τ R cos φ π 2 0 = — τ R . Произведем нахождение модуля вектора напряженности в точке А , применив теорему Пифагора: E = E x 2 + E y 2 = τ R 2 + — τ R 2 = τ R 2 . Ответ: E = τ R 2 . Найти напряженность электростатического поля равномерно заряженной полусферы с радиусом R . Поверхностная плотность заряда равняется σ . Решение Следует выделить на поверхности заряженной сферы элементарный заряд d q , располагаемый на элементе площади d S . Запись, используя сферические координаты d S , равняется: d S = R 2 sin θ d θ d φ , при 0 ≤ φ ≤ 2 π , 0 ≤ θ ≤ π 2 . Элементарная напряженность поля точечного заряда в системе С И : d E → = d q 4 π ε 0 R 3 R → R . Необходимо спроецировать вектор напряженности на О х : d E x = d q cos θ 4 π ε 0 R 2 . Произведем выражение заряда через поверхностную плотность заряда: Подставим d q = σ d S в d E x = d q cos θ 4 π ε 0 R 2 , используя d S = R 2 sin θ d θ d φ , проинтегрируем и запишем: E x = σ R 2 4 π ε 0 R 2 ∫ 0 2 π d φ ∫ 0 π 2 cos θ sin θ d θ = σ 4 π ε 0 2 π · 1 2 = σ 4 ε 0 . Отсюда следует, что E = E x . Ответ: напряженность полусферы в центре равняется E = σ 4 ε 0 . http://skysmart.ru/articles/physics/napryazhennost-elektricheskogo-polya http://zaochnik.com/spravochnik/fizika/elektricheskoe-pole/vektor-naprjazhennosti-elektricheskogo-polja/Материальные уравнения для векторов электрического поля
<\varepsilon <\varepsilon >_0>=\frac<\rho Sx><\varepsilon <\varepsilon >_0>\ \left(1.1\right),\]
Готовые работы на аналогичную тему
Напряженность электрического поля
Что такое электрическое поле
Определение напряженности электрического поля
Единицы измерения и формулы
Принцип суперпозиции
Напряженность поля точечного заряда
Закон Кулона
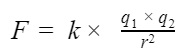
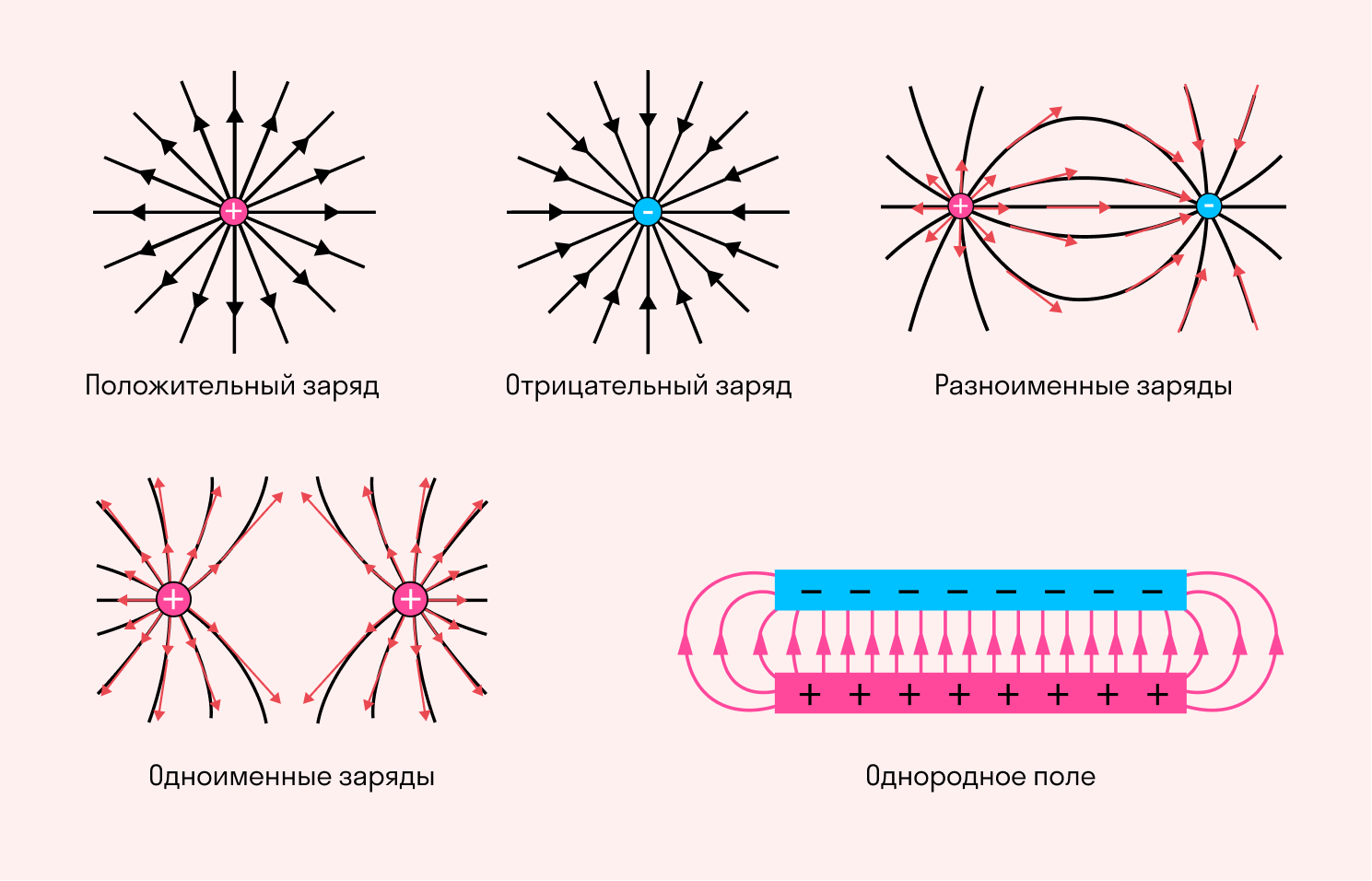
Линии напряженности
Вектор напряженности электрического поля
Характеристика электрического поля
Силовые линии
Что называется напряженностью электрического поля