Движение заряженных частиц в электрических и магнитных полях
Страницы работы
Содержание работы
Движение заряженных частиц в электрических и магнитных полях
Неквантовомеханическое описание движения заряженных частиц в заданных электромагнитных полях осуществляется на языке систем обыкновенных дифференциальных уравнений. Исчерпывающи математический алгоритм решения таких систем существует лишь в случае, когда входящие в них уравнения являются линейными и имеют постоянные коэффициенты. Этому соответствует нерелятивистское движение частиц в пространственно однородных электрических и постоянных во времени магнитных полях.
11.1. Уравнение движения
В случаях, когда квантовомеханические эффекты несущественны, описание движения заряженных частиц в электромагнитных полях может строиться на базе второго закона Ньютона в импульсной формулировке (11.1), применимого не только в классическом приближении, но и в релятивистском случае. В качестве сил, действующих на частицу следует рассматривать электрические, магнитные и диссипативные силы, вводимые для описания потерь механической энергии движущимся зарядом (11.2). Последние обычно считаются пропорциональными скорости движения частиц (аналогичная зависимость возникает при медленном движении тел в вязкой жидкости). В случае движения заряженных частиц в электромагнитных полях выбор линейной зависимости от скорости величины диссипативной скорости силы обусловлен двумя причинами. Первая состоит в том , что с токи зрения решения дифференциальных уравнений наличие в них линейных слагаемых всегда предпочтительно. Вторая причина имеет более глубоких физический смысл: потери механической энергии частицами, движущимися с ускорением, обусловлены излучением ими электромагнитных волн. Приближенное выражение для соответствующей силы радиационного трения может быть получено в рамках последовательной релятивистской теории и оказывается пропорциональным производной по времени от ускорения (11.3.). В часто встречающихся на практике случаях гармонических колебаниях и при движении по окружности (последнее сводится к двум взаимно перпендикулярным гармоническим колебаниям) вторая производная от скорости оказывается пропорциональной самой скорости, что в некоторой степени и оправдывает сделанный выбор для зависимости диссипативной силы.(11.4).
Следует иметь ввиду, что эффект радиационного трения имеет релятивистскую природу, что часто приводит к противоречиям при попытках его классического толкования. Например, возникает проблема выбора второго тела, взаимодействие с которым приводит к возникновению сил радиационного трения. Другим примером возникающих трудностей является получающийся при подстановке одной только силы радиационного трения в классическое уравнение движения явно абсурдный результат, соответствующий саморазгону заряженной частицы в пустом пространстве. Последний означает, что учет этой силы оправдан только в тех случаях, когда она проявляется на фоне других, более эффективных сил.
В приближении малых скоростей уравнение движения заряда в постоянном магнитном и пространственно однородном электрическом поле при наличии сил вязкого трения с точки зрения математики представляет собой систему обыкновенных линейных дифференциальных уравнений первого порядка относительно декартовых компонент вектора скорости. Поскольку подобные системы уравнений весьма часто встречаются в физике, представляется целесообразным на частных примерах движения частиц в электромагнитных полях познакомиться с общими методами их решения. При решении уравнения движения полезно иметь ввиду теорему существования и единственности решения обыкновенного дифференциального уравнения порядка N, для которого поставлено N начальных условий.
Релятивистское уравнение движения частицы в силовом поле (аналог второго закона Ньютона).
Силы, действующие на заряженную частицу, движущуюся в электромагнитном поле.
Julia и движение заряженной частицы в электромагнитном поле
Закрепляем навыки решения и визуализации дифференциальных уравнений на примере одного из самых распространенных эволюционных уравнений, вспоминаем о старом-добром Scilab и пытаемся понять, а надо ли оно нам… Под катом картинки (килобайт на семьсот)
и приступим к постановке задачи
Движение заряженных частиц в электромагнитном поле
На заряженую частицу с зарядом движущуюся в ЭМП со скоростью
действует сила Лоренца:
. Данная формула справедлива при ряде упрощений. Пренебрегая поправками на теорию относительности, считаем массу частицы постоянной, так что уравнение движения имеет вид:
Направим ось Y вдоль электрического поля, ось Z — вдоль магнитного поля и предположим для простоты, что начальная скорость частицы лежит в плоскости XY. В этом случае вся траектория частицы также будет лежать в этой плоскости. Уравнения движения примут вид:
Обезразмерим: . Звёздочками обозначены размерные величины, а
— характерный размер рассматриваемой физической системы. Получим безразмерную систему уравнений движения заряженной частицы в магнитном поле:
В качестве начальной конфигурации модели выберем: Тл,
В/м,
м/с. Для численного решения воспользуемся пакетом DifferentialEquations:
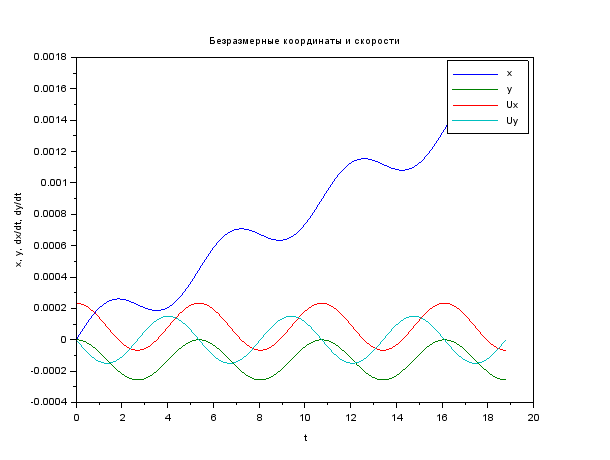
Здесь используется метод Эйлера, для которого задаётся количество шагов. Также сохраняется в матрицу ответов не всё решение системы, а только 1 и 2 индексы, то есть координаты икс и игрек (скорости нам не нужны).
Проверим результат. Введем вместо х новую переменную . Таким образом осуществляется переход в новую систему координат, движущуюся относительно исходной со скоростью u в направлении оси Х:
Если выбрать и обозначить
, то система упростится:
Электрическое поле исчезло из последних равенств, и они представляют собой уравнения движения частицы, находящейся под действием однородного магнитного поля. Таким образом, частица в новой системе координат (х, у) должна двигаться по окружности. Так как эта новая система координат сама перемещается относительно исходной со скоростью , то результирующее движение частицы будет складываться из равномерного движения по оси X и вращения по окружности в плоскости XY. Как известно, траектория, возникающая при сложении таких двух движений, в общем случае представляет собой трохоиду. В частности, если начальная скорость равна нулю, реализуется простейший случай движения такого рода — по циклоиде.
Удостоверимся, что скорость дрейфа вышла действительно равной Е/В. Для этого:
- подпортим матрицу ответов, поставив вместо первого элемента (максимального) заведомо меньшее значение
- найдем номер максимального элемента во втором столбце матрицы ответов, который откладывается по ординате
- вычислим безразмерную скорость дрейфа, разделив значение абсциссы в максимуме на соответствующее значение времени
Out: 8.333333333333332e-5
С точностью до седьмого порядка!
Для удобства определим функцию, принимающую параметры модели и подпись графика, которая будет также служить названием файла png, создаваемого в папке с проектом (работает в Juno/Atom и Jupyter). В отличии от Gadfly, где графики создавались в слоях, а потом выводились функцией plot(), в Plots, чтобы в одном фрейме наделать разных графиков, первый из них создается функцией plot(), а последующие добавляются использованием plot!(). Названия функций меняющих принимаемые объекты в Джулии принято оканчивать восклицательным знаком.
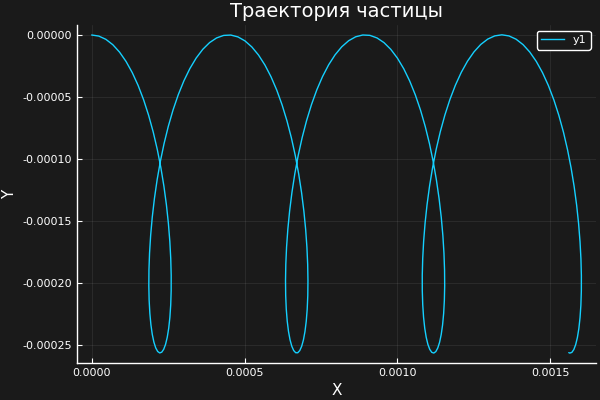
При нулевой начальной скорости, как и предполагалось, получаем циклоиду:
Получим траекторию частицы при занулении индукции, напряженности и при смене знака заряда. Напомню, что точка значит поочередное выполнение функции со всеми элементами массива
Немного о Scilab
На Хабре уже есть достаточно информации о Сайлабе, например 1, 2, а тут про Octave поэтому ограничимся ссылками на Википедию и на домашнюю страницу.
От себя добавлю, про наличие удобного создания интерфейса с флажками кнопками и выводом графиков и довольно интересного инструмента визуального моделирования Xcos. Последний можно использовать, например, для моделирования сигнала в электротехнике:

И здесь очень удобное руководство:
Собственно, нашу задачу вполне можно решить и в Scilab:
Здесь информация по функции для решения дифуров ode. В принципе напрашивается вопрос
А зачем нам Julia?
… если и так есть такие замечательные штуки как Scilab, Octave и Numpy, Scipy?
Про последние два не скажу — не пробовал. Да и вообще вопрос сложный, так что прикинем навскидку:
Scilab
На харде займет чуть больше 500 Мб, запускается быстро и сходу доступно и дифуросчитание, и графика и всё остальное. Хорош для начинающих: отличное руководство (по большей части локализованное), есть много книг на русском. Про внутренние ошибки уже было сказано тут и здесь, и так как продукт очень нишевый, сообщество вялое, и дополнительные модули весьма скудны.
Julia
По мере добавления пакетов (особенно всякой питонщины а-ля Jupyter и Mathplotlib) разрастается от 376 Мб до вполне-таки шести с лишним гигабайт. Оперативку она тоже не щадит: на старте 132 Мб и после того, как в Юпитере намалевать графиков, до 1 ГБ спокойно дойдёт. Если работать в Juno, то всё почти как в Scilab: можно выполнять код сразу в интерпретаторе, можно печатать во встроенном блокноте и сохранять как файл, есть обозреватель переменных, журнал команд и интерактивная справка. Лично у меня вызывает возмущение отсутствие clear(), т. е. запустил я код, потом начал там поправлять и переименовывать, а старые переменные-то остались (в Юпитере нет обозревателя переменных).
Но всё это не критично. Scilab подходит вполне на первых парах, сделать лабу, курсач или посчитать чего промежуточного — очень даже подручный инструмент. Хоть здесь тоже есть поддержка параллельного вычисления и вызов сишных/фортрановских функций, для чего серьезного его использовать не получается. Большие массивы повергают его в ужас, чтоб задать многомерные, приходится заниматься всяким мракобесием, а вычисления за рамками классических задач вполне могут обронить всё вместе с операционкой.
И вот после всех этих болей и разочарований можно смело переходить на Julia, чтоб огрести ещё и здесь. Будем учиться дальше, благо комьюнити очень отзывчивое, проблемы утрясаются быстро, да и у Джулии есть еще много интересных особенностей, которые превратят процесс обучения в увлекательное путешествие!
Физика дома
Задачи на движение заряженной частицы в электрическом поле — встречаются на экзаменах довольно часто. Это, как правило, комбинированные задачи, для решения которых необходимо использовать кинематические и динамические формулы. Также решение таких задач не обходится без знания формулы силы Кулона и умения решать системы уравнений. Для того, чтобы решать задачи на движение заряженной частицы в электрическом поле, можно использовать алгоритм, с которым я предлагаю ознакомиться ниже.
Рассмотрим данный алгоритм на примере решения следующей задачи.
Положительно заряженная частица влетает в пространство между пластинами плоского воздушного конденсатора, с начальной скоростью v0, направленной параллельно пластинам. Напряженность электрического поля Е, расстояние между пластинами конденсатора d. Определить смещение заряженной частицы по вертикали.
- Для начала необходимо сделать хороший рисунок (не микроскопический). На рисунке указываем начальные характеристики (начальную скорость, ее направление, полярность пластин конденсатора, направление вектора напряженности электрического поля)
- На любое заряженное тело (частицу) со стороны электрического поля действует сила Кулона, направление этой силы определяется чисто математически (если частица имеет положительный заряд, то направление силы Кулона совпадает с направлением вектора напряженности электрического поля, если частица имеет отрицательный заряд — то направление силы и вектора напряженности электрического поля — противоположны друг другу). Определив направление силы Кулона, указываем направление вектора ускорения, сообщаемого заряженной частице силой Кулона. Направление силы Кулона и вектора ускорения всегда совпадают!
Из этих уравнений определяем ускорение заряженной частицы в электрическом поле.
- изображаем траекторию движения частицы. Поскольку на заряженную частицу действует одна сила, и направление вектора скорости и вектора ускорения взаимно перпендикулярны друг другу, траектория движения представляет собой параболу (в пределах конденсатора)
- Изобразим вектор перемещения частицы в поле конденсатора. Записываем кинематические формулы для определения перемещения или скорости тела для равноускоренного движения
- Выбираем удобное направление координатных осей
- Записываем кинематические уравнения в проекциях на выбранные оси. Важно! Проекция вектора перемещения на ось ох численно равна длине пластин конденсатора, а проекция вектора перемещения на ось оy численно равна смещению заряженной частицы по вертикали.
- Решаем получившуюся систему уравнений относительно неизвестных величин.
- Если в вопросе к задаче речь идет о скорости заряженной частицы после вылета из конденсатора (направлении вектора скорости в какой-то момент времени), то на рисунке изображаем вектор скорости и определяем его компоненты. А далее определяем неизвестную величину.
Как видно из алгоритма, решение задач на движение частицы в электрическом поле конденсатора, не представляет особой сложности. Надо лишь последовательно выполнять те действия, которые описаны выше. И быть внимательными.
http://habr.com/ru/post/429790/
http://fizika-doma.ru/eto-nado-znat/algoritm-resheniya-zadach-na-dvizhenie-chasticy.html





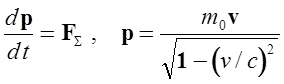
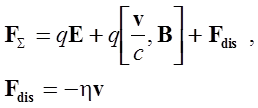








 Из этих уравнений определяем ускорение заряженной частицы в электрическом поле.
Из этих уравнений определяем ускорение заряженной частицы в электрическом поле.





