Уравнение движения для физического маятника

1.1. Уравнение гармонических колебаний

В этом разделе мы покажем, что уравнения колебательного движения многих систем, в сущности, одинаковы, так что различные физические процессы могут быть описаны одними и теми же математическими формулами.

Пружинный маятник — это система, состоящая из шарика массой m, подвешенного на пружине длиной .

Рис. 1.2. К выводу уравнения движения для пружинного маятника

В положении равновесия (рис. 1.2) сила тяжести уравновешивается упругой силой :

где – статическое удлинение пружины. Направим ось x вниз и выберем начало отсчета так, что координата x = 0 соответствует положению неподвижного шарика в положении равновесия.

Если теперь оттянуть шарик от положения равновесия на расстояние x, то полное удлинение пружины станет равным . По закону Гука проекция результирующей силы на ось ОХ будет тогда равна

Знак минус означает, что сила стремится уменьшить отклонение от положения равновесия. Полученное выражение соответствует упругой силе слабо деформированной пружины.

Запишем теперь уравнение второго закона Ньютона:

Его можно также представить в виде:

Математический маятник

Математический маятник — это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.

Будем характеризовать отклонение маятника от положения равновесия углом , который образует нить с вертикалью (рис. 1.3).

Рис. 1.3. К выводу уравнения движения математического маятника

При отклонении маятника от положения равновесия на материальную точку массой m действуют сила тяжести и сила натяжения нити . Соответственно, уравнение движения этой материальной точки имеет вид

.

Проецируя его на направления нормали и касательной к траектории (окружности радиуса ), получаем

Модуль скорости равен , учитывая, что при движении точки к положению равновесия угол убывает, а скорость точки растет, напишем

.

Тогда второе из написанных выше уравнений движения приобретает вид

При малых отклонениях маятника от вертикали, когда ,

Физический маятник

Физический маятник — это протяженное колеблющееся тело, закрепленное на оси. Его размеры таковы, что его невозможно рассматривать как материальную точку.

Пример физического маятника приведен на рис. 1.4.

Рис. 1.4. К выводу уравнения движения физического маятника

При отклонении маятника от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен

где m – масса маятника, а l – расстояние 0C между точкой подвеса 0 и центром масс C маятника.

Рассматривая как вектор, связанный с направлением поворота правилом правого винта, противоположность знаков и можно объяснить тем, что векторы и направлены в противоположные стороны. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, как I, для маятника можно записать основное уравнение динамики вращательного движения:

Ограничимся рассмотрением малых отклонений от положения равновесия:

В этом случае уравнение колебаний принимает вид:

В случае, когда физический маятник можно представить как материальную точку, колеблющуюся на нити длиной l, момент инерции равен

и мы приходим к уравнению (1.6) движения математического маятника.

Колебания поршня в сосуде с идеальным газом

Рассмотрим цилиндр с площадью поперечного сечения , в который вставлен поршень массы (рис. 1.5). Под поршнем в цилиндре идеальный газ с показателем адиабаты , над поршнем воздух с постоянным (атмосферным) давлением . Поршень может двигаться в цилиндре вверх и вниз без трения. Будем считать, что в равновесии объем идеального газа под поршнем равен и изменения объема газа, обусловленные движением поршня, происходят адиабатно, то есть без теплообмена со стенками цилиндра и поршнем.

Рис. 1.5. Колебания поршня, закрывающего сосуд с идеальным газом

В состоянии равновесия давление в газе под поршнем складывается из атмосферного давления и давления , оказываемого поршнем. Обозначим это результирующее давление :

Переместим поршень на расстояние x вверх. Объем сосуда увеличится и станет равным

Соответственно уменьшится давление. В силу предположения об отсутствии теплообмена, новое давление в газе можно найти из уравнения адиабаты Пуассона

Здесь — показатель адиабаты, зависящий от числа степеней свободы молекул газа.

При малых колебаниях, когда изменение объема газа много меньше его «равновесной» величины , то есть когда

выражение (1.11) можно разложить в ряд Тейлора:

На поршень действуют три силы: сила атмосферного давления , сила давления газа под поршнем и сила тяжести . Знаки сил соответствуют выбору положительного направления оси x вверх. Используя (1.10) и (1.12), находим для равнодействующей этих сил:

Используя (1.13), уравнение движения поршня

Физического маятника

Определение момента инерции тел методом колебаний

Физический маятник – это твёрдое тело, способное совершать колебания вокруг оси, лежащей выше его центра масс. Такое «устройство» оказывается весьма полезным. Так, с его помощью очень просто и с огромной степенью точности определяется ускорение силы тяжести. Также физический маятник позволяет определять моменты инерции различных твёрдых тел.

Малые колебание маятника вокруг оси – это его небольшие повороты в противоположные стороны, поэтому понять колебания физического маятника – это понять механику вращения. Механика вращения имеет тесную аналогию с механикой поступательного движения. Аналогия проявляется в основных понятиях механики, её идеях и закономерностях, и как следствие – в формулах и уравнениях, что удобно представить в виде «таблицы аналогий », которую следует твердо усвоить:

Поступательное движение Вращательное движение

Основной закон динамики (уравнение движения)

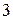a=F/m

ε =M/Iz

(Рекомендуем студенту дополнить этот перечень аналогий для кинематики равномерного и равноускоренного движения, а также для работы, энергии и законов сохранения).

Мы видим, что в динамике вращения появились три новые величины с замысловатыми названиями: момент силы, момент инерции, момент импульса (он же угловой момент, он же вращательный импульс!). Да не болит голова у читателя по поводу таких названий; они появились в результате терминологических недоразумений прошлых веков с добавкой неадекватности перевода с иностранных языков; совершенно бесполезно вникать в смысл этих названий. Их надо просто запомнить. Для момента импульса это недоразумение достигает максимума – целых три названия. К счастью, одно из них оказалось порядочным – вращательный импульс, что просто отражает его аналогию соответствующей величине поступательного движения – обычному импульсу.

Дадим пояснения моменту силы M и моменту инерции I_z .

Момент силы. Возьмём твёрдое тело, закреплённое на оси. Приложим к нему в некоторой точке силу, и пусть линия действия силы пересекает ось вращения. Такая сила либо изогнёт ось вращения, либо вырвет ось из своего укрепления вместе с телом, ничего более.

Изменим немного опыт – сдвинем линию действия той же силы от оси на расстояние l . Эффект скажется незамедлительно: тело начнёт легко поворачиваться. Сила приобрела способность поворачивать тело. Эту способность силы поворачивать называют «моментом силы». Повседневный опыт говорит, что способность силы поворачивать тело зависит не только от силы, но и от «плеча силы» l (кратчайшего расстояния от линии действия силы до оси вращения). В итоге величина момента силы равна произведению силы на плечо:

Момент инерции относительно оси. Как уже было отмечено в «таблице аналогий», момент инерции (не обращать внимание на заумное название!) – величина, характеризующая инертность тела при вращении. Рассмотрим два совершенно одинаковых по форме и размерам волчка, но с заметно отличающими массами, скажем, алюминиевый и свинцовый. Мы легко обнаружим, что раскрутить до некоторой скорости (а так же потом остановить!) алюминиевый волчок гораздо легче, чем свинцовый. Значит, инертность тела при его вращении пропорциональна массе.

Далее, если бы у нас была возможность сильно расплющить любой волчок, отодвинув значительную часть его массы как можно дальше от оси вращения, превратив его в диск, то мы бы тот час обнаружили, что раскручивать (и останавливать) его стало заметно труднее, по сравнению с тем, когда он был компактным. Значит, инертность тела при вращении зависит не только от массы, но и от степени удаления её частей от оси вращения.

Момент инерции материальной точки массы m, находящейся на расстоянии r относительно оси z(рис.1), есть величина, равная произведению её массы на квадрат расстояния до оси вращения

I_z = mr 2 (2)

А чему равен момент инерции произвольного тела (рис.2)? Опыт показывает, что он равен сумме моментов инерции частей, на которые можно разбить любое тело. Замечательно при этом, что величина момента инерции не зависит от способа разбиения целого на части (это свойство называется аддитивностью; оно нам при годится для проверки результатов лабораторной работы). Разбивая тело на весьма малые, почти точечные массы Dm_i , каждая из которых отстоит от оси вращения на расстоянии r_i, учитывая аддитивность момента инерции и определение (2) для I_z материальной точки, получаем общее выражение момента инерции произвольного тела относительно оси Zв виде суммы моментов инерции материальных точек, на которые разбито тело:

(3)

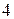
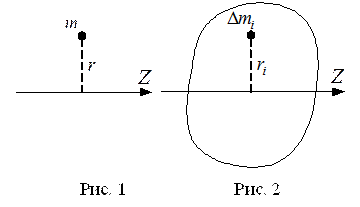
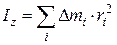
В пределе, когда Dm_i строго превращаются в материальные точки, сумма(3)сводится к интегралу по объёму тела, и для тел простой (правильной) формы она точно вычисляется (таблицу моментов инерции тел правильной формы можно найти в справочниках и учебниках по общей физике). Отметим в заключение полезную формулу, известную как теорема Штейнера, позволяющую найти момент инерции тела относительно произвольной оси Z, если известен момент инерции тела I_c относительно оси, проходящей через центр инерции C (он же — центр масс, он же — центр тяжести) и параллельной данной оси:

здесь m – масса тела, a – расстояние между осями.

Теперь мы готовы к рассмотрению колебаний физического маятника (рис.3). Если отклонить его от положения равновесия на малый угол φ и предоставить самому себе, он начнёт совершать «малые» колебания. Для описания колебаний будем использовать один из основных способов решения физических задач – метод уравнения движения.

Уравнение движения в динамике вращения уже записано в «таблице аналогий»; оно отражает основной закон динамики вращения: если на тело действует внешняя сила, приводящая к возникновению момента силы, то тело вращается, причём его угловое ускорение пропорционально моменту силы и обратно пропорционально его моменту инерции:

(5)

Будем считать, что сила тяжести – единственная сила в нашей задаче, приложена к центру масс маятника (в теоретической механике этот прием строго обосновывается). Эта сила создает относительно оси вращения момент, равный

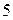
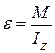
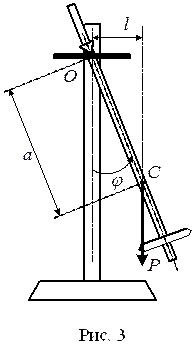
M = -Pl = — Pa sinφ = — mga sinφ ≈ — mgaφ (6)

Здесь учтено, что при малых отклонениях маятника синус угла можно заменить его аргументом (выраженным в радианах) sinφ ≈φ. Знак минус говорит о том, что при отклонении маятника на угол φ против часовой стрелки возникает момент силы тяжести, стремящийся повернуть маятник по часовой стрелке, т.е. возвратить его к положению равновесия.

В уравнении (5) искомая величина I_z. Остаётся расшифровать угловое ускорение. Угол отклонения φ (угловой путь!)зависит от времени, а угловое ускорение всегда есть вторая производная углового пути по времени (см. «таблицу аналогий»):

(7)

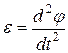
Подставляя (6) и (7) в (5), получаем уравнение движения малых колебаний физического маятника:

. (8)

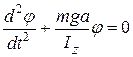
Из математики известно, что решение такого уравнения существенно зависит от знака коэффициента при φ . Величина mga/I_Z заведомо положительна. Чтобы подчеркнуть это важное обстоятельство, mga/I_Z записывают в виде квадрата некоторой действительной величины w_o:

(9)

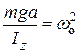
Теперь уравнение движения маятника принимает вид стандартного уравнения движения для гармонических колебаний

(10)

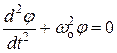
Решение этого уравнения представляет собой гармоническую функцию:

Это легко доказать, подставляя из (11) выражение для φ и в (10), в результате чего получаем 0=0.

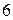
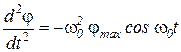
В гармоническом колебании (10) φ_max – амплитуда колебаний, а w_oобретает точныйсмысл циклической частоты – числа колебаний за 2π секунд. (Учитывая, что за период колебания Т аргумент косинуса возрастает на 2π, имеем w_o(t+T)=w_ot+2π, откуда w_o =2π/T, т.е. именно число периодов за 2π секунд).

(12)

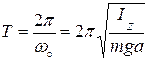
В итоге получаем формулу для экспериментального определения момента инерции физического маятника:

(13)

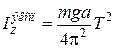
Физический маятник

Как выглядят колебания и период физического маятника. Узнайте про период колебаний, уравнение и формулу физического маятника, вращательный момент и инерцию.

Период у физического маятника находится в зависимости от момента инерции точки поворота и дистанции к центру масс.

Задача обучения

• Вычислить параметры, воздействующие на период физического маятника.

Основные пункты

• Физический маятник – обобщенный случай простого. Представлен любым твердым телом, осуществляющим колебания вокруг точки поворота.
• В случае небольших амплитуд период основывается исключительно на моменте инерции вокруг точки поворота и дистанции от оси вращения к центру масс:
• На период колебания маятника не влияет общая масса твердого объекта и массовое распределение. Изменение формы, размера и распределения массы повлияет на момент инерции и период.

Термины

• Физический маятник – стержень или нить не лишены массы и способны увеличивать свой размер.
• Массовое распределение – пространственное распределение и вычисление центра масс в объекте.

Физический маятник

Простой маятник представлен подвешенным грузом к безмассовой нити или стержню, лишенным трения. Здесь можно не учитывать эффекты от нити. А вот в физическом маятнике нить приобретает вес и способна растягиваться. Тогда период зависит от момента инерции вокруг точки поворота.

Мы видим, как силы влияют сквозь центр масс. Можно вычислить период маятника, выявив момент инерции вокруг точки поворота

Гравитация влияет сквозь центр масс твердого тела. Тогда длина маятника приравнивается к линейной дистанции между осью вращения и центром массы (h).

Уравнение вращательного момента:

τ = Iα (α – угловое ускорение, τ – вращательный момент, I – момент инерции).

Гравитация создает вращательный момент:

τ = mghsinθ (h – дистанция от центра масс к точке поворота, а θ – угол от вертикали).

То есть при небольшом угловом приближении:

Та же форма, что и у обычного простого маятника, где период:

И частота физического маятника:

Если мы располагаем моментом инерции, то можем вычислить период у физического маятника. Рассмотрим однородный стержень, повернутый из рамы. Центр масс расположен на дистанции L/2 от точки подвеса:

Жесткий стержень с равномерным распределением массы свисает с точки поворота. Это пример физического маятника

Момент инерции жесткого стержня вокруг его центра:

Также нужно выявить момент инерции относительно точки поворота, а не центра масс, поэтому применим теорему о параллельной оси:

Добавим результат к уравнению за период:

Только отметьте, что период физического маятника все еще зависит от массы. Зато лишен влияния массового распределения твердого тела. Перемены в форме, размере или распределении массы повлияют и на момент инерции, а это изменит период.