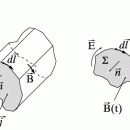
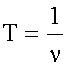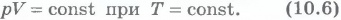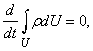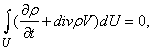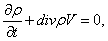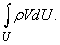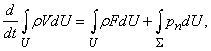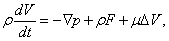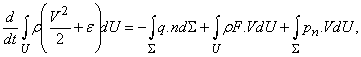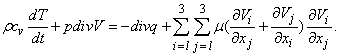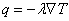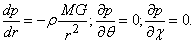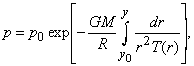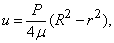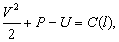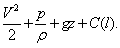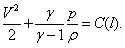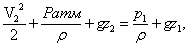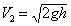Кинематическое описание движения жидкости. Уравнение движения и равновесия жидкости. Идеальная жидкость.
Кинематическое описание движения жидкости. Уравнение движения и равновесия жидкости. Идеальная жидкость.
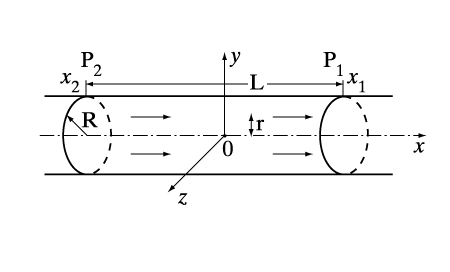
Движение жидкостей называется течением. Совокупность частиц движущейся жидкости называется потоком. Линия тока — это линия, проведенная так, что касательная к ней совпадает по направлению с вектором скорости жидкости в соответствующих точках пространства. Часть жидкости, ограниченная линиями тока, называется трубкой тока. Рассмотрим движение идеальной жидкости. Выделим внутри неё некоторый объём V. Согласно второму закону Ньютона, ускорение центра масс этого объёма пропорционально полной силе, действующей на него. В случае идеальной жидкости эта сила сводится к давлению окружающей объём жидкости и, возможно, воздействию внешних силовых полей. Предположим, что это поле представляет собой силы инерции или гравитации, так что эта сила пропорциональна напряжённости поля и массе элемента объёма. Тогда
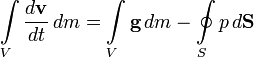
где S — поверхность выделенного объёма, g — напряжённость поля. Переходя, согласно формуле Гаусса — Остроградского, от поверхностного интеграла к объёмному и учитывая, что 

В силу произвольности объёма V подынтегральные функции должны быть равны в любой точке:
Выражая полную производную через конвективную производную и частную производную:
получаем уравнение Эйлера для движения идеальной жидкости в поле тяжести:
 |
Идеальная жидкость — это жидкость, в которой отсутствуют силы внутреннего трения .
Гармонический осциллятор. Собственные колебания математического, физического и пружинного маятников.
Гармоническим осциллятором называется система, которая совершает колебания, описываемые выражением вида d 2 s/dt 2 + ω0 2 s = 0 или
где две точки сверху означают двукратное дифференцирование по времени.

Из формулы (1) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω0t+φ) с циклической частотой
(2) и периодом 
Формула (3) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2) и формулу потенциальной энергии предыдущего раздела, равна
2.Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси. Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы.
где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, Fτ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления Fτ и α всегда противоположны;
При малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω0 и периодом
где введена величина L=J/(ml) — приведенная длина физического маятника.
Билет 21
Гармонический осциллятор. Затухающие колебания и их характеристика.
Гармоническим осциллятором называется система, которая совершает колебания, описываемые выражением вида d 2 s/dt 2 + ω0 2 s = 0 или
где две точки сверху означают двукратное дифференцирование по времени.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Свободные затухающие колебания линейной системы описываются уравнением:
где 

Период затухающих колебаний определяется формулой:
Билет 23
Длина волны — это расстояние, на которое распространяется волна за один период колебаний.
то 
Билет 25.Статические и термодинамические методы исследования вещества. Состояние, процесс, термодинамические параметры. Термодинамическое решение. Модель идеального газа. Газовые законы. Основное уравнение молекулярно-кинетической теории.
Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц. Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных законах, установленных в результате обобщения опытных данных.
Переход из одного термодинамического состояния в другое называется термодинамическим процессом. Равновесным состоянием — состоянием термодинамического равновесия — называется такое состояния термодинамической системы, в котором отсутствуют всякие потоки (энергии, вещества, импульса и т. д.), а макроскопические параметры системы являются установившимися и не изменяются во времени. Если какая-либо термодинамическая система находится в термодинамическом равновесии с двумя другими системами, то и эти две системы находятся в термодинамическом равновесии друг с другом.
Модель идеального газа: 1)Число молекул в газе велико: N >> 1, среднее расстояние между отдельными молекулами много больше их размеров (l >> a).; 2)Молекулы газа совершают неупорядоченное, хаотическое движение; 3)Движение отдельных молекул подчиняется законам механики, молекулы рассматриваются как материальные точки, совершающие только поступательное движение. Величина потенциальной энергии взаимодействия мала по сравнению со средней кинетической энергией.; 4)Все соударения молекул друг с другом и со стенками сосуда, в котором находится газ, являются абсолютно упругими При ударе о стенку компонента импульса молекулы, перпендикулярная стенке, меняет знак. Выполняются законы сохранения импульса и энергии для молекул газа.
Произведение давления идеального газа на его объем пропорционально плотности числа молекул в газе и средней кинетической энергии поступательного движения отдельной молекулы,т.е.

Изобарный процесс. Процесс изменения состояния термодинамической системы при постоянном давлении 

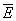


Билет 26.Теплоемкость. Применение первого начала к изопроцессам: изобарный. изохорный, изотермический.
Удельная теплоемкость вещества — величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
Молярная теплоемкость—величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К: 
где ν=m/М—количество вещества.
Единица молярной теплоемкости — джоуль на моль•кельвин (Дж/(моль•К)).
Первое начало термодинамики, выражая закон сохранения и превращения энергии, не позволяет установить направление протекания термодинамических процессов.
Изохорный процесс(V = const). При изохорном процессе газ не совершает работы над внешними телами, т. е. dA=pdV = 0. из первого начала термодинамики (dQ=dU+dA) для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии:
Изобарный процесс(р=const). При изобарном процессе работа газа при расширении объема от V1до V2 равна



Из этого выражения вытекает физический смысл молярной газовой постоянной R:если T2 —T1 =1 К, то для 1 моль газа R=A, т. е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К.
В изобарном процессе при сообщении газу массой т количества теплоты

Билет 30.
Билет 31.
Кинематическое описание движения жидкости. Уравнение движения и равновесия жидкости. Идеальная жидкость.
Движение жидкостей называется течением. Совокупность частиц движущейся жидкости называется потоком. Линия тока — это линия, проведенная так, что касательная к ней совпадает по направлению с вектором скорости жидкости в соответствующих точках пространства. Часть жидкости, ограниченная линиями тока, называется трубкой тока. Рассмотрим движение идеальной жидкости. Выделим внутри неё некоторый объём V. Согласно второму закону Ньютона, ускорение центра масс этого объёма пропорционально полной силе, действующей на него. В случае идеальной жидкости эта сила сводится к давлению окружающей объём жидкости и, возможно, воздействию внешних силовых полей. Предположим, что это поле представляет собой силы инерции или гравитации, так что эта сила пропорциональна напряжённости поля и массе элемента объёма. Тогда
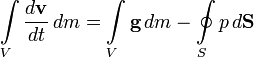
где S — поверхность выделенного объёма, g — напряжённость поля. Переходя, согласно формуле Гаусса — Остроградского, от поверхностного интеграла к объёмному и учитывая, что 

В силу произвольности объёма V подынтегральные функции должны быть равны в любой точке:
Выражая полную производную через конвективную производную и частную производную:
получаем уравнение Эйлера для движения идеальной жидкости в поле тяжести:
 |
Идеальная жидкость — это жидкость, в которой отсутствуют силы внутреннего трения .
Кратко о гидродинамике: уравнения движения
Написав предыдущий пост, исторический и отчасти рекламный (хотя потенциальные абитуриенты такое вряд ли читают), можно перейти и к разговору «по существу». К сожалению, высокой степени популярности описания добиться вряд ли получится, но всё же постараюсь не устраивать курс сухих лекций. Хотя, от сухости избавиться не удалось, да и пост писался в результате ровно месяц.
В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.
Понятие сплошной среды
В, если можно так выразиться, «традиционной» гидродинамике, сложившейся исторически, фундаментом является модель сплошной среды. Она отвлекается от молекулярной структуры вещества, и описывает среду несколькими непрерывными полевыми величинами: плотностью, скоростью (определяемой через суммарный импульс молекул в заданном элементе объёма) и давлением. Модель сплошной среды предполагает, что в любом бесконечно малом объёме содержится ещё достаточно много частиц (как принято говорить, термодинамически много — числа, близкие по порядку величины к числу Авогадро — 10 23 шт.). Таким образом, модель ограничена снизу дискретностью молекулярной структуры жидкости, что в задачах типичных пространственных масштабов совершенно несущественно.
Однако, такой подход позволяет описать не только воду в пробирке или водоёме, и оказывается куда более универсальным. Поскольку наша Вселенная на больших масштабах практически однородна, то, как ни странно, она начиная с некоторого масштаба превосходно описывается как сплошная среда, с учётом, конечно же, самогравитации.
Другими, более приземлёнными применениями сплошной среды являются описание свойств упругих тел, динамики плазмы, сыпучих тел. Также можно описывать топлу людей как сжимаемую жидкость.
Параллельно с приближением сплошной среды, в последние годы набирает обороты кинетическая модель, основанная на дискретизации среды на небольшие частицы, взаимодействующие между собой (в простейшем случае — как твердые шарики, отталкивающиеся при столкновении). Такой подход возник в первую очередь благодаря развитию вычислительной техники, однако существенно новых результатов в чистую гидродинамику не превнёс, хотя оказался крайне полезен для задач физики плазмы, которая на микроуровне не является однородной, а содержит электроны и положительно заряженные ионы. Ну и опять же для моделирования Вселенной.
Уравнение неразрывности. Закон сохранения массы
Самый элементарный закон. Пусть у нас есть какой-то совершенно произвольный, но макроскопический объём жидкости V, ограниченный поверхностью F (см. рис.). Масса жидкости внутри него определяется интегралом:
И пусть с жидкостью внутри него не происходит ничего, кроме движения. То есть, там нет химических реакций и фазовых переходов, нет трубок с насосами или чёрных дыр. Ну и всё происходит с маленькими скоростями и для малых масс вещества, потому никакой теории относительности, искривления пространства, самогравитации жидкости (она становится существенна на звёздных масштабах). И пусть сам объём и границы еего неподвижны. Тогда единственное, что может изменить массу жидкости в нашем объёме — это её перетекание через границу объёма (для определённости — пусть масса в объёме убывает):
где вектор j — поток вещества через границу. Точкой, напомним, обозначается скалярное произведение. Поскольку границы объёма, как было сказано, неподвижны, то производную по времени можно внести под интеграл. А правую часть можно преобразовать к такому же, как слева, интегралу по объёму по теореме Гаусса-Остроградского.
В итоге, в обеих частях равенства получается интеграл по одному и тому же совершенно произвольному объёму, что позволяет приравнять подинтегральные выражения и перейти к дифференциальной форме уравнения:
Здесь (и далее) использован векторный оператор Гамильтона. Образно говоря, это условный вектор, компоненты которого — операторы дифференцирования по соответствующим координатам. С его помощью можно очень кратко обозначать разного рода операции над скалярами, векторами, тензорами высших рангов и прочей математической нечистью, основные среди которых — градиент, дивергенция и ротор. Не буду останавливаться на них детально, поскольку это отвлекает от основной темы.
Наконец, поток вещества равен массе, переносимой через единичную площадку за единицу времени:
Окончательно, закон сохранения массы (называемый также уравнением неразрывности) для сплошной среды таков:
Это выражение наиболее общее, для среды, обладающей переменной плотностью. В реальности, эксперимент свидетельствует о крайне слабой сжимаемости жидкости и практически постоянном значении плотности, что с высокой точностью позволяет применять закон сохранения массы в виде условия несжимаемости:
которое с не менее хорошей точностью работает и для газов, пока скорость течения мала по сравнению со звуковой.
Уравнение Эйлера. Закон сохранения импульса
Весь относительно громоздкий процесс колдовства преобразования интегралов, использованный выше, даёт нам не только уравнение неразрывности. Точно такие же по сути преобразования позволяют выразить законы сохранения импульса и энергии, и получить в итоге уравнения для скорости жидкости и для переноса тепла в ней. Однако пока не будем сильно торопиться, и займёмся не просто сохранением импульса, а даже сохранением импульса в идеальной несжимаемой жидкости — т.е. рассмотрим модель с полным отсутствием вязкости.
Рассуждения практически те же самые, только теперь нас интересует не масса, а полный импульс жидкости в том же самом объёме V. Он равен:
При тех же самых условиях, что и выше, импульс в объёме может меняться за счёт:
- конвективного переноса — т.е. импульс «утекает» вместе со скоростью через границу
- давления окружающих элементов жидкости
- просто за счёт внешних сил, например — от силы тяжести.
Соответствующие интегралы (порядок отвечает списку) дают такое соотношение:
Начнём их преобразовывать. Правда, для этого нужно воспользоваться тензорным анализом и правилами работы с индексами. Конкретнее, к первому и второму интегралам применяется теорема Гаусса-Остроградского в обобщённой форме (она работает не только для векторных полей). И если перейти к дифференциальной форме уравнения, то получится следующее:
Крестик в кружочке обозначает тензорное произведение, в данном случае — векторов.
В принципе, это уже уравнение Эйлера, однако его можно чуток упростить — ведь закон сохранения массы никто не отменял. Раскрыв здесь скобки в дифференциальных операторах и приведя затем подобные слагаемые, мы увидим, что три слагаемых благополучно собираются в уравнение неразрывности, и потому дают в сумме ноль. Итоговое уравнение оказывается таким:
Если перейти в систему отсчёта, связанную с движущейся жидкостью (не будем заострять внимание на том, как это делается), мы увидим, что уравнение Эйлера выражает второй закон Ньютона для единицы объёма среды.
Учёт вязкости. Уравнение Навье-Стокса
Идеальная жидкость, это, конечно, хорошо (правда, всё равно точно не решается), но во многих случаях учёт вязкости необходим. Даже в той же конвекции, в течении жидкости по трубам. Без вязкости вода вытекала бы из наших кранов с космическими скоростями, а малейшая неоднородность температуры в воде приводила бы к её крайне быстрому и бурному перемешиванию. Потому давайте учтём сопротивление жидкости самой себе.
Дополнить уравнение Эйлера можно различными (но эквивалентными, конечно же) путями. Воспользуемся базовой техникой тензорного анализа — индексной формой записи уравнения. И пока также отбросим внешние силы, чтобы не путались под руками / под ногами / перед глазами (нужное подчеркнуть). При таком раскладе всё, кроме производной по времени, можно собрать в виде дивергенции одного такого тензора:
По смыслу, это плотность потока импульса в жидкости. К нему и нужно добавить вязкие силы в виде ещё одного тензорного слагаемого. Поскольку они явно приводят к потере энергии (и импульса), то они должны вычитаться:
Идя обратно в уравнение с таким тензором, мы получим обобщённое уравнение движения вязкой жидкости:
Оно допускает любой закон для вязкости.
Принято считать очевидным, что сопротивление зависит от скорости движения. Вязкость же, как перенос импульса между участками жидкости с различными скоростями, зависит от градиента скорости (но не от самой скорости — тому мешает принцип относительности). Если ограничиться разложением этой зависимости до линейных слагаемых, получится вот такой жутковатый объект:
в котором величина перед производной содержит 81 коэффициент. Однако, используя ряд совершенно разумных предположений об однородности и изотропности жидкости, от 81 коэффициента можно перейти всего к двум, и в общем случае для сжимаемой среды, тензор вязких напряжений равен:
где η (эта) — сдвиговая вязкость, а ζ (зета или дзета) — объёмная вязкость. Если же среда ещё и несжимаема, то достаточно одного коэффициента сдвиговой вязкости, т.к. второе слагаемое при этом уходит. Такой закон вязкости
носит название закона Навье, а полученное при его подстановке уравнение движения — это уравнение Навье-Стокса:
Точные решения
Главной проблемой гидродинамики является отсутствие точных решений её уравнений. Как бы с этим ни боролись, но получить действительно всеобщих результатов не удаётся до сих пор, и, напомню, вопрос существования и гладкости решений уравнений Навье-Стокса входит в список Проблем тысячелетия института Клэя.
Однако, несмотря на столь грустные факты, некоторые результаты есть. Здесь будут представлены далеко не все, а лишь самые простые случаи.
Потенциальные течения
Особый интерес представляют течения, в которых жидкость не завихряется. Для такой ситуации можно отказаться от рассмотрения векторного поля скорости, поскольку она выражается через градиент скалярной функции — потенциала. Потенциал же удовлетворяет хорошо изученному уравнению Лапласа, решение которого полностью определяется тем, что задано на границах рассматриваемой области:
Более того, при отсутствии вязкости из уравнения Эйлера можно однозначно выразить и давление, что вовсе замечательно и приводит нас к полному решению задачи. Ах, если бы так было всегда… то гидродинамики, наверное, уже бы и не было как современной и актуальной отрасли.
Дополнительно можно упростить задачу предположением, что течение жидкости двумерно — скажем, всё движется в плоскости (x,y), и ни одна частица не перемещается вдоль оси z. Можно показать, что в таком случае скорость может быть также заменена скалярной функцией (на этот раз — функцией тока):
которая при потенциальном течении удовлетворяет условиям Коши-Лагранжа из теории функций комплексной переменной и воспользоваться соответствующим математическим аппаратом. Полностью совпадающим с аппаратом электростатики. Теория потенциальных течений развита на высоком уровне, и в принципе хорошо описывает большой спектр задач.
Простые течения вязкой жидкости
Решения для вязкой жидкости чаще всего удаётся получить, когда из уравнения Навье-Стокса благодаря свойствам симметрии задачи выпадает нелинейное слагаемое.
Сдвиговое течение Куэтта
Самая элементарная задачка. Канал с неподвижной нижней и подвижной верхней стенкой, которая движется равномерно с некоторой скоростью. На границах жидкость прилипает к ним, так что скорость жидкости равна скорости границы. Этот результат является экспериментальным фактом, и как-то даже авторы первых экспериментов не упоминаются, просто — по совокупности экспериментов.
В такой ситуации от уравнения Навье-Стокса останется уравнение вида v» = 0, и потому профиль скорости в канале окажется линейным:
Данная задача является практически базовой для теории смазки, т.к. позволяет непосредственно определить силу, которую требуется приложить к верхней стенке для её движения с конкретной скоростью.
Течение Пуазейля
Вторая по элементарности — ламинарное течение в канале. Или в трубе. Результат оказывается один — профиль скорости является параболическим:
На основе решения Пуазейля можно определить расход жидкости через сечение канала, но, правда, только при ламинарном течении и гладких стенках. С другой стороны, для турбулентного потока и шероховатых стенок точных решений нет, а есть лишь приближённые эмпирические закономерности.
Стекание слоя жидкости по наклонной плоскости
Тут — почти как в задаче Пуазейля, только верхняя граница жидкости будет свободной. Если предположить, что по ней не бегут никакие волны, и вообще сверху нет трения, то профиль скорости будет практически нижней половинкой предыдущего рисунка. Правда, если из полученной зависимости вычислить скорость течения для средней равнинной речки, она составит около 10 км/с, и вода должна самопроизвольно отправляться в космос. Наблюдаемые в природе низкие скорости течения связаны с развитой завихренностью и турбулентностью потока, которые эффективно увеличивают вязкость воды примерно в 1 млн. раз.
В следующем посте планируется рассказать о законе сохранения энергии и соответствующих ему уравнениях переноса тепла при течении жидкости.
ГИДРОАЭРОМЕХАНИКА
ГИДРОАЭРОМЕХАНИКА – наука о движении и равновесии жидкостей и газов. При планировании физических экспериментов или при их проведении необходимо создавать теоретические модели, которые либо предсказывают возможные результаты этих экспериментов, либо объясняют уже полученные. Только в тесном взаимодействии теории и эксперимента можно понять то, что происходит в окружающем нас физическом мире. Для создания той или иной количественной или качественной модели физического явления необходим математический фундамент, на основе которого строятся такие модели. Под математическим фундаментом в данном случае подразумеваются те дифференциальные уравнения и те граничные и начальные условия, с помощью которых можно было бы описывать рассматриваемое физическое явление. Гидромеханика и предлагает модели и аппарат для иcследования явлений, происходящих в жидкостях и газах.
О гипотезе сплошности среды.
Гидроаэромеханика изучает движения жидкостей и газов в приближении, когда они могут рассматриваться как сплошные среды, т.е. среды, непрерывным образом заполняющие рассматриваемое пространство течения. Чтобы решать математические проблемы, связанные с расчетом движения различных объектов (самолетов, ракет, кораблей и др.) в воздухе или воде, с изучением волновых процессов в жидкостях и газах, с их течениями по трубам и каналам и т.п., необходим математический аппарат, описывающий эти явления. Этим аппаратом и являются уравнения гидроаэромеханики, которые опираются на гипотезу сплошности среды, т.е. на гипотезу о том, что частицы жидкости или газа непрерывным образом заполняют занимаемую ими часть физического пространства.
Возникает естественный вопрос: при каких предположениях справедлива эта гипотеза? Если для жидкостей (воды, жидких металлов и т.п.) эта гипотеза более или менее очевидна, то для достаточно разреженных газов (например, занимающих космическое пространство, включая атмосферы звезд, планет и Солнца), которые состоят из отдельных атомов или молекул, а также других физических объектов, к которым применим аппарат гидроаэромеханики, она требует своего обоснования. Так, например, при расчете торможения искусственных спутников Земли использование математического аппарата гидроаэромеханики не представляется возможным, в то время как именно этот аппарат используется при расчете торможения космических объектов, входящих в плотные слои атмосфер Земли и планет (например, метеоритов или возвращаемых на Землю космических кораблей и пр.). На этот вопрос легко ответить при выводе уравнений. Однако из этого вывода следует, что гипотеза сплошности среды справедлива, в частности, в том случае, когда характерный размер обтекаемого тела L (например, радиус сферического спутника) много больше длины свободного пробега атомов или молекул газа l, т.е. длины между последовательными их столкновениями.
Замкнутая система уравнений гидроаэромеханики.
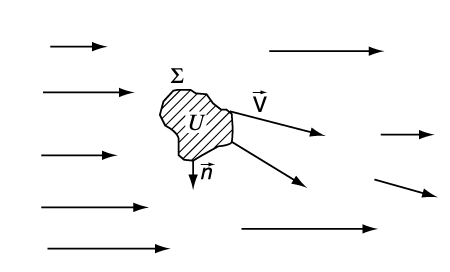
Уравнения гидроаэромеханики в их упрощенном виде представляют собой сложную систему нелинейных дифференциальных уравнений для массовой плотности r (масса жидкости или газа в единице объема), вектора скорости V и давления p, которые, в свою очередь, являются функциями пространственных координат (например, x, y и z в декартовой системе координат) и времени t. Не вдаваясь в математические подробности вывода этих уравнений, можно рассмотреть основные идеи этого вывода, тем более, что эти уравнения представляют собой известные даже из школьных учебников законы сохранения массы, импульса и энергии. Для этого рассматривается некоторый физический объем, непрерывным образом заполненный жидкостью или газом. На рис. 1 изображена движущаяся жидкость (или газ), непрерывным образом заполняющая некоторую часть физического пространства. Выделим из нее некоторый объем U (ограниченный поверхностью S), который в течение всего времени движения состоит из одних и тех же частиц жидкости (этот объем заштрихован).
Очевидно, что при своем движении масса жидкости, заключенная в объеме U, остается постоянной (если, конечно, нет каких-либо дополнительных источников этой массы), хотя сам объем может сильно деформироваться, поскольку частицы не скреплены жестко, как в твердом теле. Если выделить из рассматриваемого объема бесконечно малый элемент DU, то очевидно, что в этом элементе масса жидкости или газа будет равна rDU. Тогда закон сохранения массы, заключенной в выделенном объеме U, можно записать в виде
т.е. масса жидкости или газа, заключенная в выделенном объеме U, не изменяется со временем. Здесь интеграл берется по выделенному объему U, который меняется со временем t. Если использовать формулу производной по времени от интеграла по движущемуся объему, можно получить уравнение
где оператор дивиргенции 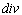
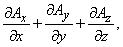
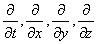
Закон сохранения массы в интегральной форме справедлив как для непрерывных, так и для разрывных функций r и V. Для непрерывных функций закон сохранения массы можно записать в дифференциальной форме
Это уравнение в гидроаэромеханике обычно называется уравнением неразрывности.
Аналогично можно записать теперь закон сохранения импульса. Импульс единицы объема жидкости, равен rV, в элементарном объеме rDU, а в выделенном объеме U –
Обобщение второго закона Ньютона на жидкие среды заключается в том, что кроме массовых сил (например, силы гравитации), которые действуют на любую частицу жидкости, находящуюся внутри выделенного объема U, действуют еще поверхностные силы, которые возникают от воздействия частиц жидкости, примыкающих к поверхности S с внешней от выделенного объема U стороне. Тогда закон сохранения импульса имеет вид
где pn– вектор поверхностной силы, который действует на элемент поверхности S с единичным вектором нормали n. Одной из основных проблем гидроаэромеханики, окончательно решенной в середине 19 в., является явное определение поверхностных сил. В рамках используемого здесь так называемого феноменологического подхода к получению уравнений гидроаэромеханики, поверхностные силы определяются эмпирически. Дифференцируя по времени интеграл слева в уравнении импульса, как это делалось при выводе уравнения неразрывности, и переходя от поверхностного интеграла справа к объемному, можно написать дифференциальные уравнения движения для непрерывных функций в виде
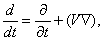
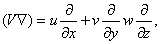
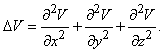
а величины u, v и w, а также 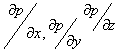
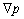
Это уравнение, называемое уравнением Навье – Стокса, выписано в наиболее простой форме для несжимаемой жидкости, где поверхностные силы сводятся к нормальному давлению р, а последний член справа представляет собой «вязкие» силы (m – коэффициент вязкости) в предположении, что r = const.
Впервые уравнение движения было выведено в середине 18 в. Л.Эйлером, когда он работал в Петербургской Академии наук. Поскольку эффекты вязкости в жидкости в то время еще не были известны, то Эйлер получил это уравнение при m = 0. В честь его эти уравнения были названы уравнениями Эйлера. Только в 1822 французским инженером Навье в уравнения Эйлера были введены силы, связанные с вязкостью, определяемой коэффициентом m. В общей форме, справедливой и для сжимаемого газа, уравнение получено Стоксом и получило название уравнения Навье – Стокса.
Для несжимаемой жидкости дифференциальные уравнения неразрывности и импульса (одно скалярное и одно векторное) являются замкнутой системой уравнений для определения вектора скорости V и скалярного давления р (r = const). Если же r № const, то требуется дополнительное уравнение. Это уравнение получается из закона сохранения энергии.
Обобщение закона сохранения энергии на случай движения жидкостей и газов получается аналогично обобщению второго закона Ньютона, однако, в силу наличия теплового движения в жидкостях и газах, энергия, приходящаяся на единицу объема, состоит из кинетической энергии rV 2 /2 и внутренней энергией re, связанной с тепловым движением частиц газа или жидкости. Полная энергия в элементе объема DU равна r(V 2 /2 + e)DU.
Изменение полной энергии в выделенном объеме U равно притоку тепла через поверхность S за счет теплопроводности, а также работе массовых и поверхностных сил, т.е. вместо закона сохранения импульса, получается уравнение
где n – единичный вектор нормали к поверхности S.
Для совершенного газа e = cv T, где сv – теплоемкость при постоянном объеме, T – температура, а для вектора потока тепла обычно принимается эмпирический закон Фурье q = – l 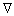
Все эти уравнения, вместе с уравнением состояния для совершенного газа
где R = (ср – сv ) – газовая постоянная, а ср – теплоемкость при постоянном давлении, и законом Фурье
Образуют замкнутую систему уравнений гидроаэромеханики для определения вектора скорости V, давления p, плотности r и температуры Т.
Если какое либо физическое явление мало зависит от диссипативных процессов (вязкости и теплопроводности), то уравнения эти уравнения сводятся к уравнениям гидроаэромеханики идеальной жидкости. В этом случае замкнутой системой уравнений для определения р, r, V и Т является система
Последнее уравнение есть адиабатический закон, который легко сводится к закону сохранения энтропии. Здесь g = сp/cv – показатель адиабаты, т.е. отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.
Гидростатика
представляет собой частный случай гидроаэромеханики, который изучает равновесие жидкостей и газов, т.е. их состояние при отсутствии гидродинамической скорости (V = 0). Результаты и методы гидростатики имеют большое значение для многих задач, важных как с практической, так и с общенаучной точек зрения. В гидростатике рассматриваются задачи, связанные с равновесием воды в водных бассейнах, воздуха в атмосфере Земли, решаются задачи расчета сил, которые действуют на тела, погруженные в жидкость или газ, определяются распределения давления, плотности, температуры в атмосферах планет, звезд, Солнца и множество других задач.
Уравнения гидростатики получаются из уравнений гидроаэромеханики при V = 0. В частности, уравнения сохранения импульса дает
Откуда, в частности, следует известный еще из школьных учебников закон Паскаля, согласно которому при отсутствии внешних массовых сил (F = 0) давление всюду является постоянным (p = const ).
Равновесие совершенного газа в поле сил тяжести.
Пусть есть газ в центральном поле сил тяжести. Уравнения равновесия в сферической системе координат будут в этом случае записываются как:
Здесь r, q и c – соответственно расстояние до притягивающего центра массы М, помещенного в начало координат, угол, отсчитываемый от полярной оси Оz, и угол в плоскости Оxy, G – гравитационная постоянная, равная 6,67Ч10 –8 дин см 2 г –2 .
Из этих уравнений видно, что в центрально-симметричном поле гравитации давление зависит только от расстояния до этого центра (легко показать, что давление не зависит и от времени). Легко также показать, что плотность и температура также зависят только от координаты r. Интегрирование первого из этих уравнений приводит к так называемой барометрической формуле, если под М понимать массу Земли, планеты, звезды, Солнца и др. При использовании уравнения состояния барометрическая формула имеет вид
где p0 – давление на некотором расстоянии r = r0 от притягивающего центра (для Земли, например, это может быть давление на уровне моря). Эта формула определяет распределение давления в атмосферах звезд, Земли, планет, Солнца и др., если известно распределение температуры Т(r), однако эту температуру часто нельзя определить из написанного ранее уравнения притока тепла, так как в нем учитывается только приток тепла за счет теплопроводности, в то время как для перечисленных атмосфер есть другие источники тепла, неучтенные в приведенном уравнении. Например, атмосфера Солнца разогревается различного рода волновыми процессами, а атмосфера Земли перерабатывает энергию солнечного излучения и т.п., поэтому для определения распределения давления в атмосферах небесных тел при помощи барометрической формулы часто используются эмпирические зависимости Т(r).
Можно, например, рассчитать распределения давления в атмосфере Земли до расстояний в 11 км от ее поверхности. Если выбрать декартову систему координат с началом на поверхности Земли и направить ось Oz вертикально вверх, тогда в барометрической формуле вместо координаты r нужно брать координату z = r – RЕ, где RЕ – радиус Земли. Поскольку этот радиус много больше толщины атмосферы (z p1), не влияют на течение в большей части этой трубы, то легко получить точное аналитическое решение уравнения Навье – Стокса в виде
где u – скорость жидкости вдоль оси х, совпадающей с осью симметрии трубы, а r – расстояние от этой оси. Из этой видно, что профиль скорости в трубе является параболическим. На стенках трубы скорость обращается в нуль вследствие прилипания жидкости из-за эффекта вязкости. Такое течение было изучено в середине 19 в. Пуазейлем и Гагеном на примере течений жидкостей в капиллярах и получило название течения Гагена – Пуазейля.
Очевидно, при постоянном потоке (не зависящем от r) жидкости у входа в трубу и на ее начальном участке профиль скорости не будет совпадать с приведенным решением. Параболический профиль устанавливается лишь на достаточно большом расстоянии от входного участка, именно поэтому для получения решения нужно предположить, что труба достаточно длинная, при этом для таких труб это точное решение хорошо совпадает с экспериментальными данными.
Полученное решение описывает стационарное, гладко-слоистое течение, которое обычно называют ламинарным. Однако из практики известно, что в трубах иногда течение бывает нестационарным, с пульсациями скорости, с перемешиванием между слоями, это течение обычно называется турбулентным. Опыты Рейнольдса, проведенные в 1883, показали, что при достаточно больших значениях числа r U L/m, где U – средняя по сечению трубы скорость жидкости, параболический профиль становится неустойчивым по отношению к малым возмущениям, а при дальнейшем увеличении этого числа течение в трубе становится турбулентным. Это число получило название числа Рейнольдса (Re), которое играет очень важную роль в различных задачах гидроаэромеханики. В частности оно характеризует отношение инерционных сил (левая часть уравнения) к силам вязкости, при этом часто силами вязкости можно пренебречь и использовать уравнения гидроаэромеханики идеальной жидкоститолько при Re >> 1.
Течения идеальных жидкостей и газов.
Часто важные в приложениях задачи рассматривают на основе уравнений гидроаэромеханики идеальной жидкости, а не на полных уравнениях. Это связано с тем, что математически уравнения идеальной гидроаэромеханики существенно проще. Если нужно определить подъемную силу крыла самолета при малых дозвуковых скоростях, то вязкие силы пренебрежимо малы и нет необходимости использовать уравнения Навье – Стокса. Однако для определения сопротивления такого крыла при движении его в воздухе вязкие силы оказываются определяющими и необходимо использовать более сложный математический аппарат, связанный с уравнениями Навье – Стокса.
Интеграл Бернулли.
При некоторых предположениях уравнения гидромеханики идеальной жидкости можно один раз проинтегрировать, они имеют решения, одним из которых является интеграл Бернулли для стационарных течений (по имени современника Эйлера математика Бернулли, впервые получившего этот интеграл)
где P (p) = т dp/r(p) – функция давления, U – потенциал внешних массовых сил, С – постоянная вдоль линии тока l (линия тока совпадает с вектором скорости течения V). Так, например, для несжимаемой жидкости в поле земного тяготения это уравнение имеет вид
Для адиабатических течений интеграл Бернулли в отсутствии внешних массовых сил имеет вид
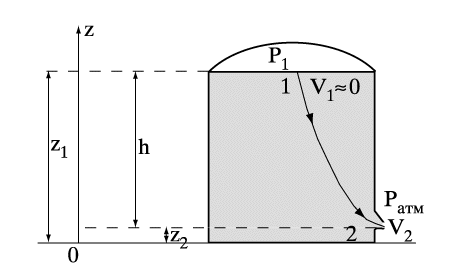
В качестве примера использования интеграла Бернулли можно определить скорость истечения несжимаемой жидкости из сосуда (рис. 5). При истечении жидкости из этого сосуда уровень жидкости понижается, т.е. скорость поверхности жидкости, вообще говоря, отлична от нуля. Однако при достаточно широком сосуде с узким отверстием вытекания можно принять, что V1 » 0. Поскольку по всей поверхности жидкости в сосуде давление р1 = const, то постоянная вдоль линии тока на всех линиях тока будет одинаковой. Интеграл Бернулли вдоль какой-нибудь линии тока, например, соединяющей точки 1 (на поверхности) и 2 (у выходного отверстия)
где ратм – атмосферное давление у выходного отверстия. Отсюда легко получить формулу для скорости истечения V2. В частном случае ратм = р1 получаем так называемую формулу Торичелли для истечения жидкости из широкого сосуда с узким выходным отверстием
по имени итальянского ученого Э.Торричелли (1608–1647). Здесь h = (z1 – z2 ). Для ванны с высотой налитой воды примерно 0,5 м скорость истечения V2 » 3,1м/сек.
Уравнения движения идеальной жидкости имеют еще один интеграл для нестационарных течений, который называется интегралом Коши – Лагранжа. Он справедлив для течений, в которых отсутствуют вихри. Его часто, например, используют при рассмотрении волновых движений жидкости или газа.
Ударные волны как одно из важных проявлений сжимаемости газа.
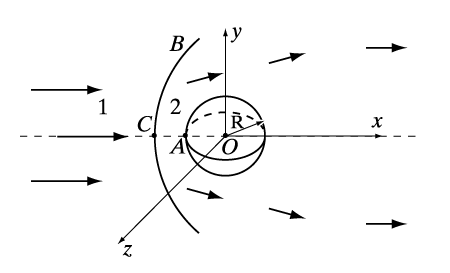
Математически уравнения идеальной гидроаэромеханики допускают разрывные решения, т.е. решения, которые имеют скачки параметров газа (плотности, давления, скорости и температуры). Одним из таких проявлений в природе является образование ударной волны около летящего со сверхзвуковой скоростью тела в плотных слоях атмосферы Земли. Например, образование ударной волны около летающих сверхзвуковых самолетов или ударных волн около метеоритов, вторгающихся в плотные слои атмосферы Земли с большими сверхзвуковыми скоростями. В условиях космического пространства хорошо известны межпланетные ударные волны, которые чаще всего являются результатом активных процессов на Солнце (например, вспышек).
Известно, что около пассажирских самолетов, летающих главным образом с большими дозвуковыми, никакие ударные волны не образуются. Пусть есть сферическое тело радиуса R (рис. 6), которое летит в воздухе со сверхзвуковой скоростью. Тогда впереди такого тела образуется ударная волна В, являющаяся границей между областями 1 и 2, которые отличаются значениями параметров газа. В системе координат, связанной с летящим телом. поток газа набегает на покоящееся тело. Пусть ось Оx направлена вдоль скорости потока, а V1, p1, r1 и T1 – скорость, давление, плотность и температура, соответственно, в невозмущенном телом потоке газа (до ударной волны). В область 1 возмущения от тела не попадают, поскольку тело движется со сверхзвуковой скоростью. Так как скорость газа в лобовой точке тела А обращается в нуль, то от точки А до точки С на ударной волне есть область дозвуковой скорости газа, которой достигают возмущения воздуха от летящего тела. Физический смысл образования ударной волны и заключается в разделении невозмущенного и возмущенного потоков газа. Если через V2, p2, r2 и T2 обозначить скорость, давление, плотность и температуру газа соответственно сразу же после ударной волны В, то справедливы неравенства
Это означает, что скорость за ударной волной уменьшается, а давление, плотность и температура возрастают. Сильным возрастанием температуры за ударной волной и объясняется оплавление возвращающихся на Землю космических аппаратов и метеоритов, вторгающихся в атмосферу с большими сверхзвуковыми скоростями. Такие ударные волны называются ударными волнами сжатия (плотность газа возрастает). Интересно, что в природе никогда не наблюдались ударные волны разрежения, в которых плотность падает. Математически образование ударных волн разрежения запрещается известной в гидроаэромеханике теоремой Цемплена
Соотношения между параметрами с индексами «1» и «2» можно получить из интегральных законов сохранения массы, импульса и энергии, поскольку они справедливы и для разрывных функций. Такие соотношения называются соотношениями Гюгонио и имеют вид (в системе координат, связанной с ударной волной)
Вместе с уравнением состояния эти соотношения позволяют определить значения параметров газа за ударной волной (индекс «2») по значениям параметров невозмущенного ударной волной потока газа (индекс «1»).
Описанный математический аппарат гидроаэромеханики используется во многих областях естественных наук, при этом для корректности использования этого аппарата требуется только выполнение критерия сплошности среды, т.е. для газов, например, длина свободного пробега частиц должна быть много меньше характерных размеров рассматриваемых объектов обтекания. В частности, в условиях космического пространства часто среда очень разрежена. В таких средах, конечно же, длина свободного пробега частиц очень велика, но размеры самих объектов исследования оказываются во многих случаях существенно больше, т.е. методы гидроаэромеханики применимы и к таким объектам.
В биомеханике при помощи методов гидромеханики исследуются интересные особенности течений биологических жидкостей по сосудам, а в гидрогеологии исследуются, например, задачи динамики внутренних слоев Земли. Все это свидетельствует о важности науки, которая называется «гидроаэромеханика».
Ландау Л.Д. и Лифшиц Е.М. Механика сплошных сред. М., ГИТТЛ, 1954
Чепмен С. и Каулинг Т. Математическая теория неоднородных газов. ИИЛ, М., 1960
Кочин Н.Е., Кибель и Розе. Теоретическая гидромеханика, т.1. Физматгиз, 1963
Кочин Н.Е., Кибель и Розе, Теоретическая гидромеханика, т.2, Физматгиз, 1963
Седов Л.И. Механика сплошной среды. М., Наука, т. 1, 1973
Седов Л.И. Механика сплошной среды. М., Наука, т. 2, 1973
Баранов В.Б. и Краснобаев К.В., Гидродинамическая теория космической плазмы, М., Изд. «Наука», 1977
Эйлер Л. Общие законы движения жидкостей. Известия РАН, сер. МЖГ, 1999, № 6
http://habr.com/ru/post/171327/
http://www.krugosvet.ru/enc/nauka_i_tehnika/fizika/GIDROAEROMEHANIKA.html