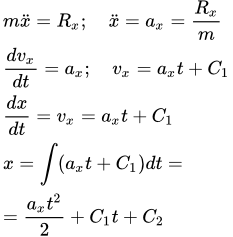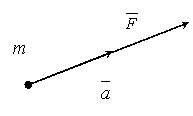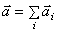Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил

Метод решения задач

Дифференциальные уравнения движения точки

Здесь мы рассмотрим движение материальной точки под действием постоянных сил. Пусть на точку массой m действуют n сил , которые постоянны на протяжении всего движения точки. Тогда удобно использовать равнодействующую , равную их векторной сумме:
.
Выберем инерциальную декартову систему координат Oxyz с началом в некоторой точке O . Закон движения точки в ней определяется вторым законом Ньютона:
(1) .
Здесь – радиус-вектор точки. То есть вектор, приведенный из начала координат O к материальной точке.

Проектируя векторное уравнение (1) на оси системы координат, получим систему дифференциальных уравнений, описывающих движение точки:
(2) .

Решение дифференциальных уравнений при действии постоянных сил

Если силы постоянны, то и их векторная сумма также постоянна. В этом случае уравнения (2) не зависят друг от друга. Поэтому каждое из этих уравнений можно решать отдельно от остальных. Рассмотрим уравнение для координаты x :
(3) .
Найдем его решение.

Разделим уравнение (3) на m и введем обозначение:
.
Тогда уравнение (3) примет более простой вид:
(4) .
Введенная нами величина является проекцией ускорения точки на ось x . В рассматриваемом нами случае постоянных сил, ускорение также постоянно.

Вторая производная координаты x по времени – это производная проекции скорости на ось x по времени. При этом применяют следующие обозначения:
(5) .
Проекция скорости на ось x – это производная координаты по времени:
(6) .

Найдем закон изменения со временем проекции скорости материальной точки на ось x : . Подставим (5) в (4):
.
Это простое дифференциальное уравнение с разделяющимися переменными. Перепишем его в следующем виде:
.
Интегрируем, используя таблицу неопределенных интегралов.
.
Здесь – постоянная интегрирования, которая определяется из начальных условий. Поскольку тоже постоянная, то, чтобы придать решению более простой вид, заменим на . В результате получим закон изменения проекции скорости на ось x :
(7) .
Как видно, скорость является линейной функцией от времени. Тот факт, что зависит от времени, можно записать так:
.

Зная значение в определенный момент времени, можно определить значение постоянной . Пусть, например, нам известно, что в начальный момент времени , проекция скорости на ось x равняется . Подставим в (7) :
.
Отсюда . Тогда закон изменения проекции скорости на ось x имеет определенный вид:
.

Теперь найдем закон изменения координаты точки x от времени: . Из (6) и (7) имеем:
;
.
Это также дифференциальное уравнение с разделяющимися переменными. Интегрируем с помощью таблицы интегралов.

.
Итак, мы получили закон изменения координаты от времени:
(8) .
Здесь – постоянные интегрирования. Их можно найти, зная скорость и координату, в какой-либо момент времени.

Пусть, например, в начальный момент времени , координата равна , и проекция скорости точки на ось x равна . Ранее мы уже нашли значение постоянной для этого случая: . Подставим в (8):
.
Подставим сюда :
.
Отсюда .
Тем самым мы получили закон изменения x координаты от времени:
.

Уравнения движения (2) для остальных переменных y и z , при постоянных силах, решаются точно так же, как и для переменной x . Далее мы приводим пример решения задачи на интегрирование дифференциальных уравнений движения материальной точки при действии на нее постоянных сил.

Задача

Условие задачи

Груз S, рассматриваемый как материальная точка массы m = 5кг, движется по шероховатой поверхности от точки A до точки B, в которой отрывается от поверхности и продолжает движение в воздухе до падения на наклонную поверхность в точке C. Движение происходит в плоскости рисунка.

В точке A, груз имел скорость м/с. Скорость в точке B: м/с. Участок AB представляет собой плоскую поверхность с углом наклона α = 30° к горизонту. На участке AB, кроме силы тяжести и силы трения, на груз действует постоянная сила Н, направленная под углом φ = 45° к поверхности. Коэффициент трения f = 0,1 .

На участке BC, груз движется под действием только силы тяжести. Сопротивлением воздуха пренебречь. Поверхность, на которую падает груз, является плоской с углом наклона β = 15° к горизонту (см. рисунок). Точка D расположена ниже точки B на расстояние |BD| = h = 1 м .

Найти: Время движения на участке AB; длину этого участка; время падения от точки B к точке C; расстояние |DC|; уравнение траектории BC.

Решение задачи

1. Движение материальной точки на участке AB

1.1. Составление уравнения движения и определение ускорения

Рассмотрим движение груза S на участке AB. Как сказано в условии, его можно рассматривать как материальную точку. То есть считаем, что размерами груза можно пренебречь.

Выберем декартову систему координат с началом в точке A. Ось x направим от A к B; ось y – перпендикулярно. Пусть в начальный момент времени , груз находился в точке A.

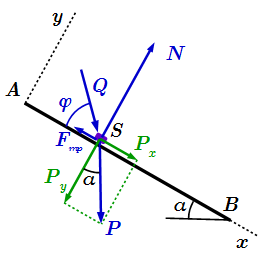
Силы, действующие на груз S на участке AB.

Рассмотрим силы, действующие на груз, и найдем их компоненты в выбранной системе координат Axy .
1) Сила тяжести , где м/с 2 – ускорение свободного падения. Она направлена вертикально вниз. Разложим ее на составляющие вдоль координатных осей по правилу параллелограмма: (см. рисунок). Поскольку вектор перпендикулярен горизонтали, а вектор перпендикулярен поверхности AB, то угол между векторами и равен углу между горизонталью и поверхностью движения, который по условию равен α . Тогда сила тяжести имеет следующие проекции на оси выбранной системы координат:
.
2) Заданная сила . По условию, она направлена под углом φ к поверхности (см. рисунок). Находим ее компоненты в системе координат Axy :
.
3) Сила давления поверхности . Она перпендикулярна поверхности. Поэтому ее компоненты:
.
4) Сила трения . Она направлена противоположно перемещению, то есть противоположно оси x . Абсолютная величина силы трения определяется по закону Амонта – Кулона:
(AB.1) .
Ее компоненты:
.

Составляем дифференциальные уравнения движения материальной точки:
.
Здесь мы учли, что движение происходит в плоскости xy . Поэтому уравнение для z компоненты тождественно обращается в нуль. Подставляем перечисленные выше компоненты внешних сил.
(AB.2) ;
(AB.3) .

Перемещение вдоль оси y отсутствует. Это означает, что координата y точки S остается постоянной при движении на участке AB. Тогда и все ее производные по времени равны нулю. Поэтому . Тогда из (AB.3) и (AB.1) имеем:
;
.

Разделим (AB.2) на m . В результате получим дифференциальное уравнение движения точки в следующем виде:
.
Вторая производная координаты по времени есть ускорение точки. Обозначим его как . Поскольку все действующие внешние силы постоянны, то ускорение постоянно.

.
В результате уравнение движения точки примет более простой вид:
(AB.4) ,
где – ускорение точки, постоянная величина.

1.2. Интегрирование уравнений движения

Итак, мы составили дифференциальное уравнение движения материальной точки S на участке AB:
(AB.4) ,
Теперь переходим к интегрированию этого уравнения.

Разберемся с обозначениями. У нас x – это координата точки, определяющая ее положение. Скорость точки – это производная координаты по времени t :
(AB.5) .
При , точка движется в сторону возрастания координаты x : от A к B. При – в противоположную сторону.
Ускорение – это производная скорости по времени, или вторая производная координаты по времени:
.

Определяем закон изменения скорости со временем. Для этого выразим уравнение (AB.4) через скорость :
.
Это простейшее дифференциальное уравнение с разделяющимися переменными. Интегрируем его, учитывая, что – это постоянная Для этого используем таблицу неопределенных интегралов.
;
;
(AB.6) .
Здесь – постоянная интегрирования. Найдем ее значение из условия, что в начальный момент времени , груз S находился в точке A и имел скорость в направлении оси x . Подставляем в (AB.6) , :
.
Отсюда . Тогда закон изменения скорости со временем принимает следующий вид:
(AB.7) .

Определяем время движения груза на участке AB. Для удобства, обозначим моменты времени, в которых груз находился в точках A и B, как и . Поскольку, по принятому нами соглашению, , то . Подставим в (AB.7) значения для точки B: . Тогда
. Отсюда
.

Теперь найдем зависимость координаты груза x от времени. Для этого воспользуемся тем, что скорость есть производная координаты по времени (см. (AB.5)):
.
Зависимость мы уже нашли: . Подставляем и интегрируем.
;
;

;
.
Здесь – постоянная интегрирования. Найдем ее из условия, что в начальный момент времени, , груз находился в точке A, в которой . Подставляем , :
.
Отсюда .
Тем самым мы нашли закон движения точки S на участке AB:
(AB.8) .

Определяем длину участка AB. Нам известно, что в момент времени , груз находился в точке A. В момент времени – в точке B. Также нам известен закон движения точки . Это позволяет найти длину участка AB:

.

1.3. Проверка решения

Сделаем проверку. Для этого воспользуемся теоремой об изменении кинетической энергии точки. Согласно этой теореме, Изменение кинетической энергии материальной точки, при переходе из точки A в точку B, равно сумме работ всех сил, приложенных к точке на этом перемещении:
(AB.9) .

Находим сумму проекций всех сил на ось x , приложенных к грузу на участке AB:

.
Находим сумму работ всех внешних сил, произведенных при перемещении груза из точки A в точку B.
.

Находим разность кинетических энергий груза при перемещении из точки A в точку B.
.

Подставим найденные значения в (AB.9):
.
Видно, что это уравнение выполняется. Различие имеется только в последней цифре. Это связано с округлениями, производимыми при вычислениях. Значит, этот этап решения выполнен верно.

2. Движение материальной точки на участке BC

2.1. Уравнения движения и их решения

Теперь рассмотрим движение груза S на участке BC. На этом участке мы выберем новую систему координат, и новый отсчет времени. Возьмем декартову систему координат с началом в точке B. Ось Bx направим по горизонтали; ось By – вертикально вверх (см. рисунок).

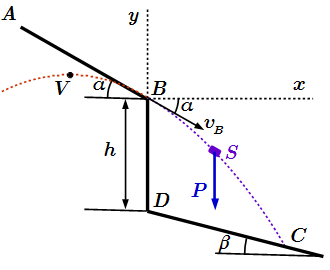
Движение груза на участке BC.

Началом движения, на участке BC, является точка B. Новый отсчет времени также будем производить от этой точки. Тогда в начальный момент времени , координаты груза равны нулю:
.
Нам известна скорость груза в точке B. Она имеет абсолютное значение , заданное в условии, и направлена вдоль прямой AB. И поэтому составляет угол α с горизонтальной осью Bx. Проекции скорости на оси координат равны:
.

На груз действует только одна сила тяжести , направленная вниз. Ее абсолютное значение . Выпишем ее компоненты в рассматриваемой системе координат (проекции силы тяжести на оси x и y):
.

Составляем уравнения движения.
.
Или
.
Разделим на m :
(BC1) ;
(BC2) .

Решаем первое уравнение (BC1). Сначала найдем закон изменения проекции скорости на ось x . Для этого, как и выше, используем следующие обозначения:
.
Выразим вторую производную в уравнении (BC1) через проекцию скорости на ось x :
;
.
Интегрируем это уравнение.
;
.
Здесь – постоянная интегрирования. Получилось, что проекция скорости груза на ось x не зависит от времени. Она постоянна для всех точек на участке BC. Поскольку нам известно значение в точке B, то . Тогда
(BC3) .
Теперь находим закон изменения координаты x от времени. Для этого воспользуемся тем, что . Подставляем в (BC3) и интегрируем.
;
;
.
Определяем постоянную интегрирования из начальных условий. В точке B . Подставляем :
.
Отсюда , и мы получаем закон изменения координаты x от времени:
(BC4) .

Аналогичным образом решаем второе уравнение:
(BC2) .
Находим закон изменения проекции скорости от времени. Используем следующие обозначения для проекции ускорения на ось y :
.
Выразим уравнение (BC2) через :
;
.
Интегрируем.
;
.
Находим значение постоянной интегрирования из начальных условий. При . Подставляем :
.
Отсюда . Так мы получили закон изменения проекции скорости на ось y :
(BC5) .
Находим закон изменения координаты y от времени. Подставляем в (BC5) и интегрируем.
;
;
.
Определяем постоянную интегрирования из начальных условий. В точке B . Подставляем :
.
Отсюда . И мы получаем закон изменения координаты y от времени:
(BC6) .

2.2. Определение координат точки C

Итак, мы получили закон движения материальной точки S в виде двух уравнений.
(BC4) ;
(BC6) .
Найдем положение точки C.

Для этого нам нужно найти уравнение прямой DC. В общем виде, уравнение прямой описывается по формуле:
(BC7) .
Здесь k – это угловой коэффициент, равный тангенсу угла наклона прямой к оси x . Положительным считается направление поворота от оси x против часовой стрелки. В нашем случае угол наклона отрицательный и равен . Поэтому
.
Найдем значение коэффициента b . Воспользуемся тем, что нам известны координаты точки D, принадлежащие прямой:
.
Подставим в (BC7):
;
.
Отсюда .
Таким образом, мы нашли уравнение прямой DC:
(BC8) ,
где .

Теперь найдем координаты точки C. Для этого нам нужно найти точку пересечения кривой, заданной уравнениями (BC4)–(BC6) и прямой (BC8). Координаты точки C удовлетворяют всем этим уравнениям:
(BC4) ;
(BC6) ;
(BC8) .
Решаем систему трех уравнений (BC4), (BC6) и (BC8). Подставляем (BC4) и (BC6) в (BC8) и выполняем преобразования:
;
.
Решаем квадратное уравнение. Подставляем численные значения.
;

;
;
.
Получаем корни уравнения:
.
Положительный корень дает момент времени, в который груз оказался в точке C . Это время движения по участку BC:
.

Находим значения координат точки C. Подставим найденное значение в (BC4):
.
Значение можно получить или из уравнения (BC6), или из (BC8). Поскольку последнее проще, то используем его:
.
Расстояние между точками D и C:
.

2.3. Траектория движения точки

Выше мы получили закон движения материальной точки S в виде двух уравнений.
(BC4) ;
(BC6) .
Теперь найдем уравнение ее траектории. Для этого мы должны исключить t из уравнений (BC4) и (BC6).

Из уравнения (BC4) находим:
.
Подставляем в (BC6) и выполняем преобразования.
;

;
;
.
Это уравнение параболы. Ее вершина V находится в точке с координатами
;
.
Фокальный параметр:
.
С этими обозначениями, уравнение параболы можно записать в каноническом виде:
.

.
Траектория движения груза на участке BC представляет собой параболу

с вершиной в точке V с координатами ,
и фокальным параметром .

Автор: Олег Одинцов . Опубликовано: 13-09-2020

Теоретическая механика: Решебник Яблонского:
Динамика материальной точки (Д1, Д2, Д3, Д4, Д5, Д6)

Бесплатный онлайн решебник Яблонского. Выберите задание и номер варианта для просмотра решения. Смотрите также способы и примеры решения задач по теме движение материальной точки.

Задание Д.1. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил

Варианты 1–5 (рис. 117, схема 1). Тело движется из точки A по участку AB (длиной l) наклонной плоскости, составляющей угол α с горизонтом, в течение τ с. Его начальная скорость v_A. Коэффициент трения скольжения тела по плоскости равен f.

В точке B тело покидает плоскость со скоростью v_B и попадает со скоростью v_C в точку C плоскости BD, наклоненной под углом β к горизонту, находясь в воздухе T с.

При решении задачи тело принять за материальную точку; сопротивление воздуха не учитывать.

Варианты с решением: 1 2 3 4 5

Варианты 6–10 (рис. 117, схема 2). Лыжник подходит к точке A участка трамплина AB, наклоненного под углом α к горизонту и имеющего длину l, со скоростью v_A. Коэффициент трения скольжения лыж на участке AB равен f. Лыжник от A до B движется τ с; в точке B со скоростью v_B он покидает трамплин. Через T с лыжник приземляется со скоростью v_C в точке C горы, составляющей угол β с горизонтом.

При решении задачи принять лыжника за материальную точку и не учитывать сопротивление воздуха.

Варианты с решением: 6 7 8 9 10

Варианты 11–15 (рис. 117, схема 3). Имея в точке A скорость v_A, мотоцикл поднимается τ с по участку AB длиной l, составляющему с горизонтом угол α. При постоянной на всем участке AB движущей силе P мотоцикл в точке B приобретает скорость v_B и перелетает через ров шириной d, находясь в воздухе T с и приземляясь в точке C со скоростью v_C. Масса мотоцикла с мотоциклистом равна m.

При решении задачи считать мотоцикл с мотоциклистом материальной точкой и не учитывать силы сопротивления движению.

Варианты с решением: 11 12 13 14 15

Варианты 16–20 (рис. 117, схема 4). Камень скользит в течение τ с по участку AB откоса, составляющему угол α с горизонтом и имеющему длину l. Его начальная скорость v_A. Коэффициент трения скольжения камня по откосу равен f. Имея в точке B скорость v_B, камень через T с ударяется в точке C о вертикальную защитную стену. При решении задачи принять камень за материальную точку; сопротивление воздуха не учитывать.

Варианты с решением: 16 17 18 19 20

Варианты 21–25 (рис. 117, схема 5). Тело движется из точки A по участку AB (длиной l) наклонной плоскости, составляющей угол α с горизонтом. Его начальная скорость v_A. Коэффициент трения скольжения равен f. Через τ с тело в точке B со скоростью v_B покидает наклонную плоскость и падает на горизонтальную плоскость в точку C со скоростью v_C; при этом оно находится в воздухе T с.

При решении задачи принять тело за материальную точку и не учитывать сопротивление воздуха.

Варианты с решением: 21 22 23 24 25

Варианты 26–30 (рис. 117, схема 6). Имея в точке A скорость v_A, тело движется по горизонтальному участку AB длиной l в течение τ с. Коэффициент трения скольжения тела по плоскости равен f. Со скоростью v_B тело в точке B покидает плоскость и попадает в точку C со скоростью v_C, находясь в воздухе T с. При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать.

Варианты с решением: 26 27 28 29 30 (решено 100%)

Задание Д.2. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил

Найти уравнения движения тела M массой m (рис. 119–121), принимаемого за материальную точку и находящегося под действием переменной силы P=Xi+Yj+Zk, при заданных начальных условиях. Во всех вариантах ось z (где показана) вертикальна, за исключением вариантов 8 и 30.

Необходимые для решения данные приведены в табл. 39, в которой приняты следующие обозначения: i, j, k – орты координатных осей (соответственно x, y, z); g – ускорение свободного падения (9,81 м/с 2 ); f – коэффициент трения скольжения; t – время, с; x, y, z, x’, y’, z’ – координаты точки и проекции ее скорости нa оси координат соответственно, м и м/с.

Во всех случаях, где сила P зависит от x, x’, z, z’, рассмотреть движение точки, при котором эти величины только положительны.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Задание Д.3. Исследование колебательного движения материальной точки

Варианты 1–5 (рис. 125). Найти уравнение движения груза D массой m_D (варианты 2 и 4) или системы грузов D и E массами m_D и m_E (варианты 1, 3, 5), отнеся их движение к оси x; начало отсчета совместить с положением покоя груза D или соответственно системы грузов D и E (при статической деформации пружин). Стержень, соединяющий грузы, считать невесомым и недеформируемым.

Варианты с решением: 1 2 3 4 5

Варианты 6–10 (рис. 125). Найти уравнение движения груза D массой m по гладкой наклонной плоскости, составляющей с горизонтом угол α, с момента соприкасания груза с пружиной или с системой пружин, предполагая, что при дальнейшем движении груз от пружин не отделяется. Движение груза отнести к оси x, приняв за начало отсчета положение покоя груза (при статической деформации пружин).

Варианты с решением: 6 7 8 9 10

Варианты 11–15 (рис. 126). Груз D массой m укреплен на конце невесомого стержня, который может вращаться в горизонтальной плоскости вокруг оси E. Груз соединен с пружиной или с системой пружин; положение покоя стержня, показанное на чертеже, соответствует недеформированным пружинам. Считая, что груз D, принимаемый за материальную точку, движется по прямой, определить уравнение движения этого груза (трением скольжения груза по плоскости пренебречь).

Движение отнести к оси x, за начало отсчета принять точку, соответствующую положению покоя груза.

Варианты с решением: 11 12 13 14 15

Варианты 16–20 (рис. 126). Найти уравнение движения груза D массой m_D (варианты 17 и 19) или системы грузов D и E массами m_D и m_E (варианты 16, 18, 20), отнеся движение к оси x; начало отсчета совместить с положением покоя груза D или соответственно системы грузов D и E (при статической деформации пружин). Предполагается, что грузы D и E при совместном движении не отделяются.

Варианты с решением: 16 17 18 19 20

Варианты 21–25 (рис. 127). Найти уравнение движения груза D массой m по гладкой наклонной плоскости, составляющей с горизонтом угол α, отнеся движение к оси x; за начало отсчета принять положение покоя груза (при статической деформации пружин).

Варианты с решением: 21 22 23 24 25

Варианты 26–30 (рис. 127). Пренебрегая массой плиты и считая ее абсолютно жесткой, найти уравнение движения груза D массой m с момента соприкасания его с плитой, предполагая, что при дальнейшем движении груз от плиты не отделяется.

Движение груза отнести к оси x, приняв за начало отсчета положение покоя этого груза (при статической деформации пружин).

Варианты с решением: 26 27 28 29 30 (решено 100%)

Задание Д.4. Исследование относительного движения материальной точки

Шарик M, рассматриваемый как материальная точка, перемещается по цилиндрическому каналу движущегося тела A (рис. 129–131). Найти уравнение относительного движения этого шарика x=f(t), приняв за начало отсчета точку O.

Тело A равномерно вращается вокруг неподвижной оси (в вариантах 2, 3, 4, 7, 10, 11, 14, 20, 23, 26 и 30 ось вращения z₁ вертикальна, в вариантах 1, 12, 15 и 25 ось вращения x₁ горизонтальна). В вариантах 5, 6, 8, 9, 13, 16, 17, 18, 19, 21, 22, 24, 27, 28 и 29 тело A движется поступательно, параллельно вертикальной плоскости y₁O₁z₁.

Найти также координату x и давление шарика на стенку канала при заданном значении t=t₁. Данные, необходимые для выполнения задания, приведены в табл. 40.

В задании приняты следующие обозначения: m – масса шарика M; ω – постоянная угловая скорость тела A (в вариантах 1–4, 7, 10–12, 14, 15, 20, 23, 25, 26, 30) или кривошипов O₁B и O₂C (в вариантах 6, 17, 22); c – коэффициент жесткости пружины, к которой прикреплен шарик M; l₀ – длина недеформированной пружины; f – коэффициент трения скольжения шарика по стенке канала; x₀, x’₀ – начальная координата и проекция начальной скорости на ось х.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Задание Д.5. Применение теоремы об изменении количества движения к определению скорости материальной точки

Телу массой m сообщена начальная скорость v₀, направленная вверх по наклонной плоскости, составляющей угол α с горизонтом. На тело действует сила P, направленная в ту же сторону (рис. 133).

Зная закон изменения силы P=P(t) и коэффициент трения скольжения f, определить скорость тела в моменты времени t₁, t₂, t₃ и проверить полученный результат для момента времени t₁ с помощью дифференциального уравнения движения.

Необходимые для решения данные приведены в табл. 41.

При построении графика изменения силы P по заданным ее значениям P₀, P₁, P₂, P₃ для моментов времени t₀, t₁, t₂, t₃ считать зависимость P=P(t) между указанными моментами времени линейной. Значение силы P, задаваемое в табл. 41 в виде дроби, указывает на то, что модуль силы в заданный момент времени претерпевает «скачок»: в числителе указан модуль силы в конце промежутка времени, а в знаменателе – в начале следующего промежутка времени.

Варианты с решением: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 (решено 100%)

Задание Д.6. Применение основных теорем динамики к исследованию движения материальной точки

Шарик, принимаемый за материальную точку, движется из положения A внутри трубки, ось которой расположена в вертикальной плоскости (рис. 135–137). Найти скорость шарика в положениях B и C и давление шарика на стенку трубки в положении C. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь h₀, отделяется от пружины.

Необходимые для решения данные приведены в табл. 42.

В задании приняты следующие обозначения: m – масса шарика; v_A – начальная скорость шарика; τ – время движения шарика на участке AB (в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27, 30) или на участке BD (в вариантах 3, 4, 6, 7, 9–13, 15–17, 19, 22, 25, 26, 28, 29); f – коэффициент трения скольжения шарика по стенке трубки; h₀ – начальная деформация пружины; h – наибольшее сжатие пружины; c – коэффициент жесткости пружины; H – наибольшая высота подъема шарика; s – путь, пройденный шариком до остановки.

Дифференциальные уравнения движения материальной точки

Динамика. Основные понятия и определения.

Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил. В разделе динамики решается более сложная и важная задача. Определяется движение тела под действием сил приложенных к нему, с учетом внешних и внутренних условий, влияющих на это движение, включая самих материальных тел.

Инертностьи представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Если, например, при действии одина­ковых сил изменение скорости первого тела происходит медленнее, чем второго, то говорят, что первое тело является более инертным, и наоборот.

Количественной мерой инертности данного тела является фи­зическая величина, называемая массой тела. В механике масса m рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.

В общем случае движение тела зависит не только от его суммар­ной массы и приложенных сил; характер движения может еще зави­сеть от формы тела, точнее от взаимного расположения образующих его частиц (т. е. от распределения масс).

Чтобы при первоначальном изучении динамики иметь возможность отвлечься от учета влияния формы тел (распределения масс), вво­дится понятие о материальной точке.

Материальной точкой называют материальное тело (тело, имеющее массу), размерами которого при изучении его движения можно пренебречь.

Точка называется изолированной, если на точку не оказывается никакого влияния, никакого действия со стороны других тел и среды, в которой точка движется.

2. Аксиомы динамики ( законы Галилея – Ньютона).

В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений над движением тел. Систематически эти законы были впервые изложены И. Ньютоном.

Первый закон (закон инерции), открытый Галилеем, гласит: изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямо­линейного движения до тех пор, пока приложенные силы не за­ставят ее изменить это состояние. Движение, совершаемое точ­кой при отсутствии сил, называется движением по инерции.

Закон инерции отражает одно из основных свойств материи — пребывать неизменно в движении и устанавливает для материальных тел эквивалентность состояний покоя и движения по инерции. Из него следует, что если F=0, то точка покоится или движется с постоян­ной по модулю и направлению скоростью ( =const); ускорение точки при этом равно нулю: = 0); если же движение точки не является равномерным и прямолинейным, то на точку действует сила.

Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной системой отсчета (иногда ее условно называют неподвижной). (По данным опыта для нашей Сол­нечной системы инерциальной является система отсчета, начало кото­рой находится в центре Солнца, а оси направлены на так называемые неподвижные звезды. При решении большинства технических задач инерциальной, с достаточной для практики точностью, можно считать систему отсчета, жестко связанную с Землей).

Второй закон (основной закон динамики) гласит: произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы.

Математически этот закон выражается векторным равенством .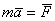

При этом между модулями ускорения и силы имеет место зависимость ma = F.

Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета. Из этого закона непо­средственно видно, что мерой инертности материальной точки является ее масса, так как две разные точки при действии одной и той же силы получают одинаковые ускорения только тогда, когда будут равны их массы; если же массы будут разные, то точка, масса кото­рой больше (т. е. более инертная), получит меньшее ускорение, и наоборот.

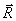
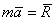
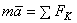
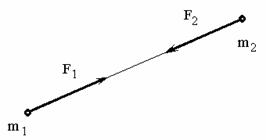
Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе, т.е. равнодействую­щей , равной геометрической сумме этих сил. Уравнение, выражаю­щее основной закон динамики, принимает в этом случае вид

или .

Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между мате­риальными телами. Для двух материальных точек он гласит: две ма­териальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.

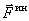
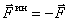
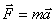
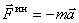
Сила, с которой материальная точка сопротивляется изменению своего движения, будем называть силой инерции этой точки — . По третьему закону она равна и противоположна действующей на точку силе , . Но на основании второй аксиомы . Поэтому .

Итак, сила инерции материальной точки по величине равна произведению её массы на ускорение

.

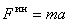
И направлена эта сила инерции в сторону противоположную вектору ускорения.

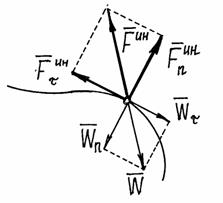
Например, при движении точки по кривой линии ускорение . Поэтому сила инерции

.

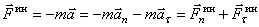
То есть её можно находить как сумму двух сил: нормальной силы инерции и касательной силы инерции.

Рис.1

Третий закон динамики, как устанавливающий характер взаимодей­ствия материальных частиц, играет большую роль в динамике системы.

Четвертый закон (закон независимого действия сил) : при одновременном действии на материальную точку нескольких сил ускорение точки относительно инерционной системы отсчета от действия каждой отдельной силы не зависит от наличия других, приложенных к точке, сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.

;

Дифференциальные уравнения движения материальной точки.

С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.

1) Определение движения точки координатным способом.

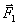
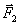
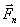
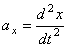
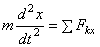
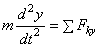
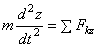
Рассмотрим свободную материальную точку, движущуюся под действием сил , . . Проведем неподвижные координатные оси Oxyz (рис.4). Про­ектируя обе части равенства на эти оси и учитывая,что и т.д., получим дифферен­циальные уравнения криволинейного дви­жения точки в проекциях на оси прямо­угольной декартовой системы координат:

, , .

Рис.4

Так как действующие на точку силы мо­гут зависеть от времени, от положения точки и от ее скорости, то правые части уравнений могут содержать время t, координаты точки х, у, z и проекции ее скорости . При этом в правую часть каждого из уравнений могут входить все эти переменные.

Чтобы с помощью этих уравнений решить основную задачу динамики, надо, кроме действующих сил, знать еще начальные условия, т.е. положение и скорость точки в начальный момент. В координатных осях Oxyz начальные условия задаются в виде: при

.

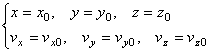
Зная действующие силы, после интегрирования уравнений найдем координаты х, y, z движущейся точки, как функции времени t, т.е. найдем закон движения точки.

2) Определение движения точки естественным способом.

Координатным способом обычно определяют движение точки, не ограниченные какими-либо условиями, связями. Если на движение точки наложены ограничения, на скорость или координаты, то определить такое движение координатным способом совсем не просто. Удобнее использовать естественный способ задания движения.

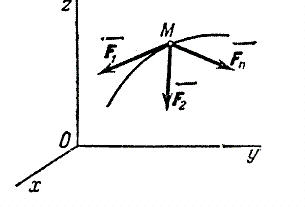
Определим, например, движение точки по заданной неподвижной линии, по заданной траектории (рис. 7).

Рис.7

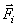
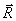
На точку М кроме заданных активных сил , действует реакция линии. Показываем составляющие реакции по естественным осям

Составим основное уравнение динамики 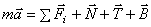и спроектируем его на естественные оси

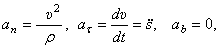
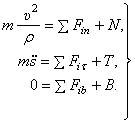
Так как то получим дифференциальные уравнения движения, такие

(5)

Здесь сила — сила трения. Если линия, по которой движется точка, гладкая, то Т = 0 и тогда второе уравнение будет содержать только одну неизвестную – координату s:

.

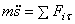
Решив это уравнение, получим закон движения точки , а значит, при необходимости, и скорость и ускорение. Первое и третье уравнения (5) позволят найти реакции и .