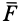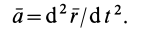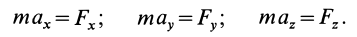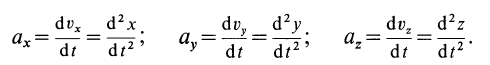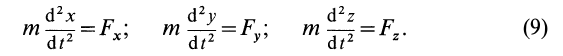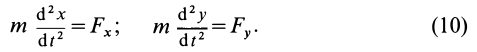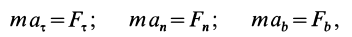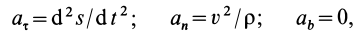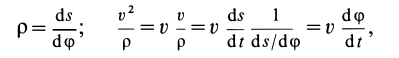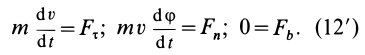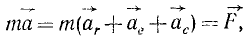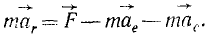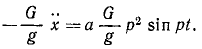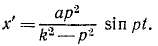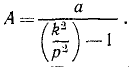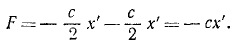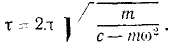Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
Здесь мы рассматриваем пример решения задачи на интегрирование дифференциальных уравнений прямолинейного движения материальной точки, находящейся под действием переменных сил. Методы, применяемые при решении задачи, подробно изложены на странице «Интегрирование дифференциальных уравнений прямолинейного движения материальной точки».
Условие задачи
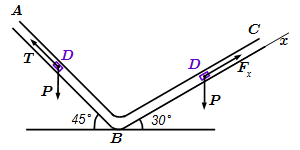
Груз D массой m, получив в точке A начальную скорость V0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости. На участке AB, длина которого l, на груз действует постоянная сила T(ее направление показано на рисунке) и сила R сопротивления среды (модуль этой силы R = μV 2 , вектор R направлен противоположно скорости V груза).
Груз, закончив движение на участке AB, в точке B трубы, не изменяя значения модуля своей скорости, переходит на участок BC. На участке BC на груз действует переменная сила F, проекция Fx которой на ось x задана.
Считая груз материальной точкой, найти закон его движения на участке BC, т.е. x = f(t), где x = BD. Трением груза о трубу пренебречь.
Дано: m = 1,8 кг , v 0 = 20 м/с , T = 15 Н , μ = 0,2 кг/м , l = 3,0 м , Fx = 5 – 2sin(3 t ) .
Решение задачи
1. Движение материальной точки на участке AB
1.1. Составление уравнения движения груза
Чтобы найти закон его движения груза D на участке BC, нам нужно найти его скорость в точке B. Для этого рассмотрим движение груза на участке AB; составим уравнение движения; решая которое, определим скорость .
Как сказано в условии, груз можно рассматривать как материальную точку. То есть, считаем, что размерами груза можно пренебречь.
Выберем декартову систему координат с началом в точке A. Направим ось от A к B. Пусть в начальный момент времени , груз находился в точке A.
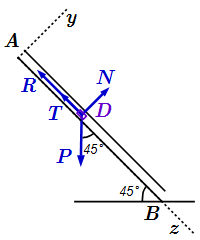
Силы, действующие на груз D на участке AB.
Рассмотрим силы, действующие на груз, и найдем их проекции на ось .
1) Сила тяжести , где м/с 2 – ускорение свободного падения. Она направлена вертикально вниз и составляет угол с осью . Абсолютное значение силы тяжести: . Проекция на ось :
.
2) Сила . Ее абсолютное значение задано: T = 15 Н . Сила направлена противоположно оси . Поэтому ее проекция на эту ось:
.
3) Сила сопротивления среды по абсолютной величине пропорциональна квадрату скорости: , и направлена противоположно скорости груза. Считаем, что скорость v направлена от A к B . Тогда вектор силы направлен противоположно оси . Его проекция на эту ось:
.
4) Сила давления поверхности . Она перпендикулярна поверхности AB , вдоль которой происходит движения груза. Поэтому ее проекция на ось равна нулю:
.
Если бы на груз действовала сила трения скольжения , то нам нужно было бы определить абсолютное значение силы давления N . Это можно сделать, приравнивая к нулю сумму проекций всех сил на ось Ay : . Но в нашей задаче, значение силы трения скольжения намного меньше величин остальных сил, поэтому мы пренебрегаем ее влиянием на движение.
На участке AB перемещение груза происходит только вдоль оси . Перемещение в перпендикулярных направлениях отсутствует. Поэтому при движении изменяется только координата . Вектор скорости груза также направлен вдоль оси . Поэтому он имеет только одну отличную от нуля компоненту . Тогда . Составляем дифференциальное уравнение движения материальной точки вдоль оси :
.
Подставляем перечисленные выше компоненты внешних сил.
;
(AB.1) .
1.2. Определение скорости vB
Выразим вторую производную координаты по времени через скорость . Поскольку , то
.
Подставляем в (AB.1):
(AB.2) .
Это дифференциальное уравнение первого порядка с разделяющимися переменными. Мы можем его решить, и найти скорость как функцию времени:
(AB.3) .
Если бы в условии было задано время движения груза на участке AB, то, подставив в (AB.3) значение , мы сразу могли бы получить искомую скорость груза в точке B.
Но у нас известно не время движения по участку AB, а его длина l . Тогда мы можем решить уравнение (AB.2), и получить зависимость . Затем нужно решить уравнение , и получить закон движения груза на участке AB: . Отсюда можно найти значение момента времени , при котором груз окажется в точке B. Зная это время, по формуле (AB.3), можно определить искомое значение скорости в точке B.
Однако есть более простой способ. Он заключается в том, чтобы искать зависимость скорости не от времени, а от координаты: . Для этого в (AB.2) применяем правило дифференцирования сложной функции, учитывая что :
.
Подставим в (AB.2):
.
Разделяем переменные.
(AB.4) .
Введем постоянную . Тогда (AB.4) примет более простой вид:
;
.
Интегрируем от точки A до точки B:
(AB.5) .
По условию, скорость в точке A равна : . Обозначим скорость в точке B как . Тогда . Поскольку мы выбрали начало координат в точке A, то . Тогда по условию, . Поставляем в (AB.5):
(AB.6) .
Интеграл в правой части элементарный:
.
В левой части делаем подстановку :
;
.
Здесь мы учли, что поскольку и , то . Поэтому убрали знак модуля. Также воспользовались свойством логарифма.
Подставляем в (AB.6).
.
Вводим постоянную , и находим :
;
;
;
.
2. Определение закона движения материальной точки на участке BC
2.1. Составление уравнения движения груза
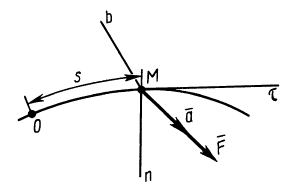
Теперь рассмотрим движение груза D на участке BC. На этом участке мы выберем новую систему координат с началом в точке B, и новый отсчет времени. Ось направим вдоль линии движения груза (см. рисунок). Ось – перпендикулярно. Пусть в момент времени , груз находился в точке B, и, как мы только что нашли, двигался со скоростью .
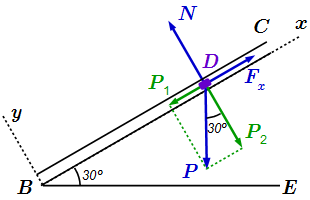
Силы, действующие на груз на участке BC.
Рассмотрим силы, действующие на груз, и найдем их проекции на ось .
1) Сила тяжести . Она направлена вертикально вниз. Разложим ее по правилу параллелограмма на составляющие и , параллельные осям координат, причем . Поскольку и , то угол между векторами и равен углу между BC и горизонталью BE. Из прямоугольника, образованного векторами , находим: . Тогда проекция силы тяжести на ось равна .
2) Сила . Ее проекция на ось задана в условии задачи: .
3) Сила давления поверхности . Она перпендикулярна поверхности BC . Поэтому ее проекция на ось равна нулю:
.
Составляем дифференциальное уравнение движения материальной точки вдоль оси :
.
Подставляем перечисленные выше компоненты внешних сил.
.
Разделим на m , и подставим численные значения величин.
;
;
.
(BC.1) .
Мы получили дифференциальное уравнение движения груза на участке BC.
2.2. Решение уравнения движения
Решаем его с помощью понижения порядка. Для этого выразим вторую производную координаты по времени через первую производную , то есть через проекцию скорости на ось :
. Подставляем в (BC.1).
(BC.2) .
Это дифференциальное уравнение первого порядка с начальным условием: при .
Интегрируем уравнение (BC.2).
.
Итак, мы получили общее решение уравнения (BC.2):
.
Здесь – произвольная постоянная. Найдем ее значение из начального условия. Подставляем :
;
;
.
Тем самым мы нашли закон изменения скорости груза со временем:
(BC.3) .
Теперь найдем закон движения груза . Для этого выразим скорость через координату: , и подставим в (BC.3):
(BC.4) .
Это дифференциальное уравнение первого порядка с начальным условием при .
Интегрируем его.
.
Итак, мы нашли общее решение уравнения (BC.4):
.
Постоянную найдем из начального условия. Подставляем :
.
Отсюда . Тем самым мы нашли закон движения груза на участке BC:
.
.
Здесь t выражено в секундах; x – в метрах.
Автор: Олег Одинцов . Опубликовано: 19-12-2020
Дифференциальные уравнения движения материальной точки в теоретической механике
Содержание:
Дифференциальные уравнения движения материальной точки:
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
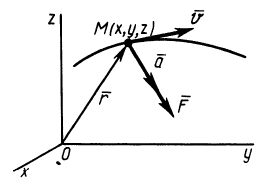
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
Из кинематики точки известно, что ускорение 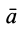
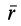
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 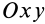
Так как 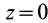
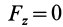
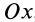
Так как при движении 
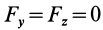
где 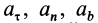
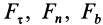
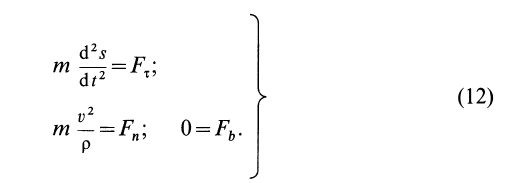
где 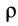
Второе уравнение из (12) можно преобразовать:
где 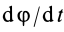
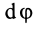
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 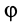
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
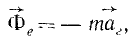
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
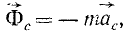
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
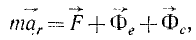
или в проекциях на оси координат:
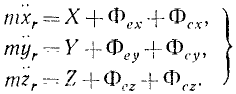
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
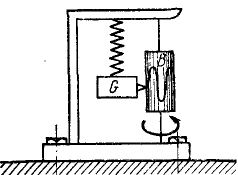
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 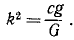
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 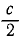
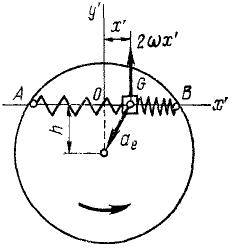
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 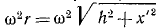
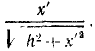
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 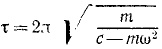
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Движение тела с переменной массой
Для начала сформулируем, что такое переменная масса.
Переменная масса – это масса тела, которая может меняться при медленных движениях из-за частичных приобретений или потерь составляющего вещества.
Уравнение движения материальной точки с переменной массой
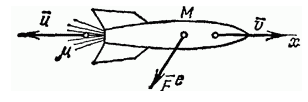
Чтобы записать уравнение движения для тела с такой массой, возьмем для примера движение ракеты. В основе ее перемещений лежит очень простой принцип: она движется за счет выброса вещества с большой скоростью, а также сильного воздействия, оказываемого на это вещество. В свою очередь выбрасываемые газы также оказывают воздействие на ракету, придавая ей ускорение в противоположном направлении. Кроме того, ракета находится под действием внешних сил, таких, как гравитация Солнца и других планет, земная тяжесть, сопротивление среды, в которой она совершает движение.
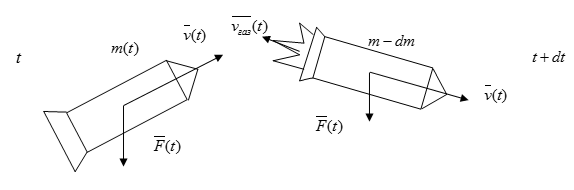
Обозначим массу ракеты в какой-либо момент времени t как m ( t ) , а ее скорость как v ( t ) . То количество движения, которая она при этом совершает, будет равно m v . После того, как пройдет время d t , обе эти величины получат приращение (соответственно d m и d v , причем значение d m будет меньше 0 ). Тогда количество движения, совершаемого ракетой, станет равно:
( m + d m ) ( v + d v ) .
Нам необходимо учитывать тот момент, что за время d t также происходит движение газов. Это количество тоже нужно добавить в формулу. Оно будет равно d m г а з v г а з . Первый показатель означает массу газов, которые образуются за указанное время, а второй – их скорость.
Теперь нам нужно найти разность между суммарным количеством движения за время t + d t и количеством движения системы во время t . Так мы найдем приращение данной величины за время d t , которое будет равно F d t (буквой F обозначена геометрическая сумма всех тех внешних сил, которые действуют в это время на ракету).
В итоге мы можем записать следующее:
( m + d m ) ( v + d v ) + d m г а з + v г а з — m v = F d t .
Поскольку нам важны именно предельные значения d m d t , d v d t и их производные, приравняем эти показатели к нулю. Значит, после раскрытия скобок произведение d m · d v может быть отброшено. С учетом сохранения массы получим:
d m + d m г а з = 0 .
Теперь исключим массу газов d m г а з и получим скорость, с которой газы будут покидать ракету (скорость струи вещества), выражающаяся разностью v о т н = v г а з — v . Учитывая эти преобразования, можно переписать исходное уравнение в следующем виде:
d m v = v о т н d m + F d t .
Теперь разделим его на d t и получим:
m d v d t = v о т н d m d t + F .
Уравнение Мещерского
Форма полученного уравнения точно такая же, как у уравнения, выражающего второй закон Ньютона. Но, если там мы имеем дело с постоянной массой тела, то здесь из-за потери вещества она постепенно меняется. К тому же помимо внешней силы нужно учитывать так называемую реактивную силу. В примере с ракетой это будет сила выходящей из нее газовой струи.
Уравнение m d v d t = v о т н d m d t + F впервые вывел русский механик И.В. Мещерский, поэтому оно получило его имя. Также его называют уравнением движения тела с переменной массой.
Формула Циолковского
Попробуем исключить из уравнения движения ракеты внешние силы, воздействующие на нее. Предположим, что движение ракеты прямолинейно, а направление противоположно скорости газовой струи v о т н . Будем считать направление полета положительным, тогда проекция вектора v о т н является отрицательной. Она будет равна — v о т н . Переведем предыдущее уравнение в скалярную форму:
m d v = v о т н d m .
Тогда равенство примет вид:
d v d m = — v о т н m .
Газовая струя может выходить во время полета с переменной скоростью. Проще всего, разумеется, принять ее в качестве константы. Такой случай наиболее важен для нас, поскольку так уравнение решить намного проще.
Исходя из начальных условий, определим, какое значение приобретет постоянная интегрирования С. Допустим, что в начале пути скорость ракеты будет равна 0 , а масса m 0 . Следовательно, из предыдущего уравнения можем вывести:
C = v о т н ln m 0 m .
Тогда мы получим соотношения следующего вида:
v = v о т н ln m 0 m или m 0 m = e v v о т н .
Это соотношение и является формулой Циолковского.
Она предназначена для расчета запаса топлива, с помощью которого ракета может набрать необходимую скорость. При этом время сгорания топлива не обусловливает величину максимальной скорости ракеты. Чтобы разогнаться до предела, нужно увеличить скорость истечения газов. Для достижения первой космической скорости следует изменить конструкцию ракеты. Она должна быть многоступенчатой, поскольку необходимо меньшее соотношение между требуемой массой топлива и массой ракеты.
Разберем несколько примеров применения данных построений на практике.
Условие: у нас есть космический корабль, скорость которого постоянна. Для изменения направления полета в ней нужно включить двигатель, который выбрасывает газовую струю со скоростью v о т н . Направление выброса перпендикулярно траектории корабля. Определите угол изменения вектора скорости при начальной массе корабля m 0 и конечной m .
Решение
Ускорение по абсолютной величине будет равно a = ω 2 r = ω v , причем v = c o n s t .
Значит, уравнение движения будет выглядеть так:
m d v d t = v о т н d m d t перейдет в m v ω d t = — v о т н d m .
Поскольку d a = ω d t является углом поворота за время d t , то после интеграции первоначального уравнения получим:
a = v о т н v ln m 0 m .
Ответ: искомый угол будет равен a = v о т н v ln m 0 m .
Условие: масса ракеты перед стартом равна 250 к г . Вычислите высоту, которую она наберет через 20 секунд после начала работы двигателя. Известно, что топливо расходуется со скоростью 4 к г / с , а скорость истечения газов постоянна и равна 1500 м / с . Поле тяготения Земли можно считать однородным.
Решение
Начнем с записи уравнения Мещерского. Оно будет иметь следующий вид:
m ∆ v 0 ∆ t = μ v о т н — m g .
Здесь m = m 0 — μ t и v 0 – скорость ракеты в заданный момент времени. Разделим переменные:
∆ v 0 = μ v о т н m 0 — μ t — g ∆ t .
Теперь решим полученное уравнение с учетом первоначальных условий:
v 0 = v о т н ln m 0 m 0 — μ t — g t .
С учетом того, что H 0 = 0 при t = 0 , у нас получится:
H = v о т н t — g t 2 2 + v о т н m 0 μ 1 — μ t m 0 ln 1 — μ t m 0 .
Добавим заданные значения и найдем ответ:
H = v о т н t — g t 2 2 + v о т н m 0 μ 1 — μ t m 0 ln 1 — μ t m 0 = 3177 , 5 м .
Ответ: через 20 секунд высота ракеты будет составлять 3177 , 5 м .
http://www.evkova.org/differentsialnyie-uravneniya-dvizheniya-materialnoj-tochki-v-teoreticheskoj-mehanike
http://zaochnik.com/spravochnik/fizika/osnovy-dinamiki/dvizhenie-tela-s-peremennoj-massoj/