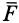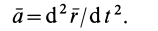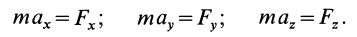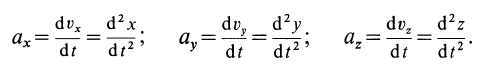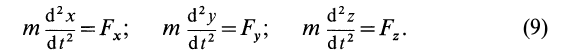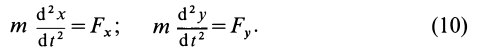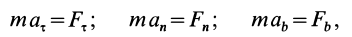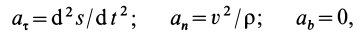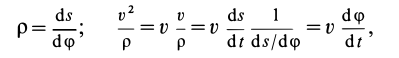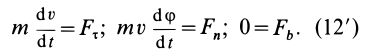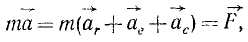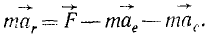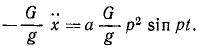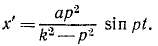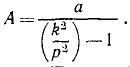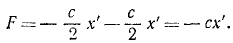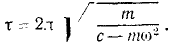Дифференциальные уравнения движения материальной точки в теоретической механике
Содержание:
Дифференциальные уравнения движения материальной точки:
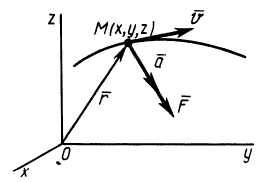
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
Из кинематики точки известно, что ускорение 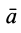
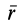
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
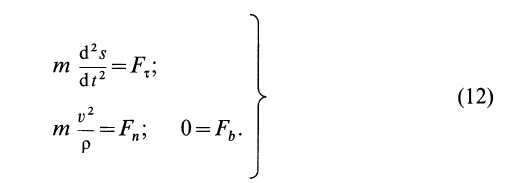
Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 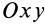
Так как 
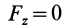
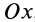
Так как при движении 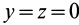
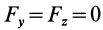
где 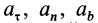
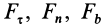
где 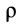
Второе уравнение из (12) можно преобразовать:
где 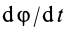
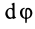
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 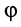
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
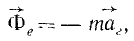
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
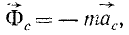
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
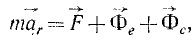
или в проекциях на оси координат:
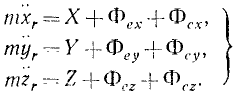
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
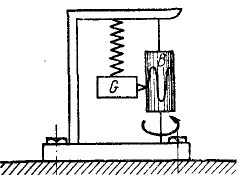
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 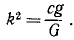
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 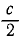
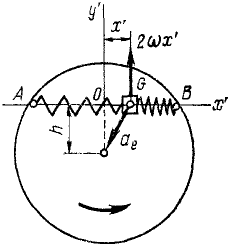
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 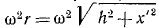
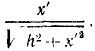
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 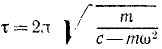
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Естественный способ задания движения точки
Содержание:
Естественный способ задания движения точки состоит в том, что в нём задаются: – траектория движения; – начало и положительное направление отсчета; – закон движения точки по траектории.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Естественный способ задания движения точки
Определим сначала кинематическое уравнение движения при натуральном способе задания движения материальной точки.
Натуральный способ задания (описания) движения материальной точки применяется тогда, когда траектория точки заранее известна. Движение изучается относительно фиксированного начала отсчета. Задается и закон движения материальной точки вдоль траектории.
Таким образом, для задания движения натуральным способом необходимо знать:
1. Траекторию АВ (рис. 2.3), которая может быть задана уравнением, графически или указанием, например точка движется вдоль окружности радиусом R.
2. Начало отсчета О криволинейной координаты S на траектории движения с указанием положительных «+» и отрицательных «–» значений. Кроме того, задается начало отсчета времени t. Обычно принимают, что t = 0 в момент, когда точка M проходит через точку O на траектории движения.
3. Закон движения материальной точки вдоль траектории. если, например, в момент времени t точка занимает положение M, криволинейная координата которого равна S, то это записывается следующим образом:
Эта функция должна быть непрерывной и по крайней мере дважды дифференцированной.
Соотношение называется кинематическим уравнением движения материальной точки в натуральной форме (или законом изменения криволинейной координаты). Это фактически расстояние подвижной точки M от начала отсчета вдоль траектории движения.
Криволинейную координату не следует путать с длиной пути, который проходит точка за определенный промежуток времени как в положительном, так и в отрицательном направлениях.
Определим кинематические характеристики движения материальной точки при
натуральном способе задания ее движения.
Скорость движения точки
Рассмотрим схему движения материальной точки M (рис. 2.3). Положение точки М соответствует моменту времени t, а положение М1 — t1. Тогда промежутку времени t1 – t = ∆t соответствует изменение криволинейной координаты S1 – S = ∆S. Отсюда можно определить среднюю скорость точки за промежуток времени ∆t:
А скорость точки в любой момент времени t можно определить, если взять предел отношения 
Модуль скорости материальной точки при натуральном способе задания ее движения равен первой производной по времени от закона движения точки.
Направление вектора скорости — по касательной к траектории движения материальной точки.
Производная по времени определяет численную алгебраическую величину скорости,
то есть, если 
отсчета, а если 
Решение.
Определим сначала положение точки на траектории движения при t1 = 1 c. Поскольку отсчет времени начался с началом момента движения, то S(0) = 0. Подставим в уравнение движения значение этого момента времени:
Для определения скорости движения точки продифференцируем по времени уравнения движения:
Из полученной функции скорости движения материальной точки можем определить (подстановкой t), что в начале движения (при t = 0): 

Переход от координатного способа задания движения материальной точки к натуральному
Для перехода от одного способа задания движения материальной точки к другому необходимо найти зависимости между основными параметрами этих движений. Сделаем это, рассматривая координатный и натуральный способы задания движения материальной точки. Так, на основании уравнения, что определяет скорость материальной точки при натуральном способе задания ее движения, можно записать
dS = 
Поскольку при координатном способе задания движения материальной точки ее скорость определяется согласно выражению:
то, подставляя его в предыдущее выражение, окончательно найдем зависимость между двумя указанными способами задания движения материальной точки:
Натуральный трехгранник
Приведем некоторые сведения из дифференциальной геометрии, которые понадобятся для определения кинематических характеристик движения материальной точки.
Предположим, что кривая АВ является траекторией точки М (рис. 2.4). В произвольной точке М и в бесконечно приближенной к ней точке М1 проведем касательные этой кривой (орты, подходящие этим касательным, обозначим через 




Плоскость, которая является предельным положением плоскости Q, когда точка M,
направляется к точке M, называется соприкасающихся плоскостью.
Через точку М проведем плоскость, перпендикулярную к касательной 

Линия пересечения нормали и стычной плоскостей определяет главную нормаль к кривой. Итак, главная нормаль — это единственная из бесконечного множества нормалей к кривой в точке M, которая расположена в соприкасающейся плоскости. Плоскость, проходящая через точку M перпендикулярна главной нормали, называется спрямляющей.
Линия пересечения спрямляющей и нормальной плоскостей определяет бинормаль
кривой. Очевидно, что бинормаль перпендикулярна к главной нормали.
Таким образом, в каждой точке кривой можно указать три взаимно перпендикулярные направления, по которым можно провести касательную в сторону роста дуговой координаты (соответствующий орт 





Прямоугольная подвижная система координатных осей с ортами 



Заметим, что плоская кривая полностью расположена в соприкасающейся плоскости, а главная нормаль является нормалью к кривой в этой плоскости. В отличии от других систем отсчета, натуральный трехгранник движется вместе с точкой и меняет свою ориентацию в пространстве в соответствии с характером траектории.
Кривизна кривой
Как видно дальше, ускорение точки в криволинейном движении зависит от кривизны траектории, поэтому рассмотрим эту характеристику. На рис. 2.5 изображена траектория AB движения точки и два близких положения M и M1. Проведем через точки M и M1 касающиеся 

Угол ∆φ между касательными в двух близких точках является углом смежности.
Кривизной кривой К в данной точке М называется предел отношения угла смежности к дуге ∆S, его взимает, когда эта дуга стремится к нулю.
Если, отношение ∆φ к ∆S является средней кривизной:
то, возведение Kc до границы дает истинное значение кривизны кривой:
Рассмотрим круг радиусом R (рис. 2.6). сделаем аналогичное геометрическое построение. Выразим ∆S по известной формуле:
и подставим в предыдущую формулу. Будем иметь:
K = 
Таким образом, круг радиусом R является кривой постоянной кривизны, значение которой равно обратной величине радиуса.
Для определения кривизны произвольной кривой достаточно подобрать такой круг, элемент дуги которого лучше всего аппроксимирует участок кривой в данной точке.
Тогда радиус круга будет радиусом кривизны кривой, а центр круга — центром кривизны.
Это показано на рис. 2.5:
K2 = 
Касательное и нормальное ускорения точки в натуральных осях координат
В декартовых осях координат мы определяли ускорение точки в проекциях на оси x, y, z. В натуральных осях координат определим проекции вектора ускорения на касательную 
равна нулю. Обратимся к рис. 2.7. Скорости близких точек M и M1 — векторы 



Перенесем параллельно вектор 



Параллельно ∆ 


и также будет расположен в соприкасающейся плоскости. А это значит, что проекция
вектора ускорения на бинормаль равна нулю.
Теперь, зная, что вектор ускорения имеет только касательную и нормальную составляющие, определим остальные.
Для этого нам понадобится схема, представленная рис. 2.8, где:
M 
M n — главная нормаль,
C — центр кривизны траектории,
ρ — радиус кривизны траектории.
Предположим, что в момент времени t точка M имеет скорость 


Переходим к проекциям ускорения материальной точки на натуральные оси координат 
Учитывая, что проекции векторов на параллельные оси одинаковы, проведем через точку М1 оси М1

Найдем проекции векторов 


Подставим значения проекций в выражения. Будем иметь:
Когда промежуток времени Δt стремится к нулю, то
Тогда уравнение может быть записано, как показано ниже, и касательное ускорение равно:
Таким образом, касательное ускорение материальной точки характеризует изменение скорости по величине в единицу времени и равна первой производной от функции скорости по времени или второй производной от закона движения.
Определим нормальное ускорение an. Преобразуем выражение для нормального ускорения, умножив числитель и знаменатель на произведение ∆φ · ∆S:
Перепишем выражение следующим образом:
Подставим значение этих границ в выражение для нормального ускорения:
Нормальное ускорение материальной точки характеризует изменение скорости по направлению в единицу времени и равна квадрату скорости, разделенном на радиус кривизны траектории в данной точке.
Вектор нормального ускорения 
Нормальное ускорение an всегда положительное, так как содержит в числителе выражение 

и отрицательным.
Вектор полного ускорения 


Угол φ между вектором 
Вектор ускорения 





где 

Следует отметить, что составляющие вектора 
Некоторые случаи движения материальной точки
1. Прямолинейное движение.
Радиус кривизны траектории, которой является прямая линия, равна 
Таким образом, скорость 

А если это движение еще и равномерно, то есть, когда 
2. Равномерное криволинейное движение.
В данном случае модуль скорости 

Таким образом, как видно из приведенных выражений, полное ускорение a материальной точки в этом случае равно нормальному ускорению an.
Вектор нормального (в данном случае полного) ускорения 


3. Равнопеременное криволинейное движение.
В этом случае движение точки является криволинейным, но ускорение a
величиной постоянной. Этот случай носит название равнопеременного движения (то есть, когда за равные промежутки времени скорость движения материальной точки изменяется на одну и ту же величину, увеличивается или уменьшается).
Определим кинематические характеристики равнопеременного движения материальной точки. Поскольку a


dv = a 
Скорость 








где 
Используем далее выражение 
dS = 
Вместо 
dS = 

Как и в предыдущем случае найдем перемещения S, взяв определенные интегралы от левой и правой частей последнего выражения. Также задаем верхние и нижние границы переменных величин, причем перемещение точки изменяется от начального значения So до конечного S:
Окончательно последнее выражение можно переписать так
где So — начальное перемещение точки.
Таким образом, при равнопеременном движении материальной точки ее скорость и перемещения определяются с помощью найденных выражений. Следует заметить, что знаки в правых частях этих формул (перед a
Пример:
Палец кривошипа дизеля движется в соответствии заданных параметрически уравнений
где x и y — в метрах; t — в секундах; b и ω — постоянные величины.
Определить траекторию движения, скорость и ускорение пальца.
Решение.
Для определения уравнения траектории движения пальца кривошипа надо исключить из заданных уравнений движения параметр времени t. Сначала определим с заданных уравнений тригонометрические функции
Поскольку тригонометрические функции являются функциями одного аргумента, то
поднимем к квадрату левые и правые части этих выражений и добавим их почленно:
Левая часть последнего выражения равна единице, поскольку sin cos 1 2 февраля t t , тогда sin 2 ω t + cos 2 ω t = 1, тогда
Таким образом, с последнего выражения видно, что траекторией движения пальца кривошипа является окружность радиуса b с центром в начале координат.
Для определения скорости движения найдем сначала проекции скорости движения пальца на координатные оси:
Модуль скорости движения будет равняться
Таким образом, с последнего выражения видно, что палец движется с постоянной скоростью, равной bω.
Найдем ускорение пальца кривошипа. Также определим его через проекции на оси координат. Для этого возьмем другие производные от заданных координат движения:
Полное ускорение будет равно:
Поскольку палец кривошипа движется по кругу, то есть по криволинейной траектории движения устойчивого радиуса b, то его ускорение можно было бы определить, если использовать выражения, описывающие натуральный способ задания движения материальной точки. Касательное ускорение пальца кривошипа будет равняться нулю, поскольку скорость bω = const. А именно:
Нормальное ускорение определим так:
Поскольку касательного ускорения нет, то полное ускорение равно нормальному:
Таким образом, как видим, ускорение пальца кривошипа, которое определено различными способами, совпадают.
Пример:
Точка на ободе барабана зерноуборочного комбайна в период разгона движется согласно уравнению S = 0,1 · t 3 (S — в метрах, t — в секундах). Радиус барабана равен R = 0,5 м. Определить касательное и нормальное ускорение точки в момент, когда его скорость равна 
Решение.
Уравнения движения точки задано натуральным способом, а потому скорость можно определить так:
По заданному значению скорости под углом 
Касательное ускорение точки будет равно:
или через 10 сек
a
Нормальное ускорение определим так:
Знак «+» перед касательным ускорением a
Услуги по теоретической механике:
Учебные лекции:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Естественная форма записи уравнений движения точки
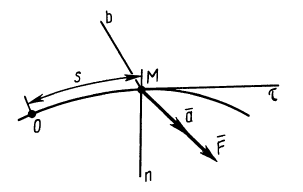
В тех случаях, когда траектория движения точки определена заранее, успешно используют в решении задач естественный способ задания движения точки. Уравнения движения точки, соответствующие данному способу, получим, проектируя обе части выражения основного закона динамики (11.1) на оси τ, n, b (рис. 12.2):
 | 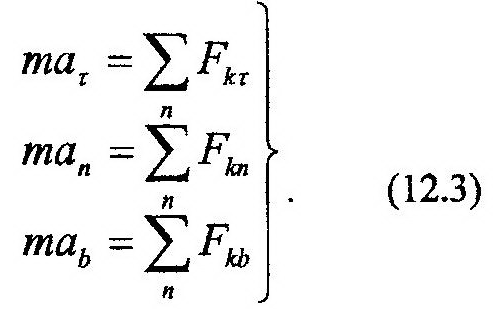 |
| получим: | Учитывая, что: |
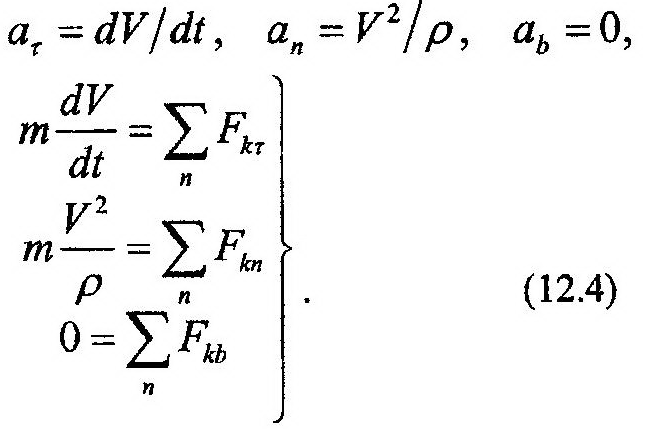 |
В (12.4) только в первые два уравнения входит кинематический параметр, характери-зующий движение точки, это – V. Последнее выражение в (12.4) по своему виду соответствует уравнению равновесия – уравнению статики. Из всех уравнений (12.4) только первое является дифференциальным. Таким образом, уравнения движения точки, соответствующие естественному способу, являются более простыми по своему виду. В этом их преимущество над уравнениями вида (12.2).
Задачи динамики
Все задачи динамики можно условно поделить на две группы: первая (прямая) и вторая (обратная) задачи. Условность деления заключается в том, что не все задачи один к одному соответствуют формулировкам, указанным ниже. Возможно и их сочетание в пределах одной задачи.
В прямых задачах: по известным уравнениям движения точки определяют силы,вызы-
Вающие его.
Таким образом, исходными для решения первой задачи динамики точки являются ее уравнения движения, записанные в одном из видов: векторном, координатном или естественном (см. тему: «способы задания движения точки»). Например, в координатной форме записи эти уравнения связывают координаты точки (x, y, z) с временем (t).
Алгоритм решения первой (прямой) задачи представлен ниже:
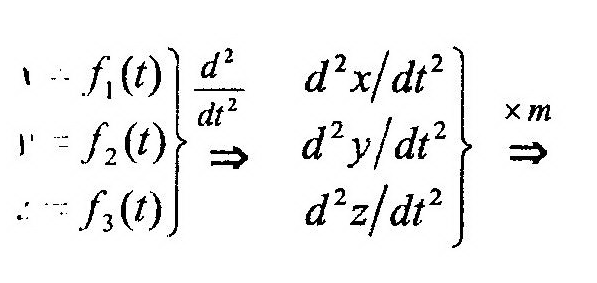 | 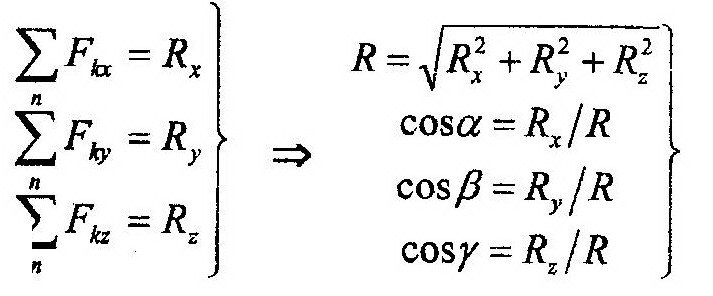 |
По известным уравнениям движения находят вторые производные от координат по времени и, умножая их на массу точки, m, определяют правые части выражений (12.2). Модуль равнодействующей, R, системы сходящихся сил, приложенных к точке, равен длине диагонали параллелепипеда, построенного на проекциях Rx, Ry, Rz как на сторонах. С помощью направляющих косинусов можно определить направление вектора равно-действующей в пространстве.
В обратных задачах: по известным силам, действующим на точку, и начальным усло-
Дата добавления: 2016-04-19 ; просмотров: 1120 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://natalibrilenova.ru/estestvennyij-sposob-zadaniya-dvizheniya-tochki/
http://helpiks.org/7-88886.html