Уравнение движения маятника вычислите циклическую частоту

Период колебаний математического маятника

Математический маятник — что это такое

Маятник — твердое тело, которое совершает под действием приложенных сил механические колебания около неподвижной точки или оси.

Простейший маятник состоит из небольшого груза массой m, подвешенного на невесомой нити или тонком стержне длиной l и совершающего колебания под воздействием земного притяжения. Если нить считать нерастяжимой, размер груза незначительным по сравнению с длиной нити, а массу нити незначительной по сравнению с массой груза, то груз можно считать материальной точкой массой m, находящейся на постоянном расстоянии l от точки подвеса. Такой маятник называют математическим.

Определение модели системы

Математические модели динамических систем часто используют для анализа самых разных технических, социально-экономических, естественнонаучных систем, в которых происходят циклические процессы.
Существуют различные классификации динамических процессов. Одна из них изображена на схеме:

Маятник Фуко

Маятник Фуко — подвес, плоскость колебаний которого со временем изменяется. Он был создан для экспериментальной демонстрации суточного вращения Земли. Впервые опыт, доказывающий, что Земля вращается, был проведен французским ученым Жаном Фуко в 1851 году в Парижской обсерватории. Маятник имел вид металлического шара массой 28 кг, подвешенного на нити длиной 67 м. Период его колебаний составлял 16,4 с.
Наблюдая за его колебаниями, можно было заметить, что плоскость, в которой они происходят, медленно поворачивается, причем в разных местах земного шара с различной скоростью. Она минимальна, т. е. равна нулю, на экваторе планеты, а максимальна — на ее полюсах.
Если мы обозначим период вращения Земли вокруг ее оси Т, а географическую широту местности — φ , тогда время t, за которое плоскость колебаний маятника совершает полный оборот, окажется равно

Отсюда следует, что если бы Земля не вращалась, данного эффекта просто не существовало бы. Это обстоятельство указывает на то, что причиной неинерциальности земной системы отсчета является вращение планеты.

Центробежное ускорение на экваторе равно 0 , 034 м / с 2 . По сравнению с экваториальным ускорением свободного падения g = 9 , 78 м / с 2 это величина малая, но она заметно влияет на изменение веса тела на экваторе по сравнению с его весом на полюсе. Если, например, взвешивать на пружинных весах тело массой 10 кг, то уменьшение веса на экваторе за счет действия центробежной силы составит около 35 г.

Период колебаний математического маятника

Период колебаний — время, за которое происходит одно полное колебание. В СИ измеряется в секундах.

Чему равен, от чего зависит частота

Если за время t совершается N колебаний, то период, обозначаемый буквой T, равен

где v — частота колебаний. Она обратно пропорциональна периоду.
Колебания можно изобразить в виде графика:

Источник: physik.ucoz.ru.
Период колебаний математического маятника можно рассчитать по формуле

g — ускорение свободного падения. Не зависит от амплитуды колебаний и массы груза.

Циклическая частота — число колебаний, которые система совершает за 2 π секунды. Также циклическую частоту называют угловой, круговой или радиальной. Кратко ее записывают греческой буквой ω . Она позволяет упростить расчеты с использованием радианов, так как при ее введении сокращаются множители 2 π .

В случае математического маятника она определяется длиной подвеса и ускорением свободного падения:

Для физического маятника в уравнение добавляются инерция и масса подвеса:

Для пружинного маятника частоту определяет жесткость пружины k:

Уравнения движения и их решение, формулы с примерами

Математический маятник — это материальная точка, имеющая массу m и подвешенная на нити с неизменяемой длиной l. Покидая положение равновесия, подвес совершает колебательные движения по дуге.

Источник: osu.ru.
Угловое ускорение ε — вторая производная от угла поворота α , вращающий момент относительно точки А создает только сила тяжести:

M = — m g × l sin α .

Угол отклонения мал, поэтому мы учитываем только то, что он отрицателен. Синус угла α считаем приблизительно равным α . Тогда:

m l 2 × α ‘ ‘ = — m g l α ;

Это дает нам дифференциальное уравнение гармонических колебаний

Из уравнения следует, что при малых углах отклонения от положения равновесия маятник будет колебаться с периодом

T = 2 π ω = 2 π l g .

Все кинематические характеристики движения меняются по гармоническим законам, т. е. по закону синуса или косинуса. Рассмотрим, от чего зависят константы амплитуды А и начальной фазы движения φ 0 .
Амплитуда колебаний определяется энергией, переданной маятнику при отклонении от положения равновесия. В случае пружинного маятника в крайнем положении скорость груза и кинетическая энергия равны нулю, полная энергия состоит только из потенциальной энергии:

E п о л н а я = k A 2 2 .

Из этого следует, что

А = 2 E п о л н а я k .

Начальная фаза зависит от того, как маятник вывели из положения равновесия. Рассмотрим ситуацию, в которой маятник отклонили от положения равновесия на расстояние А и отпустили без начальной скорости. Запишем уравнение движения колеблющегося тела с учетом того факта, что в начальный момент координата тела будет равна А:

x = A × cos ω t + φ 0 ;

x ( 0 ) = A × cos ω × 0 + φ 0 = A × cos φ 0 = А ⇒ cos φ 0 = 1 ⇒ φ 0 = 1 .

Уравнение движения маятника:

Если маятник толкнули, когда он находился в положении равновесия, начальная координата колеблющейся точки будет равна нулю:

x ( 0 ) = A × cos ω × 0 + φ 0 = A × cos φ 0 = 0 ⇒ cos φ 0 = 0 ⇒ φ 0 = ± π 2 .

Будет ли начальная координата положительной или отрицательной, определяет выбор положительного направления оси. Если направление оси совпадет с направлением начальной скорости, то в уравнении движения будет знак «плюс», если не совпадет — знак «минус».

Уравнение движения маятника:

x ( 0 ) = A × cos ω t ± π 2 = ± A × sin ω t .

Рассмотрим задачи, для которых требуется составлять и решать уравнения движения.

Необходимо определить амплитуду и частоту колебаний точки, если известно, что при смещении точки от положения равновесия на 5 см ее скорость равна 6 см/с, а при смещении на 3 см — 10 см/с.

x = A × cos ω t + φ 0 v x = x ‘ = — A ω × sin ω t + φ 0

Исключаем время из системы:

x = A × cos ω t + φ 0 v x = x ‘ = — A ω × sin ω t + φ 0 ⇒ x = A × cos ω t + φ 0 v x ω = — A × sin ω t + φ 0 ⇒ x 2 = A 2 × cos 2 ω t + φ 0 v 2 ω 2 = A 2 × sin 2 ω t + φ 0

x 2 + v 2 ω 2 = А 2 .

x 2 А 2 + v 2 v 2 m a x = 1 .

x 1 2 + v 1 2 ω 2 = А 2 x 2 2 + v 2 2 ω 2 = А 2

Преобразовав выражения и подставив значения, данные в условиях задачи, получаем:

ω = v 2 2 — v 1 2 x 1 2 — x 2 2 = 2 c — 1 ;

A = x 1 2 v 2 2 — x 2 2 v 1 2 v 1 2 — v 2 2 ≈ 5 , 57 с м ;

v = ω 2 π ≈ 0 , 32 Г ц .

Необходимо вычислить циклическую частоту колебаний точки, если известно, что при скорости 13 см/с ускорение равнялось 6 с м / с 2 , а при уменьшении скорости до 12 см/с произошло увеличение ускорения до 10 с м / с 2 .

Решение:
Координата точки меняется по закону

Запишем уравнения скорости и ускорения точки:

v x = — A × ω × sin ω t a x = — A × ω 2 × cos ω t ⇒ v x A ω = — sin ω t a x A ω 2 = — cos ω t ⇒ v 2 ω 2 + a 2 ω 4 = A 2 .

Преобразуем уравнение, исключив из него А, и подставим значения, данные в условиях задачи:

ω = a 2 2 — a 1 2 v 1 2 — v 2 2 = 1 , 6 c — 1 .

Практическое применение математического маятника

С помощью математического моделирования динамических систем можно обнаружить схожесть динамических процессов в реальных физических, технических, биологических, химических и социально-экономических системах. Разработка моделей, позволяющих предсказывать время и другие характеристики периодических процессов в этих системах, является эффективным способом анализировать, например, сельскохозяйственные или производственно-экономические процессы.

Циклическая частота колебаний

Мерой колебательного движения служит циклическая (или угловая, или круговая) частотой колебаний.

Это скалярная физическая величина.

Циклическая частота при гармонических колебаниях

Пусть колебания совершает материальная точка. При этом материальная точка через равные промежутки времени проходит через одно и то же положение.

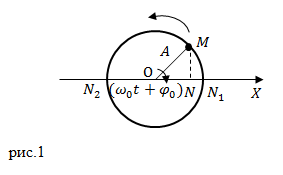
Самыми простыми колебаниями являются гармонические колебания. Рассмотрим следующую кинематическую модель. Точка M с постоянной по модулю скоростью ($v$) движется по окружности радиуса A. В этом случае ее угловую скорость обозначим $<\omega >_0$, эта скорость постоянна (рис.1).

Проекция точки $M$ на диаметр окружности (точка $N$), на ось X, выполняет колебания от $N_1$ до $N_2\ $и обратно. Такое колебание N ,будет гармоническим. Для описания колебания точки N необходимо записать координату точки N, как функцию от времени ($t$). Пусть при $t=0$ радиус OM образует с осью X угол $<\varphi >_0$. Через некоторый промежуток времени этот угол изменится на величину $<\omega >_0t$ и будет равен $<\omega >_0t+<\varphi >_0$, тогда:

Выражение (1) является аналитической формой записи гармонического колебания точки N по диаметру $N_1N_2$.

Обратимся к выражению (1). Величина $A$ — это максимальное отклонение точки, совершающей колебания, от положения равновесия (точки О — центра окружности), называется амплитудой колебаний.

Параметр $<\omega >_0$ — циклическая частота колебаний. $\varphi =(<\omega >_0t+<\varphi >_0$) — фаза колебаний; $<\varphi >_0$ — начальная фаза колебаний.

Циклическую частоту гармонических колебаний можно определить как частную производную от фазы колебаний по времени:

При $<\varphi >_0=0$, уравнение колебаний (1) преобразуется к виду:

Если начальная фаза колебаний равна $<\varphi >_0=\frac<\pi ><2>$ , то получим уравнение колебаний в виде:

Выражения (3) и (4) показывают, что при гармонических колебаниях абсцисса $x$ — это функция синус или косинус от времени. При графическом изображении гармонических колебаний получается косинусоида или синусоида. Форма кривой определена амплитудой колебаний и величиной циклической частоты. Положение кривой зависит от начальной фазы.

Циклическую частоту колебаний можно выразить через период (T) колебаний:

Циклическую частоту с частотой $?$$?$ свяжем выражением:

Единицей измерения циклической частоты в Международной системе единиц (СИ) является радиан, деленный на секунду:

Размерность циклической частоты:

Частные случаи формул для вычисления циклической частоты

Груз на пружине (пружинный маятник — идеальная модель) совершает гармонические колебания с круговой частотой равной:

$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.

Малые колебания физического маятника будут приблизительно гармоническими колебаниями с циклической частотой равной:

где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.

Примером физического маятника является математический маятник. Круговая частота его колебаний равна:

где $l$ — длина подвеса.

Угловая частота затухающих колебаний находится как:

где $\delta $ — коэффициент затухания; в случае с затуханием колебаний $<\omega >_0$ называют собственной угловой частотой колебаний.

Примеры задач с решением

Задание: Чему равна циклическая частота гармонических колебаний, если максимальная скорость материальной точки равна $<\dot>_=10\ \frac<см><с>$, а ее максимальное ускорение $<\ddot>_=100\ \frac<см><с^2>$?

Решение: Основой решения задачи станет уравнение гармонических колебаний точки, так как из условий, очевидно, что они происходят по оси X:

Скорость колебаний найдем, используя уравнение (1.1) и кинематическую связь координаты $x$ и соответствующей компоненты скорости:

Максимальное значение скорости (амплитуда скорости) равна:

Ускорение точки вычислим как:

Из формулы (1.3) выразим амплитуду, подставим ее в (1.5), получим циклическую частоту:

Вычислим циклическую частоту:

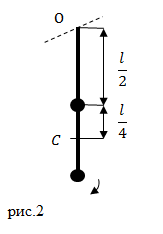
Задание: На длинном невесомом стержне закреплены два груза одинаковой массы. Один груз находится на середине стержня, другой на его конце (рис.2). Система совершает колебания около горизонтальной оси, проходящей через свободный конец стрежня. Какова циклическая частота колебаний? Длина стержня равна $l$.

Решение: Основой для решения задачи является формула нахождения частоты колебаний физического маятника:

где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника. Масса маятника по условию задачи состоит из масс двух одинаковых шариков (масса одного шарика $\frac<2>$). В нашем случае расстояние $a$ равно расстоянию между точками O и C (см. рис.2):

Найдем момент инерции системы из двух точечных масс. Относительно центра масс (если ось вращения провести через точку C), момент инерции системы ($J_0$) равен:

Момент инерции нашей системы относительно оси, проходящей через точку О найдем по теореме Штейнера:

Подставим правые части выражение (2.2) и (2.4) в (2.1) вместо соответствующих величин:

Колебательное движение. Математический маятник

п.1. Механические колебания

Кроме прямолинейного и криволинейного движения, с которыми мы уже познакомились, существует еще один вид механического движения – колебательный.

Примеры колебательных движений:

• движение маятника в часах;
• колебание автомобиля на рессорах;
• покачивание деревьев на ветру;
• раскачивание качели;
• сокращения сердца и легких;
• движение крыльев насекомых и птиц.

п.2. Математический маятник

В положении равновесия тело (шарик) находится внизу. Отклонение от положения равновесия называют смещением тела, обозначают буквой x и измеряют в метрах (в СИ). Наибольшее смещение маятника от положения равновесия называют амплитудой колебаний, обозначают буквой A. В проекции на горизонтальную ось OX смещение изменяется в интервале \(-A\leq x\leq A\). В положении равновесия x=0. Если маятник после смещения в положение 1, прошел положение равновесия 2, отклонился в положение 3, опять прошел положение 2, и вернулся в положение 1, говорят, что маятник совершил полное колебание.

п.3. Параметры колебаний математического маятника

Период и частота колебаний – взаимно обратные величины
Период в СИ измеряют в секундах, частоту – в герцах: 1 Гц=1 c -1
Формула для периода колебаний справедлива для небольших отклонений маятника (на угол порядка 15-20° от положения равновесия).

п.4. Задачи

Задача 1. Маятник совершил 3 полных колебания за 9 с. Найдите период и частоту его колебаний. Чему равна длина нити, на которой подвешен маятник (ответ дайте в см, с округлением до целых)?

Дано:
\(N=3\)
\(t=9\ c\)
__________________
\(T,\ f,\ L-?\)
Период колебаний: \(T=\frac tN\)
Частота колебаний: \(f=\frac 1T=\frac Nt\)
Длина нити: $$ T=2\pi\sqrt<\frac Lg>\Rightarrow \sqrt<\frac Lg>=\frac<2\pi>\Rightarrow \frac Lg=\left(\frac<2\pi>\right)^2\Rightarrow L=g\left(\frac<2\pi>\right)^2 $$ Подставляем: \begin T=\frac 93=3\ (c)\\ f=\frac 13\ (Гц)\\ L=9,8\cdot\left(\frac<3><2\pi>\right)^2\approx 2,234\ (м)\approx 223\ (см) \end Ответ: 3 с; 1/3 Гц; 223 см

Задача 2. Математический маятник колеблется с частотой 20?тиы кГц. Найдите период колебаний и число колебаний в минуту.

Дано:
\(f=20\ кГц=2\cdot 10^4\ Гц\)
\(t=1\ мин=60\ с\)
__________________
\(T,\ N-?\)
Период колебаний: \(T=\frac 1f\)
Частота колебаний за время \(t:\ N=ft\)
Подставляем: \begin T=\frac<1><2\cdot 10^4>=0,5\cdot 10^<-4>\ (c)=50\cdot 10^<-6>\ (c)=50\ (мкс)\\ N=2\cdot 10^4\cdot 60=1,2\cdot 10^6 \end Ответ: 50 мкс; 1,2·10 6

Задача 3. Расстояние от улья до цветочного поля 600 м. Пчела летит за нектаром со скоростью 8 м/с и машет крылышками с частотой 440 Гц. Возвращаясь в улей с нектаром, пчела летит со скоростью 5 м/с и машет крылышками с частотой 320 Гц. Найдите разность в количестве взмахов крылышками на пути туда и обратно.

Время полета из улья за нектаром \(t_1=\frac\)
Количество взмахов крылышками \(N_1=f_1 t_1=f_1\frac\)
Аналогично количество взмахов на пути назад \(N_2=f_2\frac\)
Найдем каждое из \(N\): \begin N_1=440\cdot\frac<600><8>=33000\\ N_2=320\cdot\frac<600><5>=38400 \end На пути обратно пчела с грузом делает больше взмахов. Искомая разность: $$ \triangle N=N_2-N_1=38400-33000=5400 $$ Ответ: 5400

Задача 4. Определите длину математического маятника с периодом колебаний 1с, если он находится: а) на Луне (\(g_л=1,6\ м/с^2\)); б) на Марсе (\(g_м=3,6\ м/с^2\)). Ответ запишите в см, с точностью до десятых.

Длина нити: \begin T=2\pi\sqrt<\frac Lg>\Rightarrow\sqrt <\frac Lg>=\frac<2\pi>\Rightarrow\frac Lg=\left( \frac<2\pi>\right)^2\Rightarrow L = g\left(\frac<2\pi>\right)^2 \end На Луне: $$ L_л=1,6\cdot\left(\frac<1><2\pi>\right)^2\approx 0,0405\ (м)\approx 4,1\ (см) $$ На Марсе: $$ L_м=3,6\cdot\left(\frac<1><2\pi>\right)^2\approx 0,0912\ (м)\approx 9,1\ (см) $$ Ответ: 4,1 см; 9,1 см

п.5. Лабораторная работа №4. Исследование колебаний математического маятника

Цель работы
Исследовать, от каких величин зависит период колебаний математического маятника.

Теоретические сведения
При малых отклонениях (порядка 15-20° от вертикали) период колебаний математического маятника определяется формулой: $$ T=2\pi\sqrt <\frac Lg>$$ где \(L\) – длина маятника, \(g\) – ускорение свободного падения.
Для работы принять \(g\approx 9,80665\ м/с^2\).
При заданном периоде колебаний для длины маятника получаем: $$ L=g\left(\frac<2\pi>\right)^2 $$

Приборы и материалы
Два лабораторных грузика по 100 г, крепкая нить (1,5-2 м), линейка (30-50 см), штатив, секундомер.

Ход работы
1. Рассчитайте длину нитей, необходимых для создания маятников с периодами колебаний \(T_1=1 с;\ T_2=2 с\).
2. Закрепите один грузик на нити и подвесьте его на штативе так, чтобы длина подвеса была равна расчетной длине \(L_1\).
3. Отклоните грузик на небольшой угол, отпустите его и с помощью секундомера измерьте время, за которое маятник совершит 10 полных колебаний. Повторите опыт 5 раз. Проведите расчеты для определения периода колебаний \(T_<1\ эксп>\) по методике, изложенной в лабораторной работе №2 (см. §4 данного справочника).
4. Теперь подвесьте грузик так, чтобы длина подвеса была равна расчетной длине \(L_2\). Повторите серию из 5 экспериментов и определите \(T_<2\ эксп>\).
5. При длине подвеса \(L_2\) подвесьте к первому грузику второй. Повторите серию из 5 экспериментов и определите \(T ‘\). Сравните \(T ‘\) и \(T_<2\ эксп>\).
6. Сделайте выводы о проделанной работе.

Результаты измерений и вычислений

Расчет длины нитей \begin L=g\left(\frac<2\pi>\right)^2\\ T_1=1\ c,\ \ L_1=9,80665\cdot\left(\frac<1><2\pi>\right)^2\approx 0,248\ (м)=24,8\ (см)\\ T_2=2\ c,\ \ L_1=9,80665\cdot\left(\frac<2><2\pi>\right)^2\approx 0,9994\ (м)=99,4\ (см) \end

Определение \(T_<1\ эксп>\)
Инструментальная погрешность секундомера \(d=\frac<\triangle><2>=0,1\ c\)
Время 10 колебаний

\begin t_=\frac<50><5>=10\\ \triangle_=\frac 15=0,2 \end Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ \triangle t=max\left\\right\>=max\left\<0,1;0,2\right\>=0,2\ \text $$ Результат измерения времени 10 колебаний: \begin t=t_0\pm\triangle t,\ \ t=(10,0\pm 0,2)\ c \end Период колебаний в 10 раз меньше: $$ T_<1\ эксп>=\frac<1><10>(t_0\pm\triangle t),\ \ T_<1\ эксп>=(1,00\pm 0,02)\ c $$ Относительная погрешность измерений: $$ \delta_T=\frac<\triangle T>>\cdot 100\text<%>=\frac<0,02><1>\cdot 100\text<%>=2,0\text <%>$$

Определение \(T_<2\ эксп>\)
Время 10 колебаний

\begin t_=\frac<99,5><5>=19,9\\ \triangle_=\frac 15=0,2 \end Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ \triangle t=max\left\\right\>=max\left\<0,1;0,2\right\>=0,2\ \text $$ Результат измерения времени 10 колебаний: \begin t=t_0\pm\triangle t,\ \ t=(19,9\pm 0,2)\ c \end Период колебаний в 10 раз меньше: $$ T_<2\ эксп>=\frac<1><10>(t_0\pm\triangle t),\ \ T_<2\ эксп>=(1,99\pm 0,02)\ c $$ Относительная погрешность измерений: $$ \delta_T=\frac<\triangle T>>\cdot 100\text<%>=\frac<0,02><1,99>\cdot 100\text<%>\approx 1,0\text <%>$$

Определение \(T ‘\) (с двумя грузиками)
Время 10 колебаний

\begin t_=\frac<99,8><5>=19,96\\ \triangle_=\frac<1,24><5>\approx 0,25 \end Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ \triangle t=max\left\\right\>=max\left\<0,1;0,25\right\>=0,25\ \text $$ Результат измерения времени 10 колебаний: \begin t=t_0\pm\triangle t,\ \ t=(19,96\pm 0,25)\ c \end Период колебаний в 10 раз меньше: $$ T’=\frac<1><10>(t_0\pm\triangle t),\ \ T’=(1,996\pm 0,025)\ c $$ Относительная погрешность измерений: $$ \delta_T=\frac<\triangle T>\cdot 100\text<%>=\frac<0,025><1,996>\cdot 100\text<%>\approx 1,3\text <%>$$

Полученные на опыте интервалы для \(T_<2\ эксп>\) и \(T’\) (одинаковая длина нити \(L_2\) и разные массы грузиков – 100 г и 200 г соответственно): \begin 1,97\leq T_<2\ эксп>\leq 2,01\\ 1,971\leq T’\leq 2,021 \end Таким образом, \(T_<2\ эксп>\approx T’\), т.е. период колебаний математического маятника не зависит от массы груза.

Выводы
На основании проделанной работы можно сделать следующие выводы.

В работе с помощью расчетной формулы были определены длины нитей подвеса для маятников с периодами колебаний \(T_1=1\ с;\ T_2=2\ с\).
Полученный на опыте период колебаний для подвеса с \(L_1=24,8\ см\) с грузиком 100 г равен $$ T_<1\ эксп>=(1,00\pm 0,02)\ c,\ \ \delta=2,0\text <%>$$ Полученный на опыте период колебаний для подвеса с \(L_2=99,4\ см\) с грузиком 100 г равен $$ T_<2\ эксп>=(1,99\pm 0,02)\ c,\ \ \delta=1,0\text <%>$$ Полученный на опыте период колебаний для подвеса с \(L_2=99,4\ см\) с грузиком 200 г равен $$ T’=(1,996\pm 0,025)\ c,\ \ \delta=1,3\text <%>$$ Формула \(T=2\pi\sqrt<\frac Lg>\) данными экспериментами подтверждена.
Период колебаний математического маятника зависит от длины подвеса и не зависит от массы грузика на подвесе.