Уравнение движения механизма в конечной форме

УРАВНЕНИЕ ДВИЖЕНИЯ МЕХАНИЗМА

После выполнения приведения сил и масс, любой механизм с одной степенью подвижности можно заменить его динамической моделью (рисунки 4.1; 4.5). Эта модель имеет переменный приведенный момент инерции I_пр и приведенный момент М_пр. Закон движения модели такой же, как и закон движения начального звена (уравнение 4.1).

Основой для составления уравнения движения механизма служит теорема об изменении кинетической энергии

, (4.8)

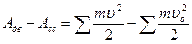
где υ – скорость в конце движения, υ_о – скорость в начале движения, А_дв – работа движущих сил, А_сс – работа сил сопротивления. При этом работу совершают все силы и моменты, а также силы трения.

Уравнение движения в энергетической форме. Если привести все силы и массы к звену приведения, то уравнение примет вид

, (4.9)

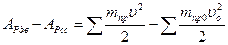
где А_Рдв – работа приведенной к звену приведения движущей силы, А_Рсс – работа приведенной силы сопротивления, m_пр и m_пр0 — приведенные массы, соответствующие конечному и начальному положениям.

Обычно удобнее в левую часть уравнения вводить работу приведенных моментов А_Мдв и М_Рсс, а правую часть выражать через приведенные моменты инерции I_пр и I_пр0. Тогда выражение (4.9) примет вид

. (4.10)

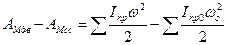
Уравнение движения в дифференциальной форме.Уравнение движения механизмов машинного агрегата запишем через приведенные силы и массы, для чего продифференцируем уравнение (4.9)

, (4.11)

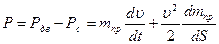
где Р_дв – движущая силы, Р_с – сила сопротивления.

То же самое уравнение можно записать, если воспользоваться приведенным моментом и приведенным моментом инерции, для чего продифференцируем уравнение (4.10)

. (4.12)

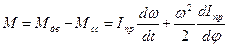
Уравнение движения в интегральной форме.В дифференциальное уравнение движения механизма машинного агрегата входят приведенные моменты движущих сил и сил сопротивления. Эти моменты могут быть функциями обобщенной координаты φ или ее первой производной φ’ = ω, или времени t. Тогда уравнение (4.12) запишем в виде

. (4.13)

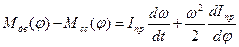
Интегрируя данное выражение по обобщенной координате, получим

. (4.14)

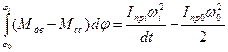
Уравнение движения механизма

Выполнив приведение сил и масс, любой механизм с одной степенью свободы (рычажный, зубчатый, кулачковый и др.), сколь бы сложным он ни был, можно заменить его динамической моделью (рис. 5.2). Эта модель в общем случае имеет переменный приведенный момент инер- ции и к ней приложен суммарный приведенный момент . Закон движения модели такой же, как и закон движения начального звена механизма (см. 5.1).

Рис. 5.2. Динамическая модель механизма с W = 1

после приведения сил и масс

Основой для составления уравнения движения механизма с одной степенью свободы служит теорема об изменении кинетической энергии:

Работу совершают все активные силы и моменты и силы трения во всех кинематических парах механизма.

Уравнение движения в энергетической форме. Запишем формулу для кинетической энергии модели, учитывая уравнение (5.1):

(5.3)

Так как вся нагрузка, приложенная к модели, выражается суммарным приведенным моментом , то сумма работ равна

_(5.4)

Здесь переменная интегрирования φ_м заменена координатой φ₁ начального звена, так как φ_м = φ₁.

Подставив выражения (5.4) в (5.2), получим уравнения движения в энергетической форме:

_(5.5)

где искомой величиной является угловая скорость φ₁ начального звена механизма.

В общем случае верхний предел φ₁ интегрирования в равнении (5.5) считается переменным. Если вся нагрузка, приложенная к механизму, зависит только от его положения, то и суммарный приведенный момент есть функция только координаты φ₁. В этом случае уравнение (5.5) решается непосредственно относительно искомой величины ω₁:

(5.6)

Укажем, что интеграл под корнем имеет знак, который необходимо учитывать.

Уравнение движения в дифференциальной форме.

Продифференцируем (5.5) по координате φ₁:

Определим производную, стоящую в левой части уравнения, помня, что в общем случае переменной величиной является не только угловая скорость ω₁, но и . Поэтому

(5.7)

Это и есть уравнение движения в дифференциальной форме, поскольку искомая переменная величина – угловая скорость ω₁ начального звена механизма – стоит под знаком производной. При пользовании уравнением (5.7) следует помнить, что суммарный приведенный момент , а также производная d/dφ₁ величины алгебраические и подставляются со своими знаками.

В том случае, когда исследуется механизм, имеющий = const (например, зубчатый механизм с круглыми центроидами), уравнение его движения упрощается и приобретает вид

(5.8)

Уравнение движения в дифференциальной форме (5.7) может быть получено также и из уравнения Лагранжа второго рода.

Для определения углового ускорения ₁ начального звена используем уравнение (5.7) и решаем его относительно

(5.9)

Величины и d/dφ₁ подставляются в уравнение (5.9) со своими знаками. Если угловое ускорение ₁ получится со знаком, противоположным знаку угловой скорости ω₁, значит, начальное звено механизма движется замедленно.

Производную d/dφ₁ подсчитывают численным дифференцированием или графическим дифференцированием. Необходимо отметить, что существует другой значительно более точный (но и более трудоемкий) способ определения производной d/dφ₁ , который можно найти в специальной литературе.

Уравнения движения механизма

Уравнения движения механизма

Выполнив приведение сил и масс, любой механизм с одной степенью свободы (рычажный, зубчатый, кулачковый и др.), сколь бы сложным он ни был, можно заменить его динамической моделью (рис. 7.1). Эта модель в общем случае имеет переменный приведенный момент инерции и к ней приложен суммарный приведенный момент . Закон движения модели такой же, как и закон движения начального звена механизма (см. уравнение 7.1).

(7.1)

Работу совершают все активные силы и моменты и силы трения во всех кинематических парах механизма.

Уравнение движения в энергетической форме. Запишем формулу для кинетической энергии модели, учитывая уравнение (7.1):

Рекомендуемые файлы

. (7.2)

Так как вся нагрузка, приложенная к модели, выражается суммарным приведенным моментом , то сумма работ равна

(7.3)

Здесь переменная интегрирования заменена координатой начального звена, так как

Учитывая (5.16) и подставив выражения (7.2) и (7.3) в основное уравнение (7.1), получим уравнение движения в энергетической форме:

(7.4)

где искомой величиной является угловая скорость начального звена механизма. В общем случае верхний предел интегрирования в уравнении (7.4) считается переменным.

Если вся нагрузка, приложенная к механизму, зависит только от его положения, то и суммарный приведенный момент есть функция только координаты . В этом случае уравнение (7.4) решается непосредственно относительно искомой величины :

(7.5)

Укажем, что интеграл под корнем имеет знак, который надо учитывать.

Уравнение движения в дифференциальной форме. Продифференцируем уравнение (7.4 по координате :

Определим производную, стоящую в левой части уравнения, помня, что в общем случае переменой величиной является не только угловая скорость , но и . Поэтому:

(7.6)

Это и есть уравнение движения в дифференциальной форме, поскольку искомая переменная величина — угловая скорость начального звена механизма — стоит под знаком производной. При пользовании уравнением (7.6) надо помнить, что суммарный приведенный момент , а также производная суть величины алгебраические и подставляются со своими знаками.

В том случае, когда исследуется механизм, имеющий (например, зубчатый механизм с круглыми колесами), уравнение его движения упрощается и приобретает такой вид:

(7.7)

Уравнение движения в дифференциальной форме (7.6) может быть получено также и из уравнений Лагранжа II рода [2], [4].

Для определения углового ускорения начального звена используем уравнение (7.6), решим его относительно :

(7.8)

Величины и подставляются в уравнение (7.8) со своими знаками. Если угловое ускорение получится со знаком, противоположным знаку угловой скорости , то это значит, что начальное звено механизма движется замедленно.

Производная подсчитывается или численным дифференцированием на ЭВМ, или графическим дифференцированием (см. § 4.2). Другой значительно более точный (но и более трудоемкий) способ определения производной можно найти в литературе

(см.: Минут С. Б. Об определении производной приведенного момента инерции массы звеньев механизма// Науч. тр. МВТУ им. Н. Э. Баумана, 1970; Зиновьев В. А., Бессонов А. П. Основы динамики машинных агрегатов. М., 1964).

Основные режимы движения машины.

При установившемся режиме III скорость главного вала изменяется периодически. В частном случае скорость может быть постоянной. В установившемся режиме работает большинство энергетических и технологических машин. Часто установившееся движение чередуется с разгонами (при повышениях скоростного режима II) и торможениями (при понижениях скоростного режима IV). Так работают, например, автомобильный двигатель и различные другие транспортные машины. Многие механизмы в установившемся режиме вообще не работают. Это особенно характерно для целого ряда приборов (реле, контакторы и т. п.). Их механизм во время срабатывания (режим VI) переходит из одного положения в другое, не совершая замкнутого повторяющегося кинематического цикла.

Неустановившийся режим движения машины имеет место тогда, когда ее пускают в ход и она, набирая скорость, выходит на установившийся режим, а также тогда, когда для остановки машины ее двигатель выключают и она продолжает двигаться за счет накопленного запаса кинетической энергии; при этом машина постепенно теряет скорость из-за действия сил трения или каких-либо других сил сопротивления, в том числе и специальных тормозных сил. В этих случаях необходимо знать, насколько быстро происходят переход из неподвижного состояния в рабочее и обратный переход до полной остановки. Применительно к транспортным машинам изучение обратного перехода особенно важно для надежного расчета длины тормозного пути. Исследование неустановившегося режима движения дает возможность определить время срабатывания механизма, что абсолютно необходимо для проектирования многих приборов, таких, как фотозатворы, средства автоматической защиты и др.

Разгоны (разбеги) и торможения могут происходить с большим ускорением. Это вызывает значительное динамическое нагружение механизма, что, в свою очередь, может привести к перенапряжениям и даже к поломкам.

Во время разбега и выбега угловая скорость многих машин проходит через критическую (резонансную) зону. Во избежание динамической перегрузки механизма и возможной аварии проход этой зоны должен быть достаточно быстрым, что надо обеспечить при проектировании, сделав расчет обеих фаз неустановившегося режима. Решение многих других динамических задач также связано с исследованием этого режима.

Таким образом, изучение неустановившихся (переходных) процессов весьма существенно для грамотного динамического проектирования механизма, машины или прибора.

Для определения закона движения механизма при неустановившемся режиме должны быть известны следующие исходные данные: кинематическая схема механизма; характеристики геометрии масс всех подвижных звеньев; механические характеристики сил и моментов; начальные условия движения. Последнее важно для исследования именно неустановившегося режима.

Рассмотрим механизм, нагруженный силами и моментами, которые являются функциями только перемещения своих точек приложения. Пусть приведенный момент инерции рассматриваемого механизма имеет переменную величину . Требуется определить зависимость скорости начального звена от его угла поворота, т. е. . Подобная задача является весьма распространенной. В качестве примеров можно привести механизмы дизель-компрессоров, буровых станков и подъемных кранов с приводом от двигателей внутреннего сгорания, различных устройств с пневмоприводом, приборов с пружинными двигателями и др.

Неустановившееся движение механизма

(переходные режимы работы)

Способами, изложенными в предыдущих лекциях строим диаграммы и , таким образом динамическая задача сводится к следующей: известны зависимости и , требуется определить закон изменения угловой скорости и углового ускорения звена приведения (модели).

Для решения данной задачи нужно взять уравнение движения, составленное в энергетической форме:

(7.9)

Порядок определения искомой угловой скорости таков:

1. Выполняют приведение масс и строят суммарную диаграмму приведенного момента инерции ;

2. По механическим характеристикам строят диаграммы приведенного движущего момента, затем диаграмму суммарного приведенного момента

Если силы тяжести и силы трения значительны, то их приведенные моменты должны войти слагаемыми в величину , т.е.

3. Графическим интегрированием строим диаграмму работы суммарного приведенного момента.

По уравнению (7.9) c учетом начальных условий определяют угловую скорость начального звена (модели) и строят зависимость

Если , то (7.10)

Если , то

Для определения углового ускорения начального звена (модели) используем уравнение движения, составленное в дифференциальной форме и решим его относительно

(7.11)

из уравнения видно, что для подсчета величины необходимо знать и в том положении начального звена, для которого определяется , а также нужно знать зависимость , по которой находят

Производную определяют графическим дифференцированием

Следует напомнить что величины и подставляют в уравнение (7.11) со своими знаками. Заметим, что графическое дифференцирование зависимости вносит некоторую ошибку во второй член уравнения.

Для тихоходных машин второй член уравнения (7.11) мал по сравнению с первым, поэтому ошибка существенного значения не имеет.

Для быстроходных машин второе слагаемое, зависящее от квадрата угловой скорости, может быть весьма значительным. В этом случае следует точно определить производную путем использования передаточных функций скоростей и ускорений (предложенных Минутом С.Б.), угловое ускорение величина алгебраическая.

Существует другой менее точный, но более простой способ определения , основанный на применении диаграммы = — метод поднормалей.

(7.12)

где — масштаб углового ускорения, = (по построению)

Величина и знак производной определяются по диаграмме аналогично определению производной

— угол наклона касательной, проведенной к кривой , с положительным направлением оси x.

(7.13)

Определение продолжительности переходного процесса

Рассмотрим построение кривой времени (рис. 7.5) по заданной диаграмме . При интегрировании обратной функции применяем метод трапеций. В пределах выбранных участков 01, 12,… кривую заменяем ступенчатым графиком с ординатами . Величины указанных ординат определяются из условия равенства площадей криволинейных трапеций и соответствующих прямоугольников. Ординаты и т.д. переносим на ось ординат, затем и на отрицательную полуось абцисс и получаем точки 1’, 2’,… i’. Отложив на оси ординат отрезок интегрирования К, соединяем точки 1’, 2’,… i’ с концом отрезка интегрирования. На диаграмме в пределах каждого участка проводим линии, параллельные линиям 1’K, 2’K,… i’K и т.д. Через точки 0, 1”, 2”…i” проводим кривую, которая является кривой времени , в масштабе мм/с. Масштаб вычисляем из равенства углов на кривой и .