Уравнение движения планет солнечной системы

Законы движения планет

В начале 17 века немецкий математик и астроном Иоганн Кеплер вывел три закона движения планет в Солнечной системе. Они были выведены на основании наблюдений за небесными телами, сделанных Браге и другими исследователями космического пространства того времени.

Первый закон Кеплера

Кеплер обратил внимание, что результаты наблюдений Браге расходятся с представлениями о круговой траектории обращения планет вокруг Солнца. Особенно это касалось Марса, чья траектория движения по наблюдения датчанина никак не могла описывать идеальный круг. Браге был очень точен в своих расчетах и сомнений в их правдивости у его последователя не возникло.

Тогда немецкий математик принял орбиты за эллипсы, у каждого из которых есть два фокуса. Это условные точки, выбранные таким образом, что сумма расстояний от них до любой точки эллипса – величина постоянная. При этом для эллиптической орбиты в одном из фокусов находится Солнце.

Форма эллипса вычисляется благодаря отношению фокального расстояния к большой полуоси орбиты. Полученное значение описывает эксцентриситет орбиты. Если он равен нулю – орбита представляет собой идеальную окружность, от нуля до единицы – эллипс различной вытянутости, больше единицы – параболу.

Второй закон Кеплера

Если орбита – это эллипс, то каким образом происходит движение небесного тела по ней? В каких отрезках орбитального пути оно ускоряется и замедляется?

Немецкий ученый обнаружил, что есть взять два любых отрезка орбитального пути, которые планета Солнечной системы проходит за одинаковые промежутки времени, провести от их концов радиус-векторы к центральной звезде, то площади полученных образований будут одинаковы. Это упрощенная формулировка второго закона.

Для того, чтобы постоянство площадей сохранялось, тело должна двигаться в разных точках орбиты с разной скоростью. Так, например, Земля в наибольшем приближении к Солнцу движется быстрее, чем в максимальном удалении от него

Третий закон Кеплера

Третий постулат о движении небесных тел в Солнечной системе как раз касается понятий перигелия и афелия. Если провести между ними условную линию, получится большая ось траектории обращения планеты. Соответственно, половина этого отрезка – большая полуось.

Кеплер на основании наблюдений вывел, что отношение полных оборотов вокруг центральной звезды для двух любых планет системы, возведенных в квадрат, всегда равняется отношению больших полуосей орбитальных путей этих тел, возведенных в куб.

Трудность в доказательстве и принятии трех законов состояла в том, что он вывел их эмпирически. Но в конце 17 века Ньютоном был открыта классическая теория тяготения. Он и помог установить правильность суждений немецкого астронома и описал движение планет по эллипсу вокруг Солнца. Ньютон установил, что кроме массы объекта и его удаления от звезды никакие другие свойства не влияют на гравитационное притяжение.

Также Ньютон внес корректировки и в третий постулат Кеплера. Он открыл, что для соблюдения соотношения необходимо учитывать массу космического объекта. Данная трактовка третьего закона помогает установить массу планеты или спутника, зная величину его орбиты и период обращения.

Законы Иоганна Кеплера помогли установить форму планетарной траектории, вычислить период обращения планет, их скорость и ее изменения по мере приближения и удаления от Солнца. Ученый вывел Землю из ранга особенных астрономических объектов системы и установил, что она подчиняется всем трем законом, как и любая другая планета нашей звездной системы.

Расчет положения небесных тел на небосводе. Часть 1

Не так давно очень активно обсуждалась тема Марса. В то время у меня возник вопрос от которого в силу своего наивного любопытства я никак не мог избавится: «Где Марс находится в данный момент, в какой стороне?» и смежный с ним: «Да и вообще, как определить положение остальных планет?». Очевидно, что траектории движения планет относительно земли будут весьма хитрыми. Конечно, можно воспользоваться планетариями, например таким, но как вы уже поняли, это не наш путь.

В данном цикле статей, я постараюсь максимально просто рассказать о сложном. В результате мы напишем простую программу, которая подскажет где искать планеты нашей Солнечной системы для любой заданной точки на поверхности земли в заданный момент времени. Своей целью я ставлю донести читателю суть того, что скрывается за Кеплеровой моделью орбиты, поэтому я не буду использовать никакие общеизвестные факты кроме законов Ньютона и закона всемирного тяготения.

Всех любопытных прошу под кат.

Стоит отметить, что дальнейшее изложение подразумевает, что читатель немного знаком с законами Ньютона, основными сведениями из геометрии, векторной алгебры и дифференциального исчисления.

Так как же движутся планеты?

В реальности, если учитывать взаимное влияние планет, смещение центра тяжести солнечной системы относительно центра тяжести солнца и т.д. движение планет окажется чрезвычайно сложным и не поддающимся строгому аналитическому определению. Стоит отметить что даже задача о движении трех тел не может быть решена аналитически. Поэтому давайте сразу оговорим в рамках каких моделей мы будем работать. Мы будем рассматривать Кеплерову модель орбиты. Существует большое множество других моделей, но все они являются полуаналитическими и в итоге большинство из них сводится к определению параметров Кеплеровой орбиты в интересующий момент времени. Другими словами, Кеплерова орбита является аппроксимацией сложного движения планеты в заданный момент времени. Кеплеровы параметры орбит планет можно посмотреть здесь nssdc.gsfc.nasa.gov/planetary/factsheet, там же указана эпоха (другими словами момент времени) в момент которой данные параметры Кеплеровой орбиты дают точное положение небесного тела. Обычно этим исходным моментом времени является эпоха J2000.0 (полдень 1 января 2000 года). Расчет движения тел на небольшой промежуток времени при помощи Кеплеровой модели является достаточно точным. Точности вполне хватит, чтобы не заметить ошибку визуально или в небольшой телескоп. Конечно, для расчета траектории полета к другой планете нужны более точные модели.

Кеплерова орбита

Итак, по порядку. Начнем с основных допущений данной модели. Предполагается, что масса Солнца много больше массы всех планет вместе взятых, откуда можно сделать вывод, что взаимодействие между планетой и планетой пренебрежимо мало по сравнению с взаимодействием между солнцем и планетой. Таким образом, поставленную задачу можно свети к задаче о взаимодействии двух тел (т.е. можно рассмотреть взаимодействии каждой планеты с солнцем отдельно). Более того предполагаем, что масса планеты много меньше массы Солнца, то взаимодействие получается одностороннее, т.е. планета никак не влияет на движение Солнца. Таким образом, мы можем рассматривать планету, как материальную точку, движущуюся в гравитационном поле, центр которого неподвижен. Примерно так:

Гравитационное взаимодействие

Что такое гравитационное взаимодействие? Это универсальное фундаментальное взаимодействие между всеми материальными телами. О гравитации можно говорить много и долго, но нам нужен только ключевой момент. Согласно классической теории тяготения Ньютона, сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть: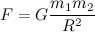

Здесь — G гравитационная постоянная (некий коэффициент пропорциональности). Нам важно отметить лишь то, что сила гравитации направлена от центра тяжести одного тела к центру тяжести другого и обратно пропорциональна квадрату расстояния между ними (закон обратных квадратов).
Отметим, что на нашу сферическую планету в вакууме материальную точку не действует никакая другая сила, кроме силы притяжения со стороны Солнца. В нашем случае, поле сил тяготения является центральным полем сил. В центральное поле сил, направление силы действующей на тело в любой точке такого поля, всегда проходит через центр этого поля (в нашем случае через центр тяжести солнца), а величина такой силы зависит только от расстояния до этого центра.

Второй закон Ньютона

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Такая формулировка хоть и менее точная (нужно сделать оговорки про системы отчета, но нас это пока не интересует), но куда более понятная. Под количеством движения здесь понимается так называемый импульс тела, равный произведению массы тела на его скорость: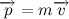

Таким образом, запишем словесную формулировку в символьном виде: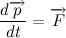

Или же если мы распишем, чему равен импульс тела и вынесем массу как константу (масса не всегда константа, но в нашем случае это так) за знак дифференциала то получим следующую всем известную формулу:

Где вектор — ускорении тела. Не забываем, что ускорение, импульс, скорость и сила величины векторные. Давайте условимся, что если над векторной величиной стоит знак вектора, то понимается именно вектор, в противном случае его модуль.

Второй закон Кеплера

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Да знаю, «получили закон» звучит не хорошо, но что поделаешь, он так называется. Причина в том, что Кеплер его не выводил, а интуитивно подобрал на основе своих наблюдений, т.е. получил его эмпирическим путем, в этом случае это действительно был закон.
Ниже приведена иллюстрация данного закона (рисунок взят из статьи на википедии).

Дифференциальное уравнение орбиты

Давайте все же подробнее рассмотрим векторное произведение радиус вектора на скорость. Радиус вектор можно представить в виде произведения модуля радиус вектора (расстояние от начала координат до точки) на вектор единичной длины, совпадающий по направлению с радиус вектором: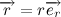


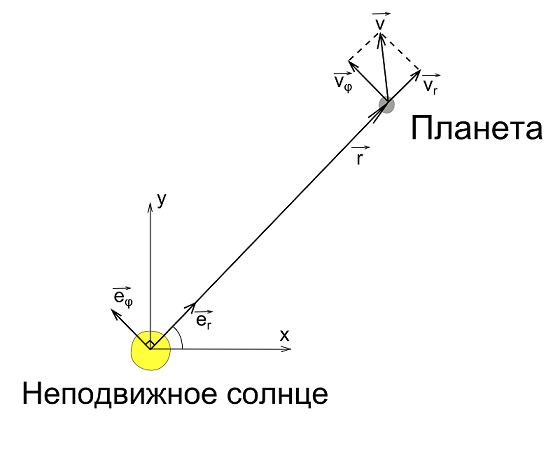
Тогда вектор скорости будет равен: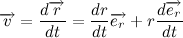

А векторное произведение радиус вектора на скорость в свою очередь: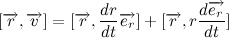

Учитывая тот факт, что вектора и совпадают по направлению, а следовательно совпадают по направлению и вектора и , получаем, что . Тогда:

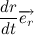
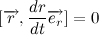
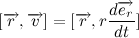
Давайте разберем, что такое производная единичного вектора по времени:

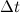
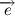
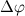
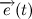
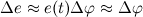
Из рисунка видно, что за время вектор поворачивается на угол . Разность векторов и равна вектору . Для малых углов справедливо следующее соотношение:

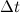
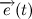
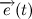
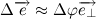
В пределе, когда устремляется к нулю, направления векторов и совпадают, а направление вектора перпендикулярно к ним. Введем единичный вектор , перпендикулярный к и совпадающий с направлением движения его конца, тогда:

Таким образом, переходя к пределу, получим: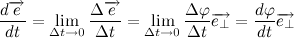

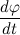
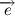
Где это угловая скорость вектора . Обозначим
Вернемся к нашему произведению радиус вектора на скорость, учитывая, что получим:

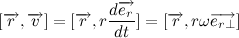
Несложно заметить, что вектора и взаимно перпендикулярны. Введем еще один единичный вектор , который перпендикулярен к векторам и . Таким образом, вектора , и образуют ортонормированный базис. Исходя из определения векторного произведения, получим:

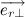
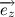
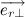
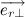
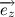
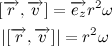
Следовательно, 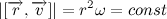. Введем обозначение, . Так же стоит отметить, что:

Вернемся к второму закону ньютона. Вектор силы действующей на тело распишем сразу как величину гравитационной силы, умноженную на орт :

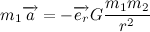
Где m₁ и m₂ — масса планеты и солнца соответственно.
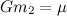
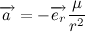
Давайте на массу планеты сразу сократим, и нигде далее про массу планеты вспоминать не будем, так как она совершенно не влияет на траекторию движения. Будем считать, что мы работаем с телом единичной массы. Введем обозначение, , тогда:

Теперь давайте распишем вектор ускорения: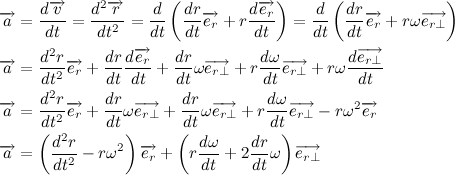

Рассмотрим содержимое второй скобки: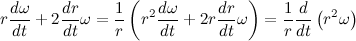

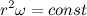
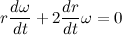
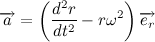
Но мы уже знаем, что , отсюда следует, что , тогда:

Введем обозначение . Напомню, что раннее мы ввели обозначение , очевидно, что .
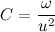
Теперь распишем производную от модуля радиус вектора через С: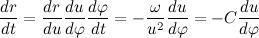

Теперь распишем вторую производную от модуля радиус вектора через С: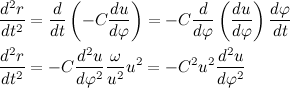

Учитывая полученный результат, перепишем выражение для вектора ускорения: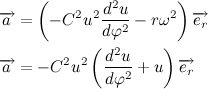

Тогда второй закон Ньютона примет вид: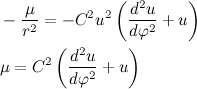

Перепишем полученное дифференциальное уравнение в более привычный вид: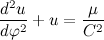

Я думаю многие из вас догадались, что представляет из себя полученное дифференциальное уравнение, но я пожалуй закончу на этом первую часть чтобы не перегружать читателя и себя.

Мы получили дифференциальное уравнение, описывающее траекторию движения материальной точки в гравитационном поле, которое вполне применимо для описания траектории планет и некоторых других небесных тел.

Что нам еще предстоит

В полученном дифференциальном уравнении отсутствует временной параметр, поэтому мы ничего не знаем о характере движения, поэтому необходимо как-то привязаться ко времени. Также далее будут рассмотрены различные системы координат и их преобразования для того чтобы получить координаты планет в системе привязанной к наблюдателю.

Законы Кеплера

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

В микромире при взаимодействии элементарных частиц – атомов, молекул – ядерные и электромагнитные взаимодействия являются главенствующими. Наблюдать гравитационное взаимодействие элементарных частиц практически невозможно. Ученым приходится прибегать к очень большим ухищрениям для того, чтобы измерить гравитационное взаимодействие тел, масса которых составляет сотни, тысячи килограмм. Однако в космических масштабах все остальные взаимодействия, кроме гравитационного, практически незаметны. Движение планет, спутников, астероидов, комет, звезд в галактике полностью описывается гравитационным взаимодействием.