Уравнение движения планеты вокруг солнца

Закон Кеплера

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Форма Земли

Сейчас нам сложно представить, что раньше люди верили, будто Земля плоская. У греков, например, плоскость просто парила в воздухе и была окружена ледниками. А в Индии верили, что планета покоится на трех слонах, которые стоят на черепахе. Впрочем, кое-кто до сих пор так думает. Доказательств того, что наша планета на самом деле не плоская — много, но вот вам парочка, чтобы можно было поддержать светскую беседу.

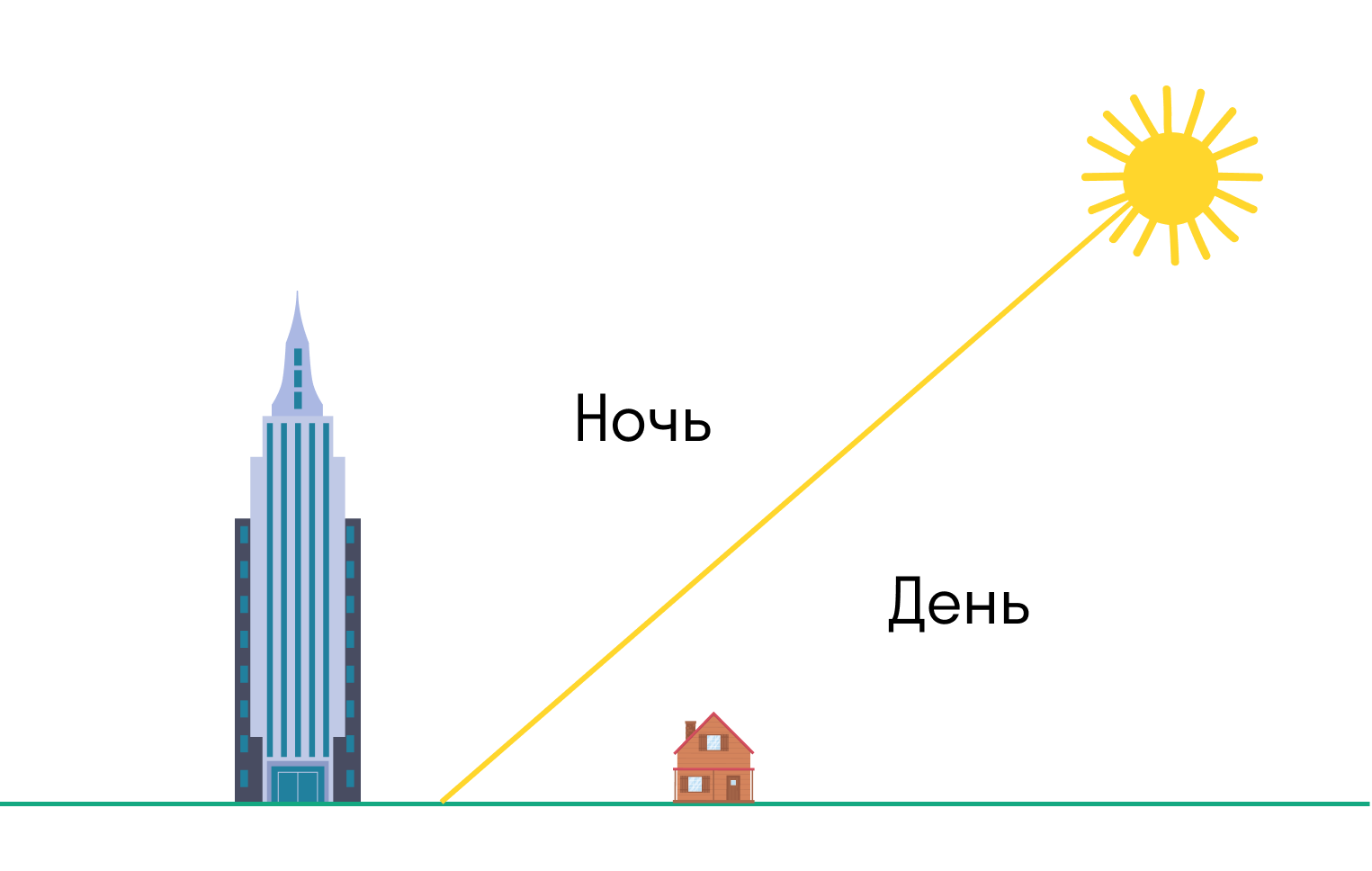
Смена дня и ночи

По представлениям приверженцев плоской Земли, день и ночь сменяются, потому что Луна и Солнце вращаются над Землей — вот как-то так:

Но — упс! — эта модель вызывает целый ряд вопросов:

Почему длина дня и ночи меняется в течение года?

Чем объясняется цвет заката и восхода?

Почему иногда мы можем увидеть Луну и Солнце одновременно?

Почему Луна и Солнце не появляются каждый раз из одной и той же точки?

Если нет гравитационного притяжения, почему они вообще крутятся?

Лунные затмения

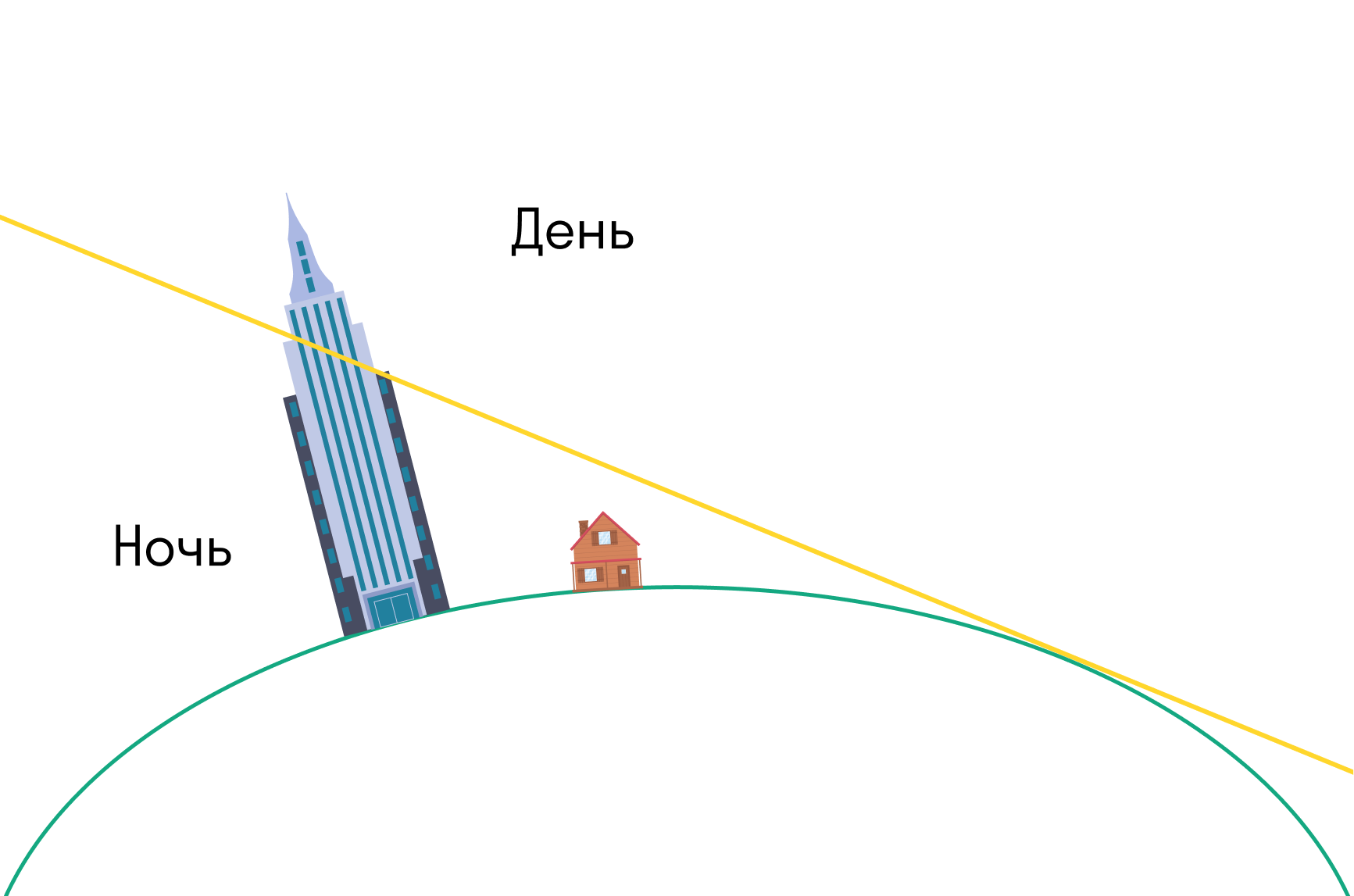
Если Земля плоская, то непонятно, как объяснить лунные затмения. Чтобы затмение произошло, нужно, чтобы Солнце находилось по одну сторону от диска, а Луна — по другую. Тогда ломается концепция дня и ночи, которую мы описали выше, ведь день и ночь будут наступать для всей Земли одновременно.

На плоскую Землю свет от Солнца падал бы, как свет от фонаря. То есть высокие объекты в противоположном от Солнца направлении после заката оставались бы в тени.

А на шарообразной Земле небоскребы или горы будут освещены Солнцем после заката или перед рассветом.

Именно это вы увидите, если застанете рассвет или закат в горах — или посмотрите на фотографии.

Окей, Земля все-таки не плоская — с этим разобрались. Но и шаром ее назвать нельзя: Земля имеет форму эллипсоида.

Эллипсоид — это такой приплюснутый шар, в одном из сечений у которого эллипс. Именно по траектории эллипса вращаются все спутники.

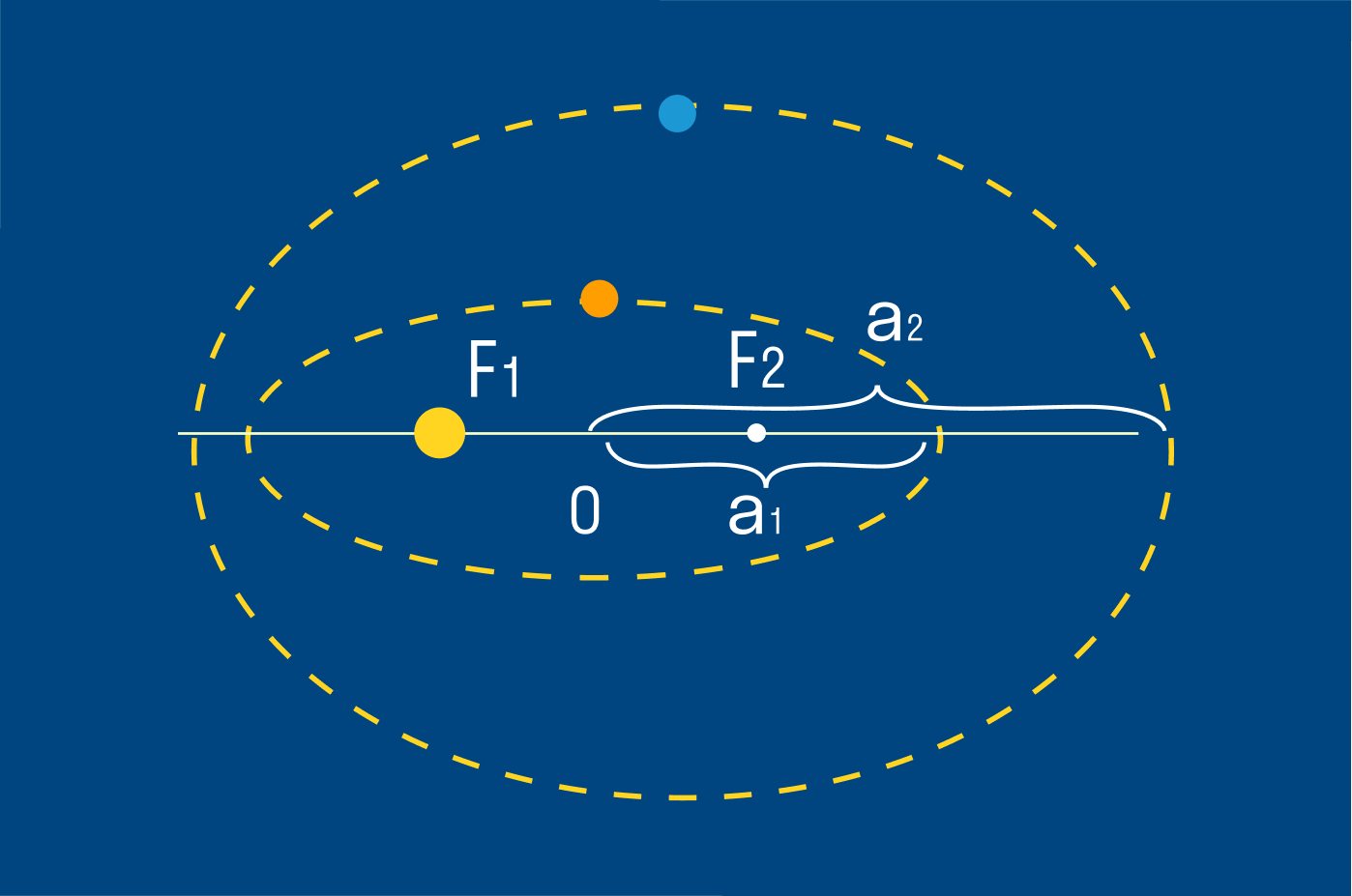
Эллипс

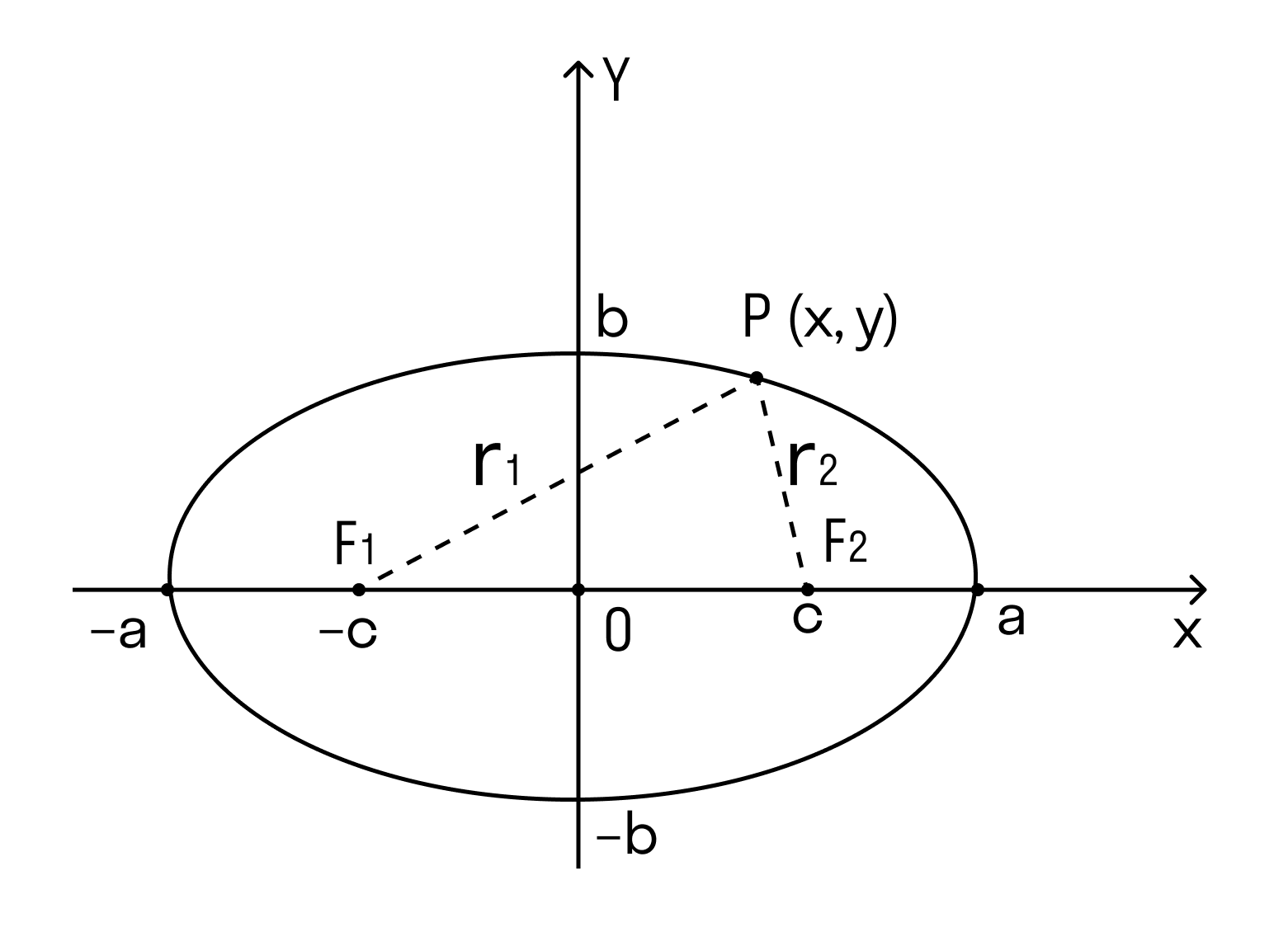
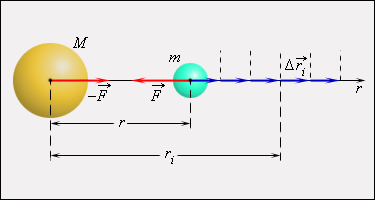
Эллипс — это замкнутая прямая на плоскости, частный случай овала. У эллипса две оси симметрии — горизонтальная и вертикальная, которые состоят из двух полуосей.

А еще у эллипса два фокуса — это такие точки, сумма расстояний от которых до любой точки P(x,y) является постоянной величиной.

Эллипс

F₁ и F₂ — фокусы

с — половина расстояния между F₁ и F₂

a — большая полуось

b — малая полуось

r₁ и r₂ — фокальные радиусы

Теперь мы знаем все необходимые понятия, чтобы разобраться, в чем состоят законы Кеплера.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

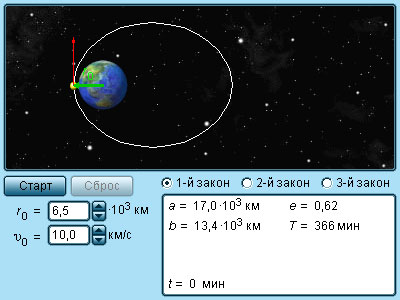
Первый закон Кеплера

Каждая планета солнечной системы вращается вокруг Солнца по эллипсоидной орбите, в одном из фокусов которого находится Солнце.

Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка B траектории называется перигелием, а точка A, наиболее удаленная от Солнца — афелием.

Первый закон Кеплера достаточно простой, но важный, так как в свое время он сильно продвинул астрономию. До этого открытия астрономы считали, что планеты движутся исключительно по круговым орбитам. Если же наблюдения противоречили этому убеждению, ученые дополняли главное круговое движение малыми кругами, которые планеты описывали вокруг точек основной круговой орбиты. Кеплер получил доступ к огромной базе наблюдений Тихо Браге и, изучив их, перешагнул старые идеи.

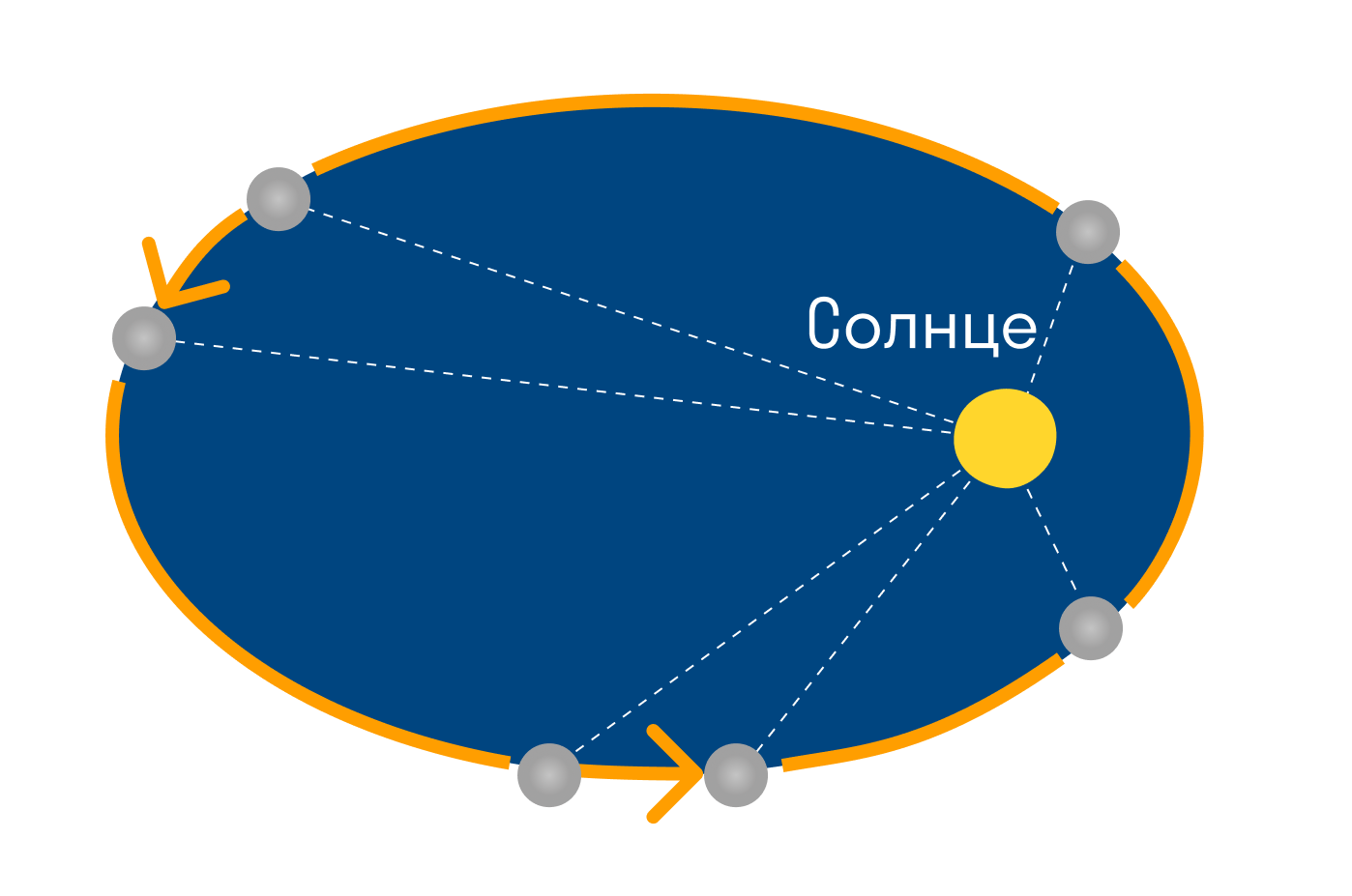
Второй закон Кеплера (закон площадей)

Радиус-вектор, соединяющий планету и Солнце, описывает в равные промежутки времени равные площади.

Каждая планета перемещается в плоскости, проходящей через центр Солнца. За равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Таким образом, тела движутся вокруг Солнца неравномерно: в перигелии они имеют максимальную скорость, а в афелии — минимальную.

На практике это можно заметить по движению Земли. Ежегодно в начале января наша планета проходит через перигелий и перемещается быстрее. Из-за этого движение Солнца по эклиптике (линии, показывающей путь Солнца по небу) также происходит быстрее, чем в другое время года. В начале июля Земля движется через афелий, из-за чего Солнце по эклиптике перемещается медленнее. Поэтому световой день летом длиннее, чем зимой.

Третий закон Кеплера

Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.

Согласно третьему закону Кеплера, между периодом обращения планет вокруг Солнца и большими полуосями их орбит устанавливается связь. Этот закон выполняется как для планет, так и для спутников с погрешно­стью менее 1%.

Третий закон Кеплера

T₁ и T₂ — периоды обращения двух планет [c]

a₁ и a₂ — большие полуоси орбит планет [м]

На основании этого закона можно вычис­лить продолжительность года (времени полного оборота вокруг Солнца) любой планеты, если известно ее расстояние до Солнца в афелии.

Также можно проделать обратное — рассчитать орбиту, зная период обращения.

Закон всемирного тяготения

Законы Кеплера — это результаты наблюдений и обобщений. Впоследствии они легли в основу закона всемирного тяготения, который звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Формула силы тяготения согласно этому закону выглядит так:

Закон всемирного тяготения

F — сила тяготения [Н]

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

G = 6,67 · 10 −11 м 3 · кг −1 · с −2

Ньютон был первым исследователем, который пришел к выводу, что между любыми телами в космосе действуют гравитационные силы, и именно они определяют характер движения этих тел.

Первая и вторая космические скорости

Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.

В серии книг Дугласа Адамса «‎Автостопом по Галактике»‎ говорится, что летать — это просто промахиваться мимо Земли. Чтобы промахнуться мимо Земли и стать ее искусственным спутником, нужно достичь первой космической скорости 7,9 км/с. Вот как это происходит:

Искусственный спутник Земли — космический летательный аппарат, который вращается вокруг Земли по геоцентрической орбите. Чтобы у него это получалось, аппарат должен иметь начальную скорость, которая равна или больше первой космической.

Первая космическая скорость

v₁ — первая космическая скорость [м/с]

g — ускорение свободного падения на данной планете [м/с 2 ]

R — радиус планеты [м]

На планете Земля g ≈ 10 м/с 2 .

Есть еще вторая и третья космические скорости. Вторая космическая скорость — это скорость, которая нужна, чтобы корабль стал искусственным спутником Солнца, а третья — чтобы вылетел за пределы солнечной системы.

Вторая космическая скорость

v₂ — вторая космическая скорость [м/с]

g — ускорение свободного падения на данной планете [м/с 2 ]

Законы Кеплера

Гравитационное взаимодействие проще всего наблюдать на космических объектах, обладающих огромной массой. В окружающей нас повседневности действие гравитации между предметами наблюдать сложно, даже если вес предметов составляет сотни и тысячи килограммов. В микромире силы гравитационного взаимодействия малы настолько, что ими можно пренебречь, потому на первый план выходят другие виды взаимодействий между элементарными частицами и атомами.

Гравитация удерживает живых существ и предметы на поверхности планеты, определяет характер движения планет вокруг Солнца. Именно гравитационное воздействие определяет тот факт, что планеты удерживаются вокруг своих звезд, а спутники не могут уйти в космическое пространство и продолжат движение по орбите вокруг своей планеты.

Закон всемирного тяготения или как его еще называют, теория гравитации, был открыт именно при наблюдении за планетами Солнечной системы.

Если наблюдать за движением небесных тел с Земли, то может показаться, что все эти тела движутся по сложной траектории. Так, например, древний ученый Птолемей, первооткрыватель законов движения планет, поместил Землю в центр вселенной и предположил, что другие планеты и звезды движутся вокруг Земли по большим и малым орбитам.

Рисунок 1 . 24 . 1 . Условное изображение наблюдаемого движения Марса на фоне неподвижных звезд.

Законы движения планет, установленные Птолемеем никем из исследователей не оспаривалась на протяжении 14 веков и только в середине 16 столетия была заменена Коперником на гелиоцентрическую систему, согласно которой все планеты движутся вокруг Солнца.

На основе гелиоцентрической системы объяснить траектории движения небесных тел стало намного проще. На основании трудов Коперника и наблюдений за движением планет астронома из Дании Браге немецкий астроном Кеплер сформулировал три эмпирических закона движения планет в Солнечной системе.

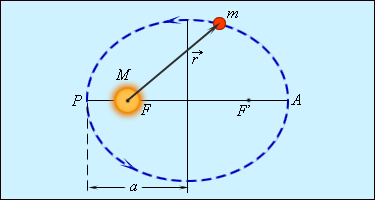
Первый закон Кеплера

Планеты Солнечной системы движутся по эллиптическим орбитам. В одном из фокусов такой орбиты находится Солнце.

Мы проиллюстрировали первый закон Кеплера рисунком. На нем изображена планета, чья масса меньше массы звезды. Звезда находится в одном из фокусов эллипса, по которому движется планета. Точкой Р мы обозначили ближайшую к звезде траекторию, носящая название перигелия. Точка А – это наиболее удаленная от звезды точка траектории, которая называется афелием. Большая ось эллипса располагается между точками афелии и перигелия.

Рисунок 1 . 24 . 2 . Эллиптическая орбита планеты массой m M . a – длина большой полуоси, F и F ‘ – фокусы орбиты.

В Солнечной системе все планеты за исключением Плутона движутся по орбитам, которые близки к круговым.

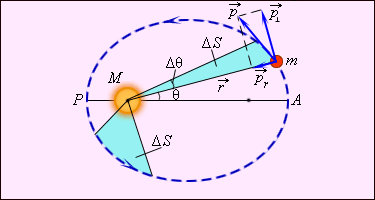
Второй закон Кеплера, или закон площадей

Радиус-вектор планеты описывает в равные промежутки времени равные площади.

Рисунок 1 . 24 . 3 . Закон площадей – второй закон Кеплера.

Эквивалентом второго закона Кеплера можно считать закон сохранения момента импульса. На рисунке, расположенном выше, изображен вектор импульса тела p → и составляющие его p r → и p ⊥ → . Площадь, заметенная радиус-вектором за малое время Δ t , приближенно равна площади треугольника с основанием r Δ θ и высотой r :

∆ S = 1 2 r 2 ∆ θ или ∆ S ∆ t = 1 2 r 2 ∆ θ ∆ t = 1 2 r 2 ω ; ( ∆ t → 0 ) .

Здесь ω = ∆ θ ∆ t ; ( ∆ t → 0 ) – угловая скорость.

Момент импульса L по абсолютной величине равен произведению модулей векторов p r → и p ⊥ → :

L = r p ⊥ = r ( m v ⊥ ) = m r 2 ω так как v ⊥ = r ω .

Из этих отношений следует:

∆ S ∆ t = L 2 m , ∆ t → 0

Поэтому, если по второму закону Кеплера ∆ S ∆ t = co n s t , то и момент импульса L при движении остается неизменным.

В частности, поскольку скорости планеты в перигелии v P → и афелии v A → направлены перпендикулярно радиус-векторам r P → и r A → из закона сохранения момента импульса следует:

r P v p = r A u A

Третий закон Кеплера

Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.

Формула третьего закона Кеплера имеет вид:

T 2 a 3 = c o n s t или T 1 2 a 1 3 = T 2 2 a 2 3

Точность, с которой третий закон Кеплера выполняется для всех планет, составляющих Солнечную систему, составляет выше 1 % .

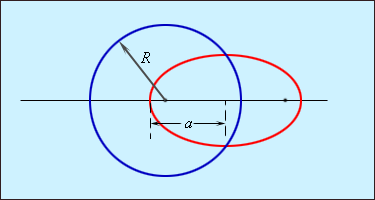
На рисунке изображены две орбиты, по которым небесные тела движутся вокруг звезды. Одна из орбит круговая с радиусом R , а другая – эллиптическая с большой полуосью a . Если R = a , то согласно третьему закону Кеплера периоды обращения планет по таким орбитам будут одинаковы.

Рисунок 1 . 24 . 4 . Круговая и эллиптическая орбиты. При R = a периоды обращения тел по этим орбитам одинаковы.

Рисунок 1 . 24 . 5 . Модель законов Кеплера.

Законы Кеплера очень долго были правилами, полученными эмпирически на основе наблюдений за движением небесных тел. Для того, чтобы получить возможность опираться на них в создании рабочих теорий, не хватало теоретического обоснования законов.

Таким обоснованием стало открытие закона всемирного тяготения Исааком Ньютоном:

Закон всемирного тяготения:

где M и m – массы Солнца и планеты, r – расстояние между ними, G = 6 , 67 · 10 – 11 Н · м 2 / к г 2 – гравитационная постоянная.

Ньютон был первым из исследователей, кто пришел к выводу о том, что между любыми телами в космосе действуют гравитационные силы, которые и определяют характер движения этих тел. Частным случаем такого взаимодействия является сила тяжести, воздействующая на тела, расположенные на поверхности и вблизи планет.

Для круговых орбит первый и второй закон Кеплера выполняются автоматически, а третий закон утверждает, что T 2

R 3 , где Т – период обращения, R – радиус орбиты. Отсюда можно получить зависимость гравитационной силы от расстояния. При движении планеты по круговой траектории на нее действует сила, которая возникает за счет гравитационного взаимодействия планеты и Солнца:

ω 2 R = 2 π 2 R T 2 .

Свойство консервативности гравитационных сил позволяет ввести понятие потенциальной энергии. Для сил всемирного тяготения удобно потенциальную энергию отсчитывать от бесконечно удаленной точки.

Потенциальная энергия тела массы m , находящегося на расстоянии r от неподвижного тела массы M , равна работе гравитационных сил при перемещении массы m из данной точки в бесконечность.

Математическая процедура вычисления потенциальной энергии тела в гравитационном поле состоит в суммировании работ на малых перемещениях.

Рисунок 1 . 24 . 6 . Вычисление потенциальной энергии тела в гравитационном поле.

Закон всемирного тяготения применим не только к точеным массам, но и к сферически симметричным телам. Работа ∆ A i гравитационной силы F → на малом перемещении ∆ s i → = ∆ r i → есть:

∆ A i = — G M m r i 2 ∆ r i

Полная работа при перемещении тела массой m из начального положения в бесконечность находится суммированием работ Δ A i на малых перемещениях:

В пределе при Δ r i → 0 эта сумма переходит в интеграл. В результате вычислений для потенциальной энергии получается выражение:

E p = A r ∞ = — G M m r

Знак «минус» указывает на то, что гравитационные силы являются силами притяжения.

Если тело находится в гравитационном поле на некотором расстоянии r от центра тяготения и имеет некоторую скорость v , его полная механическая энергия равна

E = E k + E p = m v 2 2 — G M m r = c o n s t

В соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной.

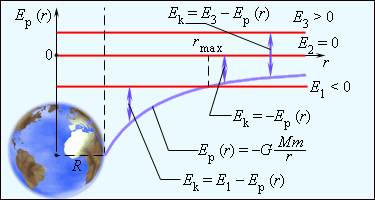
Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела (рис. 1 . 24 . 6 ).

При E = E 1 0 тело не может удалиться от центра притяжения на расстояние r > r m a x . В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы).

Рисунок 1 . 24 . 7 . Диаграмма энергий тела массой m в гравитационном поле, создаваемом сферически симметричным телом массой M и радиусом R .

При E = E 2 = 0 тело может удалиться на бесконечность. Скорость тела на бесконечности будет равна нулю. Тело движется по параболической траектории.

При E = E 3 > 0 движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии.

Первая и вторая космические скорости

Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.

Первой космической скоростью называется скорость движения спутника по круговой орбите вблизи поверхности Земли.

m v 1 2 R 3 = G M m R 3 2 = g m , отсюда v 1 = G M R 3 = g R 3 = 7 , 9 · 10 3 м / с .

Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории.

E = m v 2 2 2 — G M m R 3 = 0 , отсюда v 2 = 2 G M R 3 = 2 g R 3 = 11 , 2 · 10 3 м / с .

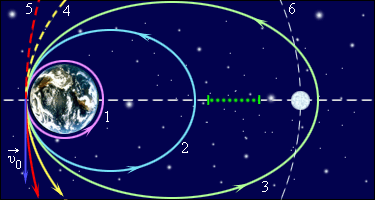
Мы проиллюстрировали понятие первой и второй космической скорости рисунком. Если скорость космического корабля равна v 1 = 7 . 9 · 10 3 м / с и направлена параллельно поверхности Земли, то корабль будет двигаться по круговой орбите на небольшой высоте над Землей. При начальных скоростях, превышающих v 1 , но меньших υ 2 = 11 , 2 · 10 3 м / с , орбита корабля будет эллиптической. При начальной скорости v 2 корабль будет двигаться по параболе, а при еще большей начальной скорости – по гиперболе.

Рисунок 1 . 24 . 8 . Космические скорости. Указаны скорости вблизи поверхности Земли. 1 : v = v 1 – круговая траектория; 2 : v 1 v v 2 – эллиптическая траектория; 3 : v = 11 , 1 · 10 3 м / с – сильно вытянутый эллипс; 4 : v = v 2 – параболическая траектория; 5 : v > v 2 – гиперболическая траектория; 6 : траектория Луны.

Расчет положения небесных тел на небосводе. Часть 1

Не так давно очень активно обсуждалась тема Марса. В то время у меня возник вопрос от которого в силу своего наивного любопытства я никак не мог избавится: «Где Марс находится в данный момент, в какой стороне?» и смежный с ним: «Да и вообще, как определить положение остальных планет?». Очевидно, что траектории движения планет относительно земли будут весьма хитрыми. Конечно, можно воспользоваться планетариями, например таким, но как вы уже поняли, это не наш путь.

В данном цикле статей, я постараюсь максимально просто рассказать о сложном. В результате мы напишем простую программу, которая подскажет где искать планеты нашей Солнечной системы для любой заданной точки на поверхности земли в заданный момент времени. Своей целью я ставлю донести читателю суть того, что скрывается за Кеплеровой моделью орбиты, поэтому я не буду использовать никакие общеизвестные факты кроме законов Ньютона и закона всемирного тяготения.

Всех любопытных прошу под кат.

Стоит отметить, что дальнейшее изложение подразумевает, что читатель немного знаком с законами Ньютона, основными сведениями из геометрии, векторной алгебры и дифференциального исчисления.

Так как же движутся планеты?

В реальности, если учитывать взаимное влияние планет, смещение центра тяжести солнечной системы относительно центра тяжести солнца и т.д. движение планет окажется чрезвычайно сложным и не поддающимся строгому аналитическому определению. Стоит отметить что даже задача о движении трех тел не может быть решена аналитически. Поэтому давайте сразу оговорим в рамках каких моделей мы будем работать. Мы будем рассматривать Кеплерову модель орбиты. Существует большое множество других моделей, но все они являются полуаналитическими и в итоге большинство из них сводится к определению параметров Кеплеровой орбиты в интересующий момент времени. Другими словами, Кеплерова орбита является аппроксимацией сложного движения планеты в заданный момент времени. Кеплеровы параметры орбит планет можно посмотреть здесь nssdc.gsfc.nasa.gov/planetary/factsheet, там же указана эпоха (другими словами момент времени) в момент которой данные параметры Кеплеровой орбиты дают точное положение небесного тела. Обычно этим исходным моментом времени является эпоха J2000.0 (полдень 1 января 2000 года). Расчет движения тел на небольшой промежуток времени при помощи Кеплеровой модели является достаточно точным. Точности вполне хватит, чтобы не заметить ошибку визуально или в небольшой телескоп. Конечно, для расчета траектории полета к другой планете нужны более точные модели.

Кеплерова орбита

Итак, по порядку. Начнем с основных допущений данной модели. Предполагается, что масса Солнца много больше массы всех планет вместе взятых, откуда можно сделать вывод, что взаимодействие между планетой и планетой пренебрежимо мало по сравнению с взаимодействием между солнцем и планетой. Таким образом, поставленную задачу можно свети к задаче о взаимодействии двух тел (т.е. можно рассмотреть взаимодействии каждой планеты с солнцем отдельно). Более того предполагаем, что масса планеты много меньше массы Солнца, то взаимодействие получается одностороннее, т.е. планета никак не влияет на движение Солнца. Таким образом, мы можем рассматривать планету, как материальную точку, движущуюся в гравитационном поле, центр которого неподвижен. Примерно так:

Гравитационное взаимодействие

Что такое гравитационное взаимодействие? Это универсальное фундаментальное взаимодействие между всеми материальными телами. О гравитации можно говорить много и долго, но нам нужен только ключевой момент. Согласно классической теории тяготения Ньютона, сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть: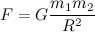

Здесь — G гравитационная постоянная (некий коэффициент пропорциональности). Нам важно отметить лишь то, что сила гравитации направлена от центра тяжести одного тела к центру тяжести другого и обратно пропорциональна квадрату расстояния между ними (закон обратных квадратов).
Отметим, что на нашу сферическую планету в вакууме материальную точку не действует никакая другая сила, кроме силы притяжения со стороны Солнца. В нашем случае, поле сил тяготения является центральным полем сил. В центральное поле сил, направление силы действующей на тело в любой точке такого поля, всегда проходит через центр этого поля (в нашем случае через центр тяжести солнца), а величина такой силы зависит только от расстояния до этого центра.

Второй закон Ньютона

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Такая формулировка хоть и менее точная (нужно сделать оговорки про системы отчета, но нас это пока не интересует), но куда более понятная. Под количеством движения здесь понимается так называемый импульс тела, равный произведению массы тела на его скорость: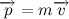

Таким образом, запишем словесную формулировку в символьном виде: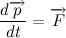

Или же если мы распишем, чему равен импульс тела и вынесем массу как константу (масса не всегда константа, но в нашем случае это так) за знак дифференциала то получим следующую всем известную формулу:

Где вектор — ускорении тела. Не забываем, что ускорение, импульс, скорость и сила величины векторные. Давайте условимся, что если над векторной величиной стоит знак вектора, то понимается именно вектор, в противном случае его модуль.

Второй закон Кеплера

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Да знаю, «получили закон» звучит не хорошо, но что поделаешь, он так называется. Причина в том, что Кеплер его не выводил, а интуитивно подобрал на основе своих наблюдений, т.е. получил его эмпирическим путем, в этом случае это действительно был закон.
Ниже приведена иллюстрация данного закона (рисунок взят из статьи на википедии).

Дифференциальное уравнение орбиты

Давайте все же подробнее рассмотрим векторное произведение радиус вектора на скорость. Радиус вектор можно представить в виде произведения модуля радиус вектора (расстояние от начала координат до точки) на вектор единичной длины, совпадающий по направлению с радиус вектором: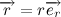


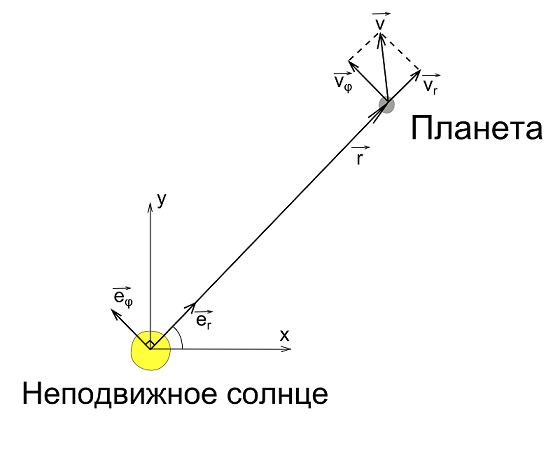
Тогда вектор скорости будет равен: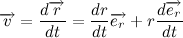

А векторное произведение радиус вектора на скорость в свою очередь: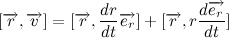

Учитывая тот факт, что вектора и совпадают по направлению, а следовательно совпадают по направлению и вектора и , получаем, что . Тогда:

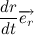
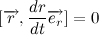
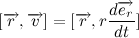
Давайте разберем, что такое производная единичного вектора по времени:

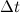
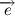
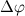
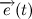
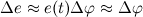
Из рисунка видно, что за время вектор поворачивается на угол . Разность векторов и равна вектору . Для малых углов справедливо следующее соотношение:

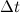
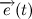
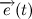
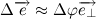
В пределе, когда устремляется к нулю, направления векторов и совпадают, а направление вектора перпендикулярно к ним. Введем единичный вектор , перпендикулярный к и совпадающий с направлением движения его конца, тогда:

Таким образом, переходя к пределу, получим: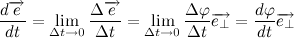

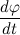
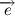
Где это угловая скорость вектора . Обозначим
Вернемся к нашему произведению радиус вектора на скорость, учитывая, что получим:

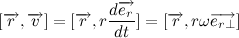
Несложно заметить, что вектора и взаимно перпендикулярны. Введем еще один единичный вектор , который перпендикулярен к векторам и . Таким образом, вектора , и образуют ортонормированный базис. Исходя из определения векторного произведения, получим:

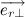
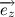
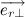
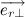
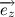
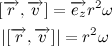
Следовательно, 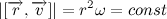. Введем обозначение, . Так же стоит отметить, что:

Вернемся к второму закону ньютона. Вектор силы действующей на тело распишем сразу как величину гравитационной силы, умноженную на орт :

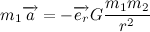
Где m₁ и m₂ — масса планеты и солнца соответственно.
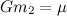
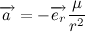
Давайте на массу планеты сразу сократим, и нигде далее про массу планеты вспоминать не будем, так как она совершенно не влияет на траекторию движения. Будем считать, что мы работаем с телом единичной массы. Введем обозначение, , тогда:

Теперь давайте распишем вектор ускорения: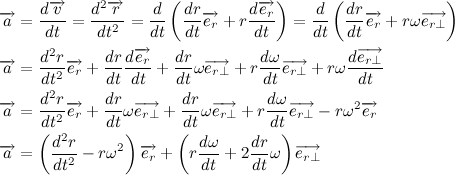

Рассмотрим содержимое второй скобки: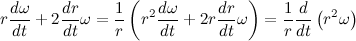

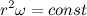
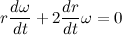
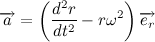
Но мы уже знаем, что , отсюда следует, что , тогда:

Введем обозначение . Напомню, что раннее мы ввели обозначение , очевидно, что .
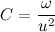
Теперь распишем производную от модуля радиус вектора через С: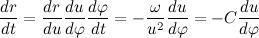

Теперь распишем вторую производную от модуля радиус вектора через С: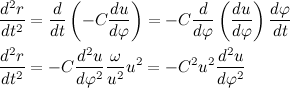

Учитывая полученный результат, перепишем выражение для вектора ускорения: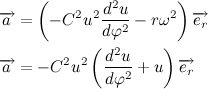

Тогда второй закон Ньютона примет вид: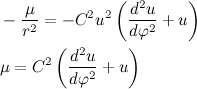

Перепишем полученное дифференциальное уравнение в более привычный вид: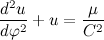

Я думаю многие из вас догадались, что представляет из себя полученное дифференциальное уравнение, но я пожалуй закончу на этом первую часть чтобы не перегружать читателя и себя.

Мы получили дифференциальное уравнение, описывающее траекторию движения материальной точки в гравитационном поле, которое вполне применимо для описания траектории планет и некоторых других небесных тел.

Что нам еще предстоит

В полученном дифференциальном уравнении отсутствует временной параметр, поэтому мы ничего не знаем о характере движения, поэтому необходимо как-то привязаться ко времени. Также далее будут рассмотрены различные системы координат и их преобразования для того чтобы получить координаты планет в системе привязанной к наблюдателю.