Уравнение движения по эллиптической орбите
В статье численными методами решаются уравнения Кеплера, необходимые для визуализации движения небесных тел в пределах солнечной системы.
Содержание
Заголовок окна
Для удобства мы будем выводить в заголовке окна информацию о скорости симуляции солнечной системы. Для этого следует внести изменения в класс CAbstractWindow, добавив новый метод SetTitle, использующий свободную функцию SDL_SetWindowTitle для изменения заголовка окна:
Задача двух тел
Задача двух тел (ru.wikipedia.org) состоит в том, чтобы определить движение двух точечных частиц, которые взаимодействуют только друг с другом. Движение Луны и Земли вокруг их общего центра масс можно описать как задачу двух тел, если пренебречь гравитационным влиянием Солнца и других планет солнечной системы.
Прелесть задачи двух тел в том, что она прекрасно решается аналитически: достаточно знать зависимость силы притяжения или, например, силы кулоновского отталкивания от координат тел. Движение космических тел по эллиптической орбите в задаче двух тел описывается уравнением Кеплера (ru.wikipedia.org):
- E — эксцентрическая аномалия (параметр, из которого выводится переменная величина удалённости тела от точки, вокруг которой оно вращается)
- e — эксцентриситет орбиты, то есть степень отклонения эллиптической орбиты от правильной окружности
- M — длина участка орбиты, пройденного с момента последнего прохождения перицентра (в солнечной системе перицентры планет называются перигелиями)
На данной иллюстрации перицентр (перигелий) орбиты тела под числом 3 обозначен числом 6, а апоцентр — числом 7:
Задача трёх (и более) тел
К сожалению, при добавлении в систему Луна-Земля влияния Солнца, а также при добавлении любого третьего тела в систему из двух тел задача нахождения координат в любой момент времени становится неразрешимой аналитическими методами. Иными словами, не существует способа с помощью решения системы уравнений точно определить траектории в системе из трёх тел.
Отсутсвие точного решения не мешает искать приближённые решения с помощью численного решения приближённых уравнений. То есть на практике задачу двух тел можно решить с любой заданной точностью — но невозможно решить абсолютно точно, за исключением некоторых частных случаев.
Движение планет по эллиптическим орбитам
В солнечной системе присутствует как минимум Солнце и 8 планет (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун). Однако, для визуализации движения планет по их орбитам мы можем пренебречь взаимным влиянием планет и разбить Солнечную Систему на 8 подсистем “Солнце-планета”.
В каждой подсистеме “Солнце-планета” путём численного решения уравнения Кеплера можно определить зависимость координат планеты от времени. Для этих целей создадим вспомогательный класс CEllipticOrbit:
Численное решение уравнения Кеплера
Численные методы поиска корней уравнений позволяют найти решения уравнения с заданной степенью точности. Если вспомнить, что числа в памяти компьютера сами по себе ограничены в точности представления, то несложно сделать вывод, что в дискретном мире компьютеров численное решение по своей точности мало чем отличается от аналитического. Какая разница, как вы находите √2, если √2 невозможно точно представить как float или double ?
Именно поэтому мы воспольуемся численным алгоритмом поиска корней под названием метод Халли. Для сокращения кода воспользуемся готовой реализацией этого алгоритма в функции boost::math::tools::halley_iterate .
Для запуска этой функции мы должны сформировать функтор, который будет для заданного параметра x возвращать кортеж из трёх значений:
- значение функции для аргумента x
- значение первой производной этой функции для аргумента x
- значение второй производной этой функции для аргумента x
В C++98 нам бы пришлось писать новый класс с перегруженным оператором вызова, но в C++11 мы можем применить лямбда-функции:
Теперь можно написать функцию-обёртку, использующую функтор с алгоритмом “метод Халли”:
Теперь, обладая способом решения уравнения Кеплера для заданного момента времени, мы можем реализовать остальные методы. Кроме того, мы добавим релизацию геттеров свойств:
Реализуем класс CSolarSystem
Теперь мы добавим класс, инкапсулирующий в себе информацию о Солнце, планетах и взаимодействии между ними. В целом он будет похож на класс CParticleSystem, хотя законы движения кардинально изменились: больше нет никакой случайности и хаотичности, на смену им пришли законы небесной механики.
Так выглядит объявление CSolarSystem:
В конструкторе CSolarSystem зададим все 8 планет, планетоид Плутон и комету Галлея:
Теперь добавим реализации Update и Draw. Планеты и Солнце мы будем рисовать как точки фиксированного размера, а орбиты — с помощью пунктирной линии. В любом случае, параметры эллипса орбиты и позицию планеты в заданный момент времени можно узнать у помощью объекта класса CElipticOrbit:
Методы для запроса свойств и управляющие методы для изменения масштаба и скорости течения времени можно реализовать так:
Реализуем класс CWindow
Практически все возможности программы уже реализованы, в CWindow остаётся лишь управляющий код. Поэтому объявление класса CWindow будет кратким:
В первую очередь рассмотрим реализацию конструктора, обновления состояния и рисования сцены:
Метод SetupView подвергся модификациям: теперь матрица ортографического проецирования должна учитывать масштаб Солнечной Системы:
Управляющие клавиши
Последним штрихом добавим в CWindow::OnKeyDown обработку управляющих клавиш. Список горячих клавиш:
- клавиша “+” (точнее, клавиша “=”) увеличивает масштаб
- клавиша “-“ уменьшает масштаб
- клавиша “влево” уменьшает скорость течения времени, и может даже обратить время вспять
- клавиша “вправо” увеличивает скорость течения времени
Поскольку вся необходимая работа уже проделана в классе CSolarSystem, в методе OnKeyDown мы просто отображаем события на методы:
Уравнение Кеплера
Статьи по небесной механике пользуются на Хабре некоторой популярностью, поэтому я решил рассказать
об одном фундаментальном уравнении движения, а именно, уравнении Кеплера.
Как известно, финитное движение небесных тел в Солнечной системе происходит по эллипсу. Однако, если необходимо
установить, в какой точке небесное тело находится в заданный момент времени, этой информации недостаточно и надо воспользоваться уравнением Кеплера.
Выведем это уравнение.
Напомню, что эллипс — это сплюснутая на величину
окружность. Здесь e — эксцентриситет.
Площадь эллипса равна
где a — большая полуось.
Согласно второму закону Кеплера, который гласит, что площадь, заметаемая радиус-вектором небесного тела пропорциональна времени, можно написать
где T — период обращения, t — текущее время, t0 — момент времени прохождения перигелия (ближайшей к Солнцу точки орбиты).
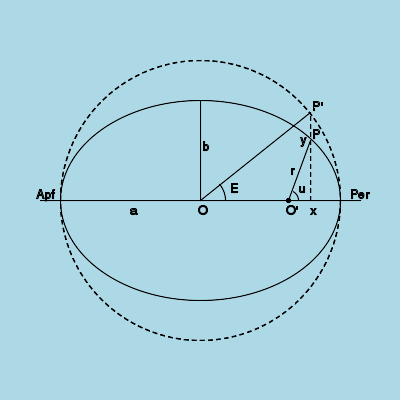
Найдем теперь зависимость этой площади от положения небесного тела на орбите, то есть от величины радиус-вектора r и истинной аномалии — угла между перигелием и небесным телом, если смотреть с Солнца.
Для этого введем дополнительную переменную — эксцентрическую аномалию E.
Направим ось x от Солнца (начала координат), которое находится в одном из фокусов эллипса, в сторону перигелия по линии апсид (прямой, соединяющей перицентр с апоцентром).
Создадим также вспомогательную окружность с радиусом, равным большой полуоси эллипса.
Абсцисса небесного тела в точке P будет равна
ордината будет, соответственно, равна
Таким образом, получаем
Для вычисления площади S рассмотрим вспомогательные фигуры:
сектор окружности P’-O-Per:
Сектор эллипса P-O-Per:
Отсюда, прощадь S равна:
Сравнивая это выражение с выведенным ранее из второго закона Кеплера,
получаем:
где M(t)=2*pi*(t — t0) / T
Это и есть уравнение Кеплера.
Заметим, что это трансцендентное уравнение относительно E и получить явное решение в общем случае не удается.
Для вычисления координат небесного тела необходимо найти эксцентрическую аномалию по известному M и e, a затем определить радиус-вектор и угол и, если необходимо x и y по приведенным выше формулам.
Интересным вопросом остается нахождение методов решения уравнения Кеплера.
Этим занимались лучшие умы человечества на протяжении последних четырехсот лет.
Результатом было обогащение математики множеством интересных идей, но описание этого требует отдельной статьи.
Наблюдение искусственных спутников Земли
Глава 1: Как движутся ИСЗ?Перед тем, как приступить к рассмотрению вопросов наблюдения ИСЗ, нужно выяснить как они движутся — по каким орбитам и каковы характеристики этих орбит. Без понимания этих вопросов наблюдение ИСЗ превращается в охоту за неведомым зверем, который неизвестно где обитает. § 1. Законы Кеплера и типы орбитИз курса средней школы нам известно, что тело, движущееся по орбите вокруг другого тела, подчинено трём законам Кеплера. Нас будут интересовать только два из них — первый и третий. Согласно первому закону Кеплера, тело, обращающееся вокруг Земли (в нашем случае) движется по эллипсу, в одном из фокусов которого находится центр Земли (см. рис. 2). Мы специально не упоминали тут, что тело может двигаться по трём видам орбит — эллипс, гипербола и парабола. Нас интересуют только периодические орбиты, а из перечисленных такой является эллипс.
Элементы эллипса показаны на рис. 2. «F1« и «F2« — фокусы эллипса; «a» — большая полуось; «b» — малая полуось; «е» — эксцентриситет эллипса, который определяется следующим образом:
Таким образом, первое важное положение — ИСЗ движутся вокруг Земли по эллипсам . Согласно третьему закону Кеплера, квадраты периодов обращения «T» спутников относятся как кубы их больших полуосей «a»:
§ 2. Орбитальные элементыДля того, чтобы задать параметры и ориентацию орбиты ИСЗ в пространстве, нужно указать 6 т.н. кеплеровских элементов (орбитальных элементов) (см. рис. 3):
Итак, наше второе важное положение — орбита ИСЗ полностью задаётся шестью орбитальными элементами . § 3. Круговая орбитаРассмотрим частный случай эллиптической орбиты — круговая орбита. Если значение эксцентриситета орбиты ИСЗ е = 0, то орбита представляет собой окружность с центром в центре Земли. Для того, чтобы тело стало спутником Земли, оно должно обладать определённой скоростью при полёте вокруг неё. Если бы у Земли не было атмосферы, то минимальная скорость, необходимая для того, чтобы тело двигалось по окружности вокруг Земли, равна vк0 = 7,91 км/с. Но в реальности такого быть не может — спутник будет сильно тормозится в атмосфере Земли. Если ИСЗ начнёт двигаться на высоте менее примерно 160 км от поверхности Земли, то он сможет сделать лишь пару оборотов, после чего начнёт необратимо терять скорость и сгорит в плотных слоях атмосферы. Для примерного расчёта скорости ИСЗ на круговой орбите можно воспользоваться формулой [1]:
где R = 6371 км — средний радиус Земли, r = R + h — расстояние от центра Земли до ИСЗ, h — высота ИСЗ над поверхностью Земли. При наблюдениях важно знать период обращения ИСЗ Т — время, необходимое на один полный оборот вокруг Земли. Для круговой орбиты период Т можно вычислить по формуле [1]:
Из (4) видно, что минимальное время, необходимое ИСЗ для одного оборота, равно Tк0 = 84,4 минуты — при нулевой высоте над поверхностью. Никакое тело не может быстрее обогнуть поверхность Земли. При примерных оценках периода обращения ИСЗ по круговой орбите полезно помнить, что период обращения увеличивается примерно на 1 минуту при увеличении высоты ИСЗ на каждый 50 км. Этой оценкой можно пользоваться для ИСЗ не выше 1000 км. Наше третье важное положение — ИСЗ не может двигаться долгое время по орбите вокруг Земли ниже 140-160 км. При этом, период обращения по круговой орбите является минимальным и для диапазона высот 160-1000 км изменяется всего с 87,6 до 105 минут . § 4. Эллиптическая орбитаТеперь рассмотрим общий вид орбиты ИСЗ — эллиптическая орбита (см. рис. 4). Как было указано выше, из первого закона Кеплера следует, что в фокусе эллиптической орбиты будет находится Земля (З), вокруг которой вращается ИСЗ. Двигаясь по эллиптической орбите, ИСЗ ближе всего подлетает к центру Земли в точке «П» — в перигее, а дальше всего находится в точке «А» — в апогее. Линия, соединяющая перигей и апогей называется линией апсид. Из наблюдений ИСЗ можно определить большую полуось и эксцентриситет орбиты, из которых можно вычислить значения перигейного «q» и апогейного «Q» расстояний:
Из (5) видно, что Q + q = 2a. При движении по орбите изменяется расстояние «r» от Земли до ИСЗ — величина радиус-вектора «r» задаётся выражением [3]:
Скорость ИСЗ в любой точке эллиптической орбиты задаётся выражением [2]:
Период обращения для спутника на эллиптической орбите вычисляется по формуле (4), в которой вместо «r» нужно подставить значение большой полуоси «a». Наше четвёртое важное положение — скорость движения ИСЗ по эллиптической орбите не равномерна: максимальна она в перигее, а минимальна в апогее. Период обращения теперь определяется не только большой полуосью «a», но и значением эксцентриситета «e» . § 5. Эволюция орбиты ИСЗВ этом параграфе мы рассмотрим, как изменяются параметры реальной орбиты ИСЗ под воздействием определённых факторов. Прежде всего следует отметить следующее: если бы Земля имела форму идеального шара с равномерным распределением вещества, была лишена атмосферы, а Луна и Солнце отсутствовали бы, то ИСЗ вечно бы вращался по своей орбите, ориентация которой в пространстве не изменялась. Если бы спутник совершал 14 оборотов в сутки (при этом его период равен примерно 103 минуты), то за время одного витка ИСЗ Земля повернётся на 1/14 полного оборота (это примерно 26°). Это означает, что с каждым новым траектория ИСЗ смещалась к западу на 26° за каждый виток. Прецессия орбитыВ реальности форма Земли — геоид, полярный радиус которого RП = 6356,8 км, а экваториальный — RЭ = 6378,2 км, т.е. экваториальный радиус больше полярного на 21,4 км. Земля имеет экваториальный «горб», который своей массой оказывает влияние на движение ИСЗ. Влияние это не такое уж явное — масса «горба» не вызывает изменения наклонения «i» орбиты за счёт притягивания плоскости орбиты к плоскости экватора, как можно было бы ожидать — плоскость орбиты медленно поворачивается вокруг земной оси в направлении, противоположном вращению ИСЗ (см. рис. 5).
Этот процесс называется прецессией. Угол прецессии плоскости орбиты ИСЗ остаётся неизменным. Угловая скорость прецессии «X1« (градусов в сутки) определяется, в основном, наклонением орбиты [1]:
где «i» — наклонение орбиты, «e» — эксцентриситет, RЭ — экваториальный радиус Земли, «а» — большая полуось орбиты ИСЗ. Если спутник движется в запада на восток, орбита поворачивается с востока на запад. Чем меньше наклонение ИСЗ, тем больше значение прецессии (см. рис. 6). Если спутник вращается с востока на запад (обратное движение ИСЗ), то прецессия орбиты происходит в обратную сторону. При этом линия узлов также поворачивается (см. рис. 7).
Теперь посмотрим, к каким изменениям условий наблюдения спутника приводит прецессия. Как известно, Земля делает полный оборот за 23 ч 56 м 4,09 с (звёздные сутки) — за 24 ч (средне-солнечные сутки) небо нам кажется повернувшимся на 361° (т.к. звёздные сутки короче средне-солнечных на 4 минуты — за это время небо повернётся на 1°). Если бы плоскость орбиты ИСЗ не прецессировала, то через 24 ч он появлялся бы на небе на 1° западнее, чем накануне (если движение ИСЗ прямое). Но за счёт прецессии орбита поворачивается на Х1 градусов за сутки, поэтому ИСЗ через 24 ч окажется на Х1 + 1 градус западнее (при обратном движении — на 1 — Х1 градус к западу). Период обращения спутника не кратен целой части суток. Если через сутки спутник будет пересекать ту же широту Земли на n минут позже, он окажется ещё на n/4 градусов западнее, т.к. за 1 минуту Земля поворачивается на 1/4 минуты. Следовательно, суммарный суточный сдвиг к западу составит (Х1 + 1 + n/4) градусов [1]. Вращение эллиптической орбитыСледующим важным эффектом, влияющим на эволюцию орбиты ИСЗ, является поворот плоскости эллиптической орбиты. Эффект этот, как и предыдущий, обязан своим существованием экваториальному «горбу» Земли, но в отличие от прецессии, действует только на эллиптичные орбиты. Эффект заключается в том, что эллиптическая орбита постоянно поворачивается в своей плоскости вперёд для спутников с нулевым наклонением, и назад — для спутников с наклонением, близким к 90°. За счёт этого точки перигея движутся вперёд или назад по орбите (см. рис. 8).
Скорость вращения «X2« эллиптической орбиты определяется выражением [1]:
На рис. 9 показаны графики зависимости X2(i) для ИСЗ с разными значениями больших полуосей «a».
Вращение происходит в том же направлении, что и движение спутника, если наклонение i 63,4°. При i = 63,4° поворот орбиты отсутствует. Наше пятое важное положение — движение ИСЗ подвержено возмущениям из-за несферичности Земли. За счёт прецессии орбита спутника может смещаться с угловой скоростью до 9°/сутки, а за счёт поворота эллиптической орбиты — до 15°/сутки. При этом, чем меньше наклонение, тем сильнее оба эффекта, но действовать они могут как в одну сторону, так и в противоположные . Атмосферное торможениеПрецессия орбиты и поворот её плоскости связаны с действием несферичности Земли. Но кроме этого Земля окружена атмосферой, которая прослеживается до 2000 км над её поверхностью. Из этого следует, что на движение ИСЗ, особенно на низких орбитах, влиянием атмосферы мы пренебрегать не можем. Атмосферное давление падает с высотой экспоненциально — на высоте 200 км оно составляет 10 -12 мбар (на уровне моря атмосферное давление составляет 1013 мбар), а на высоте 900 км — уже только 10 -42 мбар [6]. Тем не менее, даже такая разреженная атмосфера может приводить к изменению орбиты ИСЗ. Сила сопротивления движущемуся в атмосфере телу определяется выражением [4]:
где «cx« — безразмерный коэффициент сопротивления, для верхней атмосферы равный 2-2,5; «S» — площадь максимального сечения спутника, перпендикулярного налетающему воздушному потоку; «v» — скорость ИСЗ, «ρ» — плотность атмосферы на высоте полёта ИСЗ. Торможение ИСЗ определяется его парусностью — чем больше площадь и меньше масса, тем больше торможение. Для спутника, движущемся по круговой орбите, сопротивление атмосферы будет сказываться следующим образом: спутник будет медленно опускаться по спирали с постоянно увеличивающейся скоростью. Угол снижения спутника на круговой орбите можно оценить из выражения [1]:
где «m» — масса ИСЗ, «g» — ускорение свободного падения. Снижение по спирали будет продолжаться до тех пор, пока спутник не опустится до высоты 160 км — ниже этой высоты сила сопротивления настолько велика, что спутник начинает резкое снижение и сгорит в атмосфере. На высоте 160 км период обращения равен примерно 88 минут — любой ИСЗ с меньшим периодом обречён. Если орбита эллиптическая, то результат действия сопротивления атмосферы будет следующим: т.к. сопротивление сильно уменьшается с высотой, то максимальное сопротивление ИСЗ будет испытывать в перигее, а минимальное — в апогее. Это слабо меняет высоту перигея, но уменьшает высоту апогея — в результате эллиптичность орбиты уменьшается и спутник начинает спуск по спирали. На рис. 10 показано снижение ИСЗ в случае эллиптической орбиты.
Оценить время жизни спутника можно из выражения (12) [1]:
где e0 — начальный эксцентриситет орбиты, T0 — начальный период обращения, ΔT — суточное изменение периода. Тогда измение периода будет определятся выражением [1]:
а изменение эксцентриситета [1]:
Формулы (13) и (14) справедливы для значений e = 0,02-0,2. На атмосферное торможение сильно влияет время суток (в подсолнечной точке атмосфера подымается выше), а также активность Солнца. Как видно, время жизни спутника определяется его эксцентриситетом и большой полуосью. В таблице ниже представлены времена жизни ИСЗ для разных значений перигея и апогея [5]:
Наше шестое важное положение — сопротивление атмосферы Земли вызывает уменьшение большой полуоси орбиты ИСЗ, в результате чего он по спирали спускается вниз. При достижении высоты около 160 км спутник сможет сделать всего пару оборотов и сгорит в атмосфере, войдя в резкий и необратимый спуск . Давление светаВпервые идею о том, что свет производит давление на тела, высказал в 1619 г. И. Кеплер — для объяснения эффекта отклонения кометных хвостов от Солнца. Современная теория даёт значение давления следующим выражением (формула Максвелла-Бартоли) [3]: где «E» — мощность электромагнитного излучения, приходящаяся на единицу площади тела, «η» — коэффициент отражения тела, «c» — скорость света. Для абсолютно поглощающего тела вблизи Земли давление света равно 4,3 · 10 -6 Н/м 2 . Для абсолютно отражающего тела эта величина в два раза больше. Световое давление становится ощутимым для лёгких спутников выше 500 км, т.к. ниже большее значение имеют колебания плотности атмосферы. В заключении параграфа нужно отметить, что перечисленные факторы влияния на эволюцию орбиты спутника не составляют полный список. Например, на ИСЗ воздействуют своим притяжением Солнце и Луна, но это воздействие в 10000 раз слабее действия экваториального «горба» Земли, но его нужно учитывать для орбит с большим эксцентриситетом. Экваториальный «горб» также вызывает незначительные колебания плоскости орбиты ИСЗ при пересечении экваториальной плоскости. Наконец, неравномерность распределения масс под поверхностью Земли также сказывается на движении спутника. Как видим, движение спутника не так просто, как может показаться на первый взгляд. В наше время расчёты эволюции орбиты значительно упростились с точки зрения затраты времени, т.к. современные компьютеры имеют огромную вычислительную мощность. Даже любители, используя специальные программы (см. далее), могут довольно точно расчитывать положение спутников на нужную им дату и время, причём на любой промежуток времени — в начале космической эры любители могли об этом только мечтать. источники: http://habr.com/ru/post/209106/ http://www.sat.belastro.net/glava1/glava1.php | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

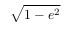
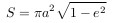
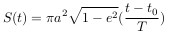
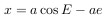
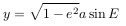
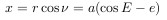
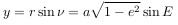
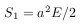
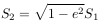
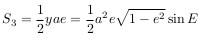
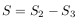
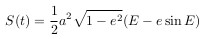
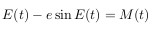

 ,     (1)
,     (1)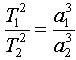 ,     (2)
,     (2)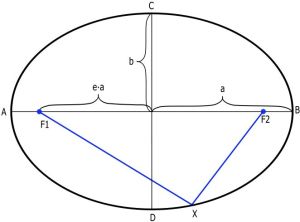

 ,     (3)
,     (3) ,     (4)
,     (4) .     (5)
.     (5)
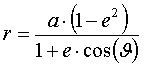 .     (6)
.     (6)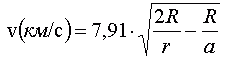 .     (7)
.     (7)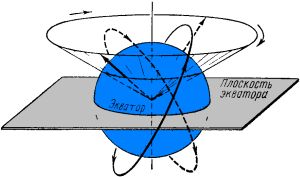
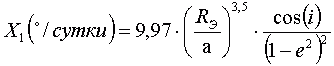 ,     (8)
,     (8)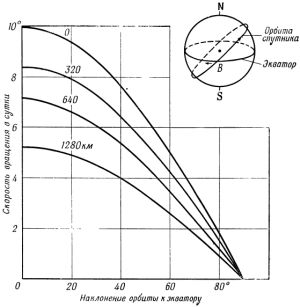


 .     (9)
.     (9)
 ,     (10)
,     (10)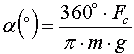 ,     (11)
,     (11)
 ,     (12)
,     (12) ,     (13)
,     (13) .     (14)
.     (14)