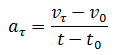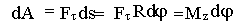Уравнение движения по окружности в полярных координатах

Кинематическое уравнение равномерного движения по окружности в полярных координатах

Кинематическое уравнение движения с постоянным ускорением

r = r0 + v0 t + at2/2, где v₀ скорость объекта в момент t₀

Уравнение для скорости тела при движении с постоянным ускорением

Кинематическое уравнение равномерного движения по окружности в полярных координатах

Кинематическое уравнение гармонических колебаний вдоль оси X
х = А Cos (ω t + φ₀)

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением

Средняя скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:

Мгновенной скоростью называется предел отношения перемещения к интервалу времени, в течение которого это перемещение произошло, если интервал времени стремится к нулю.

V_мгн=lim(t->0) ΔS/Δt

2. Ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:

или

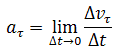
Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.

3. Вращательное движение тела вокруг неподвижной направленной оси — движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой хх, называемой осью вращения. Угловое перемещение — векторная величина, характеризующая изменение угловой координаты в процессе её движения. Угловая скорость — векторная величина, характеризующая быстроту вращения материальной точки. Вектор направлен вдоль оси вращения таким образом, чтобы, смотря с его конца, вращение казалось происходящим против часовой стрелки. Угловая скорость (ед. измерения — радиан в секунду рад/с) равна первой производной от угла-поворота радиуса-вектора по времени. Формула угловой скорости: w=df/dt. Угловое ускорение — векторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела Угловое ускорение равно первой производной от угловой скорости по времени. Формула угловой скорости: Единица углового ускорения — рад в секунду в квадрате.

4. Работа переменной силы А=Fs; Графически A=Интеграл(a, b)F(s)dx. Потенциальная энергия силы тяжести W_п=mgh. Работа сила тяжести равна изменению потенциальной энергии, взятому с противоположным знаком. Т.е., если потенциальная энергия увеличивается (тело поднимается), то сила тяжести совершает отрицательную работу и наоборот. A=-mgh

5. Направив координатную ось вдоль прямой движения, можно рассматривать F, s, υ и a как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A = Fs. При равноускоренном движении перемещение s выражается формулой

Отсюда следует, что

Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

6. Механическая система (система материальных точек) — это совокупность конечного числа материальных точек, выделенных для рассмотрения.

Внутренние силы — это силы, с которыми точки системы действуют друг на друга.

Внешние силы — это силы, источники которых лежат вне системы, т.е. это силы, действующие со стороны тел, не принадлежащих системе. Центр инерции, геометрическая точка, положение которой характеризует распределение масс в теле или механической системе.

Центр масс механической системы движется как материальная точка с массой равной массе всей системы, под действием всех приложенных к точкам системы внешних сил.

7. Импульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:

.

Обозначим скорости тел массами m₁ и m₂ до взаимодействия через и , а после взаимодействия — через и .

По третьему закону Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; поэтому их можно обозначить и .

Для изменений импульсов тел при их взаимодействии на основании равенства (16.2) можно записать

,

,

где t — время взаимодействия тел. Из этих выражений получаем

. (16.3)

Таким образом, векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия.

8. (ИСО) — система отсчёта, в которой справедлив первый закон Ньютона

1 закон Ньютона: В инерциальной системе отсчета тело, на которое не действуют другие тела, или, когда действие всех сил скомпенсировано, движется равномерно и прямолинейно или покоится.

2 закон Ньютона: Ускорение тела пропорционально результирующей силе, дейсвующей на тело, и обратно пропорционально массе тела а=F/m

3 закон Ньютона: Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. F12=-F21

9. Консервативные — такие силы, РАБОТА которых не зависит от траектории, а определяются только начальным и конечным положением материальной точки. Силы, не обладающие только что названным свойством, называют неконсервативными. Для того чтобы узнать, консервативна сила либо нет, надо вычислить ее работу. Потенциальная энергия может быть введена только для поля консервативных сил.Так как их работа не зависит от траектории, а только от начального и конечного положений материальной точки, то эту работу можно записать в виде разности двух чисел: одно — Wn1 — будет зависеть от начального положения тела, второе — Wn2 — от конечного положения тела. Wn1 — потенциальная энергия тела в положении 1; Wn2 — в положении 2.

10. Сила упругости пропорциональна деформации: Fх упр= -kx, где Fxупр — проекция силы упругости на ось х; k — коэффициент упругости (для пружины — жесткость), (На всякий случай, знак минус ука­зывает, что F_{x упр} направлена в сторону, противоположную деформации х.По третьему закону Ньютона, дефор­мирующая сила равна по модулю силе упругости и противоположно ей направле­на, т. е. F_x=-F_{x упр}=kx)

Элементарная работа dA, совершаемая силой F_xпри бесконечно малой деформации dx, равна dA = F_x dx = kxdx, а полная работа идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела П=kx 2 /2.

11. Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. (ниже хз что за чушь)

Если под действием приложенной силы твердое тело может совершать вращение вокруг некоторой точки, то для того, чтобы охарактеризовать вращательный эффект силы вводится понятие – момент силы относительно точки (или центра).Моментом силы относительно точки (рисунок 1.1) называется векторное произведение радиус-вектора точки приложения силы на вектор силы. Mo(F) = r ⊗ F . Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки. Вектор момента характеризует положение плоскости и направление вращательного действия силы, а также дает меру этого действия

|Mo(F)| = F⋅r⋅sinα = F⋅h,. (. F — с вектором.) где h – плечо силы (кратчайшее расстояние от точки O – центра момента – до линии действия силы). Если сила проходит через точку, то ее момент относительно этой точки равен нулю.Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия. Если силы расположены в одной плоскости, то используется понятие алгебраического момента силы.

12. Связь вектора момента силы и момента импульса

Продифференцируем (10) по времени:

Т.к. полюс неподвижен, то первое слагаемое равно нулю (т.к. первая производная перемещения по времени равна скорости). Тогда коллинеарны, а произведение коллинеарных векторов равно нулю.

Поэтому

Согласно II закону Ньютона ,

значит (15) будет иметь вид:

или

Выражение (17) устанавливает связь между и .

связь между и

— производная вектора момента импульса по времени относительно неподвижного полюса равна вектору момента силы, действующей на эту м.т. относительно того же полюса

13. (тоже хз что за чушь) , векторное произведение. Mz — момент силы Ft относительно оси вращения z. При повороте тела на малый угол вокруг оси Z совершается работа

14. Закон сохранения механической энергии

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:

По теореме о кинетической энергии эта работа равна изменению кинетической энергии:

Или Ek1 + Ep1 = Ek2 + Ep2.

15. Момент импульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Момент импульса замкнутой системы сохраняется.

Момент импульса частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса:

где — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчета начала отсчёта, — импульс частицы. В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

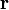
Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L:

Поскольку уравнение вращательного движения можно представить в виде:

Окончательно будем иметь:

Это уравнение, полученное здесь для случая, когда I = const, справедливо и в общем случае, когда момент инерции тела изменяется в процессе движения.

Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = Iω относительно данной оси сохраняется:

ΔL = 0, если M = 0.

Закон сохранения момента импульса: = ( + )ω

17. Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

где: 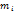— масса i-й точки, — расстояние от i-й точки до оси.

Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.

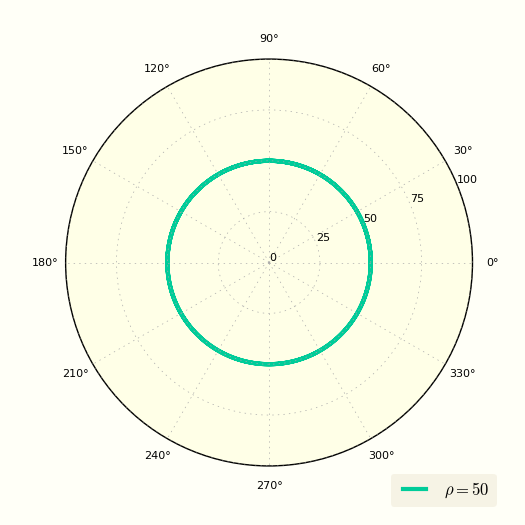
Окружность в полярных координатах

Уравнение окружности в полярных координатах выглядит очень просто

Это уравнение показывает, что ρ вообще не зависит от угла φ.

Построение окружности по простому уравнению в полярной системе координат

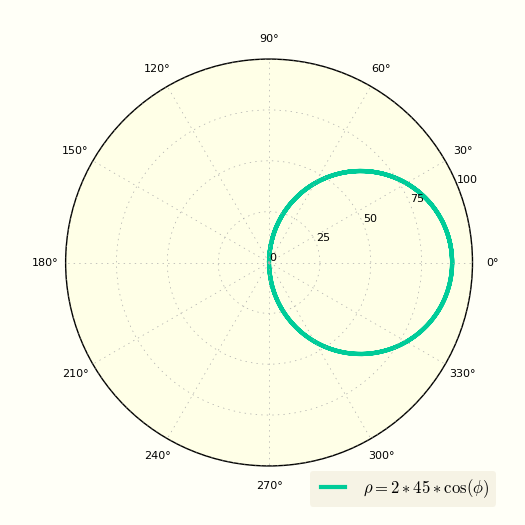
Еще одно уравнение окружности в полярных координатах

Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.

Известно, что окружность в декартовой прямоугольной системе координат описывается уравнением:

Используя эти формулы и подставив их в (1) мы получим:

Уравнение окружности в полярных координатах

Изначально после подстановки имеем

И этого уравнения получается система

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.

В итоге получаем:

Построение окружности в полярной системе координат

Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах

В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.

При таком смещении окружность описывается уравнением:

И этого уравнения получается система

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.

Уравнение окружности в полярной системе координат.

Определим уравнение окружности, проходящей через полюс системы координат, центр которой C расположен на полярной оси, а радиус равен R. Выполним построения:

Далее отметим на окружности любую точку А и В, причем точка В — конец диаметра. Соединим выбранную пару точек. Угол ОАВ — прямой, а потому, так как диаметр равен 2R, из прямоугольного треугольника АОВ имеем:

Если же центр является началом координат, то уравнение принимает вид:

Так же уравнение может принимать вид:

Для ситуации, когда центр окружности расположен на прямой перпендикулярной полярной оси и проходящей через полюс: