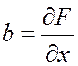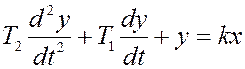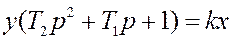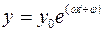2. Математическое описание систем автоматического управления
Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.
На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).
При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.
Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др
Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).
где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.
В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.
Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:
где, m — масса тела, Fj — все силы воздействующие на тело (поршень демпфера)
Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:
где — сила тяжести;
— сила сопротивления пружины,
— сила вязконо трения (пропорциональна скорости поршеня)
Размерности сил и коэффициентов, входящих в уравнение (2.1.2):
Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть
перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:
если , то уравнение принимает вид:
Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).
Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:
тогда, разделив на k, имеем:
Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!
«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:
Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [
].
Тогда уравнение (2.1.6) можно записать в операторной форме:
, что эквивалентно
где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную
.
Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.
Введем новые нормированные (безразмерные) переменные:
Подставляя эти соотношения в уравнение (2.1.2), имеем:
Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на
, получаем:
где: — коэффициент усиления, причем безразмерный.
Проверим размерность коэффициента
Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.
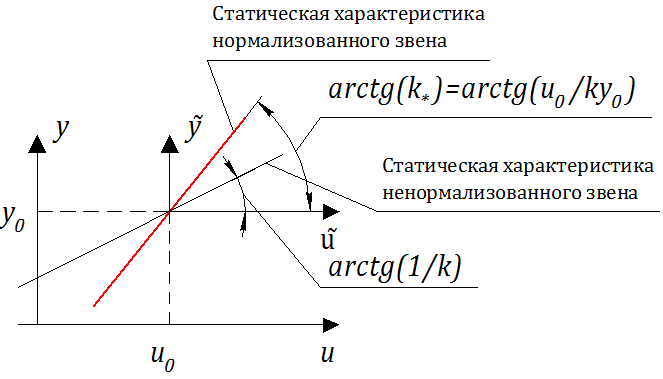
На рис. 2.1.4 представлены статические характеристики для механического демпфера:
Процедура нормировки отклонений позволяет привести уравнения динамики к виду:
где дифференциальные операторы.
Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).
А если – нелинейные дифференциальные операторы, или
, то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).
Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»
2.2. Линеаризация уравнений динамики САУ (САР)
Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:
- Нелинейностью статической характеристики.
- Нелинейностью динамических членов в уравнениях динамики.
- Наличием в САУ принципиально нелинейных звеньев.
Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).
Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N0 Рис. 2.2.1 – Пример изменения мощности реактора
Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:
Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:
Перенесем в левую часть уравнения и запишем уравнение в виде%
где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.
Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:
Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .
Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки
будет выглядеть так:
C учетом вышеприведенного разложение принимает вид:
Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку
, получаем:
Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:
Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.
В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:
где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора
выше порядка оператора
:
Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.
Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).
Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:
Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>
Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на
, то уравнение принимает вид:
или в операторном виде:
Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.
Пример
Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x0, y0), если полное уравнение динамики имеет вид:
Нелинейность полного уравнения динамики проявляется в следующем:
• во-первых, в нелинейности статической характеристики:
• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.
Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x0, y0) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.
Преобразования выполним в следующей последовательности:
- Перейдем к безразмерным переменным (нормализованным);
- Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.
Перейдем к новым безразмерным переменным:
Заметим, что: .
Подставляя значения x(t) и y(t) в исходное уравнение:
Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости:
, получаем следующее уравнение:
Вводим новые обозначения:
Получаем уравнения в «почти» классическом виде:
Если в правой части вынести за общую скобку и разделить все уравнение на
, то уравнение (линеаризованное) принимает вид:
Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).
2.3. Классический способ решения уравнений динамики
Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.
Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:
Переходя к полной символике, имеем:
Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.
Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).
Требуется найти y(t) при известных начальных условиях.
где: — решение однородного дифференциального уравнения
y_<част.>(t) $inline$ — частное решение. $inline$
Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).
Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием
, поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:
Напомним этапы решения:
1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:
2) Записываем характеристическое уравнение:
3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:
если среди нет повторяющихся корней (кратность корней равна 1).
Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:
Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:
5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…
Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .
6) Суммируя полученные составляющие (собственную и вынужденную), имеем:
7) Используя начальные условия (t = 0), находим значения постоянных интегрирования .
Обычно получается система алгебраических уравнений.
Решая систему, находим значения постоянных интегрирования
Пример
Найти аналитическое выражение переходного процесса на выходе звена, если
Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем:
тогда:
где — неизвестные (пока) постоянные интегрирования.
По виду временной функции в правой части запишем как:
Подставляя в исходное уравнение, имеем:
Суммируя , имеем:
Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:
Решая систему уравнений относительно и
, имеем:
Тогда окончательно:
Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:
Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).
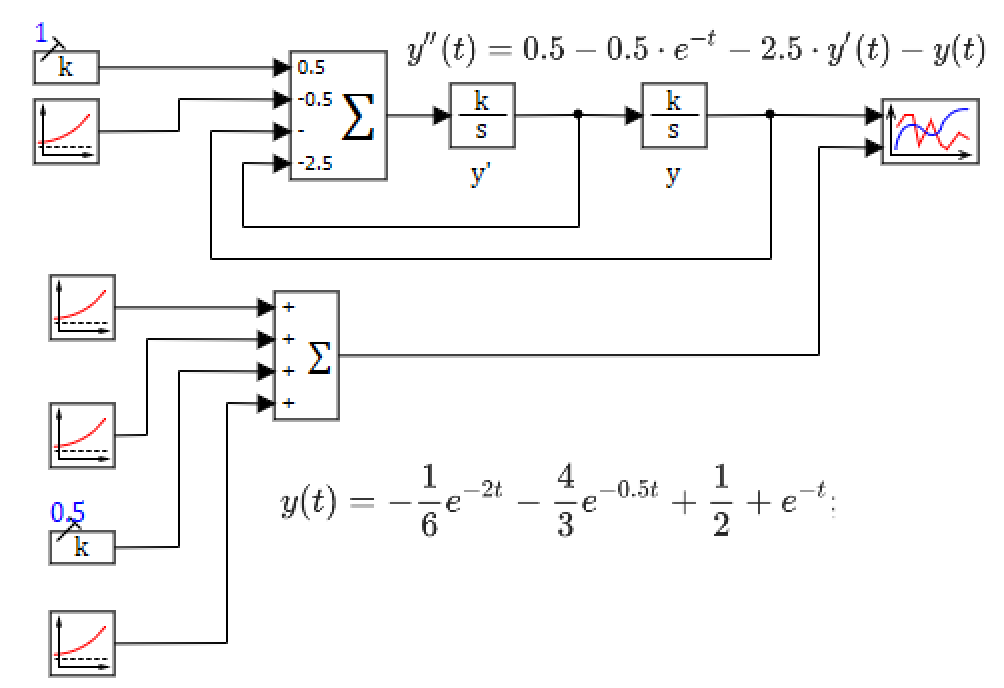
Рис. 2.3.1 – структурная схема для проверки решения
На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).
Уравнения систем автоматического управления
Для того, чтобы провести анализ системы автоматического управления САУ необходимо иметь ее математическое описание – интегродиффернциальные или дифференциальные уравнения. Если система с распределенными параметрами, то уравнения представлены в частных производных. Они будут определять поведение системы автоматического регулирования САР в динамических режимах – переходные процессы, а также приложение или снятие возмущающих воздействий.
Ели уравнения описывают изменения входящих в них переменных во времени, то их называют уравнениями динамики. Не прилагая особых усилий из уравнений динамики можно получить уравнения статики – если предположить, что все входящие в них воздействия и производные равны нулю или равны константам (постоянны). Уравнениями статики описываются системы в установившемся режиме.
Для упрощения записи уравнений динамики САР ее, как правило, разбивают на отдельные звенья, и записывают уравнения каждого звена по отдельности. Созданную таким образом систему уравнений можно преобразовать к одному уравнению, путем исключения промежуточных переменных.
Уравнения звена необходимо составлять так, чтоб оно выражало зависимость между выходящим и входящим сигналом. Также следует учитывать, что звено может иметь не одно входное значение (при наличии обратных связей), а также следует учесть, что звено может иметь возмущение из вне.
Дифференциальные уравнения составляются на основании законов физических процессов, которые будут протекать в звене.
Все факторы или переменные, от которых зависит изучаемый процесс, выявляются при составлении дифференциального уравнения. Уравнения статики не линейны для большого диапазона изменений регулируемой величины. Если рассмотреть на примере генератора независимого возбуждения, то при небольшом изменении напряжения возбуждения уравнение цепи будет иметь линейный вид:
Где: Uг – выходное генераторное напряжение, Uв – напряжение на обмотке возбуждения, α – коэффициент, выражающий зависимость Uв от Uг.
Если изменения магнитного поля машины будут существенны, то тогда придется учитывать режим насыщения, а это вводит в систему определенную нелинейность:
Если для малых отклонений регулируемой величины вполне можно использовать линеаризованные уравнения, то для больших отклонений используют нелинейные уравнения вида:
Где x, y, z – значения абсолютные регулируемой величины, а также регулирующего и возмущающего воздействий.
Изображение данных статических уравнений называют статическими характеристиками – кривыми, построенными в координатах x, z или x,y.
В качестве примера такой характеристики может послужить характеристика статическая электронного усилителя постоянного тока Uвых = f(Uвх):
Или же машины постоянного тока Ω = f(Uу):
Где: Ω – скорость вала, рад/с; Uу — якорное напряжение управления;
Из показанных выше характеристик видно, что они не линейные. Для того, чтоб упростить себе жизнь и не проводить расчет нелинейной САУ было введено понятие линеаризация, которая возможна для небольшого диапазона изменений входных и выходных величин:
Точка С, на характеристике Ω = f(Uу), имеет координаты Ω0 и Uу0, которые соответствуют номинальной скорости вращения машины. Величины ΔΩ и ΔUу — достаточно малые отклонения напряжения и скорости, поэтому нелинейный участок характеристики принадлежащий точке С вполне можно заменить прямой (секущей или касательной). Рассматриваемый участок кривой можно рассматривать в отдельных осях (ΔΩ и ΔUу), которые обозначают отклонение величин Ω и ΔUу от их номинальных значений. Замену нелинейной характеристики линейной, основанной на малых отклонениях, называют линеаризацией. Рабочий участок можно обновить формулой ΔΩ = k0ΔUу, где k0 – крутизна характеристики, k0 = tgα.
Также необходимо отметить, что существую и САР со значительно нелинейными характеристиками, которые не подлежат линеаризации. Такие системы рассматривает раздел нелинейной теории автоматического регулирования.
Лекция 5. Системы автоматического регулирования. Задачи теории автоматического регулирования. Методы описания переходных процессов в САР
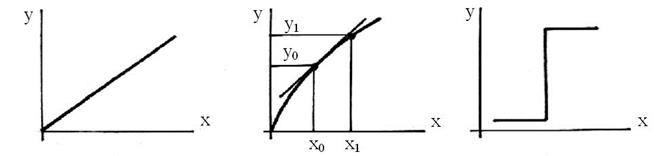
Задачей любой теории, направленной на решение вопросов проектирования технических устройств и систем, является создание формализованных математических моделей, в той или иной степени адекватных реальным механизмам, работающим в реальных условиях. Лишь в этом случае возможно проектирование с уверенностью, что изготовленная затем конструкция будет удовлетворять предъявляемым требованиям и давать желаемый эффект. Любые устройства и системы имеют два режима работы: статический и динамический (переходный), который происходит при перенастройке во время работы или как результат появления возмущений (изменение нагрузки, изменение окружающей среды и т. п.). Статический режим характеризуется статической характеристикой, т. е. зависимостью выходной величины от входной. Статические характеристики могут быть линейными, нелинейными, но линеаризуемыми при небольших отклонениях от рабочего режима заменой кривой касательной или секущей, и нелинейными, не поддающимися линеаризации, когда на характеристике имеется скачок, участки не зависимые от параметра входной величины и т. п. (рис. 47).
Рис. 47. Статические характеристики: а – линейная; б – нелинейная линеаризуемая в окрестностях рабочей точки; в – нелинейная нелинеаризуемая
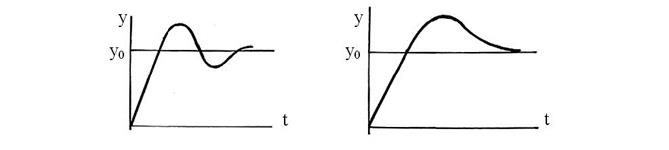
Переходный режим (иначе режим движения) характеризуется динамической характеристикой y = f(t) при изменении x(t) (рис. 48).
Рис. 48. Динамические характеристики: а – с колебаниями; б – апериодическая
Если в динамической характеристике колебания затухают и у становится постоянным, то такая система называется устойчивой и пригодна к эксплуатации, если окончательное значение у имеет допустимую ошибку. Если колебания постоянны с постоянной амплитудой, то это системы с ограниченной устойчивостью, и эксплуатация их возможна, если размах амплитуд меньше допустимой ошибки. Если же величина отклонения от данного значения у с течением времени лишь увеличивается, то это – неустойчивые системы, и эксплуатироваться они не могут. Таким образом, до воплощения системы в реальную конструкцию необходимо знать, будет ли она устойчива в диапазоне возможных изменений параметров, а кроме этого, насколько точно и быстро будет устраняться ошибка. Исходя из этого исследование переходного процесса наиболее полно отражает работоспособность автоматической системы, и поэтому задачами теории автоматического регулирования (ТАР) являются:
– выбор схемы и параметров элементов системы, исходя из предъявляемых требований процесса — синтез;
– исследование САР с целью изучения характеристик ее рабочих процессов, т. е. устойчивости и качества регулирования (точности и быстродействия) – анализ.
Накопленный опыт создания автоматических систем, работающих в промышленности, показал, что структурная схема любой системы включает устройства с определенными функциями (см. рис. 4). Исходя из этого для технических систем задача синтеза сводится к задаче коррекции, т. е. выбору дополнительных элементов, включение которых в структурную схему обеспечит нужный запас устойчивости и требуемое качество регулирования.
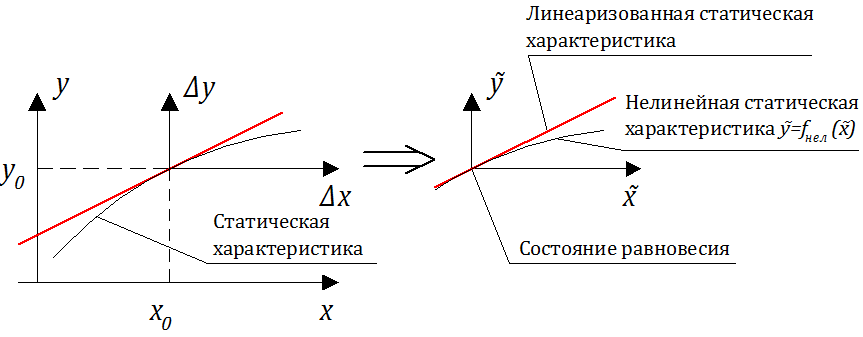
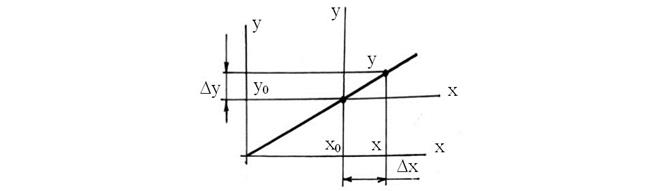
Для решения задачи анализа необходимо исследовать переходные процессы, происходящие в системе. Согласно структурной схеме, появление возмущения вызывает изменение по входу каждого элемента. Таким образом, действуя на вход элемента или системы известным сигналом, можно получить переходную характеристику как одного элемента, так и всей системы. Для упрощения рассмотрения переходных процессов в ТАР работа системы в установившемся режиме до появления возмущения не рассматривается, что равносильно переносу начала координат на статической характеристике в точку, которая соответствовала предыдущему режиму до возмущения (рис. 49), т. е. исключаются из рассмотрения постоянные значения.
Рис. 49.Условия для рассмотрения переходного процесса: х0, у0 – параметры постоянного рабочего режима до возмущения; х, у – параметры режима после
возмущения
Так как по своему назначению САР препятствует отклонению от заданного режима, то изменение Δх и Δу не могут быть значительными и, таким образом, если статическая характеристика и нелинейна, то ее короткий отрезок можно заменить прямой (касательной или секущей) без существенной погрешности, т. е. линеаризовать. Поэтому, несмотря на то, что в реальной действительности нет линейных зависимостей, в ТАР нелинейные непрерывные характеристики линеаризуются, о чем уже говорилось ранее. Учитывая все вышеизложенное, переходный процесс может быть представлен некоторой функцией F(y,x, ỷ,ÿ) = 0, зависящей от у,х и их производных ỳ,ÿ и т. д. Функция F может быть записана с помощью степенного ряда Тейлора как линейное дифференциальное уравнение (правая часть линейна):
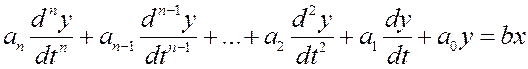
Здесь имеется в виду, что у и х – достаточно малые отклонения от первоначального значения, а коэффициенты 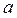
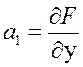
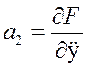
и являются постоянными (линейная зависимость – производные постоянны) для так называемых стационарных систем, таких, чьи параметры не зависят от времени (технические устройства) и определяются только конструкцией элементов. Поделив уравнение на 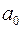
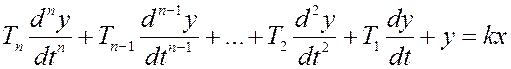
Если переходный процесс закончился, то все производные станут равны 0 и получаем линейную статическую характеристику у = kх. Коэффициент пропорциональности k, определяющий крутизну статической характеристики, называют коэффициентом усиления. Таким образом, для устройства, имеющего один вход и один выход, можно записать уравнение переходного процесса. Для анализа работы САР, учитывая принятое, система разбивается на динамические звенья, т. е. на устройства или узлы, входящие в них, имеющие один вход и один выход, поведение которых может быть описано с помощью линейных дифференциальных уравнений. При этом справедливым является принцип суперпозиции: результирующий эффект от нескольких независимых воздействий есть сумма эффектов, вызываемых каждым воздействием в отдельности. Исходя из этого можно рассматривать каждое динамическое звено отдельно и затем суммировать результат их поведения в переходном процессе, переходя к поведению всей системы.
Система, все звенья которой описываются линейными дифференциальными уравнениями, называется линейной. Если хотя бы одно звено системы нелинейно, то и вся система становится нелинейной и вышеизложенное к ней неприемлемо.
Анализ линейных САР производят следующим образом.
1. Расчленяют САР на динамические звенья.
2. Определяют статические характеристики каждого звена и, если они могут быть линеаризованы, то и всей системы.
3. Составляют уравнения динамики каждого звена.
4. Составляют динамическую структурную схему системы (связь отдельных звеньев) – графическое изображение уравнения движения системы.
5. Составляют общее уравнение динамики системы.
6. Анализируют уравнение, определяя устойчивость системы и качество регулирования.
Чтобы получить динамическую характеристику звена, и всей системы, необходимо решать дифференциальные уравнения. Решить дифференциальное уравнение – значит, найти такую функцию от заданного аргумента (в ТАР от t), которая удовлетворяет данному уравнению, т. е. при подстановке ее вместо у обращает это уравнение в тожество. Чтобы упростить составление общего дифференциального уравнения системы, в ТАР используют операторный метод, при котором функции времени заменяют соответствующими операторными изображениями. Операторное изображение дает возможность при составлении общего уравнения заменить операции дифференцирования и интегрирования на алгебраические действия. После получения общего уравнения в операторной форме можно перейти от изображения к реальной функции.
Операторным изображением функции времени f(t), которую называют оригиналом, является функция F(р) комплексной переменной 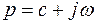
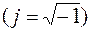
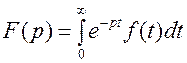
Преобразование Лапласа для типовых математических операций дается в виде таблиц в справочниках по математике. Обратное преобразование Лапласа :
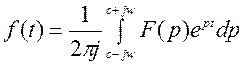
Эту формулу при анализе в TAP обычно не используют, а применяют другие способы. Практически же, чтобы записать дифференциальное уравнение в операторной форме преобразования Лапласа, нужно знак производной в дифференциальном уравнении заменить на символ оператора:
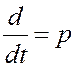
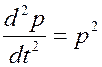

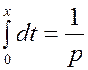
Оператор р рассматривается как число, которое можно подвергнуть алгебраическим действиям.
Запись дифференциальных уравнений дает возможность перейти к передаточным функциям, характеризующим звено и всю систему. Такой переход упрощает расчеты и не требует применения сложного математического аппарата. Дифференциальное уравнение в операторной форме звена или системы может быть представлено как: y(p) = W(p) х(p), где W(p) – передаточная функция оператора р .Часто запись упрощают, имея в виду все вышесказанное:
Таким образом, чтобы найти W(p), необходимо разделить у на х. Например, для дифференциального уравнения второго порядка
операторная формула 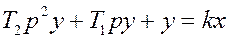
и находим передаточную функцию 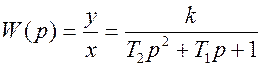
По передаточным функциям звеньев можно определить передаточную функцию всей системы, а затем уравнение движения.
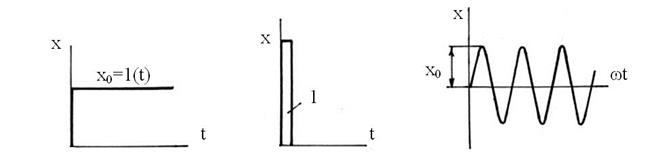
Реальные законы внешних воздействий, приложенных к системе, неизвестны, т. е. случайны. Поэтому в ТАР для анализа работы САР приняты типовые законы воздействия, имеющие место в реальных условиях: мгновенный скачок входной величины х (резкое увеличение нагрузки); синусоидальные колебания входной величины с постоянной амплитудой и изменяющейся частотой (вибрация); импульс бесконечно малой величины и бесконечно малой длительности (помеха). Если взять часть системы – звено, то можно любой сложный сигнал рассматривать через регулярные воздействия: единичное значение скачка (рис. 50, а), импульса, единичной амплитуды синусоидальных колебаний. Для линейных звеньев (правая часть дифференциального уравнения kx) переходную характеристику при регулярном скачкообразном воздействии x = x0 = 1(t) обозначают как h(t). Зная h(t) можно определить выходную величину у(t) при любом x(t) через интеграл Дюамеля (интеграл свертки в теории вероятности).
Рис. 50. Регулярные воздействия: единичный скачок (a), импульс единичной
площади (б) и синусоидальные колебания с единичной амплитудой (в)
Единичный импульс δ(t) – дельта функция, 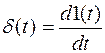

Реакция звена y(t) на единичный импульс – импульсная переходная функция – используется при анализе нестационарных линейных систем.
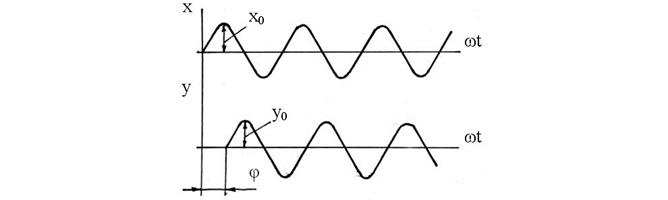
Для анализа реакции звена и системы на периодический сигнал на вход подается регулярный сигнал y = y0sin 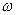
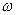
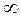
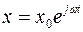
где 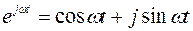
В результате на выходе звена сформируется сигнал
или 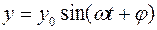
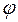
Рис. 51. Реакция звена на периодический сигнал
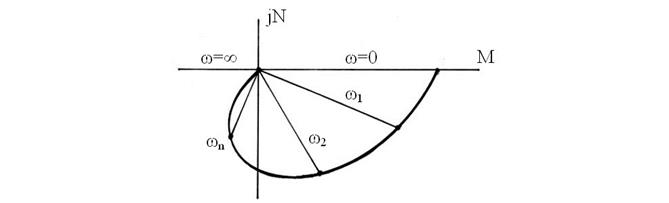
По мере увеличения частоты у0 будет уменьшаться, а угол 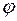
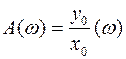
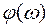
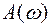
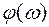
Рис. 52. Амплитудно-фазовая частотная характеристика
Представим связь между х и у при частотном воздействии в операторной форме как
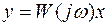
где 
Тогда 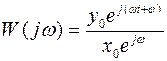

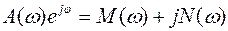
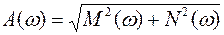
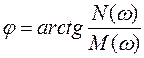
Для звеньев, которые описываются линейными дифференциальными уравнениями, существует однозначная связь между передаточной функцией 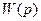
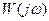
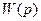
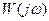
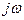
Построение и применение частотных характеристик упрощается при использовании логарифмических характеристик: амплитудно-частотной ЛАЧХ и фазочастотной. Для построения ЛАЧХ на оси абсцисс откладывают частоту 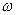
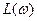
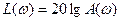
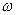
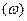

Рис. 53. Логарифмические частотные характеристики
Получить 
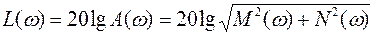
По логарифмическим частотным характеристикам чаще всего определяют поведение системы в переходном процессе. Логарифмическая характеристика 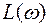

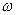
http://elenergi.ru/uravneniya-sistem-avtomaticheskogo-upravleniya.html
http://helpiks.org/7-54420.html