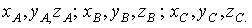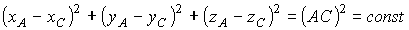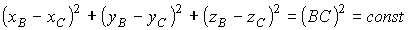Уравнение движения свободного твердого тела в векторной форме

Магия тензорной алгебры: Часть 15 — Движение несвободного твердого тела

Введение

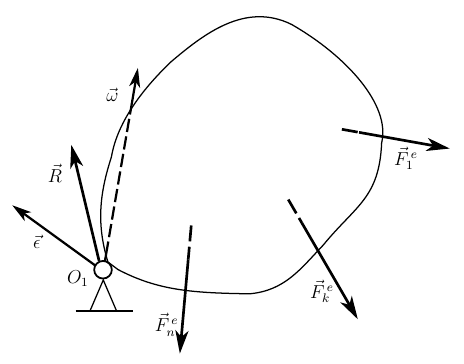
В прошлый раз мы рассмотрели один из способов получения дифференциальных уравнений движения твердого тела исходя из принципа Даламбера. Мы остановились на общей форме уравнений движения

Однако, внимательно взглянув на эти уравнения, меня следовало бы раскритиковать — дело в том, что в данных уравнениях число неизвестных слишком велико. К неизвестным следует отнести ускорение полюса и угловое ускорение тела , а также реакции связей . И если движение тела ограничено хотя бы одной связью, число неизвестных величин в (1) и (2) превышает число уравнений.

Это происходит потому, что левая часть уравнений (1) и (2) содержит ускорения, вычисляемые для случая свободного движения тела, то есть в них имеются избыточные координаты. Поэтому, систему (1), (2) следует дополнить уравнениями связей, описывающими ограничения, налагаемые связями на координаты, скорости и ускорения точек тела.

Этим мы сейчас и займемся — посмотрим, во что превращаются уравнения (1) и (2) при добавлении уравнений связей, и что дают нам полученные уравнения в практическом смысле.

1. Уравнения движения свободного твердого тела

Свободным называют такое тело, движение которого не ограничено связями. Соответственно в уравнениях (1) и (2) пропадают лишние неизвестные и они превращаются в

И для свободного тела нет смысла использовать произвольный полюс — лучше сменить центр приведения систем сил инерции на центр масс тела, записав уравнения движения в более простой форме

Уравнения (5) и (6) — дифференциальные уравнения свободного движения твердого тела. Они могут быть разрешены относительно ускорений и проинтегрированы численно, при заданных начальных условиях.

2. Уравнения движения твердого тела с одной неподвижной точкой

А теперь предположим, что движение тела ограничено сферическим шарниром, расположенным в точке . Тогда, выбрав полюс в этой неподвижной точке, мы можем добавить уравнение связи

Реакция сферического шарнира, выражается одной силой , поэтому, с учетом (7) уравнения (1) и (2) можно переписать в виде

причем , так как сила приложена в точке , значит, получаем окончательно

Уравнение (8) позволяет определить угловое ускорение тела, исходя из начальных условий задачи и известных активных сил, приложенных к телу, а уравнение (9) дает возможность, зная угловое ускорение, найти реакцию сферического шарнира. Таким образом мы получаем дифференциальные уравнения сферического движения.

3. Вращательное движение тела. Момент инерции тела относительно оси

Вращательным называется движение тела, когда две его точки остаются неподвижными в любой момент времени. Если выразить этот факт с помощью уравнений, то мы можем записать следующие уравнения связей

Условие (10) выражает неподвижность одной из точек тела, а условие (11) — неизменность направления оси вращения тела. Исходя из (11) можно выписать угловую скорость и угловое ускорение тела через параметры конечного поворота

Подставляем (12) и (10) в уравнение (2)

учитывая, что у нас две связи, и соответственно две реакции от подшипников, на которых происходит поворот тела. Причем сразу можно учесть, что , так как первая реакция приложена в точке . Кроме того выполним скалярное умножение последнего уравнения на орт оси вращения

Учтем, что момент второй реакции можно вычислить как , при этом , то есть получаем

Вторые слагаемые в обеих частях данного уравнения — смешанные произведения компланарных векторов и равны нулю, в итоге имеем

— дифференциальное уравнение вращения тела вокруг неподвижной оси, где

называют моментом инерции твердого тела относительно оси вращения, а

— проекция векторного момента относительно неподвижной точки на ось проходящую через эту точку или — момент силы относительно оси.

Выражение (14) крайне интересно. Если переписать его в тензорной форме, то мы получим формулу

позволяющую, по известному тензору инерции твердого тела определить его момент инерции относительно интересующей нас оси вращения, направление которой в пространстве задано ортом . Момент инерции (16) является скалярной величиной, характеризующей распределение массы тела вокруг оси вращения. Эта величина, равно как и уравнение (13) хорошо известны из общего курса теоретической механики.

4. Поступательное движение тела

При поступательном движении, связи, наложенные на тело препятствуют его вращению. В этом случае мы можем записать очевидные равенства

Полагая идеальность связей, мы можем записать условие, накладываемое на их реакции

где — вектор, касательный к траекториям точек тела. В случае поступательного движения, траектории всех его точек одинаковы, а значит и вектор касательной к траектории одинаков для всех точек. С учетом (17) и (18) можно переписать уравнение (1)

— дифференциальное уравнение поступательного движения тела в проекциях на касательную к траекториям его точек.

Заключение

В данной статье мы рассмотрели, как преобразуются общие уравнения движения твердого тела (1) и (2) если дополнить их уравнениями связей. При этом, мы легко и непринужденно построили дифференциальные уравнения движения для всех частных случаев движения тела, изучаемых теоретической механикой.

Благодарности

при подготовке данной статьи использован метод, предложенный пользователем SeptiM. В связи с очевидным удобством работы, хочу выразить признательность автору, за проделанную им работу.

Общий случай движения свободного твердого тела

Общий случай движения свободного твердого тела

• Разложение свободного движения твердого тела на перемещение и вращение Рассмотрим общее движение свободного твердого тела, то есть объекта с 6 степенями свободы. Наиболее распространенным движением свободного твердого тела является На рисунке 82 показано, что оно состоит из поступательного движения с любой точкой на теле и вращательного движения вокруг этой точки. Положение тела относительно системы координат O1x1u121 полностью определяется путем указания трех точек тела, которые не находятся на одной прямой линии, или путем указания треугольника, прикрепленного к телу (рисунок 82).

Треугольник ABC и связанное с ним тело можно перевести одним переводом вместе с любой точкой на теле из одного положения I в другое (например, точка A, когда перемещается система координат перемещения) Вы можете двигаться, вращая движущуюся систему координат Hxijizi, то есть вокруг оси, проходящей через эту точку. Поступательная часть движения тела зависит от выбора точки, в которой перемещается тело, а вращательная часть движения вокруг оси или точки не зависит от выбора точки. Поступательная часть смещения может быть заменена вращающейся частью, и, наконец, они могут выполняться одновременно.

Следовательно, для существования возможной диаграммы равновесия с определенной волной, если давление T меньше этого предела, единственной возможной диаграммой равновесия должна быть прямая линия. Людмила Фирмаль

Это означает, что вы можете вращать тело вокруг точки на требуемый угол при перемещении из одного положения в другое. Если два положения тела близки к бесконечности, истинное базовое движение свободного твердого тела заменяется базовым поступательным движением с базовым вращением вокруг любой точки тела и мгновенной оси, проходящей через эту точку. Он выполняется одновременно с настоящим движением. Таким образом, свободные движения твердого тела могут быть заменены серией поступательных движений с точкой тела, которая работает одновременно с истинным движением и вращением вокруг этой точки.

Перевод и движение по точкам тела Система координат Ax’iy’tZ’i является переносным движением, а движение тела относительно этой движущейся системы координат представляет собой вращение вокруг мгновенной оси, которая проходит через эту точку движения тела в каждый момент и является относительным. Это движение. Таким образом, движение свободного твердого тела может состоять из поступательного движения с движущейся системой координат и сферического движения, связанного с этой системой координат. Для относительного сферического движения можно ввести угловую скорость и угловое ускорение.

Это первая производная по времени от ©, как в случае вращения объекта вокруг фиксированной точки. Угловую скорость и ускорение относительного вращательного движения вокруг любой точки на теле обычно называют угловой скоростью и ускорением свободного твердого тела. Эти значения не зависят от выбора точки на теле. Только поступательное движение тела зависит от выбора точек на теле. Уравнение движения свободного твердого тела В общем случае, чтобы определить положение свободного твердого тела относительно системы координат Oixlylzi, задайте положение другой системы координат Ox’ij’iZi относительно этой системы координат и первой системы вместе с точкой O с рассматриваемым объектом.

• Для системы координат Ox’iy’iz’i достаточно системы координат Oxyz, связанной с движущимся телом (рис. 83). Для простоты будем считать, что оси Ox \, Oy \, Oz \ параллельны осям Otxlt Olyl, Olzl соответственно. Следовательно, положение свободного твердого тела относительно системы координат полностью определяется, когда: В связи с этой системой координаты точки O объекта как единой функции времени и движущейся системы координат Oxyz закреплены за движущимся телом относительно системы координат Ox \ y \ z, которая переводится вместе с точкой O объекта Укажите угол Эйлера. —0-LI: ♦ — /. (‘); • — /, (* Ф ”ЛИ (, О | Уравнение (20) является уравнением движения свободного твердого тела в случае общего движения.

Есть шесть из этих уравнений. Другими словами, это то же самое, что и степень свободы свободного тела. Первые три уравнения (20) определяют подвижное движение тела вдоль точки О, а вторые три уравнения определяют вращательное движение вокруг этой точки. Первые три уравнения для движения свободного твердого тела зависят от выбора точки объекта O. Последние три уравнения (углы Эйлера) не зависят от выбора точки O, в которой учитывается вращение объекта.

Однако если снаряд сферический и не вращается, то результат получается в вертикальной плоскости, включающей скорость центроида, а траектория этой точки плоская из-за симметрии. Людмила Фирмаль

Скорость и ускорение свободной жесткой точки в общем случае Поскольку движение свободного твердого тела в общем случае может быть выражено как сложное движение, как скорость, так и ускорение в любой точке M этого объекта могут быть рассчитаны в соответствии с теоремой сложения скорости и ускорения (рис. 84). Следовательно, для скорости v в точке М Конкретное движение, похожее на фигуру, представляет собой поступательное движение тела вдоль точки O этого тела. Следовательно, поступательная поступательная скорость одинакова во всех точках тела и равна скорости b0 в точке O.

Поскольку относительное движение представляет собой вращение вокруг точки O, скорость относительного движения можно рассчитать с использованием векторного уравнения Эйлера. Рисунок 84 Где r — радиус-вектор точки М, взятый из точки 0. Скорость вращения тела вокруг точки O, или ось мгновенного движения, проходящая через точку O Наконец, получим следующее уравнение для скорости точки М: v = vo + mxr. (21) Уравнение (21) может быть получено путем прямой дифференциации векторного уравнения. p = p0 + r Справедливо в любой момент. Возьмем суммарную производную по времени по обеим сторонам уравнения, учитывая изменение вектора относительно фиксированной системы координат Oixiylzl. У нас есть дп / д т-дп0 / др + др / др Здесь dp / dr = v и dp0 / dr = «0» — скорости точек объектов M и O.

Модуль вектора r как отрезка, соединяющего две точки объекта, равен Поэтому в соответствии с формулой производной по времени от модуля постоянного вектора: dr / dr = «> xr. Объедините результаты, чтобы получить уравнение (21). Как и в случае жесткого плоского движения, часть скорости hx можно интерпретировать как скорость от вращения объекта вокруг точки O Ускорение a в точке M (рис. 85) в конкретном случае, когда переносное движение представляет собой поступательное движение, составляет a = ae + ag.

Ускорение удельного движения всех точек тела равно ускорению a0 в точке O, потому что движение вдоль точки O считается поступательным движением. Как и в случае вращения тела вокруг неподвижной точки, ускорение относительного движения состоит из вращательного компонента и непрерывного компонента. ar = Exh + a> x «5r = exp + a> x (wxr), (22) Где е — угловое ускорение тела. Окончательное уравнение для ускорения точки M свободного тела в случае общего движения a = a0 + exr + ^ / dz = d

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Уравнение движения свободного твердого тела в векторной форме

Абсолютно твердым телом в механике называют идеализированную систему материальных точек, все расстояния между которыми при движении системы не изменяются с течением времени.

Чтобы однозначно определить положение твердого тела достаточно задать положение каких-либо трех точек А, В, С, не лежащих на одной прямой. Положение точек можно задать их прямоугольными координатами

Эти девять координат, однако, не независимы, а связаны тремя соотношениями:

поскольку длины АВ, АС, ВС не изменяются при движении твердого тела. Независимых координат остается только шесть — твердое тело имеет шесть степеней свободы. Отметим, что твердое тело, одна из точек которого неподвижно закреплена, может только вращаться вокруг этой неподвижной точки, имеет три степени свободы. Твердое тело, которое может только вращаться вокруг закрепленной оси, имеет одну степень свободы.

Если же твердое тело может скользить вдоль закрепленной оси и одновременно вращаться вокруг нее, то число степеней свободы равно двум.

Уравнение движения и равновесия твердого тела

Так как твердое тело является механической системой с шестью степенями свободы, то для описания его движения требуется шесть независимых числовых уравнений или два независимых векторных уравнения.

Одно из них — это уравнение движения центра масс С

, где . (1)

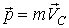
Второе — уравнение моментов

. (2)

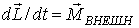
Если твердое тело покоится, то уравнения (1) и (2) переходят в

. (3)

Это необходимые условия равновесия твердого тела. Но они не являются достаточными. При их выполнении центр масс может двигаться прямолинейно и равномерно с произвольной скоростью, а само тело может вращаться с сохранением момента импульса. Такое движение твердого тела называют свободным. Следует отметить, что даже свободное движение твердого тела может быть очень сложным. Поэтому сначала рассмотрим простейший случай движения твердого тела.