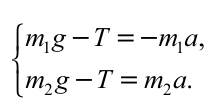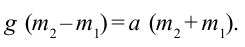Магия тензорной алгебры: Часть 14 — Нестандартное введение в динамику твердого тела
Введение
Динамика твердого тела — раздел механики, который в своё время задал четкий вектор развития этой науки. Это один из самых сложных разделов динамики, и задача интегрирования уравнения сферического движения для произвольного случая распределения массы тела не решена до сих пор.
В этой статье мы начнем рассматривать динамику твердого тела, применяя аппарат тензорной алгебры. Эта пилотная статья о динамике ответит на ряд фундаментальных вопросов, касающихся, например, такого важного понятия как центр масс тела. Что такое центр масс, что отличает его от остальных точек тела, почему уравнения движения тела составляют в основном относительно этой точки? Ответ на эти, и некоторые другие вопросы находится под катом.
Интегрирование уравнений движения этой детской игрушки — одна из до сих пор не решенных задач механики.
1. Старый, как мир, принцип Даламбера
Для начала рассмотрим движение материальной точки. Непосредственно из аксиом вытекает основное уравнение динамики точки
ускорение помноженное на массу есть векторная сумма приложенных к точке сил. И о силах, которые приложены к точке надо поговорить подробнее. В разделе механики, называемом аналитической механикой, силы, прикладываемые к точкам механической системе подлежат строгой классификации.
Силы, стоящие в правой части (1) разделяются на две группы
- Активные силы. Этой группе сил можно дать следующее определение
Активными называют силы, величину которых можно определить из условия задачи
Говоря формальным языком, активная сила определяется вектор функцией
где — обобщенная координата точки;
— обобщенная скорость точки. Из данного выражения видно, что начиная решать задачу о движении и имея начальные условия (момент времени, положение и скорость) можно сразу рассчитать активную силу.
Сила тяжести, упругости, Кулоновская сила взаимодействия заряда с электрическим полем, сила Ампера и сила Лоренца, сила вязкого трения и аэродинамического сопротивления — всё это примеры активных сил. Выражения для их расчета известны и эти силы можно посчитать, зная положение и скорость точки.
Реакции связей. Самые неприятные силы, которые только можно придумать. Напомню одну из аксиом статики, именуемую аксиомой о связях
Связи приложенные к телу можно отбросить, заменив их действие силой, или системой сил
Изображенная на рисунке точка — не свободная точка. Её движение ограничено связью, условно представленной в виде некой поверхности, в пределах которых располагается траектория движения. Приведенная выше аксиома дает возможность убрать поверхность, приложив к точке силу , действие которой эквивалентно наличию поверхности. При этом данная сила не является известной заранее — её величина удовлетворяет ограничениям на положение, скорость и ускорение, накладываемыми связью, ну и, разумеется вектор реакции зависит от приложенных активных сил. Реакции связей подлежат определению в процессе решения задачи. К реакциям связей относится так же и сухое трение, наличие которого даже в простой задаче существенно осложняет процесс её решения.
Исходя из данной классификации, уравнение движения точки (1) переписывают в виде
где — равнодействующая активных сил, приложенных к точке;
— равнодействующая реакций, наложенных на точку связей.
А теперь проделаем простейший фокус — ускорение с массой перенесем в другую часть уравнения (2)
и введем обозначение
Тогда, уравнение (2) превращается в
Сила, представляемая вектором (3) называется силой инерции Даламбера. А уравнение (4) выражает принцип Даламбера для материальной точки
Материальная точка находится в равновесии под действием приложенных к ней активных сил, реакций связей и сил инерции
Позвольте, о каком равновесии может идти речь, если точка движется с ускорением? Но ведь уравнение (4) есть уравнение равновесия, и приложив к точке силу (3) мы можем заменить движение точки её равновесием.
Достаточно распространен спор о том, являются ли силы инерции (3) физическими силами. В инженерной практике используется понятие центробежной силы, которая есть сила инерции, связанная с центростремительным (или осестремительным) ускорением, искривляющим траекторию точки. Моё личное мнение таково, что силы инерции есть математический фокус, продемонстрированный выше, позволяющий перейти к рассмотрению равновесия вместо движения с ускорением. Сила инерции (3) определяется ускорением точки, но оно, в свою очередь определяется действием на точку приложенных к ней сил, и в соответствии аксиоматикой Ньютона сила первична. Поэтому ни о какой «физичности» сил инерции говорить не приходится. Природа не знает активных сил, зависящих от ускорения.
2. Принцип Даламбера для твердого тела. Главный вектор и главный момент сил инерции
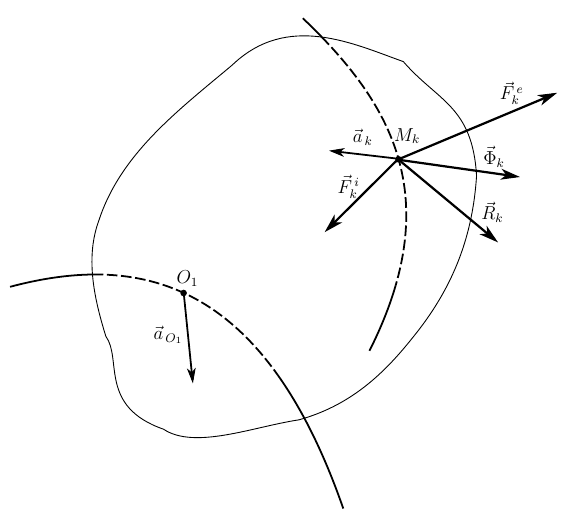
Теперь распространим уравнение (4) на случай движения твердого тела. В механике его рассматривают как неизменяемую механическую систему, состоящую из множества точек, расстояние между которыми в каждый момент времени остается неизменным. Все точки тела движутся по различным траекториям, но уравнение движения каждой точки соответствует (2)
Силы, действующие на конкретную точку можно разделить на внешние активные , реакции внешних связей
, и внутренние силы
, представляющие собой силы взаимодействия рассматриваемой точки с остальными точками тела (по сути — внутренние реакции). Все упомянутые силы есть равнодействующие соответствующей группы сил, приложенных к точке. Применим к этому уравнению Принцип Даламбера
где — сила инерции, приложенная к данной точке тела.
Теперь, когда все точки тела находятся в равновесии, мы можем воспользоваться условием равновесия твердого тела, которое дает нам статика
Твердое тело находится в равновесии под действием приложенной к нему системы сил, если главный вектор и главный момент этой системы сил, относительно выбранного центра O, раны нулю
Главный вектор системы сил — это векторная сумма всех сил, приложенных к телу. Сумма сил, приложенных к каждой точке тела определяется последним уравнением, поэтому складывая уравнения для всех точек, в левой его части получим главный вектор
При этом, сумма внутренних сил равна нулю, как следствие из третьего закона Ньютона. Аналогично вычисляем сумму моментов всех сил относительно выбранного произвольного центра O, что дает нам равный нулю главный момент системы сил
причем, как показывается в классическом курсе динамики, сумма моментов внутренних сил, приложенных к системе материальных точек, равна нулю, то есть . Уравнения (5) и (6) уже выражают принцип Даламбера применительно к твердому телу, но лишь с одной необходимой поправкой.
Число активных сил и реакций связей в уравнениях (5) и (6) конечно. Большинство слагаемых в соответствующих суммах равны нулю, ибо активные внешние силы и реакции внешних связей, вообще говоря, приложены лишь в некоторых точках тела. Чего нельзя сказать о силах инерции — силы инерции приложены к каждой точке тела. То есть сумма сил инерции, и сумма их моментов относительно выбранного центра есть суммы интегральные. Систему сил инерции принято сводить к главному вектору и главному моменту и мы можем написать, что
главный вектор и главный момент сил инерции, приложенных к твердому телу. Интегралы (7) и (8) берутся по всему объему тела, а — радиус вектор точки тела относительно выбранного центра O.
Исходя из данного соображения мы можем переписать (5) и (6) в окончательном виде
Уравнения (10) и (11) выражают принцип Даламбера для твердого тела
Теврдое тело находится в равновесии под действием приложенных к нему внешних сил, реакций связей, главного вектора и главного момента сил инерции.
По сути (10) и (11) есть форма записи дифференциальных уравнений движения твердого тела. Они довольно часто применяются в инженерной практике, однако с точки зрения механики, такая форма записи уравнений движения не является самой удобной. Ведь интегралы (7) и (8) можно вычислить в общем виде и придти к более удобным уравнениям движения. В этой связи (10) и (11) следует рассматривать как теоретическую основу построения аналитической механики.
3. На сцену выходят центр масс и тензор инерции
Вернемся к нашим тензорам и с их помощью вычислим интегралы (7) и (8) для общего случая движения твердого тела. В качестве центра приведения выберем точку O1. Эта точка выбрана в качестве полюса и в ней определен локальный базис связанной с телом системы координат. В одной из прошлых статей мы определили тензорное соотношение для ускорения точки тела в таком движении
Умножив (12) на массу точки со знаком минус, мы получим силу инерции, приложенную к элементу объема твердого тела
Выражение (13) — ковариантное представление вектора силы инерции. Двойное векторное произведение в (12) перепишем в более удобной форме, используя тензор Леви-Чивиты и псевдовекторы угловой скорости и углового ускорения
Подставляем (14) в (13) и берем тройной интеграл по всему объему тела, учитывая, что угловая скорость и угловое ускорение одинаковы в каждой точке этого объема, то есть их можно вынести за знак интеграла
Интеграл в первом слагаемом — это масса тела. Интеграл во втором слагаемом более интересная штука. Вспомним одну из формул курса теоретической механики:
где — контравариантные компоненты радиус-вектора центра масс рассматриваемого тела. Не в даваясь в смысл понятия центра масс просто заменим интегралы в (15) в соответствии с формулой (16), учтя, что во втором слагаемом (15) используются ковариантные компоненты.
Ага, выражение (17) тоже нам знакомо, представим его в более привычной векторной форме
Первое слагаемое в (18) — сила инерции, связанная с поступательным движением тела вместе с полюсом. Второе слагаемое — центробежная сила инерции, связанная с осествемительным ускорением центра масс тела при его движении вокруг полюса. Третье слагаемое — вращательная составляющая главного вектора сил инерции, связанная с вращательным ускорением центра масс вокруг полюса. В общем-то всё находится в соответствии с классическими соотношениями теормеха.
Пытливый читатель скажет: «зачем применять тензоры для получения этого выражения, если в векторном виде оно было бы получено не менее очевидным способом?». В ответ я скажу, что получение формул (17) и (18) — это была разминка. Теперь мы получим выражение главного момента сил инерции относительно выбранного полюса, и тут тензорный подход проявляет себя во всей красе.
Возьмем уравнение (13) и умножим его векторно слева на радиус вектор точки тела относительно полюса. Тем самым мы получим момент силы инерции, приложенной к элементарному объему тела
Снова выполним подстановку (14) в (19), но не станем торопится брать интеграл
Не знаю как у вас, а у меня рябит в глазах, даже при моей привычности к таким формулам. Слагаемые расположены в более естественном порядке — переставлены местами вращательная и центробежная составляющие. Кроме того, от первого слагаемого ко второму возрастает сложность преобразующих выкладок. Будем упрощать их по очереди, сначала упростим первое, сразу взяв интеграл
Тут снова появился радиус вектор центра масс. Здесь ничего сложного — ускорение полюса у нас одно и мы вынесли его за знак интеграла. Интерпретацией займемся чуть позже, а пока преобразуем второе слагаемое (20). В нем мы можем выполнить свертку произведения тензоров Леви-Чивиты по немому индексу k
Здесь мы воспользовались свойством дельты Кронекера заменять свободный индекс вектора/ковектора при выполнении свертки. Теперь возьмет интеграл, учтя, что угловое ускорение постоянно для всего объема тела
Во как! Малопонятный «крокодил», путем формальных тензорных преобразований схлопнулся в компактную формулу. Я лукавлю, мы ввели новое обозначение:
Но это не просто абстрактная формула. По структуре выражения (24) видно, что оно отражает распределение массы тела вокруг полюса и называется оно — тензор инерции твердого тела. Эта величина имеет поистине фундаментальное значение для механики, и о ней мы поговорим подробнее, пока лишь скажу, что (24) — тензор второго ранга, компонентами которого являются осевые и центробежные моменты инерции тела в выбранной системе координат. Он характеризует инертность твердого тела при вращении. Обращаю внимание читателя и на то, как быстро мы получили выражение для тензора инерции, по сути действуя формальным способом. С векторными соотношения без ломки мозгов не обойтись, в этом я убедился на личном опыте.
Ну и наконец обратимся к последнему слагаемому (20). При взятии интеграла в нём тоже должен получится тензор инерции, и мы будем преобразовывать его таким образом, чтобы достичь этой цели. В этой части выражения (20) должно фигурировать соотношение между тензором инерции и угловой скоростью тела. Приступим, для начало свернув произведение тензоров Леви-Чивиты
Налицо существенное упрощение выражения — за счет свойств дельты Кронекера и того, что векторное произведение . Но тензора инерции в (25) не видно. С целью его получить проведем ряд эквивалентных преобразований
Здесь мы снова учли, что , воспользовались свойствами дельты Кронекера и операцией поднятия/опускания индексов при умножении на метрический тензор. И, теперь мы интегрируем (26)
Здесь мы снова видим тензор инерции:
с учетом которого получаем компактное выражение для составляющей главного момента сил инерции, связанного с центробежными силами
Выражение (27) эквивалентно векторно-матричному соотношению:
И хоть меня и переполняют пафосные фразы, отложу их на потом, а сейчас аккуратно выпишу итоговый результат в векторной форме.
В общем случае движения твердого тела главный вектор и главный момент сил инерции, приложенных к твердому телу, равны
А теперь все же восхитимся — не смотря на то, что вышеприведенные преобразования похожи на египетские иероглифы, они формальны, мы просто выполняли действия над индексами тензоров и использовали свойства тензорных операций. Нам не надо было упражняться с векторами, расписывать векторные операции в компонентах и сводить получившиеся проекции векторов к результатам матричных операций. Все матричные и векторные операции конечных выражение вышли у нас автоматически. К тому же, естественным образом получены такие фундаментальные характеристики как координаты центра масс тела и тензор инерции.
Читая лекции студентам я задался целью вывести (29) и (30) оперируя векторами. После того как я перевел стопку бумаги и изрядно поломав мозги я пришел к результату. Поверьте на слово — вышеприведенные преобразования просто семечки, в сравнении с тем, через что надо пройти не используя тензоров.
К тому же, выражения (29) и (30) получены нами для произвольного центра приведения сил, в качестве которого мы взяли полюс O1. Эти выражения помогут нам понять что такое центр масс тела и его важность для механики.
4. Особая роль центра масс
Используя формулы (29) и (30) вернемся к уравнениям (10) и (11) и, выполнив подстановку, придем к дифференциальным уравнениям движения твердого тела
Чем плохи эти уравнения? А тем, что они зависят друг от друга — ускорение полюса будет зависеть от углового ускорения и угловой скорости тела, угловое ускорение — от ускорения полюса. Вектор определяет положение центра масс тела по отношению к полюсу. А что если мы выберем полюс прямо в центре масс? Тогда ведь
и уравнения (31), (32) примут более простой вид
Узнаете эти уравнения? Уравнение (33) — теорема о движении центра масс механической системы, а (34) — динамическое уравнение Эйлера сферического движения. И эти уравнения независимы друг от друга. Таким образом, центр масс твердого тела — это точка, относительно которой силы инерции приводятся к наиболее простому виду. Поступательное движение вместе с полюсом и сферическое вокруг полюса — динамически развязаны. Тензор инерции тела, вычисляется относительно центра масс и называется центральным тензором инерции.
Уравнения (33), (34) в зарубежной литературе называют уравнениями Ньютона-Эйлера, и, в настоящее время весьма активно используются для построения ПО, предназначенного для моделирования механических систем. В рамках цикла о тензорах мы ещё не раз о них вспомним.
Заключение
Прочитанная вами статья имеет две цели — в ней мы ввели базовые понятия динамики твердого тела и проиллюстрировали мощность тензорного подхода при упрощении громоздких векторных соотношений.
В дальнейшем мы подробнее остановимся на тензоре инерции и изучим его свойства. Погрузившись в дебри аналитической механики, сведем уравнения (31) — (34) к уравнениям движения в обобщенных координатах. В общем, рассказать ещё есть о чем. А пока, благодарю за внимание!
Движение тел под воздействием нескольких сил в физике — формулы и определение с примерами
Движение тел под воздействием нескольких сил:
Во время изучения второго закона Ньютона рассматривался случай, когда на тело действовала одна сила. Третий закон Ньютона описывает процесс взаимодействия тел при участии нескольких сил. В повседневной жизни тоже не наблюдаются случаи, где на тело действует только одна сила. На двигающиеся тела, кроме силы притяжения, также действует и сила трения. На тело с массой
Здесь воспользуемся понятием равнодействующая сила. Равнодействующей силой принято считать геометрическую сумму всех приложенных к телу сил, т.е. результирующую силу. В данном случае получаем:
Берется алгебраическая сумма силы притяжения и силы трения. В этом случае силы, действующие на тело, направлены противоположно, и ее модуль определяется как:
Полученное телом ускорение по второму закону Ньютона определяется из выражения:
Рассмотрим две задачи, в которых на тело действует несколько сил.
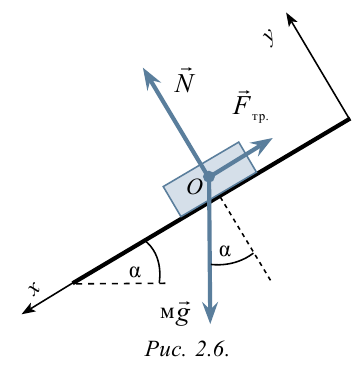
1. Рассмотрим условия равновесия и ускорение падения тела, установленного на наклонной плоскости (рисунок 2.6). Здесь 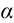
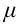
На доску, находящуюся на наклонной плоскости, действуют: сила тяжести 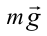
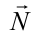
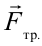
Ось 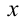
Чтобы тело оставалось в равновесии на наклонной плоскости, равнодействующая сила действующих на него сил должна быть равна нулю:
Исходя из этого составим системы уравнений для проекции на оси
координат:
- По оси
;
- По оси y: mg cosα + N = 0.
Чтобы тело оставалось в равновесии на наклонной плоскости, должно выполняться неравенство: 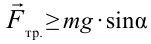
Согласно первого уравнения 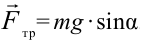
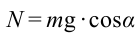
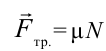
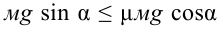
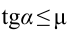
Таким образом, при выполнении условия 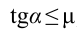
При условии 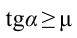
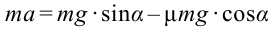
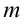
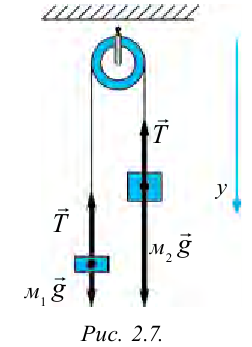
2. На неподвижный блок, с ничтожной малой массой подвешены грузы с массами 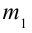
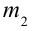
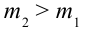
На каждый груз действуют две силы: сила тяжести и сила натяжения нити. Требование не учитывать массу блока и нити, а также силу трения означает, что они одинаковы на обоих сторонах нити. Силу натяжения нити обозначим 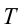
В связи с тем, что нить не растяжима, модуль перемещения грузов и соответственно скорость и ускорение будут равными. Модуль ускорения грузов обозначим как 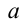
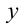
вниз, для проекции на ней составим систему уравнений:
Из второго уравнения вычитаем первое уравнение:
Решаем оба уравнения относительно Т и получаем 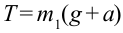
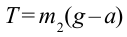
Из этой формулы находим вес каждого груза.
Основные понятия, правила и законы:
| Формулировка пер- вого закона динамики по Галилею. | Если на тело не действуют другие тела, то оно сохраняет свое состояние покоя или прямолинейного равномерного движения относительно Земли. |
| Первый закон динамики | Существуют такие системы отсчета, называемые инерциальными, относительно которых тело движется прямолинейно и равномерно, или покоится, если на него не действует сила, или действие внешних сил взаимно скомпенсировано. |
| Сила | Количественное измерение причины получения ускорения тел в результате взаимодействия друг с другом. |
| Инертная масса | Физическая величина, определяемая соотношением 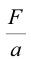 |
| Второй закон динамики | Полученное телом ускорение прямо пропорционально приложенной к нему силе и обратно пропорционально массе тела: 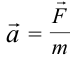 ; произведение ; произведение массы тела на ускорение равно действующей на тело силе: 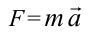 (под «силой» понимается (под «силой» понимается равнодействующая всех сил). |
| Третий закон динамики | Действие равно противодействию. Тела действуют друг на друга с силами, направленными противоположно вдоль одной и той же прямой, и равными по значению: 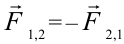 . . |
| Инерциальные системы отсчета | Системы отсчета, относительно которых материальная точка находится в покое или двигается прямолинейно и равномерно. |
| Неинерциальные системы отсчета | Системы отсчета, которые двигаются криволинейно или с ускорением. |
| Сила инерции | Сила, которая появляется в результате движения с ускорением |
| Первая космическая скорость | Скорость, которая необходима телу, чтобы стать искусственным спутником Земли – 7,91 км/с. |
| Вторая космическая скорость | Скорость, необходимая для полета к планетам солнечной системы – 11,2 км/с. |
| Третья космическая скорость | Скорость, необходимая для преодоления силы притяжения Солнечной системы и выхода за ее пределы – 16,7 км/с. |
| Вес тела при движении вертикально с ускорением 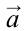 | 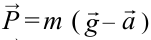 – вес тела, опускающегося вниз. – вес тела, опускающегося вниз. 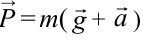 – вес тела, поднимающегося вверх. – вес тела, поднимающегося вверх. |
| Невесомость | Состояние, при котором сила взаимодействия тела с опорой или подвесом равна нулю. |
| Перегрузка | 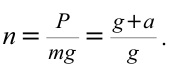 |
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
- Движение тела, брошенного под углом к горизонту
- Принцип относительности Галилея
- Движение в гравитационном поле
- Зависимость веса тела от вида движения
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Динамика твердого тела и системы. Все определения, законы и теоремы
Механическая система. Основные понятия
Свойства внутренних сил
Приводимые ниже свойства внутренних сил являются третьим законом Ньютона для системы материальных точек.
Свойство 1
Векторная сумма (главный вектор) всех внутренних сил системы равна нулю:
.
Свойство 2
Векторная сумма моментов всех внутренних сил системы, относительно произвольной точки O равена нулю:
.
Дифференциальные уравнения движения точек системы
Согласно второму закону Ньютона, дифференциальное уравнение движения материальной точки k массой mk , входящей в систему, имеет вид:
.
Спроектировав это уравнение на оси декартовой системы координат Oxyz , получим для каждой точки три уравнения:
.
Общие теоремы динамики механической системы
Общие теоремы динамики – это теорема о движении центра масс механической системы, теорема об изменении количества движения, теорема об изменении главного момента количества движения (кинетического момента) и теорема об изменении кинетической энергии механической системы.
Теорема о движении центра масс механической системы
Теорема о движении центра масс механической системы
Произведение массы системы на ускорение ее центра масс равно векторной сумме всех действующих на систему внешних сил:
.
Здесь – масса системы; – ускорение центра масс системы: ;
– скорость центра масс системы: ;
– радиус вектор (координаты) центра масс системы: ;
– координаты и массы точек, из которых состоит система.
Теорема об изменении количества движения (импульса)
Теорема об изменении количества движения в дифференциальной форме
Производная по времени от количества движения (импульса) системы равна векторной сумме всех действующих на систему внешних сил:
.
Теорема об изменении количества движения в интегральной форме
Изменение количества движения (импульса) системы за некоторый промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени:
.
Закон сохранения количества движения (импульса)
Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянным. То есть все его проекции на оси координат будут сохранять постоянные значения.
Если сумма проекций внешних сил на какую-либо ось равна нулю, то проекция количества движения системы на эту ось будет постоянной.
Тело переменной массы. Движение ракеты
Уравнение Мещерского
Дифференциальное уравнение движения точки переменной массы называется уравнением Мещерского:
.
Здесь – масса тела, которая является функцией от времени t ; – векторная сумма приложенных к телу внешних сил; – скорость отделяющихся частиц относительно тела.
Реактивная сила направлена в сторону, противоположную истечению отделяющихся частиц (топлива), и определяется по формуле:
,
где – расход топлива (кг/с).
Формула Циолковского
Скорость v движения ракеты под действием одной только реактивной силы определяется по формуле Циолковского:
.
Здесь – начальная скорость ракеты; u – скорость истечения реактивных газов относительно ракеты; – масса сгоревшего топлива; – масса корпуса ракеты с остатками топлива. Когда топливо выгорает полностью, то – это масса корпуса ракеты с полезной нагрузкой.
Отношение первоначальной массы ракеты (с полным запасом топлива) к массе корпуса ракеты называется числом Циолковского:
.
Для достижения первой космической скорости км/с , при , требуется, чтобы скорость истечения реактивных газов была не менее км/с . В современных жидкостных двигателях удается получить скорость истечения км/с . Поэтому, для достижения космических скоростей, ракеты должны быть многоступенчатыми.
Теорема об изменении главного момента количества движения (теорема моментов)
Теорема моментов в инерциальной системе координат
Главный момент количества движения (или кинетический момент) системы является характеристикой вращательного движения. Возьмем систему координат Oxyz с началом в точке O . Тогда , проекции кинетического момента системы на оси координат являются моментами количества движения системы относительно этих осей:
;
;
.
Если система состоит из нескольких частей, то главный момент количества движения системы равен сумме моментов количеств движения отдельных ее частей.
Теорема об изменении главного момента количества движения (теорема моментов)
Производная по времени от главного момента количества движения системы относительно некоторого неподвижного центра O равна сумме моментов всех внешних сил системы относительно того же центра:
(М2) .
Выпишем компоненты уравнения (М2) в неподвижной системе координат Oxyz :
;
;
.
Закон сохранения главного момента количества движения (момента импульса)
Если сумма моментов всех приложенных к системе внешних сил относительно данного неподвижного центра O равна нулю, то главный момент количества движения системы относительно этого центра будет постоянным. То есть все его проекции на оси координат будут сохранять постоянные значения:
.
Часто встречаются случаи, когда система вращается вокруг неподвижной оси. Тогда нужно спроектировать векторное уравнение (М2) на направление этой оси. В результате получим теорему моментов, применительно к вращению относительно оси.
Производная по времени от кинетического момента системы относительно некоторой неподвижной оси равна сумме моментов всех внешних сил системы относительно этой оси. Если сумма моментов всех приложенных к системе внешних сил относительно некоторой неподвижной оси равна нулю, то кинетический момент системы относительно этой оси будет постоянным.
Теорема моментов в системе координат, связанной с центром масс
Кинетический момент системы относительно неподвижного центра удобно использовать в тех задачах, в которых система имеет одну или несколько закрепленных точек. Например при вращении тела или системы тел вокруг точки или оси. Когда таких точек нет, то наиболее удобным в использовании является кинетический момент относительно центра масс в системе координат, в которой центр масс покоится, а оси остаются параллельными осям инерциальной системы отсчета. В общем случае, система отсчета, связанная с центром масс, не является инерциальной, но она не вращается относительно инерциальной системы отсчета.
Главным моментом количества движения системы относительно ее центра масс C называется величина , равная векторной сумме моментов количеств движения всех точек системы относительно центра масс в системе отсчета, в которой центр масс покоится, а оси системы координат параллельны осям инерциальной системы координат:
(М3) .
Здесь – скорости точек системы и скорость ее центра масс в инерциальной системе отсчета. Тогда – скорость точки массой в системе отсчета, связанной с центром масс.
Связь кинетических моментов в различных системах отсчета
Кинетический момент системы относительно неподвижной точки O равен сумме кинетического момента центра масс C , если в нем сосредоточить всю массу системы, и кинетического момента системы относительно центра масс :
(М4) .
То есть можно сказать, что вращение системы вокруг неподвижной точки O складывается из вращения центра масс C вокруг точки O , и вращения элементов системы вокруг центра масс C .
В (М2) ⇑ мы использовали кинетический момент системы, вычисляемый относительно произвольной неподвижной точки в инерциальной системе отсчета. Уравнения для кинетического момента имеют тот же вид, если в качестве полюса взять центр масс C системы.
Теорема моментов относительно центра масс системы
Производная по времени от главного момента количества движения системы относительно ее центра масс C , равна сумме моментов всех внешних сил системы относительно того же центра:
(М5) .
В (М5) мы используем неинерциальную систему координат, начало которой, в течении всего движения системы, находится в центре масс, а оси параллельны осям инерциальной системы координат. Естественно, что если мы выберем инерциальную систему координат, начало которой в данный момент времени совпадает с центром масс, то теорема моментов не изменит своего вида (М5). То есть центр масс обладает такой особенностью, что теорема моментов относительно него имеет одну и ту же форму, как в инерциальной системе отсчета, так и в неинерциальной системе, начало которой на всем протяжении движения совпадает с центром масс, а оси параллельны осям инерциальной системы отсчета. Такая особенность возникает только для центра масс системы. Для других точек, уравнение моментов в неинерциальной системе отсчета не имеет вида (М5).
Кинетический момент твердого тела
Пусть твердое тело вращается с угловой скоростью ω вокруг неподвижной оси Oz . Тогда его кинетический момент относительно этой оси равен произведению момента инерции относительно этой оси на угловую скорость вращения:
.
Если на твердое тело действуют внешние силы, то применяя теорему моментов, находим:
.
Если момент сил относительно оси Oz равен нулю: , то угловая скорость постоянна: .
В произвольном случае, кинетический момент выражается через компоненты угловой скорости и тензора инерции. Пусть, в данный момент времени, скорость точки O тела равна нулю: . То есть точка O является мгновенным центром вращения тела. Тогда компоненты кинетического момента тела относительно точки O определяется по формуле:
.
Здесь – компоненты тензора инерции тела ⇑ относительно точки O . Они связаны с моментами инерции формулами ⇑. Также подразумевается, что индексы p, q принимают значения x, y, z :
.
Здесь мы выбрали в качестве полюса неподвижную (в рассматриваемый момент времени) точку. Если, в качестве полюса выбрать центр масс тела, то компоненты момента импульса определяются по аналогичной формуле:
.
Для других точек, момент импульса выражается через угловую скорость более сложным образом.
В большинстве случаев, наиболее удобным полюсом оказывается центр масс C тела. Тогда, для компонент кинетического момента относительно произвольного центра O , имеем:
.
Здесь – радиус-вектор, проведенный из точки O в точку центра масс C ; m – масса тела; – скорость центра масс; – компоненты тензора инерции относительно точки C . Как видно, первое слагаемое является кинетическим моментом материальной точки, находящейся в центре масс тела и движущейся со скоростью центра масс. Второе слагаемое является вкладом вращения тела относительно его центра масс. То есть, как было указано выше ⇑, кинетический момент твердого тела относительно произвольной неподвижной точки O равен сумме кинетического момента поступательного движения центра масс относительно точки O и кинетического момента вращательного движения тела относительно его центра масс.
Теорема об изменении кинетической энергии
Кинетической энергия системы
Если система состоит из нескольких тел, то кинетическая энергия системы равна сумме кинетических энергий тел, составляющих систему.
Теорема Кенига
Кинетическая энергия системы равна сумме кинетической энергии центра масс C системы, масса m которого равна массе всей системы: , и кинетической энергии этой системы в ее движении относительно центра масс:
.
Здесь – скорость движения центра масс.
Если тело массы m совершает поступательное движение со скоростью , то скорости всех его точек равны . Кинетическая энергия поступательного движения:
(К1) .
Если тело вращается с угловой скоростью ω вокруг неподвижной оси Oz , то кинетическая энергия вращательного движения определяется по формуле:
(К2) ,
где – момент инерции тела относительно оси вращения.
В произвольном случае, кинетическая энергия равна сумме кинетической энергии поступательного движения центра масс и энергии вращательного движения относительно центра масс:
(К3) .
Здесь ω – абсолютное значение угловой скорости вращения тела; CL – ось, проведенная через центр масс, параллельно направлению вектора угловой скорости; – момент инерции относительно оси CL . Направление оси вращения может меняться со временем. Указанная формула дает мгновенное значение кинетической энергии.
Формула (К3) удобна, если тело вращается вокруг неподвижной оси. Если же вектор угловой скорости может менять направление относительно тела, то нам пришлось бы вычислять момент инерции относительно каждого положения оси вращения. В этом случае удобно выразить кинетическую энергию вращения через компоненты тензора инерции относительно центра масс тела:
(К4) .
Работа сил и мощность
Все сказанное в отношении работы и потенциальной энергии в разделе «Динамика материальной точки», имеет место и для динамики системы тел.
См. Работа силы. Мощность Силовые поля и потенциальная энергия
Единственное отличие заключается в том, что там силы приложены только к одной исследуемой точке. Для системы, внешние силы могут быть приложены к разным точкам, составляющих систему. При этом одна сила приложена только к одной точке, но этих сил может быть много. Точку, к которой приложена сила называют точкой приложения силы.
При рассмотрении твердых тел, мы можем упростить реальную систему сил, воспользовавшись результатами статики. Для этого нужно преобразовать сложную систему реальных сил на эквивалентную ей, более простую, систему. Так например, систему сил тяжести, действующих на каждую точку тела, можно заменить одной равнодействующей силой, приложенной к центру масс тела. Тогда все вычисления можно выполнять только для одной силы с точкой приложения в центре масс тела.
Работа при перемещении точки
Элементарная работа , которую совершает сила , при элементарном перемещении ее точки приложения, равна скалярному произведению векторов силы и перемещения:
;
.
То есть она равна произведению модуля вектора силы , перемещения и косинусу угла между ними. Это, в свою очередь, равно произведению касательной компоненты силы к траектории движения, и модуля элементарного перемещения . Здесь – скорость точки приложения силы; – промежуток времени, в течении которого происходит перемещение.
Мощность равна скалярному произведению векторов силы и скорости:
.
Работа , которую совершает сила , при перемещении точки ее приложения из точки в точку , равна сумме (интегралу) элементарных работ:
.
Работа при движении тела
Если тело движется поступательно, то скорости и перемещения всех его точек равны. В этом случае, работа и мощность вычисляются также как и при перемещении точки. Этот случай рассмотрен выше.
Для тела, вращающегося вокруг неподвижной оси Oz , элементарная работа равна произведению момента силы относительно этой оси на элементарный угол поворота dφ :
.
Здесь – мгновенное значение угловой скорости вращения; dt – время, в течении которого происходит поворот на угол dφ .
Мощность равна произведению момента силы на угловую скорость:
.
Для тела, вращающегося вокруг неподвижной точки O , элементарная работа равна скалярному произведению вектора момента силы относительно этой точки на вектор элементарного угла поворота :
.
Вектор элементарного поворота направлен вдоль вектора мгновенной угловой скорости : .
Мощность равна скалярному произведению векторов момента силы и угловой скорости:
.
При произвольном движении твердого тела, мы, произвольным образом, выбираем точку O , связанную с телом, которую называем полюсом. Тогда элементарная работа равна работе, которую совершает сила при перемещении полюса , и работе момента силы относительно полюса при элементарном повороте тела:
.
Заметим, что элементарный угол поворота и угловая скорость вращения не зависят от выбора полюса.
Мощность:
.
Теорема об изменении кинетической энергии системы
Теорема об изменении кинетической энергии системы в дифференциальной форме.
Дифференциал (приращение) кинетической энергии системы при некотором ее перемещении равно сумме дифференциалов работ на этом перемещении всех приложенных к системе внешних и внутренних сил:
.
Теорема об изменении кинетической энергии системы в интегральной форме.
Изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил:
.
Неизменяемая система – это механическая система, в которой расстояние между любыми двумя взаимодействующими точками остается постоянным во все время движения.
Идеальные связи – это связи, для которых сумма элементарных работ их реакций на любом возможном перемещении системы равна нулю.
Для систем с идеальными связями и неизменяемых систем, сумма работ внутренних сил равна нулю: . Для таких систем, изменение кинетической энергии системы равно сумме работ всех внешних сил, приложенных к системе:
.
Коэффициент полезного действия
В машинах и механизмах, совершающих некоторую полезную работу, силы можно разделить на следующие виды.
Движущие силы – это силы, совершающие положительную работу Aзатр .
Силы полезного сопротивления – это силы, совершающие отрицательную работу – Aпол. сопр , но выполняют полезное действие.
Силы вредного сопротивления – это силы, совершающие отрицательную работу – Aвр. сопр , и не выполняющие полезных действий.
Попеременные силы – это силы, совершающие то положительную, то отрицательную работу, но за достаточно большой промежуток времени, их сумма работ равна нулю. Механический коэффициент полезного действия машины – это величина, равная отношению работы полезных сил сопротивления (полезной работы) к работе движущих сил (затраченной на приведение машины в движение):
.
Пусть Nмаш – полезная мощность машины; Nдв – мощность двигателя. Тогда
.
Закон сохранения полной механической энергии
Если система движется под действием потенциальных сил, то сумма кинетической T и потенциальной Π энергий сохраняет постоянное значение:
.
Механическая энергия – это сумма кинетической и потенциальной энергии.
Уменьшение механической энергии, как правило, связано с ее превращением в тепловую, электрическую, электромагнитную энергию, энергию звука и электромагнитных колебаний (свет, электромагнитные волны). Увеличение механической энергии связано с обратными процессами превращения различных видов энергии в механическую.
Геометрия масс
Моменты и тензор инерции твердого тела
В этом разделе мы рассматриваем величины, характеризующие распределение массы системы в пространстве.
Сложившаяся система обозначений
Тензор инерции твердого тела
Для вычисления момента импульса и кинетической энергии твердого тела, нам нужно знать всего несколько характеристик тела, величины которых зависят от распределения масс точек, составляющих тело. Эти величины составляют компоненты, так называемого, тензора инерции , который определяется относительно некоторого, предварительно выбранного, центра O , и вычисляется по формуле:
(И1) .
Здесь – координаты точки массы в декартовой системе координат, с началом в выбранном центре O ; при p = q , при p ≠ q . Индексы координат нумеруют цифрами, придерживаясь следующих обозначений:
.
Тензор инерции имеет следующие шесть компонент:
;
;
.
Если в качестве полюса O выбрать центр масс C тела, то компоненты момента импульса и кинетическая энергия тела T вычисляются по относительно простым формулам:
.
Здесь – скорость центра масс тела, – компоненты угловой скорости.
Моменты инерции твердого тела
Пользоваться тензором инерции (И1) ⇑ удобно, поскольку, при решении задач, мы сразу можем применить результаты теории тензорного исчисления. Однако сложилось так, что вместо тензора инерции вводят его отдельные компоненты, придав им специфические названия и обозначения.
Осевые моменты инерции:
;
Центробежные моменты инерции:
.
Все это может привести к путанице. Поэтому компоненты тензора инерции мы будем обозначать буквой I . А сложившиеся названия и обозначения его отдельных компонент – буквой J .
Определения моментов инерции
Свойства моментов инерции
Сумма осевых моментов инерции
Знаки моментов инерции
Осевые моменты инерции не могут быть отрицательными:
.
Центробежные моменты инерции могут быть положительными, отрицательными, или равными нулю.
Симметричность моментов инерции
Центробежные моменты инерции симметричны относительно своих индексов:
.
Все моменты инерции имеют размерность [кг·м 2 ].
Для вычисления моментов инерции сплошных тел, мы от суммирования переходим к интегрированию. При этом массу точки mk мы заменяем на дифференциал: . Дифференциал массы dm выражаем через плотность μ и элемент объема : . Далее интегрируем по объему тела V :
.
Моменты инерции в разных системах координат
Если мы от начальной системы координат Oxyz перейдем к другой системе O′x′y′z′ , то величины моментов инерции в новой системе будут отличаться от моментов в старой системе координат. Такие переходы называются преобразованиями системы координат.
Повороты системы координат
Сначала рассмотрим случай, когда две декартовы системы координат Oxyz и Ox′y′z′ имеют общее начало O . То есть вторая система получена из первой поворотом вокруг общего центра O . Согласно тензорной алгебре, любой симметричный тензор, поворотом системы координат можно привести к диагональному виду. То есть можно найти такую декартову систему координат, относительно которой все центробежные моменты равны нулю. Оси такой системы координат называются главными осями инерции тела.
Главная ось инерции тела , относительно некоторой точки O – это ось, для которой оба центробежных момента инерции, содержащие индекс этой оси, равны нулю. Например, если ось z – главная ось инерции, то .
Главный момент инерции тела , относительно некоторой точки O – это момент инерции относительно главной оси инерции.
Главная центральная ось инерции тела – это главная ось, проходящая через центр масс тела.
Главный центральный момент инерции тела – это момент инерции относительно главной центральной оси инерции.
Любое тело в пространстве имеет три главные оси инерции и три значения главных моментов инерции (относительно предварительно выбранной точки O ). При этом главные моменты инерции могут иметь равные значения.
Стоит подчеркнуть, что главные оси определяются относительно определенной точки тела. При выборе другой точки, главные оси могут иметь другие направления.
Тело с плоскостью симметрии
Если распределение массы тела в пространстве имеет плоскость симметрии, то любая ось, перпендикулярная к этой плоскости, будет главной осью инерции тела, а две другие главные оси лежат в плоскости симметрии.
Тело с осью симметрии
Если распределение массы тела в пространстве имеет ось симметрии, то эта ось является главной центральной осью инерции.
Параллельность главных осей
Если точка O расположена на главной центральной оси тела, то главные оси, проходящие через эту точку, параллельны главным центральным осям.
Главная ось, не проходящая через центр масс
Главная ось инерции, не проходящая через центр масс тела, является главной осью инерции только в одной точке.
Инвариантность суммы осевых моментов инерции
Если от одной системы координат Oxyz , мы перейдем к другой Ox′y′z′ с тем же началом, то сумма осевых моментов инерции не изменится при переходе от одной системы к другой:
.
По этой причине, величина полярного момента инерции не зависит от поворотов системы координат. То есть является инвариантом относительно поворотов системы координат. Она зависит от выбранного центра, относительно которого определяются моменты инерции.
Момент инерции относительно произвольной оси
Пусть нам известны моменты инерции тела относительно осей Oxyz . И пусть OL – произвольная ось, проходящая через начало O , составляющая углы с осями Ox, Oy, Oz . Тогда момент инерции тела относительно оси OL определяется по формуле:
.
Если оси x,y,z являются главными осями, то
.
Перенос системы координат. Теорема Гюйгенса-Штейнера
Отсюда следует, что осевой момент инерции будет иметь наименьшее значение относительно той оси, которая проходит через центр масс тела.
Моменты инерции некоторых тел
Однородный стержень
Рассмотрим тонкий однородный стержень длины l и массы m . Выберем начало координат O на одном из его концов. Направим ось Ox вдоль стержня; оси Oy и Oz – перпендикулярно. Эти оси будут главными осями инерции стержня относительно центра O . Осевые моменты инерции имеют следующие значения:
.
Центр масс стержня находится по его середине, в точке C ; . Проведем через нее оси координат Cxy′z′ , параллельные предыдущим. Эти оси являются главными центральными осями инерции со следующими значениями осевых моментов:
.
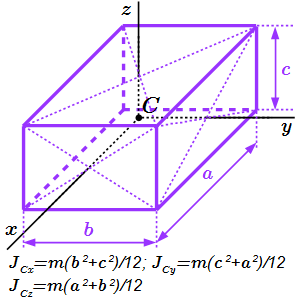
Прямоугольный параллелепипед
Рассмотрим прямоугольный параллелепипед с длинами ребер a, b, c (см. рисунок). Его центр масс C находится в центре параллелепипеда. Оси, проведенные через центр масс параллельно сторонам, будут главными центральными осями инерции. Моменты инерции прямоугольного параллелепипеда:
.
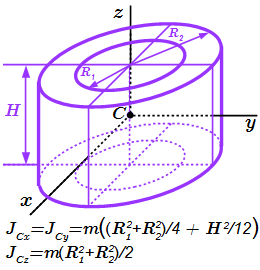
Полый цилиндр
Рассмотрим полый цилиндр высоты H и радиусами . Его центр масс находится на оси цилиндра, на расстоянии от основания. Через точку C проводим главные центральные оси инерции: ось Cz – вдоль оси цилиндра; оси Cx, Cy – перпендикулярно. Моменты инерции полого цилиндра:
.
Однородный сплошной диск
Тонкий обруч
Динамика твердого тела
Свободное движение твердого тела
Рассмотрим твердое тело массы m , перемещение которого не ограничено в пространстве. Пусть на тело действуют внешние силы , приложенных в точках . Для определения уравнений движения, мы воспользуемся теоремой о движении центра масс ⇑, теоремой моментов относительно центра масс системы ⇑, и выражением кинетического момента тела через компоненты угловой скорости ωq и тензора инерции Ipq тела (в системе координат с началом в центре масс, оси которой параллельны осям неподвижной системы):
(Т1) ;
(Т2) ;
(Т3) .
Здесь – радиус-вектор, проведенный в центр масс тела.
При известных внешних силах , из уравнения (Т1) можно определить закон движения центра масс тела.
Уравнения (Т2)–(Т3) определяют закон движения тела при его вращении. Они записаны в системе отсчета, начало которой находится в центре масс C , а оси параллельны осям инерциальной системы отсчета. Чтобы ими воспользоваться, мы должны найти способ, с помощью которого можно задать положение тела при его вращении. Это можно сделать с помощью углов Эйлера. Тогда оси вращающейся системы координат, связанной с телом, удобно направить вдоль главных центральных осей инерции тела ⇑. Тогда правые части уравнений (Т3) будут выражаться через главные центральные моменты инерций тела ⇑, три угла Эйлера и их производные по времени. Дифференцируя (Т3) и подставляя в (Т2), получим систему дифференциальных уравнений второго порядка для трех углов Эйлера.
Поступательное движение твердого тела
Рассмотрим поступательное движение твердого тела. Для него угловая скорость и угловое ускорение равны нулю: . Тогда момент количества движения постоянен и равен нулю: . Из (Т2) следует, что и главный момент всех внешних сил относительно центра масс должен равняться нулю: .
Дифференциальные уравнения поступательного движения определяются по формулам (Т1) ⇑:
.
Здесь – проекции внешней силы на оси координат. При поступательном движении, все точки тела имеют равные скорости и равные ускорения. Потому определив закон движения одной точки – центра масс , мы получаем закон движения произвольной точки A :
.
Плоское движение твердого тела
Рассмотрим плоское движение твердого тела. Выберем инерциальную систему координат Oxyz . Оси Ox и Oy направим в плоскости движения. Тогда положение тела полностью определяется тремя величинами – двумя компонентами радиус-вектора центра масс C : ; и углом поворота φ . Внешние силы также лежат в рассматриваемой плоскости. Кинетический момент направлен вдоль оси z и выражается через угловую скорость и момент инерции относительно оси, проходящей через центр масс C , перпендикулярно плоскости движения: .
Уравнения (Т1)-(Т3) ⇑ принимают вид:
(Т4) ;
(Т5) .
Здесь – проекции внешней силы на оси координат; – это алгебраический момент силы относительно центра C – то есть проекция момента силы на ось Oz .
Вращение твердого тела вокруг неподвижной оси
Рассмотрим вращение твердого тела вокруг неподвижной оси Oz . Выберем декартову систему координат. Ось Oz направим вдоль оси вращения; оси Ox и Oy – перпендикулярно. Считаем, что перемещение параллельно оси вращения отсутствует. Тогда это плоское движение. Оно происходит в плоскости Oxy . Положение тела определяется только углом поворота φ вокруг оси вращения.
Применяя теорему моментов ⇑ и связь момента с угловой скоростью ⇑, получим дифференциальное уравнение вращения твердого тела вокруг неподвижной оси:
(Т6) .
Здесь – момент инерции тела относительно оси вращения; – вращающий момент – то есть сумма моментов всех внешних сил относительно оси вращения.
Вводя угловое ускорение , дифференциальное уравнение вращения примет вид:
.
Оно аналогично уравнению прямолинейного движения под действием силы Fx :
.
Если вращающий момент является постоянной величиной: , то уравнение (Т6) имеет решение:
.
Здесь – угол поворота и угловая скорость вращения в начальный момент времени ; – угловое ускорение, постоянная величина.
Физический и математический маятники
Далее мы будем приводить данные только для плоского движения маятника. То есть мы считаем, что маятник совершает колебания вокруг неподвижной оси.
Уравнение вращательного движения физического маятника имеет вид:
.
Здесь ось вращения проходит через точку O ; φ – угол поворота между осью маятника и вертикальной прямой; JO – момент инерции маятника относительно оси вращения; P =mg – сила тяжести, действующая на маятник массы m ; a – расстояние от оси вращения O до центра масс C маятника; g – ускорение свободного падения. Введем обозначение: . Тогда
.
Рассмотрим малые колебания . При этом . И мы получаем уравнение гармонических колебаний:
.
Общее решение этого уравнения имеет вид:
.
Здесь – постоянные, которые определяются из начальных условий.
Во многих случаях удобно выразить общее решение уравнения малых колебаний через амплитуду α и начальную фазу колебаний β :
.
Величина k называется угловой частотой колебаний. Период колебаний: . Для малых колебаний, период не зависит от амплитуды. Этот результат является приближенным. При увеличении амплитуды такая зависимость появляется.
Математический маятник – это материальная точка, подвешенная на нерастяжимой невесомой нити, и совершающая колебания под действием силы тяжести. 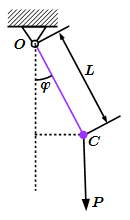
Математический маятник является частным случаем физического маятника. Пусть L – длина нити математического маятника. Его центр масс C находится в материальной точке: L = |OC| . Момент инерции: . Выразив силу тяжести P через массу m и ускорение свободного падения g , получим угловую частоту колебаний:
.
Теперь вернемся к физическому маятнику. Если положить , то частота физического маятника будет совпадать с частотой математического маятника длины L :
.
Приведенная длина физического маятника – это длина математического маятника, частота колебаний которого совпадает с частотой колебаний рассматриваемого физического маятника.
Центром качаний физического маятника называется точка K на оси физического маятника, находящаяся на расстоянии его приведенной длины от точки подвеса.
Свойство взаимности
Если физический маятник подвесить за центр качаний K , то его частота колебаний не изменится, а прежняя точка подвеса O станет центром качаний нового маятника.
Положение центра качания
Центр качаний всегда расположен ниже центра масс:
.
Принцип Даламбера
Суть принципа Даламбера состоит в том, чтобы задачи динамики свести к задачам статики. Для этого предполагают (или это заранее известно), что тела системы имеют определенные (угловые) ускорения. Далее вводят силы инерции и (или) моменты сил инерции, которые равны по величине и обратные по направлению силам и моментам сил, которые по законам механики создавали бы заданные ускорения или угловые ускорения
Принцип Даламбера
Если в любой момент времени к каждой точке системы приложить силы инерции и реально действующие силы, то полученная система сил будет находиться в равновесии, и к ней можно применять уравнения статики.
Рассмотрим пример. Путь тело массы m совершает поступательное движение и на него действуют внешние силы . Далее мы предполагаем, что эти силы создают ускорение центра масс системы . По теореме о движении центра масс, центр масс тела имел бы такое же ускорение, если бы на тело действовала сила . Далее мы вводим силу инерции:
.
После этого задача динамики:
.
Превращается в задачу статики:
;
.
Для вращательного движения поступают аналогичным образом. Пусть тело вращается вокруг оси z и на него действуют внешние моменты сил . Мы предполагаем, что эти моменты создают угловое ускорение εz . Далее мы вводим момент сил инерции M И = – Jz εz . После этого задача динамики:
.
Превращается в задачу статики:
;
.
Принцип возможных перемещений
Принцип возможных перемещений применяется для решений задач статики. В некоторых задачах, он дает более короткое решение, чем составление уравнений равновесия. Особенно это касается систем со связями (например, системы тел, соединенные нитями и блоками), состоящих из множества тел
Принцип возможных перемещений.
Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.
Возможное перемещение системы – это малое перемещение, при котором не нарушаются связи, наложенные на систему.
Общее уравнение динамики (принцип Даламбера — Лагранжа)
Принцип Даламбера — Лагранжа – это объединение принципа Даламбера с принципом возможных перемещений. То есть, при решении задачи динамики, мы вводим силы инерции и сводим задачу к задаче статики, которую решаем с помощью принципа возможных перемещений.
Принцип Даламбера — Лагранжа.
При движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы равна нулю:
.
Это уравнение называют общим уравнением динамики.
Уравнения Лагранжа
Число обобщенных координат n совпадает с числом степеней свободы системы.
Если, при возможном перемещении системы, изменяются все координаты, то работа, совершаемая внешними силами при таком перемещении, имеет вид:
δA = Q 1 δq 1 + Q 2 δq 2 + . + Qn δqn .
Тогда обобщенные силы являются частными производными от работы по перемещениям:
.
Для потенциальных сил с потенциалом Π ,
.
Уравнения Лагранжа – это уравнения движения механической системы в обобщенных координатах:
Здесь T – кинетическая энергия. Она является функцией от обобщенных координат, скоростей и, возможно, времени. Поэтому ее частная производная также является функцией от обобщенных координат, скоростей и времени. Далее нужно учесть, что координаты и скорости являются функциями от времени. Поэтому для нахождения полной производной по времени нужно применить правило дифференцирования сложной функции:
.
Использованная литература:
А. П. Маркеев, Теоретическая механика, «Ижевская республиканская типография», 1999.
Н. Н. Никитин, Курс теоретической механики, «Высшая школа», 1990.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.
А. А. Яблонский, Курс теоретической механики, часть 2, динамика «Высшая школа», 1986.
Автор: Олег Одинцов . Опубликовано: 20-07-2015 Изменено: 23-08-2019
http://www.evkova.org/dvizhenie-tel-pod-vozdejstviem-neskolkih-sil-v-fizike
http://1cov-edu.ru/mehanika/dinamika-tel/


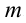
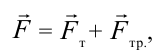
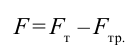

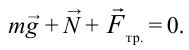
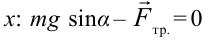 ;
;