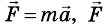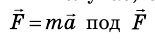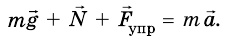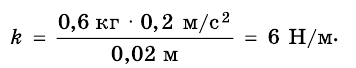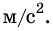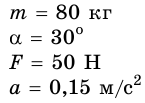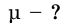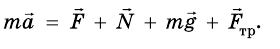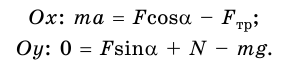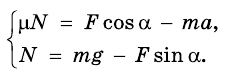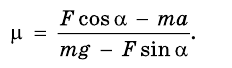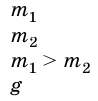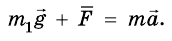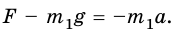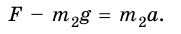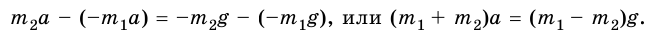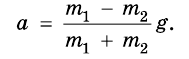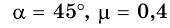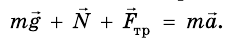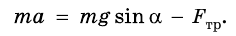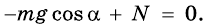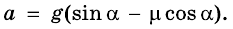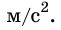Движение тела под действием нескольких сил в физике — определение и формулы с примерами
Движение тела под действием нескольких сил:
B 7-м классе вы рассматривали движение тела, на которое действует только одна сила — сила упругости, сила притяжения или сила трения. В действительности такие движения в земных условиях почти никогда не происходят. Это следует уже из того, что рядом с силами упругости или тяготения всегда действует сила трения.
Вам известно, что если тело движется равномерно прямолинейно, то на него действуют силы, которые компенсируются. Если к телу приложены несколько сил и равнодействующая сила будет направлена в сторону движения, то тело будет двигаться равноускоренно, а если в противоположную сторону — равнозамедленно.
Если решать задачи по механике, когда на тело действует несколько сил, то следует напомнить, что в уравнении, которое выражает второй закон Ньютона
Начиная решать задачу, надо сначала выбрать направление координатных осей и изобразить на рисунке векторы всех сил и вектор ускорения тела, если известно его направление. Потом надо найти проекции всех векторов на эти оси координат. Наконец, записать уравнение второго закона Ньютона для проекций на каждую ось и решить вместе найденные уравнения.
Часто бывает так, что в движении участвуют несколько тел, так или иначе связанных между собой, как говорят, система тел. Примером такого движения может быть движение спортсмена на водных лыжах, который направляется за катером, или движение грузов на нити, переброшенных через блок. При этом на каждое из тел могут действовать несколько сил. Как в таких случаях решать задачи? Общий порядок решения задач остается таким, как рассматривали ранее. Только его надо применить к каждому из тел системы: уравнение второго закона Ньютона записывают для каждого из тел системы сначала в векторной форме, а потом в скалярной (для проекций) и решают вместе найденные уравнения.
В случае, если сумма сил, действующих на тело, равна нулю в формуле
Пример №1
Пружина одним концом прикреплена к бруску массой 0,6 кг, который расположен на гладком горизонтальном столе. Свободный конец пружины начали перемещать прямолинейно вдоль стола с ускорением 0,2 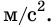
а = 0,2
Выполним рисунок.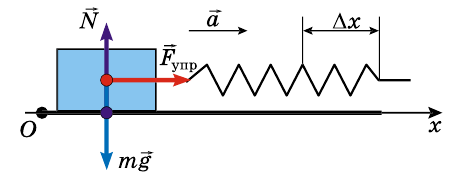
На брусок действуют: сила тяжести 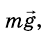
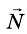
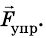
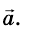
Запишем второй закон Ньютона в векторной форме:
Выберем ось Ох и найдем проекции векторов. Учитывая, что 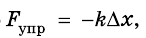
имеем: 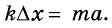
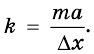
Подставив значения известных величин, определим:
Ответ: жесткость пружины равна 6 Н/м.
Пример №2
По горизонтальной дороге тянут за веревку под углом 30° груз, общая масса которого 80 кг. Сила натяжения 50 Н. Определите коэффициент трения скольжения, если груз движется с ускорением 0,15
На груз действуют силы: сила тяжести 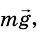
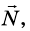
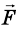
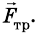
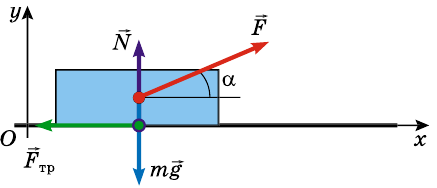
Запишем второй закон Ньютона для груза в векторной форме:
В проекциях на координатные оси данное уравнение имеет вид:
Поскольку 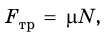
Подставим выражение mg — Fsina в первое уравнение вместо N, и выразим переменную:
Учитывая значения известных величин, вычислим:
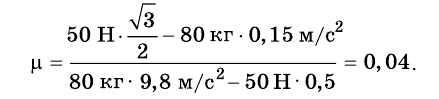
Полученное значение коэффициента трения скольжения приблизительно совпадает с табличными данными. Значит, задача решена правильно.
Ответ: 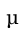
Пример №3
Через неподвижный блок перекинута нить, к концам которой прикреплены тела массами 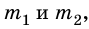
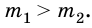
Дано:
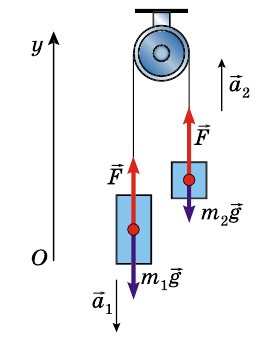
В этой задаче в движении участвуют два тела.
Если систему тел привести в движение, то тело массой 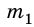
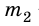
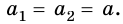
Координатную ось Оу направим по вертикали вверх.
На тело массой 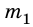
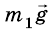
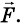
Из рисунка видно, что проекция 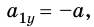
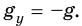
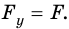
На тело массой 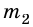
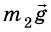
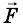
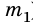
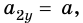
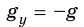
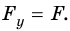
Вычтем из второго уравнения первое:
Таким образом, для ускорения а имеем:
Зная, что разность 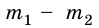
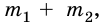
Блоки иногда и используются для того, чтобы заставить тело падать с ускорением, меньшим g. На этом основывается применение противовеса в лифтах и других подъемных механизмах.
Пример №4
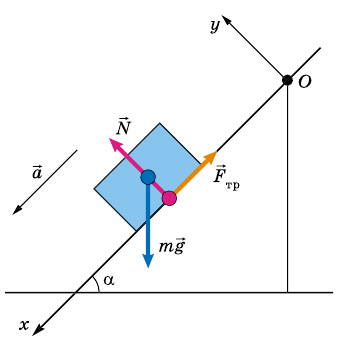
Тело движется вниз по наклонной плоскости, угол наклона которой 45° к горизонту. Коэффициент трения 0,4. Определите ускорение движения тела.
На это тело действует Земля, притягивающая его с силой 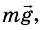
Кроме того, на тело действует наклонная плоскость с силой 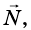
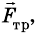
и записи условия задачи выполним рисунок.
Запишем второй закон Ньютона в векторной форме:
В этом случае координатные оси удобнее всего направить вдоль наклонной плоскости и перпендикулярно к ней. В этом случае перемещения вдоль оси Оу при движении не будет, а следовательно, ускорение 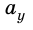
Запишем второй закон Ньютона в проекциях на координатные оси.
Проекция силы 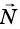
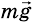
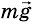
Проекция силы 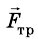
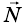
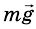
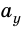
Эти два уравнения содержат неизвестные: т, a, N, 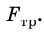
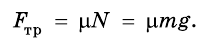
Учтя все выражения, получим уравнение: 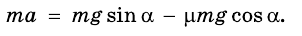
Сократив на m, получим:
Подставив значение, определим ускорение движения тела: а
Ответ: 4,16
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Наклонная плоскость в физике
- Давление газов и жидкостей
- Движение жидкостей и газов
- Гидравлические машины в физике
- Механическое давление в физике
- Столкновения в физике
- Рычаг в физике
- Блоки в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Свободные колебания.
Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинетической) при отсутствии внешних воздействий.
Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.
Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют систему тел, которая называется колебательной системой.
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины (см. рис. ниже), входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.
Другим классическим примером механической колебательной системы является математический маятник (см. рис. ниже). В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия.
Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называются силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свободные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.
Условиями возникновения свободных колебаний являются:
1) возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;
2) отсутствие трения в системе.
Динамика свободных колебаний.
Колебания тела под действием сил упругости. Уравнение колебательного движения тела под действием силы упругости F (см. рис.) может быть получено с учетом второго закона Ньютона (F = mа) и закона Гука (Fупр = -kx), где m — масса шарика, а — ускорение, приобретаемое шариком под действием силы упругости, k — коэффициент жесткости пружины, х — смещение тела от положения равновесия (оба уравнения записаны в проекции на горизонтальную ось Ох). Приравнивая правые части этих уравнений и учитывая, что ускорение а — это вторая производная от координаты х (смещения), получим:

Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени (ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.
Колебания математического маятника. Для получения уравнения колебания математического маятника (рисунок) необходимо разложить силу тяжести FT = mg на нормальную Fn (направленную вдоль нити) и тангенциальную Fτ (касательную к траектории движения шарика — окружности) составляющие. Нормальная составляющая силы тяжести Fn и сила упругости нити Fynp в сумме сообщают маятнику центростремительное ускорение, не влияющее на величину скорости, а лишь меняющее ее направление, а тангенциальная составляющая Fτ является той силой, которая возвращает шарик в положение равновесия и заставляет его совершать колебательные движения. Используя, как и в предыдущем случае, закон Ньютона для тангенциального ускорения maτ = Fτ и учитывая, что Fτ = -mg sinα, получим:
Знак минус появился потому, что сила и угол отклонения от положения равновесия α имеют противоположные знаки. Для малых углов отклонения sin α ≈ α. В свою очередь, α = s/l, где s — дуга OA, I — длина нити. Учитывая, что аτ = s», окончательно получим:

Вид уравнения 

Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.
Решением уравнений 

То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими:
В уравнении x = xm cos ω0 t (или x = xm sin ω0 t), хm — амплитуда колебания, ω0 — собственная циклическая (круговая) частота колебаний.
Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:

Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.
Для математического маятника выполняются равенства:

Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).
Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.
Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятника, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.
Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции (x = xm cos ω0 t (или x = xm sin ω0 t)), получим выражение для скорости:
где am = ω 2 0 xm — амплитуда ускорения. Таким образом, амплитуда скорости гармонических колебаний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания.
Движение под действием силы тяжести
Подбросим мяч вертикально вверх. Он поднимется на какую-то высоту, после чего упадет вниз.
Земля притягивает мяч, значит на мяч действует нескомпенсированная сила притяжения. Как гласит второй закон Ньютона, скорость мяча из-за этого меняется.
Движение тела под действием силы тяжести, называется свободным падением. Когда тело падает свободно, оно испытывает невесомость.
Для удобства будем рассматривать отдельно свободное движение мяча вверх и, его свободное падение вниз.
Движение вверх
Рассмотрим рисунок 1. В левой части рисунка — 1а) изображено движение мяча вверх, а в правой – 1б) – движение вниз. Сплошным кружком обозначено начальное положение мяча, а пунктирным – конечное. Красными стрелками обозначена скорость мяча на различных высотах.
При движении вверх скорость тела уменьшается, так как вектор ускорения и вектор скорости направлены в противоположные стороны (рис. 1а). Движение вверх равнозамедленное.
Выражение для скорости при движении мяча вверх:
Вертикальное перемещение мяча при его движении вверх выражается такой формулой:
В верхней точке траектории скорость мяча будет равна нулю. Эта точка для движения вверх будет конечной, а для движения вниз – начальной.
Поэтому, для движения вверх нулю равна конечная скорость мяча \(v_
Движение вниз
При движении вниз – наоборот, скорость будет увеличиваться, так как векторы скорости и ускорения сонаправлены (рис. 1б). Движение вниз равноускоренное.
Выражение для скорости при движении мяча вниз:
Вертикальное перемещение при движении вниз выражается формулой:
Таким образом, под действием силы тяжести мяч движется по вертикали, меняя свою скорость.
Пока мяч находится в полете, он не давит на опору и не растягивает подвес. Проще говоря, он находится в невесомости (ссылка) – то есть, не имеет веса.
Масса есть всегда, а вес тела (ссылка) может отсутствовать! Кроме того, одна и та же масса в различных ситуациях может обладать разным весом.
Из рисунка 1 так же, следует, что
если тело при падении вернется на уровень, с которого оно стартовало, то:
— скорость, с которой мы подбросим тело, по модулю будет равна скорости, с которой тело упадет \( \large \left|\vec
— время подъема равняется времени спуска \( \large t_<\text<вверх>> = t_<\text<вниз>> \);
Когда перемещение вверх не равно перемещению вниз
Рассмотрим теперь следующий рисунок. На рисунке 2а представлен случай, когда путь, пройденный вверх больше пути, пройденного при движении вниз. Предположим, мы подбросили мяч вертикально вверх и, он упал на крышу какого-то строения, например, гаража.
В таком случае на подъем потребуется больше времени, чем на спуск
И скорость, с которой мяч подбрасывали вверх будет больше скорости, с которой мяч ударится о крышу
На рисунке 2б путь при движении вверх меньше пути вниз. Такое может быть, если мы заберемся на крышу гаража и, находясь на крыше, подбросим мяч вертикально вверх.
Теперь на спуск мяча до земли потребуется больше времени, чем на подъем
http://www.calc.ru/Svobodnyye-Kolebaniya.html
http://formulki.ru/mehanika/dvizhenie-pod-dejstviem-sily-tyazhesti