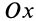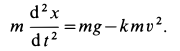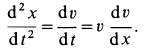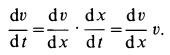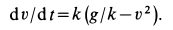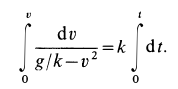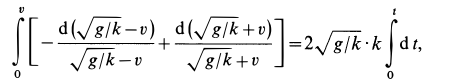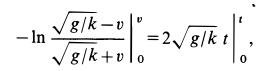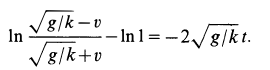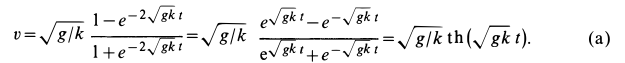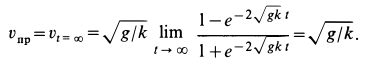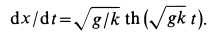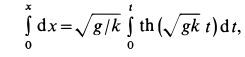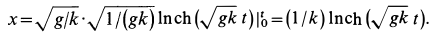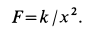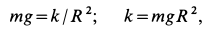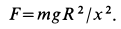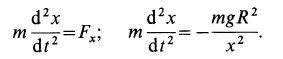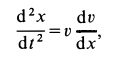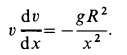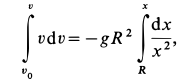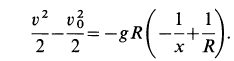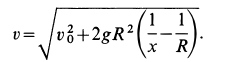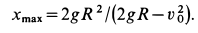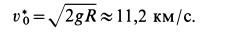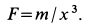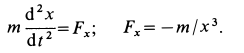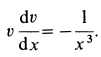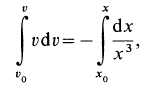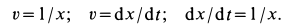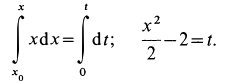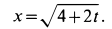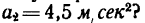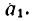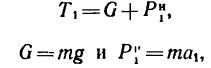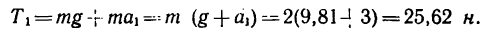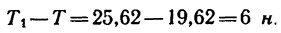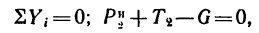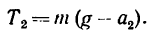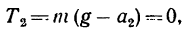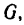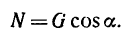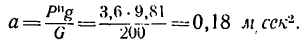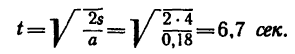Прямолинейное движение точки в теоретической механике
Содержание:
Основные виды прямолинейного движения точки:
Дифференциальное уравнение прямолинейного движения точки вдоль оси
если рассматривается случай зависимости силы только от времени, координаты и скорости.
Начальные условия можно задать в форме 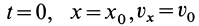
Наиболее важные случаи прямолинейного движения материальной точки получаются тогда, когда сила 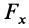
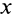
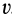
Силу, зависящую от координаты 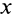
Отметим, что в перечисленных случаях интегрирование дифференциального уравнения (1Г) выполняется наиболее просто и его можно довести до конца в квадратурах. В более общем случае, если сила одновременно зависит от времени 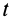
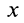
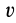
Рассмотрим примеры на составление и интегрирование дифференциального уравнения прямолинейного движения точки. Эти примеры позволяют выявить некоторые особенности решения таких задач. Ниже приведены примеры, когда сила зависит только от времени, или от скорости, или от координаты.
Пример 1. Точка массой 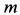
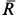
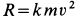
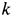
Найти уравнение движения точки.
Решение:
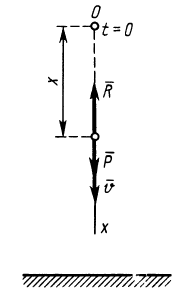
Направим ось 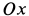
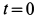
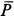
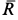
Скорость в этом случае можно определить в зависимости от времени или от координаты, используя подстановки
Последняя подстановка позволяет исключить из дифференциального уравнения время при определении скорости. Эта подстановка получается из первой умножением и одновременным делением на 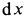
Используя первую подстановку, получаем дифференциальное уравнение движения точки в следующем виде:
Разделяя переменные и беря интегралы от обеих частей, имеем
Рис. 8
Для того чтобы не искать дополнительно произвольную постоянную интегрирования, интегралы возьмем определенные, сохраняя верхний предел переменным для последующего интегрирования, а для нижних пределов используем также условие: при 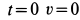
Потенцируя и решая относительно 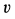
Переходя в (а) к пределу при 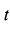
Для достижения предельной скорости требуется бесконечно большое время. Более подробные расчеты показывают, что скорость, близкая к предельной, устанавливается довольно быстро.
Отметим, что для свободного падения в воздухе парашютиста вблизи Земли без раскрытия парашюта предельная скорость равна 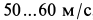
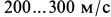
Для нахождения закона движения точки подставляем в (а) вместо скорости 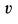
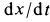
Интегрируя это уравнение после разделения переменных, имеем
Пример 2. Материальная точка массой 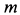
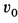
Определить зависимость скорости точки от ее расстояния до центра Земли, пренебрегая сопротивлением воздуха.
Решение:
Направив ось 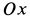
Постоянный коэффициент 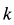
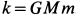
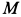
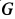
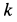
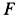
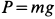
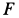
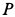
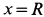
где 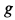
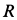
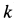
Составляем дифференциальное уравнение движения точки. Получаем
Рис. 9
Знак минус в правой части этого уравнения определяется знаком проекции силы 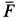
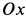
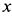
Исключая время из дифференциального уравнения подстановкой
Разделяя переменные и беря от обеих частей интегралы с учетом, что при 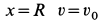
Для определения наибольшего расстояния 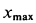
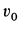
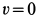
Видно, что 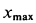
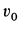
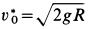
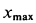
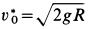
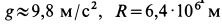
Скорость 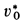
Наименьшую скорость космического корабля, при которой он становится спутником Земли, называют первой космической скоростью. Она приблизительно равна 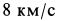
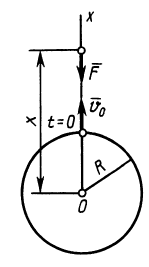
Пример 3. Материальная точка массой 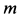
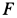
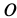
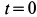
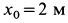
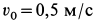
Рис. 10
Определить уравнение движения точки.
Решение:
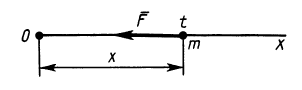
Выбирая за начало координат точку 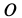
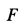
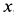
Учитывая направление силы 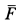
После преобразования левой части оно примет форму
Разделяя переменные и интегрируя это уравнение, имеем
После подстановки числовых значений для 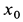
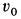
Интегрируя полученное уравнение, имеем
Закон движения точки можно выразить в форме
Прямолинейное движение точки
Обычно в задачах по динамике рассматривают так называемые несвободные материальные точки —материальные точки, движение которых ограничивается различными связями.
Приступая к решению задач, в которых рассматривается несвободная материальная точка, нужно прежде всего выявить действующие на точку активные силы (движущие силы и силы сопротивления), а также реакции связей (пассивные силы).
Выявив действующие силы, необходимо определить, находятся они в равновесии или нет? Этот вопрос в зависимости от заданных условий решается двояко.
Если, например, известно, что точка движется равномерно и прямолинейно, значит система сил уравновешена; если же известно, что точка двигается неравномерно или имеет криволинейную траекторию, то система сил неуравновешена.
Если система сил задана (все силы системы известны), то, определив проекции сил на оси координат, можно установить равновесие или неравновесие системы. В случае когда суммы проекций всех сил на каждую из осей равны нулю, заданная система сил уравновешена; когда же сумма проекций всех сил хотя бы на одну из осей не равна нулю, система сил неуравновешена; в первом случае точка движется равномерно и прямолинейно, во втором случае— имеет ускорение (вторая задача динамики).
При решении различных технических задач особенно важное значение приобретает случай, когда на материальную точку действует неуравновешенная система сил. В подобных случаях целесообразно решать задачи, применяя так называемый метод кинетостатики или принцип Даламбера, который формулируется так: активные силы, реакции связей и сила инерции образуют уравновешенную систему сил.
Применяя принцип Даламбера, необходимо очень хорошо понимать Сущность силы инерции. Нужно помнить, во-первых, что сила инерции, численно равная произведению массы точки на приобретенное ускорение, всегда направлена в сторону, противоположную вектору ускорения;
- во-вторых, что сила инерции в действительности не приложена к рассматриваемой в задаче материальной точке; она условно прикладывается к этой точке; фактически сила инерции приложена к двигающему телу или к связи;
- в-третьих, что равновесие сил, которое образуется после добавления силы инерции к силам, приложенным к точке, — равновесие фиктивное; но оно позволяет воспользоваться для решения задачи уравнениями равновесия из статики.
При решении задач с помощью метода кинетостатики рекомендуется придерживаться такой последовательности:
- выделить точку, движение которой рассматривается, и изобразить ее на рисунке;
- выявить все активные силы и изобразить их приложенными к точке на рисунке;
- освободить точку от связей, заменить связи их реакциями и также изобразить их на рисунке;
- добавить к полученной системе сил силу инерции;
- рассмотреть образовавшуюся уравновешенную систему сил и в зависимости от вида системы сил выбрать наиболее рациональный способ решения: графический, графо-аналитический или аналитический (методом проекций).
Задача №1
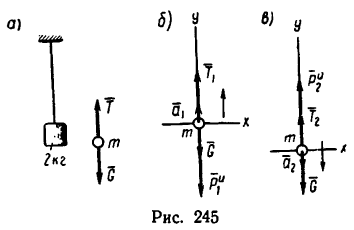
На шнуре подвешена двухкилограммовая гиря (рис. 245, а). Каково при этом натяжение шнура? Как изменится натяжение шнура, если при его помощи поднимать гирю вертикально вверх равномерно? Поднимать вертикально вверх с ускорением 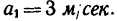
1. На гирю, которую принимаем за материальную точку массой m = 2кг, подвешенную на шнуре (см. рис. 245, а), действуют две силы: сила тяжести G и реакция нити Т, равная ее натяжению.
Других сил нет. Материальная точка (гиря) находится в покое, значит силы G и 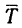
2. Если гиря, подвешенная на шнуре, поднимается вертикально вверх равномерно, то на нее действуют те же две силы и они также образуют уравновешенную систему. Происходит лишь замена статического равновесия (равновесия в состоянии покоя) динамическим равновесием (равновесием в состоянии движения — равномерного и прямолинейного).
Таким образом, и в этом случае (см. рис. 245, а) натяжение шнура T = G= 19,62 я.
3. Рассмотрим гирю в состоянии равноускоренного движения вертикально вверх с ускорением 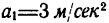
На гирю действуют также две силы: ее вес G и натяжение шнура 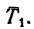
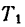
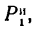
Система сил G, 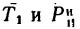
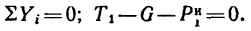
Из этого уравнения
поэтому
Как видно, при подъеме гири вверх с ускорением натяжение шнура увеличивается:
4- Рассмотрим гирю в состоянии равноускоренного движения вертикально вниз с ускорением 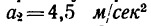
На гирю также действуют две силы: G и 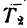
Добавим силу инерции 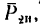
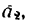
Уравнение равновесия примет вид
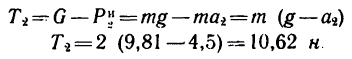
При ускоренном движении гири вниз натяжение шнура ослабевает. В данном случае по сравнению с состоянием равновесия натяжение шнура уменьшается на 9 н.
Примечание. Если решение задачи выполнить в технической системе единиц (МКГСС), то вес гири G= 2 кГ, а сила инерции получит такое выражение
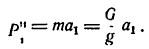
Тогда значение 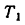
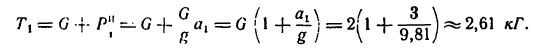
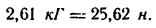
Отмстим, что выражение натяжения шнура при равноускоренном движении гири вниз
Если ускорение 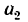
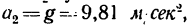
т. с. при свободном падении гири она не натягивает шнур. Образуется состояние «невесомости».
Задача №2
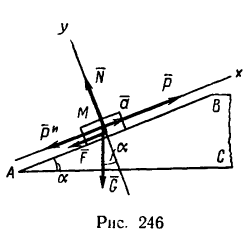
По наклонной плоскости АВ длиной 4 м и с углом подъема а=15 равноускоренно поднимают груз М весом G = 200 кГ, постоянной силой Р=65 кГ, направленной параллельно наклонной плоскости. Определить, сколько времени потребуется, чтобы переместить груз па расстояние AВ, сели коэффициент трения при движении груза по наклонной плоскости f= 0,05.
Решение — в единицах системы МКГСС.
1. Изобразим тело М на наклонной плоскости с приложенными к нему силами 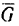
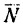
Находясь под действием этих сил, тело движется по наклонной плоскости с постоянным ускорением а.
2. Груз перемещается равноускоренно, без начальной скорости. Время его движения можно определить из уравнения движения
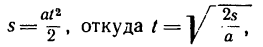
но предварительно необходимо определить ускорение а. Теперь система пяти сил 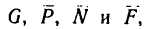
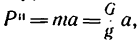
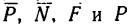
4. Выберем систему координат, как показано на рис. 238, и спроектируем все силы на оси х и у. Тогда получим два уравнения равновесия:
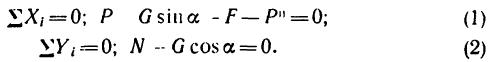
5. Из уравнения (1)
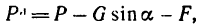
но сила трения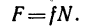
Нормальное давление найдем из уравнения (2):
поэтому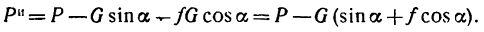
Подставим в это уравнение числовые значения 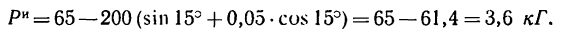
6. Из выражения 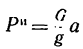
7. Подставив значение ускорения а в выражение 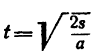
Рекомендуется повторить решение последней задачи в единицах СИ, а затем самостоятельно решить следующие задачи.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Относительное движение материальной точки
- Геометрия масс
- Кинематика сплошной среды
- Аксиомы классической механики
- Дифференциальные уравнения движения материальной точки
- Две основные задачи динамики точки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Уравнение движения точки, перемещающейся прямолинейно с постоянным ускорением, имеет вид : х = 10 + 3t + 6t ^ 2?
Физика | 10 — 11 классы
Уравнение движения точки, перемещающейся прямолинейно с постоянным ускорением, имеет вид : х = 10 + 3t + 6t ^ 2.
Координата и время измеряются в метрах и секундах соответственно.
Какова проекция вектора скорости точки через 2с?
Скорость в любой момент времени определяется уравнением
V = 3 + 12t для нашего уравнения движения
подставим время и получим
V = 3 + 12 * 2 = 27м / c.
Движение материальной точки в данной системе отсчета заданно уравнением x = 40 + 2t?
Движение материальной точки в данной системе отсчета заданно уравнением x = 40 + 2t.
Где х измеряется в метрах, а t в секундах.
Определите начальную координату точки, скорость ее движения, координату точки через 10 секунд, перемещение точки за это время.
Движение материальной точки в данной системе отсчета задано уравнением x = 44 — 3t, где x — измеряется в метрах, а t — в секундах?
Движение материальной точки в данной системе отсчета задано уравнением x = 44 — 3t, где x — измеряется в метрах, а t — в секундах.
Определите : начальную координату точки ; скорость её движения ; координату точки через 6с ; перемещение точки за это время.
Уравнение проекции скорости точки имеет видV = 2 — 4tКакова проекция перемещения точки за 4 с?
Уравнение проекции скорости точки имеет вид
Какова проекция перемещения точки за 4 с?
Уравнение координаты материальной точки имеет вид : x = 10 + 4t + 2t ^ 2(в квардате)Определить характер движения точки?
Уравнение координаты материальной точки имеет вид : x = 10 + 4t + 2t ^ 2(в квардате)Определить характер движения точки.
Найти начальную координату начальной скорости и ускорения точки.
Написать уравнение зависимости проекции скорости от времени.
Уравнение координат имеет вид x = 10 + 4t + 2t²?
Уравнение координат имеет вид x = 10 + 4t + 2t².
Нужно определить характер движения точки, найти начальную координату, начальную скорость и ускорение точки.
Написать уравнение зависимости проекции ускорения от времени.
Лыжник скатывается с горы, двигаясь прямолинейно с постоянным ускорением 0, 1 м / c2?
Лыжник скатывается с горы, двигаясь прямолинейно с постоянным ускорением 0, 1 м / c2.
Напишите уравнения, выражающие зависимость от времени координаты и проекции вектора скорости движения лыжника, если его начальные координата и скорость движения равны нулю.
Зависимость от времени координаты точки, движущейся вдоль оси х, имеет вид : x = 4 + 5t + 2t в квадрате ?
Зависимость от времени координаты точки, движущейся вдоль оси х, имеет вид : x = 4 + 5t + 2t в квадрате .
Опишите характер движения.
Каковы начальная скорость и ускорение?
Запишите уравнение для проекции скорости.
Уравнение движения точки, перемещающейся прямолинейно с постоянным ускорением, имеет вид : x = 10 + 3t + 6Координата и время измеряются в метрах и секундах соответственно?
Уравнение движения точки, перемещающейся прямолинейно с постоянным ускорением, имеет вид : x = 10 + 3t + 6
Координата и время измеряются в метрах и секундах соответственно.
Какова проекция вектора скорости точки через 2 с?
Материальная точка движется прямолинейно?
Материальная точка движется прямолинейно.
Уравнение движения имеет вид , где A = 3 м / с ; .
Найти скорость v и ускорение точки в моменты времени t1 = 0 и t2 = 3 с.
Каковы средние значения скорости и ускорения за первые 3 с движения?
Материальная точка движется прямолинейно?
Материальная точка движется прямолинейно.
Уравнение движения имеет вид s = 2t + 0, 04t3 (расстояние – в метрах, время – в секундах).
Найти скорость и ускорение точки в моменты времени t1 = 0 и t2 = 5 с.
Каковы средние значения скорости и ускорения за первые 5 с движения?
На этой странице сайта вы найдете ответы на вопрос Уравнение движения точки, перемещающейся прямолинейно с постоянным ускорением, имеет вид : х = 10 + 3t + 6t ^ 2?, относящийся к категории Физика. Сложность вопроса соответствует базовым знаниям учеников 10 — 11 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.
H = V / (a * b) = m / p * (a * b) = 2, 700 / 7200 * (1, 3 * 0, 6) = 0, 5 м = 50см Ответ : 50см.
Vcp = Sоб / tоб Sоб = s1 + v2t2 = 200 + 5×80 = 600км toб = 7 + 5 = 12ч Vср = 600 / 12 = 15км / ч Ответ 15км / ч.
№ 1 F = I * B * L * sinα F = 5 А * 0, 2 Тл * 0, 20 м = 0, 2 Н № 2 F = q * v * B * sinα q = F / (v * B * sinα) q = 2 Н / (10⁶ м / с * 50 * 10⁻³ Тл) = 8, 4 * 10⁻⁴ Кл № 3 С / n = 2 = > C = 2 * n n * C = 302 = > n * 2 * n = 302 n² = 151 n = √151≈ 12 № 4 ..
Скорости современныхтранспортных средств. Автомобиль с реактивным двигателем – 1025, 2 км / ч. Самолет с реактивным двигателем – 3529, 6 км / ч. Электропоезд – 200 км / ч. Мотоцикл – 512, 7 км / ч. Океанский лайнер «Александр Пушкин» — 40 км / ч..
1)самолет 2)машина 3)поезд 4)мотоцикл 5)трамвай.
V = v1 — v2 = 3, 2 — 1, 6 = 1, 6 m1v1 = m2v2.
Относительная скорость второго поезжа относительно пассажира V = V1 + V2 = V1 + (V1 + dU) = (2 * V1 + dU) Длина второго поезда L = (2 * V1 + dU) * t.
Q = cm(t2 — t1) Q = 4200 * 5 * 70 = 1470000Дж = 1470кДж.
Х = х(н) + V(н)t + at ^ 2 / 2 x(н) = — 0, 5 V(н) = 0 а = — 1 V = V() + at V = 1×t.
Скорость Станислава : v₁ Скорость Владислава : v₂ = 2v₁ Путь, который проехал Станислав : S₁ = v₁t₁ = 0, 5v₁ (км) Путь, который проехал Владислав : S₂ = v₂t₂ = 1 / 6 * 2v₁ = v₁ / 3 (км) Путь, который прошел Владислав : S₂’ = v₂’t₃ = 6 * t₃ (км) Так к..
Уравнение движения, графики равномерного прямолинейного движения
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.
Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: \begin
Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: \begin
п.2. Уравнение прямолинейного равномерного движения
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения \(x(t)=x_0+v_x t\) с уравнением прямой \(y(x)=kx+b\) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента \(k\) играет проекция скорости \(v_x\), а роль свободного члена \(b\) – начальная координата \(x_0\).
 | Построим графики зависимости координаты от времени для нашего примера: |
x=20+10t — машина движется вправо (в направлении оси OX)
x=20-10t — машина движется влево (в направлении, противоположном оси OX)
x=20 — машина стоит
п.5. Как найти уравнение движения по графику движения?
п.6. График скорости vx=vx(t)
Для рассмотренного примера:
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени \(t_1\) координата равна \(x_1=x_0+v_x t_1\).
Несколько позже, в момент времени \(t_2\gt t_1\) координата равна \(x_2=x_0+v_x t_2\).
Если \(v_x\gt 0\), то пройденный за промежуток времени \(\triangle t=t_2-t_1\) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x \triangle t $$ В общем случае, т.к. \(v_x\) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|\triangle t $$
Изобразим полученное соотношение на графике скорости:
Проекция скорости \(v_x\) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ \triangle x=v_x \triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите \(x_0=0\) и запишите уравнение движения.
а) Постройте график движения \(x=x(t)\) и найдите с его помощью, сколько пробежит спортсмен за \(t_1=5\ с\), за \(t_2=10\ с\);
б) постройте график скорости \(v=v(t)\) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени \(\triangle t=t_2-t_1\)?
По условию \(x_0=0,\ v_x=8\).
Уравнение движения: \(x=x_0+v_x t=0+8t=8t\)
а) Строим график прямой \(x=8t\) по двум точкам:
| t | 0 | 5 |
| x | 0 | 40 |
По графику находим: \begin
б) Скорость \(v_x=8\) м/с — постоянная величина, её график:
$$ t_1=5\ с,\ \ t_2=10\ с $$ Пройденный путь за промежуток времени \(\triangle t=t_2-t_1\) равен площади заштрихованного прямоугольника: $$ s=v_x \triangle t=8\cdot (10-5)=40\ \text <(м)>$$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения \(x=x(t)\).
Найдем скорость корабля \(v_x\): $$ v_x=\frac
б) В начальный момент времени корабль находился на расстоянии \(x_0=20\) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18\cdot 4=92\ (\text<тыс.км>) $$
г) Переведем скорость в км/с: $$ 18000\frac<\text<км>><\text<ч>>=\frac<18000\ \text<км>><1\ \text<ч>>=\frac<18000\ \text<км>><3600\ \text
а) \(x(t)=20+18t\) (\(x\) в тыс.км, \(t\) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
http://fizika.my-dict.ru/q/2436118_uravnenie-dvizenia-tocki-peremesausejsa-pramolinejno-s/
http://reshator.com/sprav/fizika/7-klass/uravnenie-dvizheniya-grafiki-ravnomernogo-pryamolinejnogo-dvizheniya/