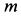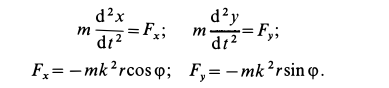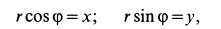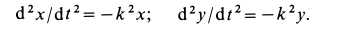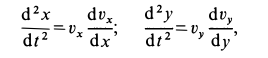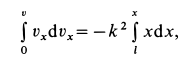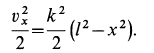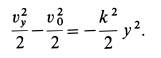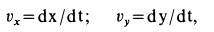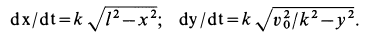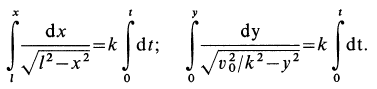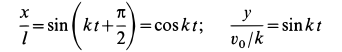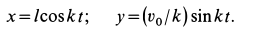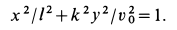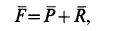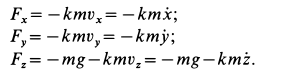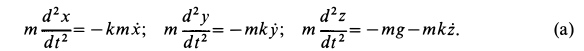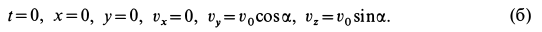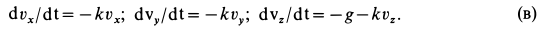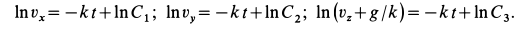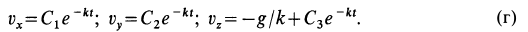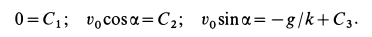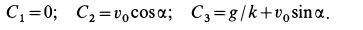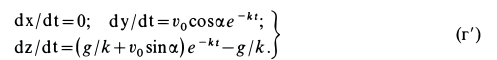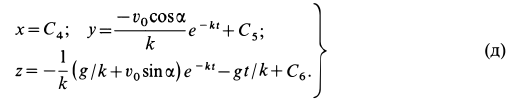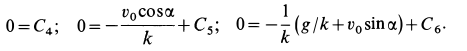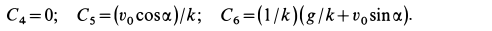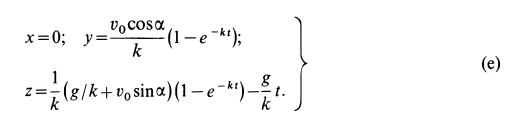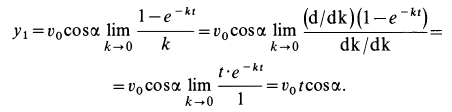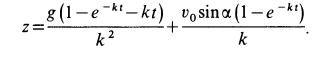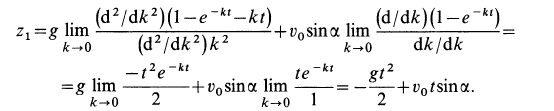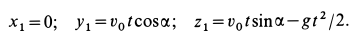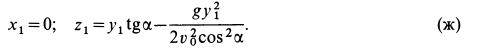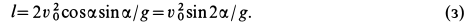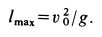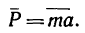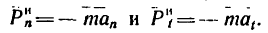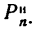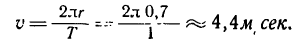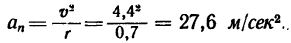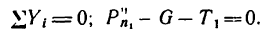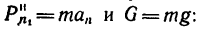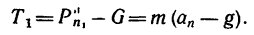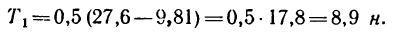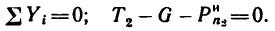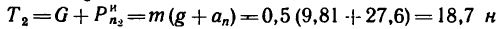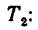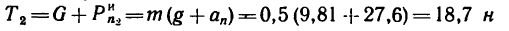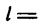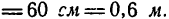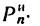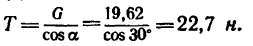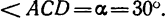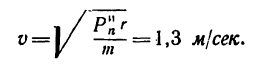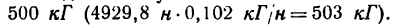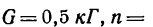Криволинейное движение материальной точки в теоретической механике
Содержание:
Криволинейное движение материальной точки:
В случае криволинейного движения по плоскости имеется два дифференциальных уравнения движения точки в декартовой системе координат, а в общем случае движения в пространстве— система трех дифференциальных уравнений. Дифференциальные уравнения криволинейного движения точки интегрируются сравнительно просто, если каждое из этих уравнений интегрируется независимо от других уравнений и при этом возможен один из трех рассмотренных случаев зависимости проекции равнодействующей силы от времени, координаты и скорости.
Рассмотрим примеры криволинейного движения точки в плоскости и в пространстве:
Пример 1. Материальная точка массой
Определить уравнения движения точки и уравнение ее траектории в координатной форме.
Решение:
Пусть в момент 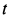
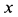
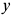
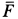
дифференциальные уравнения принимают форму
Для интегрирования этих уравнений можно применить подстановки
или интегрировать их как линейные дифференциальные уравнения с постоянными коэффициентами. Выполним интегрирование уравнений, используя подстановки. Имеем
Аналогично для 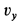
Рис. 11
Эти дифференциальные уравнения интегрируем путем разделения переменных. Получаем
Выполняя интегрирование и подставляя пределы, имеем
Рис. 12
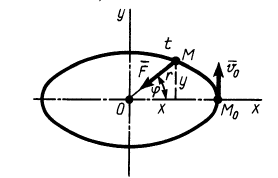
и уравнения движения точки принимают вид
Возводя в квадрат 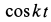
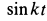
Траекторией точки оказался эллипс с полуосями 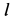
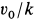
Пример 2. Материальная точка массой 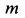
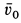
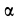
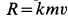
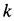
Решение:
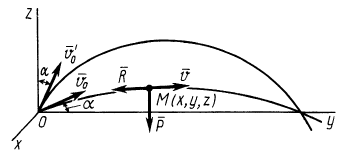
Задачу удобно решать в прямоугольной декартовой системе координат, начало которой находится в точке бросания, а ось 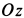
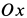
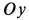
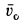
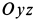
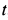
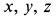
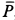
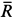
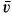
причем 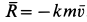
Для проекций равнодействующей силы 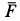
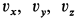
Знак минус у проекций силы сопротивления указывает на то, что их знаки противоположны знакам проекций скорости, принятым положительными.
Дифференциальные уравнения движения точки имеют вид
При сделанном выборе осей координат имеем следующие начальные условия:
Каждое дифференциальное уравнение системы в рассматриваемом случае можно интегрировать отдельно, независимо от других уравнений. После сокращения на т дифференциальные уравнения примут вид
Разделяя переменные и интегрируя каждое из уравнений системы, получаем:
После потенцирования имеем:
Подставляя в (г) начальные значения для 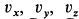
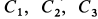
Постоянные интегрирования имеют следующие значения:
После подстановки постоянных интегрирования в (г) и замены проекций скорости на оси координат производными от координат по времени получаем
Разделяя в (г’) переменные и интегрируя каждое дифференциальное уравнение первого порядка, имеем
Подставляя в (д) начальные условия, получаем уравнения для определения постоянных интегрирования 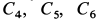
Подставляя значения постоянных в (д), получаем искомые уравнения движения точки:
Проведем некоторые исследования движения точки. Из уравнений движения (е) путем предельного перехода при 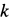
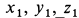
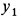
Прежде чем переходить к пределу в 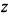
Получаем следующие уравнения движения точки под действием одной силы тяжести:
Если из этих уравнений исключить время 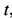
Траекторией точки является парабола, расположенная в плоскости 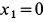
Если в (ж) принять 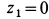
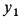
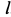
Из (з) следует, что наибольшая горизонтальная дальность получается при угле бросания 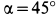
При других углах бросания 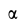
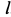
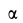
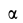
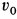
Криволинейное движение точки
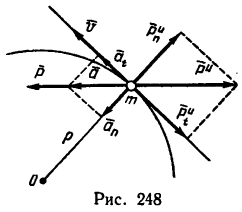
Как известно из кинематики, при движении материальной точки по криволинейной траектории ее ускорение 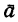
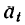
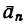
Из динамики уже известно, что ускорение 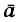
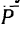
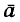
Если уравновесить силу 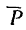
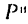
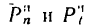
В задачах на криволинейное движение точки в основном рассматривается нормальная (центробежная) сила инерции
Числовое значение нормальной (центробежной) силы инерции можно выражать следующими формулами:

Заменим здесь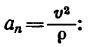

Если материальная точка, рассматриваемая в задаче, связана с каким-либо вращающимся телом, то скорость точки удобнее выражать через угловую скорость тела 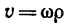
Если в последней формуле выразить массу точки через ее вес 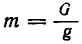
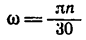
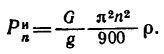
Здесь 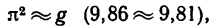
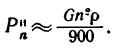
Эта формула дает приближенное значение центробежной силы инерции, но она очень удобна при решении многих задач.
Последовательность решения задач на криволинейное движение точки при помощи метода кинетостатики та же, что в предыдущем параграфе.
Задача №1
Шарик, масса которого m= 0,5 кг, привязки к нити длиной 0,7 м. Нить вместе с шариком вращается в вертикальной плоскости, затрачивая на один оборот 1 сек. Определить натяжение шнура в моменты высшего и низшего положения шарика, считая, что скорость остается постоянной при перемещении по всей длине окружности.
1. В соответствии с условием задачи считаем, что шарик движется равномерно по окружности, радиус которой равен длине нити (r=0,7 м). Следовательно, его скорость
Оставаясь численно неизменной, скорость точки непрерывно изменяет направление, значит точка имеет нормальное ускорение
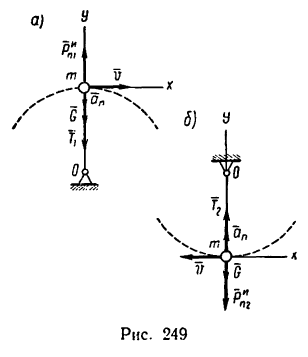
2. Рассмотрим движущийся шарик в тот момент, когда он проходит через верхнюю точку траектории (рис. 249, а).
На шарик действуют две силы: его вес 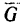
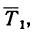
3. Добавим к силам 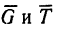
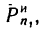
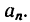
4. Из уравнения разновесия находим 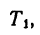
Подставим в это уравнение числовые значения:
Таким образом, находясь в верхнем положении, двигающийся шарик натягивает пить силой 8,9 н, что соответствует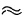
Отметим, что натяжение нити будет ослабевать при уменьшении скорости движения шарика. Следовательно, для того чтобы шарик при движении в вертикальной плоскости смог пройти верхнюю точку траектории с заданным радиусом кривизны р, он должен иметь в этой точке определенную скорость.
5. Рассмотрим теперь движущийся шарик в момент прохождения нм нижней точки траектории (рис. 249,6).
В этом положении на шарик действуют также две силы: вес 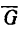
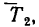
6. Добавим к силам 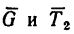
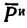
7. Находим
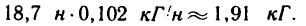
Как видно, при прохождении через нижнюю точку траектории шарик создает наибольшее натяжение нити.
Задача №2
Шарик А, масса которого 2 кг, подвешен на нити длиной 60 см, закрепленной в точке В. Он равномерно двигается по окружности в горизонтальной плоскости так, что нить описывает коническую поверхность и образует с вертикалью угол а = 30°. Определить натяжение нити и скорость шарика.
Решение 1 — с применением метода проекций.
1. Если масса шарика m=2 кг, то его вес G = mg = 2* 9,81 =19,62 н.Кроме веса, на шарик действует натяжение (реакция 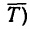
Изобразим двигающийся шарик с приложенными к нему силами G и 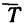
мерно, то он имеет только
6. Добавим к силам 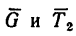
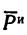
7. Находим
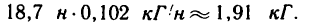
Как видно, при прохождении через нижнюю точку траектории шарик создает наибольшее натяжение нити.
Задача №3
Шарик А, масса которого 2 кг, подвешен на нити длиной 60 см, закрепленной в точке В. Он равномерно двигается по окружности в горизонтальной плоскости так, что нить описывает коническую поверхность и образует с вертикалью угол а = 30°. Определить натяжение нити и скорость шарика.
Решение 1 — с применением метода проекций.
1. Если масса шарика m=2 кг, то его вес G = mg = 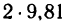
Кроме веса, на шарик действует натяжение (реакция 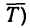
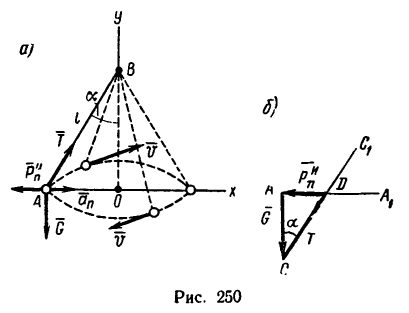
Изобразим двигающийся шарик с приложенными к нему силами 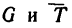
движется по окружности равно-нормальное ускорение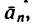
Изображая на рис. 250 силу инерции, необходимо учитывать, что она прикладывается к шарику условно. В действительности, сила инерции, как известно, приложена к двигающему телу или к связи. В данном случае нить служит для шарика и двигающим телом (через нить шарик приводится в движение), и связью (нить одновременно и ограничивает движение шарика). Поэтому сила инерции приложена к нити и отклоняет ее су вертикали.
2. Совместив оси координат с прямыми AO и ВО и спроектировав силы на оси х и у, выведем уравнения равновесия:
3. Из уравнения (2)
4 Из уравнения (1)
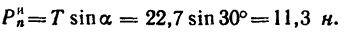
Так как 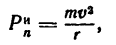
где 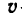
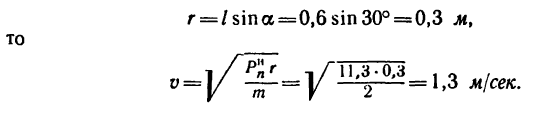
Таким образом, натяжение нити составляет 22,7 н при скорости движения шарика 1,3 м/сек.
Решение 2—с применением графо-аналитического метода.
1. Этот вариант решения начинаем так же, как и предыдущий: изображаем шарик с действующими на него силами С = 19,62 н и искомой Т, а затем добавляем силу инерции 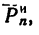
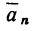
2. Силы 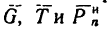
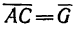
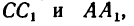
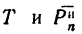
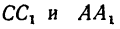
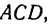
3. Из прямоугольного треугольника ACD имеем: 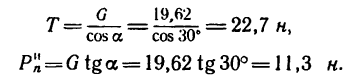
И, наконец, так же как и в первом решении, находим скорость движения шарика по окружности
Задача №4
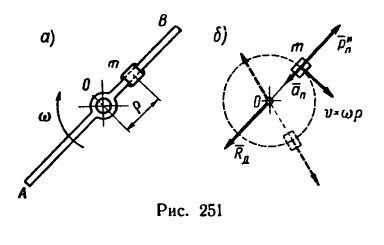
Тонкий стержень AВ, центр тяжести которого расположен на его оси О, вращается с угловой скоростью n -3009 об, мин.
На сколько увеличится нагрузка на подшипник, в котором вращается стержень, если на одну из половинок стержня прикрепить массу m — 0,5 кг, на расстоянии р = 0,1 м от оси вращения (рис. 251,а).
1. Стержень АВ без прикрепленной к нему массы т создает нагрузку на подшипник, равную его собственному весу. Причем, если стержень хорошо центрирован, т. е. его центр тяжести расположен точно на оси подшипника, то нагрузка при вращении не изменится — она также будет равна весу стержня и будет действовать на подшипник вертикально вниз.
2. Если к стержню, по условию задачи, прикрепить массу m, то эта масса (примем ее за материальную точку), двигаясь по окружности радиусом р = 0,1 м, начнет растягивать ту часть стержня, которая расположена между массой т и подшипником, силой, равной 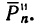
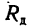
3. Так как увеличение нагрузки равно возникшей силе инерции 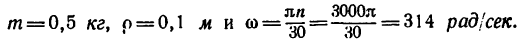
Подставим эти значения в формулу (3):
PJ| = 0,5 • 3142 • 0,1 =4929,8 н?«4,93 кн.
Таким образом, в результате прикрепления массы т нагрузка на подшипник увеличивается почти на 5 кн, что соответствует почти
4. Применив формулу (4) и положив в ней 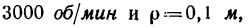
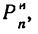
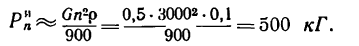
Результат, получившийся в этой задаче, подтверждает необходимость тщательной балансировки вращающихся деталей машин. Несбалансированные детали при вращении создают огромные дополнительные динамические нагрузки, которые приводят к быстрому износу подшипников.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Движение несвободной материальной точки
- Относительное движение материальной точки
- Геометрия масс
- Свойства внутренних сил системы
- Аксиомы классической механики
- Дифференциальные уравнения движения материальной точки
- Две основные задачи динамики точки
- Прямолинейное движение точки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Теоретическая механика:
Кинематика точки
Смотрите также решения задач по теме «Кинематика точки» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.
В этой главе в основном рассмотрены методы решения задач, в которых закон движения точки выражен так называемым естественным способом: уравнением s=f(t) по заданной траектории *.
* Решения задач, в которых закон движения задан координатным способом, рассмотрены в конце главы (§ 31).
В этом случае главными параметрами, характеризующими движение точки но заданной траектории, являются: s – расстояние от заданного начального положения и t – время.
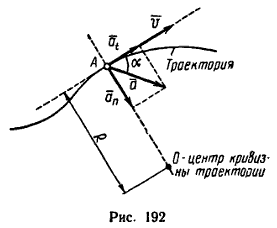
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью (v на рис. 192). Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка. Числовое значение скорости в любой момент времени выражается производной от расстояния по времени:
v = ds/dt или v = f'(t).
Ускорение a точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость – вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.
Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением at – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).
Числовое значение касательного ускорения в общем случае определяется по формуле
at = dv/dt или at = f»(t).
Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением an – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).
Числовое значение нормального ускорения определяется в общем случае по формуле
an = v 2 /R,
где v – модуль скорости точки в данный момент;
R – радиус кривизны траектории в месте, где находится точка в данный момент.
После того как определены касательное и нормальное ускорения, легко определить и ускорение a ( полное ускорение точки ).
Так как касательная и нормаль взаимно перпендикулярны, то числовое значение ускорения а можно определить при помощи теоремы Пифагора:
a = sqrt(at 2 + an 2 ).
Направление вектора a можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
sin α = an/a; cos α = at/a; tg α = an/at.
Но можно сначала определить направление полного ускорения a использовав формулу tg α = an/at,
а затем найти числовое значение a:
a = an/sin α или a = at/cos α.
Касательное и нормальное ускорения точки являются главными кинематическими величинами, определяющими вид и особенности движения точки.
Наличие касательного ускорения (at≠0) или его отсутствие (at=0) определяют соответственно неравномерность или равномерность движения точки.
Наличие нормального ускорения (an≠0) или его отсутствие (an=0) определяют криволинейность или прямолинейность движения точки.
Движение точки можно классифицировать так:
а) равномерное прямолинейное (at = 0 и an = 0);
б) равномерное криволинейное (at = 0 и an ≠ 0);
в) неравномерное прямолинейное (at ≠ 0 и an = 0);
г) неравномерное криволинейное (at ≠ 0 и an ≠ 0).
Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории.
Степень неравномерности движения точки задана уравнением s=f(t), а вид траектории задается непосредственно.
§ 27. Равномерное прямолинейное движение точки
Если at=0 и an=0, то вектор скорости остается постоянным (v=const), т. е. не изменяется ни по модулю, ни по направлению. Такое движение называется равномерным прямолинейным .
Уравнение равномерного движения имеет вид
(а) s = s0 + vt
или в частном случае, когда начальное расстояние s0=0,
(б) s = vt.
В уравнение (а) входит всего четыре величины, из них две переменные: s и t и две постоянные: s0 и v. Поэтому в условии задачи на равномерное и прямолинейное движение точки должны быть заданы три любые величины.
При решении задач необходимо выяснить все заданные величины и привести их к одной системе единиц. При этом нужно заметить, что как в системе МКГСС (технической), так и в СИ единицы всех кинематических величин одинаковы: расстояние s измеряется в м, время t – в сек, скорость v – в м/сек.
§ 28. Равномерное криволинейное движение точки
Если at = 0 и an ≠ 0, то модуль скорости остается неизменным (точка движется равномерно), но ее направление изменяется и точка движется криволинейно. Иначе, при равномерном движении по криволинейной траектории точка имеет нормальное ускорение, направленное по нормали к траектории и численно равное
an = v 2 /R,
где R – радиус кривизны траектории.
В частном случае движения точки по окружности (или по дуге окружности) радиус кривизны траектории во всех ее точках постоянный:
R = r = const,
а так как и числовое значение скорости постоянно, то
an = v 2 /r = const.
При равномерном движении числовое значение скорости определяется из формулы
v = (s — s0)/t или v = s/t.
Если точка совершит полный пробег по окружности, то путь s равен длине окружности, т. е. s = 2πr = πd (d = 2r – диаметр), а время равно периоду, т. е. t = T. Выражение скорости примет вид
v = 2πr/T = πd/T.
§ 29. Равнопеременное движение точки
Если вектор at=const (касательное ускорение постоянно как по модулю, так и по направлению), то an=0. Такое движение называется равнопеременным и прямолинейным .
Если же постоянным остается только числовое значение касательного уравнения
at = dv/dt = f'(t) = const,
то an≠0 и такое движение точки называется равнопеременным криволинейным .
При |at|>0 движение точки называется равноускоренным , а при |at| равнозамедленным .
Уравнение равнопеременного движения независимо от его траектории имеет вид
(1) s = s0 + v0t + att 2 / 2.
Здесь s0 – расстояние точки от исходного положения в момент начала отсчета; v0 – начальная скорость и at – касательное ускорение – величины численно постоянные, a s и t – переменные.
Числовое значение скорости точки в любой момент времени определяется из уравнения
(2) v = v0 + att.
Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: s0, v0, at и три переменные: s, v, t.
Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).
Если неизвестные входят в оба основных уравнения, например, неизвестны at и t, то для удобства решения таких задач выведены вспомогательные формулы:
после исключения at из (1) и (2)
(3) s = s0 + (v + v0)t / 2;
после исключения t из (1) и (2)
(4) s = s0 + (v 2 — v0 2 ) / (2at).
В частном случае, когда начальные величины s0=0 и v0=0 (равноускоренное движение из состояния покоя), то получаем те же формулы в упрощенном виде:
(5) s = att 2 / 2;
(6) v = att;
(7) s = vt / 2;
(8) s = v 2 / (2at).
Уравнения (5) и (6) являются основными, а уравнения (7) и (8) – вспомогательными.
Равноускоренное движение из состояния покоя, происходящее под действием только силы тяжести, называется свободным падением . К этому движению применимы формулы (5)–(8), причем
at = g = 9,81 м/сек 2 ≈ 9,8 м/сек 2 .
§ 30. Неравномерное движение точки по любой траектории
§ 31. Определение траектории, скорости и ускорения точки, если закон ее движения задан в координатной форме
Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат (см. § 51, п. 2 в учебнике Е. М. Никитина).
Движение точки в пространстве задается тремя уравнениями:
x = f1(t);
(1) y = f2(t);
z = f3(t);
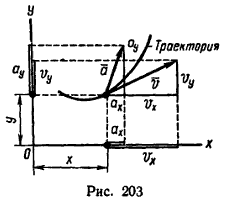
Движение точки в плоскости (рис. 203) задается двумя уравнениями:
(2) x = f1(t);
y = f2(t);
Системы уравнений (1) или (2) называют законом движения точки в координатной форме .
Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).
Если закон движения точки задан в координатной форме, то:
а) траектория плоского движения точки выражается уравнением
y = F(x),
которое образуется из данных уравнений движения после исключения времени t;
б) числовое значение скорости точки находится из формулы
v = sqrt(vx 2 + vy 2 )
после предварительного определения проекции (см. рис. 203) скорости на оси координат
vx = dx/dt и vy = dy/dt;
в) числовое значение ускорения находится из формулы
a = sqrt(ax 2 + ay 2 )
после предварительного определения проекций ускорения на оси координат
ax = dvx/dt и ay = dvy/dt;
г) направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.
§ 32. Кинематический способ определения радиуса кривизны траектории
При решении многих технических задач возникает необходимость знать радиус кривизны R (или 1/R – кривизну ) траектории. Если задано уравнение траектории, то радиус ее кривизны в любой точке можно определить при помощи дифференциального исчисления. Используя уравнения движения точки в координатной форме, можно определять радиус кривизны траектории движущейся точки без непосредственного исследования уравнения траектории. Определение радиуса кривизны траектории при помощи уравнений движения точки в координатной форме называется кинематическим способом. Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу
an = v 2 /R,
выражающую числовое значение нормального ускорения.
Скорость v точки определяется по формуле
(б) v = sqrt(vx 2 + vy 2 ).
Числовое значение нормального ускорения an входит в выражение полного ускорения точки
a = sqrt(an 2 + at 2 ),
откуда
(в) an = sqrt(a 2 — at 2 ),
где квадрат полного ускорения
(г) a 2 = ax 2 + ay 2
и касательное ускорение
(д) at = dv/dt.
Таким образом, если закон движения точки задан уравнениями
x = f1(t);
y = f2(t),
то при определении радиуса кривизны траектории рекомендуется произвести следующее:
1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
vx = f1‘(t);
vy = f2‘(t).
2. Подставив в (б’) выражения vx и vy, найти v 2 .
3. Продифференцировав по t уравнение (б), полученное непосредственно из (б’), найти касательное ускорение at, а затем at 2 .
4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
ax = f1»(t) = vx‘;
ay = f2»(t) = vy‘.
5. Подставив в (г) выражения ax и ay, найти a 2 .
6. Подставить в (в) значения a 2 и at 2 и найти an.
7. Подставив в (а) найденные значения v 2 и an, получить радиус кривизны R.
Движение тела по криволинейной траектории. Движение по окружности. Характеристики вращательного движения. Центростремительное ускорение
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Вам хорошо известно, что в зависимости от формы траектории движение делится на прямолинейное и криволинейное. С прямолинейным движением мы научились работать на предыдущих уроках, а именно решать главную задачу механики для такого вида движения.
Однако ясно, что в реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения является траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца и даже траектория движения ваших глаз, следящих сейчас за этим конспектом.
Вопросу о том, как решается главная задача механики в случае криволинейного движения, и будет посвящен этот урок.
http://exir.ru/termeh/kinematika_tochki.htm
http://interneturok.ru/lesson/physics/10-klass/mehanikakinematika/dvizhenie-tela-po-krivolineynoy-traektorii-dvizhenie-po-okruzhnosti-harakteristiki-vraschatelnogo-dvizheniya-tsentrostremitelnoe-uskorenie