Уравнение движения точки техническая механика

Динамика материальной точки. Все законы и теоремы

Законы динамики

Первый закон Ньютона (закон инерции Галилея)
Существуют такие системы отсчета, относительно которых любая материальная точка, не взаимодействующая с другими телами и точками, движется прямолинейно и равномерно. В частности, если точка покоилось в определенный момент времени, то она будет покоиться и в последующие моменты.

Не во всех системах отсчета выполняется закон инерции. Например, если мы выберем систему отсчета, связанную с ускоряющейся ракетой, то относительно этой системы, не взаимодействующие материальные точки, не будут двигаться прямолинейно и равномерно.

Инерциальная система отсчета – это система отсчета, в которой справедлив закон инерции.
Движение по инерции – это движение точки, совершаемое при отсутствии действующих на нее сил.

Второй закон Ньютона (основной закон динамики)
Взаимодействие на выбранную материальную точку со стороны других тел описывается вектором, который называется силой. При этом, в инерциальных системах отсчета, действие силы приводит к ускорению точки , которое пропорционально приложенной силе, имеет одинаковое с ней направление, и обратно пропорционально массе точки:
(1) .

Если есть радиус-вектор, проведенный из начала координат к точке, то ускорение есть вторая производная радиус-вектора по времени:
.
Производную по времени, в теоретической механике, обозначают точкой над переменной, а не штрихом, как в математическом анализе.

Если на точку действует не одна, а n сил, то в правой части производится суммирование по всем силам, действующих на точку. Тогда уравнение (1) примет вид:
(2) .

Третий закон динамики (закон равенства действия и противодействия)
Если две материальные точки действуют друг на друга, то сила, с которой первая точка действует на вторую, равна по абсолютной величине и противоположна по направлению силе, с которой вторая точка действует на первую. При этом силы направлены вдоль прямой, соединяющей точки.

Закон независимости сил
Несколько одновременно действующих на материальную точку сил сообщают точке такое ускорение, какое сообщила бы ей одна сила, равная их геометрической сумме.

То есть уравнение (2) можно записать в виде:
, где .

Задачи динамики

Первая задача динамики
Зная закон движения точки, определить действующую на нее силу.

Вторая (основная) задача динамики
Зная действующие на точку силы, определить ее закон движения.

Основные виды сил

Единицей измерения силы в СИ является 1 ньютон (1 Н = кг·м/с 2 ). Это сила, которую нужно приложить к точке массой 1 кг, чтобы она получила ускорение 1 м/с 2 .

Сила тяжести.
Сила тяжести действует на любую материальную точку, находящуюся на поверхности Земли. Она пропорциональна массе точки и равна
,
где – ускорение свободного падения, направленное вниз. Его величина зависит от широты и высоты над уровнем моря. Стандартное значение, принятое при построении систем единиц, составляет м/с 2 .

Сила тяготения.
.
Здесь – массы точек, r – расстояние между ними, Н·м 2 /кг 2 – гравитационная постоянная.

Для точки массы m на поверхности Земли имеем: . Отсюда . Тогда силу тяготения Земли можно вычислять по формуле:
,
где R = 6371 км – радиус Земли; r – расстояние от точки до центра Земли.

Сила электростатического взаимодействия.
,
где – величины зарядов; r – расстояние между ними; Н·м 2 /Кл 2 – коэффициент. Одноименные заряды отталкиваются, разноименные – притягиваются.

Сила трения скольжения
возникает при скольжении одного тела по поверхности другого. Она направлена в сторону, противоположную скорости движения. Ее величина определяется по формуле:
F = fN ,
где N – сила давления, перпендикулярная поверхности, с которой скользящее тело прижимается к поверхности; f – коэффициент трения, который зависит от материалов соприкасаемых тел.

Сила упругости.
Эта сила возникает при деформации упругих тел. Это могут быть растяжения, сжатия и изгибы. Она определяется по формуле
F = cλ ,
где λ – величина деформации; c – коэффициент, который зависит от материала упругого тела. Для пружины λ – это удлинение или сжатие пружины; c – коэффициент жесткости.

Сила вязкого трения.
При движении тела в вязкой среде с небольшими скоростями, на него действует сила трения, пропорциональная скорости движения:
F = μv ,
где v – скорость тела; μ – коэффициент сопротивления.
При больших скоростях, сила трения пропорциональна квадрату скорости.

Дифференциальные уравнения движения точки

Спроектируем уравнение (2) на оси прямоугольной системы координат. Пусть радиус вектор точки имеет в этой системе компоненты (проекции) . Тогда из векторного уравнения (2) получаем систему уравнений:
.
Это есть дифференциальные уравнения движения точки в прямоугольной системе координат.

Спроектируем уравнение (2) на оси естественного трехгранника:
.
Здесь – единичный вектор, направленный по касательной к траектории; – единичный вектор, перпендикулярный и лежащий в касательной плоскости траектории; – единичный вектор, перпендикулярный и . Поскольку , то .
Вводим пройденный путь s , измеренный вдоль дуги траектории точки. Пусть ρ – радиус кривизны траектории в рассматриваемой точке. Тогда, для естественного способа задания движения точки, уравнения движения примут вид:
.

Уравнения движения в полярных координатах для плоского движения:
.

Прямолинейное движение точки

Пусть ось x направлена вдоль линии движения точки. Тогда уравнение движения имеет вид:
(3) .
Его общее решение:
,
где – произвольные постоянные. Их находят из начальных условий:
.

Если сила F_x зависит только от времени, то из уравнения (3) сначала определяют скорость v_x , а затем координату x , последовательно интегрируя уравнения:
.
Если сила зависит только от координаты x , то выполняют преобразование:
;
;
.

Колебательное движение материальной точки

Свободные колебания

Рассмотрим движение груза на пружинке. Считаем, что груз является материальной точкой; массой пружины можно пренебречь; и отсутствует сила тяжести. Пусть движение происходит вдоль оси x . За начало отсчета выберем такое положение груза, при котором пружина не деформирована. Тогда на точку действует только восстанавливающая сила упругости пружины, которая определяется по закону Гука:
(К1) ,
где x – деформация пружины; c – коэффициент жесткости. Он равен силе, которая возникает при деформации, равной единице (один метр) и имеет размерность [Н/м]. Из (К1) видно, что сила является восстанавливающей, то есть направлена так, чтобы вернуть точку в начало координат к недеформированному состоянию. Сила такого вида возникает не только при деформации пружины, но и во многих других случаях при небольшом отклонении точки от равновесного положения.

Составим уравнение движения точки и выполняем преобразования:
.
Введем обозначение . В результате получаем.

(К2) .
Уравнение (К2) называется дифференциальным уравнением свободных колебаний. Его также называют дифференциальным уравнением гармонических колебаний. Оно является линейным однородным дифференциальным уравнением второго порядка.

Ищем его решение в виде . Получаем характеристическое уравнение:
.
Оно имеет два мнимых корня: . Тогда общее решение уравнения (К2) имеет вид:
,
где и – произвольные постоянные. Они определяются из начальных условий. Пусть – координата и скорость точки в начальный момент времени , тогда
;
.

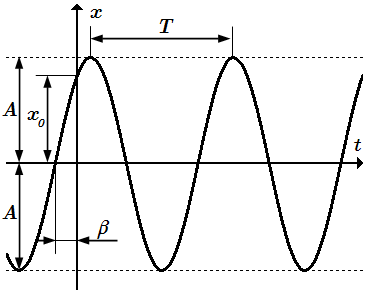
График гармонического движения точки.

Часто бывает удобно вместо постоянных интегрирования и перейти к новым постоянным A и β по формулам: . Тогда
(К3) .
Это есть уравнение гармонического колебательного движения точки. Здесь – амплитуда колебаний;
– фаза колебаний;
β – начальная фаза, ;
– циклическая частота колебаний, которую также называют угловой или собственной.
Период колебаний: .
Частота колебаний: – это число циклов колебаний, совершенных в единицу времени. Она широко применяется в технике, однако для математического описания более удобна угловая частота, которую мы будем использовать в дальнейшем и называть просто частотой.

Частота k и период T не зависят от начальных условий, а амплитуда и фаза – зависят. Кроме этого, k и T не зависят от амплитуды. Колебания, у которых частота и период не зависят от амплитуды, называют изохорными колебаниями. Если рассмотреть колебания с большой амплитудой, при которой закон Гука (К1) не выполняется, то уравнение (К2) не будет линейным и колебания не будут изохорными.

Влияние постоянной силы

Пусть теперь, наряду с восстанавливающей силой (К1), на точку действует постоянная сила P , например сила тяжести. Тогда уравнение движения примет вид:
.
Это приводит к смещению центра колебаний в сторону действия силы P на величину
δ _ст = P/c .
Это смещение называют статическим отклонением. Если P – сила тяжести, то
.

Колебания при вязком трении

Пусть на точку, кроме силы упругости пружины, действует сила сопротивления среды. При малых скоростях она пропорциональна скорости точки:
. Это так называемое вязкое трение. Составим уравнение движения:
. Обозначив μ/m= 2 b , получаем:
(К4) . Составляем характеристическое уравнение:
(К5) . Оно имеет два корня:
.

Затухающие колебания

При b , корни характеристического уравнения (К5) комплексные:
. Тогда общее решение уравнения (К4) имеет вид:
,
где . Обозначим , . Тогда
(К6) .
, ;
– амплитуда (переменная величина);
b – коэффициент затухания;
– частота затухающих колебаний;
– период затухающих колебаний. Он больше периода свободных колебаний. При небольшом коэффициенте затухания (при b/k ≪ 1 ) T ₁ ≈ T .
Колебания, происходящие по закону (К6) называются затухающими. График затухающих колебаний заключен между двумя кривыми x = ±Ae –bt , симметричными относительно оси t .

Затухающие колебания можно рассматривать как гармонические колебания с переменной амплитудой . Относительное изменение переменной амплитуды за период колебания называется декрементом колебаний. Он равен
. Модуль логарифма декремента называется логарифмическим декрементом. Он равен .

Апериодическое движение точки

При (или ) корни характеристического уравнения (К5) действительные. Поэтому движение точки является апериодическим.
При (или ) характеристическое уравнение (К5) имеет два различных действительных корня:
. Тогда общее решение уравнения (К4) имеет вид:
(К7) .
Сюда не входят тригонометрические функции. Поэтому это апериодическое движение. Точка может пройти через положение равновесия x = 0 не более одного раза.

Закон движения (К7) можно выразить через гиперболические функции, если положить: . Тогда
.
Перейдем к новым постоянным интегрирования A и β , выполнив подстановку:
. Тогда
.

При b = k характеристическое уравнение (К5) имеет два кратных вещественных корня . Общее решение уравнения (К4) имеет вид:
.
Движение также апериодическое. Точка может пройти через положение равновесия x = 0 не более одного раза.

Вынужденные колебания

Рассмотрим случай, когда кроме восстанавливающей силы , на точку действует возмущающая сила, меняющаяся по гармоническому закону:
(К8) . Составим уравнение движения:
.
Введем обозначение h=H/m . Разделив на m , получаем дифференциальное уравнение вынужденных колебаний:
(К9) .

Это линейное неоднородное дифференциальное уравнение с постоянными коэффициентами со специальной неоднородной частью. Его общее решение равно сумме общего решения однородного уравнения и частного (то есть любого, отличного от нулевого) решения данного уравнения:
;
;
.
Общее решение однородного уравнения: .
Ищем частное решение в виде . В результате получаем:
;
.

Коэффициент динамичности. Действие постоянной возмущающей силы величины H приводит к статическому отклонению . Периодическая возмущающая сила (К8) с амплитудой H приводит к периодическим колебаниям с амплитудой . В связи с этим вводят коэффициент динамичности: .
Он показывает, во сколько раз амплитуда колебаний превосходит статическое отклонение.

Явление резонанса и биения

Когда частота возмущающей силы равна частоте собственных колебаний p = k , коэффициент динамичности стремится к бесконечности, амплитуда колебаний неограниченно возрастает. Это явление называется резонансом. Уравнение движения точки при p = k имеет вид:
(К10) .
Оно имеет частное решение
.
Общее решение уравнения (К10):
.
Это уравнение показывает, что амплитуда вынужденных колебаний возрастает пропорционально времени. Фаза вынужденных колебаний отстает от фазы возмущающей силы на π/ 2 .

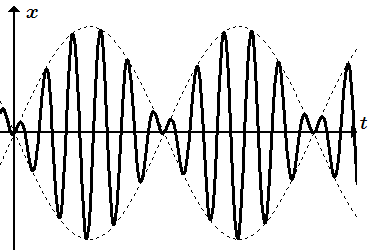
Биения.

Когда частота p возмущающей силы близка к собственной частоте k колебания точки, p/k ≈ 1 , возникает явление, называемое биениями. В этом случае частное решение уравнения (К9) имеет вид:
,
где .
Происходит наложение колебаний. Их можно рассматривать как вынужденные колебания частоты с переменной амплитудой, которая является периодической функцией с частотой .

Вынужденные колебания при наличии вязкого трения

Составим уравнение движения вынужденных колебаний при наличии вязкого трения:
.
Получаем дифференциальное уравнение:
.
Его общее решение имеет вид.
1) при b :
;
2) при b > k :
;
3) при b = k :
.
Здесь ;
ε определяется из уравнений:
.
Величины A и β являются постоянными интегрирования. Они определяются из начальных условий.

Общие теоремы динамики точки

Теорема об изменении количества движения материальной точки

Теорема об изменении количества движения материальной точки в дифференциальной форме
Изменение количества движения материальной точки за бесконечно малый промежуток времени dt равно элементарному импульсу равнодействующей сил, приложенных к этой точке:
.
Эту теорему можно сформулировать так:
Производная по времени от количества движения материальной точки равна равнодействующей сил, приложенных к этой точке:
(Т1) .

Проектируя это векторное уравнение на оси координат, получаем три скалярных уравнения:
.

Если проинтегрировать уравнение (Т1) по времени от начального момента времени t = 0 до конечного момента t = t₁ , то получим теорему в интегральной форме.

Теорема об изменении количества движения материальной точки в интегральной форме
изменение количества движения материальной точки за конечный промежуток времени [0,t₁] равно импульсу силы, приложенной к этой точке, за тот же промежуток времени:
.
Здесь – скорость точки в моменты времени t = 0 и t = t ₁ , соответственно.

Теорема об изменении момента количества движения материальной точки

Теорема об изменении момента количества движения материальной точки
Производная по времени от момента количества движения материальной точки, относительно произвольного центра O , равна моменту равнодействующей силы, приложенной к точке, относительно того же центра:
.

Проектируя это векторное уравнение на оси координат, получаем три скалярных уравнения:
.

Если на точку действует несколько сил , то равнодействующая сила равна их геометрической сумме:
.
Тогда можно записать эту теорему так:
.

Далее будем считать, что точка O выбрана в начале координат. Тогда .

Центральная сила. Второй закон Кеплера

Пусть на точку действует центральная сила с центром в начале координат O . Тогда ее момент относительно O равен нулю. По теореме об изменении момента количества движения материальной точки имеем:
.
Если ввести секторную скорость , то она оказывается постоянной
.
Получаем второй закон Кеплера (закон площадей).

Второй закон Кеплера (закон площадей)
Под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью. То есть радиус-вектор точки заметает равные площади в любые равные промежутки времени.

Работа силы. Мощность

Основные понятия

Единицей измерения работы в СИ является 1 джоуль (1 Дж = 1 Н·м = кг·м 2 /с 2 ).

Работа силы при движении материальной точки от точки M ₁ до точки M ₂ равна сумме (интегралу) элементарных работ:
.
Если ввести скорость точки , то
.

Теорема о работе силы
Работа A равнодействующей силы на некотором перемещении равна алгебраической сумме работ A_k составляющих сил на том же перемещении:
.

Мощность – это величина работы, произведенная за единицу времени.
.

Единицей измерения мощности в СИ является 1 ватт (1 Вт = 1 Дж/с). Другие единицы мощности: 1 кВт (киловатт) = 1000 Вт; 1л.с.(лошадиная сила) = 736 Вт = 75 кгс·м/с.

Работа основных видов сил

Работа силы тяжести:
,
где P – сила тяжести, действующая на точку. Если начальная точка выше конечной, то работа положительна; если начальная точка ниже конечной, то отрицательна.

Работа силы упругости:
.
Здесь – деформация пружины в начальном положении; – в конечном.

Работа силы трения. Если сила трения постоянна, то
,
где s – длина пройденного точкой пути; – сила трения, которая всегда направлена в сторону, противоположную перемещению; f – коэффициент трения; N – нормальная реакция поверхности. Работа силы трения всегда отрицательна.

Работа силы тяготения.
На точку, находящуюся вблизи планеты Земля, на расстоянии r ≥ R от ее центра, действует сила притяжения
,
где R = 6371 км – радиус Земли. Тогда при перемещении точки из положения M₁ в положение M₂, сила тяготения совершит работу
.
Она не зависит от траектории движения тела.

Теорема об изменении кинетической энергии точки

Теорема об изменении кинетической энергии точки в дифференциальной форме
Дифференциал кинетической энергии точки равен сумма элементарных работ всех действующих на точку сил:
.

Проинтегрировав обе части этого уравнения вдоль траектории движения точки от положения M₁ до M₂, получим теорему в интегральной форме.

Теорема об изменении кинетической энергии точки
Изменение кинетической энергии материальной точки, при переходе ее из начального положения M₁ в конечное положение M₂, равно сумме работ всех сил, приложенных к точке на этом перемещении:
.

Силовые поля и потенциальная энергия

1. Работа сил стационарного поля при перемещении точки из положения M₁ в положение M₂ зависит только от начального положения M₁, конечного положения M₂, и формы траектории, но не зависит от закона движения точки.

2. Работа, совершенная полем при перемещении точки из положения M₁ в M₂ равна по модулю и обратна по величине работе, совершенной полем при перемещении точки из M₂ в M₁ при перемещении по той же траектории:
.

Для нестационарных полей эти свойства на выполняются.
Примеры стационарных полей: поле силы тяжести на поверхности Земли; электростатическое поле от неподвижно закрепленного заряда; поле силы упругости пружины, один конец которой закреплен.

Потенциальное силовое поле – это стационарное силовое поле, работа сил которого зависит только от начального M₁ и конечного M₂ положений точки, и не зависит от формы ее траектории. Потенциальное силовое поле также называют консервативным.

В потенциальном поле существует такая функция, через которую можно выразить вектор силы , действующей на точку.

Силовая функция – это функция, зависящая от координат точки ( x, y, z ) , через которую выражаются проекции силы потенциального поля на оси координат:
.

Отсюда следует, что сила не изменится, если к силовой функции прибавить постоянную. Таким образом, силовая функция определена с точностью до произвольной постоянной.

В потенциальном поле элементарная работа является дифференциалом от силовой функции:
.
Работа при конечном перемещении из точки в точку равна разности силовой функции в этих точках:
.
Таким образом, в потенциальном поле, работа сил поля не зависит от формы траектории. На замкнутом перемещении работа равна 0. Для более наглядной физической интерпретации, вводят понятие потенциальной энергии. Она равна, с точностью до произвольной постоянной, силовой функции, взятой с обратным знаком.

Потенциальная энергия П – это работа, которую нужно совершить при перемещении точки в потенциальном поле из данного положения в произвольным образом выбранное нулевое положение.

Так, для поля деформации, в качестве нулевого положения обычно принимают не деформированное положение; для гравитационного и электростатических полей за нулевое выбирают положение, бесконечно удаленное от тела или заряда. Для силы тяжести в поле Земли принимают любое, удобное для расчета положение. Таким образом, потенциальная энергия равна силовой функции, взятой с обратным знаком плюс постоянная, зависящая от выбора нулевого положения:
.

Пусть – нулевое положение. Тогда
;
.

Работа сил поля при перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий: .

Эквипотенциальные поверхности – это поверхности равного потенциала:
.

Сила направлена перпендикулярно эквипотенциальной поверхности.

Закон сохранения механической энергии
Если точка находится в потенциальном поле, то сумма ее кинетической и потенциальной энергий является постоянной:
.
Если на точку действуют несколько сил от разных потенциальных полей, то в качестве потенциальной энергии нужно взять сумму потенциальных энергий от каждого силового поля:
.

Основные виды потенциальных полей

В поле силы тяжести, потенциальная энергия зависит от высоты. Направив ось z вертикально вверх, получим: .

Поле силы упругости пружины. В этом поле, потенциальная энергия зависит от деформации λ пружины:
.
В качестве нулевого положения выбирают положение без деформации: λ = 0 .

Сила гравитационного притяжения и космические скорости

Между любыми двумя точками массами m ₁ и m ₂ , действует сила всемирного тяготения. Так, на точку 2 действует сила притяжения со стороны точки 1:
,
направленная вдоль прямой, проходящей через точку 1. Здесь r – расстояние между точками; Н·м 2 /кг 2 – гравитационная постоянная.

В результате притяжения, обе точки получают ускорения и движутся друг относительно друга. Мы рассмотрим более простой, но важный случай, когда масса M = m ₁ одного из тел намного больше массы m = m ₂ второго тела. Тогда точка с меньшей массой практически не оказывает влияния на движение более массивной точки. Выберем начало инерциальной системы координат в точке 1. Тогда силу гравитационного притяжения можно рассматривать как центральную силу и представить ее в векторном виде:
(П1) .
Потенциальная энергия точки 2:
(П2) .
Здесь нулевое положение выбрано на бесконечности: .

Формулы (П1) и (П2) справедливы, если объект 1 является шаром с плотностью, зависящей только от расстояния r до его центра. Пусть R – радиус такого шара. Тогда в формулах (П1) и (П2) r – это расстояние от центра шара 1 до точки 2. Они справедливы при .

Эти формулы можно использовать при расчете движения спутников вокруг Земли. Поскольку Земля вращается вокруг своей оси, то ее форма является эллипсоидом. Но в первом приближении Землю можно считать шаром радиуса R = 6371 км. Из таких допущений можно оценить космические скорости, необходимые для выведения летательных аппаратов на космические орбиты.

Первая космическая скорость – это скорость, которую необходимо сообщить телу на поверхности Земли, чтобы оно вышло на круговую орбиту. Она равна км/с. Если у тела первая космическая скорость, то оно может вращаться по круговой орбите, не падая на Землю, то есть стать ее спутником.
Вторая космическая скорость – это скорость, которую необходимо сообщить телу на поверхности Земли, чтобы оно вышло на параболическую орбиту. Она равна км/с. Если у тела скорость больше второй космической, то ее траекторией является гипербола, и, при отсутствии помех, оно будет удаляться от Земли и никогда не вернется назад.

Однако Солнце является той преградой, которая не даст спутнику со второй космической скоростью удалиться на бесконечное расстояние. Чтобы тело могло покинуть пределы солнечной системы, ему необходимо сообщить третью космическую скорость км/с.

Использованная литература:
А. А. Яблонский, Курс теоретической механики, часть II, динамика. Москва, «Высшая школа», 1966.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.

Автор: Олег Одинцов . Опубликовано: 11-12-2019

Тема 1.6. Основные понятия кинематики

§1. Кинематика точки. Введение в кинематику.

Кинематикой (от греческого «кинема» — движение) называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.

Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

Механическое движение — это изменение положения тел (или частей тела) относительно друг друга в пространстве с течением времени.

Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета.

Тело отсчета — тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.

Система отсчета — это система координат, связанная с телом отсчета, и выбранный способ измерения времени (рис. 1).

Рис.1. Система отчета

Изображать систему отсчета будем в виде трех координатных осей (не показывая тело, с которым они связаны).

Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство.

Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время t принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматриваются как изменяющиеся с течением времени, т.е. как функции времени t.

Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано).

Кинематически задать движение или закон движения тела (точки) — значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.

Основная задача кинематики точки твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих дан­ное движение.

Положение тела можно определить с помощью радиус-вектора или с помощью координат.

Радиус-вектор точки М — направленный отрезок прямой, соединяющий начало отсчета О с точкой М (рис. 2).

Координата х точки М — это проекция конца радиуса-вектора точки М на ось Ох. Обычно пользуются прямоугольной системой координат Декарта. В этом случае положение точки М на линии, плоскости и в пространстве определяют соответственно одним (х), двумя (х, у) и тремя (х, у, z) числами — координатами (рис. 3).

Рис.2. Радиус-вектор

Рис.3. Координаты точки М

Материальная точка — тело, размерами которого в данных условиях можно пренебречь.

Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.

Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движе­нии все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.

В дальнейшем под словом «тело» будем понимать «материальная точка».

Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. Вид траектории зависит от выбора системы отсчета.

В зависимости от вида траектории различают прямолинейное и криволинейное движение.

Путь s — скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s> 0.Единицы измерения в системе СИ: м (метр).

Перемещение тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное (точка М₀) и конечное (точка М) положение тела (см. рис. 2):

где и — радиус-векторы тела в эти моменты времени.Единицы измерения в системе СИ: м (метр).

Проекция перемещения на ось Ох: ∆r_x =∆х = х-х₀, где x₀ и x — координаты тела в начальный и конечный моменты времени.

Модуль перемещения не может быть больше пути: ≤s.

Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.

Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:

Видео-урок «Механическое движение»

§2. Способы задания движения точки

Для задания движения точки можно применять один из следую­щих трех способов:

1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки.

Пусть точка М движется по отношению к некоторой си­стеме отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор , проведенный из на­чала координат О в точку М (рис. 4).

Рис.4. Движение точки М

При движении точки М вектор будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргу­мента t:

Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.

Геометрическое место концов вектора , т.е. годограф этого вектора, определяет траекторию движущейся точки.

2. Координатный способ задания движе­ния точки.

Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z (рис.4), которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т.е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

3. Естественный способ задания движе­ния точки.

Рис.5. Движение точки М

Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О’, которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).

Тогда положение точки М на тра­ектории будет однозначно определяться криволинейной коорди­натой s, которая равна расстоянию от точки О’ до точки М, изме­ренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M₁, М₂. . следовательно, расстояние s будет с течением времени изменяться.

Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость s=f(t).

§3. Вектор скорости точки

Одной из основных кинематических характеристик движе­ния точки является векторная величина, называемая скоростью точки. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.

Скорость — мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.

Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.

Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.

Для равномерно-прямолинейного движения ∆r=v∆t, где v – постоянный вектор скорости.

Из соотношения видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени.

Техническая механика

Кинематика

Кинематика точки

Кинематика – часть теоретической механики, в которой изучаются движения материальных тел без учета их масс и действующих на них сил.

Когда в механике говорят о движении тела, то подразумевают под этим изменение с течением времени его положения в пространстве по отношению к другим телам.
Обычно с телом, по отношению к которому изучают движение, связывают какую-нибудь систему координат, которую вместе с выбранным способом измерения времени называют системой отсчета. Если координаты всех точек тела в выбранной системе отсчета остаются неизменными во времени, то тело находится в покое.
Если рассматривается движение тела по отношению к условно неподвижной системе отсчета, то движение называют абсолютным ; движение тела по отношению к подвижной системе отсчета называют относительным .

В мире все находится в непрерывном движении, поэтому все движения являются относительными, однако условно можно представить себе и абсолютное движение, например, движение по отношению к Земле.

Итак, движение тело совершается в пространстве с течением времени. Пространство и время, как и движение, согласно учению диалектического материализма – формы существования материи.

Классическая механика полагает, что пространство и время имеют абсолютный, независимый друг от друга характер, и что их свойства не зависят от распределения и движения материи.

Такая точка мировоззрения господствовала в науке до начала XX века, пока гениальный А. Эйнштейн (1879-1955) не поставил ее под сомнение своей теорией относительности. Этот человек сломал вековое представление человечества о самом главном – об абсолютности времени и пространства. Теория относительности Эйнштейна – это современная физическая теория пространства и времени, связывающая эти доселе незыблемые независимые постулаты с движением, массой и энергией.

До А. Эйнштейна считалось, что все в мире относительно. Если тело движется по отношению к какой-либо подвижной системе, то оно имеет другой характер движения по отношению к той системе, относительно которой движется данная система. Это утверждение являлось одним из китов, на которых восседала наука до начала прошлого века.
Теория относительности Эйнштейна основывается на том, что скорость света является постоянной величиной, не зависящей от скорости источника этого света. На основании этого противоречащего здравому смыслу вывода можно утверждать, что и пространство, и время – суть понятия относительные, зависящие от скорости света.
Гениальность Эйнштейна заключается в том, что он увидел и объял неочевидное. Современная физика, на основании множества экспериментов, опытов и исследований полностью подтвердила его теорию.

Тем не менее, несмотря на открытия Эйнштейна, классическая механика не потеряла свою актуальность, так как при скоростях движения, далеких от скорости света, результаты, даваемые классической механикой, ничтожно мало отличаются от результатов механики теории относительности и вполне пригодны для практики. Можно сказать, что классическая механика является частным случаем механики теории относительности, предполагающая упрощенные расчеты с допустимыми погрешностями.

Основные определения кинематики

Чтобы понять смысл определений кинематики следует ознакомиться с понятиями и определениями другого раздела технической механики – теорией механизмов и машин, которая занимается приложением законов теоретической механики для практических расчетов деталей, механизмов и машин.

Механизмом называется совокупность связанных между собой тел, имеющих определенные движения и служащих для передачи и преобразования движения.

Машиной называют механизм или сочетание механизмов, служащих для преобразования энергии (энергетические машины), изменения формы, свойств, состояния и положения предмета труда (рабочие машины), или для сбора, переработки и использования информации (информационные машины).
Таким образом, любая машина состоит из одного или нескольких механизмов, но не всякий механизм является машиной, т. е. машина – понятие более широкое.

Простейшей частью любой машины является ее звено – одно тело или неизменяемое во время работы машины сочетание группы тел.
Два звена, соединенные между собой и допускающие относительное движение, называются кинематической парой .
Кинематические пары бывают низшие и высшие . Звенья низших пар соприкасаются по поверхностям (поступательные, вращательные и винтовые пары), звенья высших пар соприкасаются по линиям и точкам (зубчатые пары, подшипники качения и т. п.).

Совокупность кинематических пар называется кинематической цепью .
Кинематические пары и цепи могут быть плоскими и пространственными. Механизм – это кинематическая цепь, у которой одно из звеньев лишено движения (закреплено). Такое звено называют станиной или стойкой .
Звено, вращающееся вокруг неподвижной оси, называют кривошипом , качающееся вокруг неподвижной оси – балансиром или коромыслом .
Звено, совершающее сложное движение параллельно какой-то плоскости, называют шатуном . Звено, совершающее возвратно-поступательное движение по станине или стойке, называют ползуном .

Ведущим звеном механизма считается то, которому извне сообщается определенное движение, передаваемое посредством этого звена другим звеньям, называемым ведомыми .

Кинематика изучает закономерности относительного движения и перемещения отдельных звеньев механизмов, без учета сил, вызывающих эти движения и перемещения.

Основными физическими величинами, которыми оперирует кинематика, являются расстояние (длина) и время. Единицей измерения длины в системе СИ является метр (м), единицей измерения времени – секунда (с).

Способы задания движения точки

Знание законов движения тела означает знание законов движения каждой его точки, поэтому изучение кинематики основывается на изучении геометрии движения точки.

Траекторией точки называется множество (геометрическое место) положений движущейся точки в рассматриваемой системе отсчета. Проще говоря, траектория движения – это линия, которую описывает подвижная точка относительно выбранной системы отсчета. В зависимости от формы траектории различают прямолинейное и криволинейное движение.

Движение любой точки тела можно описать (задать) тремя способами – естественным, векторным и координатным (см. рисунок 1) .

Естественный способ (рис. 1а) заключается в том, что движение точки задается ее траекторией, началом отсчета и уравнением движения по этой траектории (законом движения).
В общем виде уравнение движения записывается так: s = f(t) , где s – расстояние от точки до начального положения (начала отсчета), являющееся функцией времени; t – время движения точки от начального отсчета.

Зная траекторию и закономерность (уравнение) движения точки по этой траектории, можно в любой момент времени определить, где она находится.

При своем движении точка проходит некоторый путь, который также является функцией времени. Следует отметить, что путь, пройденный точкой, совпадает с расстоянием от начала отсчета лишь в том случае, если траектория движения точки представляет собой прямую линию, и точка движется по ней в одном направлении, а начало движения точки совпадает с началом отсчета.

Векторный способ (рис. 1б) основывается на том, что положение точки в пространстве однозначно определяется радиусом-вектором r , проведенным из некоторого неподвижного центра к данной точке. При этом положение точки в данный момент времени определяется направлением и модулем вектора. Математически функция изменения радиуса-вектора от времени записывается так:

Координатный способ (рис. 1в) заключается в том, что движение точки задается движением ее проекций вдоль осей координат. В общем виде уравнение движения точки можно записать следующим образом:

Зная уравнения движения точки в координатной форме, можно, подставив в эти уравнения время, определить положение проекций точки, а следовательно, и самой точки в любой момент времени.
Если точка движется в плоскости, то для определения ее местоположения в данный момент времени достаточно знать две координаты, если движение происходит по прямой – достаточно одной координаты.