Уравнение движения точки в некоторой системе отсчета

Уравнение движения материальной точки

Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.

Имеет смысл говорить только о движении в некоторой системе отсчета.

Система отсчета. Системы координат

Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.

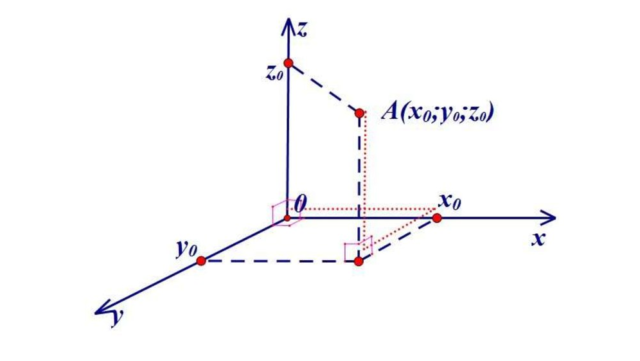
В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:

• сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
• цилиндрическая система с координатами p , z , α ;
• на полярной плоскости с параметрами r , φ .

В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.

Кинематическое уравнение движения материальной точки

Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.

При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.

Это возможно при использовании кинематического уравнения движения:

Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.

Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:

x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .

Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.

Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.

Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:

r = r ( t ) , φ = φ ( t ) ( 3 ) .

Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как

q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .

Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.

Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:

Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.

Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.

Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.

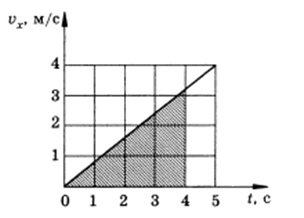
Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.

Дано: x = 0 , 4 t 2 , t = 4 c

Найти: υ x ( t ) , S — ?

Решение

При решении необходимо учитывать зависимость скорости от времени:

υ x = υ 0 x + a x t .

Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:

x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .

Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .

После подстановки данных в уравнение:

Определим точки, изобразим график:

υ x = 0 , t = 0 , υ x = 4 , t = 5

Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:

Уравнение движения материальной точки

Вы будете перенаправлены на Автор24

Система отсчета. Системы координат

Под движением материальной точки в пространстве понимают изменение ее положения относительно некоторых тел с течением времени. В связи с этим можно говорить только о движении в некоторой системе отсчета.

Сами по себе точки пустого пространства неразличимы между собой, поэтому говорить о той или иной точке пространства можно, если в ней находится материальная точка. Ее положение и определяется относительно тела отсчета с помощью измерений, для чего с телом (телами) отсчета жестко связывается некоторая система координат; в ней и измеряются пространственные координаты. Например, на поверхности Земли это географическая широта и долгота точки.

В теоретических рассуждениях часто наиболее удобна декартова прямоугольная система координат, в которой положение точки определяется радиус-вектором $\overline$ с тремя проекциями $x,y,z$ — координатами точки. Но возможно и использование других систем координат, например:

• сферической, где положение точки и ее радиус-вектор определены координатами $r,\vartheta ,\varphi $;
• цилиндрической: с координатами $p,z,\alpha $;
• на плоскости — полярной: $r,\varphi $.

В теоретических рассуждениях часто не принимают во внимание реальную систему отсчета, сохраняя только систему координат, которая и служит математической моделью системы отсчета, применяемой при измерениях на практике.

Кинематическое уравнение движения материальной точки

Итак, в любой системе отсчета и системе координат имеется возможность определить координаты материальной точки в любой момент времени.

Если положение материальной точки в каждый момент времени определено в данной системе отсчета, то движение ее задано или описано.

Это задание достигается в виде кинематического уравнения движения:

Аналитически положение точки всегда определяется совокупностью трех независимых между собой чисел. Этот факт выражают словами: свободная точка имеет три степени свободы движения.

Готовые работы на аналогичную тему

Движение точки согласно уравнению (1) полностью определено, если указано ее положение в любой момент времени $t$. Для этого достаточно задать декартовы координаты точки как однозначные и непрерывные функции времени:

Прямоугольные декартовы координаты $x,y,z$ являются проекциями радиус-вектора $\overline$, проведенного в точку из начала координат, т.е.:

Длина и направление вектора $\overline$находятся из известных соотношений:

Здесь, $\alpha ,\beta ,\gamma $ — углы, образованные радиус-вектором с координатными осями.

Равенства (2) являются кинематическими уравнениями движения материальной точки в декартовых координатах. Но уравнения могут быть записаны в любой другой системе координат, связанной с декартовой взаимно однозначным преобразованием. При движении точки в плоскости Оху часто бывает удобно пользоваться полярными коордиинатами $r,\varphi $, связанными с декартовыми преобразованием:

В этом случае кинематические уравнения движения точки имеют следующий общий вид:

$r=r(t),\varphi =\varphi (t)$. (3)

В криволинейных координатах $q_ <1>,q_ <2>,q_ <3>$ связанных с декартовыми преобразованием:

кинематические уравнения движения точки запишутся так:

(Это могут быть сферические, цилиндрические и другие координаты).

Годограф радиус-вектора точки, т.е. кривая, описываемая концом вектора $\overline$при движении точки, совпадает с траекторией движения этой точки. Уравнение траектории в параметрической форме, когда параметром служит время $t$, дано кинематическими уравнениями движения (2), (5). Для получения уравнения траектории в координатной форме достаточно исключить из кинематических уравнений время.

Движение точки может быть определено по-другому: заданием траектории и мгновенным положением точки на ней. Положение точки на кривой определяется указанием только одной величины — расстояния, измеряемого вдоль кривой от некоторой начальной точки. При этом должно быть указано положительное направление кривой. Тогда мгновенное положение точки на заданной кривой определяется функцией:

Это уравнение является уравнением движения точки по траектории. Такой способ задания движения называется естественным или траекторным.

Координатный и естественный способы задания движения точки физически (в смысле фиксации ее положения в пространстве)

эквивалентны. Что же касается математической стороны дела, то в одних задачах оказывается проще применение координатного, а в другом — естественного метода.

Закон движения точки по траектории может быть задан аналитически, графически или в виде таблицы. Оба последних способа широко применяются на транспорте (например, графики и расписания движения поездов).

Уравнение движения материальной точки имеет вид $x=0,4t^ <2>$. Написать формулу зависимости $v_ (t)$ и построить график зависимости скорости точки от времени. Показать на графике площадь, численно равную пути, пройденному точкой за 4 секунды, и вычислить этот путь. \end

Решение: Зависимость скорости от времени имеет вид:

Запишем уравнение зависимости координаты от времени и сравним его с данным:

Из сравнения видно, что $x_ <0>=0$, $v_ <0x>=0$, $a_ =0,8$м/с2.

Подставим полученные данные в уравнение скорости и получим:

Определим точки и построим график:

Путь, пройденный телом, численно равный площади фигуры, ограниченной графиком и может быть найден по следующей формуле:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 01 07 2021

Уравнение движения точки

Средняя оценка: 4.5

Всего получено оценок: 33.

Средняя оценка: 4.5

Всего получено оценок: 33.

Кинематика — это раздел физики, который изучает движение без исследования его причин. С помощью кинематических закономерностей движения можно рассчитать, в каком месте будет находиться тело в тот или иной момент времени. Эти закономерности описываются с помощью математических формул, называемых «уравнения движения». Рассмотрим эту тему более подробно.

Движение материальной точки

Материальная точка — это тело, имеющее массу, размерами которого в данный момент можно пренебречь. Понятие материальной точки очень удобно в кинематике и динамике, поскольку позволяет исключить несущественные стороны исследуемого движения и сосредоточиться на основных параметрах.

Рис. 1. Материальная точка.

Материальная точка находится в некоторой системе отсчёта, поэтому ей можно приписать некоторые координаты — одну, две или три, в зависимости от числа координатных осей.

Движение материальной точки состоит в том, что некоторые из координат меняются с течением времени. Следовательно, для описания движения необходимо сопоставить каждому моменту времени соответствующие координаты. Сделать это можно различными способами, например, просто составив таблицу, в первом столбце которой стоят моменты времени, а в остальных столбцах — соответствующие координаты. Однако удобнее найти математическую формулу, в которой в качестве исходной независимой переменной берётся время, а результатом формулы является координата.

Рис. 2. Точка в системе координат

Уравнения движения точки

Математические формулы, с помощью которых можно найти координаты точки в любой момент времени, называются уравнениями движения материальной точки.

Примером самого простого уравнения движения точки является формула:

Несмотря на крайнюю простоту, эта формула обладает всеми чертами уравнения движения. В ней есть координата $x$, и, подставляя разные моменты времени, можно её найти. В данном случае, какой бы момент времени не взять, координата всегда будет равна нулю, то есть точка покоится в начале координат.

Возьмём пример немного сложнее. Если точка движется с постоянной скоростью, то, как известно к 9 классу, умножив скорость на время движения, мы получаем пройденное расстояние. В виде формулы это выразится, например, следующим образом:

С помощью этой формулы мы можем выяснить, что в начальный момент времени точка находилась в начале координат (подставив нулевое время, мы получим нулевую координату). Подставляя другие значения времени, мы найдём соответствующую координату. Кроме того, из формулы можно получить и скорость, с которой движется материальная точка — 5 метров в секунду, или других единиц, принятых в системе отсчёта.

Если в начальный момент точка имела некоторую координату, допустим, 1 (метр), то её уравнение движения примет вид:

Часто в кинематических уравнениях движения используются буквы-обозначения, а для определения конкретных координат они заменяются конкретными числами. В последнем примере скорость можно заменить буквой $v$, а начальную координату — $x_0$. Уравнение движения примет вид:

Наконец, в системе отсчёта может быть не одна, а несколько координатных осей. В этом случае движение материальной точки описывается системой уравнений. Например:

В данном случае описывается движение в трёхмерном пространстве точки, которая в начальный момент имела координаты (1; 3; 5) и скорость которой равна 7.

Для описания движения в системе отсчёта с несколькими координатами нередко используется векторный способ описания, когда все переменные в уравнении являются векторами. Записи получаются более компактными, хотя описывают те же самые координаты и движения.

Что мы узнали?

Уравнения движения точки — это математические формулы, связывающие время в принятой системе отсчёта с координатами точки в ней. Подставляя в эти уравнения различные моменты времени, можно получить положения точки в эти моменты. Кроме того, из уравнений движения можно получить скорость, с которой движется точка.