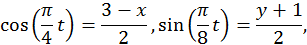Уравнение движения точки в плоскости xy

Координатный способ задания движения точки

Рассматривается движение точки М в неподвижной системе отсчёта OXYZ (рис. 2.1). Единичные векторы (орты) i, j, k показывают положительные направления отсчёта координат X, Y, Z. Движущаяся точка описывает в пространстве некоторую линию, которую называют траекторией движения точки. По виду траектории все движения точки делятся на прямолинейные и криволинейные. Положение точки М в неподвижной системе отсчёта (НСО) определяется тремя координатами X, Y, Z. При движении точки М её координаты изменяются с течением времени. Следовательно, коорди
наты X, Y, Z движущейся точки М являются функциями времени t.

Систему трёх уравнений X = f₁(t); Y = f₂(t); Z = f₃(t) называют уравнениями движения точки в пространстве в декартовых координатах.

Пример: X = 10·t 2 + 1; Y = 7·t 3 + t 2 + 1; Z = 10·sin(p·t). Действительно, имея эти уравнения, можно для любого момента времени найти значения соответствующих координат X, Y, Z и по ним определить положение точки в пространстве в этот момент времени.

Движение точки М на плоскости (рис. 2.2) определяется двумя уравнениями: X = f₁(t); Y = f₂(t). Эти выражения называют уравнениями движения точки на плоскости в декартовой системе отсчёта.

Пример. Заданы уравнения движения точки в плоскости OXY. X = 3·t 2 + t 2 + t; Y = 7·cos(p·t).

Уравнения движения, определяющие координаты точки в любой момент времени, рассматривают как параметрические уравнения траектории точки. При исключении параметра t из уравнений движения получают уравнение траектории точки в координатной форме (Y = f(t)).

Пример. Заданы уравнения: X = 4·t (см); Y = 16·t 2 – 1 (см) движения точки в плоскости OXY. Определить вид траектории движения точки, построить её график и найти положение точки на траектории движения в момент времени t₁ = 0,5 с.

Решение. Из уравнения X = 4·t находим t = X/4. Значение времени t подставляем в уравнение Y = 16·t 2 – 1. Получаем

Y = 16·(X/4) 2 – 1 = X 2 – 1.

Выражение Y = X 2 – 1 есть уравнение параболы (y= a·x 2 +b·x+c) с вершиной в точке с координатами (0, – 1). В момент времени t₁ = 0,5 с определяем координаты:

Y(t₁) = 16·(t₁) 2 – 1 = 16·(0,5) 2 – 1 = 3 см >0.

Показываем положение точки на траектории её движения (рис. 2.3).

Пример. Дано: X = 3·sin(p·t), см (1); Y = 3·cos(p·t), см (2); t₁ = 0,25 c. Определить вид траектории движения точки и её положение на траектории движения в момент времени t₁.

Решение. Уравнения движения точки представим в следующем виде: (X) 2 = (3·sin(p·t)) 2 (1 I ); (Y) 2 = (3·cos(p·t)) 2 (2 I ). Для решения используем тригонометрическую формулу sin 2 (α) + cos 2 (α) = 1.

Складывая левые и правые части уравнений (1 I ) и (2 I ), получим (X) 2 + (Y) 2 = 3 2 ·(sin 2 (p·t) + cos 2 (p·t)) = 3 2 ·1 или (X) 2 + (Y) 2 = 3 2 . Известно, что уравнение (X) 2 + (Y) 2 = R 2 есть уравнение окружности радиусом R с центром в начале координат. Таким образом, точка
движется по окружности радиусом R = 3 см (рис. 2.4).

Определяем положение точки на траектории движения в момент времени t₁.

X(t₁) = 3·sin(p·t₁) = 3·sin(p·0,25) = 3·0,707 = 2,121 см > 0.

Y(t₁) = 3·cos(p·t₁) = 3·cos(p·0,25) = 3·0,707 = 2,121 см > 0.

Показываем точку на траектории её движения (см. рис. 2.4).

ВНИМАНИЕ! Если точка не попадает на траекторию её движения, то:

1) неверно определен вид траектории движения;

2) неверно рассчитаны значения координат X(t₁), Y(t₁).

Прямолинейное движение точки М определяется одним уравнением движения X = f(t).

Пример. Дано: X = 10·t 2 + sin(2·p·t) + 3, см (рис. 2.5).

Определить положение точки на траектории движения в начальный момент времени t₀ = 0 и в момент времени t₁ = 1 c.

Решение.

X(t₀) = 10·(t₀) 2 + sin(2·p·t₀) + 3 = 10·0 2 + sin(2·p·0) + 3 = 3 см > 0.

X(t₁) = 10·(t₁) 2 + sin(2·p·t₁) + 3 = 10·1 2 + sin(2·p·1) + 3 = 13 см > 0.

Значения координат X(t₀), X(t₁) наносим на рис. 2.5.

Условия задач по кинематике.

Задача К-1

Под номером К1 помещены две задачи К1а и К1б, которые надо решить.

Условие. Задача К1а.Точка В движется в плоскости ху (рис. К1.0 – К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: , , где х и у выражены в сантиметрах, t – в секундах.

Найти уравнение траектории точки; для момента времени t₁ = 1с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Зависимость указана непосредственно на рисунках, а зависимость дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7-9 в столбце 4). Как и в задачах С1-С4, номер рисунка выбирается по последней цифре шифра, а номер условия в табл. К1 – по предпоследней.

Задача К1б.Точка движется по дуге окружности радиуса R = 2м по закону , заданному в табл. К1 в столбце 5 (s – в метрах, t – в секундах), где s = AM – расстояние точки от некоторого начала А, измеренное вдоль дуги окружности.

Определить скорость и ускорение точки в момент времени t₁ = 1с. Изобразить на рисунке векторы и , считая, что точка в этот момент находится в положении М, а положительное направление отсчета s – от А к М.

Указания.Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения.

В задаче все искомые величины нужно определить только для момента времени t₁ = 1с.

В некоторых вариантах задачи К1а при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы: ; .

Номер условия
рис. 0–2	рис. 3–6	рис. 7–9

Пример выполнения задачи К1а. Даны уравнения движения точки в плоскости xy:

(x, y – в сантиметрах, t – в секундах).

Определить уравнение траектории точки; для момента времени t₁=1 c найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Решение. 1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Поскольку t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу

или (1)

Из уравнений движения находим выражения соответствующих функций и представляем в равенство (1). Получим

Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис.К1а):

2. Скорость точки найдем по ее проекциям на координатные оси:

3. Аналогично найдем ускорение точки:

см/с, _1y = см/с 2 , ₁= 0,88 см/с 2 . (4)

4. Касательное ускорение найдем, дифференцируя по времени равенство . Получим

(5)

Числовые значения всех величин, входящих в правую часть выражения (5), определены и даются равенствами (3) и (4). Подставив в (5) эти числа, найдем сразу, что при t₁=1 c = 0,66 см/с 2 .

5. Нормальное ускорение точки . Подставляя сюда найденные числовые значения , получим, что при t₁=1 c = 0,58 см/с 2

6. Радиус кривизны траектории . Подставляя сюда числовые значения ʋ₁ и , найдем, что при t₁=1 c ρ₁=3,05 см.

Ответ: ʋ₁=1,33 см/с, 0.88 см/с 2 , =0,66 см/с 2 , 0,58 см/с 2 , ρ₁=3,05 см.

Пример выполнения задачи К1б.Точка движется по дуге окружности радиуса R=2 м по закону (s – в метрах, t – в секундах), где (рис. К1б). Определить скорость и ускорение точки в момент времени t₁=1 c.

Решение. Определяем скорость точки:

При t₁=1 c получим

Ускорение находим по его касательной и нормальной составляющим:

При t₁=1 c получим, учтя, что R=2 м,

м/с 2

Тогда ускорение точки при t₁=1 c будет

м/с 2 .

Изобразим на рис. К1б векторы , учитывая и и считая положительным направление от А к М.

Контрольные вопросы:

1. Что такое кинематика?

2. Что такое траектория точки?

3. Как определить скорость точки?

4. Как определить ускорение точки?

5. Что такое нормальное ускорение точки?

6. Что такое касательное ускорение точки?

7. Сформулировать способы задания движения точки

8. Определение скорости и ускорения точки при естественном задании движения

9. Как перейти от координатного задания движения точки к естественному?

10. Как определяется движение точки при векторном способе задания?

Задача К-3

Условие.Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна В или Е (рис. К3.0 – К3.7) или из стержней 1, 2, 3 и ползунов В и Е (рис. К3.8, К3.9), соединенных друг с другом и с неподвижными опорами О₁, О₂ шарнирами; точка D находится в середине стержня АВ. Длины стержней равны соответственно l₁ = 0,4м, l₂ = 1,2м, l₃ = 1,4м, l₄ = 0,6м. Положение механизма определяется углами α, β, γ, φ, θ. Значения этих углов и других заданных величин указаны в табл. К3а (для рис. 0-4) или в табл. К3б (для рис. 5-9); при этом в табл. К3а ω₁ и ω₄ – величины постоянные.

Определить величины, указанные в таблицах и в столбцах «Найти».

Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например угол γ на рис. 8 следует отложить против хода часовой стрелки и т.д.).

Построение чертежа начинать со стержня, направление которого определяется углом α; ползун с направляющими для большей наглядности изобразить так, как в примере К3 (см. рис. К3б).

Заданные угловую скорость и угловое ускорение считать направленными против часовой стрелки, а заданные скорость и ускорение – от точки В к b (на рис. 5-9).

Указания.Задача К3 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.

При определении ускорений точек механизма исходить из векторного равенства , где А – точка, ускорение которой или задано, или непосредственно определяется по условиям задачи (если точка А движется по дуге окружности, то ); В – точка, ускорение которой нужно определить.

Таблица К3а (к рис. К3.0 – К3.4)

Таблица К3б (к рис. К3.5 – К3.9)

Пример выполнения задачи К3.Механизм (рис. К3а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О₁ и О₂ шарнирами.

Дано: α=60º, β=150º, γ=90º, φ=30º, θ=30º, AD=DB, l₁=0,4 м, l₂=1,2 м, l₃=1,4 м, ω₁=2 с -1 , ε₁= 7 с -2 (направления и – против хода часовой стрелки).

Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. К3б; на этом рисунке изображаем все векторы скоростей).

2. Определяем ʋ_B. Точка В принадлежит стержню АВ. Чтобы найти ʋ_B, надо знать скорость какой-нибудь другой точки этого стержня и направление _B. По данным задачи, учитывая направление ω₁, можем определить _A; численно

_A⊥О₁А (1)

Направление _B найдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная _A и направление _B, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор _B (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим

(2)

3. Определяем . Точка E принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить , надо сначала найти скорость точки D, принадлежащей одновременно стержню. Для этого, зная _A и _B, строим мгновенный центр скоростей (МЦС) стержня АВ; это точка C₃, лежащая на пересечении перпендикуляров к _A и _B, восставленных из точек А и В (к _A перпендикулярен стержень l). По направлению вектора _A определяем направление поворота стержня АВ вокруг МЦС C₃. Вектор _D перпендикулярен отрезку C₃D, соединяющему точки D и C₃, и направлен в сторону поворота. Величину υ_D найдем из пропорции

(3)

Чтобы вычислить C₃D и заметим, что – прямоугольный, так как острые углы в нем равны 30º и 60º, и что Тогда является равносторонним и . В результате равенство (3) дает

C₃D. (4)

Так как точка Е принадлежит одновременно стержню О₂Е, вращающемуся вокруг О₂,то . Тогда восставляя из точек Е и D перпендикуляры к скоростям и _D , построим МЦС C₂ стержня DE. По направлению вектора _Dопределяем направление поворота стержня DE вокруг центра C₂. Вектор направлен в сторону поворота этого стержня. Из рис. К3б видно, что , Составив теперь пропорцию, найдем, что

(5)

4. Определяем ω₂. Так как МЦС стержня 2 известен (точка C₂) и , то

c -1 (6)

5. Определяем (рис. К3в, на котором изображаем все векторы ускорений). Точка В принадлежит стержню АВ. Чтобы найти , надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию точки В. По данным задачи можем определить , где численно

;

(7)

Вектор направлен вдоль AO₁, а – перпендикулярно AO₁; изображаем эти векторы на чертеже (см. рис. К3в). Так как точка В одновременно принадлежит ползуну, то вектор параллелен направляющим ползуна. Изображаем вектор на чертеже, полагая, что он направлен в ту же сторону, что и _B.

Для определения воспользуемся равенством

(8)

Изображаем на чертеже векторы (вдоль ВА от В к А) и (в любую сторону перпендикулярно ВА); численно . Найдя с помощью построенного МЦС C₃ стержня 3, получим

-1 и . (9)

Таким образом, у величин, входящим в равенство (8), неизвестны только числовые значения и ; их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси.

Чтобы определить , спроектируем обе части равенства (8) на направление ВА (ось х), перпендикулярное неизвестному вектору . Тогда получим

(10)

Подставив в равенство (10) числовые значения всех величин из (7) и (9), найдем, что

2 (11)

Так как получилось , то, следовательно, вектор направлен как показано на рис. К3в.

6. Определяем . Чтобы найти , сначала определим . Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим

(12)

Подставив в равенство (12) числовые значения всех величин из (11) и (7), найдем, что м/с 2 . Знак указывает, что направление противоположно показанному на рис. К3в.

Теперь из равенства получим

c -2 .

Ответ: м/с; м/с; с -1 ; м/с 2 ; с -2 .

Примечание. Если точка В, ускорение которой определяется, движется не прямолинейно (например, как на рис. К3.0 – К3.4, где В движется по окружности радиуса О₂В), то направление заранее неизвестно.

В этом случае также следует представить двумя составляющими ( ) и исходное уравнение (8) примет вид

(13)

При этом вектор (см. например, рис.К3.0) будет направлен вдоль ВО_2, а вектор — перпендикулярно ВО₂ в любую сторону. Числовые значения определяются так же, как в рассмотренном примере (в частности, по условиям задачи может быть или , если точка А движется прямолинейно).

Значение также вычисляется по формуле , где l– радиус окружности О₂В, а определяется так же, как скорость любой другой точки механизма.

После этого в равенстве (13) остаются неизвестными только значения и и они, как и в рассмотренном примере, находятся проектированием обеих частей равенства (13) на две оси.

Найдя можем вычислить искомое ускорение . Величина служит для нахождения (как в рассмотренном примере).

Контрольные вопросы:

1. Что такое плоскопараллельное движение твердых тел?

2. Из каких простейших движений состоит плоскопараллельное движение тела?

3. Как определить скорость точки тела при плоскопараллельном движении?

4. Как определяется ускорение точек тела при плоскопараллельном движении?

5. Сформулировать теорему о проекциях скоростей двух точек тела

6. Что такое мгновенный центр скоростей?

7. Как определить мгновенный центр скоростей тела если известно направление векторов скоростей двух точек тела?

8. Где находится мгновенный центр скоростей тела совершающего качание по неподвижной поверхности?

9. Что такое мгновенное поступательное движение тела?

10. Чему равна угловая скорость тела при мгновенном поступательном движении?

Задача К-4

Условие. Прямоугольная пластина (рис. К4.0 – К4.4) или круглая пластина радиусом R = 60см (рис. К4.5 – К4.9) вращается вокруг неподвижной оси по закону , заданному в табл. К4. Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. На рис. 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3, 4, 7, 8, 9 ось вращения ОО₁ лежит в плоскости пластины (пластина вращается в пространстве).

По пластине вдоль прямой BD (рис. 0 – 4) или по окружности радиусом R (рис. 5 – 9) движется точка М; закон ее относительного движения, т.е. зависимость (s выражено в сантиметрах, t – в секундах), задан в таблице отдельно для рис. 0 – 4 и для рис. 5 – 9; там же даны размеры b и l. На рисунках точка М показана в положении, при котором (при точка М находится по другую сторону от точки А).

Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t₁ = 1с.

Указания.Задача К4 – на сложное движение точки. Для ее решения воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка М на пластине в момент времени t₁ = 1с, и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунках к задаче).

В случаях, относящихся к рис. 5 – 9, при решении задачи не подставлять числового значения R, пока не будут определены положение точки М в момент времени t₁ = 1с и угол между радиусами СМ и СА в этот момент.

Номер условия	Для всех рисунков	Для рис. 0 – 4	Для рис. 5 – 9
b, см		l

Рассмотрим два примера решения этой задачи.

Пример выполнения задачи К4а.Пластина OEAB₁D(OE=OD рис. К4а) вращается вокруг оси, проходящей через точку О перпендикулярно плоскости пластины, по закону (положительное направление отсчета угла φ показано на рис. К4а дуговой стрелкой). По дуге окружности радиуса R движется точка В по закону (положительное направление отсчета s – от А к В).

Дано: R=0,5 м, (φ – в радианах, s – в метрах, t – в секундах).

Определить: .

Решение. Рассмотрим движение точки В как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам:

(1)

где, в свою очередь,

Определим все, входящие в равенства (1) величины.

1. Относительное движение. Это движение происходит по закону

. (2)

Сначала установим, где будет находится точка В на дуге окружности в момент времени . Полагая в уравнении (2) с, получим

Знак минус свидетельствует о том, что точка В в момент с находится справа от точки А. изображаем ее на рис. К4а в этом положении (точка B₁).

Теперь находим числовые значения .

где – радиус кривизны относительной траектории, равный радиусу окружности R. Для момента с, учитывая, что R=0,5 м, получим

(3)

Знаки показывают, что вектор направлен в сторону положительного отсчета расстояния s, а вектор – в противоположную сторону; вектор направлен к центру С окружности. Изображаем все эти векторы на рис. К4а.

2. Переносное движение. Это движение (вращение) происходит по закону . Найдем сначала угловую скорость ω и угловое ускорение ε переносного вращения:

и при с

(4)

Знаки указывают, что в момент с направления ω и ε противоположны направлению положительного отсчета угла φ; отметим это на рис. К4а.

Для определения 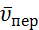и находим сначала расстояние точки от оси вращения О. Из рисунка видно, что м. Тогда в момент времени с, учитывая равенства (4), получим

м/с

(5)

Изображаем на рис. К4а векторы и с учетом направлений ω и ε и вектор (направлен к оси вращения).

3. Кориолисово ускорение. Модуль кориолисова ускорения определяем по формуле , где α – угол между вектором и осью вращения (вектором ). В нашем случае этот угол равен 90º, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор . Численно в момент времени с, так как в этот момент м/с и , получим

Уравнение движения точки в плоскости xy

Разделы

Дополнительно

Задача по физике — 3293

Точка движется в плоскости $xy$ по закону: $x = at, y = at (1 — \alpha t)$, где $a$ и $\alpha$ — положительные постоянные, $t$ — время. Найти:
а) уравнение траектории точки $y(x)$; изобразить ее график;
б) скорость $v$ и ускорение $w$ точки в зависимости от времени;
в) момент $t_<0>$, в который вектор скорости составляет угол $\pi /4$ с вектором ускорения.

Задача по физике — 3294

Точка движется в плоскости $xy$ по закону $x = a \in \omega t, y = a (1 — \cos \omega t)$, где $a$ и $\omega$ — положительные постоянные. Найти:
а) путь $s$, проходимый точкой за время $\tau$;
б) угол между векторами скорости и ускорения точки.

Задача по физике — 3295

Частица движется в плоскости $xy$ с постоянным ускорением $\vec$, направление которого противоположно положительному направлению оси $y$. Уравнение траектории частицы имеет вид $y = ax — bx^<2>$, где $a$ и $b$ — положительные постоянные. Найти скорость частицы в начале координат.

Задача по физике — 3296

Небольшое тело бросили под углом к горизонту с начальной скоростью $\vec_<0>$. Пренебрегая сопротивлением воздуха, найти:
а) перемещение тела в функции времени $\vec(t)$;
б) средний вектор скорости $\langle v \rangle$ за первые $t$ секунд и за все время движения.

Задача по физике — 3297

Тело бросили с поверхности Земли под углом $\alpha$ к горизонту с начальной скоростью $v_<0>$. Пренебрегая сопротивлением воздуха, найти:
а) время движения;
б) максимальную высоту подъема и горизонтальную дальность полета; при каком значении угла $\alpha$ они будут равны друг другу;
в) уравнение траектории $y(x)$, где $y$ и $x$ — перемещения тела во вертикали и горизонтали соответственно;
г) радиусы кривизны начала и вершины траектории.

Задача по физике — 3298

Имея в виду условие предыдущей задачи, изобразить примерные графики зависимости от времени модулей векторов нормального $w_$ и тангенциального $w_< \tau>$ ускорений, а также проекции вектора полного ускорения $w_$ на направление вектора скорости.

Задача по физике — 3299

Шарик начал падать с нулевой начальной скоростью на гладкую наклонную плоскость, составляющую угол $\alpha$ с горизонтом. Пролетев расстояние $h$, он упруго отразился от плоскости. На каком расстоянии от места падения шарик отразится второй раз?

Задача по физике — 3300

Пушка и цель находятся на одном уровне на расстоянии 5,10 км друг от друга. Через сколько времени снаряд с начальной скоростью 240 м/с достигнет цели в отсутствие сопротивления воздуха?

Задача по физике — 3301

Из пушки выпустили последовательно два снаряда со скоростью $v_ <0>= 250 м/с$: первый — под углом $\theta_ <1>= 60^< \circ>$ к горизонту, второй — под углом $\theta_ <2>= 45^< \circ>$ (азимут один и тот же). Пренебрегая сопротивлением воздуха, найти интервал времени между выстрелами, при котором снаряды столкнутся друг с другом.

Задача по физике — 3302

Воздушный шар начинает подниматься с поверхности Земли. Скорость его подъема постоянна и равна $v_<0>$. Благодаря ветру шар приобретает горизонтальную компоненту скорости $v_ = ay$, где $a$ — постоянная, $y$ — высота подъема. Найти зависимости от высоты подъема:
а) величины сноса шара $x(y)$;
б) полного, тангенциального и нормального ускорений шара.

Задача по физике — 3303

Частица движется в плоскости $xy$ со скоростью $\vec = a \vec + bx \vec$, где $\vec$ и $\vec$ — орты осей $x$ и $y$,$a$ и $b$ — постоянные. В начальный момент частица находилась в точке $x = y = 0$. Найти:
а) уравнение траектории частицы $y(x)$;
б) радиус кривизны траектории в зависимости от $x$.

Задача по физике — 3304

Частица А движется в одну сторону по некоторой заданной траектории с тангенциальным ускорением $w_ < \tau>= \vec \vec< \tau>$, где $\vec$ — постоянный вектор, совпадающий по направлению с осью $x$(рис. ), а $\tau$ — единичный вектор, совпадающий по направлению с вектором скорости в данной точке. Найти зависимость от х скорости частицы, если в точке $x = 0$ ее скорость пренебрежимо мала.

Задача по физике — 3305

Точка движется по окружности со скоростью $v = at$, где $a = 0,50 м/с^<2>$. Найти ее полное ускорение в момент, когда она пройдет $n = 0,10$ длины окружности после начала движения.

Задача по физике — 3306

Точка движется, замедляясь, по окружности радиуса $R$ так, что в каждый момент времени ее тангенциальное и нормальное ускорения по модулю равны друг другу. В начальный момент $i = 0$ скорость точки равна $v_<0>$. Найти:
а) скорость точки в зависимости от времени и от пройденного пути $s$;
б) полное ускорение точки в функции скорости и пройденного пути.

Задача по физике — 3307

Точка движется по дуге окружности радиуса $R$. Ее скорость зависит от пройденного пути $s$ по закону $v = a \sqrt$, где $a$ — постоянная. Найти угол $\alpha$ между вектором полного ускорения и вектором скорости в зависимости от $s$.