Уравнение движения центра массы тела

Движение центра масс системы

Допустим, что у нас есть некоторая система, состоящая из n -ного количества материальных точек. Возьмем одну из них и обозначим ее массу как m k . Приложенные к точке внешние силы (как активные силы, так и реакции связей) имеют равнодействующую F k e . Внутренние силы имеют равнодействующую F k l . Наша система находится в движении, следовательно, нужная точка будет иметь ускорение a k . Зная основной закон динамики, мы можем записать следующую формулу:

m k a k = F k e + F k l .

Ее можно применить к любой точке системы. Значит, для всей системы целиком можно сформулировать следующие уравнения:

m 1 a 1 = F 1 e + F 1 l , m 2 a 2 = F 2 e + F 2 l , ⋯ m n a n = F n e + F n l .

Данная формула состоит из дифференциальных уравнений, описывающих движение системы в векторной форме. Если мы спроецируем эти равенства на соответствующие координатные оси, то у нас получатся дифференциальные уравнения движения в проекциях. Но в конкретных задачах чаще всего вычислять движение каждой точки системы не требуется: можно ограничиться характеристиками движения всей системы в целом.

Движение центра масс: основная теорема

Характер движения системы можно определить, зная закон, по которому движется ее центр масс.

Центр инерции системы (центр масс) – это воображаемая точка с радиус-вектором R , выражаемым через радиус-векторы r 1 , r 2 , . . . соответствующих материальных точек по формуле R = m 1 r 1 + m 2 r 2 + . . . + m n r n m .

Здесь сумма показателей в числителе m = m 1 + m 2 + . . . + m 3 выражает общую массу всей системы.

Для нахождения этого закона нам нужно взять уравнения движения системы, приведенные в предыдущем пункте, и сложить их правые и левые части. У нас получится, что:

∑ m k a k ¯ = ∑ F k ¯ e + ∑ F k ¯ l .

Взяв формулу радиус-вектора центра масс, получим следующее:

Теперь возьмем вторую производную по времени:

Здесь буквой a c ¯ обозначено ускорение, которое приобретает центр масс системы.

Свойство внутренних сил в системе гласит, что F k l равно нулю, значит, окончательное равенство будет выглядеть так:

M a c ¯ = ∑ F k ¯ e .

Это уравнение является записью закона движения центра масс. Запишем его:

Движение центра масс системы идентично движению материальной точки той же массы, что и вся система целиком, к которой приложены все действующие на систему внешние силы.

Иначе говоря, произведение ускорения центра масс системы на массу самой системы будет равно геометрической сумме всех внешних сил, действующих на эту систему.

Возьмем полученное выше уравнение и спроецируем его правую и левую части на соответствующие координатные оси. У нас получится:

M x c ¨ = ∑ F k x ¯ e , M y c ¨ = ∑ F k y ¯ e , M z c ¨ = ∑ F k z ¯ e .

Эти равенства являются дифференциальными уравнениями движения центра масс в проекции на оси в декартовой системе координат.

Практическое значение теоремы о движении центра масс

Данная теорема имеет большую практическую ценность. Поясним, в чем именно она заключается.

1. Любое тело, движущееся поступательно, может быть рассмотрено в качестве материальной точки, масса которой равна массе всего тела. Во всех других случаях такой подход возможен лишь тогда, когда для определения положения тела в пространстве нам будет достаточно знать, в каком положении находится его центр масс. Также важно, чтобы условия задачи допускали исключение вращательной части движения тела.
2. С помощью теоремы движения центра масс системы мы можем не рассматривать в задачах неизвестные нам заранее внутренние силы.

Разберем пример применения теоремы для решения практической задачи.

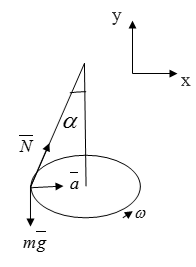
Условие: к оси центробежной машины на нити подвешено кольцо из металла. Оно совершает равномерные вращательные движения с угловой скоростью, равной ω . Вычислите, на каком расстоянии центр кольца находится от оси вращения.

Решение

Очевидно, что система находится под воздействием силы тяжести N N ¯ α α . Также необходимо учесть силу натяжения нити и центростремительное ускорение.

Второй закон Ньютона для системы будет выглядеть так:

Теперь создадим проекции обеих частей равенства на оси абсцисс и ординат и получим:

N sin α = m a ; N cos α = m g .

Мы можем разделить одно уравнение на другое:

Поскольку a = υ 2 R , υ = ω R , то нужное нам уравнение будет выглядеть так:

Физический факультатив. Тема: «Импульс, центр масс, движение центра масс»

В работе рассмотрены некоторые задачи на движение центра масс, рассматриваемые на школьном факультативе по физике в Лицее научно-инженерного профиля города Королева. Представляется, что данная статья может быть полезной как для учителей физики школ с углубленным изучением предмета, так и для абитуриентов.

Импульс или количество движения материальной точки есть вектор, равный произведению массы этой точки m на вектор ее скорости v: .

Импульс силы – это вектор, равный произведению силы на время ее действия: . Если сила не является постоянным вектором, то под F следует понимать среднее значение вектора силы за рассматриваемый интервал времени.

Теорема об изменении импульса материальной точки. Пусть на материальную точку m действует постоянная сила F. Тогда

, или . Таким образом изменение импульса материальной точки равно импульсу силы, действующей на нее.

Импульс системы материальных точек равен по определению сумме импульсов всех N точек системы:

Изменение импульса системы материальных точек равно импульсу равнодействующей внешних сил, действующих на систему.

Изолированная (замкнутая) система – это такая система материальных точек, на которую не действуют внешние силы или их равнодействующая равна нулю.

Закон сохранения импульса: импульс изолированной системы материальных точек сохраняется, каково бы ни было взаимодействие между ними:

Если внешние силы, действующие на систему не равны нулю, но существует такое неизменное направление (например, ось OX), что сумма проекций внешних сил на это направление равна нулю, то проекция импульса системы на это направление сохраняется.

Центр масс системы материальных точек. Центром масс N материальных точек m₁, m₂,…, m_N, положения которых заданы радиус-векторами , называют воображаемую точку, радиус-вектор которой определяется формулой:

.

Тогда координаты центра масс равны:

,

,

.

Скоростью центра масс является вектор

,

где – скорость i-й точки.

Ускорением центра масс является вектор

где – ускорение i-й точки.

Теорема об ускорении центра масс системы материальных точек. Произведение суммы масс точек системы на ускорение центра масс равно сумме внешних сил, действующих на точки системы.

Если на систему материальных точек не действуют внешние силы, то скорость центра масс относительно любой инерциальной системы отсчета сохраняется, каково бы ни было взаимодействие внутри системы.

Если при этом скорость центра масс относительно некоторой инерциальной системы была равна нулю, то сохраняется и положение центра масс.

Два этих утверждения являются прямыми следствиями закона сохранения импульса.

Задача 1. Частица массы m движется со скоростью v, а частица массы 2m движется со скоростью 2v в направлении, перпендикулярном направлению движения первой частицы. На каждую частицу начинают действовать одинаковые силы. После прекращения действия сил первая частица движется со скоростью 2v направлении, обратном первоначальному. Определите скорость второй частицы. [1]

Изменение импульса частицы массой m вследствие действия импульса силы равно 3mv, следовательно вторая частица приобретает точно такой же импульс перпендикулярно направлению ее движения. Полный импульс второй частицы находится векторным сложением его составляющих по двум перпендикулярным направлениям и равен 5mv. Скорость второй частицы тогда равна 5v/2.

Задача 2. Ящик с песком массы М лежит на горизонтальной плоскости, коэффициент трения с которой равен µ. Под углом ? к вертикали в ящик со скоростью v влетает пуля массы m и почти мгновенно застревает в песке. Через какое время после попадания пули в ящик, начав двигаться, остановится? При каком значении ? он вообще не сдвинется? [1]

Решение. Изменение импульса системы материальных точек равно импульсу равнодействующей внешних сил, действующих на систему. По горизонтальной и вертикальной оси:

где u – скорость ящика сразу после того, как пуля в нем застрянет, N – реакция опоры, – время, за которое пуля застревает в песке. Из этих уравнений следует

Так как пуля застревает почти мгновенно последним членом в правой части можно пренебречь. После того, как пуля застрянет, ящик тормозит под действие силы трения с ускорением . Ящик останавливается за время . Ящик не сдвинется, если .

Задача 3. По наклонной плоскости, составляющей угол а с горизонтом, с постоянной скоростью v съезжает ящик с песком массой M. В него попадает летящая горизонтально пуля массой m, и ящик при этом останавливается. С какой скоростью u летела пуля?

Решение. Вдоль наклонной плоскости изменение импульса системы

Поперек наклонной плоскости

Тогда

и с учетом того, что (ящик съезжает с постоянной скоростью)

Задача 4. Обезьяна массы m уравновешена противовесом на блоке А. Блок А уравновешен грузом массы 2m на блоке В. Система неподвижна. Как будет двигаться груз, если обезьяна начнет равномерно выбирать веревку со скоростью u относительно себя? Массой блоков и трением пренебречь. [1]

Решение. Обезьяна получает импульс силы и начинает двигаться со скоростью v к потолку. Точно такой же импульс силы получает груз m и тоже движется со скоростью v к потолку. Груз массой 2m получает импульс силы и тоже движется со скоростью v к потолку. Блок А опускается вниз со скоростью v. груз m движется относительно блока А вверх со скоростью 2v. Веревка справа от блока А движется от потолка со скоростью 3v. относительно обезьяны веревка движется вниз со скоростью 4v. Отсюда .

Задача 5. Из однородной круглой пластины радиусом R вырезали круг вдвое меньшего радиуса, касающийся края пластины. Найти центр тяжести полученной пластины.

Решение. Пусть масса пластины до вырезания равна M. Тогда масса вырезанной части равна M/4. Предположим, что имеется в наличии вещество с отрицательной массой, Тогда вырез можно получить наложением на пластину пластинки с отрицательной массой —M/4. Тогда, поместив начало координат в центр круга и направив ось X направо, положение центра масс получаем из формулы для координаты центра масс:

.

Задача 6. На гладком полу стоит сосуд, заполненный водой плотности p₀; объем воды V₀. Оказавшийся на дне сосуда жук объема V и плотности p через некоторое время начинает ползти по дну сосуда со скоростью u относительно него. С какой скоростью станет двигаться сосуд по полу? Массой сосуда пренебречь, уровень воды все время остается горизонтальным. [1]

Решение. Пусть скорость сосуда v, тогда скорость жука относительно пола u+v. Импульс системы по горизонтальной оси сохраняется и равен нулю. Удобно рассматривать жука как совокупность воды массой и сублимированного вещества жука массой , которое перемещается относительно всей воды. Тогда импульс системы

и

Задача 7. На дне маленькой запаянной пробирки, подвешенной над столом на нити, сидит муха, масса которой равна массе пробирки, а расстояние от поверхности стола равно длине пробирки l. Нить пережигают, и за время падения пробирки муха перелетает со дна в верхний конец пробирки. Определить время, за которое пробирка достигнет стола.

Решение. Ускорение центра масс системы определяется силами тяжести, действующими на пробирку и муху, и равно g. За время падения центр масс системы переместился на l/2. Отсюда время падения .

Задача 8. На нити, перекинутой через блок, подвешены два груза неравной массы (m₂ > m₁). Определить ускорение центра масс этой системы. Массой блока и нити пренебречь. [2]

Решение. Ускорение тяжелого груза направлено вниз и, как известно, равно . Ускорение легкого груза такое же по модулю, но направлено вверх. Ускорение центра масс находим по формуле из теоретического раздела

Задача 9. В сосуде, наполненном водой плотности p, с ускорением а всплывает пузырек воздуха, объем которого V. Найдите силу давления со стороны сосуда на опору. Масса сосуда вместе с водой равна m. [1]

Решение. Будем рассматривать системы как совокупность сосуда с водой массой и шарика с отрицательной массой , который поднимается вверх с ускорением a. Тогда ускорение центра масс системы

и направлено вниз. Из теоремы об ускорении центра масс

, и отсюда сила давления на опору, численно равная реакции опоры N,

Задачи для самостоятельного решения.

Задача 10. С горы с уклоном a () съезжают с постоянной скоростью сани с седоком общей массой M. Навстречу саням бежит и запрыгивает в них собака массой m, имеющая при прыжке в момент отрыва от поверхности горы скорость v, направленную под углом () к горизонту. В результате этого сани продолжают двигаться по горе вниз со скоростью u. Найти скорость саней до прыжка собаки. (Билет 3, 1991, МФТИ) [3]

Ответ:

Задача 11. Человек, находящийся в лодке, переходит с носа на корму. На какое расстояние S переместится лодка длиной L, если масса человека m, а масса лодки M? Сопротивлением воды пренебречь.

Ответ:

Задача 12. На поверхности воды находится в покое лодка. Человек, находящийся в ней, переходит с кормы на нос. Как будет двигаться лодка, если сила сопротивления движению пропорциональна скорости лодки?

Ответ: Лодка сместится, а затем вернется в исходное положение.

Задача 13. На первоначально неподвижной тележке установлены два вертикальных цилиндрических сосуда, соединенных тонкой трубкой. Площадь сечения каждого сосуда S, расстояние между их осями l. Один из сосудов заполнен жидкостью плотности p. Кран на соединительной трубке открывают. Найдите скорость тележки в момент времени, когда скорость уровней жидкости равна v. Полная масса всей системы m. [1]

Ответ:

Задача 14. На тележке установлен цилиндрический сосуд с площадью сечения S, наполненный жидкостью плотности p. От сосуда параллельно полу отходит длинная и тонкая горизонтальная трубка, небольшой отрезок которой вблизи конца загнут по вертикали вниз. Расстояние от оси сосуда до отверстия трубки равно L. Уровень жидкости в сосуде опускается с ускорением а. Какой горизонтальной силой можно удержать тележку на месте? [1]

Ответ:

Литература.

1. Задачи по физике: Учеб. пособие/ И.И. Воробьев, П.И. Зубков, Г.А. Кутузова и др.; Под ред. О.Я. Савченко. ? 2-е изд., перераб. М.: Наука. Гл. ред. физ.-мат. лит. 1988. — 416 с.

2. Дмитриев С.Н., Васюков В.И., Струков Ю.А. Физика: Сборник задач для поступающих в вузы. Изд. 7-е, доп. М: Ориентир. 2005. – 312 с.

3. Методическое пособие для поступающих в вузы / Под. ред. Чешева Ю.В. М.: Физматкнига, 2006. – 288 с.

Уравнение движения центра массы тела

При поступательном движении все точки тела получают за один и тот же промежуток времени равные по величине и направлению перемещения, поэтому скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Поэтому достаточно определить движение одной из точек тела (например, его центра инерции) для того, чтобы полностью охарактеризовать его движение.

При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.

Любое движение твердого тела может быть представлено как суперпозиция двух вышеуказанных основных видов движения. Покажем это на примере плоского движения, при котором все точки тела перемещаются в параллельных плоскостях. Таким образом, например, происходит качение цилиндра по плоскости. Элементарное перемещение какой-либо точки тела можно разложить на два — «поступательное» и «вращательное»:

причем для всех точек тела одно и то же. Разделив на соответствующий промежуток времени dt, получим скорость точки:

где — одинаковая для всех точек тела скорость поступательного движения и — различная для разных точек тела скорость вращательного движения.

Линейная скорость точки с радиус-вектором , обусловленная вращением твердого тела, равна:

Следовательно, скорость этой точки при сложном движении тела имеет значение:

1.5.2. Движение центра инерции
(центра масс) твердого тела

Разбив тело на элементарные массы Δm_i, можно представить его как систему МТ, взаимное расположение которых остается неизменным. Любая из этих элементарных масс может находиться под воздействием внутренних и внешних сил. Напишем для каждой элементарной массы уравнение второго закона Ньютона:

где — результирующие всех внутренних и всех внешних сил, действующих на данную элементарную массу. Суммируя, для всех элементарных масс имеем:

Однако сумма всех внутренних сил, действующих в системе, равна нулю. Поэтому (1.5.5) можно упростить так:

Используя определение центра инерции, можно записать:

Дифференцируя (1.5.7) дважды по времени, можно получить:

Подставляя (1.5.8) в (1.5.6), имеем:

Следовательно, центр инерции твердого тела движется так, как двигалась бы МТ с массой, равной массе тела, под действием всех приложенных к телу сил.

1.5.3. Момент силы

Рассмотрим схему установки на Рис. 1.5.1.

Рис. 1.5.1. Схема установки для исследования
равно-ускоренного вращательного движения

Под действием груза Р крестовина будет вращаться с возрастающей угловой скоростью, и вращение будет равно-ускоренным. Варьируя величину груза Р, радиус шкива l, массу грузов m и их расстояние R от оси вращения, можно прийти к заключению, что угловое ускорение β:

1. прямо пропорционально натяжению нити f и радиусу шкива l;
2. обратно пропорционально массе грузов m и квадрату их расстояния R от оси вращения.

Следовательно, ускорение вращательного движения зависит не только от величины действующей на тело силы, но и от расстояния l от оси вращения до линии, вдоль которой действует сила. Произведение fl дает величину так называемого момента силы относительно оси вращения.

Из этого опыта следует также, что на величину углового ускорения влияет не только масса вращающегося тела, но и распределение массы относительно оси вращения. Величина, которая это учитывает, называется моментом инерции тела относительно оси вращения.

Моментом силы относительно некоторой точки О называется величина , равная векторному произведению:

где — радиус-вектор, проведенный из точки О в точку приложения силы (Рис. 1.5.2).

Рис. 1.5.2. К определению момента силы

Вектор , по определению, перпендикулярен плоскости векторов и и направлен от нас. Это — аксиальный вектор. Модуль вектора равен:

где α — угол между направлениями векторов и , а l = r sinα — длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила. Эта длина называется плечом силы относительно точки О.

Если можно представить силу в виде суммы сил, имеющих общую точку приложения , то формулу (1.5.10) можно записать так:

Парой сил называются две равные по величине и противоположно направленные силы, не действующие вдоль одной и той же прямой (Рис. 1.5.3). Расстояние l между прямыми, вдоль которых действуют силы, называется плечом пары сил .

Рис. 1.5.3. Момент пары сил

Покажем, что момент пары сил относительно любой точки будет один и тот же. Пусть точка лежит в плоскости, в которой действуют силы, и выполняется . Момент силы равен fl₁ и направлен к наблюдателю, момент силы равен fl₂ и направлен от наблюдателя. Результирующий момент силы направлен от наблюдателя и равен:

Полученное выражение не зависит от положения точки О на плоскости, в которой лежит пара сил.

Суммарный момент внутренних сил Силы, с которыми взаимодействуют друг с другом две любые элементарные массы, лежат на одной и той же прямой (Рис. 1.5.4).

Рис. 1.5.4. Момент внутренних сил

Их моменты относительно произвольной точки О равны по величине и противоположны по направлению. Поэтому моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы МТ, в частности, для твердого тела, всегда равна нулю.

1.5.4. Момент импульса материальной точки.
Закон сохранения момента импульса

Аналогично моменту силы введем момент импульса МТ относительно некоторой точки О:

где — радиус-вектор, проведенный из точки О в точку пространства, в которой находится МТ (Рис. 1.5.5).

Рис. 1.5.5. К определению момента импульса

Введя плечо l = rsinα, можно получить модуль вектора момента импульса в виде:

Продифференцируем (1.5.16) по времени:

Первое слагаемое равно нулю в силу того, что оно представляет собой векторное произведение векторов одинакового направления: . Вектор . Поэтому соотношение (1.5.17) можно переписать так:

где — момент приложенных к МТ сил, взятый относительно той же точки О, относительно которой рассчитан момент импульса . Для замкнутой системы из N материальных точек легко получить аналогичное (1.5.18) соотношение. В отсутствие или при взаимной компенсации внешних сил их суммарный момент , действующий на тела системы, равен нулю. В результате этого суммарный момент импульса не зависит от времени. Таким образом, формулируется закон сохранения момента импульса : момент импульса замкнутой системы материальных точек остается постоянным.

1.5.5. Уравнение динамики
вращательного движения

Если МТ вращается по окружности радиуса r (Рис.1.5.6), то момент ее импульса относительно оси вращения О равен:

Рис. 1.5.6. К выводу уравнения динамики вращательного двмжения

Пусть ω — угловая скорость вращения, тогда v = ωr, и (1.5.18) будет иметь вид:

Если вокруг оси О вращается система МТ с одной и той же угловой скоростью ω, то:

где, момент инерции системы МТ относительно оси вращения, равный сумме произведений масс МТ на квадраты их расстояний до оси вращения.

Если угловая скорость и момент инерции — переменные величины, то, подставляя (1.5.21) в (1.5.18), получим:

где М — момент внешних сил относительно оси вращения. Соотношение (1.5.22) — это основное уравнение динамики вращательного движения вокруг неподвижной оси.

Важным частным случаем является вращение неизменяемой системы МТ или твердого тела вокруг неподвижной оси. В этом случае момент инерции I остается постоянным при вращении, и уравнение (1.5.22) будет иметь вид:

Сопоставляя уравнения динамики вращательного движения с уравнениями динамики поступательного движения, легко заметить, что при вращательном движении роль силы исполняет момент силы, роль массы — момент инерции и т д. (Табл. 1.5.1).

Сопоставление закономерностей
поступательного и вращательного движений

— сила	— момент силы
— масса	— момент инерции
— линейная скорость	— угловая скорость
— линейная скорость	— угловая скорость
— линейное ускорение	— угловое ускорение
— импульс	— момент импульса

Предположим, что твердое тело может изменять свою конфигурацию в результате перераспределения масс. Пусть в результате происходит изменение момента инерции от значения I₁ до I₂. Если такое перераспределение осуществляется при отсутствии моментов внешних сил, то согласно закону сохранения момента импульса должно выполняться равенство:

где ω₁ — исходное, а ω₂ — конечное значение угловой скорости тела. Следовательно, изменение момента инерции влечет за собой соответственное изменение угловой скорости тела. Этим объясняется такое явление: человек, стоящий на вертящейся скамье, разводя руки в стороны, начинает вращаться медленнее, а, прижимая руки к туловищу, будет вращаться быстрее.

1.5.6. Момент инерции. Теорема Штайнера

Из определения момента инерции:

следует, что момент инерции — величина аддитивная. Это означает, что момент инерции тела равен сумме моментов инерции его частей. Каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции.

Распределение массы в пределах тела можно охарактеризовать с помощью физической величины, называемой плотностью. Если тело однородно, то его плотность может быть вычислена так:

где m — масса, V — объем тела. Для тела с неравномерно распределенной массой соотношение (1.5.26) дает среднюю плотность. Плотность в данной точке определяется в этом случае так:

Уменьшение объема в (1.5.27) следует производить до тех пор, пока не будет получен физически бесконечно малый объем, который достаточно мал, чтобы в его пределах макроскопические свойства вещества можно было считать одинаковыми, и достаточно велик, чтобы не могла проявиться дискретность (атомарное строение) вещества.

Согласно (1.5.27), элементарная масса тела может быть вычислена так:

Следовательно, момент инерции следует записать в виде:

Если плотность постоянна, ее можно вынести за знак суммы:

Устремляя ΔV_i к нулю, можно в (1.5.30) перейти к интегрированию:

В качестве примера найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (Рис. 1.5.7).

Рис. 1.5.7. К расчету момента инерции диска

Разобьем диск на кольцевые слои толщиной dr. Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном r. Объем такого слоя равен:

где b — толщина диска. Поскольку диск однороден, плотность можно вынести за знак интеграла:

где R₀ — радиус диска. Применяя обозначение для массы диска , получим для момента инерции однородного диска:

В данном случае вычисление момента инерции упрощалось благодаря однородности и симметричности тела. Если бы нужно было отыскать момент инерции относительно оси О’О’ (Рис. 1.5.7), перпендикулярной к диску и проходящей через его край, вычисления оказались бы значительно сложнее. В таких случаях отыскание момента инерции облегчается, если воспользоваться теоремой Штайнера : момент инерции I относительно произвольной оси равен сумме момента инерции I C относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:

В соответствии с теоремой Штайнера момент инерции диска относительно оси О’О’ равен:

1.5.7. Работа и кинетическая энергия
вращающегося твердого тела

Если МТ вращается по окружности с радиусом r, то элементарная работа при повороте на угол dφ равна:

Такое же выражение получится и для твердого тела, так как его можно рассматривать как систему МТ, вращающихся с общей угловой скоростью ω. Роль силы в (1.5.37) играет момент внешних сил, роль линейного перемещения — угловой поворот.

Кинетическая энергия твердого тела, вращающегося с угловой скоростью ω, может быть записана так:

Это выражение напоминает соответствующую формулу для кинетической энергии МТ и может быть получено из нее формальной заменой m → I, v → ω.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2013