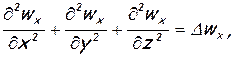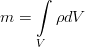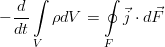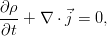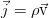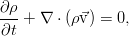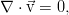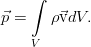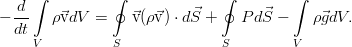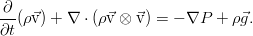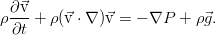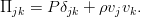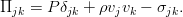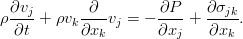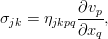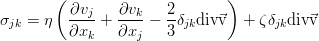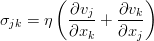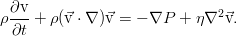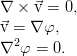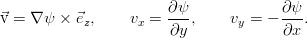Шпаргалка: Основы гидрогазодинамики
| Название: Основы гидрогазодинамики Раздел: Рефераты по физике Тип: шпаргалка Добавлен 07:14:42 04 сентября 2010 Похожие работы Просмотров: 6092 Комментариев: 20 Оценило: 6 человек Средний балл: 4.2 Оценка: 4 Скачать | |||||||||||
,
и величине этой площадки при стремлении ее к нулю. Величина напряжения зависит от выбора направления площадки.
— нормальное напряжение
— касательное напряжение
(1)
(2)
(3)
).
в жидкости отсутствуют источники или стоки. При 
имеется источник, при 
имеется сток. Уравнение 
— элемент контура АВ
.
, это указывает на наличие вращающихся объемов, вихрей жидкости. Интерес представляют течения для которых 
, такие течения называются безвихревыми или потенциальными,. Т.к. в этом случает существует потенциал вектора скорости φ, который связан с составляющими вектора скорости следующими соотношениями:
; 
; 
; 
. Для жидкой частицы основная теорема кинематики гласит, что скорость движения любой точки жидкой частицы складывается из скорости квазитвердого движения и деформационного. Квазитвердое состоит из поступательного вращательного: 
. Для доказательства рассмотрим движение точки М с координатами x , y , z , которая находится в окрестности точки М0 (x 0 , y 0 , z 0 ) и составляющая для точки М0 скорости ( u 0 , υ 0 , w 0 ) , тогда раскладывая функцию скорости в ряд Тейлора и сохраняя компоненты первого порядка малости, составляющие скорости для точки М можно записать:
; 
, входящие в скорость деформации, могут быть представлены в виде матрицы, которая называется тензором скоростей деформации: |
— диагональные компоненты.
Тензор симметричен относительно главной диагонали 
Рассмотрим диагональные компоненты. В жидкости выделим отрезок АВ длиной dx (отрезок на оси х ). Рассмотрим перемещение отрезка вдоль оси х . Скорости в точках А и В не равны. Через время dt отрезок займет положение 
. Произошла линейная деформация отрезка АВ на величину:
Если разделим линейную деформацию на длину отрезка:
скорость линейной деформации – скорость растяжения или сжатия линейного отрезка расположенного на оси х в направлении оси х . Аналогично:
скорости относительных линейных деформаций вдоль соответствующих осей. Сумма диагональных компонент определяет дивергенцию вектора скорости, т.е.
закон относительного изменения объема.
Рассмотрим перемещение отрезка АВ расположенного на оси х и длиной dx в направлении оси dy ) .
Ввиду малости угла
угловая деформация линейного отрезка в направлении оси у .
скорость угловой деформации или скорость скашивания в направлении оси у . Если отрезок расположить на оси у , то 
— скорость скашивания в направлении оси х . 
— средняя скорость угловой деформации в плоскости ху.
Таким образом недиагональные компоненты характеризуют скорости скашивания или угловых деформаций в соответствующих плоскостях.
7. Уравнение сплошности
Уравнение сплошности – это уравнение закона сохранения массы:
Выделим в жидкости элементарный объем 
с плотностью ρ.
Второй член полученного уравнения выражает закон относительного изменения объема,. Т.е. дивергенцию.
Плотность в общем случае зависит от координат и времени: 
уравнение сплошности (неразрывности).
Если течение стационарное, то уравнение упрощается: 
Если жидкость несжимаемая, т.е. 
, то 
8. Нормальное и касательное напряжение, действующие в движущейся жидкости
Закон сохранения количества движения для неизолированной системы может быть записан в виде:
где 
— главный вектор количества движения системы
— главный вектор внешних сил, действующих на систему
В жидкости выделим элементарный тетраэдр с гранями 
, 
, 
, 
. Индекс показывает перпендикулярно какой оси расположены грани, — наклонная грань. К граням приложены соответствующие напряжения 
, 
, 
, 
(не перпендикулярные граням). Масса тетраэдра 
. На тетраэдр действуют массовые и поверхностные силы. Массовые характеризуются вектором плотности 
, поверхностные – напряжениями.
— скорость центра инерции тетраэдра
— третий порядок малости
— второй порядок малости
Членами третьего порядка малости пренебрегаем.
и т.д.
Получим связь напряжений, действующих на грани выделенного тетраэдра:
В проекциях на координатные оси это уравнение может быть переписано:
В записанной системе 
называются нормальными напряжениями, а 
и т.д. называются касательными напряжениями. Все напряжения могут быть записаны в матричной форме в виде симметричного тензора напряжений:
Первый индекс определяет ось, относительно которой расположена грань, второй – ось на которую проецируется напряжение.
9. Уравнение движения сплошной среды в напряжениях
Рассмотрим элементарный параллелепипед с ребрами 
. Объем его 
. На него действуют массовые и поверхностные силы определяемые главным вектором внешних сил 
. К параллелепипеду применим закон сохранения количества движения:
Для определения главного вектора поверхностных сил рассмотрим все силы, дающие проекцию на ось х . Для граней перпендикулярных х проекцию дают только силы, создаваемые нормальными напряжениями. Поэтому равнодействующая этих сил равна:
Аналогично для граней перпендикулярных z получим равнодействующую равную:
Равнодействующая поверхностных сил в проекции на ось х равна:
Тогда закон сохранения количества движения в проекции на х можно записать:
Полученная система называется системой уравнений движения сплошной среды в напряжениях. В левой части стоит полная производная от скоростей, которые могут быть расписаны через локальные и конвективные составляющие ускорения. При определенных условиях левая часть значительно упрощается (стационарное, двухмерное или одномерное течение).
Т.к. 
систему можно записать в виде одного уравнения в векторной форме записи:
10. Напряжения, действующие в идеальной жидкости
В идеальной жидкости отсутствуют силы трения, следовательно касательные напряжения равны нулю. Применительно к элементарному тетраэдру проекция напряжения, приложенного к произвольной наклонной грани на ось х равна:
С другой стороны:
Аналогично для проекций на у :
и 
Таким образом в идеальной жидкости величина нормального напряжения в любой точке не зависит от направления площадки к которой напряжение приложено. В идеальной жидкости величина нормального напряжения в точке называется гидродинамическим давлением в этой точке. Модель идеальной жидкости упростила постановку и решение многих задач, в которых влиянием сил трения можно пренебречь.
Знак «минус» ставится, т.к. жидкость оказывает давление на выделенный объем в направлении противоположном внешней нормали.
11. Уравнение движения идеальной жидкости (Эйлера)
Для вывода воспользуемся уравнениями движения в напряжениях:
— система уравнения Эйлера для идеальной жидкости.
Справедлива, как для сжимаемой, так и для несжимаемой жидкости. Если жидкость сжимаемая, то необходимо ввести функцию координаты от времени: 
Если жидкость несжимаемая, то 
12. Уравнение движения идеальной жидкости (Эйлера) в форме Громека
Все преобразования выполним на первом уравнении:
— система уравнений движения для и.ж. в форме Громека
Рассмотрим далее движение, предполагая, что массовая сила имеет потенциал и течение баротропное.
Первое предположение утверждает, что у массовых сил имеется потенциал, связанный соотношениями с массовыми силами:
; 
; 
,
U — потенциал массовых сил.
Второе: баротропным считается течение, у которого ρ считается только функцией давления.
Например, баротропными течением является:
1) ρ= const – газ или жидкость несжимаемы
2) движение среды изотермическое — 
3) движение среды адиабатное — 
Условие баротропности предполагает, что существует некоторая функция Р , зависящая от давления, которая определяется выражением:
Функция Р связана с р и ρ соотношениями:
; 
; 
.
Подставим в систему уравнений Громека потенциал массовых сил и функцию Р :
— система уравнений Эйлера в форме Громека
Достоинство системы заключается в том, что отдельно выделен ротор, который при определенных условиях может быть равен нулю и система значительно упрощается. Последний член равен нулю, если: 1) 
— статическая задача; 2) 
— течение безвихревое или потенциальное.
Сумма, стоящая во второй компоненте, имеет определенный физический смысл. В векторной форме система может быть записана в виде одного уравнения:
13. Теорема Бернулли
Рассмотрим стационарное баротропное течение под действием массовых сил, т.е. можно записать:
умножим уравнение скалярно на вектор скорости, тогда последний член равен нулю, т.к. идет скалярное перемножение перпендикулярных векторов.
— единичный вектор в направлении вектора скорости. Вектор скорости направлен по касательной к линии тока или к траектории, т.к. течение стационарное, следовательно:
— производная по направлению.
выражение отражает теорему Бернулли: при стационарном баротропном течении идеальной жидкости под действием потенциальных массовых сил сумма кинетической энергии единицы объема, функции давления приведенного к единице массы потенциала массовых сил сохраняет постоянное значение вдоль любой линии тока.
Если бы скалярно умножили исходное уравнение на вектор угловой скорости, то получили бы аналогичный результат вдоль вихревой линии.
Если течение потенциальное, то и сразу же получается:
и 
во всем потоке, т.е. трехчлен Бернулли сохраняет постоянное значение во всей области потенциального потока.
Рассмотрим потенциальное течение несжимаемой жидкости под действием сил тяжести. Т.к. жидкость несжимаема то :
У сил тяжести потенциал равен: 
, z – координата.
(1), 
— удельный вес
Все эти составляющие имеют размерность давления и называются напорами: 
— скоростной или динамический напор; р – пьезометрический напор; 
— геометрический напор; ро – полный напор
При стационарном течении идеальной несжимаемой жидкости полный напор, равный сумме 
, сохраняет постоянное значение вдоль любой линии тока, а при потенциальном течении во всей области потока.
В задачах, в которых можно пренебречь влиянием геометрического напора, уравнение Бернулли упрощается и приобретает вид: 
Уравнение (1) разделим на 
, тогда:
все компоненты измеряются в метрах и называются высотами: 
— скоростная высота, 
— пьезометрическая высота, z – нивелирная высота, Н – гидравлическая высота. При стационарном движении идеальной несжимаемой жидкости высота
сохраняет постоянное значение вдоль любой линии тока (или вихревой линии), а при потенциальном течении во всем токе.
14. Основные понятия и определения потенциальных течений
Потенциальные течения – это течения, у которых 
во всем потоке, следовательно существует функция φ , называемая потенциалом, зависит φ(х,у, z , t ) и связана с составляющими U соотношениями:
то есть 
Записанные соотношения могут быть записаны и для любой другой функции, которая отличается от φ на константу: 
. Таким образом, уравнение потенциала определяется с точностью до константы. Геометрическое место точек с одинаковым значением φ образуют эквипотенциальные поверхности, уравнения которых: 
. Так как 
, следовательно вектор U расположен по перпендикулярам в любой точке эквипотенциальной поверхности. Так как вектор U касателен к линии тока, то линии тока перпендикулярны эквипотенциальной поверхности.
Рассмотрим стационарное плоское течение, то есть 
, тогда
и 
.
Уравнение сплошности имеет вид:
Таким образом, потенциал U удовлетворяет уравнению Лапласа, следовательно является гармонической функцией.
Введем в рассмотрение функцию ψ, связанную с составляющими U уравнениями:
и 
Функция ψ удовлетворяет уравнению сплошности, т.к.
ψ – функция тока, она также определяется с точностью до постоянной.
Уравнение 
называется уравнением линии тока.
В плоских течениях эквипотенциальные поверхности дают проекции на плоскость (х,у) в виде линии, поэтому часто в задачах рассматриваются эквипотенциальные линии которые перпендикулярны линии тока.
В потенциальном потоке , в плоском течении 
функция тока ψ гармоническая
Сравнение потенциала φ и ψ позволяет записать:
—
15. Комплексный потенциал, комплексная скорость
Из теории комплексной переменной известно, что если две функции φ и ψ, зависящие от х и у , удовлетворяют условиям Коши-Римана, то комплексная величина 
будет не просто зависеть, а являться функцией от комплексной переменной 
, то есть существует некоторая функция 
, действительной частью которой является φ , а мнимой ψ . 
.
Функция имеет большое значение при изучении плоских потенциальных течений и называется комплексным потенциалом или характеристической функцией течения.
Так как 
является аналитической функцией от 
, то ее производная не зависит от направления дифференцирования, а зависит только от положения точки в пространстве, то есть
по условию Коши-Римана:
Если вектор U разложить в комплексной плоскости годографа U , то 
.
Производная от комплексного потенциала дает зеркальное изображение комплексной U относительно действительной оси. Обозначим ее как
.
В теории комплексной переменной числа 
и 
называют сопряженными, назовем 
как сопряженную U . Таким образом, производная от комплексного потенциала определяет .
Таким образом, если изменяется какое-то плоское потенциальное течение, то для него можно подобрать уравнение комплексного потенциала, проанализировать его и просчитать составляющие U в любой точке. С другой стороны для любого потенциала можно определить вид течения.
16. Частные случаи плоских потенциальных течений
1. Плоско параллельный поток:
Рассмотрим комплексный потенциал — 
, где а – действительное число
и
— семейство прямых, параллельных оси у . 
— уравнение функции тока.
Линии тока 
— семейство прямых, параллельных оси х . 
— уравнение эквипотенциальных поверхностей.
Для построения поля скоростей возьмем производные
;
Таким образом, рассмотренный потенциал описывает плоское течение потока вдоль оси х . Величину а можно рассматривать как скорость внешнего (набегающего) потока, 
. 
2. Источник и сток.
Рассмотрим комплексный потенциал 
, а – действительное число (
), тогда
Уравнение для потенциала: 
. 
— эквипотенциальные линии, семейство окружностей с центром в точке (0,0) .
— уравнение функций тока. 
— семейство прямых, проходящих через точку (0,0) .
Характер (вид) течения определяет знак при а . Если a >0, то это источник, если a Reкр – силы инерции. Re характеризует движение при соизмеримости инерции и вязкости. Если в потоке преобладает какой-то один вид сил характер перестает зависеть от величины Re. В этом случае говорят, что течение автомодельно относительно критерия Re.
2) Критерий гидродинамической гомохронности 
— определяет соотношение между периодом темпа внешних воздействий на поток и периодом перестройки скоростного поля. Используют только для нестационарных задач. 
— время, за которое проходит частица, движущаяся со скоростью V 0 , путь l 0 . Если в задаче время подлежит определению, то рассматривается не критерий, а число Струхала: 
3) Критерий Фруда 
— определяет соотношение между силами инерции и тяжести в потоке. Используется только в задачах, в которых гравитационные эффекты имеют важное значение. Однако в таких задачах часто сложно задать характерную скорость (при естественной конвекции), поэтому строится критерий, в котором исключается скорость:
— критерий Галилея.
При гравитационном движении важное значение имеет параметрический критерий: 
.
Причем ρ и ρ 0 – плотности не только в разных точках, но и в различных фазах. 
— критерий Архимеда.
При гравитационном течении однофазной жидкости движение возникает в результате расширения: 
— коэффициент объемного расширения.
— критерий Гросгофа.
4) Число Эйлера 
— определяет соотношение сил давления и сил инерции; определяемая величина; т.к. часто давление в потоке неизвестно, то больший интерес представляет определение перепада давления на рассматриваемом участке 
.
— безразмерный коэффициент сопротивления при очень низких скоростях, когда течение ламинарное 
, 
, в этих случаях рассматривают число Лагранжа, которое принимает постоянное значение:
22. Моделирование ГГД явлений
Одним из средств исследования потока является аэродинамический эксперимент. Достаточно сложно, дорого, а порой и невозможно выполнить эксперимент на действующем оборудовании. Для того, чтобы результаты полученные на моделях могли быть перенесены и использованы в действующих расчетах необходимо соблюдать условия подобия Кирпичева-Гухмана, т.е. течение в модели и образце должны иметь одинаковую физическую природу и описываться одними и теми же безразмерными уравнениями. Течения должны происходить в геометрически подобных каналах и должны быть подобраны все условия однозначности. Безразмерные критерии подобия должны иметь одинаковую величину. Рассмотрим условия моделирования вынужденного течения в цилиндрической трубе с прямой осью. Для соблюдения подобия необходимо, чтобы: 
Свяжем одноименные величины с помощью констант подобия:
— условие, определяющее выбор констант подобия
Например, если в модели и образце используется одинаковая жидкость с одинаковой температурой, то 
. Это значит если размер модели в п раз меньше, чем размер образца, то для соблюдения подобия необходимо чтобы скорость в модели была в п раз больше. При моделировании часто возникает необходимость соблюдения подобия по нескольким критериям. В этом случае часто прибегают к приближенному моделированию, т.е. когда исследуется зависимость течения от одного критерия при условии, что от других критериев при этом же течение не зависит, т.е. автомодельно.
23. Ламинарное и турбулентное движение
При низких скоростях потока отмечается, что отдельные частицы или струйки жидкости движутся по плавным непересекающимся траекториям. Такое течение называется ламинарным, что означает слоистое. При увеличении скорости потока траектории отдельных струек приобретают волнообразный характер и через некоторое время струйка исчезает, перемешиваясь с жидкостью. Характер течения при этом изменился. Траектории отдельных частиц приобретают хаотичный неустановившийся характер. Такое течение называется турбулентным – хаотичным, вихревым. Рейнольдс установил, что смена режима происходит при значении 
. Причина перехода обусловлена влиянием возмущений, исходящих от стенок или вносимых в поток извне. Установлено, что если ликвидировать возмущение, т.е. отполировать тубу, сделать плавный вход потока в канал, то границу перехода можно значительно переместить в область более высоких 
. При 
любые возмущения гаснут, следовательно 
— нижняя граница значения области перехода. Смена режима происходит не сразу: сначала в потоке возникают отдельные очаги турбулентного движения, которые появляются и исчезают. Такое явление называют перемежаемостью:
— общее время наблюдения за какой-то точкой
— время существования режима в этой точке
При 
— ламинарное
При 
— турбулентное
— переход
Переход ламинарного движения в турбулентное имеет очень большое практическое значение, т.к. определяет условия теплообмена, сопротивления потока, перемешивания жидкостей.
24. Пограничный слой и его характерные толщины
При обтекании любого тела потоком реальной жидкости поток как бы «прилипает» к поверхности. По мере удаления от поверхности скорость возрастает и, начиная с некоторого расстояния, скорость равна скорости набегающего или невозмущенного потока. В этом состоит проявление вязкости жидкости. Прандтль определил, что толщина слоя в котором проявляется вязкость увеличивается по мере продвижения потока. Чем меньше скорость набегающего потока, тем больше толщина слоя, в котором проявляется вязкость. Прандтль назвал эту часть жидкости у поверхности гидродинамическим пограничным слоем. Все течение он разбил на 3 части: 1 – гидродинамический пограничный слой – область, где сосредоточено влияние вязкости, 2 – след, 3 – невозмущенный поток. Во внешнем потоке вязкость можно не учитывать и считать жидкость идеальной, то есть без трения. Таким образом общая задача обтекания разбивается на 2 части: 1) течение жидкости в пограничном слое; 2) течение идеальной жидкости. Результаты решений должны совпадать на внешней границе пограничного слоя. Поскольку скорость в пограничном нарастает от 0 до скорости внешнего течения постепенно — асимптотически, поэтому δ определяется достаточно условно. Принято считать за δ такое значение у поперечной координаты, при котором скорость u отличается от U не более чем на 1-2%. u / U =0,98..0,99. Теория погранслоя использует и другие более точно определяемые толщины. Рассмотрим как влияет вязкость на кинематику (положение линий тока) и динамику (потерю количества движения).
Из-за торможения жидкости линия тока отклоняется от поверхности на расстояние δ. Расход жидкости между поверхностью и линией тока в плоском течении будет равен: 
Если бы жидкость была идеальной, то та же линия тока располагалась бы ближе к поверхности на величину δ: 
Максимальное значение δ будет равняться: δ= δmax = δ*
— толщина вытеснения.
Это более точно вычисляемая величина чем δ.
δ* может быть представлена, как линейный отрезок через который проходит секундный объемный расход идеальной жидкости, равный потере расхода через сечение погранслоя из-за торможения в реальном течении. Из-за торможения снижается и количество движения жидкости в погранслое. С количеством движения связана толщина потери импульса:
Толщина потери импульса может быть представлена как линейный отрезок, через который проходит количество движения жидкости равный потере количества движения через сечение в пограничном слое из-за торможения в реальном течении.
25. Переход ламинарного ПС в турбулентный
При обтекании поверхности потоком вязкой жидкости, начиная от критической точки образуется погранслой. Причем сначала слой является ламинарным, толщина его δ увеличивается, течение теряет устойчивость и происходит смена течения погранслоя. Смена происходит в некоторой области. Часто для упрощения считают, что переход происходит в точке.
Т.к. коэффициент сопротивления поверхности при ламинарном и турбулентном погранслое значительно отличаются по величине, меняются условия теплообмена. Определение границ перехода имеет большое практическое значение. Для определения границы перехода существуют теоретические и экспериментальные методы. В теоретических методах исследуется устойчивость течения ламинарного погранслоя и за границу перехода принимают точку потери устойчивости. Экспериментальные методы основаны на измерении распределений скорости или напряжения поверхностного трения. В точке перехода трение потока о стенку резко возрастает.
Если перемещать микротрубку вдоль обтекаемой поверхности на одинаковом расстоянии от нее, то по мере погружения микротрубки в ламинарный погранслой значение скорости, которое она будет показывать с увеличением х будет убывать. Вначале перехода ламинарного погранслоя в турбулентный (хкр1 ) профиль скорости начинает перестраиваться – становится более заполненным – прижимается к пластине, поэтому скорость возрастает. При x >хкр2 микротрубка погружается уже в турбулентный погранслой и поэтому скорость будет уменьшаться. За точку перехода принимают значение х, в которой скорость достигает минимума. Для определения границы перехода используют:
На положение хкр значительное влияние может оказать скорость изменения внешнего потока 
.
В конфузорной области, т.е. при разгоне внешнего потока переход затягивается, т.е. ламинарная зона увеличивается.
В диффузорной области ламинарный погранслой раньше теряет устойчивость, поэтому хкр уменьшается. Причины, вызывающие смену режима следующие:
— возмущения, которые вносятся в погранслой из внешнего потока (внешний поток турбулизирован)
— возмущения, исходящие от поверхности (шероховатости, стыки поверхностей)
Рассмотрим влияние турбулентности внешнего потока. Если степень турбулентности внешнего потока меньше 0,1%, то возмущение не влияет:
Если 
, то с увеличением ε хкр1 и хкр2 уменьшаются. Влияние шероховатости приводит к более ранней смене режимов.
Рассмотрим влияние величины U . Чем больше U , тем меньше хкр .
При турбулентном режиме течение у поверхности всегда существует область ламинарно текущей жидкости – вязкий подслой, толщина которого 
от δ. Распределение скорости в вязком подслое линейное и описывается уравнением:
(1)
В турбулентном ядре распределение скорости может быть описано универсальным логарифмическим профилем распределения:
(2)
Между подслоем и ядром часто выделяют буферную область в которой физическая и критическая вязкость одного порядка. Поэтому уравнение (2) дает расхождение с экспериментальными данными в буферной области и на внешней границе пограничного слоя, где поток взаимодействует с нетурбулизированным потоком.
Т.к. при турбулентном погранслое коэффициент сопротивления значительно больше, то для снижения общего сопротивления хорошо обтекаемых тел (крыло, пластина, судно) необходимо затягивать переход, т.е. увеличивать протяженность ламинарного участка погранслоя. Для плохо обтекаемых тел (цилиндр, сфера) сопротивление определяется в первую очередь сопротивлением формы (давления). Сопротивление трения имеет малое значение. Сопротивление формы зависит от области отрыва потока. Чем больше область отрыва, тем больше сопротивление. При малых скоростях набегания (Re Re кр на цилиндре сначала образуется ламинарный погранслой, который преобразуется в турбулентный, который срывается при угле 140°.
Турбулентный погранслой лучше обменивается энергией с внешним потоком, чем ламинарный. Увеличение запаса энергии в турбулентном погранслое приводит к затягиванию точки отрыва до 140° и зона отрывного течения за цилиндром резко уменьшается, течение как бы приближается к идеальному, коэффициент сопротивления резко снижается. Это явление называется кризисом обтекания плохо обтекаемых тел.
УРАВНЕНИЯ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ
Особенности напряженного состояния вязкой жидкости.
Нормальные и касательные напряжения. Тензор напряжений.
Закон трения Ньютона. Законом трения Стокса.
Поперечный и продольной градиент скорости.
Динамический и кинематический коэффициент вязкости.
Скорости угловой и линейной деформации. Тензор скоростей деформаций
Давление в вязкой жидкости. «Вторая вязкость».
Уравнение Навье Стокса.
Уравнения движения идеальной жидкости рассматривались в разделе Уравнения движения[1], где они были представлены в форме Эйлера и в форме Громеки. В настоящем разделе изучается движение вязкой жидкости. Это более сложное явление. В отличие от идеальной жидкости, где поверхностными силами являются только силы нормального давления (нормальные напряжения сжатия), в вязкой жидкости эти силы получаются несколько иными, а именно: появляются касательные напряжения, приложенные к поверхностям, которые ограничивают рассматриваемый объем, нормальные напряжения зависят не только от давления, но и от сил вязкости.
Уравнения движения вязкой жидкости выводятся тем же методом, что и уравнения Эйлера, только расширяется комплект действующих сил — добавляются касательные напряжения, а нормальные напряжения вычисляются более сложно. Поэтому, прежде чем приступить к выводу, необходимо выяснить, как определяются напряжения.
В элементарном объеме, изображенном на рисунке 5, полагая, что жидкость вязкая, векторы поверхностных сил будут направлены не перпендикулярно к площадкам (например, АDЕF, ВСКL), а под косыми углами к ним. Это связано с тем, что векторы напряжений поверхностных сил имеют не только нормальные компоненты, но и касательные. Заметим также, что в теории вязкой жидкости положительными нормальными напряжениями считаются напряжения растяжения. Поэтому на схемах подобных рисунку 5, напряжения от поверхностных сил изображают векторами, направленными не внутрь рассматриваемого объема, а наружу.
Для обозначения проекций вектора напряжения поверхностной силы применяется двойная индексация. Первый индекс указывает ту площадку, на которой рассматриваются напряжения. Этому индексу дается наименование той координатной оси, которая нормальна к заданной площадке. Так, например, для площадки, параллельной координатной плоскости хоу, при обозначении любых напряжений первым индексом будет z. Второй индекс указывает ту ось, на которую проектируется вектор напряжения. Таким образом, на каждой площадке рассматриваются два касательных и одно нормальное напряжение. Касательные имеют разноименные индексы, нормальные — одноименные (см. рисунок 109).
Поскольку частицу жидкости можно представить как элементарный объем кубической формы, то вполне очевидно, что для характеристики ее напряженного состояния нужно задать следующие девять величин:
Если составить моменты сил, вызываемые касательными напряжениями, приложенными к граням кубика, и рассмотреть условия их равновесия относительно координатных осей [2], то нетрудно доказать, что
т.е. касательные напряжения, приложенные к смежным граням и действующие в одной плоскости, численно равны. Это дает значительное упрощение, так как позволяет сократить число рассматриваемых напряжений с девяти до шести.
Для дальнейших рассуждений необходимо связать напряжения со скоростью движения жидкости.
Наиболее простую зависимость касательных напряжений от скорости дает закон жидкостного трения Ньютона
(6.1)
Здесь τ — касательное напряжение, ∂w/∂n — изменение скорости по нормали к линии тока, или поперечный градиент скорости. Коэффициент пропорциональности в этой формуле μ — называется динамическим коэффициентом вязкости, или динамической вязкостью. Он зависит от рода жидкости и характеризует вязкость. Кроме того, он зависит от температуры. Для капельных жидкостей с ростом температуры и уменьшается, следуя зависимости
(6.2)
где а и b — постоянные для данного рода жидкости коэффициенты, t — температура в градусах Цельсия, μ0 — динамический коэффициент вязкости при t=0°. Для газов μ возрастает с увеличением температуры. Эта зависимость хорошо описывается формулой Сатерлэнда
(6.3)
в которой с — коэффициент, зависящий только от рода газа, Т — абсолютная температура в градусах Кельвина, μ0 — коэффициент вязкости при Т=Т0. Для воздуха можно пользоваться также приближенной зависимостью
(6.4)
Наряду с динамическим коэффициентом вязкости применяется еще кинематический коэффициент вязкости
(6.5)
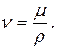
Его размерность [м 2 /сек] не содержит динамических величин, а только кинематические, откуда он и получил свое название.
Единицы измерения дляμ и ν в различных системах следующие:
| СИ | СГС | МКГС (техническая) | |
| μ | 1  | 1  | 1  |
| ν | 1  | 1  | 1 |
В системе СГС эти единицы имеют специальные названия: 1 дин сек/см 2 = 1 пуаз; 1 см 2 /сек = 1 стокс. Соотношение между единицами в различных системах такое:
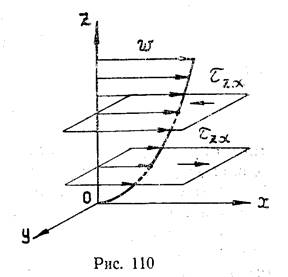
Применяя формулу Ньютона (6.1) к потоку, движущемуся параллельно плоскости хоу (см. рисунок 110), можно записать
(6.6)
Если рассмотреть два бесконечно близко расположенных слоя, которые на рисунке 110 изображены параллельными плоскостями, то можно заметить, что касательные напряжения на верхний слой со стороны нижнего действуют против движения, а на нижний со стороны верхнего — по движению. Иначе говоря, верхний слой стремится увлечь за собой нижний, а нижний слой тормозит верхний. Объем жидкости, находящийся между такими слоями, деформируется, получая деформацию сдвига (см. рисунок 111). Согласно формуле (1.5)[3] скорость угловой деформации определится как
что при 
=0 (так как wz=0) даст
(6.7)
Таким образом, между касательным напряжением и скоростью угловой деформации существует линейная зависимость с коэффициентом пропорциональности 2μ.
В более общем виде связь между напряжениями и скоростями деформации жидкости устанавливается законом трения Стокса. Этот закон имеет формальную аналогию с законом Гука для твердого тела, применяемом в теории упругости или в сопротивлении материалов. По закону Гука напряжения, возникающие в твердом теле, пропорциональны деформациям: нормальные напряжения пропорциональны линейным относительным деформациям, а касательные — угловым. Согласно закону Стокса напряжения пропорциональны не деформациям, а скоростям деформации: нормальные — скорости линейной деформации, а касательные — скорости угловой деформации. Коэффициент пропорциональности, как это следует из рассмотренного выше частного примера, равен 2μ [4].
Обращаясь к теореме Коши-Гельмгольца (1.7)[5] видим, что при движении жидкого объема в общем случае имеют место следующие скорости деформации:
скорости линейной деформации 
скорости угловой деформации 
Тогда, принимая во внимание формулы (1.5), можно записать касательные напряжения в таком виде:
(6.8)
а нормальные напряжения, возникающие только от действия сил вязкости, представить так:
(6.9)
Нужно обратить внимание, что полные величины нормальных напряжений рхх, руу, рzz отличаются от записанных формулой (6.9) на величину давления в газе р0, которое определяется молекулярно-кинетическими процессами. (Давление в газе или жидкости существует и тогда, когда влияние вязкости отсутствует, например, в идеальной жидкости или в неподвижной реальной жидкости). Таким образом,
(6.10)
Знак минус перед величиной р0 связан с тем, что давление создает напряжения сжатия, в то время как положительными считаются нормальные напряжения растяжения.
Вычитая из утроенной величины рxх сумму напряжений, можно записать
(6.11)
Теперь следует ввести понятие о том, что такое давление в вязкой жидкости.
Если за величину давления принять нормальные напряжения рхх, рyy, рzz, то возникает неудобство, так как в одной и той же точке эти напряжения различны по величине. В этом случае пришлось бы в каждом направлении рассматривать свою величину давления. Для того чтобы понятия давления в вязкой жидкости и в идеальной жидкости сохранялись идентичными, надо отыскать такую комбинацию, составленную из трех напряжений рхх, рyy и рzz, которая не зависела бы от ориентации системы координат, иначе говоря, которая не зависела бы от ориентации площадки, проведенной внутри жидкости для подсчета действующих на нее сил давления. Таким свойством обладает средняя арифметическая величина
Она и принимается в качестве давления в вязкой жидкости.
Пользуясь таким представлением о давлении, можно записать выражение (6.11) для рхх и аналогичные ему для рyy и рzz в следующем виде:
(6.13)
В случае несжимаемой жидкости, согласно уравнению неразрывности divw=0, тогда последние слагаемые в правой части обращаются в нуль и уравнения (6.13) упрощаются. Сопоставляя их с формулами (6.10), нетрудно заметить, что в этом случае р=р0.
Попутно заметим, что «давление движущейся жидкости имеет свойства гидростатического, если не учитывать сил вязкости. Действительно, для невязкой жидкости силы, являющиеся причиной движения, не отличаются от сил, действующих в покоящейся жидкости (массовые силы, силы инерции). Поэтому доказательство того, что давление образует скалярное поле (см. Гидростатику), полностью распространяется и на движущуюся невязкую жидкость».
Для вывода уравнений движения вязкой жидкости рассмотрим элементарный объем АВСDЕFLК (см. рисунок 112), движущийся под действием сил: поверхностных нормальных 
, поверхностных касательных 
и массовых 
. Равнодействующая этих сил, в соответствии со вторым законом Ньютона, должна равняться массе жидкого объема, умноженной на ускорение. Запишем это уравнение сначала в проекциях на ось x, подсчитав предварительно проекции действующих сил
здесь 
— масса, а 
— проекция ускорения на ось х. После подстановки сюда вычисленных значений проекций сил, приведения подобных и сокращения на 
, это уравнение приобретает вид:
(6.14)
Подставим теперь вместо напряжений их выражения через скорости деформаций, пользуясь формулами (6.13) и (6.8) и считая μ=соnst. Тогда
и уравнение (6.14) после небольших преобразований принимает такой вид:
Применяя здесь операторы Δ и div
Поделив обе части равенства на ρ и приняв во внимание, что 
, представим уравнение движения в проекциях на ось х и аналогичные ему в проекциях на оси у и z в окончательном виде
(6.15)
Они называются уравнениями Навье-Стокса [6].
В заключение нужно отметить, что существует кроме зависимости (6.12) еще одна, которая может представлять давление в вязкой жидкости, а именно
Эта величина также не зависит от ориентации площадки, на которую рассматривается действие сил давления. Коэффициент μ’ называется второй вязкостью.
На формальную возможность такого представления давления указывали еще Стокс и Кирхгоф, однако физическое истолкование явление второй вязкости получило в 1937 году в работах Л.И.Мандельштама и М.А.Леонтовича. Вторая вязкость связана с явлениями неравновесности и проявляется в быстропротекающих процессах. Если в движущемся газе происходит очень быстрое изменение плотности, то наблюдается некоторое отставание в изменении других величин. Восстановление равновесия протекает с диссипацией энергии, т.е. с необратимым преобразованием части энергии в тепло. Таким образом, этот эффект аналогичен вязкости.
Если провести вывод уравнений Навье–Стокса, воспользовавшись формулой (6.16) вместо (6.12), то они принимают такой вид:
(6.17)
Нужно заметить, что в несжимаемой жидкости вторая вязкость не проявляется (divw=0), а в газах при сравнительно медленных процессах последний член в формуле (6.16) мал, поэтому в обычных случаях давление в вязкой жидкости определяют по формуле (6.12), а уравнения Навье — Стокса берут в форме (6.15).
«Дифференциальные уравнения газовой динамики, записанные в координатной форме, сложны, их вывод требует большого времени и большого количества бумаги. Значительно удобнее при их получении использовать векторную алгебру и самые начала тензорного анализа: тензорные обозначения и простейшие тензорные преобразования».
Кратко о гидродинамике: уравнения движения
Написав предыдущий пост, исторический и отчасти рекламный (хотя потенциальные абитуриенты такое вряд ли читают), можно перейти и к разговору «по существу». К сожалению, высокой степени популярности описания добиться вряд ли получится, но всё же постараюсь не устраивать курс сухих лекций. Хотя, от сухости избавиться не удалось, да и пост писался в результате ровно месяц.
В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.
Понятие сплошной среды
В, если можно так выразиться, «традиционной» гидродинамике, сложившейся исторически, фундаментом является модель сплошной среды. Она отвлекается от молекулярной структуры вещества, и описывает среду несколькими непрерывными полевыми величинами: плотностью, скоростью (определяемой через суммарный импульс молекул в заданном элементе объёма) и давлением. Модель сплошной среды предполагает, что в любом бесконечно малом объёме содержится ещё достаточно много частиц (как принято говорить, термодинамически много — числа, близкие по порядку величины к числу Авогадро — 10 23 шт.). Таким образом, модель ограничена снизу дискретностью молекулярной структуры жидкости, что в задачах типичных пространственных масштабов совершенно несущественно.
Однако, такой подход позволяет описать не только воду в пробирке или водоёме, и оказывается куда более универсальным. Поскольку наша Вселенная на больших масштабах практически однородна, то, как ни странно, она начиная с некоторого масштаба превосходно описывается как сплошная среда, с учётом, конечно же, самогравитации.
Другими, более приземлёнными применениями сплошной среды являются описание свойств упругих тел, динамики плазмы, сыпучих тел. Также можно описывать топлу людей как сжимаемую жидкость.
Параллельно с приближением сплошной среды, в последние годы набирает обороты кинетическая модель, основанная на дискретизации среды на небольшие частицы, взаимодействующие между собой (в простейшем случае — как твердые шарики, отталкивающиеся при столкновении). Такой подход возник в первую очередь благодаря развитию вычислительной техники, однако существенно новых результатов в чистую гидродинамику не превнёс, хотя оказался крайне полезен для задач физики плазмы, которая на микроуровне не является однородной, а содержит электроны и положительно заряженные ионы. Ну и опять же для моделирования Вселенной.
Уравнение неразрывности. Закон сохранения массы
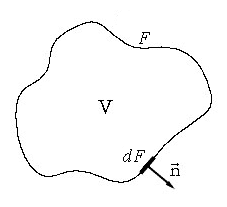
Самый элементарный закон. Пусть у нас есть какой-то совершенно произвольный, но макроскопический объём жидкости V, ограниченный поверхностью F (см. рис.). Масса жидкости внутри него определяется интегралом:
И пусть с жидкостью внутри него не происходит ничего, кроме движения. То есть, там нет химических реакций и фазовых переходов, нет трубок с насосами или чёрных дыр. Ну и всё происходит с маленькими скоростями и для малых масс вещества, потому никакой теории относительности, искривления пространства, самогравитации жидкости (она становится существенна на звёздных масштабах). И пусть сам объём и границы еего неподвижны. Тогда единственное, что может изменить массу жидкости в нашем объёме — это её перетекание через границу объёма (для определённости — пусть масса в объёме убывает):
где вектор j — поток вещества через границу. Точкой, напомним, обозначается скалярное произведение. Поскольку границы объёма, как было сказано, неподвижны, то производную по времени можно внести под интеграл. А правую часть можно преобразовать к такому же, как слева, интегралу по объёму по теореме Гаусса-Остроградского.
В итоге, в обеих частях равенства получается интеграл по одному и тому же совершенно произвольному объёму, что позволяет приравнять подинтегральные выражения и перейти к дифференциальной форме уравнения:
Здесь (и далее) использован векторный оператор Гамильтона. Образно говоря, это условный вектор, компоненты которого — операторы дифференцирования по соответствующим координатам. С его помощью можно очень кратко обозначать разного рода операции над скалярами, векторами, тензорами высших рангов и прочей математической нечистью, основные среди которых — градиент, дивергенция и ротор. Не буду останавливаться на них детально, поскольку это отвлекает от основной темы.
Наконец, поток вещества равен массе, переносимой через единичную площадку за единицу времени:
Окончательно, закон сохранения массы (называемый также уравнением неразрывности) для сплошной среды таков:
Это выражение наиболее общее, для среды, обладающей переменной плотностью. В реальности, эксперимент свидетельствует о крайне слабой сжимаемости жидкости и практически постоянном значении плотности, что с высокой точностью позволяет применять закон сохранения массы в виде условия несжимаемости:
которое с не менее хорошей точностью работает и для газов, пока скорость течения мала по сравнению со звуковой.
Уравнение Эйлера. Закон сохранения импульса
Весь относительно громоздкий процесс колдовства преобразования интегралов, использованный выше, даёт нам не только уравнение неразрывности. Точно такие же по сути преобразования позволяют выразить законы сохранения импульса и энергии, и получить в итоге уравнения для скорости жидкости и для переноса тепла в ней. Однако пока не будем сильно торопиться, и займёмся не просто сохранением импульса, а даже сохранением импульса в идеальной несжимаемой жидкости — т.е. рассмотрим модель с полным отсутствием вязкости.
Рассуждения практически те же самые, только теперь нас интересует не масса, а полный импульс жидкости в том же самом объёме V. Он равен:
При тех же самых условиях, что и выше, импульс в объёме может меняться за счёт:
- конвективного переноса — т.е. импульс «утекает» вместе со скоростью через границу
- давления окружающих элементов жидкости
- просто за счёт внешних сил, например — от силы тяжести.
Соответствующие интегралы (порядок отвечает списку) дают такое соотношение:
Начнём их преобразовывать. Правда, для этого нужно воспользоваться тензорным анализом и правилами работы с индексами. Конкретнее, к первому и второму интегралам применяется теорема Гаусса-Остроградского в обобщённой форме (она работает не только для векторных полей). И если перейти к дифференциальной форме уравнения, то получится следующее:
Крестик в кружочке обозначает тензорное произведение, в данном случае — векторов.
В принципе, это уже уравнение Эйлера, однако его можно чуток упростить — ведь закон сохранения массы никто не отменял. Раскрыв здесь скобки в дифференциальных операторах и приведя затем подобные слагаемые, мы увидим, что три слагаемых благополучно собираются в уравнение неразрывности, и потому дают в сумме ноль. Итоговое уравнение оказывается таким:
Если перейти в систему отсчёта, связанную с движущейся жидкостью (не будем заострять внимание на том, как это делается), мы увидим, что уравнение Эйлера выражает второй закон Ньютона для единицы объёма среды.
Учёт вязкости. Уравнение Навье-Стокса
Идеальная жидкость, это, конечно, хорошо (правда, всё равно точно не решается), но во многих случаях учёт вязкости необходим. Даже в той же конвекции, в течении жидкости по трубам. Без вязкости вода вытекала бы из наших кранов с космическими скоростями, а малейшая неоднородность температуры в воде приводила бы к её крайне быстрому и бурному перемешиванию. Потому давайте учтём сопротивление жидкости самой себе.
Дополнить уравнение Эйлера можно различными (но эквивалентными, конечно же) путями. Воспользуемся базовой техникой тензорного анализа — индексной формой записи уравнения. И пока также отбросим внешние силы, чтобы не путались под руками / под ногами / перед глазами (нужное подчеркнуть). При таком раскладе всё, кроме производной по времени, можно собрать в виде дивергенции одного такого тензора:
По смыслу, это плотность потока импульса в жидкости. К нему и нужно добавить вязкие силы в виде ещё одного тензорного слагаемого. Поскольку они явно приводят к потере энергии (и импульса), то они должны вычитаться:
Идя обратно в уравнение с таким тензором, мы получим обобщённое уравнение движения вязкой жидкости:
Оно допускает любой закон для вязкости.
Принято считать очевидным, что сопротивление зависит от скорости движения. Вязкость же, как перенос импульса между участками жидкости с различными скоростями, зависит от градиента скорости (но не от самой скорости — тому мешает принцип относительности). Если ограничиться разложением этой зависимости до линейных слагаемых, получится вот такой жутковатый объект:
в котором величина перед производной содержит 81 коэффициент. Однако, используя ряд совершенно разумных предположений об однородности и изотропности жидкости, от 81 коэффициента можно перейти всего к двум, и в общем случае для сжимаемой среды, тензор вязких напряжений равен:
где η (эта) — сдвиговая вязкость, а ζ (зета или дзета) — объёмная вязкость. Если же среда ещё и несжимаема, то достаточно одного коэффициента сдвиговой вязкости, т.к. второе слагаемое при этом уходит. Такой закон вязкости
носит название закона Навье, а полученное при его подстановке уравнение движения — это уравнение Навье-Стокса:
Точные решения
Главной проблемой гидродинамики является отсутствие точных решений её уравнений. Как бы с этим ни боролись, но получить действительно всеобщих результатов не удаётся до сих пор, и, напомню, вопрос существования и гладкости решений уравнений Навье-Стокса входит в список Проблем тысячелетия института Клэя.
Однако, несмотря на столь грустные факты, некоторые результаты есть. Здесь будут представлены далеко не все, а лишь самые простые случаи.
Потенциальные течения
Особый интерес представляют течения, в которых жидкость не завихряется. Для такой ситуации можно отказаться от рассмотрения векторного поля скорости, поскольку она выражается через градиент скалярной функции — потенциала. Потенциал же удовлетворяет хорошо изученному уравнению Лапласа, решение которого полностью определяется тем, что задано на границах рассматриваемой области:
Более того, при отсутствии вязкости из уравнения Эйлера можно однозначно выразить и давление, что вовсе замечательно и приводит нас к полному решению задачи. Ах, если бы так было всегда… то гидродинамики, наверное, уже бы и не было как современной и актуальной отрасли.
Дополнительно можно упростить задачу предположением, что течение жидкости двумерно — скажем, всё движется в плоскости (x,y), и ни одна частица не перемещается вдоль оси z. Можно показать, что в таком случае скорость может быть также заменена скалярной функцией (на этот раз — функцией тока):
которая при потенциальном течении удовлетворяет условиям Коши-Лагранжа из теории функций комплексной переменной и воспользоваться соответствующим математическим аппаратом. Полностью совпадающим с аппаратом электростатики. Теория потенциальных течений развита на высоком уровне, и в принципе хорошо описывает большой спектр задач.
Простые течения вязкой жидкости
Решения для вязкой жидкости чаще всего удаётся получить, когда из уравнения Навье-Стокса благодаря свойствам симметрии задачи выпадает нелинейное слагаемое.
Сдвиговое течение Куэтта
Самая элементарная задачка. Канал с неподвижной нижней и подвижной верхней стенкой, которая движется равномерно с некоторой скоростью. На границах жидкость прилипает к ним, так что скорость жидкости равна скорости границы. Этот результат является экспериментальным фактом, и как-то даже авторы первых экспериментов не упоминаются, просто — по совокупности экспериментов.
В такой ситуации от уравнения Навье-Стокса останется уравнение вида v» = 0, и потому профиль скорости в канале окажется линейным:
Данная задача является практически базовой для теории смазки, т.к. позволяет непосредственно определить силу, которую требуется приложить к верхней стенке для её движения с конкретной скоростью.
Течение Пуазейля
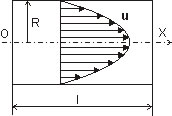
Вторая по элементарности — ламинарное течение в канале. Или в трубе. Результат оказывается один — профиль скорости является параболическим:
На основе решения Пуазейля можно определить расход жидкости через сечение канала, но, правда, только при ламинарном течении и гладких стенках. С другой стороны, для турбулентного потока и шероховатых стенок точных решений нет, а есть лишь приближённые эмпирические закономерности.
Стекание слоя жидкости по наклонной плоскости
Тут — почти как в задаче Пуазейля, только верхняя граница жидкости будет свободной. Если предположить, что по ней не бегут никакие волны, и вообще сверху нет трения, то профиль скорости будет практически нижней половинкой предыдущего рисунка. Правда, если из полученной зависимости вычислить скорость течения для средней равнинной речки, она составит около 10 км/с, и вода должна самопроизвольно отправляться в космос. Наблюдаемые в природе низкие скорости течения связаны с развитой завихренностью и турбулентностью потока, которые эффективно увеличивают вязкость воды примерно в 1 млн. раз.
В следующем посте планируется рассказать о законе сохранения энергии и соответствующих ему уравнениях переноса тепла при течении жидкости.
http://lektsii.org/1-21881.html
http://habr.com/ru/post/171327/