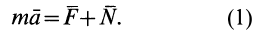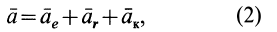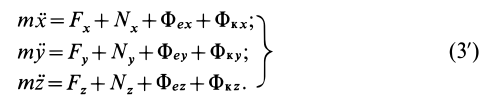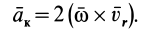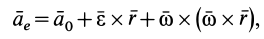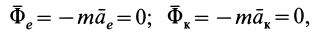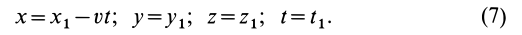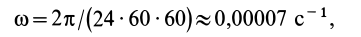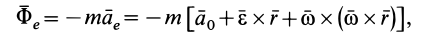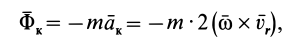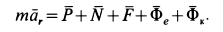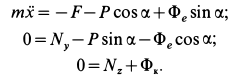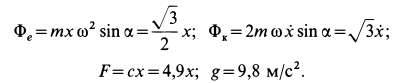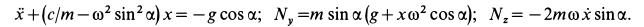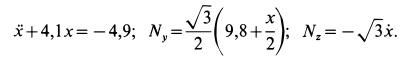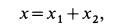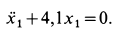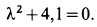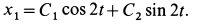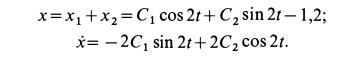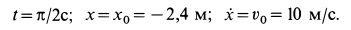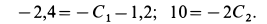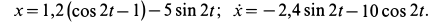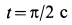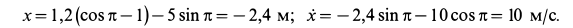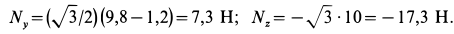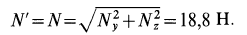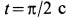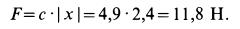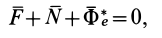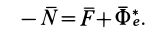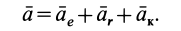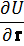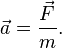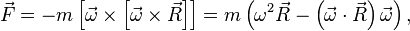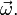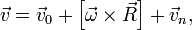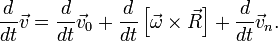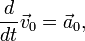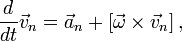Относительное движение материальной точки в теоретической механике
Содержание:
Относительное движение материальной точки:
Во многих задачах динамики рассматривается движение материальной точки относительно системы отсчета, движущейся относительно инерциальной системы. Дифференциальные уравнения движения материальной точки относительно таких подвижных, в общем случае неинерциальных, систем отсчета получают из уравнений движения точки относительно инерциальной системы отсчета и кинематической теоремы Кориолиса о сложении ускорений.
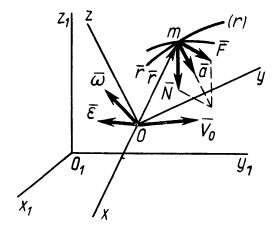
Имеем инерциальную систему отсчета
Рис. 14
Если ввести другую, неинерциальную, систему отсчета 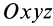
где 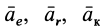
Подставляя значение абсолютного ускорения 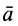
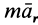
где 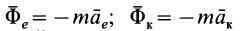
Силы инерции 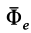
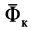
Если координаты движущейся точки относительно подвижной системы координат 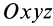
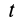
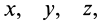
Это дифференциальные уравнения движения точки относительно подвижной системы координат в проекциях на декартовы подвижные оси координат. Они отличаются от дифференциальных уравнений абсолютного движения относительно инерциальной системы отсчета только наличием поправок на неинерциальность системы отсчета.
Относительное движение по инерции
Если материальная точка движется относительно подвижной системы отсчета прямолинейно и равномерно, то такое движение называют относительным движением по инерции. В этом случае относительная скорость 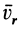
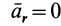
Это условие для сил при относительном движении точки по инерции.
Относительное равновесие
При покое материальной точки относительно подвижной системы отсчета ее относительные скорость и ускорение равны нулю, т. е. 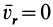
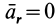
Из (3) получаем условие относительного равновесия для сил:
При абсолютном движении по инерции или абсолютном равновесии относительно инерциальной системы отсчета имеем для сил одно и то же условие 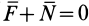
Инерциальные системы отсчета
Переносное ускорение в общем случае вычисляется по формуле
где 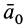
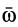
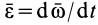
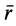
Пусть подвижная система отсчета все время движется относительно основной инерциальной системы поступательно, равномерно и прямолинейно. В этом случае переносная и кориолисова силы инерции равны нулю, т. е.
так как при поступательном движении 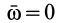
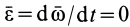
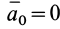
которое совпадает с уравнением движения относительно инерциальной системы отсчета (1).
Все подвижные системы отсчета, которые движутся поступательно, равномерно и прямолинейно относительно основной инерциальной системы отсчета, называются тоже инерциальными. Относительно всех инерциальных систем отсчета получаются одинаковые уравнения движения материальной точки. Ускорения материальной точки относительно всех инерциальных систем отсчета одинаковы.
Отсутствие принципиальной возможности каким-либо механическим опытом, основанным на наблюдении за движением материальных тел, отличить одну инерциальную систему отсчета от другой находится в основе принципа относительности классической механики — принципа Галилея — Ньютона, который утверждает: все механические явления в различных инерциальных системах отсчета протекают одинаково, или никаким механическим опытом нельзя обнаружить инерциальное движение системы отсчета, участвуя вместе с ней в этом движении. Наоборот, неинерциальную систему отсчета можно обнаружить и отличить одну от другой по поправкам на неинерциальность.
Скорости материальной точки относительно различных инерциальных систем отсчета разные, но нет возможности из наблюдений за движением материальной точки в различных системах отсчета сделать утверждение, какая из инерциальных систем отсчета является основной, неподвижной, а какая — подвижной.
В специальной теории относительности имеет место принцип относительности Эйнштейна, который утверждает: все физические явления во всех инерциальных системах отсчета протекают одинаково. Физические явления кроме механических включают также электромагнитные процессы.
Рис. 15
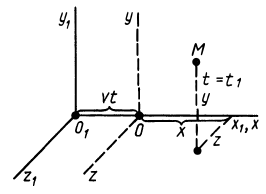
Возьмем две инерциальные системы отсчета: 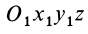
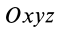
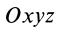
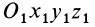
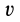
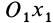
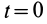
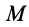
Эти соотношения называются преобразованиями Галилея в частном случае движения двух инерциальных систем отсчета друг относительно друга.
Преобразования Галилея не изменяют формы уравнения движения точки (1), т. е. оно инвариантно по отношению к преобразованиям Галилея.
Движение точки относительно земли
Для неинерциальной системы отсчета уравнение движения материальной точки под действием силы отличается от уравнения движения относительно инерциальных систем отсчета. Согласно (3), оно имеет форму
Наличие поправок на неинерциальность систем отсчета в виде сил инерции 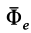
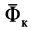
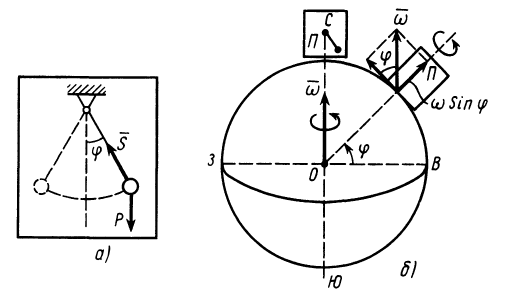
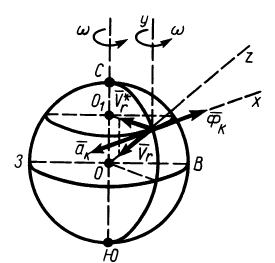
Система отсчета, скрепленная с земным шаром, не является инерциальной. Земной шар движется относительно гелиоцентрической инерциальной системы отсчета. При рассмотрении движения материальных тел относительно Земли должны проявлять себя эффекты, связанные с неинерциальностью системы отсчета. Земной шар движется относительно гелиоцентрической системы отсчета как свободное твердое тело. Его центр перемещается по эллиптической орбите, близкой к окружности. Кроме того, он вращается вокруг оси, проходящей через его центр, с почти постоянной по модулю и направлению угловой скоростью, совершая один оборот за сутки. Угловая скорость вращения Земли
т. е. величина малая по сравнению с единицей.
В общем случае переносная сила инерции
где 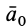
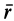
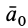
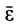
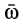
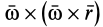
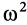
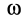
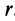
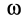
где 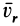
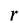
Маятник Фуко
Если подвесить на длинной нити груз достаточно малых размеров, то действующая на него сила 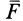
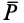
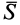
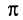
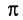
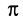
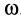
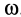
Рис. 16
Рис. 17
Если тело маятника имеет выступ, который при колебаниях может оставлять след, например на песке, то этот след при движении маятника в одну сторону будет отличаться от следа при движении в противоположную сторону из-за вращения Земли. Это отличие тем больше, чем длиннее нить маятника. Фуко в 1857 г. использовал маятник длиной 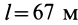
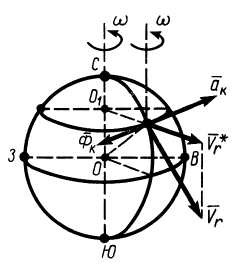
Отклонение движущихся тел вправо в Северном полушарии
В Северном полушарии из-за дополнительного действия силы инерции Кориолиса, вызванной вращением Земли, все движущиеся тела должны смещаться в правую сторону, если смотреть в направлении движения. Пусть материальная точка движется со скоростью 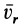
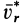
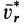
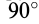
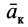
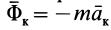
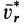
Если рассмотреть поступательное движение железнодорожного вагона, то для него сила инерции Кориолиса пройдет через центр его тяжести слева направо, если смотреть по движению вагона. Это приведет к увеличению давления на правый рельс и к его уменьшению на левый. На двухколейных железных дорогах правый рельс изнашивается быстрее левого.
Для частички воды в реке действие силы Кориолиса слева направо, если смотреть по течению реки, приведет к прижиманию этой частички к правому берегу, способствуя большему его подмыванию. Правый берег рек в Северном полушарии более подмыт, чем левый на прямолинейных участках реки. Этот эффект известен в географии как закон Бэра. На закруглениях реки вследствие центробежных сил инерции может оказаться подмытым и левый берег.
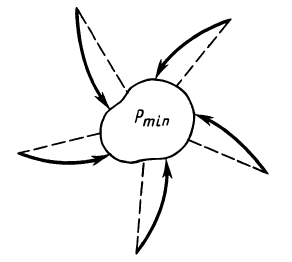
Действие силы инерции Кориолиса на летящие самолеты, ракеты, снаряды, движущийся воздух, морские течения приводит к их отклонению в правую сторону в Северном полушарии. В Южном полушарии отклонение будет в левую сторону. Сила инерции Кориолиса способствует образованию циклонов, антициклонов, вихрей, смерчей и т. д. Если в каком-то месте образовалось пониженное давление, например вследствие местного нагревания воздуха, то к этому месту начнет двигаться воздух из мест с повышенным давлением. Сила инерции Кориолиса отклонит движущиеся частички воздуха вправо, создав местный вихрь (рис. 18), а для больших масс воздуха— циклон. Аналогично, в местах с повышенным давлением образуются антициклоны.
Отклонение падающих тел к востоку
Рассмотрим в Северном полушарии тело, падающее вертикально вниз под действием силы тяжести без начальной скорости. Действие силы инерции Кориолиса в этом случае в первом приближении сведется к отклонению падающего тела к востоку. Действительно, если скорость тела 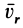
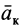
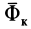
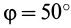
Пример:
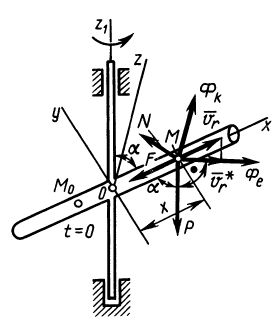
Внутри трубки, имеющей гладкую поверхность, находится шарик массой 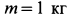
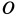
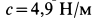
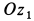
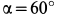
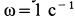
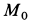
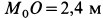
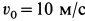
Определить закон движения шарика по трубке, принимая его за точку; силу давления шарика на стенку трубки и силу притяжения в момент времени 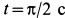
Решение:
Выберем систему подвижных осей координат 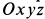
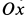
Векторное уравнение движения шарика относительно подвижной системы координат имеет вид
В проекциях на подвижные оси координат
Здесь 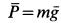
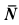
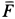
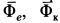
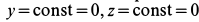
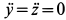
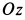
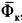
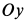
Подставляя эти значения сначала в общем виде в уравнения движения, после простых преобразований получаем:
После подстановки числовых значений величин имеем
Дифференциальное уравнение является линейным неоднородным; следовательно, его решение
где 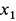
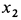
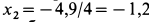
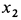
Общее решение однородного уравнения 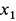
Его характеристическое уравнение
Корни характеристического уравнения 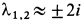
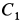
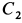
Начальные условия задачи
Подставляя их в выражения для 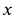
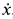
Их решения 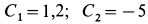
Уравнения движения шарика с учетом значений постоянных принимает вид
В момент времени
Подставляя эти значения 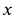
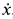
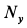
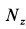
Давление шарика 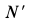
Сила притяжения 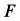
Невесомость
Динамическая теорема Кориолиса позволяет рассмотреть состояние невесомости, которое, в частности, возникает при движении космических кораблей как искусственных спутников Земли. При рассмотрении невесомости материальной точки целесообразно ее представлять как твердое тело, имеющее поверхность, которой оно может соприкасаться с другими телами. Будем предполагать, что скорости и ускорения всех точек тела одинаковы, а реакции соприкасающихся тел приводятся к равнодействующей.
Под невесомостью такой материальной точки понимают отсутствие давления этой точки на каждое из тел, с которым она может соприкасаться. В частности, невесомая материальная точка не давит на площадку весов (не имеет веса), находящихся в покое по отношению к той системе отсчета, относительно которой покоится материальная точка.
Систему отсчета, относительно которой материальная точка находится в покое и, следовательно, имеет относительно нее скорость и ускорение, равные нулю, назовем собственной системой отсчета материальной точки. Все величины относительно этой системы отсчета условимся обозначать специальным индексом 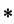
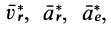
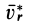
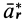
Невесомая материальная точка (тело), прикрепленная на пружине к любому телу, покоящемуся относительно ее собственной системы отсчета, не деформирует эту пружину. Учитывая, что давление точки на какое-либо тело по модулю совпадает с силой реакции тела на эту точку, невесомость наблюдается при равенстве нулю силы реакции от любого тела, соприкасающегося с рассматриваемой невесомой материальной точкой.
Если в общем случае рассматривать невесомость материального тела, а не точки, то реакции окружающих его тел сведутся к распределенным силам по поверхности его соприкосновения с этими телами. Сила реакции, отнесенная к единице площади поверхности соприкосновения (напряжение силы реакции), должна при невесомости тела быть равна нулю в каждой точке его поверхности. Это является условием невесомости для любого тела, не обязательно твердого.
Для абсолютно твердого тела при его невесомости вместо равенства нулю напряжения поверхностной силы в каждой точке его поверхности соприкосновения достаточно равенства нулю главного вектора и главного момента этих сил относительно любого центра приведения.
Ограничимся рассмотрением невесомости материальной точки, т. е. абсолютно твердого тела, для которого все поверхностные силы приводятся только к одной равнодействующей силе — реакции тел, соприкасающихся с ним. Невесомость материальной точки не связана с системой отсчета или с наблюдателем, находящимся в той или иной системе отсчета. Но для выявления сил, действие которых испытывает материальная точка, выберем ее собственную систему отсчета, по отношению к которой ее относительные скорость и ускорение равны нулю, т. е. 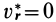
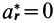
где 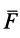
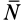
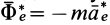
Из условия относительного равновесия сил имеем
Согласно определению невесомости, 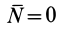
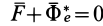
Таким образом, условие невесомости через силы можно выразить как 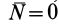
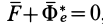
Согласно теореме о сложении ускорений, абсолютное ускорение в общем случае определяется по формуле
Если абсолютное ускорение рассматривать относительно инерциальной системы отсчета, а в качестве подвижной системы отсчета выбрать собственную систему отсчета, то 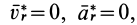
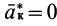
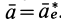
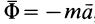
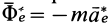
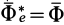
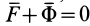
Проверим выполнение условия невесомости для материальной точки, находящейся в космическом корабле, который движется поступательно относительно Земли в качестве ее искусственного спутника за пределами атмосферы. За инерциальную систему отсчета можно принять систему отсчета, скрепленную с Землей.
Пусть материальная точка неподвижна относительно космического корабля. Тогда собственной системой отсчета будет система отсчета, скрепленная с кораблем. Силой от действия тел, не соприкасающихся с точкой, является сила тяготения Земли 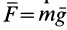
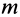
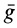
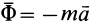
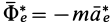
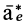
Если корабль не испытывает действия других сил, кроме силы тяготения Земли, то его ускорение от этого тяготения тоже равно 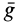
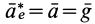
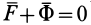
В космическом корабле, который кроме поступательного движения имеет также и вращение, каждая из материальных частиц корабля не находится в состоянии невесомости, хотя весь корабль как целое находится в состоянии невесомости. Для него главный вектор и главный момент поверхностных сил равны нулю, так как нет тел, с которыми корабль соприкасается своей поверхностью.
Материальная точка внутри кабины корабля находится в состоянии невесомости, пока она не соприкасается со стенками корабля и с другими телами, скрепленными с кораблем.
Кажется, что для невесомости тела необходима невесомость каждой его точки. Это приводит к требованию отсутствия взаимных давлений между точками тела или к отсутствию внутренних напряжений в теле. Но такие напряжения всегда имеются при невесомости вследствие естественной связи точек тела друг с другом, на которую можно влиять, например, термообработкой, изменением температуры и т. д. При невесомости тела как целого не обязательно отсутствие даже дополнительных напряжений, создаваемых движением тела. Достаточно равенства нулю напряжений в точках поверхности тела, создаваемых другими, соприкасающимися телами (связями), а для абсолютно твердого тела — равенства нулю главного вектора и главного момента поверхностных сил.
В невесомости находятся земной шар и другие планеты Солнечной системы, их спутники, если пренебречь действием на них метеоритов, космического излучения и т. д.
В состоянии невесомости находилось бы свободно падающее тело вблизи Земли, если бы не было действия воздуха. Невесомость можно создать искусственно вблизи Земли в герметизированной кабине летательного аппарата, заставив его с помощью двигателей совершать поступательное движение с ускорением 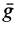
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Геометрия масс
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Неинерциальные системы отсчета
Ни для кого не секрет, что законы Ньютона могут быть выполнены лишь в инерциальных системах отсчета.
Системы отсчета, совершающие ускоренное движение относительно инерциальной системы, носят название неинерциальных.
В таких системах законы Ньютона применяться не могут. Несмотря на это, законы динамики можно использовать и в условиях подобных систем в случае, если, кроме обусловленных взаимным воздействием тел друг на друга сил, будет введено понятие силы инерции.
С учетом сил инерции второй закон Ньютона будет справедлив для любой системы отсчета: произведение массы тела на ускорение в рассматриваемой системе отсчета эквивалентно совокупности всех оказывающих воздействие на данное тело сил F , в список которых включены и инерционные.
Наряду с этим, силы инерции F i n должны быть такими, чтобы в сумме с силами F они придавали движению приведенного объекта ускорение a ′ , которым оно обладает в неинерциальных системах отсчета, таким образом:
По причине того, что F = m a , где a является ускорением тела в инерциальной системе отсчета.
Силы инерции вызваны ускоренным движением системы отсчета относительно исследуемой системы, из-за чего, в общем случае, стоит учитывать следующие варианты возникновения данных сил:
- Силы инерции в условиях ускоренного поступательного движения системы отсчета.
- Силы инерции, оказывающие воздействие на тело, покоящееся во вращающейся системе отсчета.
- Силы инерции, действующие на движущееся во вращающейся системе отсчета тело.
Рассмотрим приведенные случаи.
Силы инерции в условиях ускоренного поступательного движения системы отсчета
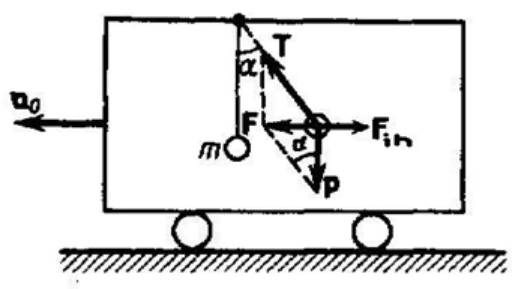
К расположенному на тележке штативу с помощью нити подвешен шарик с некоторой массой m (рис. 1 ). Во время того, как тележка покоится или движется прямолинейно и равномерно, удерживающая шарик нить, находится в вертикальном положении, а сила тяжести P компенсируется силой натяжения нити T .
В условиях, в которых тележка обладает ускорением a 0 , нить будет отклоняться от вертикали в обратную по отношению к направлению движения сторону до некоторого угла a до тех пор, пока результирующая сила F = P + T не приведет ускорение шарика к ускорению, равному a 0 . Таким образом, результирующая сила F сонаправлена с ускорением тележки a 0 и для установившегося движения шарика (так как теперь он движется вместе с тележкой с ускорением a 0 ) эквивалентна F = m g · t g α = m a 0 , соответственно t g a = a 0 g . Выходит, что угол отклонения нити от вертикали тем больше, чем выше значение ускорения тележки. В системе отсчета, которая связана с ускоренно движущейся тележкой, шарик находится в состоянии покоя. Такое становится возможным, если сила F компенсируется равной и противоположно направленной ей силой F i n , представляющей собой силу инерции, так как действия на шарик каких-либо других сил эффекта не возымеют.
Следовательно: F i n = — m a 0 .
Силы инерции, оказывающие воздействие на тело, покоящееся во вращающейся системе отсчета
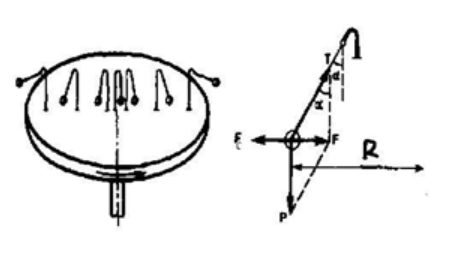
Пускай диск равномерно вращается с угловой скоростью ω ( ω = c o n s t ) вокруг ортогональной (то есть перпендикулярной) ему оси, проходящей через его центр. На диске расположены маятники, на различных расстояниях от оси вращения и на нитях прикреплены шарики массой m . Во время вращения диска, шарики отклоняются от вертикали на некоторый угол (рис. 2 ).
В инерциальной системе отсчета, связанной, к примеру, с помещением, в котором расположен диск, происходит равномерное вращательное движение шарика по окружности с радиусом R . Следовательно, на него оказывает воздействие сила, эквивалентная F = m ω 2 R и направленная ортогонально оси вращения диска. Она представляет собой равнодействующую сил тяжести и натяжения нити T : F = P + T . В момент, когда движение шарика установится, F = m g · t g a = m ω 2 R , соответственно: t g α = ω 2 R g . Таким образом, углы отклонения нитей маятников будут тем больше, чем больше величины угловой скорости вращения и расстояния R от центра шарика до оси вращения диска. Относительно системы отсчета, связанной с вращающимся диском, шарик покоится, что возможно лишь в том случае, если сила F будет скомпенсирована равной и противоположно направленной ей силой F c , представляющей собой силу инерции, так как действия на шарик каких-либо других сил эффекта не возымеют. Сила F c , носящая название центробежной силы инерции, направлена по горизонтали от оси вращения диска и равняется:
F c = — m a 0 ω 2 R .
Исходя из формулы, расположенной выше, можно заключить, что центробежная сила инерции, воздействующая на тела во вращающихся системах отсчета и направленная в сторону радиуса от оси вращения, обладает зависимостью от угловой скорости вращения ω системы отсчета и радиуса R , однако не имеет зависимости от скорости тела относительно вращающихся систем отсчета. Таким образом, центробежная сила инерции во вращающихся системах отсчета оказывает влияние на любые удаленные от оси вращения на конечное расстояние объекты. При данном условии не имеет значения, покоятся ли они в подобной системе отсчета, как нами предполагалось до этих пор, или совершают движение относительно нее с некоторой скоростью.
Силы инерции, действующие на движущееся во вращающейся системе отсчета тело
Пускай шарик массой m совершает движение в условиях постоянной скорости υ ‘ вдоль радиуса равномерно вращающегося диска
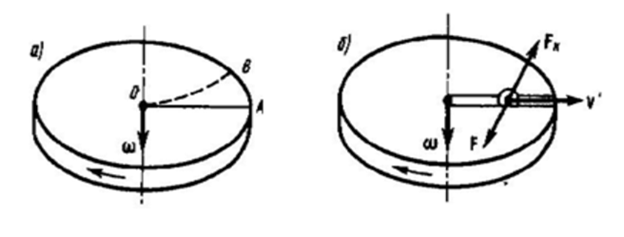
( υ ‘ = c o n s t , ω = c o n s t , υ ‘ ортогонально ω ). В случае, если диск не начинает вращательное движение, шарик перемещается по радиальной прямой и попадает в точку А . Если же диск приводится во вращение в указанном стрелкой направлении, то шарик катится по кривой O В (рис. 3 а ), при этом относительно диска его скорость υ ‘ меняет свое направление. Такое возможно только в том случае, если на шарик оказывает влияние сила, перпендикулярная скорости υ ‘ .
Чтобы спровоцировать качение шарика по вращательно двигающемуся диску вдоль радиуса, будем применять жестко укрепленный вдоль него стержень, на котором шарик движется без трения прямолинейно и равномерно со скоростью υ ‘ (рис. 3 б ).
В случае отклонения шарика стержень воздействует на него некоторой силой F . Шарик совершает прямолинейное равномерное движение во вращающейся системе отсчета, то есть относительно диска. Данный факт основывается на том, что сила F компенсируется приложенной к шарику силой инерции F k , ортогональной скорости υ ‘ . Такая сила является кориолисовой силой инерции. Можно сказать, что вектор силы Кориолиса F k направлен под прямым углом к векторам скорости υ ‘ объекта и угловой скорости вращения системы отсчета в соответствии с правилом правого винта.
Давайте рассмотрим пример движения тела в одном из видов неинерциальных систем отсчета. Объект находится в покое на вершине наклонной плоскости.
По прошествии какого времени тело соскользнет с поверхности, если она в момент времени е = 0 начнет движение влево в горизонтальном направлении с ускорением с 1 м / с 2 ?
Длина плоскости 1 м , угол наклона плоскости по отношению к горизонту 30 ° , коэффициент трения между телом и плоскостью 0 , 6 .
Необходимо высчитать время движения тела по наклонной плоскости.
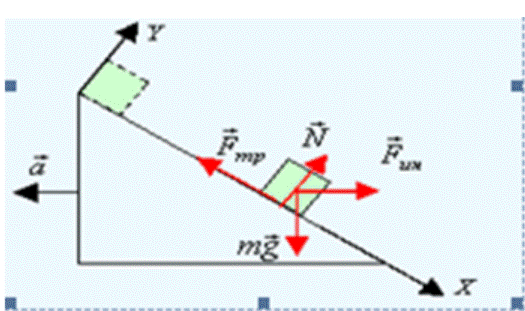
Систему отсчета будет удобно связать с наклонной плоскостью. Однако плоскость по отношению к Земле находится в состоянии ускоренного движения. Для данного движения Земля представляет собой инерциальную систему отсчета. Выходит, что связанная с наклонной плоскостью система отсчета считается, напротив, неинерциальной, и в уравнение движения тела нужно добавить поступательную силу инерции. На двигающееся тело в связанной с наклонной плоскостью системе отсчета влияют четыре силы: сила тяжести m g , сила нормальной реакции N , сила трения F т р и поступательная сила инерции F ¯ i n = — m a ¯ .
Уравнение движения тела выглядит следующим образом:
m a 1 ¯ = m g ¯ + N ¯ + F ¯ т р + F ¯ i n , где a 1 ¯ — ускорение тела.
Спроецируем это уравнение на ось X , направленную вдоль наклонной плоскости, и ортогональную к ней ось Y .
m a 1 = m g · sin α — F т р + m a · cos α , 0 = — m g · cos α + N + m a · sin α .
Если учитывать, что F т р = μ N , из этой системы уравнений получим:
a 1 = g ( sin α — μ cos α ) + a ( cos α + μ sin α ) .
По причине того, что ускорение a 1 не обладает зависимостью от времени, время движения тела по наклонной плоскости будет равняться:
t = 2 l a 1 = 2 l g ( sin α — μ cos α ) + a ( cos α + μ sin α ) ≈ 0 , 8 с
ДВИЖЕНИЕ В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ ОТСЧЕТА
Страница 1 из 2
До сих пор, рассматривая движение любой механической системы, мы всегда относили его к инерциальной системе отсчета. Только в инерциальных системах отсчета функция Лагранжа, например, одной частицы во внешнем поле имеет вид
L0 = 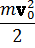
и соответственно уравнение движения
m 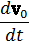
(мы будем в этом параграфе отличать индексом 0 величины, относящиеся к инерциальной системе отсчета).
Займемся теперь вопросом о том, как выглядят уравнения движения частицы в неинерциальной системе отсчета. Отправным пунктом при решении этого вопроса снова является принцип наименьшего действия, применимость которого не ограничена никаким выбором системы отсчета; вместе с ним остаются в силе и уравнения Лагранжа
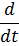
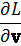
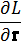
Однако функция Лагранжа уже не имеет вида (39.1), и для ее нахождения необходимо произвести соответствующее преобразование функции L0.
Это преобразование мы произведем в два приема. Рассмотрим сначала систему отсчета K’, которая движется относительно инерциальной системы K0 поступательно со скоростью V(t). Скорости v0 и v‘ частицы относительно систем K0 и K’ связаны друг с другом соотношением
v0 = v‘ + V(t). (39.3)
Подставив это выражение в (39.1), получим функцию Лагранжа в системе K’
L’ = 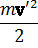
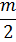
Но V 2 (t) есть заданная функция времени; она может быть представлена как полная производная по t от некоторой другой функции, и потому третий член в написанном выражении может быть опущен. Далее, v‘=dr‘/dt, где r‘ — радиус-вектор частицы в системе координат K’; поэтому
mV(t)v‘ = mV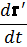
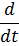
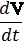
Подставив это в функцию Лагранжа и снова опустив полную производную по времени, получим окончательно:
L’ = 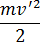
где W=dV/dt — ускорение поступательного движения системы отсчета K’.
Составляя с помощью (39.4) уравнение Лагранжа, получим
m 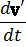
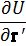
Мы видим, что в смысле своего влияния на уравнения движения частицы ускоренное поступательное движение системы отсчета эквивалентно появлению однородного силового поля, причем действующая в этом поле сила равна произведению массы частицы на ускорение W и направлена в противоположную этому ускорению сторону.
Введем теперь еще одну систему отсчета, K, которая имеет общее с системой K’ начало, но вращается относительно нее с угловой скоростьюΩ(t); по отношению же к инерциальной системе K0 система K совершает как поступательное, так и вращательное движение.
Скорость v‘ частицы относительно системы K’ складывается из ее скорости v относительно системы K и скорости [Ωr] ее вращения вместе с системой K:
v‘ = v + [Ωr]
(радиус-векторы r и r‘ частицы в системах K иK’‘ совпадают). Подставив это выражение в функцию Лагранжа (39.4), получим
L = 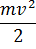
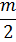
Это есть общий вид функции Лагранжа частицы в произвольной неинерциальной системе отсчета. Отметим, что вращение системы отсчета приводит к появлению в функции Лагранжа члена совершенно особого вида — линейного по скорости частицы.
В классической механике представления о силах и их свойствах основываются на законах Ньютона и неразрывно связаны с понятием инерциальная система отсчёта.
Действительно, физическая величина, называемая силой, вводится в рассмотрение вторым законом Ньютона, при этом сам закон формулируется только для инерциальных систем отсчёта [17] . Соответственно, понятие силы оказывается определённым только для таких систем отсчёта [18] .
Уравнение второго закона Ньютона, связывающее ускорение 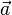
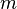
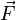
Из уравнения непосредственно следует, что причиной ускорения тел являются только силы, и наоборот: действие на тело не скомпенсированных сил обязательно вызывает его ускорение.
Третий закон Ньютона дополняет и развивает сказанное о силах во втором законе.
Учёт содержания всех законов Ньютона приводит к заключению о том, что силы, о которых идёт речь в классической механике, обладают неотъемлемыми свойствами:
· сила есть мера механического действия на данное материальное тело других тел. [19]
· в соответствии с третьим законом Ньютона силы способны существовать лишь попарно, при этом природа сил в каждой такой паре одинакова [20][21] .
· любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, силы обязательно представляют собой результатвзаимодействия тел [22] .
Никакие другие силы в классической механике в рассмотрение не вводятся и не используются [18][23] . Возможность существования сил, возникших самостоятельно, без взаимодействующих тел, механикой не допускается [22][24] .
Хотя в наименованиях эйлеровых и даламберовых сил инерции содержится слово сила, эти физические величины силами в смысле, принятом в механике, не являются
Ньютоновы силы инерции[править | править вики-текст]
Некоторые авторы используют термин «сила инерции» для обозначения силы-противодействия из третьего закона Ньютона. Понятие было введено Ньютоном в его«Математических началах натуральной философии» [26] : «Врождённая сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает свое состояние покоя или равномерного прямолинейного движения. От инерции материи происходит, что всякое тело лишь с трудом выводится из своего покоя или движения. Поэтому врожденная сила могла бы быть весьма вразумительно названа силою инерции. Эта сила проявляется телом единственно лишь, когда другая сила, к нему приложенная, производит изменение в его состоянии. Проявление этой силы может быть рассматриваемо двояко — и как сопротивление, и как напор.», а собственно термин «сила инерции» был, по словам Эйлера, впервые употреблён в этом значенииКеплером( [26] , со ссылкой на Е. Л. Николаи).
Для обозначения этой силы-противодействия некоторые авторы предлагают использовать термин «ньютонова сила инерции» во избежание путаницы с фиктивными силами, применяемыми при вычислениях в неинерциальных системах отсчёта и при использовании принципа д’Аламбера.
Отголоском ньютоновского выбора слова «сопротивление» для описания инерции является также представление о некоей силе, якобы реализующей это свойство в форме сопротивления изменениям параметров движения. В связи с этим Максвелл заметил, что с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким, так как сладким он становится не сам по себе, а лишь после добавления сахара [26] .
Существование инерциальных систем отсчёта[править | править вики-текст]
Ньютон исходил из предположения, что инерциальные системы отсчёта существуют и среди этих систем существует наиболее предпочтительная (сам Ньютон связывал её с эфиром, заполняющим всё пространство). Дальнейшее развитие физики показало, что такой системы нет, но это привело к необходимости выйти за пределы классической физики.
Движение в инерциальной СО[править | править вики-текст]
Выполнив тривиальную математическую операцию в выражении третьего закона Ньютона (5) и перенеся член из правой части в левую, получаем безупречную математически запись:
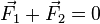
С физической точки зрения, сложение векторов сил имеет своим результатом получение равнодействующей силы.
В таком случае, прочтённое с точки зрения второго закона Ньютона выражение (6) означает, с одной стороны, что равнодействующая сил равна нулю и, следовательно, система из этих двух тел не двигается ускоренно. С другой стороны, здесь не высказаны никакие запреты на ускоренное движение самих тел.
Дело в том, что понятие о равнодействующей возникает лишь в случае оценки совместного действия нескольких сил на одно и то же тело. В данном же случае, хотя силы равны по модулю и противоположны по направлению, но приложены к разным телам и потому, касательно каждого из рассматриваемых тел по отдельности, не уравновешивают друг друга, поскольку на каждое из взаимодействующих тел действует лишь одна из них. Равенство (6) не указывает на взаимную нейтрализацию их действия для каждого из тел, оно говорит о системе в целом. [26][27]
Рис.1 Материальная точка в двух декартовых системах координат: неподвижной O, считающейся инерциальной, и подвижной O’
Повсеместно используется запись уравнения, выражающего второй закон Ньютона в инерциальной системе отсчёта:
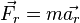
Если 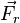
Но выражение (7) может быть, подобно (6), переписано в виде:
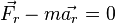
Для постороннего наблюдателя, находящегося в инерциальной системе и анализирующего ускорение тела, на основании сказанного выше такая запись имеет физический смысл только в том случае, если члены в левой части равенства относятся к силам, возникающим одновременно, но относящимся к разным телам. И в (8) второй член слева представляет собой такую же по величине силу, но направленную в противоположную сторону и приложенную к другому телу, а именно силу 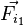
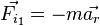
В случае, когда оказывается целесообразным разделение взаимодействующих тел на ускоряемое и ускоряющее и, чтобы отличить действующие тогда на основании Третьего закона силы, те из них, которые действуют со стороны ускоряемого тела на ускоряющее, называют силами инерции 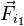
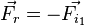
Существенно, что сила действия ускоряющего тела на ускоряемое и сила инерции имеют одно и то же происхождение и, если массы взаимодействующих тел близки друг другу настолько, что и получаемые ими ускорения сравнимы по величине, то введение особого наименования «сила инерции» является лишь следствием достигнутой договорённости. Оно так же условно, как и само деление сил на действие и противодействие.
Иначе обстоит дело, когда массы взаимодействующих тел несравнимы между собой (человек и твёрдый пол, отталкиваясь от которого, он идёт). В этом случае деление тел на ускоряющие и ускоряемые становится вполне отчётливым, а ускоряющее тело может рассматриваться как механическая связь, ускоряющая тело, но не ускоряемая сама по себе
Центробе́жная си́ла [1] — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюся неинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил.
Зачастую это бывает удобно. Например, когда вращается целиком вся лаборатория, может быть более удобным рассматривать все движения относительно нее, введя лишь дополнительно силы инерции, в том числе центробежную, действующие на все материальные точки, чем учитывать постоянное изменение положения каждой точки относительно инерциальной системы отсчета.
Часто, особенно в технической литературе, во вращающуюся с телом неинерциальную систему отсчёта переходят неявно, и говорят о проявлениях закона инерции как о центробежной силе, действующей со стороны движущегося по круговой траектории тела на вызывающие это вращение связи, и считают её по определению равной по модулю центростремительной силе и всегда направленной в противоположную ей сторону.
Однако в общем случае, когда мгновенный центр поворота тела по дуге окружности, которой аппроксимируется траектория в каждой её точке, может не совпадать с началом вектора силы, вызывающей движение, неверно называть действующую на связь силу силой центробежной. Ведь есть ещё составляющая силы связи, направленная по касательной к траектории, и эта составляющая будет изменять скорость движения тела по ней. Поэтому некоторые физики вообще избегают использовать термин «центробежная сила», как ненужный
Формулы[править | править вики-текст]
Обычно понятие центробежной силы используется в рамках классической (Ньютоновской) механики, которой касается основная часть данной статьи (хотя обобщение этого понятия и может быть в некоторых случаях достаточно легко получено для релятивистской механики).
По определению, центробежной силой называется сила инерции (то есть в общем случае — часть полной силы инерции) в неинерциальной системе отсчета, не зависящая от скорости движения материальной точки в этой системе отсчета, а также не зависящая от ускорений (линейных или угловых) самой этой системы отсчета относительно инерциальной системы отсчета.
Для материальной точки центробежная сила выражается формулой:
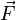
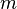
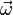
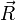
Эквивалентное выражение для центробежной силы можно записать как
если использовать обозначение 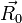
Центробежная сила для тел конечных размеров может быть рассчитана (как это обычно делается и для любых других сил) суммированием центробежных сил, действующих на материальные точки, являющиеся элементами, на которые мы мысленно разбиваем конечное тело.
Вывод[править | править вики-текст]
Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью 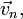
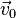
Тогда линейная скорость тела в инерциальной системе координат равна:
где 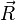
Найдём значение каждого слагаемого в инерциальной системе координат:
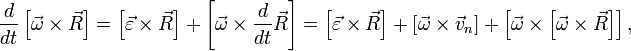
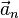
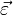
Таким образом, получаем:
Последнее слагаемое и будет центростремительным ускорением.
Раскрыв двойное векторное произведение и положив 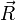
Элементарное рассмотрение и мотивировка[править | править вики-текст]
http://zaochnik.com/spravochnik/fizika/osnovy-dinamiki/neinertsialnye-sistemy-otscheta/
http://helpiks.org/6-64690.html