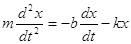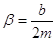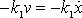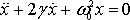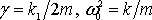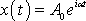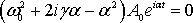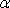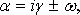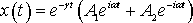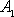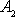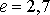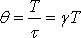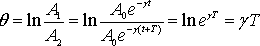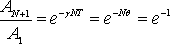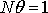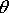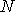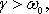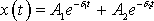Свободные колебания пружинного маятника. Общие сведения
Цель работы. Ознакомиться с основными характеристиками незатухающих и затухающих свободных механических колебаний.
Задача. Определить период собственных колебаний пружинного маятника; проверить линейность зависимости квадрата периода от массы; определить жесткость пружины; определить период затухающих колебаний и логарифмический декремент затухания пружинного маятника.
Приборы и принадлежности. Штатив со шкалой, пружина, набор грузов различной массы, сосуд с водой, секундомер.
1. Свободные колебания пружинного маятника. Общие сведения
Колебаниями называются процессы, в которых периодически изменяется одна или несколько физических величин, описывающих эти процессы. Колебания могут быть описаны различными периодическими функциями времени. Простейшими колебаниями являются гармонические колебания – такие колебания, при которых колеблющаяся величина (например, смещение груза на пружине) изменяется со временем по закону косинуса или синуса. Колебания, возникающие после действия на систему внешней кратковременной силы, называются свободными.
Рассмотрим одну из простейших колебательных систем – пружинный маятник, представляющий собой груз массой m, подвешенный на абсолютно упругой пружине с коэффициентом жесткости k
(рис. 1). Пусть l0 – длина пружины без подвешенного к ней груза. При подвешивании груза под действием силы тяжести пружина растянется на x1 так, что маятник будет находиться в положении равновесия вследствие равенства модулей силы тяжести mg и упругой силы Fупр: mg = kx1, стремящейся вернуть груз в положение равновесия (полагается, что деформации пружины идеально упругие и подчиняются закону Гука).
Если груз вывести из положения равновесия, отклонив на величину x, то сила упругости возрастает: Fупр = – kx2= – k(x1 + x). Дойдя до положения равновесия, груз будет обладать отличной от нуля скоростью и пройдет положение равновесия по инерции. По мере дальнейшего движения будет увеличиваться отклонение от положения равновесия, что приведет к возрастанию силы упругости, и процесс повторится в обратном направлении. Таким образом, колебательное движение системы обусловлено двумя причинами: 1) стремлением тела вернуться в положении равновесия и 2) инерцией, не позволяющей телу мгновенно остановиться в положении равновесия. В отсутствии сил трения колебания продолжались бы сколь угодно долго. Наличие силы трения приводит к тому, что часть энергии колебаний переходит во внутреннюю энергию и колебания постепенно затухают. Такие колебания называются затухающими.
Незатухающие свободные колебания
Сначала рассмотрим колебания пружинного маятника, на который не действуют силы трения – незатухающие свободные колебания. Согласно второму закону Ньютона c учетом знаков проекций на ось X
(1)
Из условия равновесия смещение, вызываемое силой тяжести: 
. Подставляя 
в уравнение (1), получим: 
. Разделив правую и левую часть этого уравнения на m и принимая, что a = d2x/dt2, получим дифференциальное уравнение
. (2)
Это уравнение называется дифференциальным уравнением гармонических колебаний пружинного маятника. Из этого уравнения следует, что после прекращения внешнего воздействия, приводящего к первоначальному отклонению системы от положения равновесия, движение груза обусловлено только действием упругой силы (сила тяжести вызывает постоянное смещение).
Общее решение однородного дифференциального уравнения второго порядка (2) имеет вид
. (3)
Данное уравнение называется уравнением гармонических колебаний. Наибольшее отклонение груза от положения равновесия А0 называется амплитудой колебаний. Величина 
, стоящая в аргументе косинуса, называется фазой колебания. Постоянная φ0 представляет собой значение фазы в начальный момент времени (t = 0) и называется начальной фазой колебаний. Величина
(4)
есть круговая или циклическая частота собственных колебаний, связанная с периодом колебаний Т соотношением 
. Период колебаний определяется
. (5)
Рассмотрим свободные колебания пружинного маятника при наличии силы трения (затухающие колебания). В простейшем и вместе с тем наиболее часто встречающемся случае сила трения пропорциональна скорости υ движения:
где r – постоянная, называемая коэффициентом сопротивления. Знак минус показывает, что сила трения и скорость имеют противоположные направления. Уравнение второго закона Ньютона в проекции на ось Х при наличии упругой силы и силы трения
Данное дифференциальное уравнение с учетом υ = dx/dt можно записать
, (8)
где 
– коэффициент затухания; – циклическая частота свободных незатухающих колебаний данной колебательной системы, т. е. при отсутствии потерь энергии (β = 0). Уравнение (8) называют дифференциальным уравнением затухающих колебаний.
Чтобы получить зависимость смещения x от времени t, необходимо решить дифференциальное уравнение (8). В случае малых затуханий (
) решение уравнения можно записать следующим образом:
, (9)
где А0 и φ0 – начальная амплитуда и начальная фаза колебаний;
– циклическая частота затухающих колебаний при ω >> 
ω ≈ ω0.
Движение груза в этом случае можно рассматривать как гармоническое колебание с частотой ω и переменной амплитудой, меняющейся по закону:
. (10)
На графике функции (9), рис. 2, пунктирными линиями показано изменение амплитуды (10) затухающих колебаний.
Рис. 2. Зависимость смещения х груза от времени t при наличии силы трения
Для количественной характеристики степени затухания колебаний вводят величину, равную отношению амплитуд, отличающихся на период, и называемую декрементом затухания:
. (11)
Часто используют натуральный логарифм этой величины. Такой параметр называется логарифмическим декрементом затухания:
. (12)
Если за время t‘ амплитуда уменьшается в n раз, то из уравнения (10) следует, что
. (13)
Отсюда для логарифмического декремента получаем выражение
. (14)
Если за время t‘ амплитуда уменьшается в е раз (е = 2,71 – основание натурального логарифма), то система успеет совершить число колебаний
. (15)
Следовательно, логарифмический декремент затухания – величина, обратная числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз. Чем больше θ, тем быстрее происходит затухание колебаний.
2. Методика эксперимента и экспериментальная установка
Рис. 3. Схема установки
Установка состоит из штатива 1 с измерительной шкалой 2. К штативу на пружине 3 подвешиваются грузы 4 различной массы. При изучении затухающих колебаний в задании 2 для усиления затухания используется кольцо 5, которое помещается в прозрачный сосуд 6 с водой.
В задании 1 (выполняется без сосуда с водой и кольца) в первом приближении затуханием колебаний можно пренебречь и считать гармоническими. Как следует из формулы (5) для гармонических колебаний зависимость T 2 = f (m) – линейная, из которой можно определить коэффициент жесткости пружины k по формуле
, (16)
где 
– угловой коэффициент наклона прямой T 2 от m.
Задание 1. Определение зависимости периода собственных колебаний пружинного маятника от массы груза.
1. Определить период колебаний пружинного маятника при различных значениях массы груза m. Для этого с помощью секундомера для каждого значения m трижды измерить время t полных n колебаний (n ≥10) и по среднему значению времени 
вычислить период 
. Результаты занести в табл. 1.
2. По результатам измерений построить график зависимости квадрата периода T2 от массы m. Из углового коэффициента графика определить жесткость пружины k по формуле (16).
Результаты измерений для определения периода собственных колебаний
, с
, с
Затухающие колебания
Определение затухающих колебаний
Механическое движение всегда сопровождается трением. Трение приводит к рассеянию (диссипации) механической энергии. Диссипация энергии имеется в любых не идеализированных колебательных системах, она вызывает затухание собственных колебаний.
Затухающими колебаниями называют колебания, амплитуда которых постепенно уменьшается со временем из-за потерь энергии колебательной системой.
Уравнение колебаний пружинного маятника с затуханием
Иногда, если тело движется в веществе, силу сопротивления ($<\overline
\[<\overline
где $\beta $ — коэффициент сопротивления.
Данную силу учитывают в уравнении второго закона Ньютона при описании движения. Так, уравнение, которое описывает линейные колебания по вертикали (колебания по оси X) пружинного маятника, учитывающее силу трения принимает вид:
где $\dot
(где $<\omega >_0$- циклическая частота свободных незатухающих колебаний (собственная частота колебаний при $\gamma $=0) той же колебательной системы; $\gamma $ — коэффициент затухания) уравнение колебаний пружинного маятника с затуханием (2) преобразуем к виду:
Малые собственные колебания, затухающие вследствие сопротивления среды в любой физической системе (математический маятник, физический маятник, электрические колебания . ) описывают при помощи уравнения формы (4).
Уравнение затухающих колебаний имеет точное решение:
где $\omega =\sqrt<<\omega >^2_0-<\gamma >^2>$; $A_0$ — начальная амплитуда колебаний, задаваемая начальными условиями; $\varphi $ — постоянная из начальных условий. При $\gamma \ll <\omega >_0$, $\omega \approx <\omega >_0$, параметр $A_0e^<-\gamma t>$ можно считать медленно изменяющейся во времени амплитудой колебаний.
Затухание колебаний по экспоненте связано с тем, что силу сопротивления мы приняли пропорциональной скорости. Если использовать другую зависимость силы трения от скорости, то закон затухания изменится.
Диссипация энергии при затухающих колебаниях
Пусть затухание мало, при этом потеря энергии колебательной системой за один период много меньше, чем энергия колебаний.
Рассеяние энергии за период колебаний происходит не равномерно, ввиду осцилляции кинетической энергии ($E_k$). Уравнение убывания энергии при затухающих колебаниях будет иметь вид:
\[\frac
где $\frac
Так как мы считаем затухание малым, то $\left\langle E_k\right\rangle $ можно принять равным (как при свободных колебаниях) половине полной энергии осциллятора:
\[\left\langle E_k\right\rangle =\frac
В таком случае уравнение (6) можно записать в виде:
Выражение (8) отображает «сглаженное» поведение энергии колебаний (в случае, если детали изменения энергии за один период колебаний не интересны). Оно показывает, что скорость изменения энергии пропорциональна самой энергии. Решением уравнения (8) является функция:
где $E_0$ — величина энергии колебательной системы в начальный момент времени.
Так как энергия колебаний пропорциональна квадрату амплитуды ($E\sim A^2$), изменение амплитуды колебаний за большие отрезки времени (в сравнении с периодом колебаний) запишем в виде функции:
$A_0$ — начальная амплитуда колебаний.
Время жизни колебаний. Период затухающих колебаний. Декремент затухания
Из формулы (10) видно, что амплитуда затухающих колебаний убывает по экспоненте. За время $\tau =\frac<1><\gamma >$ амплитуда убывает в $e$ раз и это не зависит от $A_0$. Время $\tau $ в этом случае называют временем жизни колебаний (или временем релаксации) (не смотря на то, что в соответствии с выражением (9) колебания должны длиться бесконечно). Тезис о малости затухания означает, что время жизни колебаний не бесконечно, а много больше, чем их период ($\tau \gg T$). За время жизни происходит много колебательных движений.
Строго говоря, затухающие колебания не являются строго периодическими движениями. Периодом в данном случае считают промежуток времени между двумя последовательными максимальными отклонениями от положения равновесия.
Период затухающих колебаний считают равным:
Пусть $A\left(t\right)\ и\ A(t+T)$ — амплитуды двух последовательных колебаний, моменты времени которых отличаются на период. Отношение этих амплитуд, следуя (10) равно:
называют декрементом затухания. Натуральный логарифм декремента затухания ($\theta $):
называют логарифмическим декрементом затухания. Для колебательной системы $\theta $ постоянная величина.
Примеры задач с решением
Задание. Каков коэффициент затухания маятника ($\gamma $), если за $\Delta t$ амплитуда его колебаний уменьшилась в $n$ раз?
Решение. За основу решения задачи примем уравнение затухающих колебаний в виде:
По условию задачи имеем:
С другой стороны:
где $t_2-t_1=\Delta t$. Найдем натуральный логарифм от правой и левой части выражения (1.2), получим:
Выразим $\gamma $ из (1.3) учтем, что $\frac
Ответ. $\gamma =\frac<<\ln n\ >><\Delta t>$
Задание. Что представляет собой фазовая траектория затухающего колебания?
Решение. Фазовой траекторией называют траекторию движения в плоскости $\left(x;;v\right).$ По оси абсцисс откладывается отклонение $x$, по оси ординат откладывают скорость $v$. Каждому движению в момент времени $t$ соответствует изображающая точка, на указанной плоскости координаты ее $\left(x,v\right),$ они однозначно определены мгновенными значениями отклонения и скорости. Точка со временем движется и описывает траекторию (рис.1). В данном случае время выступает как параметр, уравнение фазовой траектории задет функция:
Фазовая траектория затухающего колебания, если
\[<\overline
представляет собой незамкнутую спираль, которая закручивается вокруг начала координат (рис.1). Если затухание колебаний малое, то есть за время жизни колебательная система совершает множество колебаний, количество витков спирали в фазовой плоскости будет таким же.
Уравнение собственных затухающих колебаний физического и пружинного маятников
1.2 Уравнение собственных затухающих колебаний физического и пружинного маятников
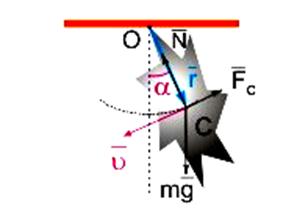
Рассмотрим движение груза, жестко зафиксированного на подвесе (металлическом стержне), закрепленном в точке O (см. приложение 1). Система «груз – подвес» в общем случае представляет собой физический маятник. Точку крепления этого маятника условно назовем точкой подвеса.
Опыт показывает, что физический маятник, выведенный из положения равновесия, совершает вращательные колебания. Согласно основному закону динамики вращательного движения произведение момента инерции системы «груз – подвес» на угловое ускорение маятника равно равнодействующему моменту внешних сил: силы тяжести m·g и силы сопротивления Fc (момент силы деформации растяжения тела N равен нулю). Спроецировав это уравнение на направление оси вращения, для случая малых колебаний получим следующее выражение:
где α(t) — угол отклонения колеблющегося груза, отсчитываемый от положения равновесия;
α’ и α» — соответственно угловая скорость и угловое ускорение маятника;
k и h — размерные константы;
I — момент инерции системы «груз – подвес»;
М = -m . g . r . sin(α) = -k . sin(α) — момент возвращающей силы (для малых колебаний М = -k . α);
Mc = -h . α’ — момент сил сопротивления (выражение справедливо для малых угловых скоростей).[5]
Поделив левую и правую части уравнения (1) на величину I и перенеся все слагаемые в левую часть, получим соотношение, аналогичное выражению, описывающему движение собственных затухающих колебаний груза на пружине.
a» + w0 2 ·a + 2b·a’ = 0, (2)
где b = h/2I — коэффициент затухания;
w0 = (k/I) 1/2 — собственная частота колебаний груза.
Решение уравнения (2) имеет вид:
a(t) = a0·e — b t ·sin(w·t + j), (3)
где w=(w0 2 — b 2 ) 1/2 — частота затухающих колебаний груза.
Как видно из уравнения (3) амплитуда углового смещения будет уменьшаться (затухать) с течением времени по экспоненциальному закону. Коэффициент затухания определяет быстроту этого процесса. Он равен промежутку времени по истечении которого, амплитуда колебаний уменьшается в e раз.
Далее рассмотрим уравнение собственных затухающих колебаний пружинного маятника.
Пружинным маятником называется система, состоящая из груза массой m и невесомой пружины жесткостью k.
Пусть масса маятника m, коэффициент упругости пружины k, сила сопротивления, действующая на маятник, F = — bv, v — скорость маятника, b — коэффициент сопротивления среды, в которой находится маятник. Так как рассматриваем только линейные системы, b = const, k = const. x — смещение маятника от положения равновесия.
(второй закон Ньютона)
Данное уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. Принято записывать его в следующем, так называемом каноническом виде:
— коэффициент затухания, — собственная частота свободных (незатухающих) колебаний пружинного маятника, то, что раньше мы обозначали просто w.
Уравнение затухающих колебаний в таком (каноническом) виде описывает затухающие колебания всех линейных систем; конкретная колебательная система отличается только выражениями для b и j0.
2. Движения маятника с различными механизмами затухания
При исследовании собственных колебаний предполагается отсутствие внешней среды. Наличие среды приводит к появлению диссипативной силы, которая, как мы показали, постепенно уменьшает первоначально переданную системе энергию. Это выражается через уменьшение собственной частоты колебаний ω0, также как постепенным уменьшением амплитуды колебаний.
Примечание: во избежание путаницы нумерация формул останется такой же как в научной литературе.[6]
Пусть на колеблющееся тело действует сила мокрого трения:
,
Уравнение движения частицы примет следующий вид:
, (1.35)
. (1.36)
Подставляя последнее в (1.35), получим:
(1.37).
Так как полученное уравнение верно для произвольного момента времени, то выражение в скобках должно быть нулем. Последнее дает для неизвестной величины 
следующее значение
(1.38)
, (1.39)
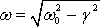
Учитывая (1.38), решение (1.36) примет следующий вид:
, (1.40)
Полученное уравнение движения описывает затухающие колебания, где
и 
– постоянные, определяемые из начальных условий.
В зависимости от соотношения коэффициента трения 
и частоты собственных колебаний 
, затухающие колебания подразделяются на два класса. Они соответствуют случаям периодического и непериодического затухания.
Периодическое затухание. Оно осуществляется при слабых силах трения:
, (1.41)
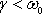
когда величина (1.39) действительна. В этом случае решение (1.40) выражается формулой (в действительной форме)
, (1.42)
Графически это колебание представлено на рисунке (см. приложение 2) и является колебанием с постоянной частотой (1.39), но убывающей с течением времени амплитудой. В этом смысле это не только не гармоническое, но даже и не периодическое колебание, поскольку колебания не повторяются в том же виде. Тем не менее, удобно говорить о периоде этих колебаний, понимая под этим промежуток времени
, (1.43)
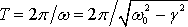
Говоря «амплитуда затухающих колебаний» понимают величину
, (1.44)
которая есть максимальное смещение частицы относительно положения равновесия во время колебаний. Из выражения (1.44) следует, что за время , (1.45) амплитуда убывает в 
раз. Этот промежуток времени называется временем затухания, а – декрементом затухания.
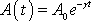
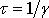
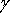
Наиболее объективной характеристикой затухания колебаний является логарифмический декремент, который является отношением периода колебаний (1.43) к времени затухания (1.45)
, (1.46)
Легко заметить, что логарифмический декремент равен натуральному логарифму отношения двух последующих амплитуд:
, (1.47)
Определим число N колебаний, в течение которых амплитуда колебаний убывает в , раз:
откуда следует, что
, (1.48)
На основании этого соотношения можно экспериментально определить логарифмический декремент затухания 
, считая соответствующее число 
колебаний.
Непериодическое затухание. При сильном трении
(1.49)
величина (1.43) становится мнимой. В этом случае удобно представить (1.42) так:
, (1.50)
, (1.51)
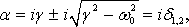
В рассматриваемом случае решение (1.42) примет вид:
, (1.52)
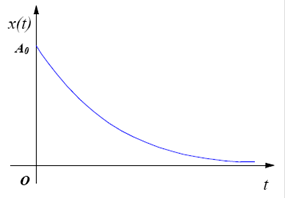
которое не описывает какое-либо колебание, а представляет экспоненциональное убывание смещения от положения равновесия (см. приложение 3). Непериодическое затухание маятника можно наблюдать, если поместить его в сильно вязкую среду (глицерин, мед).
Специальным случаем непериодического затухания является случай, когда . В этом случае решение уравнения (1.35) выражается в виде:
, (1.53).
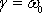
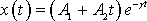
Целью данной курсовой работы являлось изучение колебаний маятника с различными механизмами затухания. Для реализации поставленной цели предполагалось решение ряда задач, что позволило сделать следующие выводы:
На основании анализа существующей литературы даны определения исходных теоретических положений, а именно: колебания, виды колебаний, маятник (физический маятник, пружинный маятник), декремент затухания, добротность колебательной системы и т.д.
Также, исходя из проработанной литературы, сделан вывод о том, что данная тема изучалась и изучается многими авторами, как зарубежными, так и советскими, и находит практическая применение в различных науках.
Получены уравнения собственных затухающих колебаний на примерах физического и пружинного маятников.
,
где — коэффициент затухания,
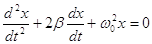
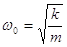
— собственная частота свободных (незатухающих) колебаний пружинного маятника.
Таково полученное уравнение собственных затухающих колебаний пружинного маятника. Это уравнение описывает затухающие колебания всех линейных систем; конкретная колебательная система отличается только выражениями для b и j0.
a(t) = a0·e — b t ·sin(w·t + j), (3)
где w=(w0 2 — b 2 ) 1/2 — частота затухающих колебаний груза.
Данное уравнение определяет быстроту процесса затухания колебаний физического маятника.
Определены два механизма затухающих колебаний: периодическое (осуществляется при слабых силах трения) и непериодическое (при сильном трении), а также получены формулы, для их расчета.
— для периодического механизма затухающих колебаний;
, — для непериодического механизма затухающих колебаний.
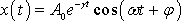
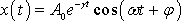
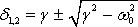
Библиографический список литературы
1. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Наука, 1991. — 568 с.
2. Анищенко В.С. Сложные колебания в простых системах. М.: Наука, 1990. – 59 с.
3. Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1994. — 408 с.
4. Владимиров С.Н., Майдановский А.С., Новиков С.С. Нелинейные колебания многочастотных автоколебательных систем. Томск: изд-во Томск. ун-та, 1993. — 203 с.
5. Горелик Г. С., Колебания и волны, 2 изд., М., 1989. — 124 с.
6. Дмитриев А.С., Кислов В.Я. Стохастические колебания в радиофизике и электронике. М.: Наука, 2001. — 280 с.
7. Капранов М.В., Кулешев В.Н., Уткин Г.М. Теория колебаний в радиотехнике. М.: Наука, 1994. — 319 с.
8. Ланда П.С. Автоколебания в системах с конечным числом степеней свободы. М.: Наука, 1991. — 360 с.
9. Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М.: Наука, 1989. — 390 с.
10. Мун Ф. Хаотические колебания: Вводный курс для научных работников и инженеров. М.: Мир, 1990. — 312 с.
11. Неймарк Ю.И., Ланда П.С. Стохастические и хаотические колебания. М.: Наука, 1995. — 424 с.
12. Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. М.: Наука, 1994. — 431 с.
13. Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 2002. — с. 597.
[1] Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Наука, 1991. — с. 137.
[2] Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М.: Наука, 1989. — с. 52.
[3] Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 2002. — с. 597.
[4] Горелик Г.С., Колебания и волны, 2 изд., М., 1989. – с. 82
[5] Мун Ф. Хаотические колебания: Вводный курс для научных работников и инженеров. М.: Мир, 1990. — с. 192.
[6] Стрелков С. П., Введение в теорию колебаний, 2 изд., М., 2002. — с. 149-154.
http://www.webmath.ru/poleznoe/fizika/fizika_46_zatuhajushhie_kolebanija.php
http://kazedu.com/referat/108041/1