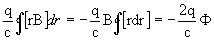Тема: Определение удельного заряда электрона методом магнетрона
Тема: Определение удельного заряда электрона методом магнетрона.
Цель работы: познакомиться с законами движения заряженных частиц в электрическом и магнитном полях, определить удельный заряд электрона с помощью цилиндрического магнетрона.
Краткие теоретические сведения: магнетроном называется электро-вакуумное устройство, в котором движение электронов происходит во взаимно перпендикулярных электрическом и магнитном полях. Магнетрон является источником электромагнитного излучения СВЧ диапазона.

При этом силовые линии электрического поля имеют радиальное направление, а линии магнитной индукции совпадают с осью электродов (рис.2).
Движение электрона в электромагнитном поле подчиняется второму закону Ньютона:

где r — радиус-вектор, m — масса электрона, e — абсолютная величина заряда электрона, V — скорость электрона, E — вектор напряженности электрического поля, В — вектор индукции магнитного поля.
Траектория движения заряженной частицы в электромагнитном поле существенно зависит от величины удельного заряда — отношения заряда к массе частицы. Уравнение траектории можно получить из решения уравнения (1), но даже в случае цилиндрической симметрии это уравнение не имеет решения в аналитическом виде.
Рассмотрим на качественном уровне движение электрона в цилиндрическом магнетроне. Для упрощения предположим, что электроны вылетают из катода с нулевой начальной скоростью, их движение происходит в плоскости, перпендикулярной оси электродов, а радиус катода много меньше радиуса анода.
При протекании тока в цепи накала, в результате термоэлектронной эмиссии с катода, в лампе образуются свободные электроны. Эмитированные катодом электроны под действием электрического поля движутся к аноду, и в анодной цепи возникает электрический ток. Постоянный ток в обмотке соленоида создает магнитное поле, искривляющее траекторию движения электронов.
Выясним характер движения электронов в магнетроне. В электрическом поле на электрон действует сила F = eE, вынуждающая его двигаться с ускорением в направлении, противоположном вектору Е. Эта сила совершает работу, которая идет на изменение кинетической энергии электрона. Скорость электронов вблизи анода может быть найдена из закона сохранения энергии:

где Ua — анодное напряжение лампы.
В магнитном поле сила действует на движущийся электрон F=-e[VB] и направлена перпендикулярно скорости электрона. Эта сила не совершает механической работы над электроном, а только изменяет направление вектора скорости и вынуждает электрон двигаться с центростремительным ускорением по окружности. В нашей модели предполагается, что V^B. Применяя второй закон Ньютона, получим:

Отсюда выразим радиус окружности:


Увеличивая индукцию магнитного поля, можно получить ситуацию, когда электрон, двигаясь по криволинейной траектории, едва не коснется анода и возвратится на катод, как на рис 3в. Криволинейная траектория в этом случае напоминает окружность, радиус которой для электрона вблизи анода приблизительно равен половине радиуса анода

где значение скорости в соответствии с формулой (2) равно

Анодный ток при этом прекращается.
Таким образом, если известна индукция критического магнитного поля при определенном анодном напряжении, то из формул (5) и (6) можно рассчитать удельный заряд электрона:

При дальнейшем увеличении магнитного поля электроны, двигаясь по криволинейным замкнутым траекториям, удаляются от катода на меньшие расстояния и не долетают до анода, как показано на рис. 3г.
Для определения удельного заряда электрона по формуле (7) нужно, задавая величину анодного напряжения, найти значение индукции критического магнитного поля, при котором анодный ток уменьшается до нуля. В данной работе измеряется ток соленоида. Индукция магнитного поля соленоида связана с силой тока соотношением

где N — число витков, l — длина соленоида. В результате расчетная формула для удельного заряда электрона принимает вид:




Соленоид подключается к источнику постоянного напряжения, а ток соленоида фиксируется амперметром. Справа изображены источник напряжения и приборы, регистрирующие параметры анодной цепи.
Подаем на лампу анодное напряжение 20В. Получили значение анодного тока Іа=0,5834.
Изменяя силу тока в соленоиде, снимаем зависимость анодного тока от тока соленоида. Данные заносим в таблицу:
По данным таблицы построим зависимость анодного тока от тока соленоида.
Графически продифференцируем эту зависимость и определим критическое значение тока соленоида. Максимум построенной функции соответствует критической силе тока в соленоиде.
Таким образом, критическое значение тока соленоида составляет Іс(кр)=320А.
По формуле 
Выводы: в выполненной работе мы познакомились с законами движения заряженных частиц в электрическом и магнитном полях, определили удельный заряд электрона с помощью цилиндрического магнетрона.
1. Что такое магнетрон и как он работает?
Ответ: Магнетроном называется электровакуумное устройство, в котором движение электронов происходит во взаимно перпендикулярных электрическом и магнитном полях. Магнетрон является источником электромагнитного излучения СВЧ диапазона.
В работе магнетрона используется процесс движения электронов при наличии двух полей — магнитного и электрического, перпендикулярных друг другу. Магнетрон представляет собой двухэлектродную лампу или диод, содержащий накаливаемый катод, испускающий электроны, и холодный анод. Магнетрон помещается во внешнее магнитное поле. Анод (анодный блок) магнетрона имеет довольно сложную монолитную конструкцию с системой резонаторов, необходимых для усложнения структуры электрического поля внутри магнетрона. Магнитное поле создается либо катушками с током (электромагнит), либо постоянным магнитом, между полюсами которого помещается магнетрон. Если бы магнитного поля не было, то электроны, вылетающие из катода практически без начальной скорости, двигались бы в электрическом поле вдоль прямых 
Траектория электрона есть циклоида, описываемая точкой, лежащей на окружности круга, равномерно катящегося по катоду. При прохождении циклоидного потока электронов мимо щелей резонаторов анодного блока, в них возбуждаются мощные электромагнитные СВЧ колебания. Высокочастотная энергия из прибора обычно выводится с помощью петли или отверстия связи, помещенных в периферийной части одного из резонаторов анодного блока.
Магнетрон разрабатывался как мощный генератор электромагнитных колебаний СВЧ диапазона для использования в системах РЛС. Эффект нагревания предметов микроволнами нашел применение в микроволновых (СВЧ) печах.
2. Изобразите направление электрического и магнитного полей в магнетроне и траектории движения электронов.
Ответ: В магнетроне электрон движется в скрещенных электрическом и магнитном полях. В отсутствии магнитного поля траектории движения электронов приведены на рис. 3а. При наложении «слабого» магнитного поля траектории электронов искривляются, но все электроны долетают до анода, как показано на рис. 3б.
3. Какие силы действуют на электрон в магнетроне? Укажите направление сил, действующих на электрон в магнетроне. Запишите второй закон Ньютона для электрона в магнетроне.

Движение электрона в электромагнитном поле подчиняется второму закону Ньютона:
где r — радиус-вектор, m — масса электрона, e — абсолютная величина заряда электрона, V — скорость электрона, E — вектор напряженности электрического поля, В — вектор индукции магнитного поля.
4. Сделайте вывод рабочей формулы.
Ответ: в электрическом поле на электрон действует сила F=eE, вынуждающая его двигаться с ускорением в направлении, противоположном вектору Е. Эта сила совершает работу, которая идет на изменение кинетической энергии электрона. Скорость электронов вблизи анода может быть найдена из закона сохранения энергии:

где Ua — анодное напряжение лампы. В магнитном поле сила действует на движущийся электрон F=-e[VB] и направлена перпендикулярно скорости электрона. Эта сила не совершает механической работы над электроном, а только изменяет направление вектора скорости и вынуждает электрон двигаться с центростремительным ускорением по окружности. В нашей модели предполагается, что V^B. Применяя второй закон Ньютона, получим:

Отсюда выразим радиус окружности:

Увеличивая индукцию магнитного поля, можно получить ситуацию, когда электрон, двигаясь по криволинейной траектории, едва не коснется анода и возвратится на катод. Криволинейная траектория в этом случае напоминает окружность, радиус которой для электрона вблизи анода приблизительно равен половине радиуса анода:

где значение скорости в соответствии с формулой (1) равно:

Анодный ток при этом прекращается.
Таким образом, если известна индукция критического магнитного поля при определенном анодном напряжении, то из формул (4) и (5) можно рассчитать удельный заряд электрона

При дальнейшем увеличении магнитного поля электроны, двигаясь по криволинейным замкнутым траекториям, удаляются от катода на меньшие расстояния и не долетают до анода.
Для определения удельного заряда электрона по формуле (6) нужно, задавая величину анодного напряжения, найти значение индукции критического магнитного поля, при котором анодный ток уменьшается до нуля. В данной работе измеряется ток соленоида. Индукция магнитного поля соленоида связана с силой тока соотношением:


где N-число витков, l-длина соленоида. В результате расчетная формула для удельного заряда электрона принимает вид:
5. Какие графики нужно построить в данной работе? Поясните ход экспериментальных кривых.
Ответ: в данной лабораторной работе нужно построить график зависимости анодного тока от тока соленоида и график зависимости скорости изменения анодного тока от тока соленоида. Первый график показывает, что при увеличении тока соленоида и соответственно значения вектора магнитной индукции анодный ток прекращается, т. к. радиус движения электронов уменьшается, и они не достигают анода. Второй график позволяет определить ток соленоида, при котором электроны перестают долетать до анода.
1. Савельев общей физики, 1978, т2, §§50,72
Уравнение электрона в магнитном поле
Итак, на предыдущих лекциях мы познакомились с квантомеханическим подходом к описанию поведения электрона в периодическом поле решетки Браве. Мы узнали также какими методами решается уравнение Шредингера для электронов, волновая функция которых удовлетворяет условию Блоха. Тем самым мы знаем, каким образом можно определить собственную волновую функцию и собственные значения энергии электрона, а точнее, зависимость энергии от квазиимпульса где n — номер зоны. В основном состоянии электроны заполняют наинизшие энергетические состояния вплоть до энергии Ферми EF(k), значение которой также зависит от направления квазиимпульса. Тем самым в k-пространстве формируются эквиэнергетические поверхности, одна из которых — есть поверхность Ферми.
Мы убедились в том, что эти задача отыскания собственных волновых функций Ψ n,k и зависимости Еn(k) не решается легко. При этом решетка предполагалась идеальной и жесткой, а внешние поля отсутствовали. Однако, именно поведение материала во внешних электрических, магнитных, тепловых полях или под действием механических сил представляет наибольший практический интерес. Естественно, что внешние поля усложняют и без того сложное описание кристаллов в рамках квантовой механики. Оказалось, что многие свойства кристаллов можно описать, сделав пол-шага назад, а именно, применив квазиклассический подход.
Основные положения квазиклассической модели. Электроны как волновые пакеты. Уравнения движения во внешних полях.
В классической механике электрон обладает траекторией, т.е. помимо энергии, в данный момент времени — координату и производные координаты по времени — скорость/импульс, ускорение и т.д.. Это, естественно, предполагалось в теории Друде. В теории Зоммерфельда утверждалось также, что для расчета динамического поведения электронов можно пользоваться обычными уравнениями классической механики, если только не требуется описывать местоположение электрона с точностью порядка межэлектолнных расстояний. Т.е., в промежутках между столкновениями, частица с импульсом hk подчиняется уравнениям:
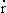


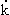

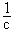
(здесь и далее — в системе CGS, в системе СИ — нужно убрать фактор 1/c перед v). Для оправдания квазиклассического подхода с точки зрения квантовой механики можно сказать, что уравнения (4.1) в действительности описывают поведение волнового пакета, составленного из уровней свободных электронов с волновыми векторами k‘ :
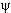
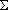

g(k‘)

где r и k -средние координата и квазиимпульс, вблизи которых сосредоточен волновой пакет
(с учетом 

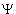
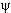
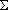
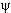
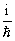
g(k‘)

Пусть ширина пакета по волновым векторам 
vg = d

что совпадает со скоростью электронов в блоховском состоянии с волновой функцией 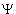
vn (k) =
Поскольку 

т.е. в. пакет “размазан” по большому числу элементарных ячеек в реальном пространстве. Полуклассическая модель описывает воздействие на электроны полей, которые медленно меняются на длине волнового пакета, и, стало быть гораздо медленней на межатомном расстоянии, т.е. 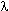

Основные положения полуклассической модели:
- Схема зонных уровней En(k) — известна. Модель применяется для расчетов кинетических коэффициентов (реакции электронов на внешние поля) по заданной (уже вычисленной) зонной структуре, а также для определения свойств зонной структуры по наблюдаемым кинетическим характеристикам. Электрон проводимости — классическая частица со сложным законом дисперсии. При движении во внешних полях En(k)играет роль кинетической энергии.
- Номер зоны — интеграл движения. Возможностью межзонных переходов пренебрегается.
- Изменение со временем координаты и волнового вектора с данным номером зоны n определяется уравнениями движения:
После интегрирования получим:
r 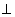

Т.е. проекция орбиты в r-пространстве есть та же орбита в k-пространстве, повернутая на 90 0 вокруг направления поля, причем размеры орбиты масштабированы с фактором 
Электронные, дырочные и открытые орбиты.
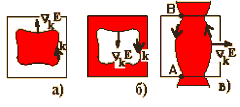 Рис. 4.1. Электронные a), дырочные б) и открытые в) орбиты |
Для электронов в магнитном поле на поверхности Ферми возможны 3 типа орбит: электронные, дырочные и открытые орбитали. На рис. 4.1. изображены схематично траектории электронов в 1-й зоне Бриллюэна в магнитном поле, перпендикулярном плоскости чертежа. Замкнутые траектории могут охватывать заполненную (рис.4.1а) и «пустую» (рис.4.1б) область. Градиент энергии направлен в сторону незаполненной области, т.е. в первом случае наружу, а во втором случае внутрь замкнутой траектории. Соответственно ур. (4.8б), направление движения в первом и во втором случае противоположны, что можно представить как движение частиц с противоположным знаком заряда. Поэтому, траектории типа рис. 4.1а и рис. 4.1б, называют, соответственно, «электроноподобные» и «дыркоподобные», или просто электронные и дырочные орбиты.
В отличие от предыдущих, траектории типа изображенных на рис. 4.1в не замкнуты 1-й зоной Бриллюэна, это т.н. открытые траектории. При достижении точки В на границе 1-й з.Б., частица перемещается в точку А, и движение повторяется.
Квантование орбит электрона во внешнем постоянном магнитном поле.
В r-пространстве. Из электродинамики известно, что полный (или обобщенный) импульс частицы р может быть представлен в виде суммы кинетического ркин и потенциального рпот слагаемых:
р = ркин + рпот
ркин = mv = 
где q-заряд, А — вектор потенциал, который удовлетворяет ур-ю
B = rotA = [ N A]
Следуя полуклассическому подходу Онсагера и Лифшица, мы полагаем, что орбиты в магнитном поле квантуются в соответствии с правилом квантования Бора-Зоммерфельда:
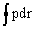


где n-целое, g =1/2 — (коррекция фаз). Тогда,
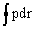
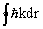
Интегрируя (4.8б), с точностью до константы имеем

Отсюда и из (4.10в) для 1-го слагаемого в правой части (4.12) имеем:
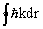
где Ф — магнитный поток через площадь, ограниченную орбитой. Для второго слагаемого
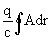
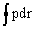
Т.о. орбита электронов квантуется т.о., что поток через нее равен
Фn = (n + γ )(2
где (2

Квантование в k-пространстве. Учитывая фактор масштабирования в (4.9) имеем:



An = (
Отсюда: Фn = 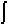



или Sn = (n+ g ) (2 p e/
Одинаковая площадь S в k-пространстве на поверхности Ферми будет для двух последовательных значений магнитного поля:
S(1/Bn+1 — 1/Bn) = 2

Равные инкрименты 1/B соответствуют подобным орбитам! Соотношение (4.20) получил Онсагер (1952), он же показал, что S — площадь экстремальной орбиты (подробнее — в следующей лекции). Это объясняет наблюдаемые осцилляторные эффекты при низких температурах в электросопротивлении, магнитной восприимчивости, теплоемкости при изменении магнитного поля (см. следующую лекцию).
Уровни Ландау для свободных электронов в магнитном поле (Ландау, 1930, 1969).
Пусть имеем образец, помещенный в магнитное поле, направленное вдоль оси z перпендикулярно торцу с квадратным сечением. Волновые векторы имеют дискретные разрешенные значения ki = 2

D S = Sn — Sn-1 = (2

Отсюда, число электронных орбит, которые вырождены в один магнитный уровень (рис.4.2в):
D = (2


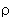
(4.22)
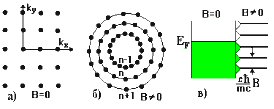 Рис. 4.2. Уровни Ландау |
где 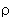


Энергия уровней Ландау.
В соответствии с классической механикой движения заряда в магнитном поле, приравнивая центростремительную силу силе Лоренца mv 2 /r = evB/c, где v — нормальная к B составляющая скорости электрона, а r — радиус орбиты, получаем для частоты кругового движения (т.н. циклотронной частоты)




В квазиклассическом приближении, движение электрона в магнитном поле представляется как колебание осциллятора с частотой 
En = (n + 1/2)
Энергетический спектр свободных электронов при В = 0 перераспределяется по магнитным уровням Ландау при В
Уровни Ландау для блоховских электронов.
Траектории блоховских электронов не являются окружностью, однако, правила квантования (4.20, 21, 22) остаются в силе. Это позволяет использовать их для исследования поверхности Ферми в реальных кристаллах. Другое отличие: — в выражении для циклотронной частоты (4.23), эффективная масса блоховской частицы (электрона или дырки), m*, может отличаться от массы свободного электрона. В общем случае из уравнений движения (4.7) следует, что ускорение, приобретаемое частицей в поле сил
a = dvn/dt = 1/











Т.е. обратная эффективная масса
1/m* = 1/ 


в общем случае является тензором, зависящим от k:
[M -1 (k)]ij = 1/ 





Так что циклотронная частота в общем виде определяется соотношением

Дополнительная литература
- АМ, Гл.12.
- Onsager L., Phil. Mag., 43, 1006 (1952)
- Ландау Л.Д., Zs. Phs., 64, 629 (1930), Собрание трудов, М., Наука, 1969, т.1., стр.47
Атом в магнитном поле
При движении электрона вокруг ядра по орбите радиуса r на него действует центростремительная сила
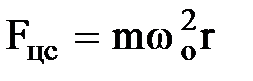
Если атом внести во внешнее магнитное поле, вектор индукции 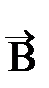
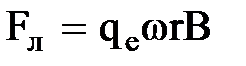
где w — круговая частота обращения электрона в магнитном поле.
Уравнение движения электрона в магнитном поле запишем в виде
mw 2 r = 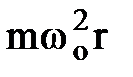
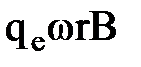
где знаки «±» выбираются в соответствии с относительной ориентацией векторов 
После преобразования последнего выражения получим
где Dw =½w-wo ½ — cреднее значение площади S^ для орбит всех электронов атома.
При суммировании орбитальных и спиновых магнитных моментов атомов может произойти их полная компенсация.
Тогда результирующий магнитный момент атома равен нулю.
Если такой компенсации не происходит, то атом имеет постоянный магнитный момент. Вещества, у которых атомы в отсутствие внешнего магнитного поля имеют постоянный магнитный момент, не равный нулю, могут быть парамагнетиками, ферромагнетиками, антиферромагнетиками или ферримагнетиками.
Дата добавления: 2016-02-09 ; просмотров: 2385 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://nuclphys.sinp.msu.ru/solidst/physmet4.htm
http://helpiks.org/6-85866.html








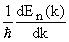
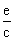 vn (k) х B(r,t) = —
vn (k) х B(r,t) = — 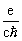
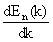 х B(r,t)
х B(r,t)