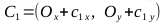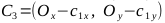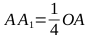Координаты точки эллипса по углу
IP76 > Координаты точки эллипса по углу
Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.
Калькулятор точки на эллипсе
Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.
Get a better browser, bro…
Параметрическое уравнение эллипса
Обратимся, как обычно, к Википедии. Находим там следующее:
Каноническое уравнение эллипса может быть параметризовано:
Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.
Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.
Подготовка
У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.
Проведем прямую из общего центра [X0;Y0] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X1;Y1] и [X2;Y2].
α – угол между прямой и осью X.
| Малая окружность | X1 = b × cos α | Y1 = b × sin α |
| Большая окружность | X2 = a × cos α | Y2 = a × sin α |
Таблица 1. Координаты точек пересечения прямой с окружностями
Нахождение зависимости
Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X0;Y0] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.
Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.
Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:
X’ = X2 = a × cos α
Y’ = Y1 = b × sin α
Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.
Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.
Тангенс угла β в этом случае равен:
(3) Тангенс угла β
Используя формулу тангенса произведем дальнейшие преобразования:
(4) Зависимость тангенса α от тангенса β
Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.
Нахождение координат
Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.
Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):
Рисование эллипса под произвольным углом в canvas на JavaScript
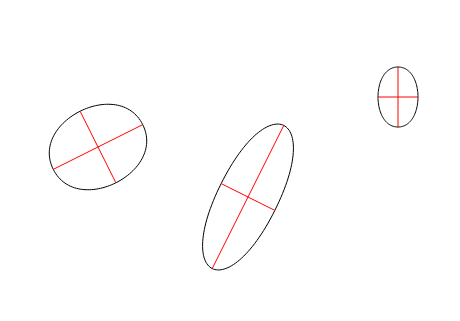
В процессе разработки одного приложения столкнулся с необходимостью рисования эллипсов под произвольным углом в canvas на JavaScript. Пользоваться какими-либо фреймворками в столь простом проекте не хотелось, так что я отправился на поиски статьи-мануала на эту тему. Поиски не увенчались успехом, так что пришлось разбираться с задачей самостоятельно, и я решил поделиться с вами полученным опытом.
Формализуем задачу. Нам требуется функция drawEllipse(coords, sizes, vector), где:
- coords — координаты центра эллипса — массив [x, y]
- sizes — длины большой и малой полуосей эллипса — массив [a, b]
- vector — вектор [x, y] наклона эллипса
В статье приведено три способа решения данной задачи.
В качестве первого метода были выбраны кривые Безье. Для построения такой кривой требуются четыре точки: начальная, конечная и две контрольные.
Искомый эллипс будет состоять из двух таких кривых, причем нетрудно догадаться, что вышеупомянутые точки у каждой из них будут вершинами прямоугольника. Давайте исследуем наш эллипс.
- Имеем некоторый вектор
Найдем единичный вектор
Найдем единичный вектор
Для этого вспомним свойство скалярного произведения векторов обращаться в ноль в случае, если они перпендикулярны:
Таким образом: - Найдем векторы
, точки A1, A2, B1, B2
- Найдем векторы
, точки C1, C2, C3, C4
- Вспомним, что для рисования эллипса нам нужны две кривые Безье:
- 1-я имеет начальную точку B1, конечную B2, проходит через точку A1
- 2-я имеет начальную точку B2, конечную B1, проходит через точку A2
Вспомним также, что для построения кривых Безье нам требуются контрольные точки. Недолго думая, я сначала подставил в качестве таковых вершины прямоугольника, в который вписан эллипс. Это решение оказалось ошибкой, ведь если мы рассмотрим построение кривой Безье, то обнаружим, что она не касается отрезка, соединяющего две контрольные точки.
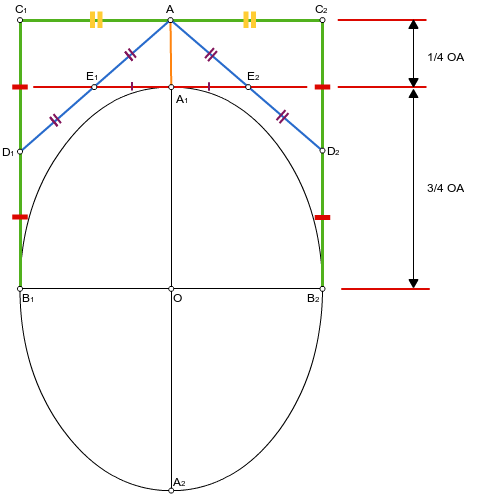
Изобразим момент построения кривой Безье в точке, в которой она (кривая) будет наиболее близка к отрезку между контрольными точками. В нашем случае это будет выглядеть так:
Из рисунка очевидно, что расстояние от этой точки (A1) до отрезка между контрольными точками (C1, C2) будет составлять четверть от расстояния между центром искомого эллипса (O) и тем же отрезком (C1, C2), то есть:



Таким образом, для получения эллипса с нужными параметрами нам необходимо умножить вектор
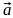 на параметр
на параметр 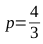 , после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.
, после чего вернуться к вычислениям, описанным в пунктах 1-4. В результате получаем наборы точек (B1, C1, C2, B2 и B2, C3, C4, B1) для построения двух кривых Безье, вместе представляющих искомую фигуру.Собственно демо и код:
Upd. Ознакомившись с комментариями, написал функцию рисования эллипса через параметрическое уравнение, и оказалось, что фигура, которая получается с помощью кривых Безье не вполне точно совпадает с эллипсом. На наложении фигур видно, что нарисованный кривыми Безье объект (красный) местами шире, чем правильный эллипс (синий). Вот демо наложения фигур.
Upd. В комментариях подсказали более нативный и простой способ отрисовки наклонного эллипса (спасибо subzey). Оставлю здесь, чтобы не затерялся. Вот демо.
http://habr.com/ru/post/255485/





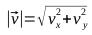
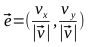


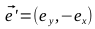
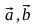 , точки A1, A2, B1, B2
, точки A1, A2, B1, B2
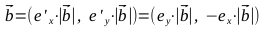

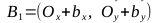


 , точки C1, C2, C3, C4
, точки C1, C2, C3, C4