Эллиптический параболоид.
Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

Уравнение (7) называется каноническим уравнением эллиптического параболоида.
Рассмотрим сечения данной поверхности координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения

из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат.
Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями


из которых следует, что при 


Уравнение (9) называется каноническим уравнением гиперболического параболоида.
Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение

из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.
рассмотрим сечение данного параболоида плоскостью Oyz (x=0).
из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения
из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10).
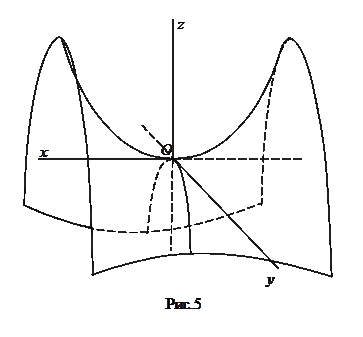
Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения

из которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h 0 и h
Поверхности второго порядка. Поверхности вращения.
Поверхность S называется поверхностью вращения вокруг оси OZ, если для любой точки M0(x0,y0,z0)
этой поверхности окружность, проходящая через эту точку в плоскости z=z0 с центром в (0,0,z0) и радиусом

Теорема (об уравнении поверхности вращения).
Если в некоторой декартовой прямоугольной системе координат поверхность S задана уравнением
F(x 2 +y 2 ,z)=0, то S — поверхность вращения вокруг оси OZ.
Эллипсоид:


Мнимый эллипсоид.
где a > 0, b > 0, c > 0. Эта поверхность не имеет ни одной вещественной точки.
Свойства эллипсоида.
1. Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что 

2. Эллипсоид обладает:
- центральной симметрией относительно начала координат,
- осевой симметрией относительно координатных осей,
- плоскостной симметрией относительно начала координат.
3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается
Однополостной гиперболоид.
Свойства однополостного гиперболоида.
1. Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что
2. Однополостной гиперболоид обладает:
- центральной симметрией относительно начала координат,
- осевой симметрией относительно всех координатных осей,
- плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается
эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.
 |  |
Двуполостной гиперболоид.
Свойства двуполостного гиперболоида.
1. Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует,
что 
2. Двуполостный гиперболоид обладает
- центральной симметрией относительно начала координат,
- осевой симметрией относительно всех координатных осей,
- плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, при
получается эллипс, при – точка, а в сечении плоскостями, перпендикулярными осям
Ox и Oy, – гипербола.
 |  |  |
 |  |
В случае, если a=b≠0, перечисленные выше (эллипсоид, однополостной гиперболоид, двуполостной
гиперболоид, эллиптический параболоид) поверхности являются поверхностями вращения.
Эллиптический параболоид.
Свойства эллиптического параболоида.
1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует,
что z ≥ 0 и принимает сколь угодно большие значения.
2. Эллиптический параболоид обладает:
- осевой симметрией относительно оси Oz,
- плоскостной симметрией относительно координатных осей Oxz и Oyz.
3. В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а
плоскостями, ортогональными осям Ox и Oy – парабола.
Уравнение эллиптического параболоида имеет вид:
Если a=b, то эллиптический параболоид представляет собой поверхность вращения, образованную
вращением параболы, параметр которой 
вершину и фокус данной параболы.
Пересечение эллиптического параболоида с плоскостью z=z0>0 является эллипсом.
Пересечение эллиптического параболоида с плоскостью x=x0 или y=y0 является параболой.
I. Теоретические сведения. 1. Эллиптический параболоид.
Читайте также:
|












 . (1)
. (1)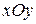 .
. (2)
(2) . (3)
. (3) , то линия пересечения эллипс;
, то линия пересечения эллипс; , то линия пересечения мнимый эллипс;
, то линия пересечения мнимый эллипс; , то линия пересечения пара мнимых пересекающихся прямых с действительной точкой пересечения.
, то линия пересечения пара мнимых пересекающихся прямых с действительной точкой пересечения.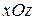 .
. (4)
(4) . (5)
. (5)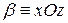 , и в сечении мы получаем параболу
, и в сечении мы получаем параболу  ;
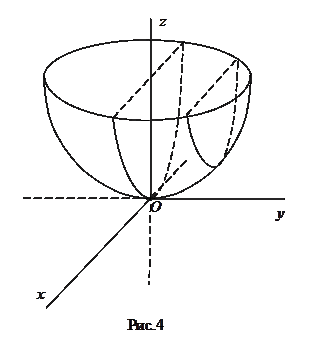
; .
.
 (6)
(6)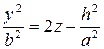 . (7)
. (7) , и в сечении мы получаем параболу
, и в сечении мы получаем параболу  .
.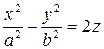 . (8)
. (8) (9)
(9) . (10)
. (10) (11)
(11) . (12)
. (12)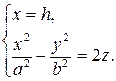 (13)
(13) Или
Или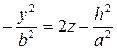 . (14)
. (14) .
. II.
II.  (15)
(15) II.
II.  (16)
(16)