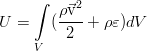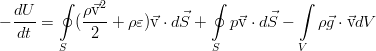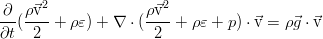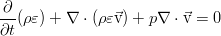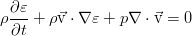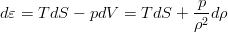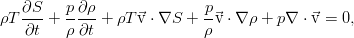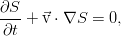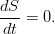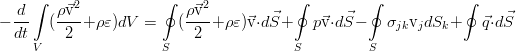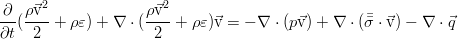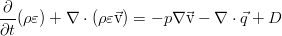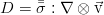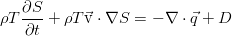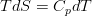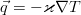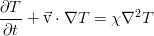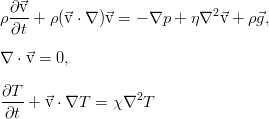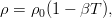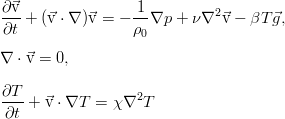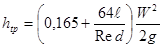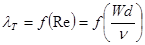Уравнение энергии для потока вязкой жидкости

Уравнение Бернулли

Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Уравнение Бернулли выглядит так:

Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.

Содержание статьи

Смысл уравнения Бернулли

По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.

Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.

В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.

Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.

Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.

Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную

Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.

В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид

Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.

Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.

Отсюда следует, что между напором и удельной энергией существует очень простая зависимость

где э – удельная энергия

Уравнение Бернулли для элементарной струйки реальной жидкости

Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.

При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.

Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет

Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается

Величина Э_1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.

Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h_1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде

Уравнение Бернулли для потока реальной жидкости

Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.

Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.

В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.

Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.

Слагаемое h_1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
— h_лп — линейные потери — сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
— h_мп — местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости

Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет

Видео по теме

Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.

Кратко о гидродинамике: сохранение энергии

В очередной раз извиняюсь за медленное написание постов в запланированной серии. В этот раз причина промедления объективна, в виде конференции в Вене, хотя и имеет значимую субъективную составляющую в виде собственного там участия и некоторых бюрократических моментов подготовки и оплаты.

Данный пост рассматривает законы сохранения энергии в идеальной и вязкой жидкости. Они заведомо необходимы для полноты описания движения, однако, в изотермическом случае теплообмена как такового нет, и потому для описания достаточно использовать уравнение Навье-Стокса и уравнение неразрывности. Надеюсь, этот пост будет последним из достаточно абстрактных постов, описывающих общую теорию и не практически привязанных к конкретным постановкам задач.

Постараюсь уменьшить количество выкладок, ибо они, конечно, важны, но результаты в виде конечных уравнений — важнее.

Перенос энергии в идеальной жидкости

Итак, сохранение энергии. Подход к описанию абсолютно стандартный — мы вводим некоторую величину, находим, какие механизмы отвечают за её изменение и пишем закон сохранения сперва в интегральной форме, а затем, сведя все поверхностные интегралы к объёмным по теореме Гаусса — в дифференциальной.

Энергия жидкости в классической гидродинамике, не учитывающей также такой эффект, как электропроводность и соответствующее взаимодействие с внешними и внутренними электромагнитными полями, складывается из внутренней и кинетической энергии. Она равна такому интегралу:

Изменяться в пределах нашего объёма V энергия может за счёт простого её перетекания вместе с потоком жидкости, работы сил давления от внешних элементов жидкости и работы внешних сил (ниже показаны на примере силы тяжести):

В идеальной жидкости нет трения, и потому нет рассеяния энергии за счёт вязкости. Кроме того, здесь пренебрегается и процессами теплопроводности, что так же присуще идеальной жидкости как отсутствие ещё одного механизма диссипации энергии. В дифференциальной форме закон сохранения полной энергии выглядит так:

Однако, его можно благополучно упростить. Воспользовавшись уравнением Эйлера (см. предыдущий пост), скалярно домноженным на скорость, можно выделить из полученного закона сохранения такую часть:

А это уже преобразуется к ещё более простому виду:

Тут уже можно вспомнить термодинамику. Первое начало термодинамики (с пометкой — для удельного объёма жидкости, т.е. объёма, масса которого равна единице):

позволяет вполне очевидным образом связать производные энергии, энтропии и плотности (как обратной объему величины). Используя эту связь дифференциалов величин в уравнении для энергии:

а также закон сохранения массы, получим ещё одно уравнение, которое описывает эволюцию энтропии в жидкости:

В движущейся системе отсчёта, привязанной к тому элементу жидкости, для которого это всё написано, уравнение упрощается ещё сильнее:

То есть, энтропия отдельной произвольной жидкой частицы (в идеальной жидкости) сохраняется. Энтропия просто пассивно переносится потоком, попутно связывая уравнением состояния давление и плотность среды.

Учёт вязкости. Уравнение теплопроводности

Теперь учтём вязкую и теплопроводную диссипацию. В интегральном виде они представляется парой добавочных слагаемых в законе сохранения:

Они описывают работу сил вязкого трения на границе элемента жидкости и тепловой поток через границу. В дифференциальной форме уравнение сохранения полной энергии:

Произведя ряд операций над этим соотношением с применением уравнения переноса импульса в общем виде (для произвольного тензора вязких напряжений) и уравнения неразрывности (а именно — домножив закон сохранения массы на половину квадрата скорости, закон сохранения импульса — на скорость, сложив их между собой и вычтя итог из уравнения для полной энергии), мы избавимся от слагаемых с кинетической энергией:

Здесь возникает диссипативная функция, равная двойной свёртке тензора вязких напряжений и тензора, который условно иногда называют градиентом скорости:

Применив здесь уравнение баланса массы и первое начало термодинамики аналогично тому, как это сделано выше, приходим к уравнению баланса энтропии:

Видно, что оно отличается от уравнения в идеальной жидкости только ненулевой правой частью. Для несжимаемой жидкости мы можем благополучно перейти от энтропии к более осязаемой величине, то бишь — к температуре, используя определение теплоёмкости при постоянном давлении:

Наконец, можно пренебречь диссипативной функцией, т.к. она описывает выделение за счёт внутреннего трения, и потому существенна только в жидкостях с очень большими вязкостями, а для потока тепла воспользоваться законом теплопроводности Фурье, позволяющим выразить его через температуру:

В итоге получается уравнение теплопроводности несжимаемой вязкой жидкости:

Согласно ему, температура элемента жидкости изменяется за счёт непосредственного конвективного переноса с потоком жидкости, а также за счёт вполне обычного механизма молекулярной теплопроводности (правая часть).

Конвекция. Приближение Буссинеска

Собственно, с описания задачи конвекции на хабре и начался весь этот гидродинамический «балаганчик». Итак, мы смотрим на баночку с несжимаемой вязкой жидкостью, например, водой. Движение её в случае неоднородной температуры в объёме описывается тремя уравнениями:

В общем случае в эту систему входит ещё уравнение состояния, связывающее плотность, давление и температуру. Однако тогда жидкость уже нельзя считать несжимаемой. Практика же (да и математика) показывает, что с достаточной точностью можно принять плотность постоянной везде, кроме слагаемого с силой тяжести. Более того, достаточно ограничиться линейным разложением по температуре:

Сразу отметим, что здесь записана уже не абсолютная температура, а уже отклонение от некоторого «нулевого» уровня, при котором плотность равна . Писать так нам позволяет уравнение теплопроводности, благо оно линейное и к таким сдвигам инвариантно. Можно выделить в слагаемом при силе тяжести независимую от температуры часть (гидростатический градиент) и спрятать её в давление:

И тогда мы приходим к уравнениям конвекции в приближении Буссинеска:

Данная модель практически общеупотребительна при изучении конвективных явлений, и на её основе было получено огромное количество самых разных по значимости результатов. В частности, в задачах устойчивости равновесия жидкости и прочих.

Проблема инструментария

Немного отступлю от темы, хотя прекрасно понимаю, что это может только разжечь лишнюю и отвлекающую дискуссию.

Знаете, что удивило в комментариях по предыдущему посту? То, что читатели уделяют много внимания вопросу математической строгости выкладок, которой тут, в общем-то, немного. Гидродинамика создана Эйлером и Навье во времена господства французского материализма, когда строгие результаты аналитической механики описали, казалось, весь мир. Но уровень строгости этих результатов таков, каким он мог быть в те времена, в едва только-только созданном Ньютоном и другими дифференциальном исчислении, и не выше. И таким он остался по сей день, и такой же является математическая строгость гидродинамики. Практически, это последняя классическая область науки, которая ещё имеет нерешённые фундаментальные проблемы. Может быть, не решены они именно потому, что сформулированы на том, старом, не сильно развитом и не богатом значительными средствами языке. Помнится, есть отдельные наработки в математике, где к уравнениям Навье-Стокса применяют аппарат, не к ночи будь помянут, биспиноров и гамма-матриц Дирака (основу квантовой теории поля) или ещё чего похуже. Но они до сих пор отдельные и практически неизвестные.

Лично я предполагаю, что развитие аппарата для решения уравнений Навье-Стокса ещё попросту не состоялось. Ведь, как известно, эти уравнения отлично описывают и упорядоченные ламинарные течения, и хаос турбулентности. А в уравнениях для этого всего-то достаточно изменить один управляющий параметр. Как в нелинейных системах (а-ля система Лоренца), которые тоже не имеют общих аналитических решений, да и, в целом, конкретного детального анализа свойств решений именно как математических функций. Многое на уровне поведения — тут хаос, там упорядочение, там синхронизация, здесь влияние параметра, а переход, по-видимому, происходит вот таким образом. Но ни о гладкости решений, ни об их существовании вопроса в таких задачах нет, в отличие от Навье-Стокса. Ведь мы же до сих пор практически не знаем — существуют ли вообще их общие гладкие решения.

Увидев в комментариях вещи навроде «набла — это 1-форма», сперва сильно задумался, не упустил ли чего в своём образовании. Да, про разного рода n-формы у меня в курсах упоминалось (но не более) в одном семестровом спецкурсе под названием теории групп в физике, из которого, правда, много вынести не удалось ввиду отсутствия серьёзной структурированности изложения. Но рассуждать о том, набла — вектор или же нет, никогда не приходится. В физике, не касающейся значительно математизированных проблем уровня, скажем, общей теории относительности и неотъемлемо нужной для неё дифференциальной геометрии, набла всегда была практически вектором. Конечно, не совсем обычным, не коммутирующим с ними и обладающим рядом иных свойств. Простой, в общем-то даже обычный оператор, который показывает, какую компоненту вектора и каким образом мы будем дифференцировать. Просто инструмент, которым мы умеем пользоваться в заданных пределах и осознаём, что нужно проверить его пригодность при выходе за границу привычной области, даже, например, при переходе от декартовых координат к тем же сферическим.

Иногда можно потратить излишне много времени на понимание устройства молотка, но так толком и не научиться забивать им гвозди. Например, почему он имеет такую форму, почему разные молоты имеют разную форму, а затем начать копать глубже — почему блестит металл, а деревянная ручка — нет, и др. Но от этого понимания сущность наиболее частого применения молотка не поменяется. Им будут забивать гвозди, выравнивать металл по оправке и т.д. — им всё равно будут стучать, желательно, не по пальцам.

На таком уровне находится моё личное знакомство с аппаратом квантовой электродинамики. По принципу — помню, что-то проходил. Более того, даже методичку в прошлом году издали с преподавателем этого предмета, но как-то оно всё равно в стороне — не занимаюсь этим.

Далее

Следующий пост будет посвящён проблемам устойчивости для равновесия и стационарного течения. Там в очередной раз мы увидим, что даже простейшие задачи гидродинамики не могут быть решены аналитически в полном виде, и потому приходится применять множество различных, на первый взгляд весьма спорных, но в то же время прекрасно работающих и обоснованных методик. Надеюсь, что уже удастся перейти от абстрактности к более осязаемым вещам.

Уравнение Бернулли для потока вязкой жидкости

При движении вязкой жидкости вдоль твердой стенки, например, в трубе происходит торможение потока вследствие влияния вязкости и в результате сил молекулярного сцепления между жидкостью и стенкой. Реализуется неравномерное распределение скоростей: у стенки скорость потока уменьшается до нуля (у смачиваемой жидкости), а в центральной части потока она максимальна (это применительно к течению в трубе). Кроме того движение вязкой жидкости часто сопровождается вращением макрочастиц жидкости, вихреобразованием и перемешиванием. Все это требует затрат энергии, поэтому удельная энергия жидкости (т.е. полный напор) не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений и, следовательно, уменьшается вдоль потока. Сказанное можно выразить следующим балансовым уравнением:

где Н_ср1 и Н_ср2 – средние значения полного напора в сечении 1 и 2 соответственно, ∑h – суммарная потеря напора (удельной энергии жидкости) на участке между рассматриваемыми сечениями.

Используя это уравнение, запись уравнения Бернулли для случая течения вязкой жидкости представляется в следующем виде

, (5)

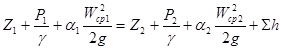
где Σh – суммарная потеря удельной энергии жидкости (напора) на участке между рассматриваемыми сечениями.

Энергия, теряемая жидкостью на рассматриваемом участке течения, не исчезает бесследно, а превращается в другую форму – тепловую. Эта энергия непрерывно рассеивается, поэтому повышение температуры жидкости практически мало заметно.

Гидравлические потери (общие сведения). Потери напора или, как их часто называют, гидравлические потери зависят от формы, размеров и шероховатости канала (трубы), от скорости течения и вязкости жидкости, но практически не зависят от абсолютного значения давления в жидкости.

Как показывает опыт, во многих случаях гидравлические потери приблизительно пропорциональны квадрату скорости потока. Поэтому в гидравлике с давних времен принят следующий общий способ выражения гидравлических потерь полного напора в линейных единицах:

(6)

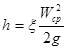
Такое выражение удобно тем, или в единицах давления

.

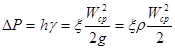
Такое выражение удобно тем, что включает в себя безразмерный коэффициент пропорциональности ξ, называемый коэффициентом сопротивления,и скоростной напор, входящий в уравнение Бернулли.

Гидравлические потери обычно подразделяют на два вида: местные потери и потери на трение.

Местные потери обусловлены так называемыми местными гидравлическими сопротивлениями, т.е. местными изменениями формы и размеров канала (трубы), вызывающими деформацию потока. При этом происходят изменения скорости потока, возникают вихреобразования. Примерами местных сопротивлений могут служить устройства типа задержек потока, сопел, диафрагм, отверстий (шайб), поворотов, вентилей, кранов, другой стендовой арматуры. Местные потери энергии (напора) определяются по формулам:

или (7)

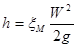
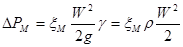
Последнее уравнение часто называют формулой Вейсбаха. В этих формулах W – средняя по сечению скорость в трубопроводе, в котором установлено местное сопротивление. Каждое местное сопротивление характеризуется своим значением коэффициента сопротивления ξ_М, которое во многих случаях приближенно можно считать постоянным для данного вида местного сопротивления.

Потери на трение, или потери по длине, — это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при установившемся течении, и возрастают пропорционально длине трубы. Этот вид потерь обусловлен трением о поверхность и внутренним трением в жидкости, а поэтому они (потери) имеют место в трубах со сколь угодно малой шероховатостью стенок.

Потерю давления на трение можно выразить по общей формуле для гидравлических потерь, т.е. 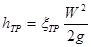, однако более удобнее будет коэффициент ξ_ТР связать с относительной длиной трубы ℓ/d соотношением ξ_ТР = λℓ/d.

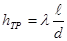
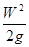
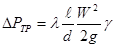
Тогда (8)

(9)

Формулу (9) обычно называют формулой Дарси. Безразмерный коэффициент λ называется коэффициентом потерь на трение или коэффициентом сопротивления трения.

Гидравлические потери в напорных потоках происходят за счет уменьшения вдоль потока удельной потенциальной энергии жидкости (Z + Р/γ). Удельная кинетическая энергия жидкости в этом случае если и меняется вдоль потока при заданном расходе, то не за счет потерь энергии, а вследствие изменения поперечного сечения канала, так как она зависит только от скорости, а скорость определяется объемным расходом Q и площадью сечения S: W = Q/S. Следовательно, в трубе постоянного сечения средняя скорость и удельная кинетическая энергия остаются строго постоянными, несмотря на наличие гидравлических потерь напора.

Расчет гидравлических потерь для разных конкретных случаев представляет собой один из основных вопросов гидравлики.

2. РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ В ТРУБАХ

Возможны два режима или два вида течения жидкостей в трубах: ламинарное, т.е. слоистое, течение и турбулентное, т.е. бурное, возмущенное.

Ламинарное течение – это течение без перемешивания слоев и частиц (макрочастиц) жидкости, без пульсаций скорости. Это течение является вполне упорядоченным и при постоянном напоре строго установившимся. Однако ламинарнре течение нельзя считать безвихревым. Хотя в нем нет ярко выраженных вихрей, но одновременно с поступательным движением жидкости имеет место упорядоченное вращательное движение отдельных частиц жидкости вокруг своих мгновенных центров вращения.

Турбулентное течение – это течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. Движение отдельных частиц оказывается неупорядоченным, траектории фрагментов жидкости имеют подчас вид замысловатых кривых. Это объясняется тем, что при турбулентном течении наряду с продольным перемещением массы жидкости имеют место поперечное и вращательное движения отдельных , как бы автономных, объемов жидкости.

Смена режима течения данной жидкости в трубе происходит при определенной скорости течения, которую называют критической (W_кр). Как показывают эксперименты, значение этой скорости прямо пропорционально кинематическому коэффициенту вязкости (ν) и обратно пропорционально диаметру трубы (d), т.е. W_кр = kν/d. Оказывается, что входящий в предыдущее соотношение безразмерный коэффициет k имеет универсальное значение, т.е. он одинаков для всех жидкостей и труб любых диаметров. Это означает, что смена режимов течения происходит при вполне определенном соотношении, которое можно выразить числом, между скоростью, диаметром трубы и вязкостью жидкости. Это безразмерное число называется критическим числом Рейнольдса по имени английского ученого, который экспериментально установил этот критерий:

(10)

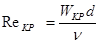
Как показывает опыт, критическое число Рейнольдса приблизительно равно 2300. Однако можно говорить не только о критическом числе Рейнольдса, определяющим смену режима течения, но и о числе Рейнольдса, характеным для того или иного потока, и выражать его через фактическую скорость потока, т.е.

(11)

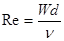
Таким образом, мы получили критерий, позволяющий судить о режиме течения жидкости в трубе. При значениях числа Rе Rе_КР течение обычно турбулентное.

Смена режимов течения при достижении числа Rе_КР объясняется тем, что один режим течения теряет устойчивость, а другой ее приобретает. При Rе Rе_КР, наоборот, турбулентный поток устойчив, а ламинарный – неустойчив. В связи с этим критическое число Рейнольдса, соответствующее переходу от ламинарного режима к турбулентному, может получиться несколько больше, чем для обратного перехода.

Гидродинамическое подобие. Гидродинамическое подобие – это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кинематическое и динамическое.

Геометрическое подобие, как известно из геометрии, означает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимается подобие поверхностей, которые ограничивают потоки жидкостей, т.е. подобие трубных каналов.

Кинематическое подобие – это геометрическое подобие канала и пропорциональность скоростей в сходственных сечениях.

Динамическое подобие означает пропорциональность сил, действующих на сходственные элементы кинематически подобных потоков

Осуществление на практике полного гидродинамического подобия оказывается весьма затруднительным, поэтому имеют, обычно, дело с частичным (неполным) подобием, при котором наблюдается пропорциональность лишь главных, основных для процесса, сил.

Физический смысл числа Рейнольдса заключается в том , что это – величина, пропорциональная отношению динамического давления к напряжению трения или, что то же самое, отношение сил инерции к силам вязкости. Поэтому закон гидродинамического подобия формулируется следующим образом: для гидродинамического подобия геометрически подобных потоков с учетом сил вязкости требуется равенство чисел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков.

МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ

Мы уже говорили, что гидравлические потери энергии делятся на две категории: местные потери и потери на трение. Рассмотрим более подробно потери, обусловленные местными гидравлическими сопротивлениями, т.е. такими элементами трубопровода, в которых вследствие изменения размеров или конфигурации канала происходит изменение скорости потока и возникают вихреобразования. Общий способ их выражения основан на экспериментальных данных и имеет следующий вид:

, (12)

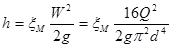
где Q – объемный расход, м 3 /с.

Задача теперь заключается в том, чтобы научиться определять коэффициенты сопротивления для различных трубных элементов, т.е. местных сопротивлений.

Простейшие местные гидравлические сопротивления можно разбить на следующие группы и подгруппы:

1. Расширение трубопровода (канала) – внезапное, плавное.

2. Сужение трубопровода (канала) – внезапное, плавное.

3. Поворот трубопровода (канала) – внезапный, плавный.

Более сложные случаи местных сопротивлений представляют собой комбинации перечисленных простейших сопротивлений. Рассмотрим некоторые местные сопротивления при турбулентном режиме течения. Следует отметить, что коэффициенты сопротивления ξ_М при турбулентном течении определяются почти исключительно формой гидравлического элемента и очень мало меняются с изменением размеров канала, скорости потока и вязкости жидкости. Поэтому их считают независящими от числа Рейнольдса, что означает автомодельность по числу Rе.

Значения коэффициентов местных сопротивлений в большинстве случаев получают экспериментальным путем, а затем пользуются обобщенными формулами или графиками. Однако для некоторых типов местных сопротивлений, а именно для внезапного расширения или для течения в диффузоре расчетные значения коэффициентов сопротивления имеют удовлетворительную точность. ДАЛЕЕ СЛЕДУЕТ ДЕМОНСТРАЦИЯ РИСУНКОВ МЕСТНЫХ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ, ВКЛЮЧАЯ СХЕМУ ВЕНТИЛЯ(рис.2)

Местные гидравлические сопротивления при ламинарном режиме.

Расчет потери напора на местных сопротивлениях при ламинарном режиме имеет особенности. Во — первых, местные сопротивления ври этом режиме играют меньшую роль по сравнению с потерями трения. Во – вторых, закон сопротивления в этом случае является более сложным и исследован в меньшей степени, чем при турбулентном режиме.

Если при турбулентном режиме потери напора на мастном сопротивлении не зависят от числа Рейнольдса, то при ламинарном режиме потерю напора h_м следует рассматривать как сумму:

где h_тр – потеря напора, обусловленная непосредственным действием сил трения (вязкости) в данном местном сопротивлении, пропорциональная вязкости жидкости и скорости в первой степени;

h_вихр – потеря, связанная с отрывом потока и вихреобразованиями, возникающими в самом местном сопротивлении или за ним, и пропорциональная квадрату скорости. Так, например, при течении через жиклер (рис. 3) слева от сечения 1. – 1 возникает потеря напора на трение, а справа – на вихреобразования. Формулу (12) можно представить в следующем виде:

, (14)

где А и В – безразмерные константы, зависящие от формы местного сопротивления. Разделив, согласно общему принципу определения коэффициента сопротивления, h_м на скоростной напор, получим общее выражение для коэффициента местного сопротивления при ламинарном режиме

(15)

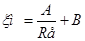
Соотношение между первым и вторым членами в формулах (14 и 15) зависит от формы местного сопротивления и числа Rе.

При широком диапазоне изменения числа Рейнольдса в одном и том же местном сопротивлении возможны как линейный (при малых числах Rе) так и квадратичный (при больших числах Rе) законы сопротивления, а также переходная между ними область сопротивления при средних числах Rе. Типичный график, иллюстрирующий сказанное, приведен на рис. . Такого рода графики для конкретных сопротивлений обычно строят на основе экспериментальных данных.

Иногда вместо двухчленной формулы выражения местных гидравлических потерь применяют степенной одночлен вида

h_м = kQ m , (16)

где k – размерная величина; m – показатель степени, зависящий от формы местного сопротивления и числа Рейнольдса и изменяющийся в пределах от 1 до 2.

ТЕЧЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ОСНОВНЫЕ РАСЧЕТНЫЕ ЗАВИСИМОСТИ

Ламинарное течение жидкости в круглой трубе.Как уже говорилось,ламинарное течение является строго упорядоченным слоистым течением без перемешивания жидкости; оно подчиняется закону трения Ньютона, суть которого в следующем: касательное напряжение в жидкости зависит от рода жидкости и характера течения и при слоистом течении изменяется прямо пропорционально поперечному градиенту скорости, т.е.

,

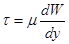
где μ – динамический коэффициент вязкости; наряду с динамическим коэффициентом вязкости μ применяется в гидравлике кинематический коэффициент вязкости ν, равный ν = μ/ρ, где ρ – плотность жидкости. (Размерность μ, н·сек / м 2 ; размерность ν, м 2 /сек).

Используя этот закон, находится распределение скоростей по сечению круглой трубы в ламинарном режиме течения жидкости и формула для определения расхода:

, (17)

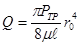
где Р_тр – перепад давления на участке трубы длиной ℓ, т.е. это потери от трения (потери трения).

Зная, что потери напора за счет трения определяются как h_тр = Р_тр/γ, находим

(18)

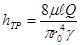
Заменяя μ через νρ и γ через ρg , а также переходя от r₀ к d = 2r₀, окончательно находится выражение

(19)

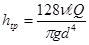
Полученный закон сопротивления показывает, что при ламинарном течении жидкости в круглой трубе потеря напора на трение пропорциональна расходу (скорости) и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон, часто называемый законом Пуазейля – Хагена, используется для расчета трубопроводов с ламинарным режимом течения.

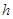
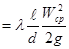
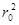
Так как по общему принципу (закон Дарси) _{тр ,} тогда, заменяя Q = W_ср π , окончательно получим . (20)

Связь средней скорости с потерей напора

Сопоставляя полученное выражение с формулой Дарси, видим,

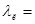
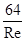
что (21)

Эту зависимость называют законом Пуазейля.

Зная закон распределения скоростей по сечению трубы и связь средней скорости с потерей напора, возможно определить значение коэффициента α, учитывающего неравномерность распределения скоростей в уравнении Бернулли (5).

Для ламинарного течения α₁ = α₂ =2

Теория ламинарного течения жидкости в круглой трубе, элементы которой были изложены в данном курсе, в общем хорошо подтверждается опытом. Полученные законы сопротивления и распределения скоростей не нуждаются в каких-либо поправках, за исключением следующих случаев.

1. При течении в начальном участке трубы, где происходит постепенное установление параболического профиля скоростей. Сопротивление на этом участке получается больше, чем на последующих участках трубы. Но это обстоятельство учитывается только при расчете очень коротких труб.

2. При течении со значительным теплообменом.

3. При очень высоких перепадах давления.

Потеря напора на участке трубы, длина которого ℓ меньше длины начального участка ℓ_нач, определяется по формулам (20 и 21), но с поправочным коэффициентом К, большим единицы. Так при ℓ = ℓ_нач К = 1,09. Для коротких труб значение поправочного коэффициента К существенно отличается от единицы. Определить длину начального участка можно по приближенной формуле Шиллера:

В литературных источниках встречаются и другие оценочные зависимости для определения длины начального участка

В том случае, когда длина трубы ℓ больше длины начального участка ℓ_нач, потеря напора будет складываться из потери на начальном участке и потери на участке стабилизированного течения:

или с учетом (21) и (22)

Если относительная длина трубопровода ℓ/d достаточно велика, то дополнительный член в скобках, равный 0,165 можно не учитывать.

Течение с теплообменом.При течении жидкости, которое сопровождается ее охлаждением, слои жидкости, непосредственно прилегающие к стенке, имеют температуру более низкую, а вязкость более высокую, чем в основном ядре потока. Это ведет к более сильному торможению пристенных слоев жидкости и уменьшению градиента скорости у стенки.

При течении, сопровождающемся нагреванием жидкости через стенку, ситуация меняется наоборот: вязкость пристенных слоев уменьшается, пристенный градиент скорости возрастает.

Таким образом, в результате теплообмена через стенку трубы происходит нарушение обычного параболического закона распределения скоростей. Это показано на рис. . Здесь 1 – распределение скоростей при изотермическом течении, 2 – при течении с охлаждением, 3 – при течении с нагреванием. Это вызывает изменение коэффициента α в уравнении Бернулли: охлаждение ведет к усилению неравномерности распределения скоростей (α > 2), нагревание ослабляет эту неравномерность (α 6 , α = 1,025,т.е. α асимптотически приближается к единице.

В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах, пользуются экспериментальными данными, систематизированными на основе гидродинамической теории подобия. Основной расчетной формулой для турбулентного течения в круглых трубах является уже рассмотренная нами универсальная формула:

,здесь λ ≡ λ_Т – коэффициент потерь на трение при турбулентном режиме

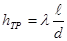
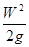
или ,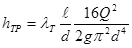

если скорость потока выразить через расход.

Видим, что при турбулентном течении потеря напора на трение пропорциональна квадрату скорости потока (и квадрату расхода). Но из закона гидродинамического подобия следует, что коэффициент λ_Т как и коэффициент λ_Л должен являться функцией числа Рейнольдса, содержащего скорость потока, вязкость жидкости и диаметр трубы

Существует ряд эмпирических и полуэмпирических формул, представляющих эту зависимость для турбулентного течения в гладких трубах. Одной из наиболее удобных и употребительных зависимостей является формула Конакова, которая имеет следующий вид:

(24)

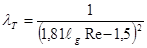
Эта формула применима от Rе = Rе_кр до Rе, равного нескольким миллионам. При числах Рейнольдса от 2300 до ≈ 10 5 можно пользоваться формулой Блазиуса

(25)

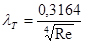
Из формул (24) и (25) видно, что коэффициент λ уменьшается с увеличением числа Рейнольдса, но это уменьшение гораздо менее значительно, чем при ламинарном режиме.

Приведенные формулы для определения коэффициента потерь на трение через число Rе справедливы для так называемых технически гладких (гидравлически гладких) труб, т.е. для таких, шероховатость которых столь мала, что практически не влияет на сопротивление. Именно такие трубы применяются в стендовой практике.

Экспериментально установлено, что при турбулентном режиме существуют три области, в которых коэффициент λ по-разному зависит от числа Rе:

1. Область гидравлически гладких труб.

2. Переходная область.

3. Область гидравлически шероховатых труб.

Физическая картина существования этих областей в одной и той же трубе объясняется следующим образом. У всякой трубы на стенке имеются выступы шероховатости. Их высота зависит от материала труб технологии их изготовления, времени эксплуатации и др. факторов. В турбулентном потоке скорости непосредственно у стенки равны нулю. Поэтому вблизи стенок образуется тонкий слой жидкости толщиной δ, где скорости столь малы, что в его пределах движение жидкости близко к ламинарному. Этот слой, толщина которого измеряется долями миллиметра, называется вязким (ламинарным) подслоем (рис. 4). Если через Δ обозначить среднюю высоту выступов шероховатости, то возможны следующие соотношения δ и Δ. При δ > Δ выступы шероховатости прикрыты вязким подслоем, турбулентная часть потока не касается выступов и скользит по ламинарному слою, как по гладкой трубе. В этом случае трубы рассматриваются как гидравлически гладкие и потери давление на трение не зависят от шероховатости трубы. Если δ