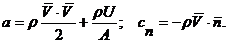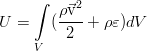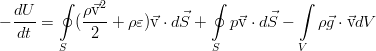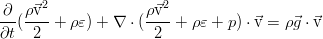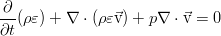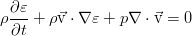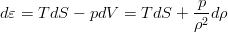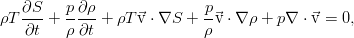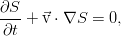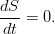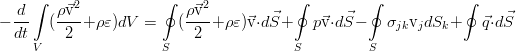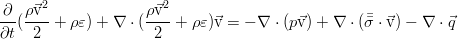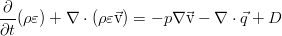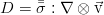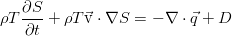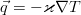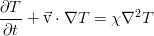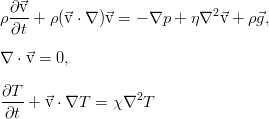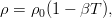Уравнение энергии в дифференциальной форме

Дифференциальное уравнение энергии и примеры

Дифференциальное уравнение энергии

• Дифференциальное уравнение энергии определяет распределение температуры в теле выводится на основе закона сохранения энергии и метода Фурье. Получаем уравнение движущейся среды, в которой внутренний источник тепла находится равномерно. Предполагается, что теплоноситель является изотропным, однородным по теплопроводности х, теплоемкости. Температура не зависит от cp и плотности p.

Рассмотрим только системы, которые могут игнорировать изменение кинетической энергии по сравнению с изменением энтальпии. Выберите основной параллелепипед, закрепленный плоскостью χχ, лукгг, и укажите количество тепла, поступающего между ними. c-это 00 ’x, ЦЦ’ ц и ^ 2.И Л0.2.1), компонент средней скорости A) X, шц, а, а>, и те, которые передают мощность внутреннего источника тепла W! это м3. Исходя из закона сохранения энергии, тепловой баланс рассматриваемого параллелепипеда принимает вид.

Частицы жидкости за пределами пограничного слоя способны двигаться, преодолевая возрастающее давление за кормовой половиной, благодаря переходу их кинетической энергии в энергию давления. Людмила Фирмаль

Разность количества тепла, поступающего в параллелепипед и выходящего из него, Л(> r-изменение внутреннего тепловыделения, энтальпия основного объема. тепло, поступающее в коробку по оси x и выходящее из нее, можно определить по формуле: ^ ’х = Д’ х(1yLxLx, (2.2） 4 Где u-плотность теплового потока, соответствующая координатам x и x + Ox соответственно. Расширьте значение$ряда Тейлора и ограничьте его первыми 2 членами ряда (2.4） Принимая во внимание формулу (2.4), разницу в количестве тепла, входящего и выходящего из параллелепипеда вдоль оси x, можно описать следующим образом.

• Общее количество тепла, накопленного параллелепипедом, составляет (2.5). Внутреннее тепловыделение определяется по формуле = IV О. (2.6). Изменения температуры в неподвижной первичной тропосфере О лелепипед вовремя-будет ah. So … а б-КФР-Ахау. (2.7） Формула(2.(2.5), (2.6) и (2.7). Вы можете получить уравнение Рассмотрим более подробно составляющие плотности теплового потока, содержащиеся в Формуле (2.8).ЗначениеX записывается как: Гдеhtepl и Chh kop-плотность теплового потока, поступающего в параллелепипед за счет теплопроводности вдоль оси x и конвективного переноса. На основе правил Фурье Конвекционный компонент-это.

Где u> x-составляющая скорости потока вдоль x-axis. So … ？х = pcrr> Х. Если X = const1, то это равенство равно Для других осей также： Здесь и находится составляющая скорости потока вдоль оси y и оси r. Если подставить эти равенства в Формулу (2.8)、 (2.12） Дифференциальное уравнение неразрывности несжимаемости! Форма жидкости является* С этой- й точки зрения уравнение (2.12) сводится к следующему виду: A. a-a-a-a-a-a-a-v-2_ ДГ ДХ делать Здесь+ Проводимость.

Как видно из фотографии, поток обтекает цилиндр с двух сторон, отрываясь от его поверхности, и у кормовой половины образуется зона с завихрениями. Людмила Фирмаль

Температурный коэффициент В общем случае I-I(x, y, r, m). Итак, используя понятие полной производной, можно записать: Л1 Д1, Д1 ЛК д! дю, Д1 ЛГ ДХ ДХ ЛГ + у ДТ ДГ ЛГ Это производное называется субстантивным, 01, 01 by. м. символ-г- Заменить левую часть равенства (2.13) значением равенства (2.14), получаем дифференциальное уравнение (2.15） В цилиндрической системе координат дифференциального уравнения(2.15) значение величины V2 имеет следующий вид: (2.16） Упрощенные предположения об инвариантности коэффициента теплопроводности могут привести к серьезным ошибкам, так как температура в системе существенно меняется, а Х во многом зависит от температуры.

Выражения (2.10) и (2.11) принимают аналогичный вид form. In в этом случае дифференциальное уравнение(2.15) описывается следующим образом: 01 ПЦР=- Рассмотренные типы дифференциальных уравнений энергии подходят как для ламинарного, так и для турбулентного течения flows. In в последнем случае формула включает в себя мгновенные или так называемые действительные значения температуры и скорости, изменения которых естественным образом пульсируют во времени. Дифференциальные уравнения энергии также могут быть описаны с использованием усредненных по времени температур и скоростей.

Временной интервал усреднения фактических параметров турбулентности выбирается таким образом, чтобы среднее значение не зависело от размера интервала. Проводимость k заменяется суммой k + X. Где X-коэффициент турбулентного теплообмена. Величина Xm зависит от расстояния до стенки: вблизи стенки Xm — > 0, а расстояние-Xm может быть во много раз больше k.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Общее уравнение энергии в интегральной и дифференциальной формах

Как уже говорилось раньше, при изучении физических свойств жидкостей вязкость существенно зависит от температуры жидкости и почти не зависит от плотности и давления. При этом коэффициент динамической вязкости m и коэффициент кинематической вязкости n у капельных жидкостей с ростом температуры уменьшаются, а у газов возрастают.

Общее уравнение энергии в интегральной форме.

Три уравнения сохранения для газов – количества движения, массы и энергии, в интегральной форме могут быть записаны следующим образом

причем в первом случае

В приведенных равенствах: – (τ) – произвольный объем жидкости, ограниченный покерхностью (S), — единичный вектор внешней нормали к (S), t₁ и t₂ — два каких-то момента времени, p – давление, ρ – плотность, — скорость (вектор), U – внутренняя энергия единицы массы в какой-либо точке объема (τ) или поверхности (S).

Общее уравнение энергии в дифференциальной форме.

Для той части жидкости, в которой гидродинамические элементы и их первые производные непрерывны, можно написать уравнения в дифференциальной форме:

уравнение движения (приращение количества движения частицы жидкости равно импульсу силы)

уравнение неразрывности (сохранения массы)

уравнение энергии (условие адиабатичности)

Здесь k – отношение теплоемкостей C_p/C_v. Для воздуха k = 1,4.

Уравнение Д.Бернулли для газов

При установившемся одномерном плавноизменяющемся адиабатичесеком движении газа, как и для несжимаемой жидкости, можно поток разбить на элементарные струйки. При этом живые сечения потока можно считать плоскими. Для такого потока газа будут справедливы:

уравнение Д.Бернулли в интегральной форме: вдоль потока

уравнение Д.Бернулли в дифференциальной форме

уравнение неразрывности (постоянства массы)

В последних равенствах w – средняя скорость течения в живом сечении потока.

Число Маха

Многие свойства потока сжимаемой жидкости и характер взаимодействия его с окружающей средой зависят от соотношения скорости движения потока и скорости звука в нем. Учитывая важность этого обстоятельства, в гидродинамике сжимаемой жидкости рассматриваются два вида одномерного движения потоков:

— дозвуковое течение, когда скорость движения потока меньше скорости звука; и

— сверхзвуковое течение, когда скорость движения потока превосходит скорость звука в нем.

Сжимаемость жидкости часто характеризуют безразмерной величиной, равной отношению скорости потока сжимаемой жидкости w к скорости звука в нем a. Это отношение называют числом Маха или числом М:

Кратко о гидродинамике: сохранение энергии

В очередной раз извиняюсь за медленное написание постов в запланированной серии. В этот раз причина промедления объективна, в виде конференции в Вене, хотя и имеет значимую субъективную составляющую в виде собственного там участия и некоторых бюрократических моментов подготовки и оплаты.

Данный пост рассматривает законы сохранения энергии в идеальной и вязкой жидкости. Они заведомо необходимы для полноты описания движения, однако, в изотермическом случае теплообмена как такового нет, и потому для описания достаточно использовать уравнение Навье-Стокса и уравнение неразрывности. Надеюсь, этот пост будет последним из достаточно абстрактных постов, описывающих общую теорию и не практически привязанных к конкретным постановкам задач.

Постараюсь уменьшить количество выкладок, ибо они, конечно, важны, но результаты в виде конечных уравнений — важнее.

Перенос энергии в идеальной жидкости

Итак, сохранение энергии. Подход к описанию абсолютно стандартный — мы вводим некоторую величину, находим, какие механизмы отвечают за её изменение и пишем закон сохранения сперва в интегральной форме, а затем, сведя все поверхностные интегралы к объёмным по теореме Гаусса — в дифференциальной.

Энергия жидкости в классической гидродинамике, не учитывающей также такой эффект, как электропроводность и соответствующее взаимодействие с внешними и внутренними электромагнитными полями, складывается из внутренней и кинетической энергии. Она равна такому интегралу:

Изменяться в пределах нашего объёма V энергия может за счёт простого её перетекания вместе с потоком жидкости, работы сил давления от внешних элементов жидкости и работы внешних сил (ниже показаны на примере силы тяжести):

В идеальной жидкости нет трения, и потому нет рассеяния энергии за счёт вязкости. Кроме того, здесь пренебрегается и процессами теплопроводности, что так же присуще идеальной жидкости как отсутствие ещё одного механизма диссипации энергии. В дифференциальной форме закон сохранения полной энергии выглядит так:

Однако, его можно благополучно упростить. Воспользовавшись уравнением Эйлера (см. предыдущий пост), скалярно домноженным на скорость, можно выделить из полученного закона сохранения такую часть:

А это уже преобразуется к ещё более простому виду:

Тут уже можно вспомнить термодинамику. Первое начало термодинамики (с пометкой — для удельного объёма жидкости, т.е. объёма, масса которого равна единице):

позволяет вполне очевидным образом связать производные энергии, энтропии и плотности (как обратной объему величины). Используя эту связь дифференциалов величин в уравнении для энергии:

а также закон сохранения массы, получим ещё одно уравнение, которое описывает эволюцию энтропии в жидкости:

В движущейся системе отсчёта, привязанной к тому элементу жидкости, для которого это всё написано, уравнение упрощается ещё сильнее:

То есть, энтропия отдельной произвольной жидкой частицы (в идеальной жидкости) сохраняется. Энтропия просто пассивно переносится потоком, попутно связывая уравнением состояния давление и плотность среды.

Учёт вязкости. Уравнение теплопроводности

Теперь учтём вязкую и теплопроводную диссипацию. В интегральном виде они представляется парой добавочных слагаемых в законе сохранения:

Они описывают работу сил вязкого трения на границе элемента жидкости и тепловой поток через границу. В дифференциальной форме уравнение сохранения полной энергии:

Произведя ряд операций над этим соотношением с применением уравнения переноса импульса в общем виде (для произвольного тензора вязких напряжений) и уравнения неразрывности (а именно — домножив закон сохранения массы на половину квадрата скорости, закон сохранения импульса — на скорость, сложив их между собой и вычтя итог из уравнения для полной энергии), мы избавимся от слагаемых с кинетической энергией:

Здесь возникает диссипативная функция, равная двойной свёртке тензора вязких напряжений и тензора, который условно иногда называют градиентом скорости:

Применив здесь уравнение баланса массы и первое начало термодинамики аналогично тому, как это сделано выше, приходим к уравнению баланса энтропии:

Видно, что оно отличается от уравнения в идеальной жидкости только ненулевой правой частью. Для несжимаемой жидкости мы можем благополучно перейти от энтропии к более осязаемой величине, то бишь — к температуре, используя определение теплоёмкости при постоянном давлении:

Наконец, можно пренебречь диссипативной функцией, т.к. она описывает выделение за счёт внутреннего трения, и потому существенна только в жидкостях с очень большими вязкостями, а для потока тепла воспользоваться законом теплопроводности Фурье, позволяющим выразить его через температуру:

В итоге получается уравнение теплопроводности несжимаемой вязкой жидкости:

Согласно ему, температура элемента жидкости изменяется за счёт непосредственного конвективного переноса с потоком жидкости, а также за счёт вполне обычного механизма молекулярной теплопроводности (правая часть).

Конвекция. Приближение Буссинеска

Собственно, с описания задачи конвекции на хабре и начался весь этот гидродинамический «балаганчик». Итак, мы смотрим на баночку с несжимаемой вязкой жидкостью, например, водой. Движение её в случае неоднородной температуры в объёме описывается тремя уравнениями:

В общем случае в эту систему входит ещё уравнение состояния, связывающее плотность, давление и температуру. Однако тогда жидкость уже нельзя считать несжимаемой. Практика же (да и математика) показывает, что с достаточной точностью можно принять плотность постоянной везде, кроме слагаемого с силой тяжести. Более того, достаточно ограничиться линейным разложением по температуре:

Сразу отметим, что здесь записана уже не абсолютная температура, а уже отклонение от некоторого «нулевого» уровня, при котором плотность равна 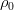. Писать так нам позволяет уравнение теплопроводности, благо оно линейное и к таким сдвигам инвариантно. Можно выделить в слагаемом при силе тяжести независимую от температуры часть (гидростатический градиент) и спрятать её в давление:

И тогда мы приходим к уравнениям конвекции в приближении Буссинеска:

Данная модель практически общеупотребительна при изучении конвективных явлений, и на её основе было получено огромное количество самых разных по значимости результатов. В частности, в задачах устойчивости равновесия жидкости и прочих.

Проблема инструментария

Немного отступлю от темы, хотя прекрасно понимаю, что это может только разжечь лишнюю и отвлекающую дискуссию.

Знаете, что удивило в комментариях по предыдущему посту? То, что читатели уделяют много внимания вопросу математической строгости выкладок, которой тут, в общем-то, немного. Гидродинамика создана Эйлером и Навье во времена господства французского материализма, когда строгие результаты аналитической механики описали, казалось, весь мир. Но уровень строгости этих результатов таков, каким он мог быть в те времена, в едва только-только созданном Ньютоном и другими дифференциальном исчислении, и не выше. И таким он остался по сей день, и такой же является математическая строгость гидродинамики. Практически, это последняя классическая область науки, которая ещё имеет нерешённые фундаментальные проблемы. Может быть, не решены они именно потому, что сформулированы на том, старом, не сильно развитом и не богатом значительными средствами языке. Помнится, есть отдельные наработки в математике, где к уравнениям Навье-Стокса применяют аппарат, не к ночи будь помянут, биспиноров и гамма-матриц Дирака (основу квантовой теории поля) или ещё чего похуже. Но они до сих пор отдельные и практически неизвестные.

Лично я предполагаю, что развитие аппарата для решения уравнений Навье-Стокса ещё попросту не состоялось. Ведь, как известно, эти уравнения отлично описывают и упорядоченные ламинарные течения, и хаос турбулентности. А в уравнениях для этого всего-то достаточно изменить один управляющий параметр. Как в нелинейных системах (а-ля система Лоренца), которые тоже не имеют общих аналитических решений, да и, в целом, конкретного детального анализа свойств решений именно как математических функций. Многое на уровне поведения — тут хаос, там упорядочение, там синхронизация, здесь влияние параметра, а переход, по-видимому, происходит вот таким образом. Но ни о гладкости решений, ни об их существовании вопроса в таких задачах нет, в отличие от Навье-Стокса. Ведь мы же до сих пор практически не знаем — существуют ли вообще их общие гладкие решения.

Увидев в комментариях вещи навроде «набла — это 1-форма», сперва сильно задумался, не упустил ли чего в своём образовании. Да, про разного рода n-формы у меня в курсах упоминалось (но не более) в одном семестровом спецкурсе под названием теории групп в физике, из которого, правда, много вынести не удалось ввиду отсутствия серьёзной структурированности изложения. Но рассуждать о том, набла — вектор или же нет, никогда не приходится. В физике, не касающейся значительно математизированных проблем уровня, скажем, общей теории относительности и неотъемлемо нужной для неё дифференциальной геометрии, набла всегда была практически вектором. Конечно, не совсем обычным, не коммутирующим с ними и обладающим рядом иных свойств. Простой, в общем-то даже обычный оператор, который показывает, какую компоненту вектора и каким образом мы будем дифференцировать. Просто инструмент, которым мы умеем пользоваться в заданных пределах и осознаём, что нужно проверить его пригодность при выходе за границу привычной области, даже, например, при переходе от декартовых координат к тем же сферическим.

Иногда можно потратить излишне много времени на понимание устройства молотка, но так толком и не научиться забивать им гвозди. Например, почему он имеет такую форму, почему разные молоты имеют разную форму, а затем начать копать глубже — почему блестит металл, а деревянная ручка — нет, и др. Но от этого понимания сущность наиболее частого применения молотка не поменяется. Им будут забивать гвозди, выравнивать металл по оправке и т.д. — им всё равно будут стучать, желательно, не по пальцам.

На таком уровне находится моё личное знакомство с аппаратом квантовой электродинамики. По принципу — помню, что-то проходил. Более того, даже методичку в прошлом году издали с преподавателем этого предмета, но как-то оно всё равно в стороне — не занимаюсь этим.

Далее

Следующий пост будет посвящён проблемам устойчивости для равновесия и стационарного течения. Там в очередной раз мы увидим, что даже простейшие задачи гидродинамики не могут быть решены аналитически в полном виде, и потому приходится применять множество различных, на первый взгляд весьма спорных, но в то же время прекрасно работающих и обоснованных методик. Надеюсь, что уже удастся перейти от абстрактности к более осязаемым вещам.