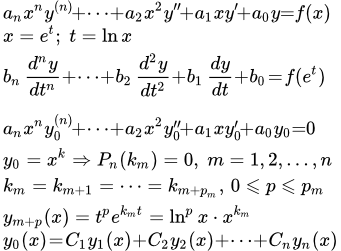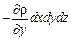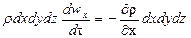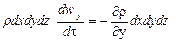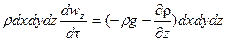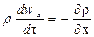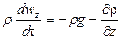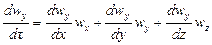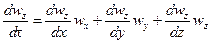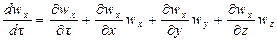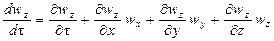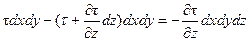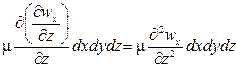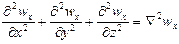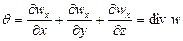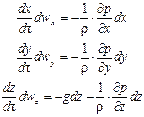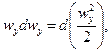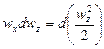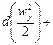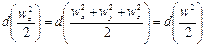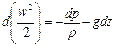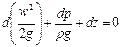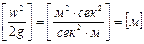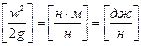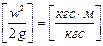Дифференциальное уравнение Эйлера и методы его решения
Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.
Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.
Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;
;
;
.
Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.
Решение однородного уравнения Эйлера
Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.
Рассмотрим действительные корни. Пусть ki – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.
Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть ki – кратный корень кратности m . Выразим комплексный корень ki через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.
После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .
Примеры
Решение неоднородного уравнения Эйлера
Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.
Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).
Пример
Неоднородное уравнение Эйлера со специальной неоднородной частью
Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.
Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.
Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020
Дифференциальные уравнения движения Эйлера
Рассмотрим установившийся поток идеальной жидкости. Как уже говорилось, она не обладает вязкостью, т.е. движется без трения.
Как и при выводе дифференциальных уравнений равновесия Эйлера, выделим в потоке элементарный параллелепипед объемом dV = dxdydz, ориентированный относительно осей координат (см. рис. II-2).
Проекции на оси координат сил тяжести и давления, действующих на параллелепипед, составляют;
для оси х:
для оси у:
для оси z: 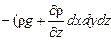
Согласно основному принципу динамики, сумма проекций сил, дейcтвующих на движущийся элементарный объем жидкости, равна произведению массы жидкости на ее ускорение.
Масса жидкости в объеме параллелепипеда
Если жидкость движется со скоростью ли, то ее ускорение равно w, то проекции ускорения на оси координат: 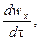
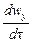
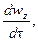
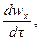
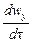

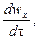
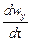
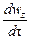
В соответствии с основным принципом динамики
или после сокращения
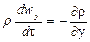
где, согласно уравнению (II,28а), субстанциональные производные соответствующих составляющих скорости равны
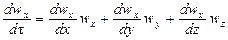
Система уравнений (II,46) с учетом выражений (II,47) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлерадля установившегося потока.
При неустановившемся движении скорость жидкости изменяется не только при перемещении частицы потока из одной точки пространства в другую, но и с течением времени в каждой точке. Поэтому, в соответствии с уравнением (II,28), составляющие ускорения в уравнении (II,46), выражаемые субстанциональными производными для неустановившихся условий, имеют вид:
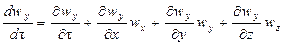
Система уравнений (II,46) с учетом выражений (II,47а) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлера для неустановившегося потока.
Интегралом уравнений движения Эйлера для установившегося потока является уравнение Бернулли, широко используемое для решения многих технических задач.
4. Дифференциальные уравнения движения Навье-Стокса
При движении реальной (вязкой) жидкости в потоке жидкости помимо сил давления и тяжести действуют также силы трения.
Действие сил трения Т на выделенный в потоке вязкой жидкости элементарный параллелепипед (рис. II-14) проявляется в возникновении на его поверхности касательных напряжений t.
Рассмотрим первоначально относительно простой случай одномерного плоского потока капельной жидкости в направлении оси х, когда проекция скорости wx зависит только от расстояния r до горизонтальной плоскости отсчета.
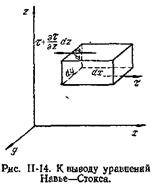

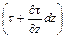
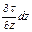
Указанные на рис. II-14 стрелками направления сил трения, приложенных к параллелепипеду на его нижней и верхней гранях, обусловлены, например, тем, что более медленные вышележащие слои жидкости затормаживают слой, в котором находится параллелепипед, а более быстрые нижележащие слои «разгоняют» его.
Тогда проекция равнодействующей сил трения на ось х
Подставив в это выражение значение касательного напряжения t по уравнению (II,12а) [t = 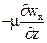
В более общем случае трехмерного потока составляющая скорости wx будет изменяться не только в направлении z, но и в направлениях всех трех осей координат. Тогда проекция равнодействующей сил трения на ось x примет вид
Сумму вторых производных по осям координат называют оператором Лапласа:
Следовательно, проекция равнодействующей сил трения на ось х может быть представлена как m 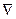
Соответственно проекции равнодействующей сил трения:
на ось у: m 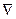
на ось z: m 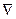
Проекции на оси координат равнодействующей всех сил (тяжести, давления и трения), действующих на элементарный объем капельной жидкости (с учетом проекций сил тяжести и давления, полученных при выводе уравнений Эйлера), составляют:
на ось х: ( 
на ось у: ( 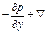
на ось z: ( 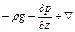
Суммы проекций сил на оси координат, в соответствии с основным принципом динамики, должны быть равны произведению массы жидкости rdxdydz (r — плотность жидкости), заключенной в элементарном объеме, на проекции ускорения на оси координат. Поэтому, приравнивая проекции равнодействующей произведениям массы на проекции ускорения, после сокращения на dxdydz, получим
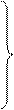
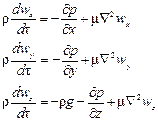
где соответствующие субстанциональные производные выражены для установившегося и неустановившегося потоков уравнениями (II,47) или (II,47а).
Уравнения (II,48) представляют собой уравнения Навье-Cтокса, описывающие движение вязкой капельной жидкости.
При движении сжимаемой жидкости (газа) в ней дополнительно возникают вызванные трением силы сжатия и растяжения, поэтому уравнения Навье-Стокса принимают вид:
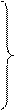
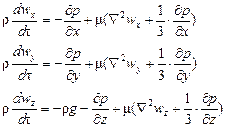
где частные производные 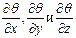
Левые части уравнений (II,48) выражают произведение массы единицы объема r на проекцию ее ускорения, т.е. представляют собой проекции равнодействующей сил инерции, возникающих в движущейся жидкости.
В правых частях тех же уравнений произведение pg отражает влияние сил тяжести, частные производные 
Каждый член уравнений (II,48) имеет размерность соответствующей силы (тяжести, давления, трения или инерции), отнесенной к единице объема жидкости.
При движении идеальной жидкости, когда силы трения отсутствуют, при подстановке m = 0 в уравнения (II,48) последние совпадают с уравнениями (II,46), т.е. уравнения движения Эйлера можно получить как частный случай уравнений Навье-Стокса.
Полное описание движения вязкой жидкости в его наиболее общей форме возможно путем решения уравнений Навье-Стокса совместно с уравнением неразрывности потока. Однако уравнения Навье-Стокса не могут быть решены в общем виде. Получены решения этой сложной системы уравнений только для некоторых частных случаев. Так, для установившегося ламинарного движения жидкости решение уравнений Навье-Cтокса позволяет вывести уравнение Пуазейля, полученное выше другим способом.
В большинстве же наиболее важных для промышленной практики случаев применение уравнений Навье-Стокса становится возможным либо при ряде упрощающих допущений, либо при преобразовании этих сравнений методами теории подобия.
5. Уравнение Бернулли
Решение уравнений движения Эйлера для установившегося потока приводит к одному из наиболее важных и широко используемых уравнений гидродинамики — уравнению Бернулли.
Умножив левые и правые части каждого из уравнений (II,46) соответственно на dx, dy и dz и разделив на плотность р жидкости, получим
Сложим эти уравнения, учитывая, что производные 
Слагаемые левой части этого уравнения могут быть представлены как
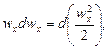
следовательно, их сумма
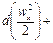
где w = 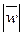
В то же время сумма членов, стоящих в скобках в правой части записанного уравнения, представляет собой полный дифференциал давления dp (при установившихся условиях давление зависит лишь от положения точки в пространстве, но в каждой данной точке не меняется со временем). Значит
Разделив обе части этого уравнения на ускорение свободного падения g и перенеся все его члены в левую часть, находим
причем для несжимаемой однородной жидкости r = const.
Сумма дифференциалов может быть заменена дифференциалом суммы, следовательно
Уравнение (II,49) для любых двух поперечных сечений 1 и 2 потока (трубопровода) можно представить в виде
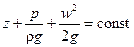
Уравнение (II,49) является уравнением Бернулли для идеальной жидкости.
Величину 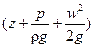
Следовательно, согласно уравнению Бернулли, для всех поперечных сечений установившегося потока идеальной жидкости гидродинамический напор остается неизменным.
Гидродинамический напор включает три слагаемых, из которых первые два слагаемых, z и 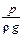
z — нивелирная высота, называемая также геометрическим, или высотным, напором (hг), представляет собой удельную потенциальную энергию положения в данной точке (данном сечении);
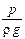
Сумма z+ 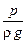
Величины z и 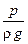
Третья составляющая, 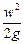
или после умножения и деления на единицу веса (н — в СИ или кгс – в системе МКГСС)
Величину называют скоростным, или динамическим напором и обозначают через hck. Скоростной напор характеризует удельную кинетическую энергию в данной точке (данном сечении).
Таким образом, согласно уравнению Бернулли, при установившемся движении идеальной жидкости сумма скоростного и статического напоров, равная гидродинамическому напору, не меняется при переходе от одного поперечного сечения потока к другому.
Вместе с тем из уравнения Бернулли в соответствии с энергетическим смыслом его членов следует, что при установившемся движении идеальной жидкости сумма потенциальной (z + 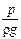
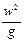
При изменении поперечного сечения трубопровода и соответственно скорости движения жидкости происходит превращение энергии: при сужении трубопровода часть потенциальной энергии давления переходит в кинетическую и, наоборот, при расширении трубопровода часть кинетической энергии переходит в потенциальную, но общее количество энергии остается постоянным. Отсюда следует, что для идеальной жидкости количество энергии, поступающей с потоком через начальное сечение трубопровода, равно количеству энергии, удаляющейся с потоком через конечное сечение трубопровода.
Таким образом, уравнение Бернулли является частым случаем закона сохранения энергии и выражает энергетический баланс потока.
Если умножить левую и правую части уравнения (II,50) на удельный вес жидкости g = rg, то уравнение Бернулли для идеальной жидкости может быть представлено в виде
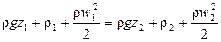
В уравнении (II,50а) каждый член выражает удельную энергию в данной точке, отнесенную не к единице веса, а к единице объема жидкости (1 м 3 ). Например
В случае горизонтально расположенного трубопровода z1 = z2 и уравнение Бернулли для идеальной жидкости упрощается:
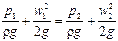

Пусть для точек, лежащих на оси трубопровода в поперечных сечениях 1—1 и 2—2, нивелирные высоты равны z1 и z2 соответственно. Установим в каждой из этих точек две вертикальные открытые так называемые пьезометрические трубки, у одной из которых нижний конец загнут навстречу потоку жидкости в трубопроводе.
В прямых вертикальных трубках (с незагнутыми нижними концами) жидкость поднимается на высоту, отвечающую гидростатическому давлению в точках их погружения, т.е. эти трубки будут измерять пьезометрические напоры в соответствующих точках.
В трубках с нижними концами, направленными навстречу потоку, уровень жидкости будет выше, чем в соседних вертикальных трубках, так как трубки с загнутыми концами будут показывать сумму пьезометрического и динамического (скоростного) напоров. Однако, согласно уравнению (II,49), во всех трубках с загнутыми нижними концами жидкость поднимается на одну и ту же высоту относительно произвольной горизонтальной плоскости сравнения, равную гидродинамическому напору Н (рис. II-15).
Площадь поперечного сечения 2—2 трубопровода меньше сечения 1—1. Поэтому скорость жидкости w2 при данном ее расходе, согласно уравнению неразрывности потока, будет больше w1. Соответственно 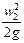

В любом поперечном сечении трубопровода скоростной напор можно измерить по разности показаний установленных здесь трубок (с загнутым и прямым нижними концами). Следовательно, эта разность должна быть больше для сечения 2—2, чем для сечения 1—1. Вместе с тем из уравнения Бернулли следует, что высота уровня жидкости в прямой трубке в сечении 2—2 должна быть меньше соответствующей высоты в прямой трубке сечения 1—1 настолько же, насколько скоростной напор в сечении 2 – 2 больше, чем в сечении 1—1.
Приведенный пример демонстрирует взаимный переход потенциальной энергии в кинетическую и, наоборот, при изменении площади сечения трубопровода, а также постоянство суммы этих энергий в любом поперечном сечении трубопровода.
При движении реальных жидкостей начинают действовать силы внутреннего трения, обусловленные вязкостью жидкости и режимом ее движения, а также силы трения о стенки трубы. Эти силы оказывают сопротивление движению жидкости. На преодоление возникающего гидравлического сопротивления должна расходоваться некоторая часть энергии потока. Поэтому общее количество энергии потока по длине трубопровода будет непрерывно уменьшаться вследствие перехода потенциальной энергии в потерянную энергию — затрачиваемую на трение и безвозвратно теряемую при рассеивании тепла в окружающую среду.
При этом для двух любых сечений 1—1 и 2—2 трубопровода, расположенных по ходу движения реальной жидкости (рис. II-15)
При движении реальной жидкости высоты ее подъема (относительно плоскости сравнения) в трубках с концами, обращенными навстречу потоку, уже не будут равны в сечениях 1—1 и 2—2, как было показано на рис. II-15 применительно к движению идеальной жидкости. Разность высот в этих трубках, обусловленная потерями энергии на пути жидкости от сечения 1—1 до сечения 2—2, характеризует потерянный напор hп.
Для соблюдения баланса энергии при движении реальной жидкости в правую часть уравнения (II,50) должен быть введен член, выражающий потерянный напор. Тогда получим уравнение Бернулли для реальных жидкостей:
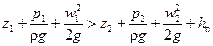
Потерянный напор hп характеризует удельную (т.е. отнесенную к единице веса жидкости) энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости.
Уравнение (II,52) может быть представлено в несколько ином виде, если умножить обе его части на pg:
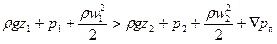
В уравнении (II,52а) величина Ñрп — потерянное давление, равное
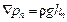
Определение потерь напора или давления является практически важной задачей, связанной с расчетом энергии, которая необходима для перемещения реальных жидкостей при помощи насосов, компрессоров и т.д. Трудность решения этой задачи обусловлена тем, что решение системы дифференциальных уравнений, описывающих движение реальной жидкости, в большинстве случаев оказывается невозможным.
Дата добавления: 2016-02-16 ; просмотров: 2766 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Уравнение эйлера дифференциальные уравнения вывод
Пример 2.1. Рассмотрим пример, который легко решить аналитически. Требуется найти экстремум функционала
при граничных условиях
Найдём частные производные и
Вычислим полную производную по x от
Составляем дифференциальное уравнение Эйлера вида
или, после упрощений
Его общее решение имеет вид
Для нахождения произвольных постоянных C1 и C2 подставим решение (2.16) в граничные условия (2.11):
Видно, что система (2.17) имеет единственное решение. Решая эту систему, найдём значения C1 и C2:
и тогда уравнение экстремали имеет вид:
Действительно ли на этой кривой достигается экстремум? И если да, то какой: минимум или максимум? Далее, в главе 13, мы рассмотрим достаточные условия экстремума . В частности, мы выведем условие Лежандра: если на экстремали выполняется условие а на функциях, близких к экстремали, для произвольных y‘ имеет место то достигается сильный минимум. В нашем случае это выполняется:
и, следовательно, на нашей экстремали достигается сильный минимум. Проверим этот результат: вычислим на нескольких функциях вида Эти функции удовлетворяют граничным условиям (2.11) и, следовательно, являются допустимыми. Для вычислений применим MATLAB.
Действительно, полученный результат не противоречит выводу о том, что на функции достигается минимум. Но, конечно же, проведенная проверка не доказывает этот факт. Ведь мы проверили только несколько из бесконечного числа функций, графики которых проходят через точки и Доказательством могут служить необходимые и достаточные условия экстремума функционала.
Пример 2.2. Найти экстремаль функционала
при граничных условиях
Выводим уравнение Эйлера вида (2.9). Частные производные:
Уравнение Эйлера после упрощений имеет вид:
Его общее решение
Находим произвольные постоянные из граничных условий (3.22). Подставляем решение (3.25) в эти граничные условия:
Мы видим, что из полученной системы уравнений можно найти только а C2 может быть произвольной. Поэтому данная вариационная задача имеет бесчисленное множество решений вида
На любой из этих функций функционал принимает постоянное значение (какое − мы сейчас посчитаем). Проверка по достаточному условию Лежандра даёт:
поэтому на экстремалях (3.27) достигается сильный минимум.
Посчитаем значение функционала (2.21) на функциях вида (2.27) и нарисуем несколько экстремалей с помощью MATLAB.
На каждой из наших функций функционал равен нулю.
2.2. Частные случаи уравнений Эйлера
Иногда решение уравнения Эйлера существенно упрощается. Рассмотрим соответствующие частные случаи.
2.2.1. Подынтегральная функция F не зависит явно от y‘
Материал этого подраздела изложен в книге.
2.2.2. Подынтегральная функция F линейно зависит от y‘
Материал этого подраздела изложен в книге.
2.2.3. Подынтегральная функция F не зависит явно от y
Материал этого подраздела изложен в книге.
2.2.4. Подынтегральная функция F зависит только от y‘
Материал этого подраздела изложен в книге.
2.2.5. Подынтегральная функция F не зависит явно от x
Материал этого подраздела изложен в книге.
2.3. Вопросы для самопроверки
- Какую вариационную задачу мы решаем?
- Как выводится дифференциальное уравнение Эйлера?
- Где используется в выводе дифференциального уравнения Эйлера основная лемма вариационного исчисления?
- Почему обращается в нуль внеинтегральное слагаемое в формуле (2.8) при интегрировании по частям?
- Чем отличается частная производная от полной?
- Какие Вы знаете методы решения дифференциальных уравнений порядка?
- Всегда ли решение вариационной задачи будет единственным? От чего это зависит?
- Какие частные случаи уравнения Эйлера Вы знаете?
- В каких случаях уравнение Эйлера перестаёт быть дифференциальным и становится конечным?
- В каких случаях вариационная задача теряет смысл?
- Как записывается интеграл уравнения Эйлера, если подынтегральная функция F не зависит явно от y?
- Каким будет решение уравнения Эйлера, если подынтегральная функция F зависит только от y‘?
- Как решается уравнение Эйлера, если подынтегральная функция F не зависит явно от y‘?
- Как решается задача о брахистохроне?
2.4. Примеры выполнения заданий
2.4.1. Задание 1
Найти экстремаль функционала
Исследовать полученную экстремаль на достаточные условия экстремума. Вычислить значение функционала на найденной экстремали и, для сравнения, на прямой, соединяющей точки и Построить график решения.
В этом примере подынтегральная функция является функцией общего вида, поэтому составим уравнение Эйлера в виде (2.9) и решим его. Затем построим график решения. Попутно исследуем на выполнение достаточных условий экстремума и вычислим значение функционала на экстремали и отрезке прямой M1M2. Применим для решения задачи MATLAB.
Очистим память. Напечатаем заголовок решаемой задачи. Если хотите, задайте другую строку для вывода (например, свою фамилию). Опишем символические переменные [58]. Для решения уравнения Эйлера используем принятые в MATLAB обозначения производных: Dy для y‘ и D2y для y». Аргумент обозначим x , а функцию − y .
Вводим подынтегральную функцию и граничные условия. Печатаем их. Здесь вы должны поставить свои исходные данные: подынтегральную функцию F и граничные условия x1, y1, x2, y2.
Начинаем вывод дифференциального уравнения Эйлера (2.9). Найдём частные производные Fy и Fy’. Напечатаем их.
В уравнение Эйлера (2.9) входит полная производная Вычислим её по обычной формуле дифференцирования сложной функции:
Напечатаем её. Напечатаем также величину необходимую для проверки достаточных условий экстремума по признаку Лежандра.
Составим левую часть дифференциального уравнения Эйлера (2.9) и упростим её. Преобразуем символическую переменную Euler в строку.
Мы составили уравнение Эйлера, теперь решим его. Команда dsolve позволяет находить как общее решение дифференциального уравнения, так и частное его решение, удовлетворяющее заданным начальным или граничным условиям. В следующих главах при решении других заданий нам нужно будет иметь общее решение уравнения Эйлера. Найдём его.
Сформируем теперь уравнения для граничных условий. Подставим в найденное аналитическое решение Sol граничные точки x1 и x2 , и приравняем их соответственно y1 и y2 .
Решаем полученную систему конечных уравнений − находим значения произвольных постоянных C1 и C2 . Присваиваем найденные решения символическим константам, полученным при решении дифференциального уравнения. Теперь вычисляем аналитическое решение Sol21 . Такое вычисление сводится к тому, что в него будут подставлены найденные значения констант C1 и C2 . Печатаем найденное уравнение экстремали.
Вычислим значения функционала (2.86) на найденной экстремали и на прямой, соединяющей точки M1 и M2. Подставим в подынтегральную функцию F аналитические выражения для этих линий и их производных, а затем проинтегрируем. Напечатаем результаты.
В данном примере условие Лежандра говорит о сильном минимуме, что подтверждается полученным результатом: значение функционала на экстремали меньше, чем на другой допустимой функции. А как в вашем варианте: какой экстремум достигается? И подтверждается ли этот результат сравнением величин Jextr и Jlin ? Если нет, то не забудьте, что найденный экстремум − только локальный, а не глобальный! Попробуйте вычислить значение функционала не на прямой M1M2, а на какой-нибудь другой допустимой кривой, достаточно близкой к экстремали. Например, можно наложить на экстремаль несколько полуволн синусоиды, смещённой и деформированной вдоль оси Ox так, что
И, наконец, строим график. Задаём массив аргументов для рисования графика функции и вычисляем значения функции. Рисуем график, подписываем заголовок и координатные оси установленным шрифтом.
2.4.2. Задание 2
Найти экстремаль функционала
Исследовать на выполнение достаточных условий экстремума. Построить график решения.
В этом примере подынтегральная функция не зависит явно от y. Первый интеграл уравнения Эйлера имеет вид (2.43). Составим программу для решения этой вариационной задачи. Вначале введём исходные данные. У нас будет первый интеграл уравнения Эйлера, поэтому ни сама функция y, ни её вторая производная y» нам не нужны, и мы их не описываем. Поставьте свою подынтегральную функцию и граничные условия.
Строим первый интеграл и решаем полученное дифференциальное уравнение. Названия констант C1 и C2 используются в команде dsolve , поэтому при составлении интеграла уравнения Эйлера обозначим константу C . Все использованные здесь функции и операторы MATLAB были описаны ранее, в примере 1.
В переменной Sol получено общее решение, произвольные постоянные обозначены C и C1 . Найдём их. Для этого подставим в Sol граничные точки. Приравняем полученные выражения соответственно y1 и y2 . Тем самым мы сформируем систему уравнений.
Решим полученную систему − найдём произвольные постоянные C и C1 . Подставим их в решение Sol . Ограничим решение 14 знаками. Напечатаем уравнение найденной экстремали.
Дальнейшие действия не отличаются от описанных в примере 1. Рисуем график и и вычисляем Fy’y’, которая нужна для проверки достаточных условий экстремума по признаку Лежандра.
Проанализируйте достаточное условие Лежандра. Достигается ли экстремум на вашей экстремали? Если да, то какой?
2.4.3. Задание 3
Решить задачу о брахистохроне, соединяющей точки и
Мы уже решили эту задачу аналитически. Нам осталось найти значение константы C1 и параметра в конечной точке t2 из решения системы уравнений (2.84). Составим программу для решения этого примера. Вначале введём исходные данные задачи. Подставьте свою правую точку.
Составляем систему уравнений (2.84). Левую часть каждого уравнения мы задаём сразу в виде строки. В правой части переводим числа x2 и y2 в их строковые представления с помощью функции num2str . Ранее мы использовали конструкцию char(sym(y2)) . Оба варианта работают правильно − вы можете это проверить. Решаем полученную систему уравнений аналитически. Печатаем решения.
Рисуем график полученной брахистохроны. Выбираем начало координат в левом верхнем углу с помощью команды axis . Задаём границы по оси Ox, чтобы график занимал всё место на рисунке. Выравниваем масштабы по осям координат, чтобы брахистохрона выглядела неискажённой. Надписываем заголовок и метки осей.
2.5. Задание
Для своего варианта функционалов 1, 2, 3 найти экстремали, построить их графики и исследовать на выполнение достаточных условий экстремума.
http://helpiks.org/7-10101.html
http://iglin.exponenta.ru/All/BookDisc/AllDocs/Part2/part2.html