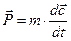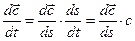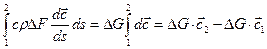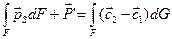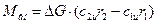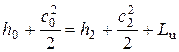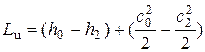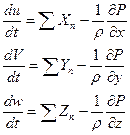Уравнение эйлера о количестве движения газа

Уравнение Эйлера об изменении количества движения.

Основные уравнения движения газа в двигателях и их элементах (продолжение)

Обобщенное уравнение Бернулли

Если из уравнения сохранения энергии вычесть уравнение 1 закона термодинамики, то получим уравнение

= L _r ,

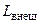
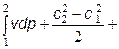
которое и называется обобщенным уравнением Бернулли. Оно, как уже отмечалось при изучении термодинамики газовых потоков, отличается от известного в гидродинамики уравнения Бернулли учетом наличия внешней работы и гидравлических сопротивлений.

При этом интеграл 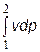называется работой сжатия газа в потоке, причем слова ²в потоке² обычно опускаются. Таким образом, согласно обобщенному уравнению Бернулли внешняя работа, подведенная к газу в потоке, расходуется на работу сжатия газа, на изменение (увеличение) его кинетической энергии и на работу по преодолению гидравлических потерь.

Уравнение Эйлера об изменении количества движения.

При проектировании газотурбинных двигателей, анализе их рабочего процесса и расчете эксплуатационных характеристик возникает необходимость определения сил взаимодействия газа с элементами двигателя, находящимися в потоке.

Например, при определении усилий, действующих на лопатки компрессора и турбины, силы тяги, создаваемой двигателем, и в других случаях.

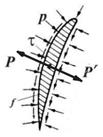
Рассмотрим аэродинамический профиль, обтекаемый потоком.

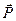
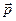
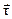
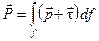
Вектор аэродинамической силы , действующей на этот профиль, можно определить, интегрируя силы давления и трения [Н/м 2 ], с которыми газ действует на поверхность f этого профиля. Тогда

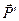
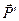
Очевидно, что профиль воздействует на газ с силой , равной по величине, но противоположно направленной, т.е. = –

Однако определение силы 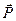интегрированием сил давления и трения газа в инженерной практике затруднительно, т.к. значения этих сил по поверхности обтекаемого тела очень сложно рассчитать.

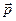
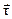
Если использовать теорему Эйлера об изменении импульса газового потока при обтекании тела, то аэродинамическую силу, действующую на тело, можно определить без знания и во всех точках обтекаемой поверхности. И это намного проще, чем интегрирование.

Как известно из курса физики, импульсом тела называется произведение его массы на его скорость. В теории авиационных двигателей для аналогичной величины применительно к потоку газа используется термин ²количество движения². Это термин мы и будем использовать в дальнейшем.

Для вывода уравнения Эйлера используем известный из механики 2-й закон Ньютона. Согласно ему равнодействующая всех внешних сил, действующих на тело, равна произведению массы тела на его ускорение:

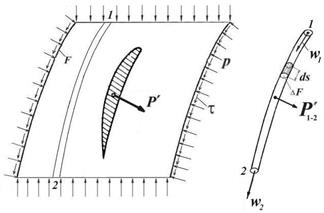
Примем, что движение газа установившимся. Выделим произвольной поверхностью F некоторый объем газа, окружающий обтекаемое тело, например, профиль. (Такую поверхность обычно называют ²контрольной поверхностью²)

Выберем в этом объеме произвольную трубку тока 1-2 и разобьем ее на элементарные частицы с массами dm = ρΔFds, где ρ – плотность газа, ΔF – площадь поперечного сечения трубки тока, s – криволинейная координата вдоль трубки тока, отсчитываемая от ее начала (сечения 1), а ds – элемент этой координаты. Массовыми силами, действующими на газ, будем пренебрегать, так как они (например, сила тяжести) несоизмеримо малы по сравнению с аэродинамическими силами, действующими на воздух или продукты сгорания в двигателе.

Согласно 2 закона Ньютона, для каждой такой элементарной частицы можно записать

(1.1)

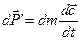
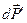
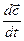
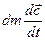
где — равнодействующая внешних сил, действующих на элементарную частицу газа с массой dm, — ускорение этой частицы. Тогда – ее сила инерции.

Так как при установившемся движении скорость в каждом сечении трубки тока не зависит от времени, то производная скорости по времени может быть представлена как

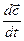
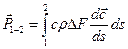
Подставив значение dm и в равенство (1.1) и проинтегрировав его вдоль трубки тока, получим

(1.2)

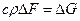
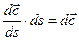
Но в равенстве (1.2) – расход газа через трубку тока, одинаковый в каждом ее сечении, а – дифференциал вектора скорости. И тогда

что после постановки в (1.2) дает

. (1.3)

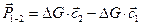
Формула (1.3) и представляет собой выражение теоремы Эйлера для трубки тока. Согласно этой формулепри установившемся течении газа и отсутствии массовых сил равнодействующая всех газодинамических сил (сил давления и трения), приложенных к поверхности отрезка трубки тока 1–2, включая ее торцы, равнаежесекундному изменению импульса (количества движения) протекающего через данную трубку тока газа.

Распространим далее полученный результат на всю массу газа, выделенную контрольной поверхностью F. Разобьем мысленно занимаемый ею объем на множество трубок тока, включая и прилегающие к обтекаемой поверхности профиля, и просуммируем выражения (1.3), записанные для каждой из них. При таком суммировании гидродинамические силы, действующие на струйки тока внутри контрольной поверхности, взаимно компенсируются, так как силы, действующие на каждый элемент поверхности соседних струек одинаковы по величине и противоположны по направлению. 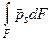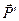Неуравновешенными при суммировании останутся силы давления и трения, действующие снаружи на массу газа, выделенную контрольной поверхностью F (обозначим их сумму, полагая площадь сечения каждой трубки тока бесконечно малой, как ) и сила , действующая на газ со стороны профиля, находящегося в выделенном контрольной поверхность объеме газа.

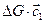
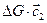
Количества движения и каждой трубки тока просуммируются при этом по всей контрольной поверхности F. Тогда получим

Таким образом, при установившемся течении газа сумма всех гидродинамических сил (сил давления и трения), действующих на выделенную произвольной контрольной поверхностью F массу газа со стороны контрольной поверхности и обтекаемых тел, равна разности количеств движения вытекающей из этой поверхности и втекающей в неё в единицу времени масс газа. (Это и есть теорема Эйлера о количества движения установившегося потока газа).

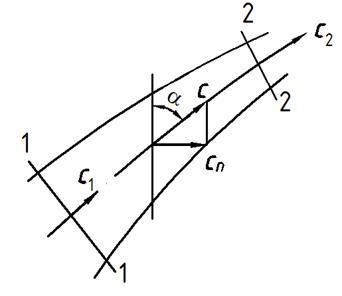
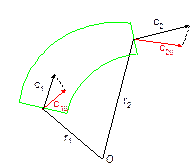
Аналогичным образом доказывается теорема Эйлера о моменте количества движения установившегося газового потока. Рассмотрим схему течения.

При установившемся течении газа сумма моментов всех гидродинамических сил, действующих на выделенную контрольной поверхностью F массу газа со стороны этой поверхности, относительно произвольной оси и момента сил относительно этой же оси, действующих на эту массу со стороны обтекаемых тел, равна разности моментов количеств движения вытекающей и втекающей в единицу времени масс газа относительно той же оси.

Дата добавления: 2018-05-10 ; просмотров: 1544 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Тема № 4: Основные уравнения газового потока в лопаточных машинах

Преобразование энергии расширения рабочего тела в энергию вращения ротора происходит в результате обтекания потоком неподвижных сопловых и рабочих решеток.

Законы течения сжимаемой жидкости имеют большое значение для изучения процессов, происходящих в ступени.

Теория лопаточных машин базируется на основных уравнениях движения газа: уравнении неразрывности, уравнении сохранения энергии, уравнении первого закона термодинамики, уравнении Бернулли и уравнениях Эйлера. Эти уравнения рассматриваются в курсе термодинамики. Здесь остановимся лишь на некоторых особенностях этих уравнений, которые связаны с их использованием в расчетах лопаточных машин. Уравнение Эйлера о количестве движения применительно к ступени турбины будет рассмотрено ниже.

Реальное течение рабочего тела в ступени турбомашины является пространственным периодически неустановившимся течением вязкого сжимаемого газа, математическое исследование которого в строгой постановке затруднительно. Для получения относительно простых уравнений, которые можно без труда использовать в инженерных расчетах, делаются некоторые упрощения:

1) рассматривают осредненные значения параметров в точке (стационарность);

2) во всех сечениях каждой ступени неизменными.

Указанные допущения означают, что число лопаток СА и РК бесконечно.

Уравнение неразрывности в случае установившегося течения формулируется следующим образом: секундный массовый расход газа через любое поперечное сечение элементарной струйки при установившемся течении сохраняется постоянным (см. рис. 4.1).

Рис. 4.1. К выводу уравнения неразрывности

Если в рассматриваемых сечениях элемента двигателя поток является равномерным или рассматриваются осредненные параметры газового потока в этих сечениях, то уравнение неразрывности с равным основанием может быть записано и для всего потока. В частности, для сечений, нормальных к оси потока:

. (2.1)

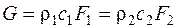
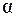
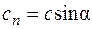
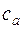
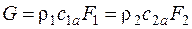
В общем случае, когда выбранное сечение не перпендикулярно к оси струйки, а составляет с ней некий угол , нужно рассматривать нормальную составляющую скорости в этом сечении (т. е. в применении к теории ступени турбомашин – осевую составляющую скорости ), а уравнение неразрывности записывается в виде:

. (2.2)

Уравнение первого закона термодинамики

Уравнением первого закона термодинамики пользуются для определения параметров состояния газа при осуществлении термодинамического процесса. Оно является частным выражением закона сохранения энергии для элементарного объема газа, написанным в системе координат, движущейся вместе с рассматриваемым элементом объема или, в частном случае, для покоящегося газа.

Для элементарного объема газа уравнение первого закона термодинамики имеет вид:

, (2.7)

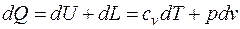
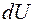
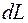
т. е. все тепло, подведенное к рассматриваемому объему газа, идет на изменение внутренней энергии и на совершение работы против сил давления, связанной с изменением объема.

Для движущегося газа удобно вместо внутренней энергии пользоваться понятием энтальпии:

. (1.8)

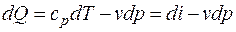
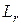
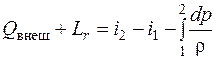
Переходя к интегральной форме записи, с учетом того, что тепло трения эквивалентно работе сил трения , можно получить:

, (1.9)

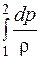
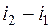
т. е. все тепло, подводимое к потоку между сечениями 1–1 и 2–2 (рис. 2.2), состоящее из тепла, подводимого извне, и тепла, выделяющегося в результате трения (работы сил трения), идет на совершение работы сжатия (расширения) и на изменение внутренней энергии потока ( ).

Уравнение первого закона термодинамики удобно для определения работы сил трения по известному значению показателя политропы 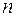, который легко определяется по термодинамическим соотношениям, если известны параметры потока в начале и в конце процесса.

Обобщенное уравнение Бернулли

Основным уравнением, на котором строятся расчеты турбомашин, является уравнение Бернулли:

. (2.10)

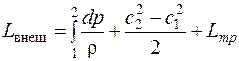
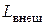
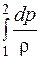
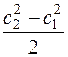
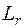
Уравнение (2.10) можно трактовать так: подведенная извне энергия идет на работу сжатия (расширения) газа , приращение кинетической энергии и преодоление гидравлического сопротивления .

Заметим, что уравнение Бернулли не зависит от теплообмена с окружающей средой. Однако теплообмен оказывает косвенное влияние на показатель политропы процесса.

Уравнение Бернулли, как и уравнение сохранения энергии, можно отнести к энергетическим и получить его из рассмотрения баланса механической энергии.

При свободном движении идеального газа, при отсутствии энергии, подведенной извне и потерь на преодоление гидравлического сопротивления:

. (1.11)

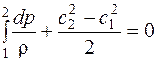
Для идеальной несжимаемой жидкости, для которой :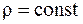

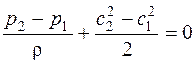
, (1.12)

т. е. для повышения давления в компрессоре динамического действия необходимо затормозить поток.

Самый простой способ достичь этого – геометрическое воздействие:

, (1.13)

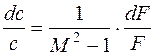
Таким образом, при дозвуковом потоке ( 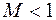) расширение канала приводит к снижению скорости потока. На замедляющийся поток набегают следующие молекулы, что приводит к снижению удельного объема (увеличению плотности), т. е. давление газа растет.

Можно сделать вывод, что рабочий процесс турбокомпрессора состоит из двух взаимосвязанных, одновременно протекающих процессов:

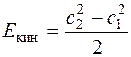
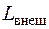
— приращения кинетической энергии за счет подводимой внешней работы (от турбины) ;

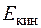
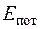
— преобразования кинетической энергии потока в энергию потенциальную , пропорциональную давлению.

Уравнение сохранения энергии

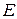
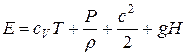
Полная энергия рабочего тела может быть записана в виде:

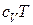
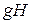
где — внутренняя энергия; P/r – потенциальная энергия давления; С 2 /2 – кинетическая энергия; — потенциальная энергия положения.

Данное выражение можно упростить.

Потенциальной энергией положения 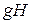можно пренебречь, т.к. по сравнению с остальными слагаемыми она ничтожна.

Внутренняя энергия рабочего тела в сумме с потенциальной энергией давления P/r будут равны энтальпии рабочего тела h, которая, таким образом, является мерой той потенциальной энергии, которой обладает поток рабочего тела.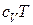

В этом случае уравнение полной энергии запишется в виде:

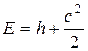
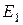
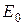
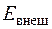
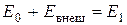
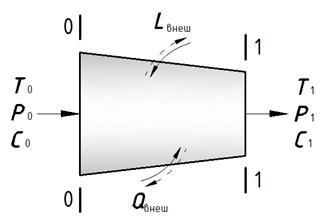
Уравнение сохранения энергии может быть сформулировано следующим образом: полная энергия газового потока на выходе из рассматриваемого элемента (рис. 4.2) больше (или меньше) полной его энергии на входе на величину энергии, подведенной (или отведенной) между рассматриваемыми сечениями :

Рис. 4.2. К выводу уравнения сохранения энергии

Поскольку при установившемся движении газа расходы через сечения 0–0 и 1–1 одинаковы, то все члены уравнения сохранения энергии принято представлять отнесенными к 1 кг газа.

Применительно к турбомашинам уравнение сохранения энергии можно записать в виде:

, (2.3)

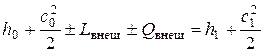
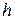
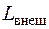
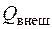
где – энтальпия газа (отвечает за внутреннюю и потенциальную энергию потока), с 2 /2 – кинетическая энергия потока; и – внешняя подведенная (отведенная) энергия, в виде механической работы и в виде тепла соответственно.

Для элементов двигателя, в которых отсутствует подвод или отвод энергии, уравнение сохранения энергии в частном случае имеет вид:

, (2.4)

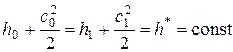
т. е. при отсутствии энергообмена полная энергия газового потока сохраняется неизменной и равна энтальпии заторможенного потока.

Запишем уравнение сохранения энергии для турбинной ступени (см. рис. 2.1). Теплообменом с окружающей средой при этом можно пренебречь, т.к. при относительно небольших площадях теплоотдачи и хорошей теплоизоляции коэффициенты теплоотдачи малы.

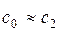
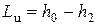
Обычно для турбинной ступени , поэтому

т.е. работа турбинной ступени фактически численно равна изменению энтальпии потока.

Заметим, что в различные записи уравнения сохранения энергии в явном виде не входит трение, а значит, это уравнение применимо как для идеального газа, так и газа, обладающего вязкостью.

Силы трения, которые возникают на стенках, ограничивающих поток газа, и силы внутреннего трения между отдельными струйками газа являются внутренними силами, а работа на их преодоление переходит практически полностью в тепло. Трение приводит лишь к преобразованию одного вида энергии в другой и не отражается на общем балансе энергии. Например, если вследствие трения уменьшается кинетическая энергия, то энтальпия в этом сечении вырастет на ту же величину.

Дата добавления: 2015-06-17 ; просмотров: 3784 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Уравнения количества движения газа в форме Л. Эйлера и И. Громеки

Многие практически важные реальные случаи сводятся к рассмотрению случаев течения потока идеального газа.

Для потока идеального газа:

— поток газа лишен сил трения

— отсутствует внутренний теплообмен и теплопроводность

( в потоке реального газа возникают градиенты температуры и совершается внутренний теплообмен между соседними частицами.

Переход рассмотрения процессов газодинамики к потоку идеального газа ( отсутствует внутренний теплообмен и теплопроводность, изоэнтропийный процесс (отсутствуют потери энергии) и μ=0) позволяет уравнения Навье- Стокса об изменении количества движения для частицы газового потока преобразовать в уравнения Эйлера, полученные в 1759 г.:

Уравнения могут быть представлены в развернутом виде;

Уравнения показывают, что ускорение частицы идеального газа вызывается соответствующими изменениями сил давления, действующих на элемент и силами внешних полей.

Переходя к рассмотрению движения потока идеального газа в цилиндрических координатах (r, θ, z) (тангенциальное ускорение, кариолисово ускорение), вводя в рассмотрение уравнения специфических элементов движения потока- компонентов вихря, потенциальной и кинетической энергии, некоторую функцию давления, выражающий потенциал объемного действия поверхностных сил давления

Некоторую потенциальную функцию U, частные производные от которой по координатам выражают проекции единичных массовых сил на оси координат

Профессор Казанского университета И. Громека в 1881 г. Вывел уравнения, названные в его честь:

(7)

Для установившегося движения ( , при отсутствии вихрей

(

(8)

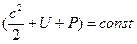
Из данного уравнения в гидродинамике было получено уравнение Бернулли для несжимаемой жидкости:

. (9)

Уравнение моментов количество движения

Данный момент имеет особое значение при изучении вращательного движения газа.

Моментом количества движения относительно некоторой точки (оси вращения) называется произведение количества движения тела на кратчайшее расстояние от точки до линии, по которой направлена скорость.

r c_1u

2 c₁

C_2u 1’

C₂ c₂_r 2’

Момент количества движения (1-1’):

(10)

Т.к.

Для сечений 1-1’

По аналогии для сечения 2-2’ момент количества движения составит:

Разность моментов количества движения равен моменту импульса.

Момент импульса- произведение величины импульса на кратчайшее расстояние от точки до линии действия силы, создающей данный импульс.

(Импульс- произведение скорости точки на массу)

(11)

P- равнодействующая внешних сил, действующих на частицу

r_o— расстояние от линии действия силы до оси вращения.

Выражение называется моментом равнодействующих внешних сил относительно оси вращения.

Для установившегося движения

Тогда выражение момента М сводится к виду:

(12)

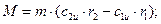
Полученное уравнение называется уравнением Эйлера для вращательного движения и широко используется при изучении особенностей движения газа в лопаточных аппаратах.

Например, рассмотрим движение потока газа в центробежном компрессоре.

Величина момента (М), окружная скорость (ω) определяют теоретическую мощность: