Уравнение эйлера остроградского для функционала примеры
Пример 5.1. Найти экстремаль функционала:
в прямоугольной области показанной на
Граничные условия: на правой стороне
на остальных сторонах
Решение примера изложено в книге.
Решение нашей задачи − это одна первая гармоника ряда (5.16):
Вот как выглядит график этой функции (мы здесь взяли
5.2. Вопросы для самопроверки
- Какую вариационную задачу мы решаем?
- Как выводится дифференциальное уравнение Эйлера-Остроградского?
- Где используется в выводе дифференциального уравнения Эйлера-Остроградского основная лемма вариационного исчисления?
- Почему мы не можем использовать формулу интегрирования по частям? Чем мы её заменяем?
- Обязательно ли будет достигаться экстремум функционала на решении дифференциального уравнения Эйлера-Остроградского?
- Какие вы знаете методы решения дифференциальных уравнений в частных производных?
- Всегда ли решение вариационной задачи будет единственным? От чего это зависит?
- Выведите систему дифференциальных уравнений Эйлера-Остроградского для функционала, зависящего от нескольких функций нескольких переменных.
5.3. Пример выполнения задания
Найти экстремум функционала
в области D, которая представляет из себя квадрат со стороной скруглённый по верхнему краю дугой окружности радиуса с добавкой полукруга слева и с вырезанной частью эллиптического очертания справа. Центр полукруга находится посередине левой стороны, а центр эллипса − на расстоянии наружу от середины правой стороны. Эллипс с полуосями и повёрнут на 30° против часовой стрелки. Начало координат выберем в центре полукруга
Граничные условия: на нижней стороне u изменяется по параболическому закону в зависимости от x с максимальным значением посередине стороны, на остальных сторонах
Составим программу для решения данной задачи. Вначале очистим рабочую область от предыдущих задач. Опишем необходимые символические переменные и введём исходные данные. Нам необходимы будут символические переменные для аргументов x и y , функции z , первых и вторых частных производных Dzx , Dzy , D2zx2 , D2zxy и D2zy2 . Вводим подынтегральную функцию F (символическое выражение), граничное условие zc там, где оно не равно нулю (также символическое выражение), и строковую переменную bc , показывающую, где именно граничное условие отлично от нуля. Не забудьте, что при вычислениях мы имеем дело с округлёнными значениями. Поэтому пишите условие bc так, чтобы захватить нужную Вам сторону.
Найдём частные производные Fz, Fp и Fq. Сформируем из них полные частные производные и При их формировании учитываем, что Используем формулу (2.87). Формируем уравнение Эйлера-Остроградского. Нам нужно будет иметь уравнение в виде (5.14), когда слева записаны частные производные и сама функция z, а справа − известные функции. Поэтому вычислим отдельно левую и правую части. Правую часть получим, когда в выражение подставим и вместо всех частных производных также подставим нуль. Тогда левая часть − это всё остальное.
Для решения дифференциальных уравнений в частных производных в MATLAB’е есть специальный инструментарий − Partial Differential Equation Toolbox (PDE) [54], в котором используется метод конечных элементов (FEM). Использование PDE Toolbox для решения дифференциальных уравнений в частных производных подробно описано в книге.
Наша область образована следующими примитивами:
- квадрат со стороной
- круг радиусом с центром в точке он отрезает от квадрата верхнюю часть;
- круг радиусом с центром в начале координат; он добавляется к области;
- эллипс с центром в точке с полуосями повёрнутый на угол он вырезается из области.
Зададим эти примитивы в виде матрицы. В столбце зададим данные для прямоугольника, во и − для кругов, и в − для эллипса. Уравняем длины всех столбцов.
Затем сформируем из этих примитивов область. Обозначим столбцы матрицы буквами a, b, c, d. Тогда область может быть получена с помощью формулы Действительно, из квадрата a кругом b вырезается область, затем к ней добавляется круг c, и из полученной области вырезается эллипс d. Напечатаем число элементарных участков границы. Изобразим полученную область графически. Выравняем масштабы по осям координат. Надпишем заголовок и метки осей.
Разбивка полученной области на треугольные конечные элементы осуществляется командой initmesh , которая возвращает 3 выходных параметра: p , e и t . Смысл их следующий:
- В переменной p возвращаются координаты узлов сформированной сетки. Массив p имеет размеры где np − число узлов. В нём содержатся:
- строка − − координаты.
- В переменной t возвращаются данные по треугольникам. Это массив размером где nel − число элементов.
- Первые 3 строки содержат номера узлов для каждого элемента в порядке обхода против часовой стрелки.
- число − это номер подобласти. Если мы удалим все внутренние границы, то у нас будет только одна подобласть, и все числа строки будут 1.
- В переменной e возвращаются данные по граничным точкам сетки. Размер массива e где nb − число участков границы в В каждом столбце массива e содержатся данные по одной граничной линии.
- и числа − это номера узлов (в том порядке, в котором они перечислены в массиве p ).
- и числа содержат значения параметра длины в начальной и конечной точках. Параметр длины точки − это отношение расстояния от начала участка границы до данной точки к общей длине участка границы.
- число содержит номер участка границы.
- и числа − это номера подобластей слева и справа от данной границы. Если мы удалим все внутренние границы, то из и чисел одно число будет равно 1, а другое − 0.
Заметим, что ne − это число элементарных участков границы (дуг окружностей или эллипсов, отрезков прямых), а nb − это число сторон конечных элементов, которые выходят на границу. Обычно
Полученную FEM-сетку можно один или несколько раз измельчить при помощи команды refinemesh . Эту команду можно использовать, например, в цикле для достижения нужной точности вычислений.
Изобразить сетку разбиения можно командой pdemesh .
Сформируем треугольную FEM-сетку и измельчим её. Напечатаем количество узлов, элементов, граничных линий. Нарисуем полученную сетку. Выравняем масштабы по осям, надпишем заголовок, метки осей.
Следующий этап − это задание граничных условий. Граничные условия можно задать или в виде матрицы граничных условий (boundary condition matrix), или в виде граничных условий (boundary M-file). Второй вариант проще. Файл граничных условий должен иметь такую структуру:
Входные параметры: p , e − данные по сетке разбиения, u − решение, time − время. Выходные параметры − матрицы граничных условий Дирихле (5.30) или Неймана (5.31). PDE позволянт решать параболические и гиперболические уравнения (зависящие от времени), а также нелинейные задачи, поэтому граничные условия и параметры дифференциального уравнения могут зависеть также от времени и решения.
Для граничных условий Неймана матрицы q и g должны содержать значения параметров q и g в средних точках границ. Размер матрицы q: где N − число уравнений системы, а nb − число сторон конечных элементов, выходящих на границу. Размер матрицы g: В каждом из столбцов этих матриц должны возвращаться коэффициенты q и g в средних точках соответствующей границы. Для нескольких уравнений элементы q должны следовать по столбцам. Так, например, для уравнений в каждом столбце матрицы q нужно возвратить q11, q21, q12, q22. В случае граничных условий Дирихле в этих матрицах должны возвращаться нулевые значения.
Для граничных условий Дирихле должны формироваться матрицы h и r . Матрица h имеет размеры и содержит значения h сперва во всех начальных точках каждой граничной линии, и сразу за ними − в конечных точках граничных линий. Размер матрицы r : этот массив заполняется аналогично.
Сформируем файл для вычисления граничных условий Дирихле. Число уравнений у нас число точек граничных линий nb находим из массива e . Формируем строки для записи в файл и записываем их. Файл размещаем в рабочем каталоге системы MATLAB. Имена всех файлов, которые мы будем записывать в каталоги MATLAB, мы будем начинать с префикса My . Файлов с такими именами в каталогах MATLAB’а нет, поэтому мы ничего не испоритм. Файл граничных условий назовём Это − обычный текстовый файл. Расширение говорит о том, что MATLAB будет воспринимать его как свою функцию, причём имя функции должно совпадать с именем файла.
Следующий этап − задание функций, входящих в дифференциальное уравнение.
Найдём C, a, f. Элементы матрицы C − это коэффициенты при частных производных. При их вычислении учтём, что коэффициенты при и одинаковые. Число a − это коэффициент при u в дифференциальном уравнении. Параметр f вычисляем вначале в узлах, а затем в центрах тяжести конечных элементов.
Решаем наше дифференциальное уравнение с помощью функции assempde . Рисуем график решения командой pdeplot . Показываем конечноэлементную сетку и не показываем линейку соответствия цветов. Команда axis возвращает или устанавливает границы рисунка по осям. Мы получили текущие границы, выравняли масштаб по осям Ox и Oy, а затем восстановили старые границы. Надписываем оси. Выбираем палитру. Показываем сетку и контур. Осталось почистить за собой: убрать из текущего каталога записанный туда файл Делаем это командой delete .
5.4. Задание
Для своего варианта функционала выведите дифференциальное уравнение Эйлера-Остроградского и решите его МКЭ. Нарисуйте область решения, сетку МКЭ и трёхмерную поверхность − график решения.
Различные обобщения уравнения Эйлера. Уравнение Пуассона-Эйлера и Остроградского.
Читайте также:
|





 ,
,  ,
,  ,
,  (2)
(2)
 , которые удовлетворяют краевым условиям (2). Тогда, очевидно, приращения δy(x) должны удовлетворять краевым условиям
, которые удовлетворяют краевым условиям (2). Тогда, очевидно, приращения δy(x) должны удовлетворять краевым условиям ,
,  (4)
(4)
 , (6)
, (6)
 ,
,  имеет вид
имеет вид

 –известна.
–известна.
 — множество непрерывно дифференцируемых функций в замыкании области Ω.
— множество непрерывно дифференцируемых функций в замыкании области Ω. (x, y) — решение вариационной задачи, а z(x, y) — любая другая функция из D(J), то
(x, y) — решение вариационной задачи, а z(x, y) — любая другая функция из D(J), то
 (2)
(2) ,
, 

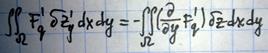
 (3)
(3) ,
,  (на Γ= ∂Ω)
(на Γ= ∂Ω)