Уравнение ферма в настоящее время неразрешимо

Уравнение ферма в настоящее время неразрешимо

О теореме Ферма и её доказательстве

Карпунин Иван Иванович,

доктор технических наук, профессор, профессор кафедры Белорусского национального университета, академик МИА и МАИТ.

Как известно, суть теоремы Ферма состоит в том, что при натуральных n 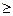3 уравнение x n +y n =z n не имеет решений в целых положительных числах. Прошло не одно столетие, когда она была высказана, многие выдающиеся математики пытались её доказать. Наибольших выдающихся результатов в этом направлении достиг Куммер, который доказал, что указанная теорема верна тогда, когда простой нечётный показатель степени р не делит числителей чисел Бернулли [1].

В 1995 году вышла обширная статья [2], в которой сообщалось о доказательстве указанной теоремы. После этого появилось множество статей, в которых также рассматривалось приведенное в [2] доказательство. Однако в литературе [3,4,19] также появились данные, что в [2] содержится принципиальная математическая ошибка. В работе [5] также показано, что теорема Рибета и теорема Мазура ( предложение 4) не могут быть одновременно верны, так как представление 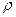_l не может быть одновременно модулярным и не модулярным уровня N / p, то есть пришли к противоречию. То есть теорема 11 в [6], из которой следует связь теоремы Ферма с гипотезой Таниямы, не является верной, теорема Рибета находится в противоречии с предложением 4.

Об ошибочном доказательстве теоремы П.Ферма Уайлзом имеются также сведения и в других источниках. Теорема Ферма сформулирована для целых положительных числах, а поэтому её доказательство должно явно указывать на новые и существующие свoйства целых чисел, которые углубляли бы их теорию. Ошибка заключается в том, что гипотетическое решение уравнения Ферма одновременно является решением алгебраического уравнения 3-й степени. Это в действительности было бы так, если бы указанная кривая являлась бы эллиптической. Однако кривая представлена в нелинейных координатах, что означает факт не существования её в линейном топологическом пространстве. Если обратиться к линейным координатам евклидова пространства, то получаются формулы, отличные от эллиптических кривых. При этом отрезки евклидовой прямой при сложении точек на такой эллиптической кривой взяты в нелинейном масштабе.

Уайлс [2] представил гипотетическое уравнение Ферма x n +y n =z n в виде группового сложения целых чисел: x n +y n +z n =0, где x n ,y n ,z n – элементы аддитивной группы 3-го порядка, имеющей обратные элементы. Эта группа изображена на диаграмме [17]. В чертеже цифры 1,2,3 соответствуют элементам группы, а стрелки между ними указывают на симметричные повороты в кольце преобразований. Причём основание группы равно 4 (количество имеющихся цифр 0,1,2,3). Фреем и Уайлсом произвольно без доказательства предполагается, что рассматриваемая группа реализуется на точках (элементах) проективной эллиптической кривой, когда это второе предположение (после 1 го, когда уравнение Ферма записывалось в целых числах). Это означает, что в приведенном Уайлсом доказательстве теоремы Ферма не доказано, что элементами группы уравнения x n +y n =z n являются отрезки прямых (точки на эллиптической кривой), а не какие-либо нелинейные элементы.

При рассмотрении числа в качестве операторов при сравнении с переменными, то они должны быть однородными величинами, т.е. иметь одинаковые степени. Это означает, что при линейных координатных системах евклидова пространства получим отличные формулы, характерные для эллиптических кривых. Анализ работы [2] показывает, что ошибка основана на предположении о том, что решение уравнения Ферма одновременно является и решением алгебраического уравнения 3 й степени, описывающего эллиптическую кривую известного вида при условии, если бы она в действительности была эллиптической. Но так как указанная кривая представлена в нелинейных координатах, то она реально не существует в линейном топологическом пространстве. Поэтому невозможно правдоподобно представить указанную зависимость, так как нет соответствия между кривой Ферма и модулярными эллиптическими кривыми. Возникает противоречие.

В отношении существования доказательства самим Фермой своей теоремы следует заметить, что не существует никаких литературных источников, в которых великий Ферма доказал свою теорему. Поэтому все высказывания о доказательстве самим Ферма высказанной им теоремы не имеют никакой основы, так как это попросту домысел. Нужны литературные источники, в которых доказательство теоремы было изложено самим Ферма.

В настоящее время, кроме «доказательства» теоремы Ферма в [2], появились и другие, изложенные в [7-13,20,21]. В указанных работах приведены «доказательства» теоремы Ферма, в которых содержатся ошибки, имеются неточности, делаются произвольные необоснованные допущения, поэтому её доказательствами по сути дела не являются и в настоящее время в литературе продолжают появляться всё новые подобные её «доказательства».

Математические журналы Российской АН даже не рассматриваютдоказательства теоремы элементарными способами. Например, журнал «Алгебра и анализ». Вот какой мы получили ответ от указанного журнала: по решению редколлегии работы, посвященные элементарным подходам к тереме Ферма, не рассматриваются, зав. редакцией Н.Б.Бажутина. Однако она не доказана и в настоящее время как элементарными, так и неэлентарными способами, и подобные « доказательства» продолжают поступать. Что касается доказательства , приведенного в [2], то оно тяжело понимаемое и громоздкое. Оно ничего нового не вносит в теорию чисел. К сожалению, аналогичным образом поступают рецензенты «ВесцI НАН БеларусI» серии физико-математических наук, давая необъективные и не представляющие никакого интереса рецензии.

Нами предложен новый метод сравнения чисел, т.е. сравнение по ненулевому рациональному модулю [14,15], которое имеет особое значение для математики в доказательстве многих высказанных предложений.

В [16] нами показан новый подход к оценке величины комплексных чисел в сравнении с обычными натуральными числами.

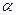
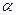
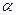
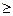
Известно [1], что Куммер поставил проблему, заключающуюся в разложении на простые сомножители чисел вида a₀ +a₁ +а₂ 2 +…+а_р-1 р-1 , где а₀ , а₁,…, а _р-1 — целые, то есть проблему разложения круговых целых. Эта проблема решаема, если применить предложенный нами способ приведения комплексных чисел к новой системе [16], a затем уже в таком случае теорема Ферма доказывается без всяких осложнений, так как соблюдается единственность разложения уравнения х n + y n = z n ( n 3), но этого можно и не делать, если учесть предложенное нами сравнение по ненулевому рациональному модулю [14.15-18]. Это означает, что при делении р на v, где р-иррегулярное число, v – регулярное число ( р выбрано большим v), получается дробное число f большее 1.

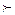
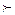
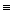
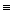
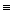
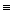
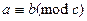
Если B_m (число числителя чисел Бернулли) делится на иррегулярное р, то имеем В_m: a₁= p (где а₁ – целое число от деления числителя чисел Бернулли). В случае, если В_m: a₂=p (где а₂ – дробное число 1 от деления числителя чисел Бернулли В_m на р), если число р было бы регулярным, но в обоих случаях В_m : (В_m: p) = p не зависимо от того р делит или не делит В_m, то есть является ли число f1 дробным или целым числом (f=B_m: p). Это также означает, что B_m 0 (mod B_m : p) 0 (mod f ), (причём B_m 0 (mod B_m : p) равноценно сравнению B_m . p 0(mod B_m ), где f принимает частные случаи, то есть может быть целым или дробным числом 1(сравнение по ненулевому рациональному модулю). Из литературных источников [1] известны свойства сравнения , т.е. два числа а и b являются сравнимыми по модулю третьего натурального числа , если имеются такие натуральные числа m и n, что а + mc = b + nc. Иначе это можно сказать, что а и b лежат в одной прогрессии с разностью с, т.е. разность а – b делится на с, а и b при делении на их на c дают одинаковые остатки.

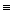
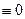
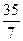
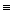
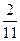
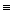
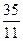
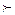
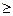
Проиллюстрируем на обычном числовом примере: 350(mod 5)(mod); 350(mod 3)0(mod ), где f может быть дробным или целым числом 1 (c=1,2,3,…,35; a=35; a:c=f). При делении а на f1, где f целое или дробное число, получается всегда целое число.

В опубликованных нами работах 17 дано обоснование сравнения по нулевому рациональному модулю и показаны его свойства. Этим и всё сказано о подлинности теоремы Ферма и бесконечности регулярных простых чисел.

1. Боревич З.И., Шафаревич Н.Р. Теория чисел. М.: Наука.—1985.-368 с.

2. Wiles A. Modular elliptic curves and Fermat ’ s last theorem – Annals of Mathematics. 1995, v.141, p.443-551.

3. Ивлиев Ю.А.Реконструкция нативного доказательства Великой теоремы Ферма. Объединённый научный журнал. 2006.№7.- с.3-9.

4. Ивлиев Ю.А.Величайшая научная афёра ХХ века: «Доказательство» последней теоремы Ферма. Естественные и технические науки.№4.-2007.-С.35-48.

5. Лещинский А.С. Ошибки Э.Уайлса в доказательстве теоремы Ферма. Материалы научн. конференции студентов и аспирантов, посвящённой 85-летию БНТУ. Минск.-2005.-с.15-17.

6. Лещинсий А.С. Гипотеза Вандивера. Сб. статей. Минск: БНТУ, 2008.-24 с.

7. Мокроносов В.С. Где собака зарыта (доказательство великой теоремы Ферма). // Естественные и технические науки.-2007.-№5.-с.35-41.

8. Галканов А.Г. Теорема о трёх корнях и два доказательства теоремыФерма. // Естественные и технические науки.-2006.- №1.-с.35-36.

9. Серединский В.Г. Решение проблемы Ферма. Изд-во Казанского университета.- 2000.- 67 с

10. Лещинский А.С. Полное доказательство великой теоремы Ферма. // Вестник БНТУ. Минск.- 2005.-№4.- с.57-61.

11. Алава М. Он закрыл великую проблему Ферма. Краснодар. Центр. инст. информатики. 2009.- с.28-30.

12. Цымбалов А.С. Теорема Ферма (очередная попытка её доказать). // Инновация в образовании.-2008.-№2.-с.108-112.

13. Камлия Р.А.Теорема Ферма и разложимость степенных вычетов. Абхазский научный центр Российской академии космонавтики им. К.Э.Циолковского. Сухум.-2008. – 68 с.

14. Карпунин И.И.Подлозный Э.Д.О делимости чисел. / Информационная среда среда вуза: Материалы ХIV Международной научно-технической конференции. Госуд.архитектурно-строительная академия. – Иваново. 2007.- С.501-506.

15. Карпунин И.И., Подлозный Э.Д. Делимость чисел на основе сравнения по ненулевому рациональному модулю. Тезисы докладов 3-й Международной конференции. – М.: МФТИ, 2008. – С.142-144.

16. Карпунин И.И., Подлозный Э.Д. О свойствах сравнения по ненулевому рациональному модулю. Материалы 13 Международной научной конференции имени академика Н.Кравчука. Институт математики НАН Украины. Национальный педагогический университет им Н.Драгоманова. Киев.-2010.- с.139

17. Карпунин И.И., Подлозный Э.Д.Особенность делимости чисел при сравнении по ненулевому рациональному модулю. // Журнал публикаций аспирантов и докторантов. Курск. 2011.- С.86-88.

18. Карпунин И.И., Подлозный Э.Д. // Журнал публикаций аспирантов и докторантов. Курск. 2011.

19. Ивлиев Ю.А. Разгадка феномена великой теоремы Ферма / Современные наукоёмкие технологии.№4, 2010.- С.38-45.

20. Калугин В.А. Решение великой теоремы и тайна уравнения. М.: URSS . Алгебраическая серия. 2010.- 22с.

21. Назаров А.А.Элементарное доказательство великой теоремы Ферма, или о невозможности разложения какой либо степени, большей чем два, на две степени с таким же показателем пос. Плесецк, Архангельской обл. Плесецкая тип.- 2010.

Почему доказательство Великой теоремы Ферма не нуждается в улучшениях

В течение десятилетий, прошедших после появления знакового доказательства великой теоремы Ферма, появилось несколько идей по поводу того, как сделать его ещё более надёжным. Однако эти попытки отражают глубокое непонимание того, что делает доказательство важным.

23 июня исполнилось 25 лет с момента взбудоражившего всех объявления от Эндрю Уайлса, в котором он заявил о получении доказательства великой теоремы Ферма – наиболее известной в математике задачи возрастом 350 лет. История, окружающая доказательство Уайлса – семь лет он тайно работал над этим проектом, разрыв в доказательстве, обнаружившийся после июньского объявления, элегантное решение, опубликованное год спустя в совместной работе, написанной Уайлсом вместе с его бывшим студентом Ричардом Тэйлором, получение рыцарского звания в 2000 – вошло в анналы математических легенд.

После прорыва Уайлса часто можно услышать рассуждения о наступлении новой «золотой эры» в математике, особенно в теории чисел – области, к которой и принадлежит теорема Ферма. Методы, представленные Уайлсом и Тейлором, сегодня являются частью инструментария специалистов по теории чисел, считающих историю Великой теоремы закрытой. Но эта история тронула не только специалистов по теории чисел.

Мне неожиданно напомнили об этом события 2017 года, когда в промежуток из нескольких дней два логика, делавших доклад на двух разных континентах, указали на способы улучшения доказательства Теоремы – и рассказали о том, насколько удивились их коллеги, когда специалисты по теории чисел не выказали к их идеям никакого интереса.

Логики выражали эти идеи на языках своих соответствующих специальностей – теории множеств и теоретической информатики. Сделанные ими предложения по сути своей были истинными, и, возможно, когда-нибудь поднимут новые вопросы, не менее интересные, чем у Ферма. Однако мне сразу же стало ясно, что эти вопросы не имеют отношения к специалистам по теории чисел, и любые иные предположения отражают глубокое непонимание природы доказательства Уайлса и целей теории чисел в целом.

Корни этого непонимания можно обнаружить в простоте утверждения Теоремы, которая и отвечает за большую часть её привлекательности: если n – любое положительное целое число, большее 2, то невозможно найти три таких положительных числа, a, b и c, что:

Это ярко контрастирует с тем случаем, когда n равно 2: любой человек, изучавший евклидову геометрию, вспомнит, что 3 2 + 4 2 = 5 2 , что 5 2 + 12 2 = 13 2 , и так далее (этот список бесконечен). За последние несколько столетий математики пытались объяснить наличие такого контраста, и каждый раз терпели неудачу, оставляя, однако, за собой целые новые ветви математики. Среди этих ветвей – крупные области современной теории чисел, привлечённой Уайлсом для своего успешного решения, а также множество фундаментальных идей в каждой части науки, затронутой математиками. И однако никто до Уайлса не мог доказать утверждение Ферма.

Специалисты по информатике недавно ощутили радостное возбуждение, узнав о прогрессе, достигнутом в автоматическом подтверждении доказательств – амбициозной попытке реализовать формалистский подход к математике на практике. Для формалистов, математическое доказательство – это список утверждений, удовлетворяющих строгим ограничениям:

1. Заявления в начале списка должны включать в себя общепринятые идеи. В строгой интерпретации сюда входят только аксиомы формальной теории множеств, обычно из формальной системы, известной, как ZFC (система Цермело — Френкеля с аксиомой выбора). Это совершенно непрактично, поэтому мы также разрешаем включать сюда уже доказанные теоремы – к примеру, Великую теорему для случая n=4, который уже сам Ферма доказал в XVII веке.
2. Каждое следующее утверждение должно получаться применением правил логической дедукции к предыдущим утверждениям.
3. Наконец, доказанная теорема должна быть на последнем месте в списке.

Математическую логику разрабатывали в надежде установить математику на прочную основу – как аксиоматическую систему, свободную от противоречий, которая способна рассуждать, не скатываясь в нелогичность. Хотя работа Курта Гёделя показала несбыточность этой мечты, многие философы от математики, а также некоторые логики (небольшое, но активное меньшинство, если верить специалистам по теории множеств), всё ещё относятся к ZFC и упомянутым требованиям, как к некоей конституции от математики.

Однако математики никогда не записывают доказательства таким способом. Логический анализ доказательства Уайлса указывает на множество шагов, не учитывающих ZFC, тая в себе потенциал для скандала: если математики придумывают правила, не проверяя их на конституционность, откуда они знают, что все они имеют в виду одно и то же?

Автоматическая проверка доказательств, кажется, предлагает решение этой проблемы. Она подразумевает переформулировку доказательства через набор раздельных заявлений, каждое из которых записано непротиворечивым языком, который компьютер может считать, а затем и подтвердить конституционную верность каждого шага. Этот трудоёмкий метод с успехом применялся ко многим длинным и сложным доказательствам, наиболее известное из которых – доказательство гипотезы Кеплера о наиплотнейшей упаковке сфер, сделанное Томасом Хейлсом. Проверка доказательства Уайлса давно считалась одной из главных целей. Поэтому мой друг, специалист по информатике, был искренне разочарован, что поиски «чистых математиков, безапелляционно поддерживающих использование автоматических инструментов в построении их аргументов», как он это сформулировал, пока не дают результатов.

«Арифметика» Диофанта издания 1670 года, в котором в основной текст включена и печально известная заметка Ферма. В переводе она звучит так: «Кубу невозможно быть суммой двух кубов, четвёртой степени невозможно быть суммой двух четвёртых степеней, или, в общем, любому числу, представляющему собою степень, большую второй, невозможно быть суммой двух таких же степеней. Я открыл воистину чудесное доказательство этого предположения, для размещения которого здесь эти поля слишком узки».

Первое, что не учитывает это разочарование — что доказательство Уайлса, пусть сложное, имеет простую основу, которую легко объяснить обывательской аудитории. Допустим, что, в противоречие с утверждением Ферма, существует тройка положительных целых чисел a, b, c таких, что

(A) a p + b p = c p

для некоего нечётного простого p (а достаточно рассматривать только простые числа). В 1985 году Герхард Фрей показал, что a, b и c можно перегруппировать в

(B) новое уравнение, под названием «эллиптическая кривая»

со свойствами, которые, как все считали, невозможны. Точнее говоря, уже давно было известно, как выразить эту эллиптическую кривую через

(С) представление Галуа

которое является бесконечным набором уравнений, связанных как с эллиптической кривой, так и друг с другом чёткими правилами.

Связь между этими шагами была хорошо известна в 1985 году. К тому времени большинство специалистов по теории чисел были убеждены – хотя доказательства пока не было – что каждому представлению Галуа можно назначить, опять-таки, по чётким правилам,

(D) модулярную функцию,

что-то вроде двумерного обобщения знакомых из тригонометрии функций синуса и косинуса.

Итоговое звено было получено, когда Кен Рибет подтвердил предположение Жан-Пьера Сера о том, что свойства модулярной функции, заданные формой эллиптической кривой Фрея, подразумевают существование

(E) ещё одной модулярной функции веса 2 и уровня 2.

Однако таких функций существовать не может. Следовательно, не существует ни модулярной функции (D), ни представления Галуа (С), ни уравнения (B), ни решения (A).

Оставалось лишь найти отсутствующее звено между (С) and (D), которое математики назвали гипотезой модулярности.

Это звено было объектом семилетних поисков Уайлса. С нашей текущей точки зрения тяжело в полной мере оценить отважность этого рискованного предприятия. Через двадцать лет после того, как Ютака Танияма и Горо Шимура в 1950-х впервые сообщили о связи между (B) и (D) через (С), математики постепенно пришли к выводу, что это должно быть так. Именно эту надежду высказал в очень популярной работе Андре Вейл, которая идеально вписалась в крайне влиятельную программу Ленглендса, названную в честь канадского математика Роберта Ленглендса. Эта связь была слишком хорошей для того, чтобы не быть правдой. Однако гипотеза модулярности казалась совершенно недостижимой. Объекты типов (С) и (D) были слишком разными.

Специалист по информатике не пояснил, связано ли его разочарование с тем, что специалистам по теории чисел было неважно, что доказательство было ограничено поисками критически важного звена между (С) и (D), или что оно простиралось на всём промежутке от (A) до (E). Не буду пытаться разобраться в этом. Но если логикам нужно было только формально подтвердить опубликованное доказательство связи между (С) и (D), то их ожидания были слишком завышенными. Во-первых, Уайлс доказал лишь чуть более, чем достаточно для того, чтобы гипотеза модулярности завершала дедукцию «от (A) до (E)». Полную гипотезу модулярности установили несколько лет спустя Кристоф Бройль, Брайан Конрад, Фред Даймонд и Ричард Тэйлор. Но это не бросает тень на работу Уайлса! Наоборот, то, что такое большое количество ведущих мировых специалистов по теории чисел пошли по стопам работы Уайлса всего через несколько месяцев после её появления, говорит о её богатстве.

К примеру, чуть позже, осенью 2016 года, 10 математиков встретились в Институте передовых исследований в Принстоне, Нью-Джерси, и смогли доказать наличие связи между эллиптическими кривыми и модулярными функциями в новых условиях. Все они использовали разные пути для понимания структуры доказательства Уайлса, появившегося, когда некоторые из них ещё были детьми. Если бы их попросили описать это доказательство в виде последовательности логических выводов, они, несомненно, выдали бы 10 разных его вариантов. Каждый из них напоминал бы путь от (A) до (E), описанный выше, но был бы гораздо более детальным.

Тем не менее – и это всегда упускают из философского взгляда на доказательства – каждый из этих десяти приписал бы авторство своего доказательства Уайлсу. Они бы ссылались на них тем же образом, что и на другие доказательства, изучаемые ими в разъяснительных статьях или на учебных курсах, которые они посещали или которые преподавали. И хотя каждый из десяти опустил бы какие-нибудь детали, в целом все они были бы правы.

Что же такое доказательства Уайлса, если оно может иметь так много разных вариантов? В математической философии принято относиться к опубликованному доказательству, как к приближению к идеальному формализованному доказательству, которое в принципе можно проверить на компьютере, применяющем правила формальной системы. Идеальное доказательство не загрязняется ничем, что находится за пределами формальной системы – так, будто бы каждый закон нёс на себе метку, подтверждающую его конституциональную оправданность.

Но такой подход противоречит тому, что сами математики говорят о своих доказательствах. Математики не применяют идеологических или философских лакмусовых тестов, но я убеждён, что большинство моих коллег согласятся с Майклом Фрэнсисом Атья, заявившим, что доказательство – «это итоговая проверка, но не основа чего-либо». Опубликованное доказательство явно не является основой чего-либо.

Уайлс и специалисты по теории чисел, уточнявшие и расширявшие его идеи, несомненно не ожидали получить предложения от двух логиков. Но – в отличие от многих людей, наблюдающих за теорией чисел издалека – они определённо понимали, что к такому доказательству, как к тому, что опубликовал Уайлс, не стоит относиться, как к некоему артефакту в себе. Наоборот, доказательство Уайлса – это стартовая точка открытого диалога, который является слишком неуловимым и живым, чтобы ограничивать его серьёзными пределами, чуждыми данной теме.

Великая теорема Ферма до сих пор не доказана

В мире можно найти не так уж много людей, ни разу не слы­шавших о Великой теореме Ферма — пожалуй, это единственная математическая задача, получившая столь широкую известность и ставшая настоящей легендой. О ней упоминается во множестве книг и фильмов, при этом главный контекст почти всех упоми­наний — невозможность доказать теорему.

Да, эта теорема очень известна и в некотором смысле стала «идолом», которому поклоняются математики-любители и про­фессионалы, но мало кому известно о том, что ее доказательство найдено, а произошло это в уже далеком 1995 году. Но обо всем по порядку.

Итак, Великая теорема Ферма (нередко называемая послед­ней теоремой Ферма), сформулированная в 1637 году блестя­щим французским математиком Пьером Ферма, очень проста по своей сути и понятна любому человеку со средним образова­нием. Она гласит, что формула a n +b n =c n не имеет натуральных (то есть не дробных) решений для n > 2. Вроде все просто и понятно, но лучшие ученые-математики и простые любители бились над поиском решения более трех с половиной веков.

Сам Ферма утверждал, что вывел весьма простое и лаконич­ное доказательство своей теории, однако до сих пор не найдено никаких документальных свидетельств этого факта. Поэтому сейчас считается, что сам Ферма так и не смог найти общего решения своей теоремы, хотя из-под его пера вышло частное доказательство для n = 4.

После Ферма над поиском доказательства работали такие ве­ликие умы, как Леонард Эйлер (в 1770 году им было предложено решение для n = 3), Адриен Лежандр и Иоганн Дирихле (эти ученые в 1825 году совместно нашли доказательство для n = 5), Габриель Ламе (нашедший доказательство для n = 7) и многие другие. К середине 80-х годов прошлого века стало понятно, что ученый мир находится на пути к окончательному решению

Великой теоремы Ферма, однако только в 1993 году математики увидели и поверили, что трехвековая эпопея по поиску доказа­тельства последней теоремы Ферма практически закончилась.

В 1993 году английский математик Эндрю Уайлс представил миру свое доказательство Великой теоремы Ферма, работа над которым продолжалась более семи лет. Но оказалось, что данное решение содержит грубую ошибку, хотя в целом и верно. Уайлс не сдался, призвал на помощь известного специалиста в теории чисел Ричарда Тейлора, и уже в 1994 году они опубликовали исправлен­ное и дополненное доказательство теоремы. Самое удивительное, что эта работа заняла целых 130 (!) полос в математическом журнале «Annals of Mathematics». Но и на этом история не закончилась — последняя точка была поставлена только в следующем, 1995 году, когда в свет вышел окончательный и «идеальный», с математи­ческой точки зрения, вариант доказательства.

С того момента прошло немало времени, однако в обществе до сих пор бытует мнение о неразрешимости Великой теоремы Фер­ма. Но даже те, кто знает о найденном доказательстве, продолжают работу в этом направлении — мало кого устраивает, что Великая теорема требует решения в 130 страниц! Поэтому сейчас силы очень многих математиков (в основном это любители, а не профессио­нальные ученые) брошены на поиски простого и лаконичного до­казательства, однако этот путь, скорее всего, не приведет никуда…