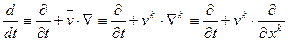Законы Фика | Основы диффузии
Итак, в основе любой теории диффузии (красителей в волокнистых материалах, компонентов в пластических массах, обмена ионов в ионообменных материалах, а также частиц в кристаллических веществах, включающих металлы, полупроводники, оксиды, керамику, стекла и т.д.), лежат законы Фика. Существуют два закона Фика – первый и второй.
Первый закон Фика
Первый закон Фика описывает квазистационарные процессы, когда проницаемая для обменивающихся местами частиц мембрана (пластинка) разделяет две среды (которые могут быть жидкими или газообразными) с существенно постоянными условиями на границах раздела. Эта мембрана может быть инертной по отношению в диффундирующим веществам (например, пористое стекло, разделяющее водные солевые растворы различной концентрации или солевого состава) или активной по отношению к одному или нескольким диффундирующим компонентам (например, палладиевая мембрана, пропускающая через себя водород при высокой температуре из-за специфических процессов сорбции на ее границе и практически не пропускающая другие газы).
Уравнение, описывающее первый закон Фика, имеет следующий вид:
где j – поток вещества через единицу поверхности, D – коэффициент диффузии (в общем случае – коэффициент взаимодиффузии), C — концентрации по толщине мембраны, равная разнице концентраций переносимого вещества по обе стороны мембраны, x — толщина мембраны.
Очевидно, что к обсуждаемым нами процессам образования цинкового покрытия это уравнение неприменимо, поскольку изучаемые нами процессы являются нестационарными.
Второй закон Фика описывает нестационарные процессы, и именно его необходимо применять для описания закономерностей, с которыми имеют дело как металлурги, так и работники других специальностей, соприкасающиеся с проблемами массопереноса в твердых телах.
Рассмотрим его действие на следующем примере. Возьмем два одинаковых образца, имеющих плоскую поверхность и состоящих из металла, который под воздействием нейтронного облучения способен создавать радиоактивные атомы той же природы. Облучим нейтронным потоком один из двух образцов с тем, чтобы создать в нем радиоактивность, соединим плотно по поверхностям облученный и необлученный образцы между собой и для убыстрения процесса будем выдерживать эту композицию при повышенной температуре. Вследствие теплового движения радиоактивные атомы из одной части образца будут диффундировать во вторую его часть, причем этот процесс будет продвинут тем более, чем более высока температура и чем больше время опыта. Затем образцы разъединим, и в каждом образце послойно измерим радиоактивность (технология этого типа эксперимента разработана очень хорошо). В результате эксперимента получаются кривые, изображенные на рис. 7.38, которые соответствующим образом обрабатываются для расчета эффективных коэффициентов диффузии. Концентрация радиоактивных ионов на межфазной границе будет равна половине той, что была в исходном левом образце, а сам процесс диффузии будет описываться уравнением:
Метод обработки таких кривых, как следует из литературы, был предложен физиком по фамилии Матано, и, как правило, называется методом Матано и иногда методом Матано- Больцмана (вероятно, из-за того, что метод возник как результат анализа решений уравнений диффузии, полученных одним из великих физиков теперь уже позапрошлого века Больцманом).
Если поверхность образца контактирует с какой-либо средой в жидкой форме, то на границе раздела концентрация данной среды, как правило, остается постоянной, но на форме фронта в железном образце эта особенность эксперимента при условии постоянства эффективного коэффициента диффузии сказывается достаточно мало (рис.7.39).
Для процесса цинкования необходимо смоделировать именно такую картинку. В этом случае концентрация диффундирующего вещества на границе двух сред является практически постоянной, и диффузия вещества в другую среду будет идти до тех пор, пока не достигнет стационара.
Рис. 7.38. Форма фронта диффузии при контакте двух твердых образцов, в одном из которых (в данном случае слева) методом нейтронного облучения созданы радиоактивные атомы, для двух значений времени эксперимента.
Рис. 7.39. Ожидаемая форма фронта в поглощающей среде при диффузии из среды с постоянной концентрацией на границе.
Второй закон Фика
Уравнение нестационарной диффузии описывается, как было уже сказано, вторым законом Фика, который для диффузии с постоянной концентрацией на границе двух фаз имеет следующий вид:
где n = 2, 1 или 0 – для шара, бесконечного цилиндра и бесконечной пластины.
Для бесконечной пластины уравнение имеет вид:
Ниже приведены соответствующие решения для степени завершения обмена как функции времени при постоянных коэффициентах диффузии:
для шара:
для пластины:
и для бесконечного цилиндра:
μ — корни функции Бесселя нулевого порядка, Bt = π 2 F0
N — степень завершения процесса обмена
F0 = D*t / l 2 — безразмерный параметр, где (D — коэффициент диффузии, t — время, l — линейный параметр)
Эти уравнения показывают, какая доля атомов (от максимально возможной) накапливается в поглощающей части образца.
Анализ показывает, что получаемые кривые, изображенные на рис. 7.39, никоим образом не напоминают типичный фронт сорбции цинка поверхностью железа, картинку которого можно видеть на рис. 7.40. Если верить кривой, полученной на рис. 7.39, наибольшей толщиной должны обладать ζ— и Г1-фазы, а δ-фаза должна иметь промежуточную толщину (о η-фазе мы поговорим несколько позже). Аналогичные результаты (то есть не совпадающие с фронтом, изображенным на рис. 7.39) были получены в значительном количестве исследований, и вот отсюда начинается игра ума.
Одни начинают искать причину в том, что поскольку изучаемое тело имеет кристаллическую структуру, то коэффициенты диффузии в различных направлениях являются различными. Действительно, на монокристаллах в ряде случаев это доказано. Но вот беда: сталь – это поликристаллическое тело, и для процесса цинкования этим вряд ли можно объяснить упомянутые выше экспериментальные закономерности.
Другие ищут причину отклонения от теоретической зависимости в методе Матано в том, что необходимо в уравнении второго закона Фика использовать не градиент концентрации, а градиент химического потенциала. В этом случае уравнение значительно усложняется, и неизвестно, какие результаты – отражающие или не отражающие действительность – будут получены.
Наконец, третьи пошли логически более правильным путем. На самом деле, при диффузии в металле с примесью (сплаве) диффундирует не один вид частиц, а, как минимум, два. Эти два вида частиц диффундируют навстречу друг другу, к тому же обладают различной подвижностью. Если отсчитывать скорость их передвижения от некоторой воображаемой плоскости (рис 7.41), то будет обнаружено, что через некоторое время эксперимента эта плоскость передвинется в сторону той части образца, которая содержит более быстрые частицы (эффект Киркендаля).
Рис. 7.40. Форма фронта, рассчитанная из содержания цинка в каждой из фаз внутри цинкового покрытия.
Рис. 7.41. Сущность эффекта Киркендаля. Пластина из латуни окружена слоем меди, нанесенной электролитически, причем на границе латунного образца предварительно закреплены метки из молибденовой проволоки. В результате выдерживания образца в течение нескольких сотен часов при повышенной температуре метки передвинулась внутрь образца.
Когда анализируют данные по кинетике образования цинк- железного покрытия на образце, исследуются дотошно любые факты, включая тип и структуру образующихся железо-цинковых сплавов, но ни в одной статье до настоящего времени не анализировалась форма фронта цинка в покрытии. Между тем, именно форма фронта говорит о многом, и именно выяснение причин ее образования может стать ключом к количественному описанию скорости образования железо-цинковых слоев.Обратим внимание на следующее. Почти во всех исследованиях в низкотемпературной области (достоверных сведений о форме фронта в высокотемпературной области нами не найдено) образуется форма обрывного фронта, близкая к изображенной на рис. 7.40. Эта форма не сильно зависит от температуры процесса, толщины образующегося покрытия и наличия или отсутствия в образце кремния (фосфора). Между тем имеется очень мало процессов, которые характеризуются такой формой фронта. Одним из таких процессов является процесс горения с быстрым отводом образующихся продуктов горения от поверхности. Для горящего шара, например, процесс горения описывается уравнением:
где R — радиус шара до начала горения, r — радиус координаты горения, D — коэффициент диффузии.
Очевидно, что если мы сделаем плоский образец с защитой боковых поверхностей, то процесс горения будет происходить только на одной из поверхностей без изменения ее реальной площади, то есть скорость уменьшения толщины образца будет пропорциональна времени. Пример такого процесса – «курение сигареты» автоматическим курильщиком с постоянной скоростью просасывания воздуха через образец.
Между тем, в огромном большинстве исследований наблюдается обратноквадратичная зависимость скорости образования слоя (скорости вымывания железа в расплав) от времени, то есть выполняется зависимость:
Однако необходимо тщательно проверить последнее утверждение, прежде чем принимать его за аксиому.
На рис. 7.42 и 7.43 приведены данные по зависимости скорости накопленияжелеза в расплаве от времени при различных температурах. В книге утверждается, что при построении этих данных в координатах получаются прямые линии для всех температур, кроме данных при 510°С, где наблюдается прямолинейная зависимость. Проверим это утверждение.
Рис. 7.42. Зависимость скорости накопления железа в расплаве с течением времени от температуры в высокотемпературной области.
Рис. 7.43. Зависимость скорости накопления железа в расплаве от времени в низкотемпературной области.
Таблица № 7.5. Определение формального порядка реакции методом сравнения с базисной зависимостью для данных по скорости вымывания железа из образца в течение процесса цинкования.
Тема №10 Кинетика диффузионных процессов в твердых телах. Определение диффузии. Первое и второе уравнения Фика
Кинетика диффузионных процессов в твердых телах.
Определение диффузии. Первое и второе уравнения Фика.
Определим диффузию как процесс переноса вещества из одной части системы в другую, происходящий под действием градиента концентрации. Отметим, однако, что градиент концентрации – важная, но не единственная причина, вызывающая перенос вещества в системе.
При свободной диффузии не взаимодействующих между собой частиц (в отсутствии приложенных внешних сил) в однородном и изотропном твердом теле поток диффузионных частиц 


где 

где 

В случае независимости коэффициента диффузии от концентрации легирующих частиц, применение закона сохранения вещества при диффузии в форме уравнения непрерывности для потока частиц позволяет перейти ко второму уравнению Фика, устанавливающему связь между концентрацией диффундирующих частиц в различных точках тела и временем диффузии:

Для трехмерного случая:


где 

Второй закон Фика, как закон сохранения вещества, можно записать в форме уравнения непрерывности:

Размерность плотности потока вещества зависит от размерности концентрации. Если 

Одним из основных параметров диффузии является коэффициент диффузии, вводимый как коэффициент пропорциональности между потоком и градиентом концентрации вещества в уравнении (10.1). В зависимости от условий проведения диффузионного опыта, различают несколько типов коэффициента диффузии.
1. Для описания взаимной диффузии при контакте двух образцов неограниченно растворимых один в одном, пользуются понятием коэффициента взаимной диффузии 
2. Подвижность каждого компонента в свою очередь характеризуется собственным коэффициентом диффузии 



3. Кроме того, подвижность 


Порциальные коэффициенты можно определить как для собственной, так и для взаимной диффузии. Все введенные до сих пор коэффициенты являются коэффициентами гитеродиффузии (химической диффузии), т. е. такой диффузии, которая имеет место при наличии только градиента концентрации.
Диффузия в реальных кристаллах происходит вследствие четырех основных механизмов:
1. Для идеальных кристаллов процесс диффузии предполагает простой обмен местами между соседними атомами вещества. В этом случае необходимо затратить значительную энергию (порядка энергии связи между соседними атомами решетки).
2. Для примесей внедрения характерно перемещение атомов по междоузлиям из-за наличия в системе некоторой концентрации дефектов.
3. При вакансионном механизме диффузии один из соседних атомов занимает близлежащую вакансию. Вакансии могут образовываться вследствие того, что некоторые атомы, совершающие тепловые колебания около положения равновесия, могут иметь энергию, значительно превышающую среднюю энергию связи. Такие атомы уходят из узлов решетки в междуузельное пространство, образуя вакансию. Такая вакансия перемещается в кристалле путем последовательного заполнения ее другими атомами.
4. Возможна также диффузия по междоузлиям путем вытеснения, когда атом выталкивает одного из ближайших соседей в междоузлие, а сам занимает его место в решетке.
Таким образом, мы видим, что в твердых телах благодаря тепловому движению происходит непрерывное перемешивание частиц. Скорость перемешивания зависит от среднего времени 

где 






В большинстве случаев коэффициент диффузии в твердых телах увеличивается с ростом температуры по закону, имеющему вид уравнения Аррениуса:

где 
Процессы взаимной диффузии в поликристаллических пленках металлов приводят к образованию интерметаллидов. При этом можно выделить следующие изменения их свойств:
1. Образуются металлические слои, структура которых имеет большое количество дефектов, через которые возможна диффузия примесей и газов.
2. Электронные характеристики пленок металлов из-за образования твердых растворов металлов и соединений изменяются.
3. Меняется толщина и состав переходного слоя.
4. Возможно развитие неоднородностей в слоях металлов и в переходном слое из-за неравномерности взаимной диффузии металлов через границу раздела.
Отмеченные выше процессы приводят к деградации электрических параметров и зависят от количества продиффундированного в структуру вещества. Поэтому особенно важно уметь находить зависимости распределения концентрации диффундирующих примесей в структурах от времени и температуры процесса диффузии. Это можно сделать, решив второе уравнение Фика или уравнение диффузии.
Уравнение диффузии представляет собой дифференциальное уравнение в частных производных и для его решения необходимо сформулировать начальные и граничные условия, которым должна удовлетворять концентрация и первоначальное распределение диффундирующего вещества. Эти условия определяют на основе анализа конкретной ситуации, в которой происходит процесс диффузии. Здесь важно отметить, что внутри твердого тела концентрация является непрерывной функцией координат и времени, а ее первая производная по времени 



Начальное распределение концентрации 


Уравнение диффузии (в физике его чаще называют уравнением теплопроводности) можно решить различными методами. Обычно в практике пользуются следующими методами его решения:
1. Метод разделения переменных (Фурье).
2. Операторный метод (Лапласа – Карсона – Хевисайда).
3. Метод источника (метод функций Грина).
4. Численные методы.
5. Метод Монте – Карло.
Следует отметить, что в настоящее время сам процесс диффузии в технологии изготовления полупроводниковых приборов и ИМС усовершенствован до такой степени, что можно создавать 
Контрольные вопросы
1. Что такое диффузия?
2. Как записывается первое уравнение Фика?
3. Как записывается второе уравнение Фика?
4. Что такое коэффициент диффузии?
5. Какие различают типы коэффициентов диффузии?
6. Как записывается зависимость изменения коэффициента диффузии от температуры в твердом теле?
7. Как процессы взаимной диффузии и образование при этом интерметаллидов изменяют свойства пленок металлов?
8. Как можно задавать начальное распределение концентрации и граничные условия (условия на поверхности) при решении уравнения диффузии?
Механика многофазных сред – наука и инженерные приложения 3 страница
II.4.2.5. Модель неньютоновских жидкостей
Определение. Жидкости, моделируемые условием 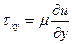
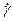
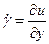
Пример. Модель степенной жидкости Оствальда
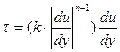
Здесь связь между τ в слоях жидкости степенная
Кажущаяся вязкость в среде –
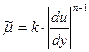
где k, n – коэффициенты в среде.
Определение. Если n 1 – среды – дилатантные (например, крахмальный клейстер).
Пример. Вязко-пластическая среда с предельным напряжением сдвига; модель “жидкости” Шведова-Бингама (сюда относятся высокопарафинистые и застывающие нефти, глинистые растворы, лаки, краски):
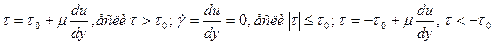
Физический смысл (6). Пока τ не превышает по mod некоторую предельную величину τ0 (является предельным напряжением сдвига), течение такой среды не начинается (в этом случае 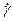
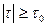
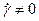
II.4.2.6. Модель упруго-деформируемого трубопровода
При схематизации процессов движения жидкостей и газов в трубопроводе используются модели трубопровода.
Модель недеформируемой трубы (МНТ), т.е. цилиндра с постоянными не изменяющимся внутренним диаметром d0 и постоянной толщиной δ стенки. Внешний диаметр D=d0 +2δ тоже остается постоянным.
При изучении гидравлического удара МНТ оказывается неточной в анализе явлений переноса В этих условиях используется модель упруго -деформируемого трубопровода (МУДТ).
Опыт показывает, что объем внутренней полости трубы хоть незначительно, но изменяется при изменении T, p среды. Поэтому для учета объемного расширения трубопровода при отклонении T от T0, имеем модель
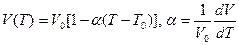
Здесь α – коэффициент объемного расширения металла, из которого сделан трубопровод. Существенно больше объем внутренней полости трубопровода изменяется от разности внутренного и внешнего давлений.
При одновременном отклонении p и T от p0 и T0 соответственно, используют модель
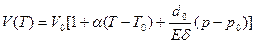
где E-модуль Юнга, δ – толщина стенки.
§ II.4.3. Уравнения движения и сплошности в однофазной области
Движение среды в любой области газожидкостной системы будет определяться уравнениями гидродинамики (Навье-Стоска):
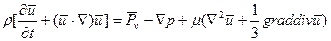
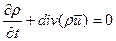
В обозначениях принято: 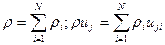
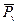
В случае многокомпонентной среды к (1), (2) добавляется уравнение диффузии индивидуальной компоненты:
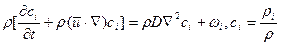
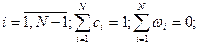
Для неизотермических условий к уравнениям (1)-(4) добавляются энергетические уравнения — теплопроводности Фурье-Кирхгоффа (5) или Фурье-Острроградского (6):
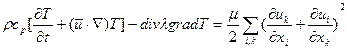
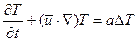
§ II.4.4. Механическое взаимодействие на границе раздела фаз
Для уравнений движения, написанных попарно для каждой из фазовых областей газожидкостной системы необходимо задать условия, связывающие поля давлений и скорости по поверхностям раздела фаз.
Выделим контрольной поверхностью F замкнутую область объема V, заключающую в себе часть поверхности раздела фаз, где F1 – поверхность тяжелого компонента — жидкость, F2 — поверхность легкого компонента – газ.
Считаем, что к поверхности F=F1+F2 приложены нормальные σ и касательные τ напряжения. Тогда условие динамического равновесия рассматриваемой области имеет вид:
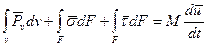
В (1) M — масса, заключенная в объеме V; 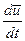
С другой стороны:
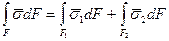
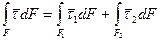
Стягивая поверхность F к заключенной в V поверхности раздела фаз Fгр, имеем:
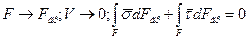
Вывод. Т.к. 
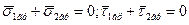
Замечание. Если прямоугольную систему координат расположить так, чтобы плоскость (xz) была касательной к поверхности раздела фаз в данной точке, а ось y нормальна к этой поверхности, то согласно уравнениям гидродинамики:
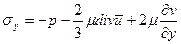
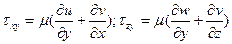
Условие отсутствия скольжения фаз на границе раздела:
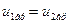
Нормальные к плоскости (xz) составляющие вектора скорости на границе раздела фаз определяются массовой скоростью фазового превращения 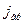
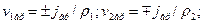
Замечание. 1. Если фазовые превращения отсутствуют, то 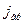
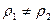
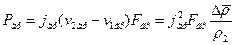
где 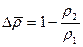
3. Если предположить, что qф — плотность теплового потока, идущего на испарение (конденсацию) на ПРФ, а скрытая теплота фазового превращения – r, то
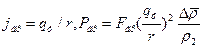
§ II.4.5. Тепловое взаимодействие на границе раздела фаз
Тепловой баланс объема V, включающего в себя ПРФ, имеет вид
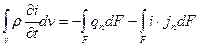
где 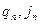
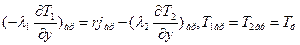
где 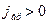
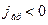
§ II.4.6. Скачок давления на границе раздела фаз
Т.к. молекулы жидкости, расположенные на ее границе с газом (твердым телом, другой жидкостью) находятся с силовом поле как остальных молекул своей среды, так и молекул другой среды, то силовое поле, действующее на поверхностный слой несимметрично. Поэтому возникает сила, направленная в сторону более плотной среды. Расстояние, на котором проявляется действие молекул, весьма мало. Молекулы поверхностного слоя имеют свободную энергию, которая изменяется при деформации ПРФ. Поскольку равновесие системы устойчиво при минимальной свободной энергии, то любая жидкость стремиться максимально сократить свою свободную поверхность. Отсюда жидкость, не подверженная действию односторонних сил, принимает форму сферы. Эти эффекты учитывает коэффициент поверхностного натяжения (КПН).
Введем этот коэффициент 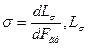
Определение. КПН – работа, которую необходимо совершить, чтобы увеличить ПРФ на единицу площади.
Замечание. Искривление ПРФ вызывает скачок давления, который определяется формулой Лапласа:
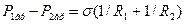
Здесь R1, R2 — главные радиусы кривизны ПРФ в данной точке.
Радиус кривизны — положительный, если направлен вглубь первой фазы. У сферы R1= R2= R, и соответственно давление в газовом потоке больше давления в окружающей жидкости на величину
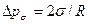
Замечание. Эффект поверхностного натяжения – давление насыщения также меняется с кривизной границы раздела фаз.
Приращение давления насыщения вследствие кривизны поверхности при одной и той же температуре определяется по формуле Кельвина
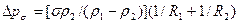
Глава II.5. Уравнения механики сплошных гетерогенных сред
§ II.5.1. Уравнения сохранения для составляющих
Запишем балансовые соотношения массы, импульса и энергии для каждой составляющей в некотором фиксированном объеме смеси V, ограниченной поверхностью S, учитывая, что имеется взаимодействие не только с внешней (по отношению к выделенному объему V) средой, но и соответствующий обмен массой, импульсом, энергией между составляющими внутри V.
II.5.1.1. Уравнение сохранения массы
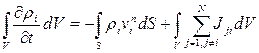
Здесь 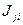
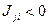
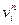
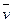
Из законов сохранения массы при различных физико-химических превращениях, имеем
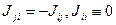
При переходе от поверхностного интеграла к объемному в (1) используется формула Гаусса-Остроградского:
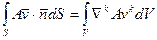
Применяя (3) к (1) имеем
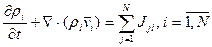
Здесь (4) – дифференциальное уравнение (ДУ) сохранения индивидуальной составляющей (i).
Уравнение (4) можно переписать, если использовать диффузионную скорость
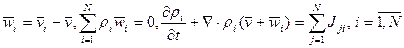
Замечание. Если просуммировать (4) или (5) по i, учитывая 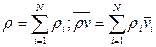

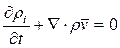
Вывод: уравнение неразрывности (6) в целом не чувствительно к относительному движению составляющих.
II.5.1.2. Уравнение импульсов
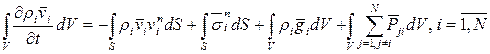
Физический смысл слагаемых правой части (7). ① — приток импульcа i-й составляющей через поверхность S; ②,③ — воздействие внешних поверхностных и массовых сил, приходящихся на i-ю составляющую и характеризуемых тензором 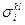
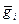
Из закона сохранения импульса при различных взаимодействиях
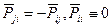
Применяя формулу Остроградского-Гаусса (3) к (7) имеем ДУ импульсов каждой составляющей:
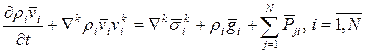
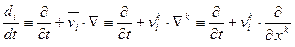
и уравнения (5) , имеем уравнение (9) в виде:
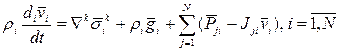
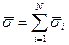
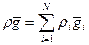
для сферы в целом, то суммируя (9) по i c учетом (12), имеем уравнение импульсов среды в целом:
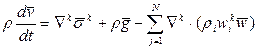
Замечание. Уравнение (13) в отличие от уравнения неразрывности (6), зависит от относительного движения составляющих.
II.5.1.3. Уравнение энергии
Замечание. Введем понятие удельной энергии смеси E (энергия приходящаяся на единицу массы среды) E=u+K, где u – внутренняя энергия, K – кинетическая энергия. В случае многофазной среды: внутренняя энергия смеси аддитивна по массе входящих в нее составляющих
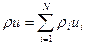
Здесь ui – удельные внутренние энергии составляющих смеси. Кинетическая энергия определяется макроскопическим движением
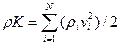
Тогда полная энергия смеси будет
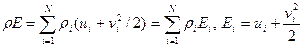
Из (15) и (5) для диффузионных скоростей (т.е. с использованием связи 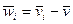
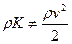
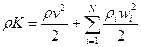
Из (16) видно, что кинетическая энергия многоскоростной среды определяется не только ее движением как целого со скоростью центра масс 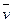
Балансовое уравнение для энергии каждой составляющей смеси в интегральной форме, имеет вид:
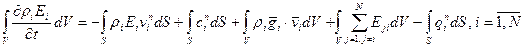
Замечание. (Физический смысл слагаемых правой части уравнения (18)):
I. ① — приток энергии i-й составляющей через S; ②,③ — работа внешних поверхностных сил [характеризуемая вектором 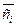
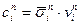
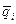
II. Для (18) справедливо: 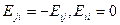
После применения формулы Гаусса-Остроградского (3) к уравнению (18) [используя уравнение неразрывности (4) –для перехода к индивидуальной компоненте ρi] следует ДУ энергии:
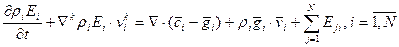
(20) – дивергентная форма ДУ. Бездивергентная форма ДУ полной энергии:
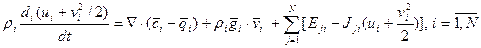
Суммируя по i уравнение (20) и учитывая (5), (6) (т.е. диффузионную скорость, уравнение неразрывности для смеси, соотношения (19) для Eji), получим уравнение энергии для смеси в целом:
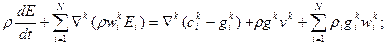
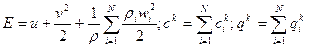
Вывод: уравнение энергии, как и уравнение импульсов (13), зависит от относительного движения составляющих.
Замечание (по обобщению понятия субстанциональной производной для величин, характеризующих смесь в целом и аддитивных величин по массам, входящих в смесь составляющих).
В отличие от обычной односкоростной СС, в данном случае понятие производной, дающей изменение параметра вдоль траектории выделенной частицы смеси, ее составляющие обладающие различными скоростями и траекториями, расходятся.
Так, в обычной односкоростной среде справедливо
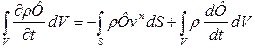
Для соотношения (24) имеем: 1. 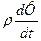
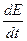
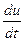
В случае многоскоростной среды выражение (24) допускает обобщение, определяющее 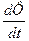
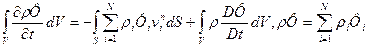
I. Введенная величина — 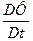
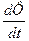
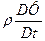
II. II. Из (25) следует выражение для 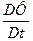
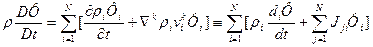
III. Из выражений для субстанциональной производной (10), а также соотношений (5), (16) следует выражение для формально определенной барицентрицеской субстанциональной производной:
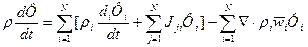
Таким образом, из (26), (27) видно отличие 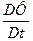
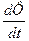
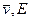
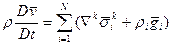
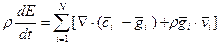
Уравнения (28), (29) – балансовые связи для скорости и энергии, могут быть использованы для описания любого многоскоростного континуума, соответствующей гомогенной и гетерогенной смеси.
§ II.5.2. Диффузионное приближение для гомогенных смесей
Определение. В гомогенной смеси, представляющей смесь газов, растворы, сплавы, ее составляющие, которые называются компонентами, размешаны и взаимодействуют на молекулярном или атомном уровне, скорости их относительного движения малы и их нужно учитывать в связи с определением концентраций компонент, и в то же время можно пренебречь динамическими и инерционными эффектами из-за относительного движения компонент.
Замечание. С формальной точки зрения при условии
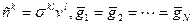
диффузионное приближение (в механике смесей) связано с пренебрежением слагаемыми, содержащими величины второго порядка относительно диффузионных скоростей 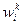
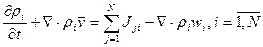
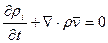
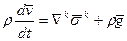
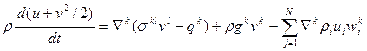
1. Уравнение реологии и состояния для всей среды в целом, задающие тензор напряжений 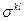
2. Считается, что тензор скоростей деформации 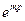
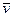
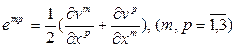
а влияние состава смеси непосредственно проявляется через физико-химические параметры, входящие в уравнение реологии и состояния
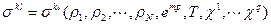
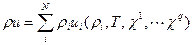
3. Относительные движения компонент, описываемые диффузионными скоростями или диффузионными потоками 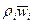
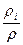
4. О законах диффузии. Устанавливаются зависимости, как правило, линейные для мгновенных значений 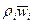
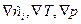
5. Модели, построенные на основе диффузионного приближения (1) для многоскоростного континуума фактически являются односкоростными, и поэтому диффузионное приближение называется одножидкостным.
6. Усложнение диффузионной теории смеси посредством учета температурных эффектов фактически не меняют существа диффузионного приближения, связанного: (i) с пренебрежением динамическими и инерционными эффектами относительного движения компонент; (ii) с применением законов диффузии для определения этого относительного движения.
§ II.5.3. Особенности математического описания гетерогенных смесей
Замечание. В отличие от ГоС ГеС, включающие газовзвеси, суспензии, эмульсии, пузырьковые жидкости, водонасыщенные грунты, углеводородные смеси, композитные материалы и т.д., описываются многоскоростной или многожидкостной моделью с учетом динамических эффектов из-за несовпадения скоростей составляющих, которые называются фазами. Это необходимо, т.к. скорости относительного движения фаз 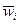
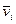
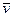
Система определяющих уравнений имеет вид:
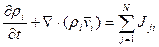
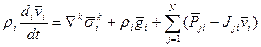
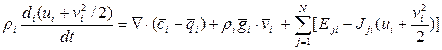
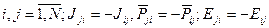
Замечание. (Отличие ГоС от ГеС).
I. В ГоС каждая компонента может рассматриваться как занимающая весь объем смеси равноправно с другими компонентами (V1 =V2=…=VN =V), в ГеС каждая фаза занимает лишь часть объема смеси (V1+ V1+…+VN =V). Для этой цели в теории ГеС используют величины αi (i=1…N), характеризующие доли объема смеси, занимаемой каждой фазой:
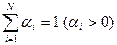
Вывод. Помимо приведенных плотностей ρi, вводятся истинные плотности вещества фаз 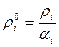
II. В ГеС необходимо учитывать, что фазы присутствуют в виде макроскопических (по отношению к молекулярным размерам) включений или в виде среды, окружающей эти включения, поэтому деформация любой фазы связана [для сравнения, в ГоС имеем 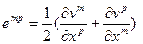
Дата добавления: 2017-01-29 ; просмотров: 1111 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://pandia.ru/text/80/099/45272.php
http://helpiks.org/8-98613.html