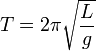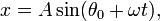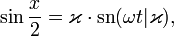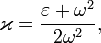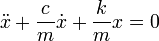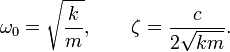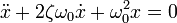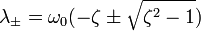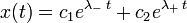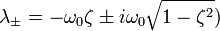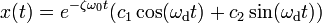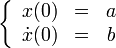Математический и физический маятники
Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.
Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая 

Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент силы относительно точки О: 
M = FL .
Момент инерции J в данном случае
Угловое ускорение:
С учетом этих величин имеем:
 | (7.8) |
Его решение

где  и и  | (7.9) |
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

 | (7.10) |
 | (7.11) |
Решение этого уравнения
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. 

Из этого соотношения определяем
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: <\displaystyle F(t)=F_<0>\cos \left(\Omega t\right)>
Примеры вынужденных колебаний: колебания мембраны телефона, иглы швейной машины, поршня в цилиндре автомобильного двигателя, рессор автомобиля, движущегося по неровной дороге, океанические приливы под действием Луны и др
Резонанс
РЕЗОНАНС (франц. resonance, от лат. resono — откликаюсь) — частотно-избирательный отклик колебат. системы на периодич. внеш. воздействие, при к-ром происходит резкое возрастание амплитуды стационарных колебаний. Наблюдается при приближении частоты внеш. воздействия к определённым, характерным для данной системы значениям. В линейных колебат. системах число таких резонансных частот соответствует числу степеней свободы и они совпадают с частотами собственных колебаний. В нелинейных колебат. системах, реактивные и диссипативные параметры к-рых зависят от величины стороннего воздействия, Р. может проявляться и как отклик на внеш. силовое воздействие, и как реакция на периодич. изменение параметров. В строгом значении термин «Р.» относится лишь к случаю силового воздействия.
Резонанс в линейных системах с одной степенью свободы. Пример простейшего случая Р. представляют вынужденные колебания, возбуждаемые сторонним источником — гармонической эдс
E0cospt с амплитудой Е0 и частотой p — в колебательном контуре (рис. 1, а).
Рис. 1. Колебательные системы с одной степенью свободы: последовательный (а) и параллельный (б) колебательные контуры, математический маятник (в) и упругий осциллятор (г),
Амплитуда x и фаза f вынужденных колебаний заряда [q(t) = xcos(pt +f)] определяются амплитудой и частотой внеш. силы:
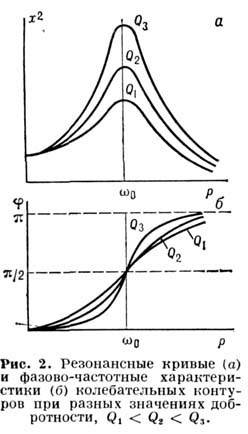
Зависимость амплитуды х стационарных вынужденных колебаний от частоты p вынуждающей силы при постоянной её амплитуде наз. резонансной кривой (рис. 2). В линейном колебат. контуре резонансные кривые, соответствующие различным F, подобны, а фазово-частотная характеристика f(p) не зависит от амплитуды силы.
Вложение энергии в колебат. контур пропорц. первой степени, а диссипация энергии пропорц. квадрату амплитуды колебаний. Это обеспечивает ограничение амплитуд стационарных вынужденных колебаний при Р. Приближение частоты p к собств. частоте w0сопровождается ростом амплитуды вынужденных колебаний, тем более резким, чем меньше коэф. затухания d. При Р. ток, протекающий через контур, I = 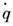
Важной характеристикой резонансных свойств колебат. системы (осциллятора) является добротностьQ ,к-рая, по определению, равна умноженному на 2p отношению энергии, запасённой в системе, к энергии, рассеиваемой за период колебаний. При воздействии на резонансной частоте амплитуда вынужденных колебаний x в Q раз больше, чем в квазистатич. случае, при 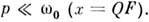

При Р. в электрич. цепях реактивная часть комплексного импеданса обращается в нуль. При этом в после-доват. цепи падения напряжения на катушке индуктивности и на конденсаторе имеют амплитуду QE0. Однако они складываются в противофазе и взаимно компенсируют друг друга. В параллельной цепи (рис. 1, б)при Р. происходит взаимная компенсация токов в ёмкостной и индуктивной ветвях. В отличие от последоват. Р., при к-ром внеш. силовое воздействие осуществляется источником напряжения, в параллельном контуре резонансные явления реализуются только в том случае, когда внеш. воздействие задаётся источником тока. Соответственно Р. в последоват. контуре называют Р. напряжений, а в параллельном контуре — Р. токов. Если в параллельный контур вместо генератора тока включить генератор напряжения, то на резонансной частоте будут выполняться условия не максимума, а минимума тока, поскольку вследствие компенсации токов в ветвях, содержащих реактивные элементы, проводимость цепи оказывается минимальной (явление антирезонанса).
Подобными чертами обладает явление Р. в механич. и др. колебат. системах. В линейных системах, согласно принципу суперпозиции, реакцию системы на периодич. несинусоидальное воздействие можно найти как сумму откликов на каждую из гармонич. компонент воздействия. Если период несинусоидальной силы равен Т, то резонансное возрастание колебаний может происходить не только при условии w0 ! 2p/Т, но в зависимости от формы E(t)и при условиях w0 ! 2pn/T, где n = 1, 2. (Р. на гармониках).
Резонансные кривые определяют, наблюдая изменение амплитуды вынужденных колебаний либо при медленной перестройке частоты p вынуждающей силы, либо при медленном изменении собств. частоты w0. При высокой добротности осциллятора (Q 


Рис. 3. Статические и динамические амплитудно-частотные характеристики резонанса при различных скоростях нарастания частоты: p(t)= w0 + t/m, m = 0(1), 0,0625 (г), 0,25(3), 0,695 (4).
t* — время, в течение к-pогo частота p находится в пределах полосы резонанса Dw. При быстрой перестройке частоты, по мере роста m, происходит уменьшение высоты и расширение резонансных кривых, причём их форма становится более асимметричной (рис. 3).
Резонанс в линейных колебательных системах с несколькими степенями свободы. Колебат. системы с неск. степенями свободы представляют собой совокупность взаимодействующих осцилляторов. Примером может служить пара колебат. контуров, связанных за счёт взаимной индукции (рис. 4). Вынужденные колебания в такой системе описываются ур-ниями
Индуктивная связь приводит к тому, что колебания в отд. контурах не могут происходить независимо друг от друга. Однако для любой колебат. системы с неск. степенями свободы можно найти нормальные координаты, к-рые являются линейными комбинациями независимых переменных. Для нормальных координат система ур-ний, подобная (2), преобразуется в цепочку ур-ний для вынужденных колебаний такого же вида, как для одиночных колебат. контуров, с тем отличием, что воздействие на каждую из нормальных координат оказывают силы, приложенные, вообще говоря, в разных частях совокупной колебат. системы. При рассмотрении законов движения в нормальных координатах справедливы все закономерности Р. в системах с одной степенью свободы.
Рис. 4. Колебательная система с двумя степенями свободы — пара контуров со связью за счёт взаимоиндукции.
Резонансное нарастание колебаний происходит во всех частях колебат. системы на одних и тех же частотах (рис. 5), равных частотам собств. колебаний системы. Нормальные частоты не совпадают с парциальными, т. е. с собств. частотами осцилляторов, входящих в совокупную систему. Если частота сторонней силы равна одной из парциальных частот, то в совокупной системе Р. не наступает. Напротив, в этом случае амплитуды вынужденных колебаний достигают минимума, аналогично случаю антирезонанса в системе с одной степенью свободы. Возможность подавления колебаний, частота к-рых равна одной из парциальных, используется в электрич. фильтрах и успокоителях механич. колебаний.
В системе, состоящей из слабо связанных осцилляторов с одинаковыми парциальными частотами, резонансные максимумы, отвечающие близким нормальным частотам, могут сливаться, так что частотная характеристика имеет один максимум (рис. 6). Увеличение связи между осцилляторами приводит к росту интервала между нормальными частотами системы. Изменение формы резонансных кривых при увеличении коэф. связи иллюстрирует рис. 6. Система осцилляторов при связи, близкой к критической, имеет частотную характеристику, уплощённую вблизи Р., причём крутизна её склонов выше, чем у одиночного осциллятора с таким же уровнем потерь. Это свойство обычно используется для создания полосовых электрич. фильтров.
Рис. 6. Резонансные кривые двухконтурной колебательной системы при gQ = 1(1), 
Резонанс в распределённых колебательных системах. В распределённых системах (см. Система с распределёнными параметрами)амплитуда и фаза колебаний зависят от пространственных координат. Линейные распределённые колебат. системы характеризуются набором нормальных частот и собств. ф-ций, к-рые описывают пространственное распределение амплитуд собств. колебаний. Резонансные свойства (добротность) распределённых систем определяются не только собств. затуханием, но и связью с окружающей средой, в к-рую происходит излучение части энергии колебаний (электрич., упругих и др.). В распределённых системах, обладающих высокой добротностью (Q 
В распределённых системах сохраняют силу все общие свойства Р. Особенностью Р. в распределённых системах (равно как и в системах с неск. степенями свободы) является зависимость амплитуд вынужденных колебаний не только от частоты, но и от пространственного распределения вынуждающей силы. Р. наступает, если пространственное распределение внеш. силы повторяет форму собств. ф-ции, а частота равна соответствующей нормальной частоте. При неблагоприятном пространственном распределении сторонней силы вынужденные колебания не возбуждаются. Это происходит, в частности, тогда, когда сосредоточенная сила прикладывается в точках, для к-рых амплитуда соответствующего нормального колебания обращается в нуль. Так, прикладывая сосредоточенную силу в точке, являющейся узловой для перемещений струны, невозможно возбудить её колебания, поскольку работа силы будет равна нулю. Если распределение сил таково, что работа, совершаемая ими в разл. частях системы, имеет противоположные знаки и в целом не приводит к изменению энергии, вынужденные колебания также не возбуждаются.
Резонанс в нелинейных колебательных системах. В упругих системах нелинейным элементом является пружина, для к-рой связь между деформацией и упругой силой нелинейна, т. е. нарушается закон Гука. В электрич. системах примером нелинейного диссипа-тивного элемента является диод, вольт-амперная характеристика к-рого не подчиняется закону Ома. Нелинейными реактивными (энергоёмкими) элементами являются конденсаторы с сегнетоэлектриком или катушки индуктивности с ферритовыми сердечниками. Параметры этих элементов — ёмкость, индуктивность, сопротивление, а также собств. частоту и коэф. затухания в нелинейных системах можно считать ф-циями тока или напряжения. При этом в нелинейных системах не выполняется суперпозиции принцип.
В нелинейных системах гармонич. сила возбуждает негармонич. колебания, в спектре к-рых имеются кратные частоты, поэтому Р. на гармониках происходит p при синусоидальной внеш. силе. В колебат. системах, обладающих достаточно высокой добротностью и частотной избирательностью, наиб. амплитуду имеет та спектральная компонента, частота к-рой близка к частоте Р. Рассматривая лишь колебания с частотой, близкой к резонансной, можно и в этом случае получить семейство резонансных кривых. Для системы с нелинейными реактивными (энергоёмкими) элементами при r ! w0 эти кривые изображены на рис. 7. Форма резонансной кривой зависит от амплитуды вынуждающей силы и по мере её увеличения становится всё более асимметричной. Поскольку частота собств. колебаний нелинейного осциллятора зависит от их амплитуды, то и максимумы на резонансных кривых сдвигаются в сторону более высоких или более низких частот. Начиная с нек-рого значения амплитуды силы, резонансные кривые приобретают неоднозначную клювообразную форму. В определённом интервале частот стационарная амплитуда вынужденных колебаний оказывается зависящей от предыстории установления колебаний (явление колебат. гистерезиса). При этом части резонансных кривых, соответствующих неустойчивым состояниям, образуют на плоскости (х, р)область физически нереализуемых режимов (на рис. 7 заштрихована).
Рис. 7. Семейство амплитудно-частотных кривых в случае нелинейного резонанса при различных амплитудах сторонней силы (F1
Малые колебания физического и математического маятников
Физическим маятником называется твердое тело любой формы, имеющее горизонтальную ось вращения, не проходящую через центр тяжести тела, называемую осью привеса.
Рассмотрим движение физического маятника под действием силы тяжести Р (рис. 115). В соответствии с (111.218) дифференциальное уравнение движения физического маятника будет
где IO — момент инерции маятника относительно оси вращения О,
h — расстояние центра инерции С от оси вращения (длина физического маятника).
При малых колебаниях маятника или при малых углах отклонения φ можно принять sin φ ≈ φ, тогда
где
Интегрируя это уравнение, найдем
Постоянные интегрирования С1 и С2 определим из начальных условий движения. Например, пусть при t = 0, φ0=α, φ0=0.
Следовательно, под действием силы тяжести (без учета силы сопротивления среды) маятник совершает гармонические колебания. Частота этих колебаний
Период Т малых колебаний физичесйого маятника равен
Формула (111.222) может быть использована для опытного определения момента инерции твердого тела.
Математический маятник представляет собой несвободную тяжелую материальную точку М, соединенную с горизонтальной осью вращения (осью привеса) z гибкой нерастяжимой невесомой нит (или абсолютно жестким невесомым стержнем), движущуюся в вертикальной плоскости. Расстояние материальной точки от оси вращения называется длиной математического маятника.
Пусть вес математического маятника равен Р, а длина — l. Рассматривая математический маятник как частный случай физического маятника, применим для вывода дифференциального уравнения движения математического маятника уравнение (111.219), в котором
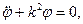
Таким образом, движение математического маятника описывается дифференциальным уравнением, аналогичным уравнению движения физического маятника.
Для круговой частоты колебаний /с и периода колебаний Т математического маятника получим
Приведенной длиной физического маятника называется длина синхронного с ним математического маятника, т. е. математического маятника, имеющего тот же период колебаний, что и физический маятник.
Приравняв периоды колебаний математического и физического маятников или выражения (111.224) и (111.222), получим
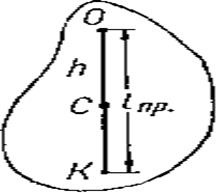
На расстоянии приведенной длины /пр от точки привеса О (рис. 116) находится точка К, которая называется центром колебаний (качаний) физического маятника.
Центр колебаний физического маятника имеет следующие свойства:
1. Центр тяжести маятника расположен между центром колебаний и точкой привеса, следовательно lпр>h.
2. Если заставить маятник колебаться вокруг оси, проходящей через центр колебаний и параллельной его оси привеса, то точка привеса О будет новым центром колебаний такого физического маятника.
Это свойство взаимозаменяемости точки привеса и центра колебаний физического маятника (теорема Гюйгенса) используется в оборотном маятнике Картера, применяемом для определения ускорения силы тяжести в различных точках земной поверхности.
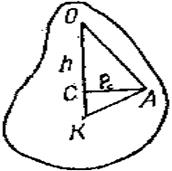
Рассмотрим графический способ нахождения центра колебаний физического маятника, основанный на том, что радиус инерции маятника относительно центральной оси ρc есть средняя пропорциональная между длиной h маятника и расстоянием КС его центра инерции от центра колебаний (рис. 116).
а на основании формулы (111.80)
Как видно из рис. 116, lпр-h=KC=h1. Поэтому 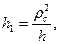
Для нахождения центра колебаний отложим из точки С перпендикулярно к отрезку h отрезок рс (рис. 117) и конец его А соединим с точкой привеса О. Затем под прямым углом к ОА проведем прямую до пересечения с продолжением ОС в искомой точке К — центре колебаний физического маятника. Заметим при этом, что ρc можно отложить как вправо, так и влево от точки С.
Дата добавления: 2015-08-08 ; просмотров: 2157 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Уравнение колебаний маятника
Рис.1
Исследуем выражение (2) в зависимости от разности фаз (φ2 — φ1):
1) φ2 — φ1 = ±2mπ (m = 0, 1, 2, . ), тогда A=A1+A2, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;
2) φ2 — φ1 = ±(2m+1)π (m = 0, 1, 2, . ), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.
Для практики представляет особый интерес случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω
23 Колебания физического маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Определения
— угол отклонения маятника от равновесия;
— начальный угол отклонения маятника;
— масса маятника;
— расстояние от точки подвеса до центра тяжести маятника;
— радиус инерции относительно оси, проходящей через центр тяжести.
— ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:

[править] Дифференциальное уравнение движения физического маятника
Основная статья: Приведённая длина
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
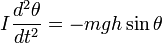
Полагая 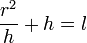
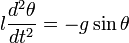
Последнее уравнение аналогично уравнению колебаний математического маятника длиной 

[править] Центр качания физического маятника
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии 
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен 
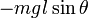
[править] Теорема Гюйгенса
[править] Формулировка
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
[править] Доказательство
Вычислим приведенную длину для нового маятника:
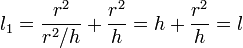
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
[править] Период колебаний физического маятника
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на 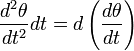
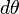
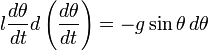
Интегрируя это уравнение, получаем.
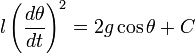
где 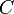
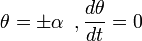
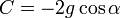
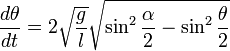
Отделяем переменные и интегрируем это уравнение:
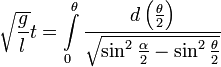
Удобно сделать замену переменной, полагая 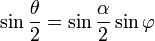
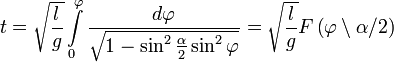
Здесь 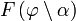
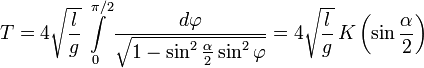
Здесь 
[править] Период малых колебаний физического маятника
Если амплитуда колебаний 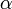
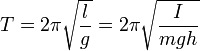
24 Колебания математического маятника
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит [1] от амплитуды и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; 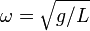
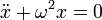
[править] Решения уравнения движения
[править] Гармонические колебания
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
где A — амплитуда колебаний маятника, θ0 — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями
[править] Нелинейный маятник
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 

Параметр 
где 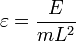
Период колебаний нелинейного маятника
где K — эллиптический интеграл первого рода.
[править] Движение по сепаратрисе
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, и останавливается, возвратившись в исходное положение.
25 Затухающие колебания. Зависимость амплитуды от времени.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида 
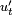
Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:
где Fc — сила сопротивления, Fy — сила упругости
или в дифференциальной форме
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения:
Величину ω называют собственной частотой системы, ζ — коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
Сделав замену x = e λt , получают характеристическое уравнение
Корни которого вычисляются по следующей формуле
[править] Решения
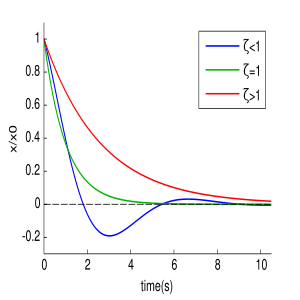
Зависимость графиков колебаний от значения ζ.
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Если 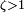
В этом случае колебания с самого начала экспоненциально затухают.
- Граница апериодичности
Если 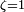
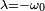
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
Если 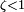
Тогда решением исходного дифференциального уравнения является
Где 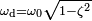
Константы c1 и c2 в каждом из случаев определяются из начальных условий:
26 Вынужденные колебания. Понятие резонанса.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: 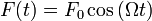
http://helpiks.org/4-64516.html
http://poisk-ru.ru/s49779t9.html
















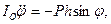
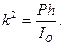
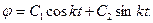
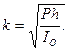
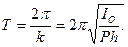
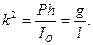
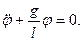
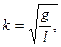
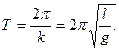
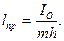
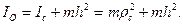
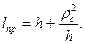
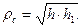
 — угол отклонения маятника от равновесия;
— угол отклонения маятника от равновесия; — масса маятника;
— масса маятника; — расстояние от точки подвеса до центра тяжести маятника;
— расстояние от точки подвеса до центра тяжести маятника; — радиус инерции относительно оси, проходящей через центр тяжести.
— радиус инерции относительно оси, проходящей через центр тяжести.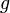 — ускорение свободного падения.
— ускорение свободного падения.