Таблица производных функций
О чем эта статья:
10 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое производная и зачем она нужна
Прежде чем переходить к таблице для вычисления производных, дадим определение производной. В учебнике оно звучит так:
Производная функции — это предел отношения приращения функции к приращению ее аргумента, при условии, что приращение аргумента стремится к нулю.
Если же говорить простыми словами, то производная функции описывает, как и с какой скоростью эта функция меняется в данной конкретной точке. Процесс нахождения производной называется дифференцированием.
Объясним на примере: допустим, Маша решила по утрам делать зарядку и стоять в планке. В первую неделю она держалась каждый день по 10 секунд, но начиная со второй недели смогла стоять в планке с каждым днем на 3 секунды дольше. Успехи Маши можно описать следующими графиками:
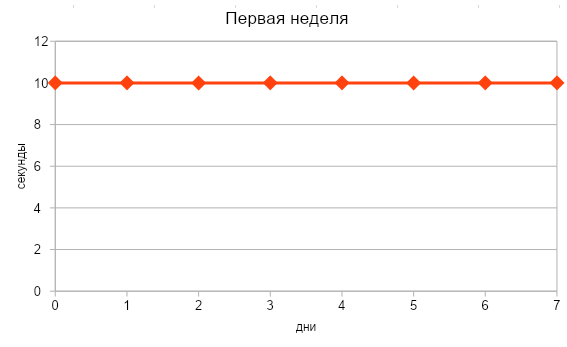
Очевидно, что в первую неделю результаты Маши не менялись (т. е. были константой), скорость прироста оставалась нулевой. Если мы заглянем в таблицу производных простых функций, то увидим, что производная константы равна нулю.
Во вторую неделю время выполнения планки с 10 сек начало увеличиваться на 3 сек ежедневно.
Снова смотрим в таблицу дифференцирования производных, где указано, что производная от х равна 1.
Вот так с помощью таблицы производных и элементарной математики мы докажем, что успехи Маши росли со скоростью 3 сек в день.
Это был очень простой пример, который в общих чертах объясняет азы дифференциального исчисления и помогает понять, для чего нужны формулы из таблицы производных функций. Но разобраться в решении задач, где скорость меняется нелинейно, конечно, не так просто.
Быстрее освоить производные поможет обучение на курсах по математике в онлайн-школе Skysmart.
Производные основных элементарных функций
Таблица производных для 10 и 11 класса может включать только элементарные часто встречающиеся функции. Поэтому приведем стандартную таблицу производных.
Примеры решения производных с ответами
Простое объяснение принципов решения производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения производных
Для вычисления производных вам потребуется таблица производных. Кроме того, существуют формулы для нахождения сложных производных.
Процесс нахождения производный называется дифференцированием.
- 0, c \neq 1″ title=»Rendered by QuickLaTeX.com» height=»20″ width=»219″ style=»vertical-align: -5px;» />
- 0, c \neq 1″ title=»Rendered by QuickLaTeX.com» height=»20″ width=»180″ style=»vertical-align: -5px;» />
0, c \neq 1″ title=»Rendered by QuickLaTeX.com» height=»20″ width=»219″ style=»vertical-align: -5px;» />
0, c \neq 1″ title=»Rendered by QuickLaTeX.com» height=»20″ width=»180″ style=»vertical-align: -5px;» />
– производная суммы (разницы).
– производная произведения.
– производная частного.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Примеры решений производных
Задача
Найти производную функции 
Решение
Заданная функция является сложной и её производная равна произведению производной от косинуса на производную от его аргумента:
Ответ
Задание
Найти производную функции 
Решение
Обозначим 
, где 
. Тогда, согласно правила вычисления производной сложной функции, получим: 
Ответ
Задача
Найти производную функции 
при 
.
Решение
. 
.
Ответ
.
Задача
Найти производную функции 
.
Решение
.
После приведения подобных членов получаем: 
.
Ответ
Задача
Найти производную функции 
.
Решение
В этом примере квадратный корень извлекается из суммы 
. Поэтому сначала вычисляем производную от квадратного корня, а затем умножаем ее на производную от подкоренного выражения: 
.
Ответ
.
Задача
Найти производную функции 
.
Решение
Применяя правила дифференцирования дробей, получаем: 
.
Применяя правила дифференцирования котангенса, получаем: 
.
Учитывая, что 
и 
, после упрощения получим: 
.
Ответ
.
Задача
Найти производную функции 
.
Решение
Применяя правила дифференцирования дробей, получаем: 
.
Ответ
.
Задача
Найти производную функции 
.
Решение
Применяя правила дифференцирования дробей, получаем: 
.
Ответ
.
Задача
Найти производную функции 
.
Решение
Дифференцирование можно произвести в два этапа: вначале продифференцировать степень функции арксинус, а затем произвести дифференцирование самого арксинуса, перемножив результаты: 
.
Ответ
.
Задача
Найти производную функции 
.
Решение
По правилам дифференцирования показательной функции с основанием 
, производная этой функции равна произведению самой функции на производную функции, являющейся показателем степени: 
.
Ответ
.
Производная
Теория к заданию 7 из ЕГЭ по математике (профильной)
Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:
Дифференцированием называют операцию нахождения производной.
Таблица производных некоторых элементарных функций
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n$ | $nx^ |
| $<1>/ | $-<1>/ |
| $√x$ | $<1>/<2√x>$ |
| $e^x$ | $e^x$ |
| $lnx$ | $<1>/ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | $<1>/ |
| $ctgx$ | $-<1>/ |
Основные правила дифференцирования
1. Производная суммы (разности) равна сумме (разности) производных
Найти производную функции $f(x)=3x^5-cosx+<1>/
Производная суммы (разности) равна сумме (разности) производных.
2. Производная произведения
Найти производную $f(x)=4x·cosx$
3. Производная частного
4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
Физический смысл производной
Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.
Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?
1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции
$v(t) = x'(t) = 1,5·2t -3 = 3t -3$
2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:
Геометрический смысл производной
Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.
Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:
Следовательно, можем составить общее равенство:
На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.
На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k 0$
Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.
Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)
$f'(x_0) = tg ВАС = 0,25$
Производная так же применяется для нахождения промежутков возрастания и убывания функции:
Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.
http://nauchniestati.ru/spravka/primery-resheniya-proizvodnyh/
http://examer.ru/ege_po_matematike/teoriya/issledovanie_funkcii