Ответы на экзаменационные вопросы. Вопросы по курсу «Теплопередача»
| Название | Вопросы по курсу «Теплопередача» |
| Анкор | Ответы на экзаменационные вопросы.doc |
| Дата | 24.04.2017 |
| Размер | 329.5 Kb. |
| Формат файла |  |
| Имя файла | Ответы на экзаменационные вопросы.doc |
| Тип | Документы #4627 |
| Категория | Физика |
| страница | 1 из 3 |
Вопросы по курсу «Теплопередача» Температурное поле. Гипотеза Фурье. Теплоотдача и теплопередача. Коэффициенты теплоотдачи и теплопередачи, их физический смысл. Теплопроводность это важнейшая техническая характеристика теплоизоляционного материала. Количественно теплопроводность определяется коэффициентом теплопроводности (λ), выражающим количество тепла, проходящее через образец материала толщиной 1 м и площадью 1 м2 при разности температур на противолежащих поверхностях 1°К за 1 час. На величину теплопроводности теплоизоляционных материалов оказывают влияние плотность материала, вид, размеры и расположение пор (пустот) и т.д. Сильное влияние оказывает также температура материала и, особенно, его влажность. Теплопроводность вакуума — 0, то есть вакуум не проводит тепло. Это абсолютный теплоизолятор. Теплопроводность воздуха зависит от его температуры и давления. В большинстве житейских случаев она колеблется возле отметки 0.02 Вт/(м*K). Теплопроводность снега зависит от его состояния. Если он только что выпал, то его теплопроводность примерно равна 0.10-0.15 Вт/(м*K), а если уже слежался, то 0.25-0.4 Вт/(м*K). Температурным полем называется совокупность значений t˚ во всех точках рассматриваемого пространства (ТВ тела) в каждый фиксированный момент времени. в данном случае температура – это скалярная величина, определяющая степень нагретости тела в каждой точке. Различают стационарное и нестационарное температурные поля. Ф-ла (1) относится к неустановившемуся тепловому режиму и называется нестационарным тепловым полем. Если тепловой режим явл установившемся, то температура в каждой точке тела с течением времени не меняется, изменяясь лишь от точек к точкам с разными координатами, такое температурно поле наз стационарным и t˚ явл функцией координат по пространству Согласно гипотезе Фурье количество теплоты dQτ, Дж, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту ∂t⁄∂n: Коэффициент теплопередачи является количественной расчетной величиной и зависит от коэффициентов теплоотдачи, термического сопротивления стенки и загрязнений. Для плоской стенки
где Коэффициент теплоотдачи Коэффициент теплоотдачи зависит от: — скорости жидкости — тепловых свойств жидкости (удельной теплоёмкости ср, теплопроводности — геометрических параметров – формы и определяющих размеров стенки (для труб – их диаметр d и длина L), а также шероховатости Вследствие сложной зависимости коэффициента теплоотдачи 2. Уравнение энергии. Уравнение Фурье-Кирхгофа (с выводом). где
Дифференциальное уравнение конвективного теплообмена или уравнение Фурье-Кирхгофа: Коэффициент температуропроводности Для твёрдых тел Следовательно, При установившемся процессе теплообмена Для практического использования уравнения Фурье-Кирхгофа его представляют в виде функции от критерия подобия. 3. Динамическое уравнение движения (уравнение Навье-Стокса). Уравнение сплошности. (неразрывности движения). Их физический смысл. Система состоит из трех уравнений: В векторном виде для несжимаемой жидкости они записываются следующим образом: где: 4. Основное уравнение теории теплопроводности (уравнение Фурье) и его физический смысл. Краевые условия. Задачи о температурном поле твердого тела, условия первого, второго и третьего рода. Коэффициент теплоотдачи Коэффициент теплоотдачи зависит от: — скорости жидкости — тепловых свойств жидкости (удельной теплоёмкости ср, теплопроводности — геометрических параметров – формы и определяющих размеров стенки (для труб – их диаметр d и длина L), а также шероховатости Вследствие сложной зависимости коэффициента теплоотдачи Краевые условия (условия однозначности) включают в себя:
Геометрическими условиями задаются форма и линейные размеры тела, в котором протекает процесс. Физическими условиями задаются физические параметры тела (c, λ, ρ и др) и может быть задан закон распределения внутренних источников теплоты. Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае начальное условие аналитически может быть записано следующим образом (при τ=0) : при равномерном распределении температуры в теле начальное условие упрощается (при τ=0) : Граничные условия могут быть заданы несколькими способами. Граничные условия I рода. Задается распределение температуры на поверхности тела для каждого момента времени. tс=f(x,y,z,τ) tс – температура на поверхности тела. В частном случае, когда температура на поверхности тела является постоянной на протяжении всего времени протекания процесса теплообмена, уравнение упрощается и принимает вид tс=const Граничные условия II рода. Задаются значения теплового потока для каждой точки поверхности тела и любого момента времени. qп=f(x,y,z,τ) qп- плотность теплового потока. В простейшем случае: qп=qo=const Граничные условия III рода. Задаются температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой. Согласно закону Ньютона-Рихмана количество теплоты, отдаваемое единицей поверхности тела в единицу времени, пропорционально разности температур поверхности тела tc и окружающей среды tж (tc>tж) где α – коэффициент пропорциональности, называемый коэффииентом теплоотдачи, Вт/(м²*К), характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Численно он равен количеству теплоты, отдаваемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой, равной одному градусу. отсюда окончательно граничное условие III рода : 5. Решение задачи определения температурного поля плоской однослойной стенки стационарном режиме в граничных условиях первого рода. Многослойная плоская стенка. Тепловой поток через однослойную и многослойную плоскую стенку. Q’ –тепловой поток, который подводится от теплоносителя к твердому телу В стационарном случае при отсутствии источников теплоты Для тепловых потоков справедливо: Для плотности тепловых потоков в сплошных телах площадь теплообмена переменна, поэтому плотности потоков будут различаться q1=-л*gradt= б*( tп1-t’)/д получили систему n+2 уравнений (n-количество слоев) с n+2 неизвестными => система имеет единственное решение t tп1-t’= (д1/л1)*q + => tc1- tс2=q(1/ б1+ д1/л1+…+1/б2) неизвестные температуры находятся последовательной подстановкой q в уравнения системы. Теплоотдача (конвективный теплообмен)4.2.1. Определение исходных понятий Обмен внутренней энергией между поверхностью твердого тела и жидкостью посредством теплопередачи в теплотехнике называется теплоотдачей или конвективным теплообменом. Термин «конвективный теплообмен» подчеркивает, что процесс переноса тепла здесь осуществляется одновременно не только теплопроводностью, но и конвекцией. Теплопроводность обусловливается градиентом температуры между слоями жидкости. Конвективные потоки макроскопических элементов жидкости (газа) возникают вследствие различия в плотности вещества разных элементов, находящихся при разной локальной температуре. Конвекция, обусловленная разницей в плотности макроскопических элементов жидкости, называют естественной конвекцией. В жидкости можно реализовать также и вынужденную конвекцию с помощью внешних возбудителей, например, перемешиванием жидкости (газа). Теплоотдача зависит и от характера движения жидкости – ламинарного (слоистого) или турбулентного (вихревого). Напомним, критерий перехода ламинарного течения в турбулентное оценивается безразмерным числом Рейнольдса Re = Теплопередача в вязком подслое осуществляется теплопроводностью, термическое сопротивление которого Явление теплоотдачи определяется тепловыми и гидродинамическими процессами. Эти процессы описываются соответствующими дифференциальными уравнениями: уравнением теплоотдачи, уравнением теплопроводности, уравнением динамики течения жидкости (газа), уравнением непрерывности. Рассмотрим эти уравнения. 4.2.2. Уравнение теплоотдачи Интенсивность теплоотдачи (конвективного теплообмена) с поверхности стенки площадью dS за время t описывается эмпирической формулой Ньютона-Рихмана где: Tст , Tж — температура стенки и жидкости соответственно; dS — элементарная площадка стенки; a — коэффициент теплоотдачи. Коэффициент теплоотдачи имеет смысл тепла, передаваемого в жидкость за единицу времени единицей поверхности при разности температур в один кельвин (один градус 0 С). Теплопередача осуществляется через вязкий подслой толщиной l, для которой справедлив закон Фурье dQ= — l где Сравнивая законы Ньютона-Рихмана и Фурье, получим: a = — Уравнение (23) называется уравнение теплоотдачи. Уравнение теплоотдачи позволяет по известному температурному полю определить коэффициент теплоотдачи. Заметим, в технических расчетах процесса теплоотдачи именно коэффициент теплоотдачи и представляет наибольший интерес. 4.2.3. Уравнение теплопроводности Фурье-Кирхгофа Выделим в потоке жидкости элементарный кубик с ребрами dx, dy, dz (рис. 4-7) и определим поток тепла через грани этого элементарного кубика. Здесь оператор d указывает, что теплота является одной из функций процесса переноса внутренней энергии (наряду с работой dA = pdV): элементарная порция подведенной теплоты dQ в общем случае не является полным дифференциалом. Однако так как энтальпия (H = U + pV) как функция состояния является полным дифференциалом, то припостоянном давлении подведенная элементарная порция тепла dQ формально становится полным дифференциалом, т.е. можно формально записать: dQ = dQ. Поток тепла через грани кубика обусловлен градиентом температуры на противоположных гранях, находящихся в перпендикулярном направлении на расстоянии dx, dy и dz соответственно. Если в направлении x на левой грани (см. рис. 4-7) температура T, то на противоположной грани на расстоянии dx температура равна (T + За время dt в направлении оси x количество тепла, проходящее через левую грань, равно (закон Фурье) Qx1 = а через правую грань Qx2 = Имеем: dQx = Qx1 — Qx2 = Аналогично по осям y и z: dQy = За счет подвода тепла наблюдаем приращение энтальпии жидкости за время dt определится уравнением dQ = dH = dQx + dQy + dQz = С другой стороны подведенную теплоту dQ (изменение энтальпии dH) можно представить также уравнением dQ =cpr где dm = r dx dy dz – масса рассматриваемого элементарного объема, cp – теплоемкость жидкости при постоянном давлении, Здесь Здесь представляет собой конвективное изменение температуры, обусловленное перемещением элементов текущей жидкости (vx, vy, vz – проекции скорости элементов жидкости). Таким образом, температурное поле в движущейся жидкости зависит и от распределения скоростей элементов жидкости. Сравнивая (24) и (25) получим уравнение cpr Уравнение (26) есть дифференциальное уравнение теплопроводности Фурье-Кирхгофа, где постоянная жидкости a = Запишем уравнение Фурье-Кирхгофа в развернутом виде Для твердых тел уравнение Фурье-Кирхгофа пример вид так как в твердых телах при наличии переноса тепла наблюдается только локальные изменения температуры, но перенос вещества отсутствует 4.2.4. Уравнение Навье-Стокса (дифференциальное уравнение Движения жидкости) Как было уже отмечено, из уравнения Фурье-Кирхгофа следует, что температурное поле зависит от распределения скоростей элементов жидкости (см., напр., уравнение 26 ** ). Динамика движения произвольного элемента жидкости массой dm описывается вторым законом Ньютона: dma = R, где R – результирующая сила, действующая на элемент. На выделенный элемент жидкости действуют: 1) сила тяжести; 2) равнодействующая сил давления по вертикали; 3) равнодействующая сил вязкого трения на боковые поверхности выделенного элемента, и обусловленная градиентом скорости жидкости в направлении оси 0y. Сила тяжести равна где gx – проекция ускорения свободного падения на ось 0х, r – плотность жидкости. Будем считать, что жидкость несжимаемая, т.е. r = const. Равнодействующая сил давления. На верхней грани давление равно p,на нижней – (p + p dy dz — (p + Равнодействующая сил вязкого трения. При ламинарном течении жидкости сила вязкого трения возникает только на боковых (левом и правом) гранях выделенного элемента жидкости. Напомним, закон касательной силы вязкого трения на единицу площади контакта (закон Ньютона) имеет вид: Ft =h где h – коэффициент вязкости (или просто – вязкость), единицей вязкости служит паскаль×секунда (Па×с). Если на левой боковой грани вязкое трение равно Ft , то на правой грани – (Ft + (Ft + Воспользовавшись законом силы вязкого трения (29), получим при h = const: Если проекция скорости vx изменяется по всем направлениям, т.е. проекция скорости vx имеет градиент по всем направлениям, то равнодействующая вязкого трения в направлении оси 0х примет вид: h Итак, проекция результирующей силы R, действующей на выделенный элемент массой dm и объемом dV, на ось 0х примет вид: Rx = [r gx — С другой стороны dmax = r dV т.е. полное изменение скорости r Теперь можно записать второй закон динамики в развернутом виде: r Дифференциальное уравнение (32), описывающее динамику движения вязкой несжимаемой жидкости (r = const), называется уравнением Навье-Стокса. Уравнение Навье-Стокса для проекций на оси 0y и 0z имеют аналогичный вид: r r Заметим, уравнение Навье-Стокса справедливо как для ламинарного, так и турбулентного потока жидкости. 4.2.5. Уравнение непрерывности (сплошности) Выделим в потоке жидкости мысленный неподвижный элементарный кубик с ребрами dx, dy, dz (рис. 4-9) и определим массу жидкости, протекающей через этот кубик за время dt. а через правую грань той же площади вытекает масса mx2 = Имеем: dmx = mx2 — mx1 = Аналогично по остальным осям: dmy = my2 — my1 = dmz = mz2 — mz1 = Полное изменение массы жидкости в выделенном объеме dV = dx dy dz равно dm = dmx + dmy + dmz = Ясно, что изменение массы жидкости в выделенном объеме с течением времени может быть обусловлено только изменением плотности жидкости со временем. Следовательно, имеем: Знак минус в (33) указывает, что если dm > 0 (т.е. из объема dV вытекает большая масса жидкости, чем втекает), то Уравнение (33) можно записать в виде: Дифференциальное уравнение (34) и есть уравнение непрерывности (уравнение сплошности) в общем виде. Если плотность жидкости постоянна, (r = const) то уравнение непрерывности (34) примет вид 4.2.6. Условия однозначности математического описания теплоотдачи (краевые условия). Подобие явлений Процесс теплоотдачи математически описываются рассмотренными выше дифференциальными уравнениями: уравнением теплоотдачи; уравнением теплопроводности; уравнением динамики движения жидкости (газа); уравнением непрерывности. Применение этих уравнений к расчету конкретного процесса теплоотдачи требует введения в структуру уравнений частных особенностей этого процесса. Эти частные особенности называются условиями однозначности или краевыми условиями решения частной задачи. К этим условиям относятся: 1) геометрические условия, которые характеризуют размеры и форму, например, диаметр и длина, гладкость или шероховатость стенок канала протекания жидкости и т.п.; 2) физические константы, характеризующие свойства среды, например, плотность, вязкость, коэффициент теплопроводности и т.д.; 3) граничные условия протекания процесса на границах раздела сред, например, условие нулевой скорости жидкости в пристеночном вязком слое трубы; 4) временные условия, например, стационарность или нестационарность физических констант. Процесс теплоотдачи – сложный процесс, и аналитическое решение системы дифференциальных уравнений возможно для ограниченного числа весьма упрощенных задач, т.к. особенности реального процесса теплоотдачи зависит от очень большого числа разного рода переменных величин, которые, к тому же, взаимосвязаны. В этой связи эксперимент приобретает решающее значение для анализа и расчета реальных процессов теплопроводности. Сам по себе эксперимент предварительно проводится на модельных объектах. Результаты эксперимента на модели выражают в форме определенного критерия подобия. Примером такого критерия подобия является число Рейнольдса. Эти критериальные оценки далее переносятся на объекты, подобные модельному объекту. Методология теории подобия основывается на трех утверждениях (трех теоремах подобия): 1) подобные явления имеют одинаковые критерии подобия (Бертран Ж.). В модельном эксперименте измеряют те величины, которые содержатся в критерии; 2) уравнения, описывающие процесс, могут быть представлены в виде зависимости между критериями подобия, определяющими процесс (Федерман А., Букингем Дж.). Результаты опыта представляют в виде критериальных уравнений; 3) подобны те явления, краевые условия которых подобны и для которых критерии подобия, составленных из краевых условий, равны (Кирпичев М.В., Гухман А.А.). Это утверждение устанавливает признак подобия процессов в модельном и рабочем объектах. Опишем некоторые критерии подобия. Все критерии представляют собой отношения одноименных величин и, следовательно, являются безразмерными величинами. Число Эйлера Eu – это соотношение между перепадом силы давления в потоке Fp = Dpl 2 и поступательной силой инерции Fi = ma = rl 3 Eu = Число Эйлера характеризует соотношение между перепадом статического давления и динамическим давлением в потоке. Число Рейнольдса Re определяет связь в потоке между поступательной силой инерции Fi = m Re = Число Рейнольдса характеризует гидродинамический режим вынужденного движения жидкости (газа). Критерии теплового подобия получают из уравнений передачи тепла. Число Фурье Fo – отношение тепла, передаваемого теплопроводностью Ql = l Fo = Число Фурье характеризует нестационарные процессы распространения тепла, определяемое скоростью изменения температурного поля, размерами тела, температуропроводностью. Число Нуссельта Nu – отношение тепла передаваемого в процессе теплоотдачи Qa = aDTl 2 t к теплу в процессе теплопроводности Ql = l Nu = Число Нуссельта характеризует интенсивность теплообмена на границе твердое тело (стенка) – жидкость. Приложение:формулы и теоремы векторного исчисления Векторные величины в тексте обозначены прямым полужирным шрифтом, скалярные – курсивом. Например, b – вектор, b – скаляр. Скалярное произведение векторов a и b записывается как(ab). Векторное произведение обозначено заключением сомножителей в квадратные скобки через запятую. Например, векторное произведение векторов a и b записывается как[a, b]. 1.1. Скалярное произведение векторов abназывается произведение модулей векторов на косинус угла между этими векторами: Выражение скалярного произведения через компоненты векторов в декартовой системе координат: где i, j, k – единичные орты, ii = jj= kk = 1, ij= jk = ki =0. 1.2. Векторное произведение двух векторов[a, b]. В результате векторного произведения векторовaи b получается новый вектор c: [a, b] = c. Модуль результата векторного произведения – модуль вектора с— по определению равен c = ab sin (a^b). В декартовой системе координат векторное произведение имеет вид [a, b] = 1.3. Смешанное (скалярно-векторное) произведение трех векторов а[bc]. Результатом такого произведения является скалярная величина: Смешанное произведение допускает циклическую (стековую) перестановку векторов: По своему геометрическому смыслу смешанное произведение равно объему параллелепипеда, построенного на векторах а, bиc. 1.4. Двойное векторное произведение[а,[bc]]: Здесь вначале выполняются скалярные произведения, стоящие в скобах (т.е. скалярные произведения acи ab), и только затем вектораb и c умножаются на соответствующие результаты скалярного произведения. Компоненты результата двойного векторного произведения имеют вид: При проведении циклической перестановки в двойном векторном произведении получаются три разных вектора, сумма которых равна нулю: 2.1. Векторный оператор набла Ñ (оператор Гамильтона) как символический вектор: Ñ = 2.2. Градиент скалярной функции (скалярного поля) j(x, y, z) – это вектор, направленный в сторону быстрейшего увеличения j и равный производной по этому направлению. В координатном представлении градиент имеет вид: gradj = Ñj (в развернутом виде Ñj = 2.3. Дивергенция некоторого вектора Eв данной точке пространства– это поток вектора Eиз бесконечно малого объема dV, находящегося в этой точке пространства. Объем dV — источник или сток вектора E. Дивергенция вектора E – скалярная величина и определяется скалярным произведением оператора набла на вектор E: div Eº ÑE. В развернутом виде ÑE = 2.4. Ротор некоторого вектора E –это вектор, порождающий циркуляцию некоторого другого вектора по бесконечно малому контуру. Например, в уравнении Максвелла rot Е= В развернутом виде [Ñ, E] = 2.5.Некоторые векторные тождества. 1. Ñ(Ñj) = Ñ 2 j = 3. Ñ[Ñ, E] = 0, где E — векторная функция. 2.6.Теоремы векторного анализа. 1. Теорема Гаусса-Остроградского. Здесь объем V ограничен замкнутой поверхностью S. Вектор dS в данной точке замкнутой поверхности направлен по внешней нормали к поверхности. а) б) 2. Теорема Стокса. Здесь замкнутый контур L ограничивает поверхность S, натянутая на контур. Вектор dl (как элемент контура L) по направлению совпадает с положительным обходом контура. Положительный обход контура связан с положительной нормалью к поверхности S правилом правого винта. а) б) ЛИТЕРАТУРА 1. Савельев, И. В. Курс общей физики [Текст]: учеб. пособие. Кн.1., Кн.2., Кн.3, Кн.4 – М.: Наука, 2003. 2. Семенов, Н.А. Техническая электродинамика [Текст]: учеб. пособие для вузов. – М.: Связь, 1973. – 480 с. 3. Матвеев, А.Н. Электричество и магнетизм [Текст]: учеб. пособие для вузов. – М.: Высшая школа, 1983. – 463 с. 4. Алешин, Н.П. и др. Ультразвуковой контроль: учебное пособие/ под общ. ред. В.В. Клюева – М.: Изд. Дом «Спектр», 2011. – 224 с., ил. 5. Будадин, О.Н. и др. Тепловой контроль: учебное пособие/ под общ. ред. В.В. Клюева – М.: Изд. Дом «Спектр», 2011. – 176 с., ил. Содержание 1. ОСНОВЫ ТЕОРИИ КОЛЕБАНИЙ И ВОЛН……………………………….7 1.1. Основные положения теории колебаний осцилляторов………………7 1.1.1. Уравнения колебаний гармонического осциллятора…………….7 1.1.2. Методы (способы) представления колебаний……………………10 1.1.3. Динамика гармонического осциллятора…………………………12 1.1.4. Динамика затухающих колебаний………………………………..15 1.1.5. Динамика вынужденных колебаний. Импеданс колебательной 1.1.6. Импеданс и фазовые соотношения между смещением и вынуждающей силой. Резонанс смещения……………………….21 1.1.7. Импеданс и фазовые соотношения между скоростью и вынуждающей силой. Резонанс скорости………………………..23 1.1.8. Устойчивость амплитуды вынужденных колебаний……………24 1.1.9. Добротность осциллятора…………………………………………26 1.1.10. Добротность и резонансная кривая поглощения 1.2. Исходные положения теории гармонических волн…………………….29 1.2.1. Волновое уравнение, описывающее бегущую волну в струне. Фазовая скорость волны. …………………………………………29 1.2.2. Стоячие волны на струне………………………………………….33 1.2.3. Импеданс среды (на примере струны)…………………………….36 1.2.4. Отражение и прохождение волны на границе двух сред с различными импедансами. Согласование импедансов………. 37 1.2.6. Затухание реальных волн в среде…………………………………41 2.1. Волновое уравнение плоской волны в газе и жидкости………………..42 2.2. Скорость акустической волны в твердом теле………………………….46 2.3. Поле плоского излучателя ультразвуковой волны……………………..47 3. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ……………………………………………..48 3.1. Электростатическое поле…………………………………………………48 3.1.1. Объекты электростатики…………………………………………..48 3.1.2. Закон Кулона. Напряженность электростатического поля и интегральная теорема Гаусса……………………………………..49 ЛЕКЦИЯ 10 ПОТЕНЦИАЛ ПЕРЕНОСА. УРАВНЕНИЕ ФУРЬЕ-КИРХГОФА ЭЛЕМЕНТЫ ТЕОРИИ ПОДОБИЯ В ТЕПЛООБМЕНЕ. Потенциал переноса
1 ЛЕКЦИЯ 10 ПОТЕНЦИАЛ ПЕРЕНОСА. УРАВНЕНИЕ ФУРЬЕ-КИРХГОФА ЭЛЕМЕНТЫ ТЕОРИИ ПОДОБИЯ В ТЕПЛООБМЕНЕ Потенциал переноса Рассмотрим газовую или жидкую сплошную среду. Примем: все точки среды находятся в неравновесном состоянии. Это приводит к возникновению полей концентраций, температур, давлений, а наличие градиентов этих параметров вызывает перенос массы и энергии. Выделим элемент объема движущейся жидкости в неоднородном поле некоторого потенциала переноса. Под потенциалом переноса понимают удельную массу или энергию (отнесѐнную к единице объѐма). (x, y, z) — скалярная величина. Из курса математики известно, что скалярная функция называется потенциалом векторной функции, если между ними существует связь в форме: q grd Под градиентом скалярной функции (10.1) grd подразумевают векторную функцию: grd i j k (10.) x y z где i, j, k базисные векторы или орты. В дальнейшем будем понимать связь между q и как пропорциональность q grd (10.) Таким образом, поток переносимой субстанции (массы или энергии) является векторной величиной q. В случае переноса массы под потенциалом переноса обычно понимают концентрацию компонента в смеси: mi (10.3) i где mi масса i-го компонента в объѐме, кг i; i концентрация i-го компонента в смеси, кг i/м 3. 1 2 При переносе энергии в качестве потенциала переноса рассматривают энтальпию единицы объема среды: c P cp (10.4) Здесь: ср изобарная теплоѐмкость среды, Дж (кг К) ; температура, К; — плотность, кг/м 3 ; объем, м 3 c Дж c Дж P P 3 м В рассматриваемой среде могут существовать, так называемые, объемные (непрерывно распределѐнные по объѐму) источники или стоки массы и энергии. В химической технологии под ними подразумеваются химические превращения. Известно, что процессы тепло- и массообмена осуществляются двумя основными механизмами: молекулярным и конвективным. Молекулярный перенос (диффузия, теплопроводность) возникает в результате стремления системы к термодинамическому равновесию, а конвективный вызывается наличием поля скоростей в жидком или газовом объѐме. Следует отметить, что в случае переноса энергии в форме теплоты существует ещѐ и радиантный перенос (тепловое излучение), вклад которого учитывают при достаточно высоких температурах. Молекулярный перенос является определяющим в неподвижных средах, хотя он вызывает естественную конвекцию и практически всегда ею сопровождается. Процессы молекулярного переноса массы и энергии описываются соответствующими феноменологическими уравнениями, являющимися, как правило, линейными градиентными законами. закону Фика: Молекулярный перенос массы (молекулярная диффузия) подчиняется первому qmm -D grd i (10.5) где коэффициент молекулярной диффузии, м с; q Mm — плотность массового потока, кг i /м с. Молекулярный перенос энергии в форме теплоты описывается законом Фурье: q M — grd (10.6) 3 где коэффициент теплопроводности, Вт/ м K; q M — плотность теплового потока, Дж /с м = Вт/ м В более общей форме закон Фурье можно переписать следующим образом: q M — cp grd cp — grd cp c grdc P P (10.7) Здесь коэффициент температуропроводности, м /с. c P Следует обратить внимание, что коэффициенты диффузии D и температуропроводности а имеют одинаковую размерность (м /с) и называются молекулярными коэффициентами переноса. Таким образом, молекулярный перенос массы и энергии описываются одинаковыми по форме законами, и они могут быть обобщены следующим выражением: q M -k grd (10.8) При конвективном переносе масса и энергия транспортируются макроскопическим путѐм, движущейся со скоростью v средой. Плотность конвективного потока массы и энергии на каждом участке поверхности А можно выразить следующим образом: v A q K v (10.9) A где А участок поверхности, ориентированный перпендикулярно вектору скорости v. Размерность q плотность потока массы или энергии, соответственно. q K v c P (10.10) Таким образом, в случае молекулярного и конвективного переноса общая плотность потока массы или энергии складывается из двух векторных величин: q q M q K (10.11) 3 4 Рис К выводу балансовых уравнений переноса В газовой или жидкой среде, находящейся в движении, выделим произвольный объѐм, ограниченный поверхностью А (рис. 10.1). На поверхности А выделим элемент поверхности dа и представим его в векторной форме, умножив на единичный вектор, нормальный к этому элементу и направленный из объѐма,. Составим балансовое уравнение по типу: Накопление внутри объёма = Вход Выход + Образование Примем, что в произвольном объеме нет источников субстанции или стоков, т.е. образование равно нулю. Плотность потока субстанции через элементарную площадку будет Знак в этом произведении делает входящие потоки положительными, а выходящие отрицательными. Результирующий поток массы или энергии (Вход минус Выход) будет получен суммированием всех потоков через замкнутую поверхность A: A q da (10.1) Таким образом, физически этот интеграл представляет разницу между входящими и выходящими потоками субстанции через всю поверхность А. 4 5 Если в объѐме происходит накопление субстанции, то это вызовет изменение d потенциала переноса во времени, которое для элементарного объѐма d можно dt d представить как d, а для всего объема как интеграл: dt M d d dt (10.13) Приравняв выражения (10.1) и (10.13), получим: q da A d d dt (10.14) Согласно теореме Остроградского-Гаусса, дающей преобразование интеграла, взятого по объѐму, ограниченному поверхностью A, в интеграл, взятый по этой поверхности, будем иметь: q da A div q d С учѐтом (10.15) соотношение (10.14) примет вид: (10.15) div q d t (10.16) Интеграл, взятый по произвольному объѐму, может быть равен нулю только в случае равенства нулю подынтегральной функции: div q 0 t (10.17) Полученное выражение (10.17) и есть основное дифференциальное уравнение переноса субстанции массы или энергии, как будет показано далее. В случае изотропных сплошных сред с его помощью можно получать поля температур или концентраций в однофазной среде. Искомой величиной является плотность потока субстанции, которая определяет удельный поток массы или энергии. 5 6 Дифференциальное уравнение конвективного теплообмена (Уравнение Фурье-Кирхгофа) Дифференциальное уравнение конвективного теплообмена является частным случаем уравнения переноса энергии в форме теплоты в однофазной сплошной изотропной среде. При этом теплоѐмкость с P, теплопроводность и плотность среды считаются постоянными; отсутствует также перенос энергии в форме теплового излучения и объѐмное источники (стоки) теплоты. Как было отмечено выше, потенциалом переноса теплоты является энтальпия единицы объѐма среды (ур. 10.4): Где q M вид: q c P (10.4) Тогда с учѐтом выражений (10.7) и (10.9), будем иметь: q q q grd c c (10.18) M K v P плотность потока теплоты, представляющая векторную сумму молекулярной и конвективной q K компонент. Основное уравнение переноса субстанции (10.17) в этом случае примет следующий cp t t div div При = const получим: c c v 0 P grd P P (10.19) grd (10.0) v 0 div grd (10.1) — оператор Лапласа. Дифференциальная операция скалярную функцию сопоставляет скалярную функцию и учѐтом div grd (10.) x y z Примем также, что гидродинамически среда является стационарной, тогда div v уравнение неразрывности имеет вид: 0 (10.3) с 6 7 Дивергенцию от v, как произведения векторной и скалярной величины, можно представить в виде: div v divv v grd (10.4) С учѐтом (10.1), (10.3) и (10.4) выражение (10.0) примет вид: v grd t 7 (10.5) Полученное выражение (10.5) называется дифференциальным уравнением конвективного теплообмена или уравнением Фурье-Кирхгофа. Оно является частным случаем дифференциального баланса энергии в форме теплоты в движущейся среде, где имеет место перенос энергии теплопроводностью. Полная форма уравнения конвективного теплообмена в скалярном виде будет: t v x vy vz (10.6) x y z x y z Левая часть этого соотношения представляет собой субстанциональную производную: D Dt vx vy vz t x y z Решением дифференциального уравнения конвективного теплообмена в общем виде является функция температур в движущейся среде. В неподвижной среде t, которая представляет собой нестационарное поле и выражение (10.5) принимает вид: (10.7) Уравнение (10.7) описывает нестационарное температурное поле в неподвижной среде, может применяться также для твѐрдых тел и нестационарной теплопроводности. имеет вид: называется уравнением Уравнение для установившегося процесса в неподвижной среде или в твердом теле 0 (10.8) Отметим, что согласно уравнению (10.7), локальное изменение температуры пропорционально коэффициенту температуропроводности, который, таким образом, характеризует теплоинерционные свойства среды. При прочих равных условиях быстрее нагреется или охладится то тело, которое имеет бόльший коэффициент температуропроводности. t 8 Граничное условие Уравнения Фурье-Кирхгофа на практике используется совместно с граничным условием, т.е. условием на границе среды у неподвижной твердой стенки. Вблизи твердой стенки теплота передается только теплопроводностью внутри пограничного слоя. Следовательно, по закону Фурье: Q da grd da n (10.9) В тоже время, количество теплоты, передаваемой из ядра потока к твердой стенке, можно выразить законом Ньютона (уравнение теплоотдачи): Q ст da (10.30) Если перенос тепла стационарный, это один и тот же тепловой поток: Q grd da ст da grd ст (10.31) Это и будет граничным условием, дополняющим уравнение Фурье-Кирхгофа. Элементы теории подобия в теплообмене Рассмотрим гидродинамически одномерный поток жидкости. Запишем уравнение Фурье-Кирхгофа: t vz z (10.3) Получим приближенное решение этого уравнения методами теории подобия. Для этого зададим константы подобия, выражающие отношения величин, входящих в уравнение Фурье-Кирхгофа:, t. v. Умножим каждый из элементов дифференциального уравнения (10.3) на соответствующую константу подобия, причем последняя как постоянная величина, выносится за знак дифференциала. v v z (10.33) t t z Для сохранения тождественности полученного и исходного уравнений необходимо выполнение следующего условия: 8 9 t v (10.34) Разделим поочередно дроби на правую дробь. Отношения будут равны единице, т.к. они все являются индикаторами подобия, а у подобных явлений индикаторы равны единице.после деления заменим константы подобия их значениями: = 1/, t = t1/t, а = а1/ а, = 1/. Первый комплекс при делении / 1 t Fo 9 t (10.35) Критерий Фурье Fo является мерой отношения между количеством теплоты, вызывающей изменение температуры в данной точке движущейся среды и количеством теплоты, передаваемой данной движущейся среде теплопроводностью. Равенство критериев Fo в сходственных точках подобных систем — необходимое условие подобия нестационарных процессов. Критерий Fo — аналог критерия Ho в гидродинамике. Второй комплекс при делении v / 1 v Pe (10.36) Критерий Пекле Pe характеризует отношение количества теплоты, передаваемой конвекцией, к количеству теплоты, передаваемой теплопроводностью. Критерий Pe можно представить так: v Pe Re Pr где: Pr (10.37) Критерий Прандтля Pr — мера соотношения между толщиной гидродинамического пограничного слоя δгидр и толщиной теплового пограничного слоя δтепл. Критерий Прандтля Pr составлен только из физических параметров. В газах при Pr = 1 поля температур и скоростей подобны, толщины теплового и гидродинамического слоев соизмеримы по масштабу δтепл δгидр. При Pr = 0,7 1, толщины теплового и гидродинамического слоев практически равны по величине. Здесь Pr мало зависит от температуры и давления. 10 В жидкостях Pr = Поэтому в капельных жидкостях толщина теплового слоя δтепл меньше толщины гидродинамического δгидр слоя, δтепл 11 3 g Ar 1 (10.40) 1 Зависимость плотности от температуры можно записать как: 1 1 ( 1 ) (10.41) где β — коэффициент объемного расширения (1/град). Отсюда 1 ( 1 ) (10.4) Критерий Грасгофа Gr: 1 g Gr 3 (10.43) Gr — критерий Грасгофа равен отношению подъемной силы, определяемой разностью плотностей в разных точках потока и 1, к силе внутреннего трения в неизотермической движущейся среде. В большинстве случаев Δ в критерии Грасгофа определяют как положительную разницу температур между ядром потока и стенкой. Поэтому, в условиях свободной конвекции стационарного процесса переноса теплоты, критериальное уравнение может быть записано так: Nu = f( Gr, Pr, Г1, Г. ) (10.44) Основным видом критериальных зависимостей, применяемых в инженерных расчетах, является степенная функция вида: Nu = ARe m Pr n Gr p Г q. (10.45) Коэффициенты: A, m, n, p, q получают, проводя экспериментальные исследования в определенных границах изменения параметров для определенной группы подобных явлений. Полученная зависимость применяется в инженерных расчетах для получения коэффициентов теплоотдачи α в указанном диапазоне величин. 11 источники: http://megaobuchalka.ru/8/34861.html http://docplayer.com/106299933-Lekciya-10-potencial-perenosa-uravnenie-fure-kirhgofa-elementy-teorii-podobiya-v-teploobmene-potencial-perenosa.html |
 , (9.28)
, (9.28) – коэффициент теплоотдачи от горячего теплоносителя, Вт/(м град);
– коэффициент теплоотдачи от горячего теплоносителя, Вт/(м град);  – толщина теплопередающей стенки аппарата, м;
– толщина теплопередающей стенки аппарата, м;  — коэффициент теплопроводности материала стенки, Вт/(м град);
— коэффициент теплопроводности материала стенки, Вт/(м град);  — коэффициент теплоотдачи от стенки к холодному теплоносителю, Вт/(м град);
— коэффициент теплоотдачи от стенки к холодному теплоносителю, Вт/(м град);  – термическое сопротивление загрязнения стенки, м 2 град/Вт.
– термическое сопротивление загрязнения стенки, м 2 град/Вт. показывает, какое количество теплоты передаётся от горячего теплоносителя к холодному через 1 м 2 поверхности при средней разности температур в 1 градус за 1 с:
показывает, какое количество теплоты передаётся от горячего теплоносителя к холодному через 1 м 2 поверхности при средней разности температур в 1 градус за 1 с:

 , её плотности
, её плотности  и вязкости
и вязкости  , т.е. переменных определяющих режим течения жидкости,
, т.е. переменных определяющих режим течения жидкости, ), а также коэффициента объёмного расширения
), а также коэффициента объёмного расширения  ,
, стенки.
стенки.

 ,
, 







 — оператор Гамильтона, Δ — оператор Лапласа,
— оператор Гамильтона, Δ — оператор Лапласа,  — вектор скорости, t — время, ν — коэффициент кинематической вязкости, ρ — плотность, P — давление,
— вектор скорости, t — время, ν — коэффициент кинематической вязкости, ρ — плотность, P — давление,  — вектор плотности массовых сил, T — температура, cp — теплоемкость при постоянном давлении.
— вектор плотности массовых сил, T — температура, cp — теплоемкость при постоянном давлении.

 [Дж]
[Дж] c1- tп1=q/б1
c1- tп1=q/б1
 , где r — плотность жидкости, h — вязкость жидкости, v – средняя скорость потока жидкости, l – характерные размеры канала (например, диаметр трубы). При больших числах Рейнольдса наблюдается турбулентное течение. Экспериментально выявлено, что критическое значение числа Рейнольдса, когда в круглой трубе происходит переход от ламинарного течения в турбулентное, примерно2×10 3 . Характер течения жидкости (газа) в трубах разного сечения будет одинаков, если каждому сечению соответствует одно и то же значение числа Re.
, где r — плотность жидкости, h — вязкость жидкости, v – средняя скорость потока жидкости, l – характерные размеры канала (например, диаметр трубы). При больших числах Рейнольдса наблюдается турбулентное течение. Экспериментально выявлено, что критическое значение числа Рейнольдса, когда в круглой трубе происходит переход от ламинарного течения в турбулентное, примерно2×10 3 . Характер течения жидкости (газа) в трубах разного сечения будет одинаков, если каждому сечению соответствует одно и то же значение числа Re. При любом виде течения (турбулентном или ламинарном) скорость жидкости в тонком слое у стенки канала равна нулю. Этот слой обычно называют вязким подслоем. На рис. 4-6 приведен график изменения температуры в жидкости при турбулентном течении. Температура в основном изменяется по толщине вязкого слоя, а в турбулентном потоке изменение температуры незначительное.
При любом виде течения (турбулентном или ламинарном) скорость жидкости в тонком слое у стенки канала равна нулю. Этот слой обычно называют вязким подслоем. На рис. 4-6 приведен график изменения температуры в жидкости при турбулентном течении. Температура в основном изменяется по толщине вязкого слоя, а в турбулентном потоке изменение температуры незначительное. представляет собой малую величину (см. формулу 7 * ). При ламинарном течении теплопередача в поперечном сечении канала трубы также осуществляется практически только за счет теплопроводности. При турбулентном течении вдали от стенки теплоотдача в объеме жидкости происходит в основном вследствие перемешивания элементов жидкости и температура в турбулентном слое по сечению трубы изменяется незначительно.
представляет собой малую величину (см. формулу 7 * ). При ламинарном течении теплопередача в поперечном сечении канала трубы также осуществляется практически только за счет теплопроводности. При турбулентном течении вдали от стенки теплоотдача в объеме жидкости происходит в основном вследствие перемешивания элементов жидкости и температура в турбулентном слое по сечению трубы изменяется незначительно. t dS ,
t dS ,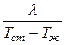
 Пренебрежем изменением давления p и будем считать, что параметры жидкости – коэффициент теплопроводности l, плотность r и удельная теплоемкость жидкости при постоянном давлении ср – постоянные константы. Из первого начала термодинамики следует, что при p = const подведенная теплота равна приращению энтальпии в выделенный объем жидкости:
Пренебрежем изменением давления p и будем считать, что параметры жидкости – коэффициент теплопроводности l, плотность r и удельная теплоемкость жидкости при постоянном давлении ср – постоянные константы. Из первого начала термодинамики следует, что при p = const подведенная теплота равна приращению энтальпии в выделенный объем жидкости: dx), где
dx), где 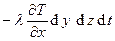 , где dS = dx dy – площадь грани,
, где dS = dx dy – площадь грани, .
. .
. , dQz =
, dQz = 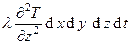 .
. . (24)
. (24) dx dy dz, (25)
dx dy dz, (25) имеет смысл субстанциальной производной. Дело в том, что изменение температуры в текущей жидкости определяется двумя факторами: 1) изменением температуры во времени в рассматриваемом объеме жидкости; 2) изменением температуры вследствие перемещения этого объема от одной точки пространства к другой:
имеет смысл субстанциальной производной. Дело в том, что изменение температуры в текущей жидкости определяется двумя факторами: 1) изменением температуры во времени в рассматриваемом объеме жидкости; 2) изменением температуры вследствие перемещения этого объема от одной точки пространства к другой: +
+  +
+  +
+  .
. +
+  +
+  ,
, . (26)
. (26) называется коэффициентом температуропроводности. Из уравнения Фурье-Кирхгофа следует, что коэффициент температуропроводности a характеризует скорость изменения температурного поля в среде. Уравнение (26) можно кратко записать посредством оператора Лапласа Ñ 2 =
называется коэффициентом температуропроводности. Из уравнения Фурье-Кирхгофа следует, что коэффициент температуропроводности a характеризует скорость изменения температурного поля в среде. Уравнение (26) можно кратко записать посредством оператора Лапласа Ñ 2 =  +
+  +
+  :
: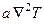 . (26 * )
. (26 * )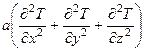 . (26 ** )
. (26 ** ) Выделим в потоке жидкости элемент жидкости массой dm в форме кубика с ребрами dx, dy, dz (рис. 4-8). Жидкость течет по вертикали вниз. Ось 0x совпадает с левой стенкой. Скорость тонкого пристеночного слоя жидкост равна нулю. По мере удаления от стенки скорость vx возрастает (на рисунке приведена эпюра скоростей жидкости).
Выделим в потоке жидкости элемент жидкости массой dm в форме кубика с ребрами dx, dy, dz (рис. 4-8). Жидкость течет по вертикали вниз. Ось 0x совпадает с левой стенкой. Скорость тонкого пристеночного слоя жидкост равна нулю. По мере удаления от стенки скорость vx возрастает (на рисунке приведена эпюра скоростей жидкости). ). Площадь верхнего и нижнего граней dS = dy dz, следовательно, равнодействующая сил давления равна
). Площадь верхнего и нижнего граней dS = dy dz, следовательно, равнодействующая сил давления равна . (28)
. (28) , (29)
, (29) ). Так как скорость жидкости растет слева направо, то сила трения на левой грани площадью dS = dx dz направлена вверх, а на правой той же площади – вниз. Равнодействующая сил трения равна:
). Так как скорость жидкости растет слева направо, то сила трения на левой грани площадью dS = dx dz направлена вверх, а на правой той же площади – вниз. Равнодействующая сил трения равна: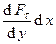 dy dz =
dy dz =  .
. dV . (30)
dV . (30)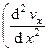 +
+  dV или hÑ 2 vx dV . (31)
dV или hÑ 2 vx dV . (31)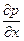 + h
+ h  ] dV.
] dV. = r
= r  +
+  +
+  +
+  dV,
dV, определяется: 1) локальной составляющей – изменением скорости во времени
определяется: 1) локальной составляющей – изменением скорости во времени  в данной точке пространства и 2) изменением в пространстве вследствие течения жидкости – конвективной составляющей
в данной точке пространства и 2) изменением в пространстве вследствие течения жидкости – конвективной составляющей  +
+  +
+  . Итак:
. Итак: +
+ 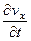 + r
+ r  +
+  + r
+ r  +
+  +
+  = r gy —
= r gy —  + h
+ h  +
+  +
+  ; (32 * )
; (32 * ) + r
+ r  +
+  +
+  = r gz —
= r gz —  + h
+ h  +
+  +
+ 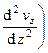 . (32 ** )
. (32 ** ) В направлении оси 0x через левую грань с площадью dS = dydz втекает за время dt масса жидкости
В направлении оси 0x через левую грань с площадью dS = dydz втекает за время dt масса жидкости dy dz.
dy dz. dx dy dz dt.
dx dy dz dt. dx dy dz dt;
dx dy dz dt;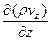 dx dy dz dt.
dx dy dz dt. +
+  dV dt.
dV dt. dV (33)
dV (33) 0, т.е. когда плотность жидкости в выделенном объеме увеличивается.
0, т.е. когда плотность жидкости в выделенном объеме увеличивается. = 0 (34)
= 0 (34) +
+  +
+  = 0.
= 0.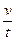 :
: =
=  =
=  .
. l 2 :
l 2 : =
=  l 2 t и поступающим в тело массой m теплом Q = rl 3 cDT:
l 2 t и поступающим в тело массой m теплом Q = rl 3 cDT: =
=  =
=  , где а – температуропроводность.
, где а – температуропроводность. .
. .
. +
+  +
+ 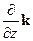 .
. +
+  +
+  ).
). +
+  +
+  .
. вектор
вектор  является ротором, который порождает вихревой вектор – напряженность вихревого электрического поля Е. Ротор вектора E – векторная величина и кратко записывается векторным произведением оператора набла на вектор E:
является ротором, который порождает вихревой вектор – напряженность вихревого электрического поля Е. Ротор вектора E – векторная величина и кратко записывается векторным произведением оператора набла на вектор E: i +
i + 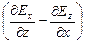 j +
j +  k).
k). , где j — скалярная функция.
, где j — скалярная функция. =
=  или в форме
или в форме  =
=  =
=  или в форме
или в форме 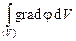 =
=  =
= 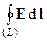 или в форме
или в форме 
 =
=  =
= 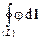 или в форме
или в форме  =
=