Реферат: Теоретическая физика: механика
| Название: Теоретическая физика: механика Раздел: Рефераты по физике Тип: реферат Добавлен 04:51:41 04 августа 2005 Похожие работы Просмотров: 2635 Комментариев: 23 Оценило: 4 человек Средний балл: 5 Оценка: неизвестно Скачать | |||||||||||||||||||||||
План-конспект занятияПо теоретической физике Студента V курса физико-математического факультета, гр. ОФ-61 Филатова Александра Сергеевича Дата проведения занятия: 20.12.2000 Тема: «Канонические преобразования. Функция Гамильтона-Якоби. Разделение переменных»Цели : Развить навык использования канонических преобразований. Закрепить умение осуществлять преобразования Лежандра для перехода к производящей функции от необходимых переменных. Научить использовать метод Гамильтона-Якоби при решении задач с разделением переменных. Сформировать понимание сути и могущественности метода. Воспитывать трудолюбие, прилежность. Тип занятия : практическое. Ход занятияКраткие теоретические сведенияКанонические преобразованияКанонические преобразования переменных – это такие преобразования, при которых сохраняется канонический вид уравнений Гамильтона. Преобразования производят с помощью производящей функции, которая является функцией координат, импульсов и времени. Полный дифференциал производящей функции определяется следующим образом: Выбирая производящую функцию от тех или иных переменных, получаем соответствующий вид канонических преобразований. Заметим, что если частная производная будет браться по «малым» Функция Гамильтона-ЯкобиПри рассмотрении действия, как функции координат (и времени), следует выражение для импульса: Из представления полной производной действия по времени следует уравнение Гамильтона-Якоби: Здесь действие рассматривается как функция координат и времени: Путем интегрирования уравнения Гамильтона-Якоби , находят представление действия в виде полного интеграла, который является функцией s координат, времени, и s +1 постоянных ( s – число степеней свободы). Поскольку действие входит в уравнение Гамильтона-Якоби только в виде производной, то одна из констант содержится в полном интеграле аддитивным образом, т.е. полный интеграл имеет вид: Константа А не играет существенной роли, поскольку действие входит везде лишь в виде производной. А определяет, что, фактически, лишь s констант меняют действие существенным образом. Эти константы определяются начальными условиями на уравнения движения, которые для любого значения А будут иметь одинаковый вид, как и само уравнение Гамильтона-Якоби. Для того чтобы выяснить связь между полным интегралом уравнения Г.-Я. и интересующими нас уравнениями движения, необходимо произвести каноническое преобразование, выбрав полный интеграл действия в качестве производящей функции. Константы тоже будут константы, поскольку Выражая из уравнения координаты Решение задачи на нахождение зависимости существенно упрощается в случае разделения переменных. Такое возможно, когда какая-то координата Итак, нахождение уравнений движения методом Гамильтона-Якоби сводится к следующему: составить функцию Гамильтона; записать уравнение Г.-Я., и определить какие переменные разделяются; Путем интегрирования уравнения Г.-Я. получить вид полного интеграла Составить систему s уравнений По необходимости найти закон изменения импульсов: Примеры решения задач№ 11.14 [] Как известно, замена функции Лагранжа
где Перепишем штрихованную функцию Лагранжа, представив полную производную функции Функции Гамильтона, соответствующие штрихованной и не штрихованной функциям Лагранжа, определяются следующим образом: Распишем Подставляя формулы и в выражение для штрихованной функции Гамильтона , получим: Взаимно сократив второе слагаемое с последним, учитывая зависимость , получим: Но согласно каноническим преобразованием с производящей функцией Ф : Полученное соотношение определяет условие на временную часть производящей функции канонического преобразования, соответствующего преобразованию функции Лагранжа . Поскольку вид обобщенных импульсов и координат при преобразовании функции Лагранжа не изменился, координатно-импульсная часть производящей функции должна соответствовать тождественному каноническому преобразованию. Как было показано в задаче №9.32 [] (д/з пред. занятия), производящая функция определяющая тождественное каноническое преобразование с неизменным гамильтонианом, имеет вид: Учитывая условие на временную часть производящей функции, окончательно получим: Полученная производящая функция определяет тождественное каноническое преобразование с заменой функции Гамильтона соответствующей замене функции Лагранжа . З
Составим функцию Гамильтона системы: Здесь потенциальная энергия состоит из энергии гармонических колебаний и потенциальной энергии шариков в поле сил земного тяготения. По определению потенциального поля: Мы имеем дело с одномерным движением, поэтому градиент в формуле заменяется производной по х . В то же время сила, является суммарной силой тяжести. Принимая во внимание принцип суперпозиции гравитационного поля, проинтегрируем последнее уравнение: Значение смещения пружины Подставив выражения и в формулу , получим вид функции Гамильтона, выраженной через импульсы и координаты явно: Переход к новым каноническим переменным производится в случае, когда возможно упростить вид функции Гамильтона, а соответственно и исходящих из нее уравнений движения. В данной ситуации удобно выбрать новые координаты так, чтобы одна описывала движение центра масс системы, а вторая колебания пружины в собственной системе отсчета. Убедимся, что заданная в условии производящая функция отвечает именно такому преобразованию. Новая координата Новая координата Сложив оба уравнения, получим:
Запишем функцию Гамильтона в новых переменных:
– суммарная масса системы. Действительно, функция Гамильтона в новых переменных распалась на две части, что соответствует двум парам канонических уравнений. Одна часть описывает колебания шариков в собственной системе отсчета, другая – движение системы как целого в поле сил тяжести. № 9.21 [] Найти полный интеграл уравнения Г.-Я. и закон свободного движения материальной точки. 1. Составим функцию Гамильтона свободной частицы: 2. Запишем уравнение Г.-Я.: 3. Произведем разделение переменных и проинтегрируем по времени. Используем начальное условие: Тогда подставляя вид функции S в уравнение Г.-Я. , последнее примет вид: Следовательно, полный интеграл уравнения Г.-Я.: 4. Закон движения определяется из канонического преобразования: Откуда сам закон движения: 5. Импульс свободно движущейся материальной точки определяется следующим образом: Действительно, частица в отсутствии внешнего поля движется с постоянным импульсом. Домашнее задание:№ 11.2 [] Найти производящую функцию вида № 9.38 [] Найти уравнение, которому удовлетворяет производящая функция № 9.23 [] Найти полный интеграл уравнения Г.-Я. для тела, движущегося по гладкой наклонной плоскости, составляющей угол с горизонтом. № 12.1 a) [] Найти траекторию и закон движения частицы в поле Литература:Л.Д. Ландау, Е.М. Лифшиц «Механика, электродинамика», — М.: «Наука», 1969 г., — 272 с. Л.Д. Ландау, Е.М. Лифшиц «Механика», — М.: «Наука», 1965 г., — 204 с. И.И. Ольховский, Ю.Г. Павленко, Л.С. Кузьменков «Задачи по теоретической механике для физиков», — М.: 1977 г., — 389 с. Г.Л. Коткин, В.Г. Сербо «Сборник задач по теоретической механике», — М.: «Наука», 1977 г., — 320 с. И.В. Мещерский «Сборник задач по теоретической механике», — М.: «Наука», 1986 г., — 448 с. Л.П. Гречко, В.И. Сугаков, О.Ф. Томасевич, А.М. Федоренко «Сборник задач по теоретической физике», — М.: «Высшая школа» 1984 г., — 319 с. Студент-практикант: Филатов А.С.
План-конспект занятияПо теоретической физике Студента V курса физико-математического факультета, гр. ОФ-61 Филатова Александра Сергеевича Дата проведения занятия: 06.12.2000 Тема: «Функция Гамильтона. Функция Рауса. Канонические уравнения»Цели : Развить у учащихся навык решения задач на составление и использование функции Гамильтона и функции Рауса. Сформировать понимание взаимосвязи между функцией Гамильтона, Рауса и функцией Лагранжа. Закрепить знание свойств функции Лагранжа. Воспитывать трудолюбие, прилежность. Тип занятия : практическое. Ход занятияКраткие теоретические сведенияФункция Гамильтона: Функция Рауса: Канонические уравнения: Схема составления функции ГамильтонаКак следует из определения функции Гамильтона для составления самой функции необходимо знать вид функции Лагранжа. Однако при подстановке функции Лагранжа в явном виде в выражение в правой части будут присутствовать переменные Итак, при решении задач на нахождение функции Гамильтона, когда вид функции кин. энергии Записать функцию Лагранжа, при возможности преобразовав ее к более простому виду (это в частном случае подразумевает выбор новых обобщенных координат). Определить зависимость Записать саму функцию Гамильтона Примеры решения задач№ 10.3 [] Определить функцию Гамильтона ангармонического осциллятора, функция Лагранжа которого: Подставляя полученное выражение в , имеем: № а) 1. Действуя согласно предлагаемой схеме составления функции Гамильтона, определим функцию Лагранжа системы: Где Согласно выбранной системе координат: Учитывая, что 2. Найдем зависимость обобщенной скорости 3. Следовательно, функция Гамильтона: б) Используя формулы , найдем уравнения движения системы: В частности, представляет интерес случай, когда Первое уравнение дает тривиальное решение Где № 9.5 [] Найти траекторию одномерного гармонического осциллятора в фазовом пространстве. Фазовым пространством называется такое 2 s -мерное пространство, по осям которого откладываются s импульсов и s координат. ( s – число степеней свободы). Изменение состояния системы соответствует непрерывной линии – траектории движения системы в фазовом пространстве. Функция Гамильтона гармонического осциллятора имеет вид: Из закона сохранения энергии Т.е. траекторией является эллипс. № 10.4 [] Найти закон движения частицы, функция Гамильтона которой: Закон движения частицы дают функции:
вид которых можно получить исходя из уравнений Гамильтона . Поделив 1-ое уравнение на 2-ое получим:
Выражая отсюда
где Или после интегрирования: Подставляя полученную зависимость в выражение , получим: Задача №1. Математический маятник массы т прикреплен к движущейся вдоль горизонтальной прямой муфте, масса которой М . Определить функцию Рауса системы. Составим функцию Лагранжа: Где Координату х можно представить в виде суммы: Где х 1 – координата муфты (координата лабораторной системы отсчета), а х 2 – координата смещения шарика мат. маятника в системе отсчета муфты. Из выражения следует: Заметим, что х 1 – циклическая переменная. Найдем обобщенный импульс Следовательно, по определению функция Рауса с учетом выражения : Подставляя в последнее выражение зависимость , окончательно получим: Запишем уравнение связи импульса с функцией Рауса: Но поскольку х 1 не входит в функцию Рауса явно, то правая часть записанного равенства есть ноль. Т.е. импульс в процессе движения остается постоянным. Следовательно, функция Рауса фактически зависит только от 2-х независимых переменных: Задача №2. Определить функцию Рауса симметричного волчка в поле Используем известное нам значение функции Лагранжа для симметричного волчка: По определению обобщенных импульсов: Следовательно, по определению функция Рауса с учетом выражения : Домашнее задание:Задача№1. Исходя из функции Гамильтона для гармонического осциллятора, получить закон движения гармонического осциллятора. № 10.5 [] Найти уравнения движения частицы, функция Гамильтона которой: Указание: получить Литература:Л.Д. Ландау, Е.М. Лифшиц «Механика, электродинамика», — М.: «Наука», 1969 г., — 272 с. Л.Д. Ландау, Е.М. Лифшиц «Механика», — М.: «Наука», 1965 г., — 204 с. И.И. Ольховский, Ю.Г. Павленко, Л.С. Кузьменков «Задачи по теоретической механике для физиков», — М.: 1977 г., — 389 с. Г.Л. Коткин, В.Г. Сербо «Сборник задач по теоретической механике», — М.: «Наука», 1977 г., — 320 с. И.В. Мещерский «Сборник задач по теоретической механике», — М.: «Наука», 1986 г., — 448 с. Л.П. Гречко, В.И. Сугаков, О.Ф. Томасевич, А.М. Федоренко «Сборник задач по теоретической физике», — М.: «Высшая школа» 1984 г., — 319 с. Студент-практикант: Филатов А.С.
План-конспект занятияПо теоретической физике Студента V курса физико-математического факультета, гр. ОФ-61 Филатова Александра Сергеевича Дата проведения занятия: 27.12.2000 Тема: «Функция Гамильтона-Якоби. Разделение переменных»Цели : Закрепить умение использования метода Гамильтона-Якоби при решении задач с разделением переменных. Сформировать понимание сути и могущественности метода. Воспитывать трудолюбие, прилежность. Тип занятия : практическое. Ход занятияКраткие теоретические сведенияПри рассмотрении действия, как функции координат (и времени), следует выражение для импульса: Из представления полной производной действия по времени следует уравнение Гамильтона-Якоби: Здесь действие рассматривается как функция координат и времени: Путем интегрирования уравнения Гамильтона-Якоби , находят представление действия в виде полного интеграла, который является функцией s координат, времени, и s+1 постоянных ( s – число степеней свободы). Поскольку действие входит в уравнение Гамильтона-Якоби только в виде производной, то одна из констант содержится в полном интеграле аддитивным образом, т.е. полный интеграл имеет вид: Константа А не играет существенной роли, поскольку действие входит везде лишь в виде производной. А определяет, что, фактически, лишь s констант меняют действие существенным образом. Эти константы определяются начальными условиями на уравнения движения, которые для любого значения А будут иметь одинаковый вид, как и само уравнение Гамильтона-Якоби. Для того чтобы выяснить связь между полным интегралом уравнения Г.-Я. и интересующими нас уравнениями движения, необходимо произвести каноническое преобразование, выбрав полный интеграл действия в качестве производящей функции. Константы тоже будут константы, поскольку Выражая из уравнения координаты Решение задачи на нахождение зависимости существенно упрощается в случае разделения переменных. Такое возможно, когда какая-то координата Итак, нахождение уравнений движения методом Гамильтона-Якоби сводится к следующему: составить функцию Гамильтона; записать уравнение Г.-Я., и определить какие переменные разделяются; Путем интегрирования уравнения Г.-Я. получить вид полного интеграла Составить систему s уравнений По необходимости найти закон изменения импульсов: Примеры решения задачНа прошлом занятии был продемонстрирован пример нахождения закона движения для свободной точки. Что же будет происходить при помещении точки в поле? № 9.22 [] Составить уравнения Г.-Я. для точки, движущейся в однородном гравитационном поле. Найти полный интеграл этого уравнения, а также траекторию и закон движения точки. 1. Направим ось Oz вверх по вертикали. Тогда функция Гамильтона точки в декартовых координатах примет вид: 2. Соответственно уравнение Г.-Я.: 3. Все переменные в этом уравнении разделяются. Здесь Тогда, к примеру, изменение х, повлечет за собой изменение лишь первого слагаемого в квадратных скобках уравнения . Слагаемое может меняться, а все выражение все равно тождественный ноль. Следовательно, это слагаемое есть константа. Выполняя такого рода действия, получим следующий вид полного интеграла уравнения Г.-Я.: Заметим, что в выражении полного интеграла уже содержится три константы. Система имеет три степени свободы. Поэтому эти три константы уже однозначно определяют уравнения движения. 4-ая константа может входить в действие только аддитивным образом и не играет существенной роли. Соответственно функция Интегрирование последнего уравнения приводит к функции: Окончательно полный интеграл: 4. Отсюда на основании теоремы Якоби: Первые два из этих уравнения показывают, что траекторией частицы является парабола, а третье уравнение представляет собой закон движения. Далее найдем, что компоненты В частности, при нулевых значениях Найдем также компоненту № 9.24 [] Найти полный интеграл уравнения Г.-Я. для мат. маятника и закон его движения в квадратуре. 1. Чтобы составить функцию Гамильтона, можно пойти двумя путями. Записать вид функции Гамильтона в полярных координатах: Но поскольку длина стержня мат. маятника – величина постоянная, то 2) Записать функцию Лагранжа, и из нее получить вид функции Гамильтона, который будет совпадать с представлением . Предлагается учащимся убедиться в этом самостоятельно в качестве домашнего задания. 2. Запишем уравнение Г.-Я.: 3. И время t и координата – разделяются. Следовательно, полный интеграл имеет вид: Подставляя его в уравнение Г.-Я. получим вид функции На основании теоремы Якоби найдем закон движения маятника: Литература:Л.Д. Ландау, Е.М. Лифшиц «Механика, электродинамика», — М.: «Наука», 1969 г., — 272 с. Л.Д. Ландау, Е.М. Лифшиц «Механика», — М.: «Наука», 1965 г., — 204 с. И.И. Ольховский, Ю.Г. Павленко, Л.С. Кузьменков «Задачи по теоретической механике для физиков», — М.: 1977 г., — 389 с. Г.Л. Коткин, В.Г. Сербо «Сборник задач по теоретической механике», — М.: «Наука», 1977 г., — 320 с. И.В. Мещерский «Сборник задач по теоретической механике», — М.: «Наука», 1986 г., — 448 с. Л.П. Гречко, В.И. Сугаков, О.Ф. Томасевич, А.М. Федоренко «Сборник задач по теоретической физике», — М.: «Высшая школа» 1984 г., — 319 с. Студент-практикант: Филатов А.С.
План-конспект занятияПо теоретической физике Студента V курса физико-математического факультета, гр. ОФ-61 Филатова Александра Сергеевича Дата проведения занятия: 13.12.2000 Тема: «Скобки Пуассона. Канонические преобразования»Цели : Развить навык обращения со скобками Пуассона. Развить навык использования канонических преобразований. Научить осуществлять преобразования Лежандра для перехода к производящей функции от необходимых переменных. Воспитывать трудолюбие, прилежность. Тип занятия : практическое. Ход занятияКраткие теоретические сведенияСкобки Пуассона: Канонические преобразования переменных – это такие преобразования, при которых сохраняется канонический вид уравнений Гамильтона. Преобразования производят с помощью производящей функции, которая является функцией координат, импульсов и времени. Полный дифференциал производящей функции определяется следующим образом: Выбирая производящую функцию от тех или иных переменных, получаем соответствующий вид канонических преобразований. Примеры решения задач№ 9.6 [] Показать, что уравнения Гамильтона можно записать в виде: № 9.7 [] Показать, что для функции № 9.10 [] С помощью скобок Пуассона показать, что импульс системы является интегралом движения, если ее гамильтониан инвариантен относительно произвольного параллельного переноса системы в пространстве. По определению обобщенный импульс есть: Но в силу однородности времени функция Лагранжа явно от времени не зависит, следовательно, и выражение для импульса также не содержит в себе явной зависимости по времени: Тогда следуя формуле : При параллельном переносе тела в пространстве координаты каждой точки этого тела преобразуются по закону: При этом изменение гамильтониана равно нулю. Но с другой стороны изменение гамильтониана равно: Где суммирование идет по всем частицам системы. Но поскольку при параллельном переносе для каждой частицы С другой стороны для каждой декартовой компоненты имеет место соотношение вида: Здесь было использовано свойство аддитивности скобок Пуассона. Запишем совокупность этих соотношений в краткой форме: Сопоставляя и находим: Что означает, что импульс системы № 9.9а) [] Доказать, что скобки Пуассона Принимая во внимание, что Проверяя равенство для всех значений i , т.е. для № 10.14 а-1) [] Вычислить скобки Пуассона В силу равенств : Компоненты вектора момента инерции можно записать как свертку тензоров (сам вектор является тензором I ранга):
где
остальные компоненты тензора равны нулю. Подставляя формулу в выражение , получим: Посчитаем по полученной формуле , к примеру, № 9.31 [] Найти каноническое преобразование, соответствующее производящей функции: Поскольку производящая функция явно от времени не зависит, Такое преобразование явно не меняет вид канонических уравнений, к тому же сводит просто к взаимному переименованию координат и импульсов. Следовательно, в гамильтоновом формализме понятие обобщенных координат и импульсов лишено их первоначального смысла. Мы всегда можем назвать координаты импульсами, а импульсы координатами (см. ). Ввиду этой условности терминологии переменные p и q в формализме Гамильтона часто называют канонически сопряженными величинами. № 9.37 [] Показать, что гамильтониан является инвариантом при бесконечно малом каноническом преобразовании с производящей функцией
где Запишем канонические преобразования: Изменение гамильтониана в случае бесконечно малого канонического преобразования есть Из канонических уравнений следует, что Выражая Подставим и в выражение для изменения гамильтониана . Получим: По условию функция f является интегралом движения. А значит С другой стороны Подставляя в последнее выражение равенства , получаем: Сопоставляя и , делаем вывод, что изменение гамильтониана
что и требовалось доказать. Т.е. гамильтониан является инвариантом при бесконечно малом каноническом преобразовании с заданной производящей функцией. Домашнее задание:№ 9.8 [] Показать, что функция Для свободной частицы: № 9.9б) [] Доказать, что скобки Пуассона № 10.14 а) [] Вычислить скобки Пуассона: № 9.32 [] Показать, что производящая функция Литература:Л.Д. Ландау, Е.М. Лифшиц «Механика, электродинамика», — М.: «Наука», 1969 г., — 272 с. Л.Д. Ландау, Е.М. Лифшиц «Механика», — М.: «Наука», 1965 г., — 204 с. И.И. Ольховский, Ю.Г. Павленко, Л.С. Кузьменков «Задачи по теоретической механике для физиков», — М.: 1977 г., — 389 с. Г.Л. Коткин, В.Г. Сербо «Сборник задач по теоретической механике», — М.: «Наука», 1977 г., — 320 с. И.В. Мещерский «Сборник задач по теоретической механике», — М.: «Наука», 1986 г., — 448 с. Л.П. Гречко, В.И. Сугаков, О.Ф. Томасевич, А.М. Федоренко «Сборник задач по теоретической физике», — М.: «Высшая школа» 1984 г., — 319 с. Принцип наименьшего действия в аналитической механикеПричина данной публикации — неоднозначная статья на тему принципа наименьшего действия (ПНД), опубликованная на ресурсе несколько дней назад. Неоднозначна она потому, что её автор в популярной форме пытается донести до читателя один из основополагающих принципов математического описания природы, и это частично ему удается. Если бы не одно но, притаившееся в конце публикации. Под спойлером приведена полная цитата данного отрывка Не все так простоНа самом деле я немного обманул, сказав, что тела всегда двигаются так, чтобы минимизировать действие. Хотя в очень многих случаях это действительно так, можно придумать ситуации, в которых действие явно не минимально. Например, возьмем шарик и поместим его в пустое пространство. На некотором отдалении от него поставим упругую стенку. Допустим, мы хотим, чтобы через некоторое время шарик оказался в том же самом месте. При таких заданных условиях шарик может двигаться двумя разными способами. Во-первых, он может просто оставаться на месте. Во-вторых, можно его толкнуть по направлению к стенке. Шарик долетит до стенки, отскочит от нее и вернется обратно. Понятно, что можно толкнуть его с такой скоростью, чтобы он вернулся в точно нужное время. Оба варианта движения шарика возможны, но действие во втором случае получится больше, потому что все это время шарик будет двигаться с ненулевой кинетической энергией. Как же спасти принцип наименьшего действия, чтобы он был справедлив и в таких ситуациях? Об этом мы поговорим в следующий раз. Так в чем же, с моей точки зрения, проблема? Проблема в том, что автор, приводя данный пример допустил ряд фундаментальных ошибок. Она усугубляется тем, что планируемая вторая часть, со слов автора, будет опираться на эти ошибки. Руководствуясь принципом наполнения ресурса достоверной информацией я вынужден выступить с разъяснением своей позиции по данному вопросу более развернуто, и формат комментариев для этого маловат. Данная статья расскажет о том, как строится механика на базе ПНД, и постарается объяснить читателю, что проблема, которую ставит автор цитируемой публикации отсутствует. 1. Определение действия по Гамильтону. Принцип наименьшего действия— функция Лагранжа, для некоторой механической системы, в которой (опуская аргументы в дальнейшем) T — кинетическая энергия системы; П — потенциальная её энергия; q(t) — вектор обобщенных координат этой системы, являющийся функцией времени. при этом полагают, что моменты времени t1 и t2 — фиксированы. Почему функционал, а не функция? Потому, что функция, по определению есть правило, по которому одному числу из области определения (аргументу функции) ставится в соответствие другое число из области значений. Функционал отличается тем, что качестве его аргумента выступает не число, а целая функция. В данном случае это закон движения механической системы q(t), определенный по крайней мере на промежутке времени между t1 и t2. Многолетние (и это мягко сказано!) труды ученых-механиков (включая умопомрачительного Леонарда Эйлера), позволили сформулировать Принцип наименьшего действия:
называемому действием по Гамильтону. Уже из самого определения ПНД следует тот факт, что данный принцип приводит к уравнениям движения лишь для ограниченного класса механических систем. Для каких? А давайте разберемся. 2. Границы применимости принципа наименьшего действия. Некоторые определения для самых маленькихКак следует из определения, опять таки, функции Лагранжа, ПНД позволяет получить уравнения движения для механических систем, силовое воздействие на которые определяется исключительно потенциальной энергией. Для того чтобы разобраться, о каких системах идет речь, дадим несколько определений, которые, для экономии объема статьи я помещаю под спойлер Рассмотрим движущуюся по траектории AB точку, к которой приложена сила Элементарной работой силы Тогда, полная работа силы на перемещении точки по траектории AB есть криволинейный интеграл
В соответствии со вторым законом Ньютона Вычислим строго стоящее под знаком интеграла скалярное произведение, для чего продифференцируем по времени скалярное произведение вектора скорости самого на себя С другой стороны, Дифференцируя это равенство по времени, имеем Сравнивая (1) и (2) приходим к выводу, что Тогда, спокойно вычисляем работу, раскрывая криволинейный интеграл через определенный, взяв в качестве пределов модуль скорости точки в начале и в конце траектории Пусть точка перемещается в пространстве по произвольной траектории AB. Вычислим, какую работу при этом совершит сила (3) Так как проекции силы на оси координат зависят исключительно от этих самых координат, всегда можно найти функцию Тогда, выражение для работы преобразуется к виду где
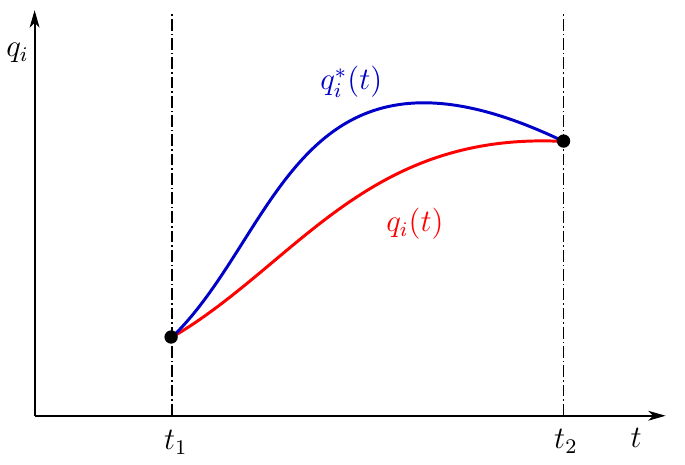
— потенциальная энергия точки в положении A, а — потенциальная энергия точки в положении B. Учитывая всё вышесказанное снова вычислим работу потенциальных сил на перемещении из точки A в точку B Таким образом, работа консервативных сил равна изменению потенциальной энергии точки, взятому с обратным знаком причем выбор уровня, на котором мы считаем потенциальную энергию равной нулю совершенно не влияет на результат. Отсюда можно сделать вывод, что уровень отсчета потенциальной энергии можно выбрать совершенно произвольно. 3. Понятие о вариациях обобщенных координат. Постановка вариационной задачигде s — число степеней свободы данной системы. Действительный, но неизвестный пока нам, закон движения данной системы определяется зависимость обобщенных координат (4) от времени. Рассмотрим одну из обобщенных координат Рисунок 1. Действительное и окольное движение механической системы На рисунке зависимость Однако, я ещё раз настаиваю на том, чтобы нижеследующий текст был прочтен внимательно! Несмотря на то, что мы задаемся начальным и конечным положением системы, ни первое положение, ни второе, нам заранее неизвестны! Равно как и неизвестен закон движения системы! Эти положения рассматриваются именно как начальное и конечное положение, безотносительно конкретных значений. Далее мы полагаем, что из начального положения в конечное система может придти разными путями, то есть зависимость будем называть изохронными вариациями обобщенных координат В данном контексте вариации (5) следует понимать как бесконечно малые функции, выражающие отклонение окольного движения от действительного. Малая «дельта» для обозначения выбрана не случайно и подчеркивает принципиальное отличие вариации от дифференциала функции. Дифференциал — главная линейная часть приращения функции, вызванного приращением аргумента. В случае с вариацией изменение значения функции при постоянном значении аргумента вызвано изменением вида самой функции! Мы не варьируем аргумент, в роли которого выступает время, поэтому вариация называется изохронной. Мы варьируем правило по которому каждому значению времени приводится в соответствие некоторое значение обобщенных координат! По сути, мы варьируем закон движения, по которому система из начального состояния перемещается в конечное состояние. Начальное и конечное состояние определяются действительным законом движения, но я ещё раз подчеркиваю — их конкретные значения нам не известны и могут быть любыми кинематически возможными, мы лишь полагаем, что они существуют и система гарантированно перемещается из одного положения в другое! В начальном и конечном положении системы мы не варьируем закон движения, поэтому вариации обобщенных координат в начальном и конечном положении равны нулю Исходя из принципа наименьшего действия, действительное движение системы должно быть таким, чтобы доставлять минимум функционалу действия. Варьирование координат вызывает изменение функционала действия. Необходимым условием достижения функционалом действия экстремального значения является равенство нулю его вариации 4. Решение вариационной задачи. Уравнения Лагранжа 2-го родаЗагоним всё под один интеграл, и так как для вариаций справедливы все операции над бесконечно малыми величинами, преобразуем этот крокодил к виду Исходя из определения обобщенной скорости Тогда выражение (8) преобразуется к виду Второе слагаемое интегрируется по частям Исходя из условия (7), имеем тогда, получаем уравнение При произвольных пределах интегрирования равенство нулю определенного интеграла обеспечивается равенством нулю подынтегральной функции С учетом того, что вариации обобщенных координат независимы, (11) справедливо только в случае равенства нулю всех коэффициентов при вариациях, то есть Никто не мешает нам умножить каждое из уравнений на (-1) и получить более привычную запись Уравнения (12) и есть решение задачи. И вот на этом моменте ещё раз внимание — решение вариационной задачи по принципу наименьшего действия, это не функция, доставляющая минимум действию по Гамильтону, а система дифференциальных уравнений, решая которое таковую функцию можно найти. В данном случае это дифференциальное уравнение Лагранжа 2-го рода, записанное через функцию Лагранжа, то есть в формулировке для консервативных механических систем. И всё, на этом принцип наименьшего действия заканчивается, а начинается теория обыкновенных дифференциальных уравнений, которая, в частности, гласит, что решением уравнения (12) является вектор-функция вида где C1. C2s — произвольные константы интегрирования.
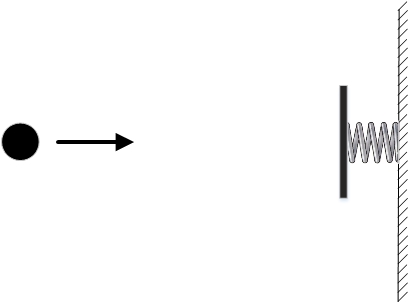
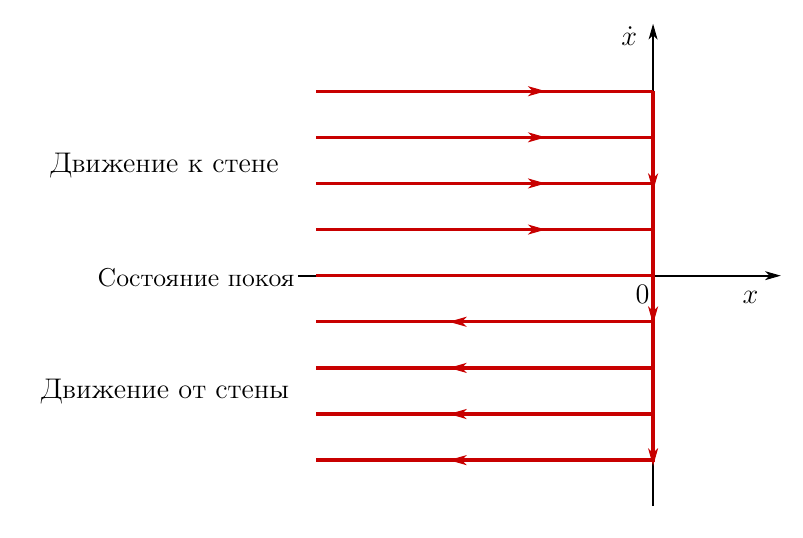
Точка! В задачах аналитической механики вышеперечисленные выкладки больше не нужно проделывать, достаточно использовать их результат (12). Функция, удовлетворяющая уравнению (12) есть закон движения системы, удовлетворяющей ПНД. 5. Задача с шариком и стенкойТеперь вернемся к той задаче, с которой всё началось — об одномерном движении шарика около абсолютно упругой стенки. Разумеется, для данной задачи можно получить дифференциальные уравнения движения. Так как это дифференциальные уравнения движения, то любое, я подчеркиваю это, любое их решение доставляет минимум функционалу действия, а значит ПНД выполняется! Общее решение уравнений движения шарика можно изобразить в виде так называемого фазового портрета рассматриваемой механической системы. Вот этот фазовый портрет Рисунок 2. Фазовый портрет системы в задаче с шариком По горизонтальной оси откладывается координата шарика, по вертикальной — проекция скорости на ось x. Может это покажется странным, но данный чертеж отражает все возможные фазовые траектории движения шарика, при любых начальных, или если вам так хочется, краевых условиях. На самом деле параллельных прямых на графике бесконечно много, на чертеже показаны некоторые из них и направление движения по фазовой траектории. Это — общее решение уравнения движения шарика. Каждая из этих фазовых траекторий доставляет минимум функционалу действия, что непосредственно следует из выкладок, проделанных выше. Что делает автор задачи? Он говорит: вот шарик покоится, и за промежуток времени от tA до tB действие равно нулю. Если шарик толкнуть к стенке, то за тот же промежуток времени действие будет больше, так как у шарика отличная от нуля и неизменная кинетическая энергия. Но почему шарик движется к стенке, ведь в покое действие будет меньше? Значит ПНД испытвает проблемы и не работает! Но мы обязательно решим это в следующей статье. То что говорит автор — бред. Почему? Да потому, что он сравнивает действия на различных ветвях одной и той же действительной фазовой траектории! Между тем, при применении ПНД, сравнивается действие на действительной траектории и на множестве окольных траекторий. То есть происходит сравнение действия на реальной траектории с действием на тех траекториях, которых нет в природе, и никогда не будет! Не понятно? Объясню ещё более доходчиво. Рассмотрим состояние покоя. Оно описывается ветвью фазового портрета, совпадающего с осью абсцисс. Координата не меняется с течением времени. Это действительное движение. А какое же движение будет окольным. Любое другое кинематически возможное. Например малые колебания шарика около рассматриваемого нами положения покоя. Задача допускает колебания шарика вдоль оси х? Допускает, значит такое движение кинематически возможно и может рассматриваться как одно их окольных Почему же шарик таки покоится? Да потому, что действие в состоянии покоя, вычисленное на фиксированном промежутке времени от tA до tB, будет меньше действия, при малых колебаниях на том же промежутке времени. Значит колебаниям и любому другому «шевелению» шарика природа предпочитает покой. В полном соответствии с ПНД. Допустим мы толкнули шарик в сторону стенки. Пусть мы толкнули его как хочет автор, со скоростью, подобранной из краевых условий, так чтобы в момент времени tB шарик оказался в том же положении, откуда стартовал. Шарик, с постоянной скоростью долетит до стенки, упруго отскочит и вернется в начальное положение в момент времени tB, опять таки с постоянной скоростью. Ок, это действительное движение. Какое движение будет одним из окольных? Например, если шарик будет двигаться к стенке и от стенки со скоростью, меняющейся со временем. Такое движение возможно кинематически? Возможно. Почему же модуль скорости шарика не меняется? Да потому, что действие на такой фазовой траектории будет иметь минимальное значение, в сравнении с любом другим вариантом, где скорость зависит от времени. Вот и всё. Ничего такого волшебного тут не происходит. ПНД работает безо всяких проблем. Выводы и пожеланияПНД — фундаментальный закон природы. Из него, в частности, вытекают законы механики, например дифференциальные уравнения движения (12). ПНД говорит нам о том, что природа устроена так, что уравнение движения консервативной механической системы выглядит именно как выражение (12) и никак иначе. Большего от него и не требуется. Не нужно придумывать проблем там где их нет. источники: http://habr.com/ru/post/425771/ |
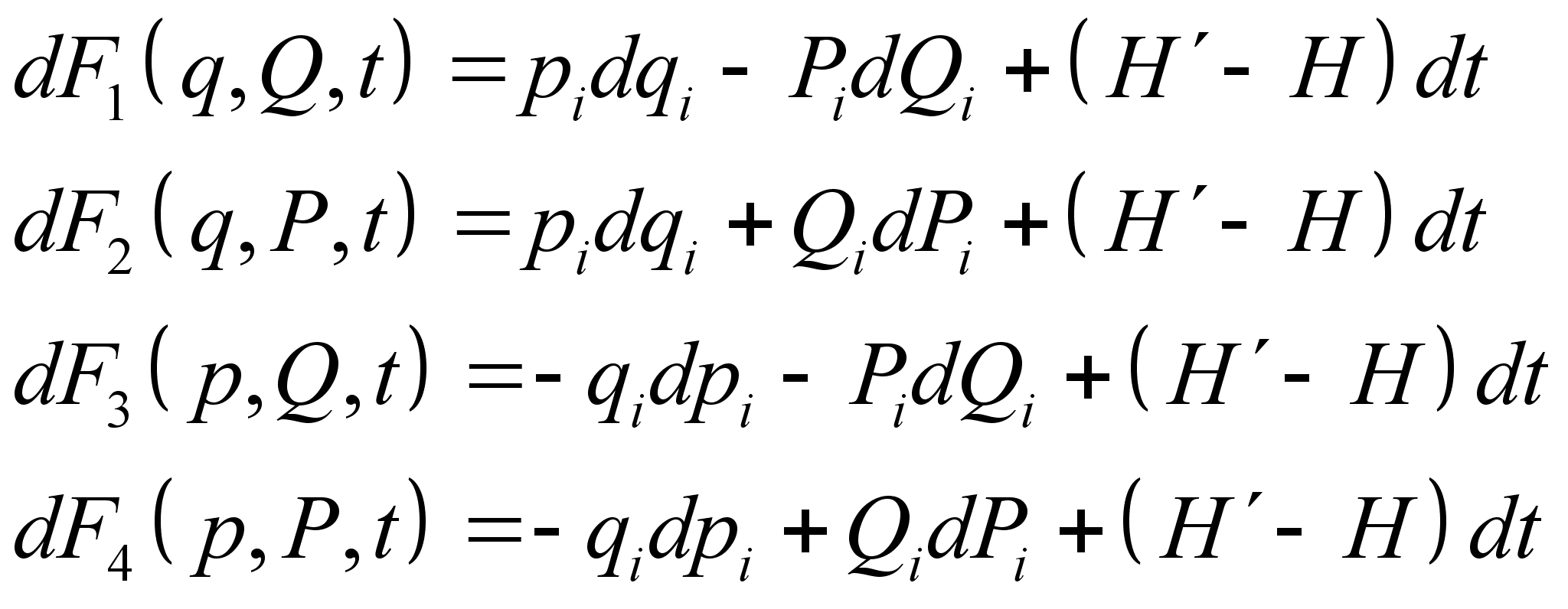
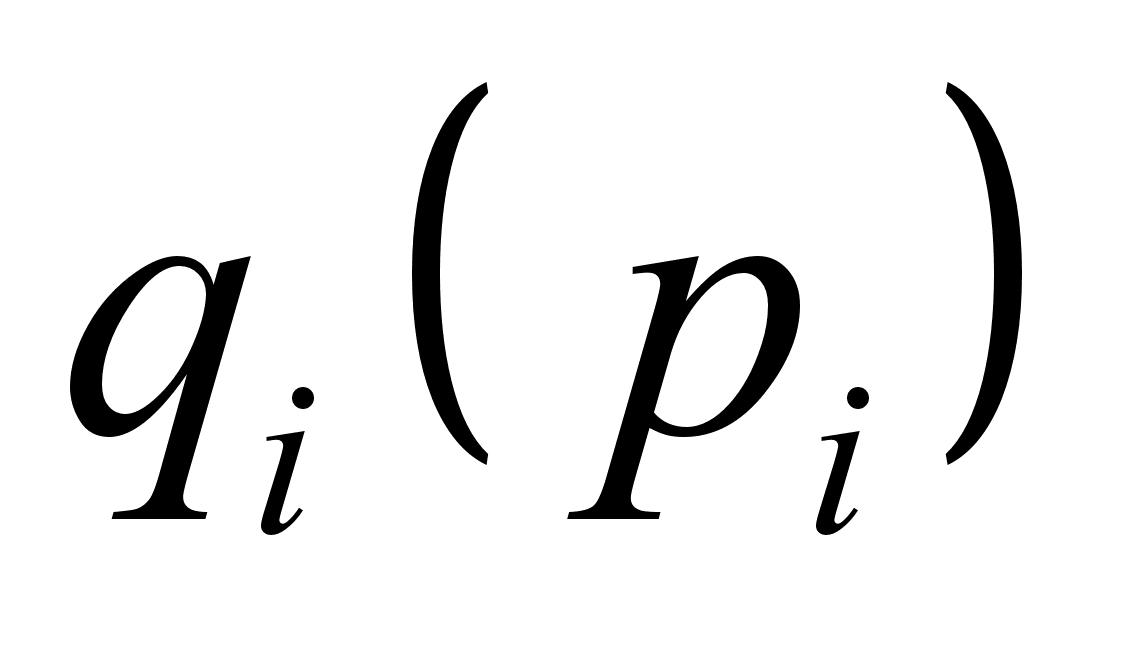 , то будем получать малое
, то будем получать малое 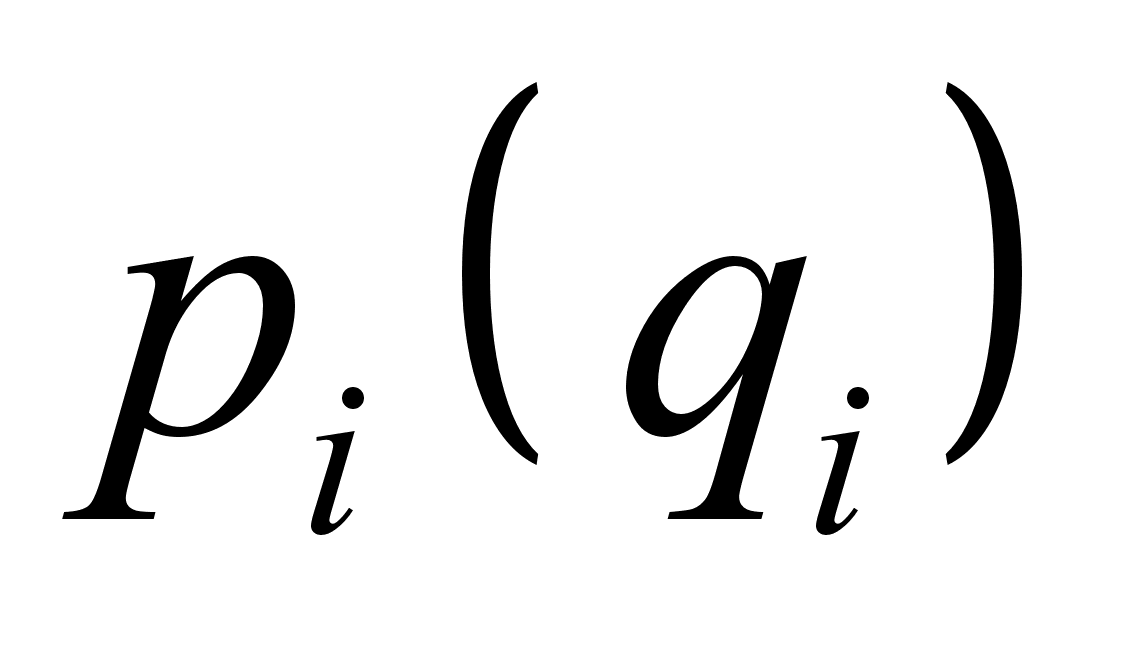 , если же по «большим»
, если же по «большим» 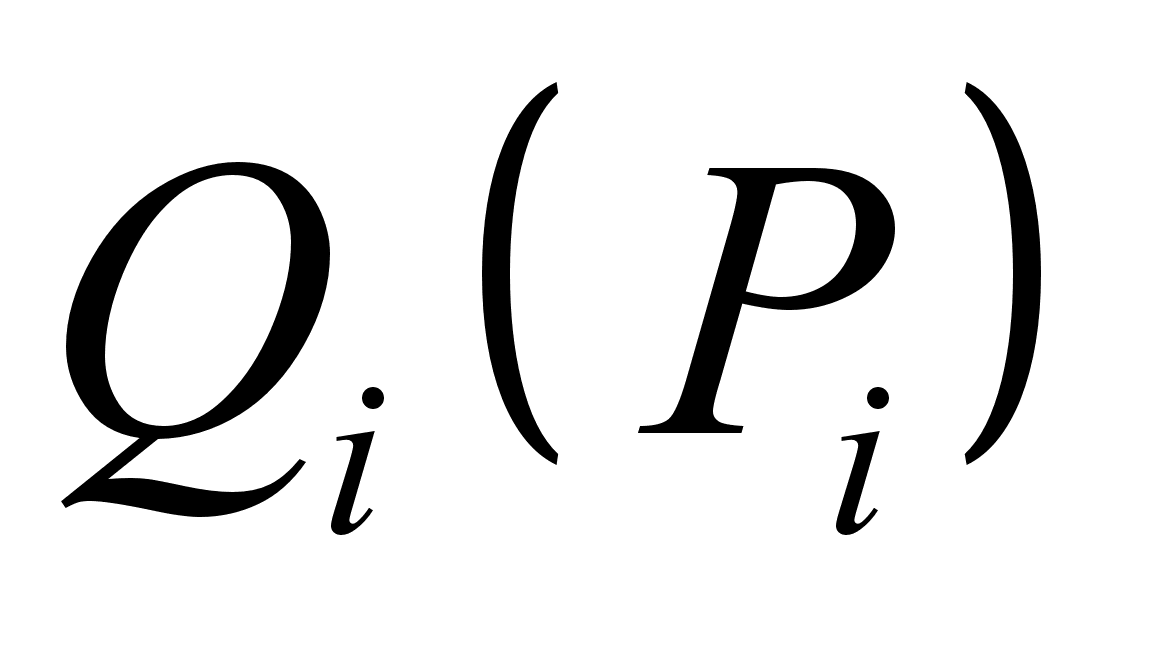 , то и получать будем соответственно
, то и получать будем соответственно 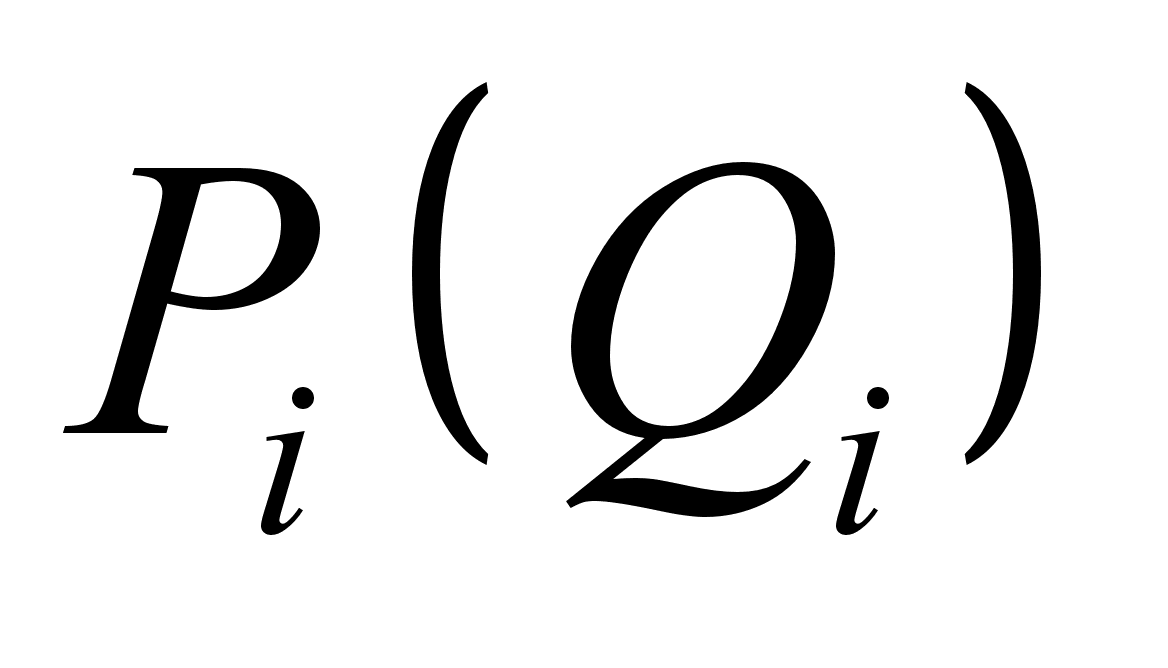 .
.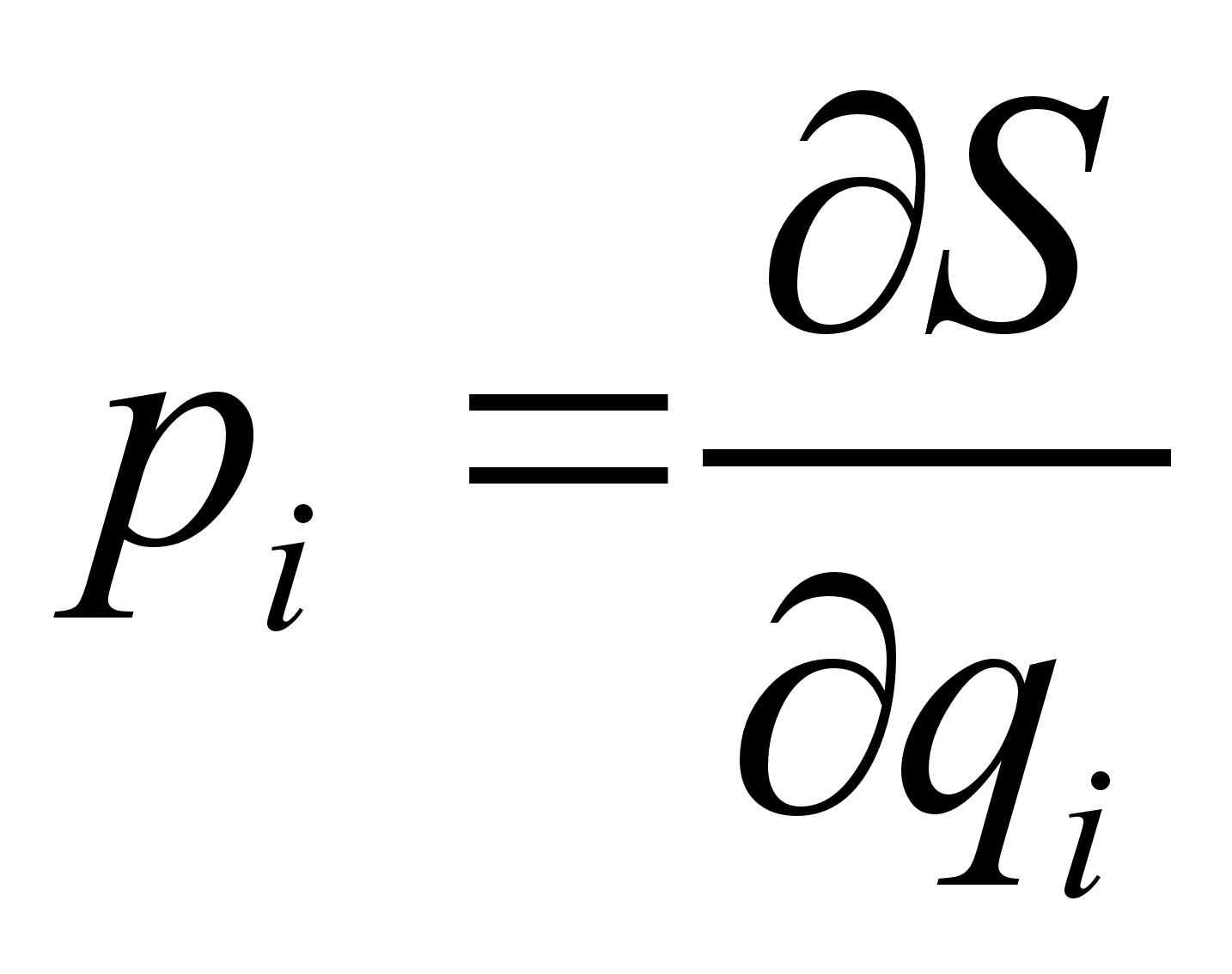
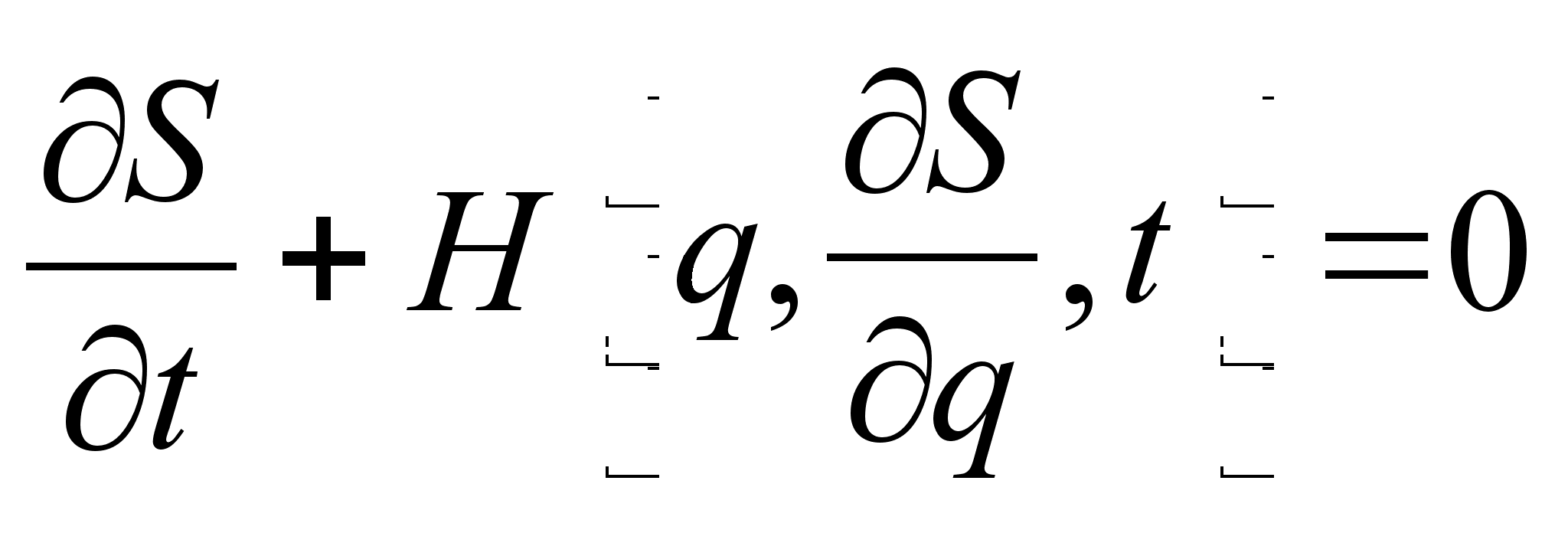
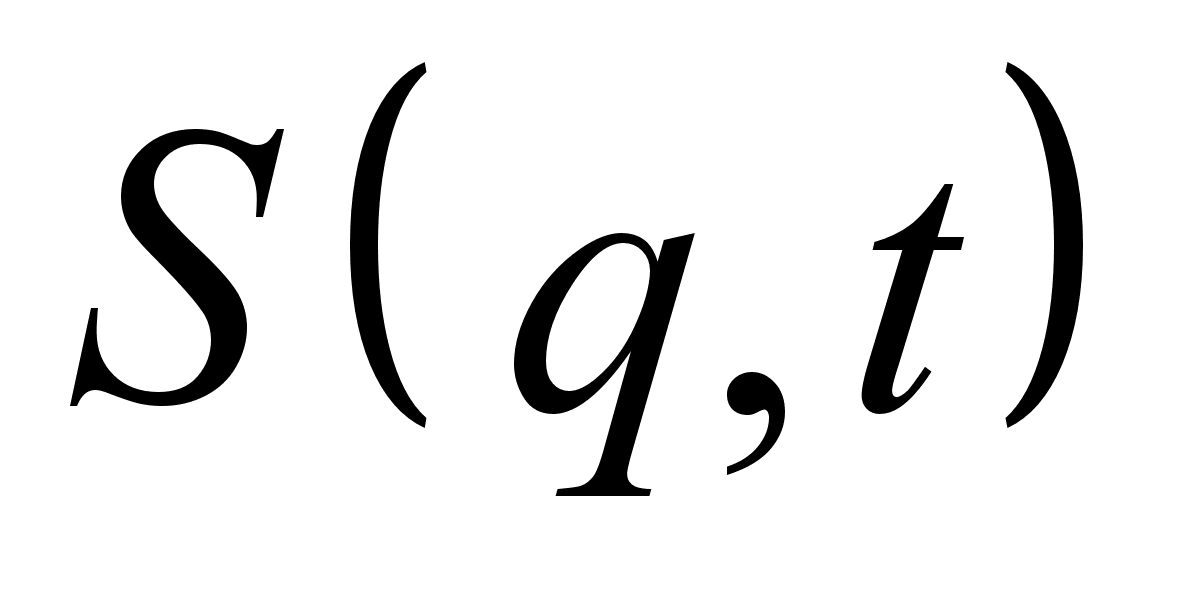 .
.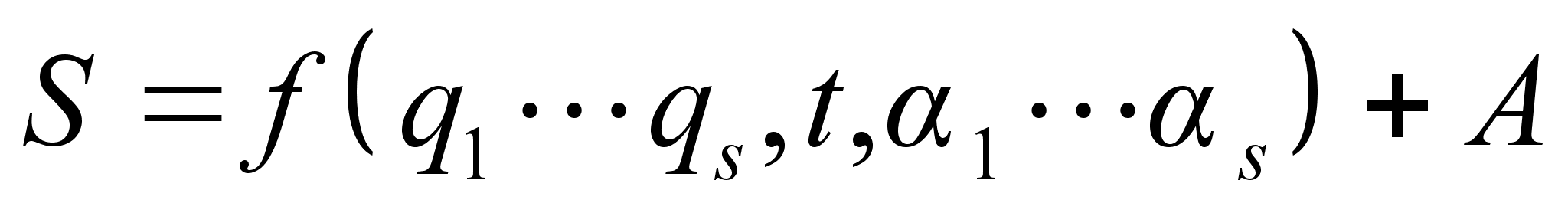
 будут выступать в качестве новых импульсов. Тогда новые координаты
будут выступать в качестве новых импульсов. Тогда новые координаты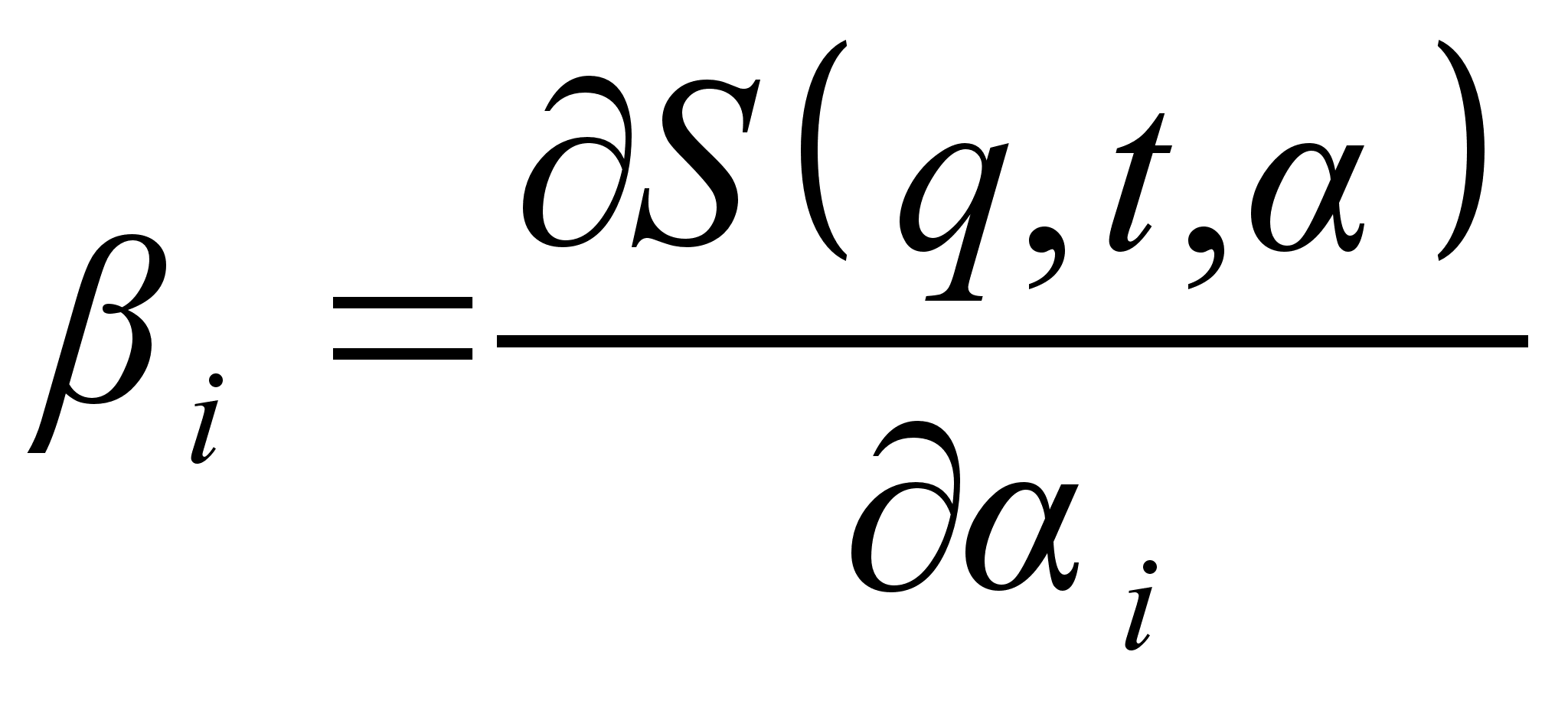
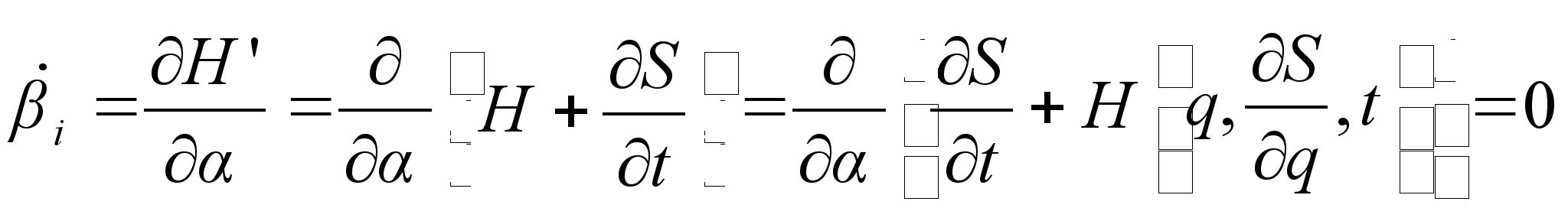
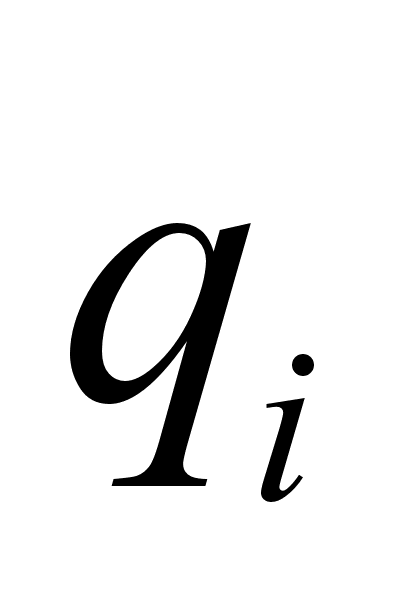 в виде функций от
в виде функций от 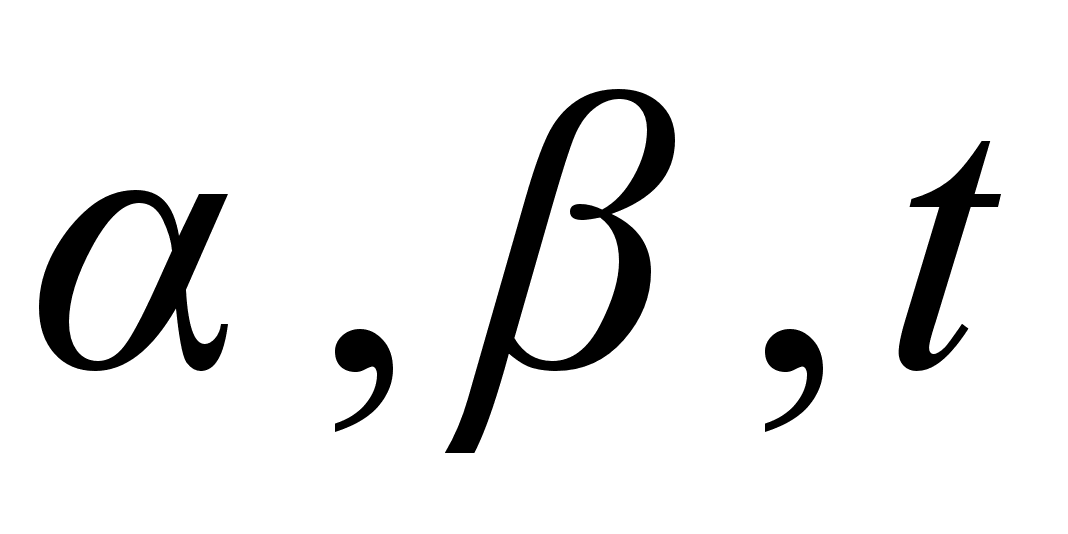 , мы и получим закон движения:
, мы и получим закон движения: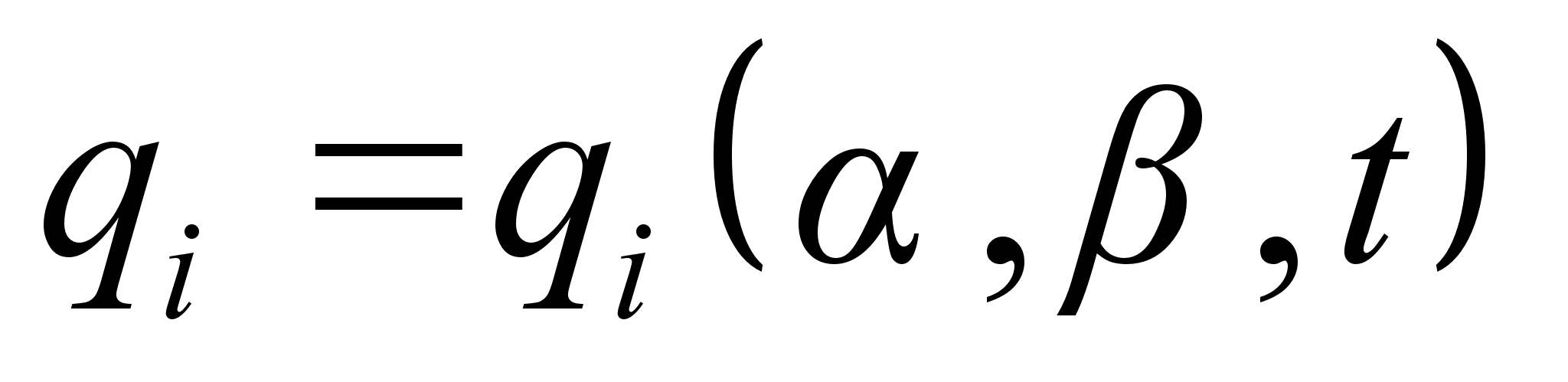
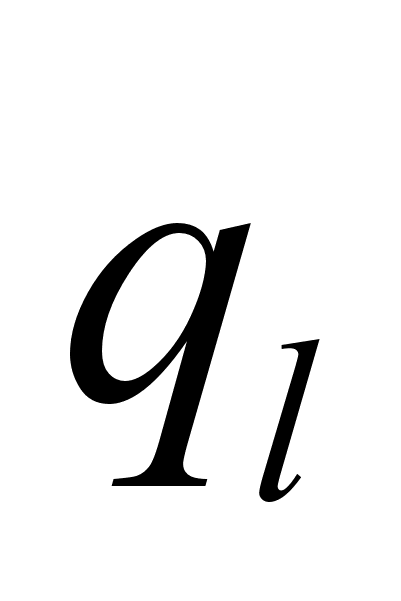 может быть связана лишь с соответствующим ей импульсом
может быть связана лишь с соответствующим ей импульсом 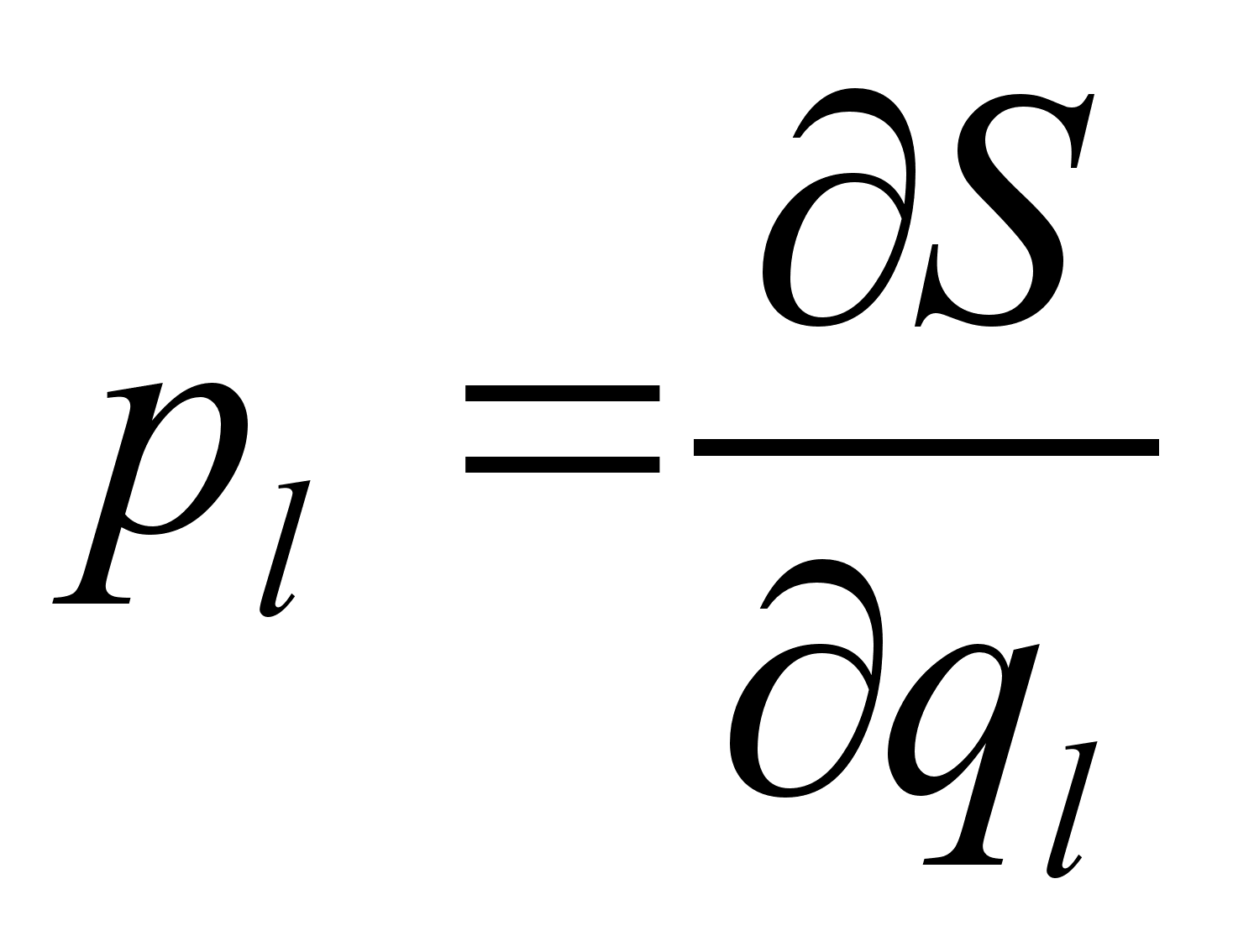 и не связана ни с какими другими импульсами или координатами, входящими уравнение Г.-Я. В частности это условие выполняется для циклических переменных.
и не связана ни с какими другими импульсами или координатами, входящими уравнение Г.-Я. В частности это условие выполняется для циклических переменных.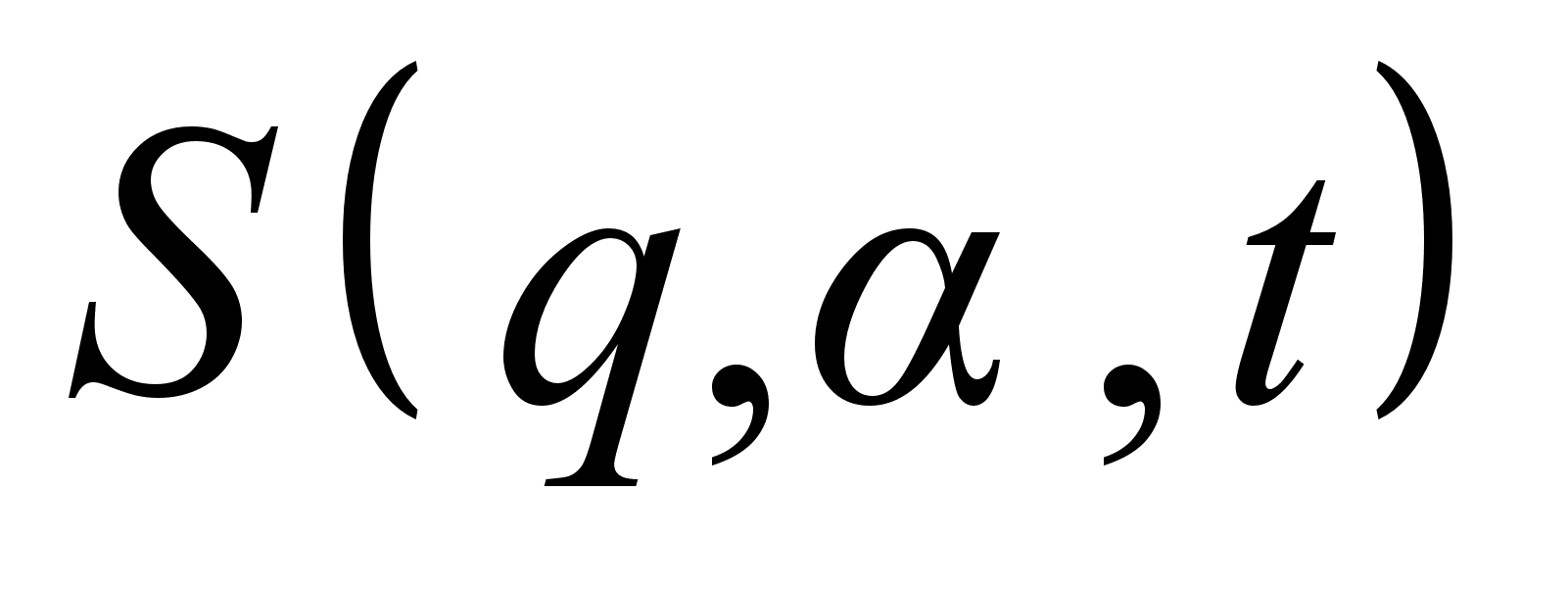 ;
;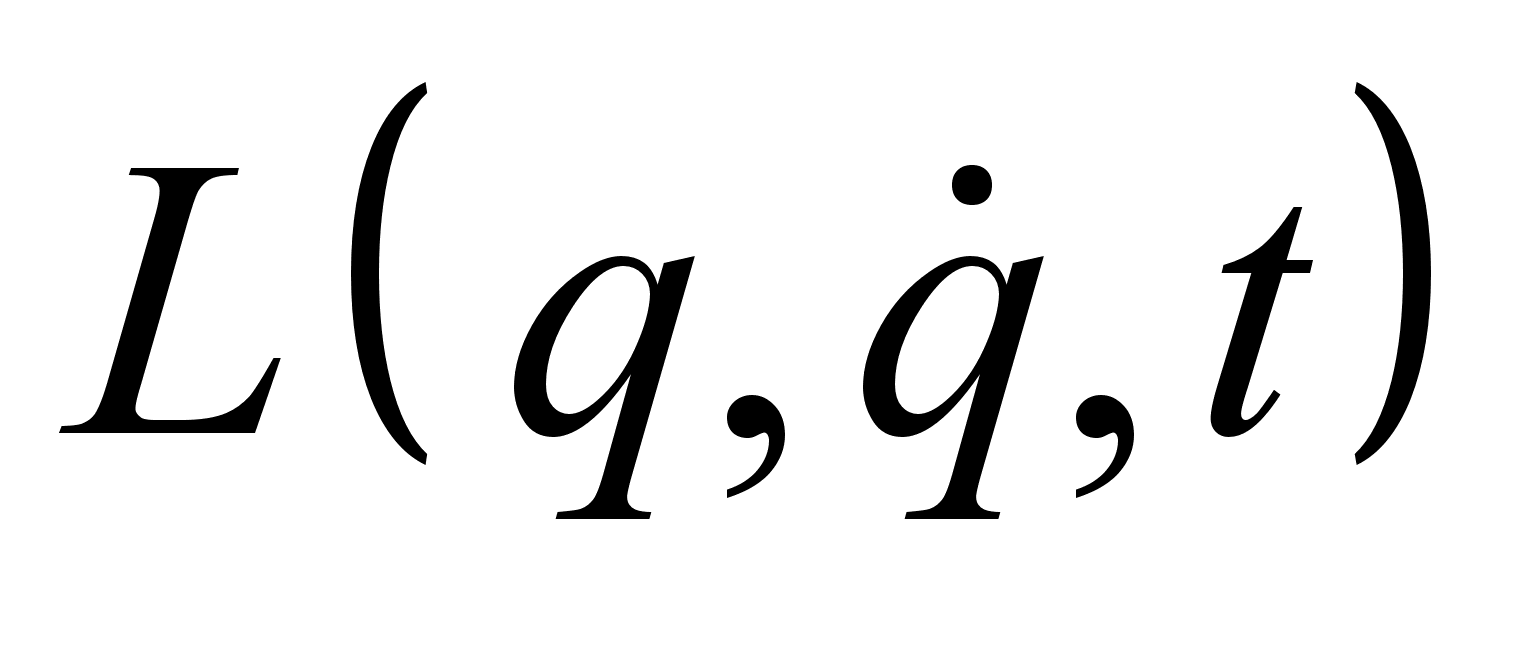 на
на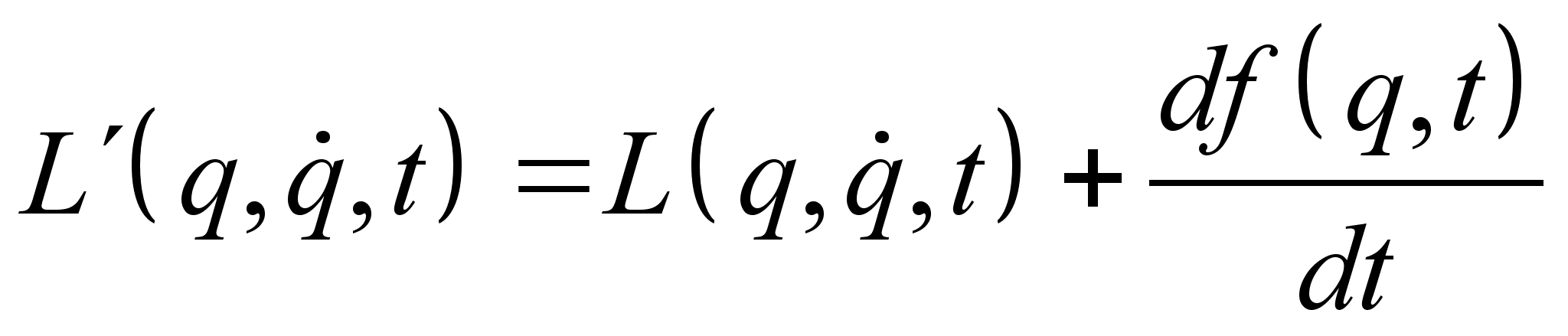 ,
,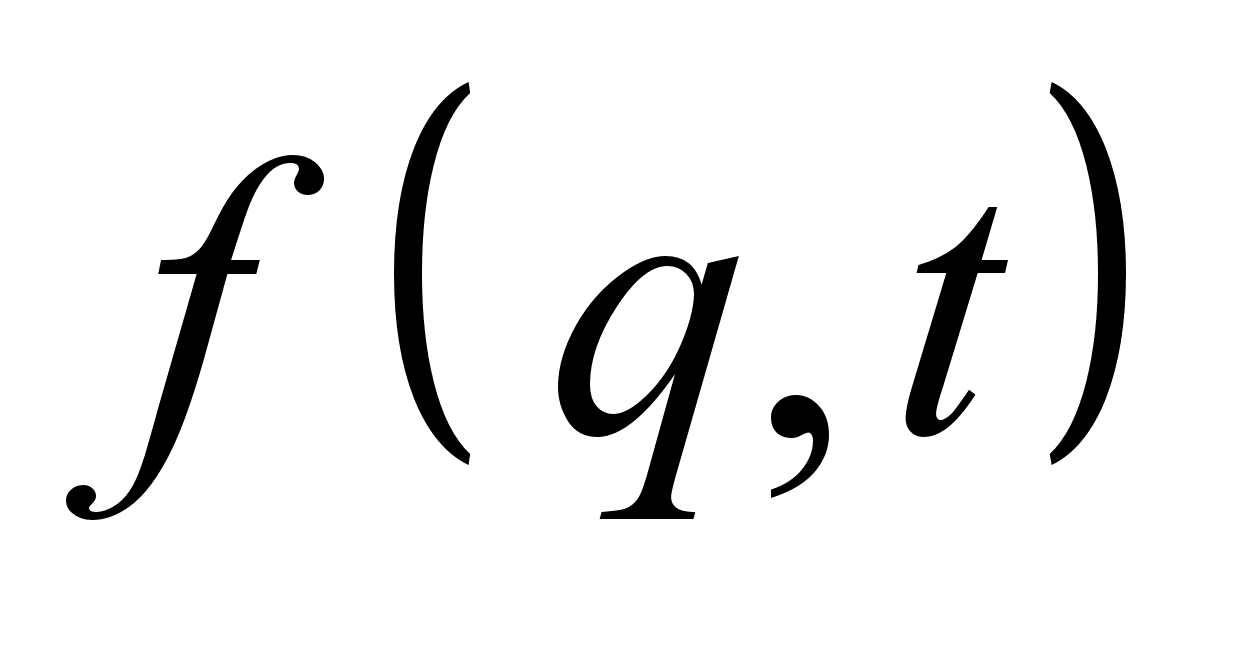 – произвольная функция, не изменяет уравнений Лагранжа. Показать, что это преобразование является каноническим, и найти его производящую функцию.
– произвольная функция, не изменяет уравнений Лагранжа. Показать, что это преобразование является каноническим, и найти его производящую функцию.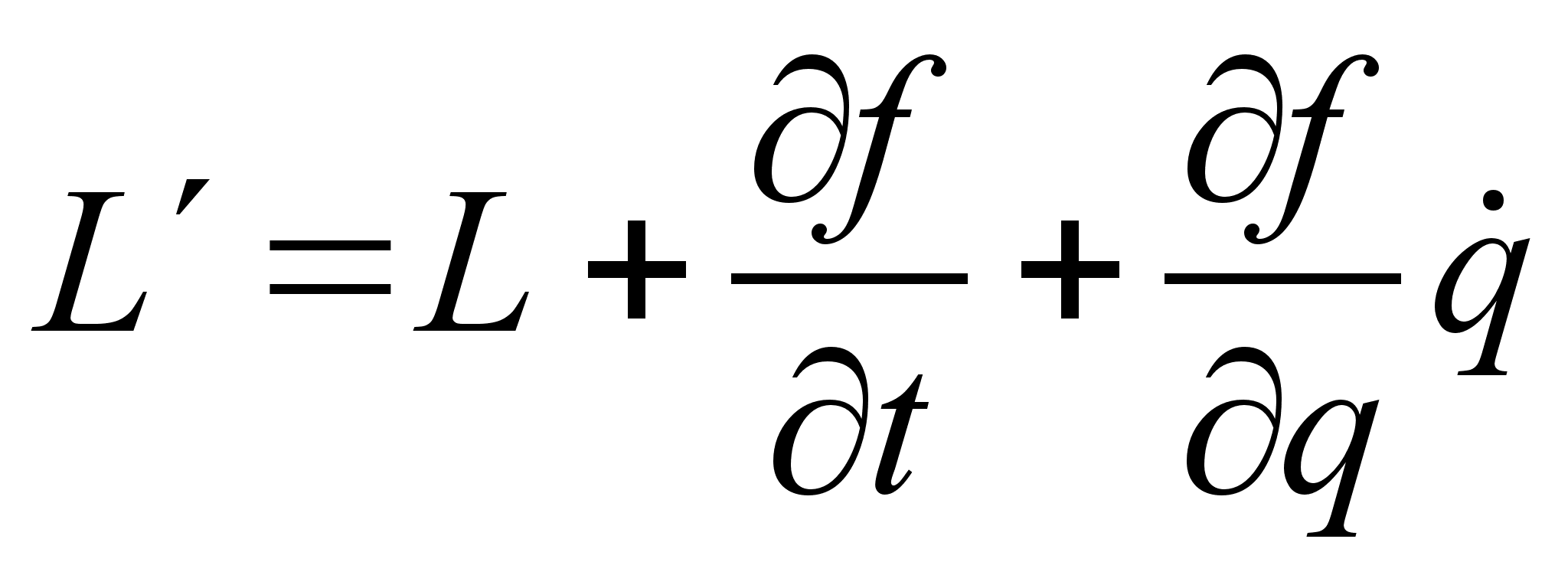
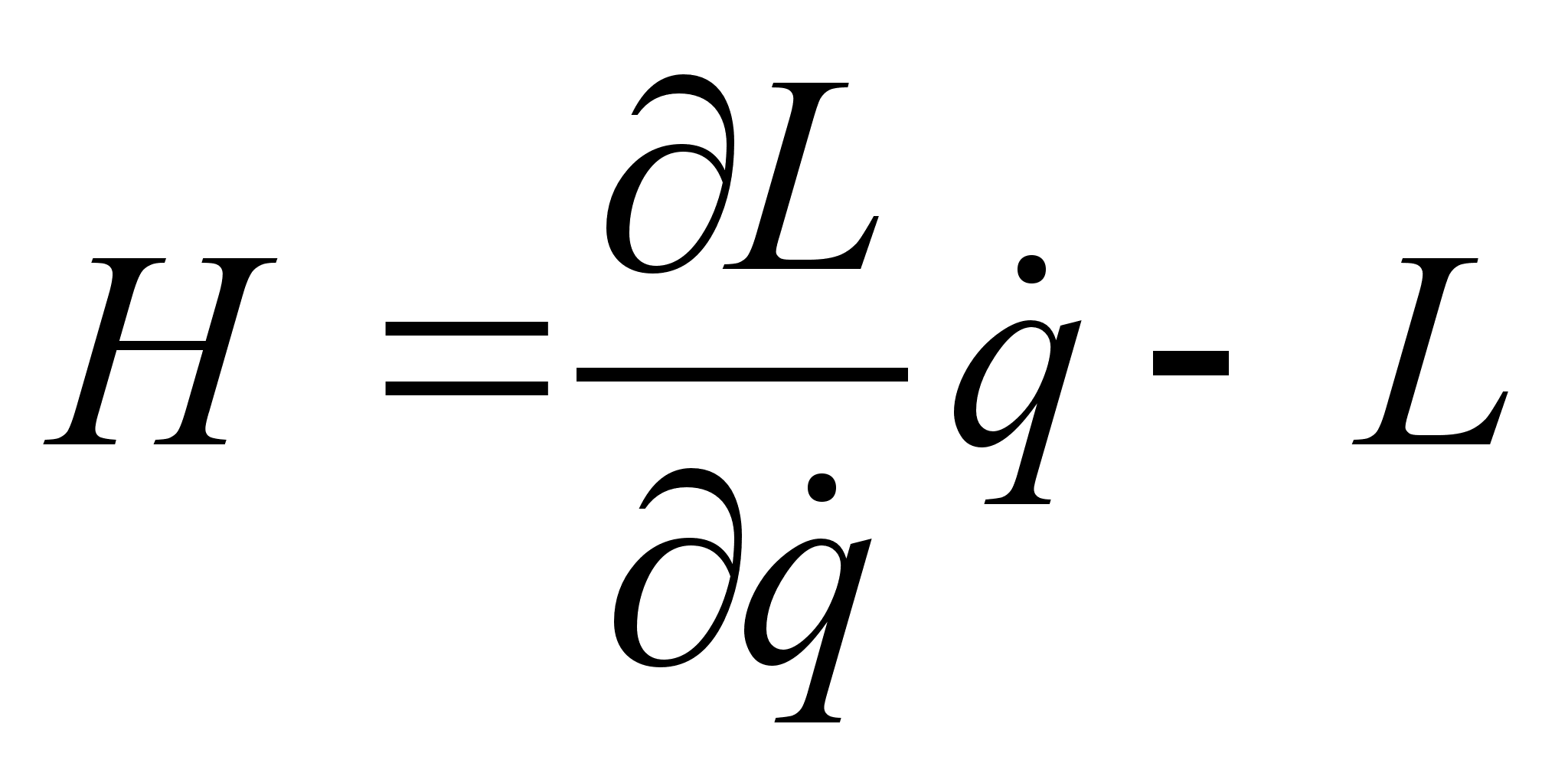
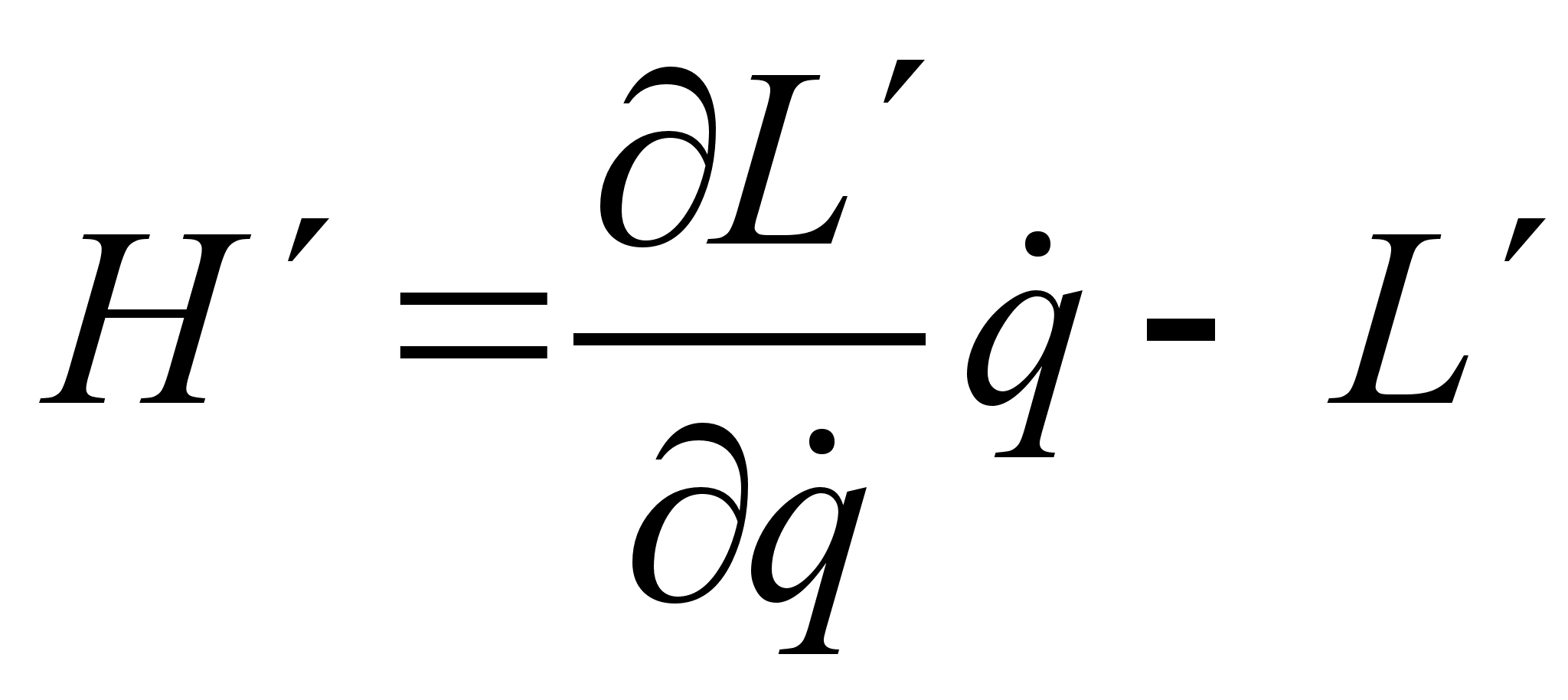
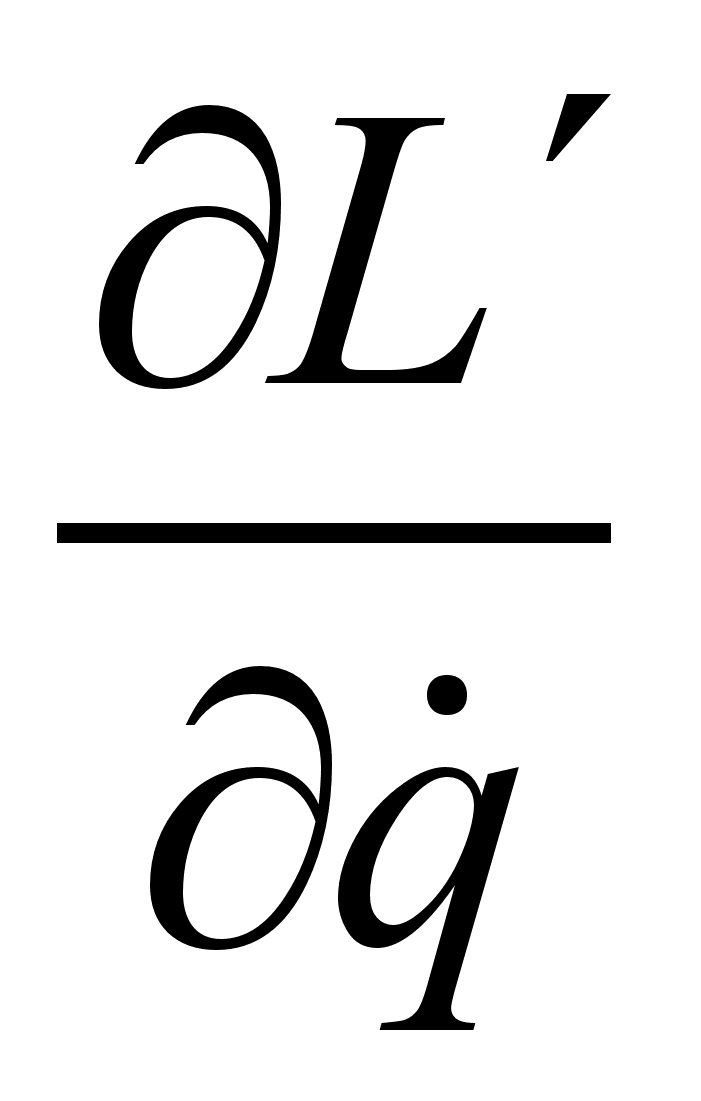 , используя представление штрихованной функции Лагранжа :
, используя представление штрихованной функции Лагранжа :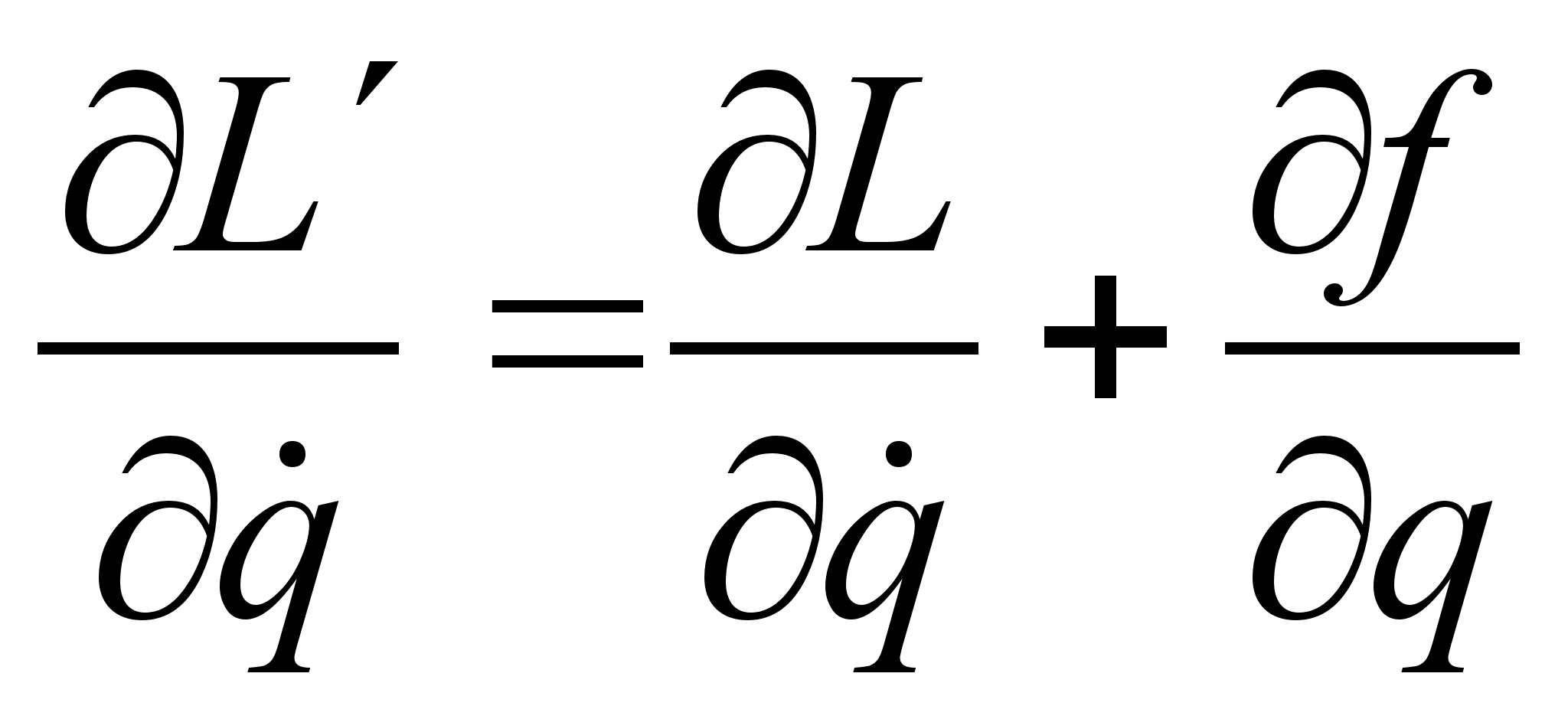
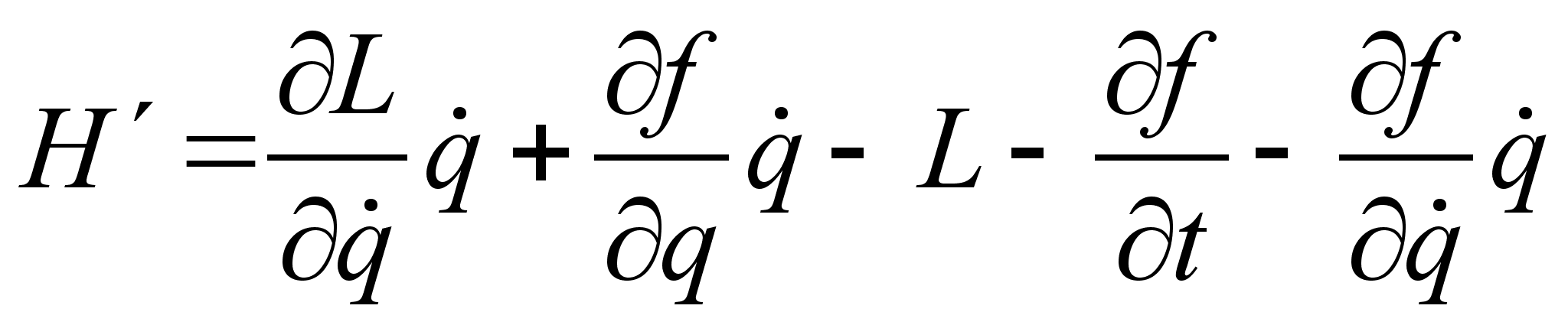
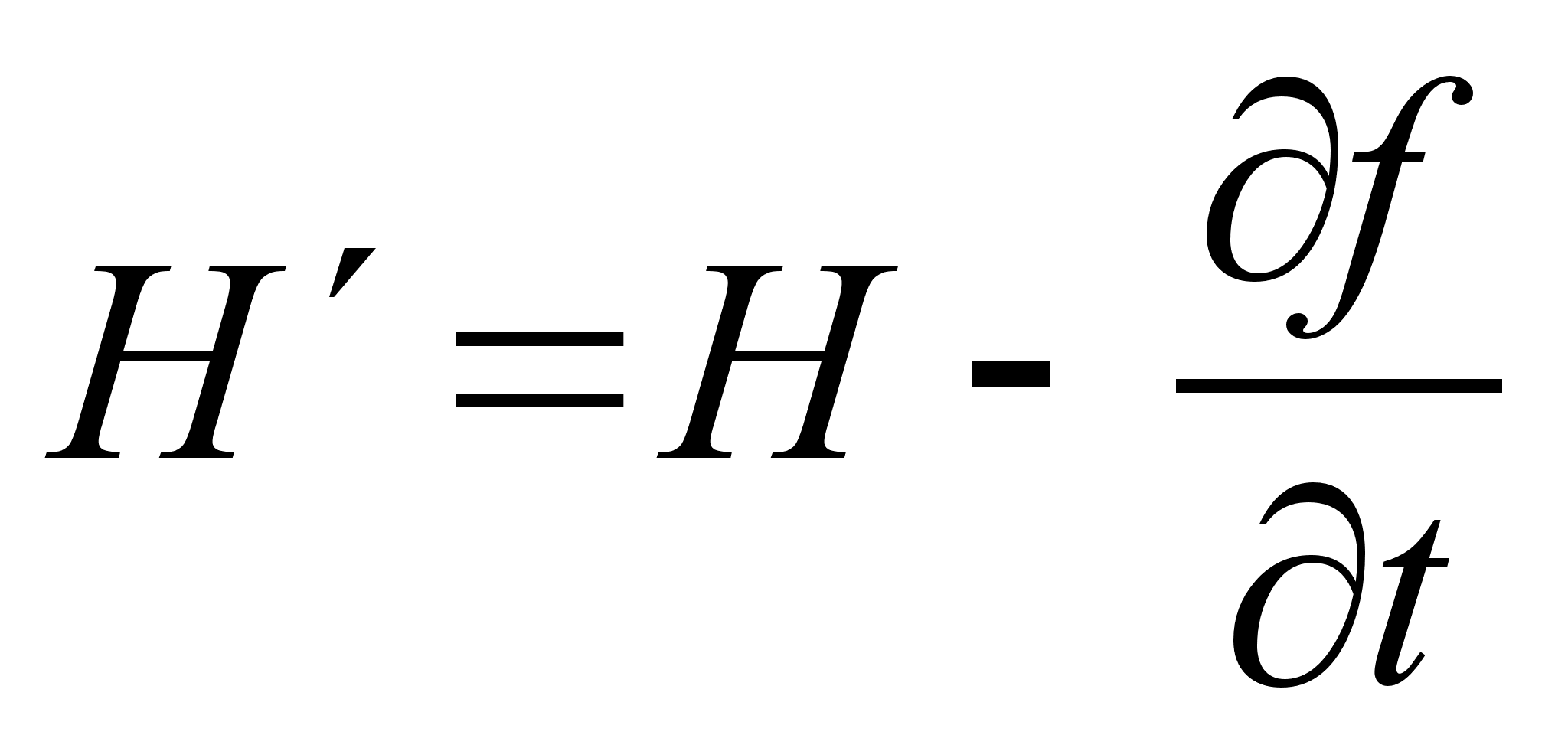

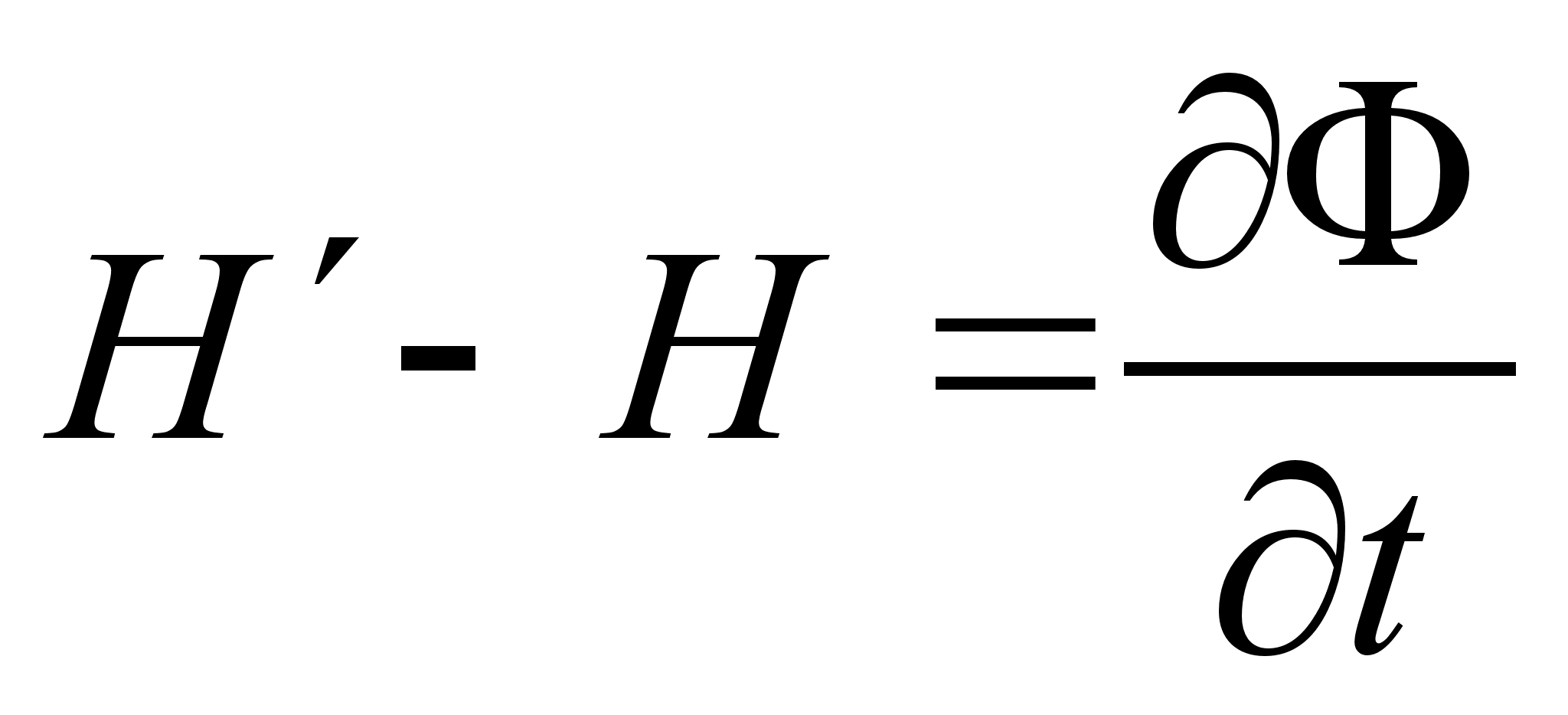
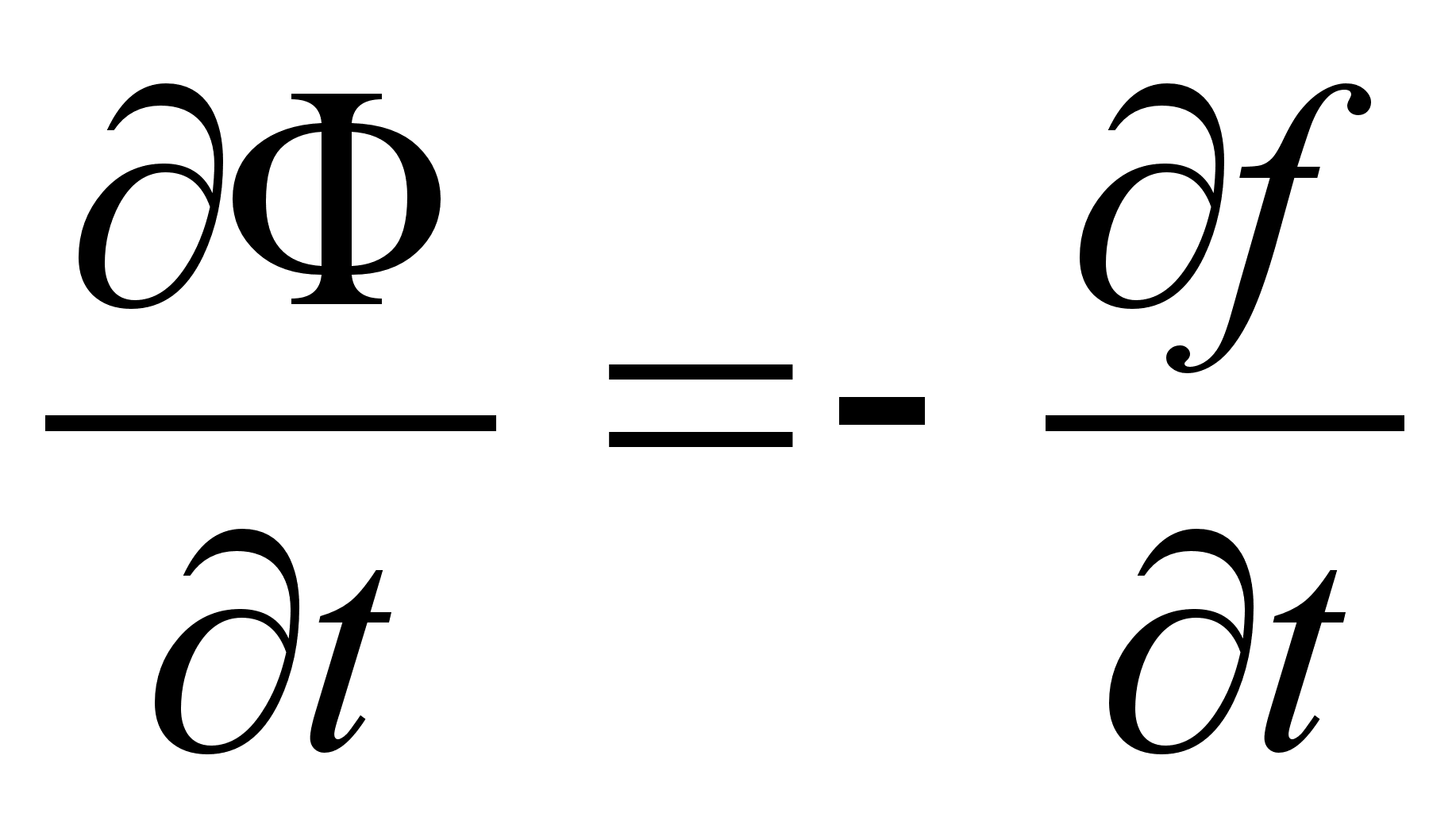
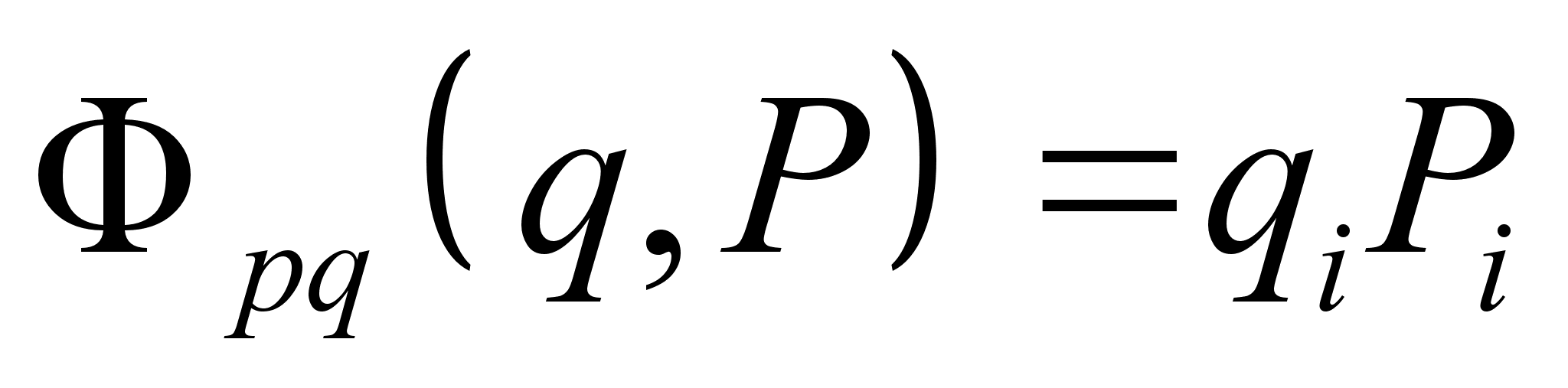
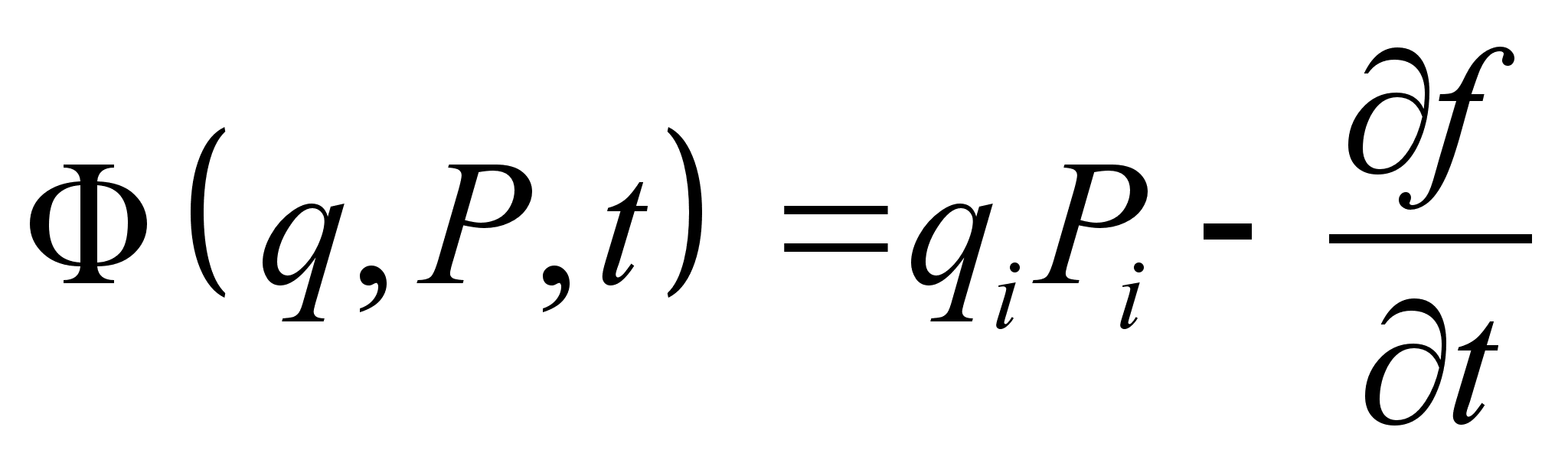
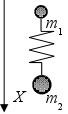 адача. Система, состоящая из двух шариков массами
адача. Система, состоящая из двух шариков массами 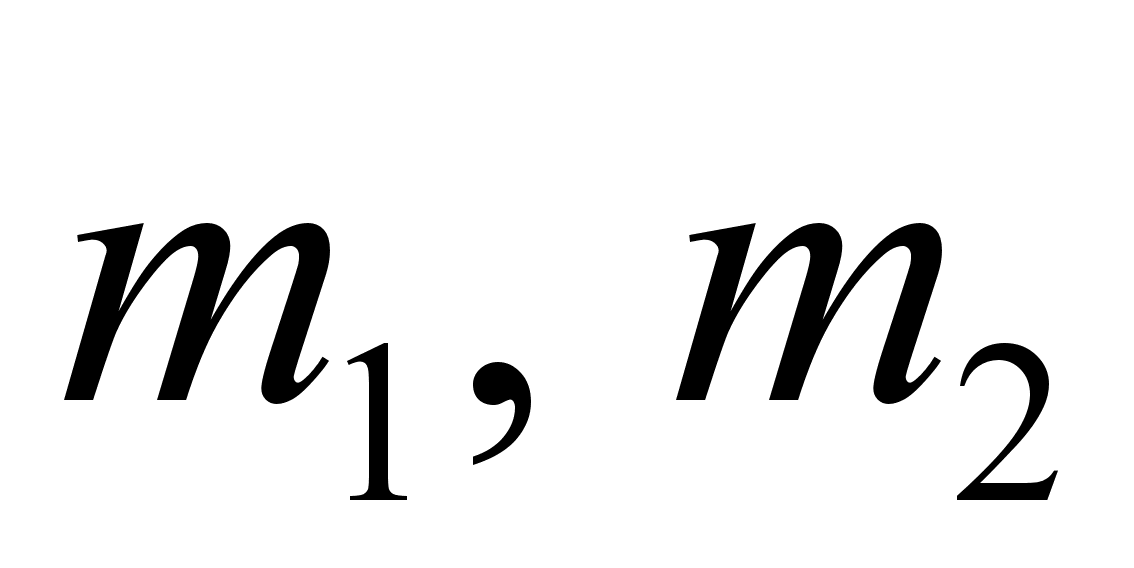 , соединенных невесомой пружиной, расположенной вертикально, начинает двигаться в поле сил тяжести. Длина пружины —
, соединенных невесомой пружиной, расположенной вертикально, начинает двигаться в поле сил тяжести. Длина пружины — 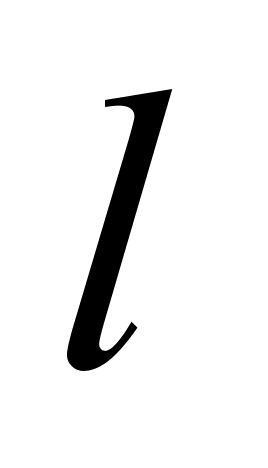 . Произвести каноническое преобразование и записать новую функцию Гамильтона, соответствующие производящей функции
. Произвести каноническое преобразование и записать новую функцию Гамильтона, соответствующие производящей функции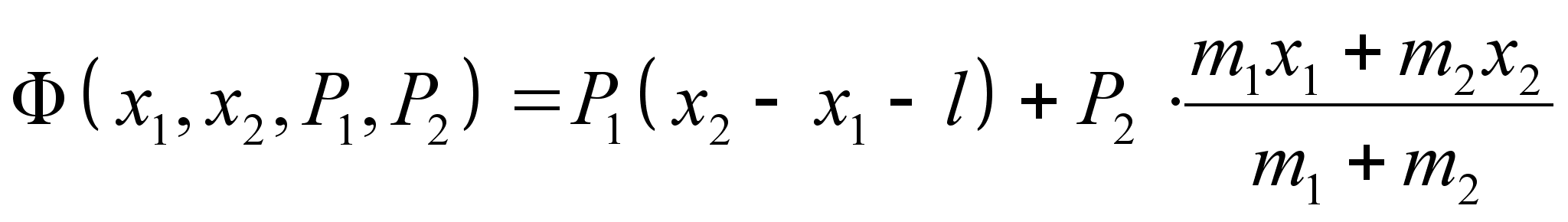 .
.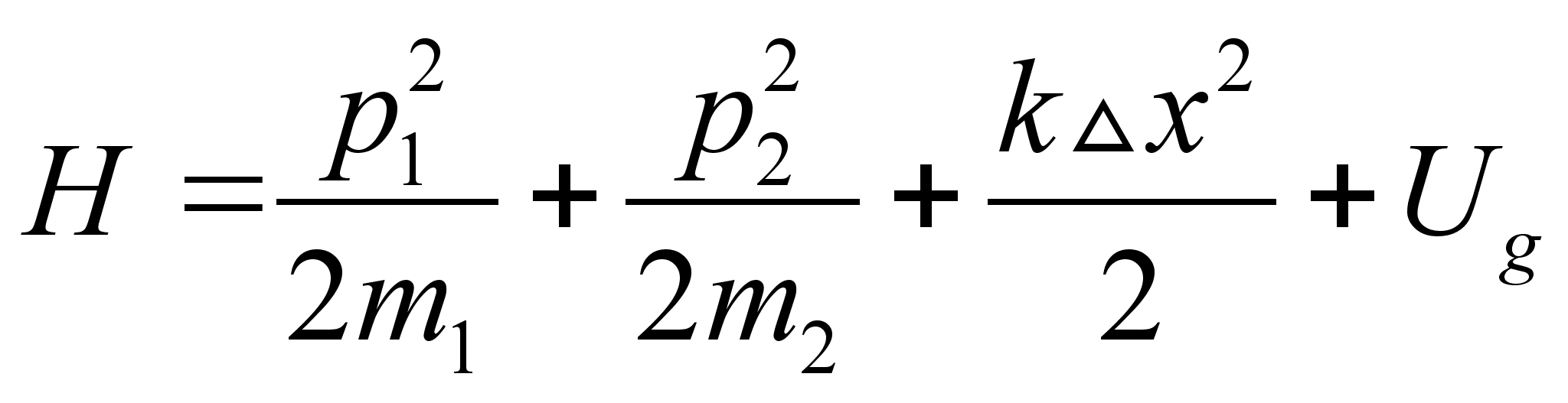
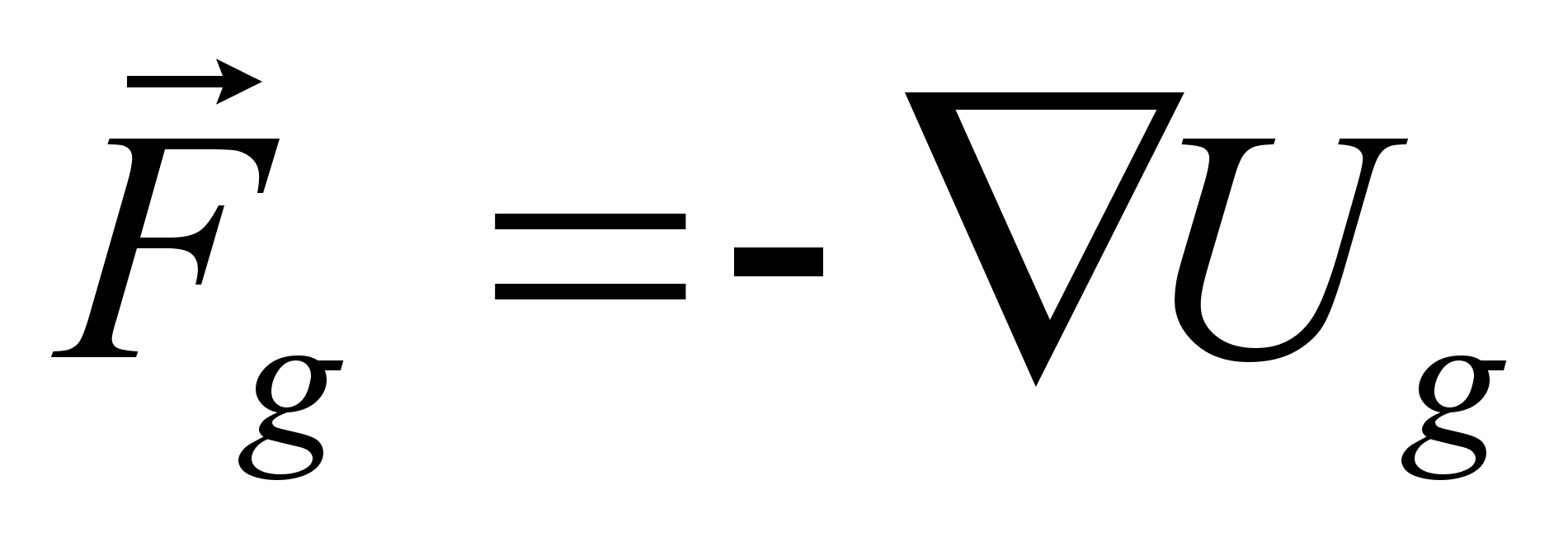
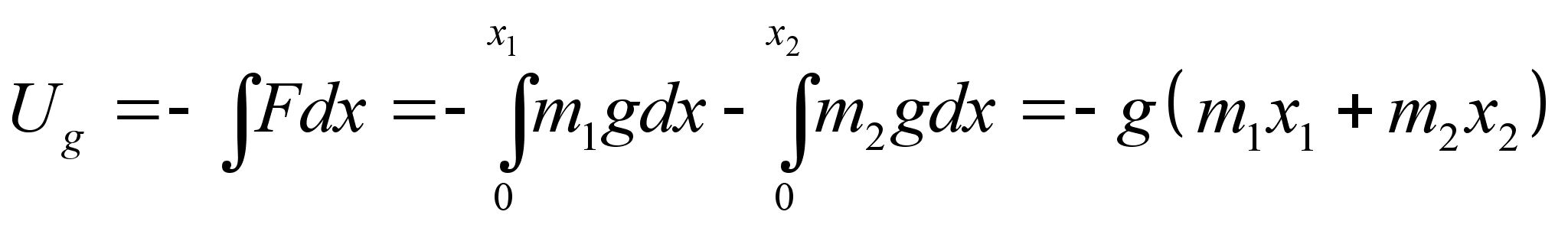
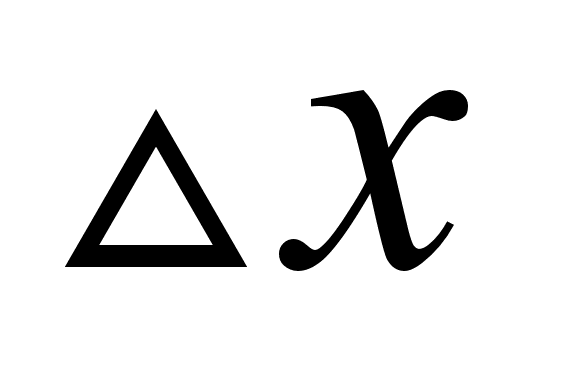 от положения равновесия будет определяться следующим образом:
от положения равновесия будет определяться следующим образом: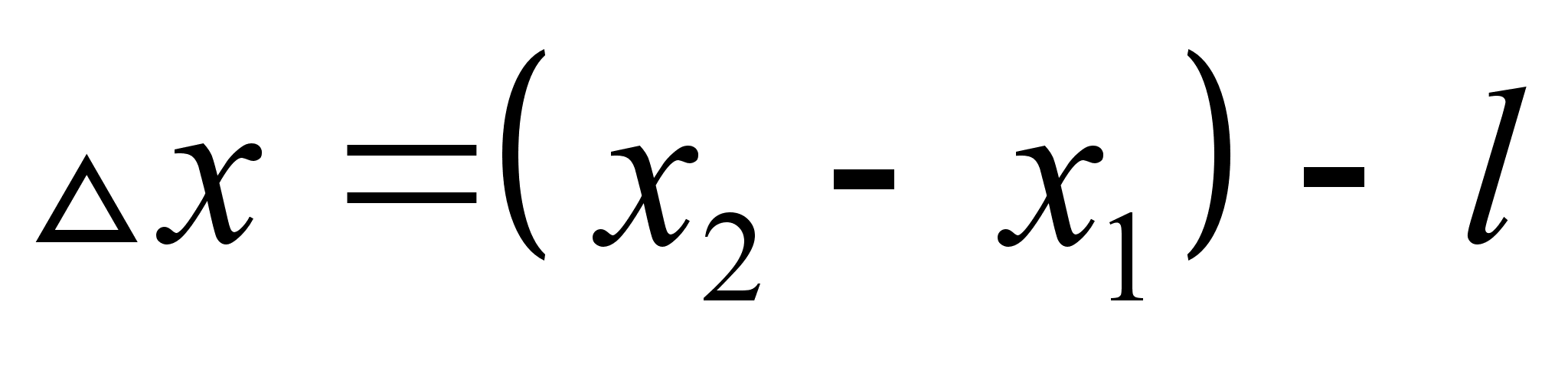
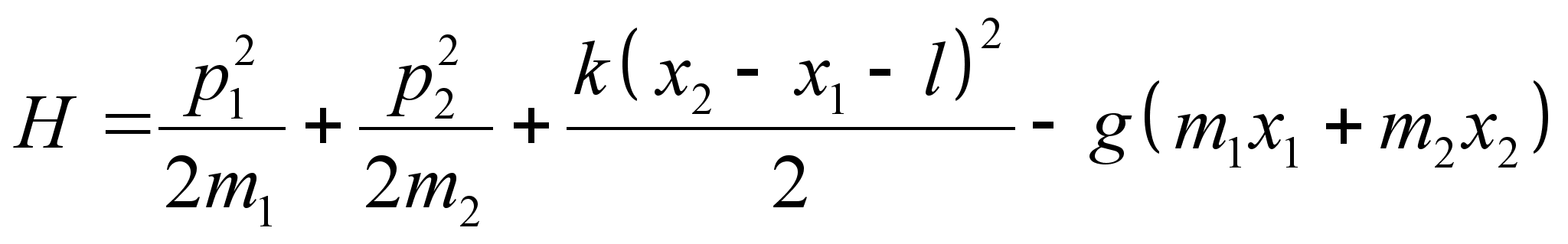
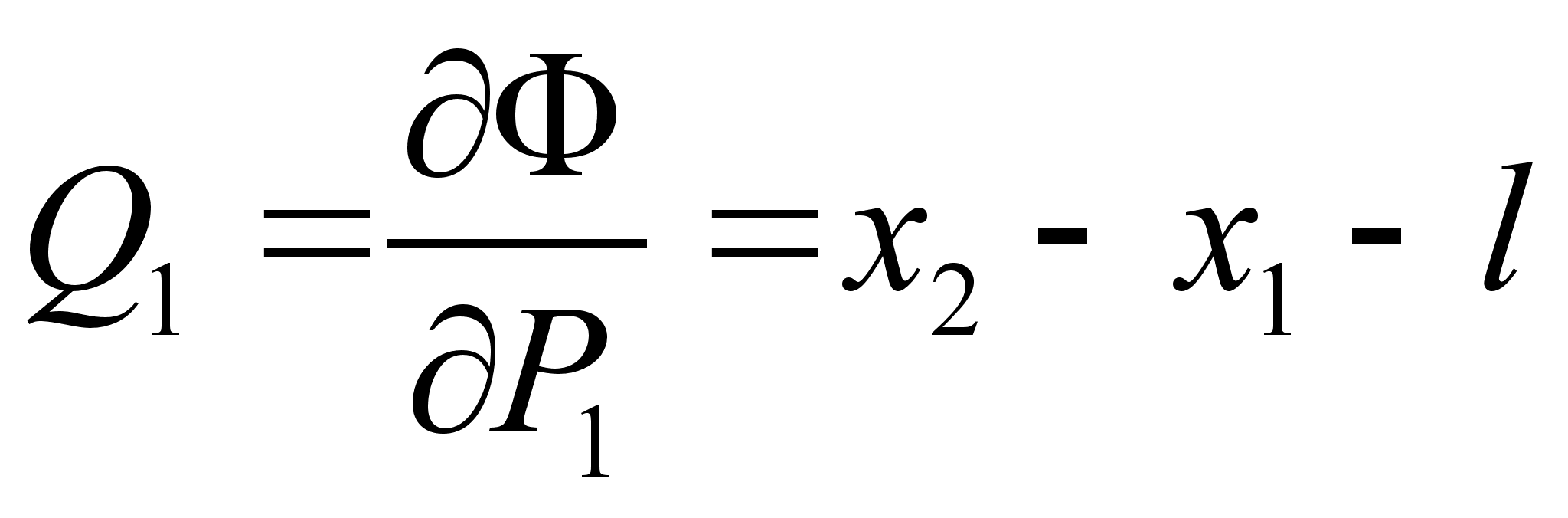
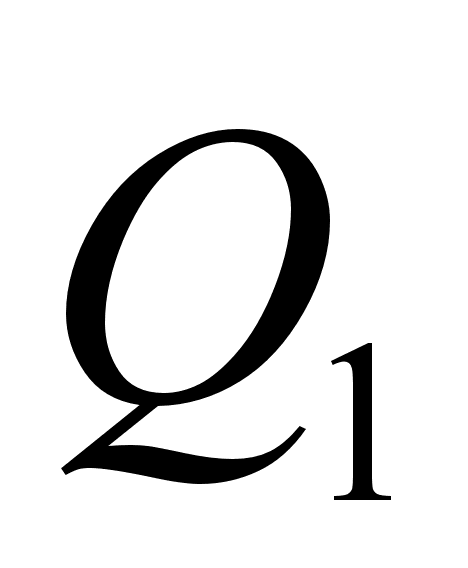 совпадает со значением смещения пружины от положения равновесия.
совпадает со значением смещения пружины от положения равновесия.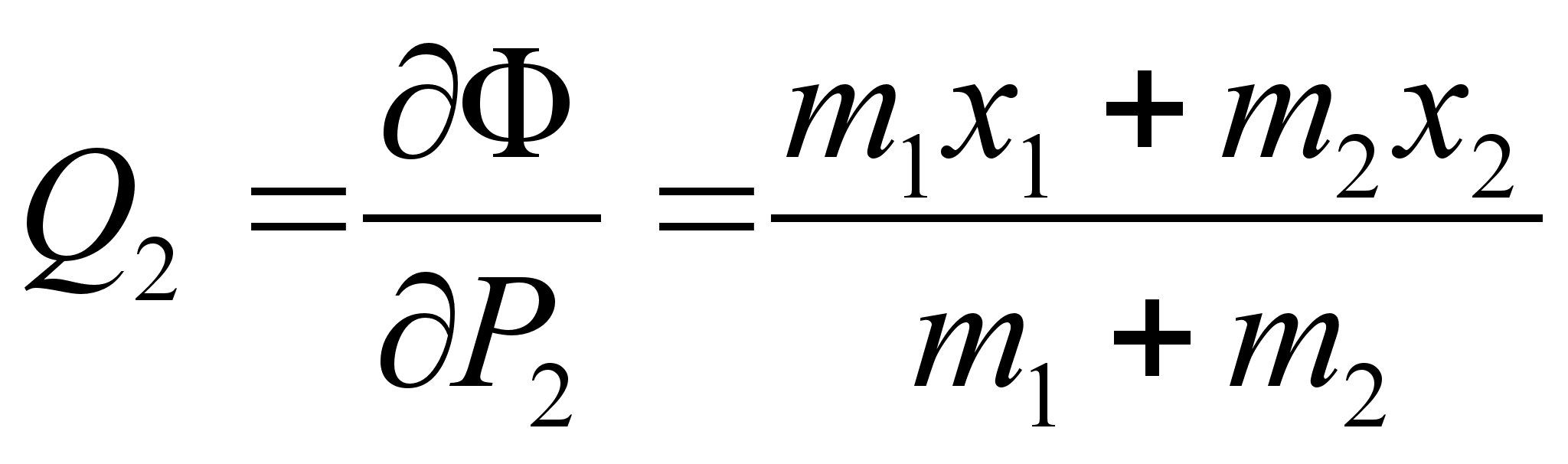
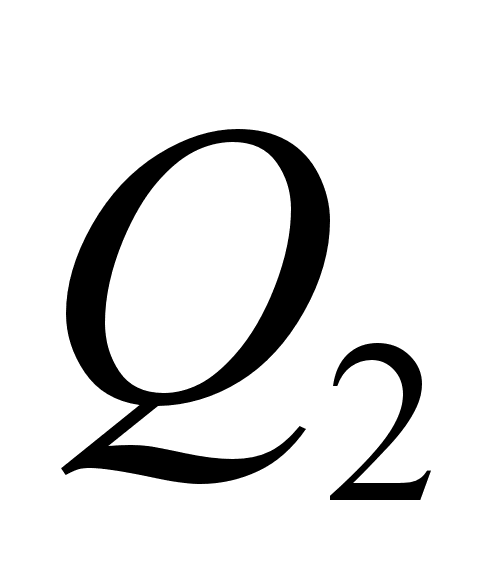 совпадает со значением положения центра масс системы.
совпадает со значением положения центра масс системы.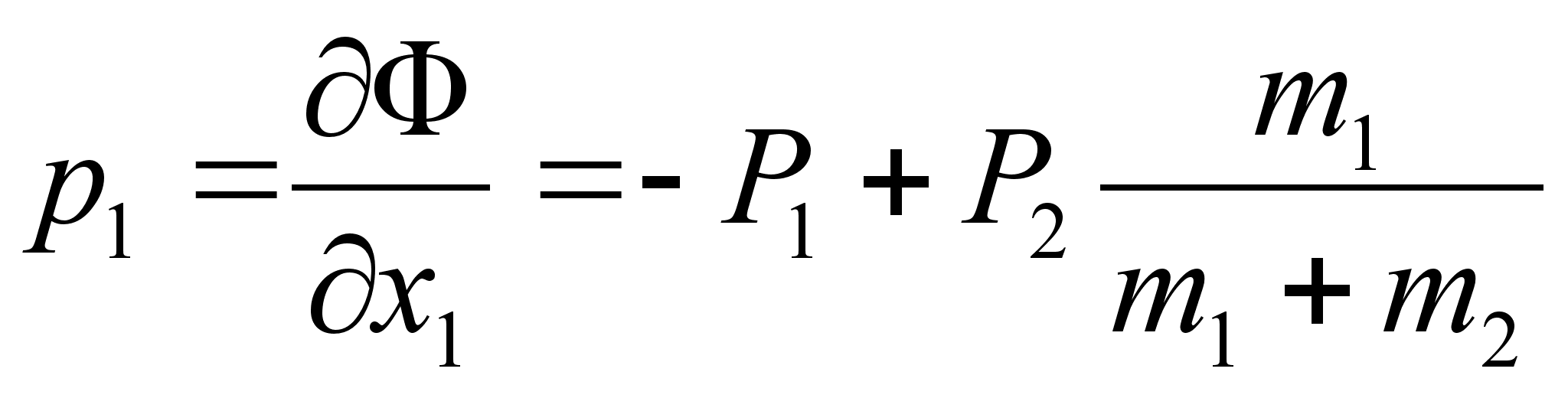
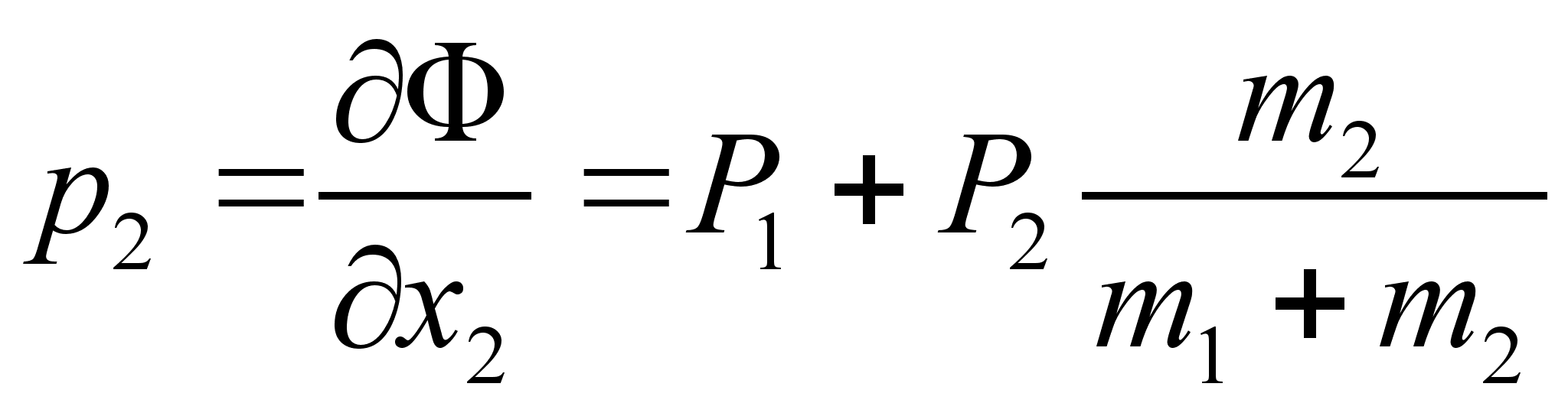
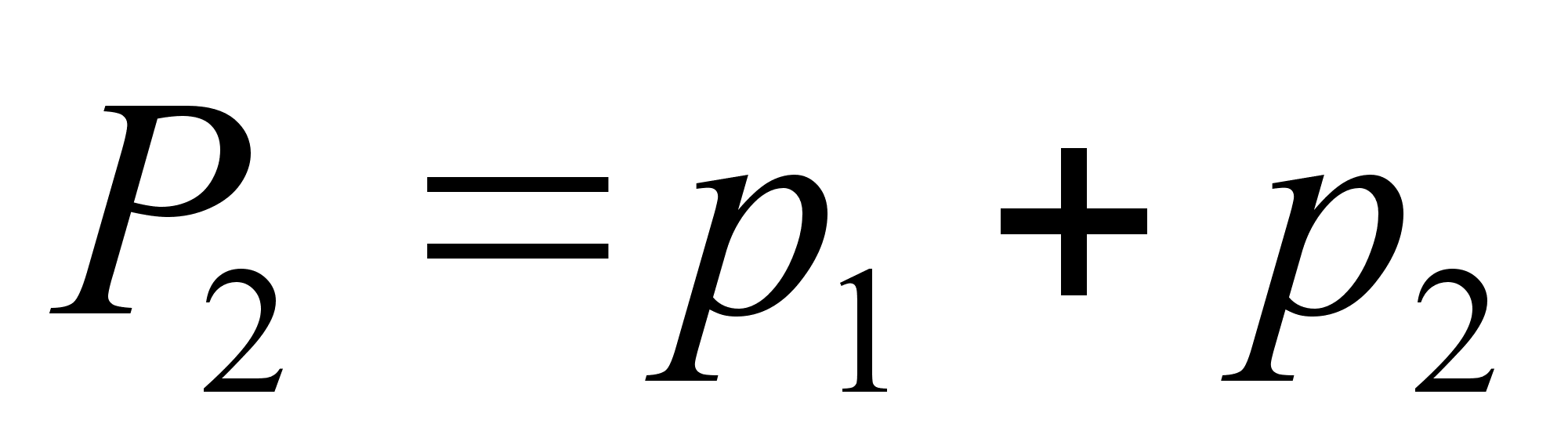
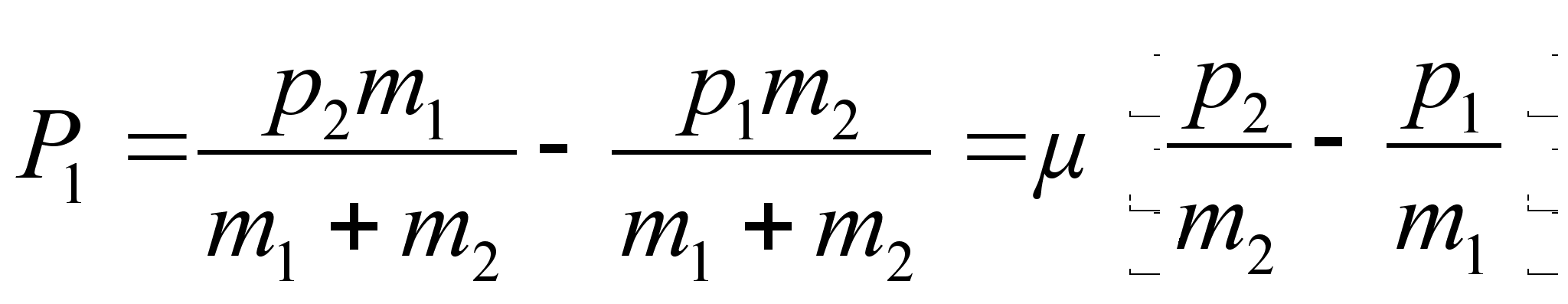 ,
,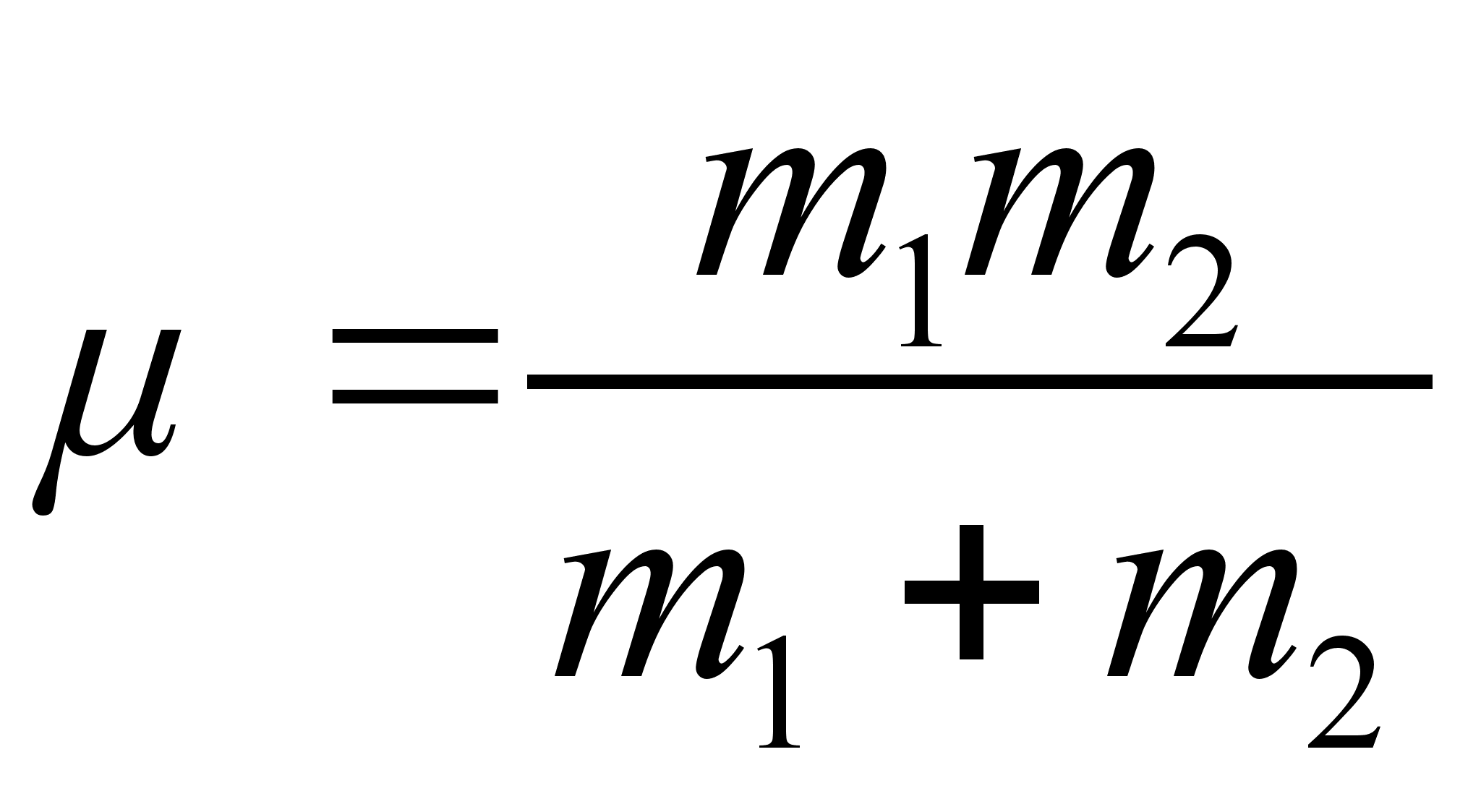 ,
,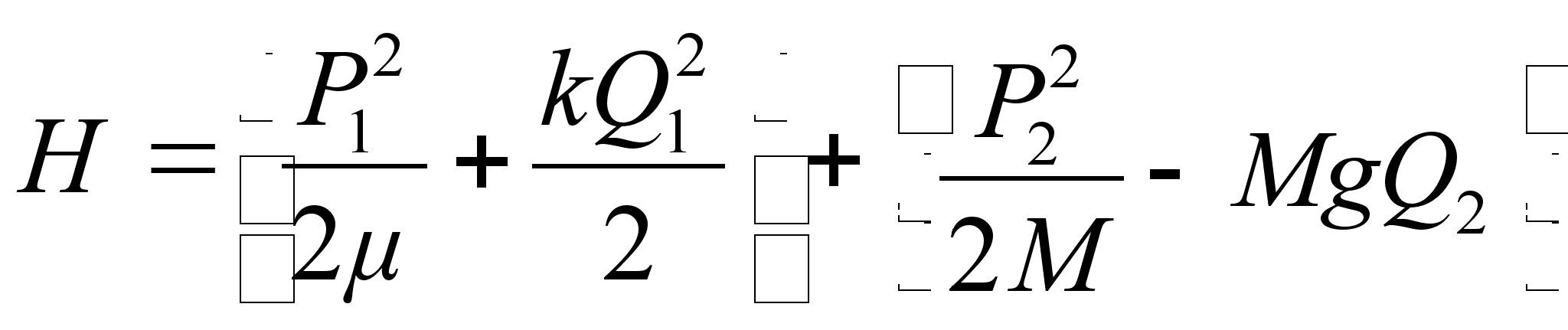 ,
,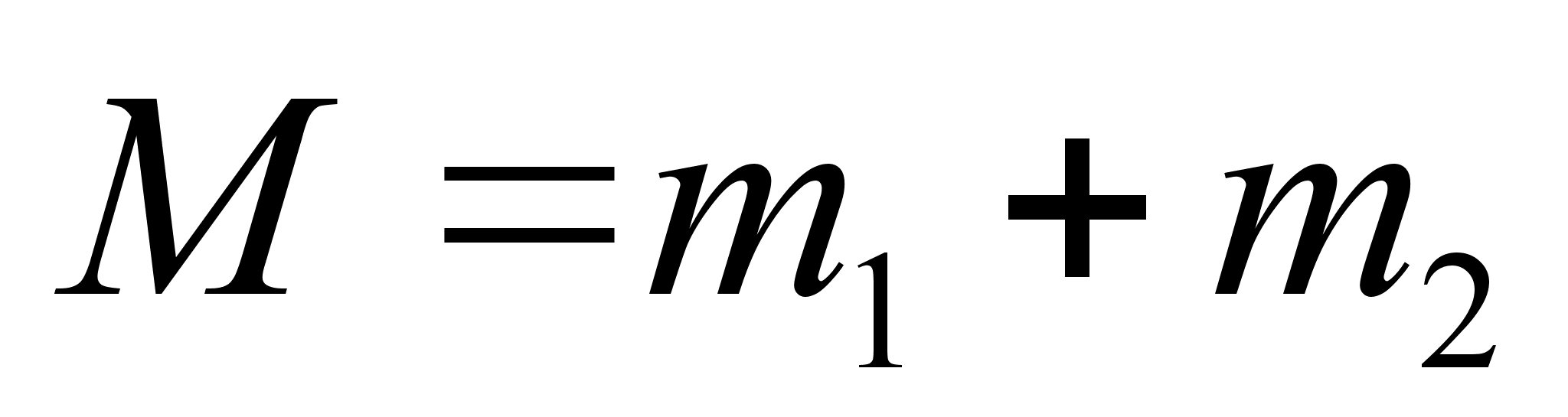 ,
,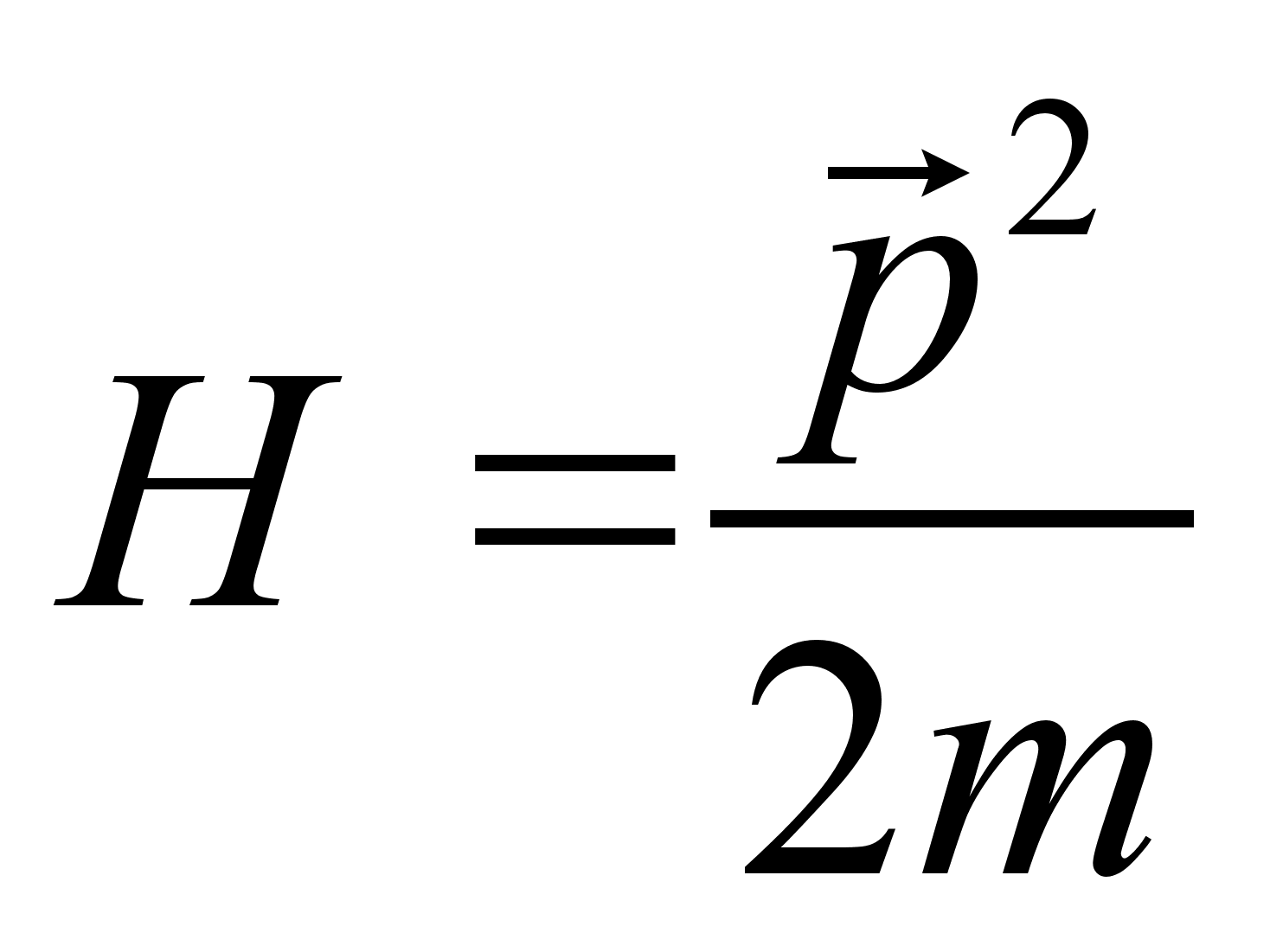
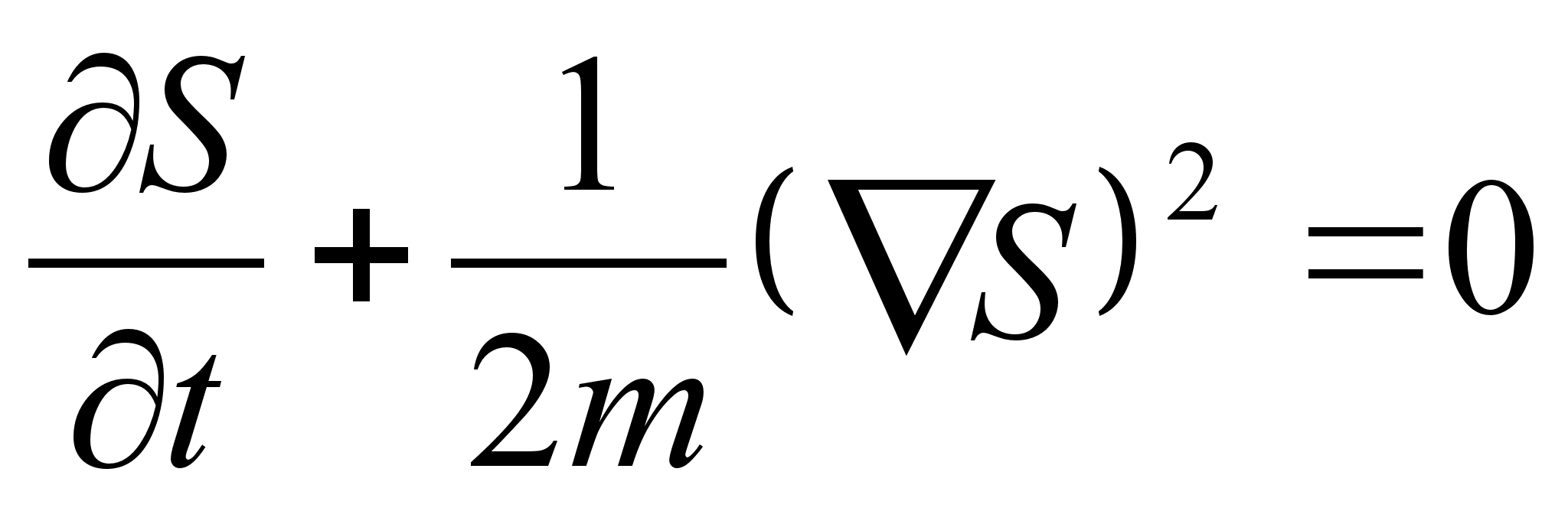
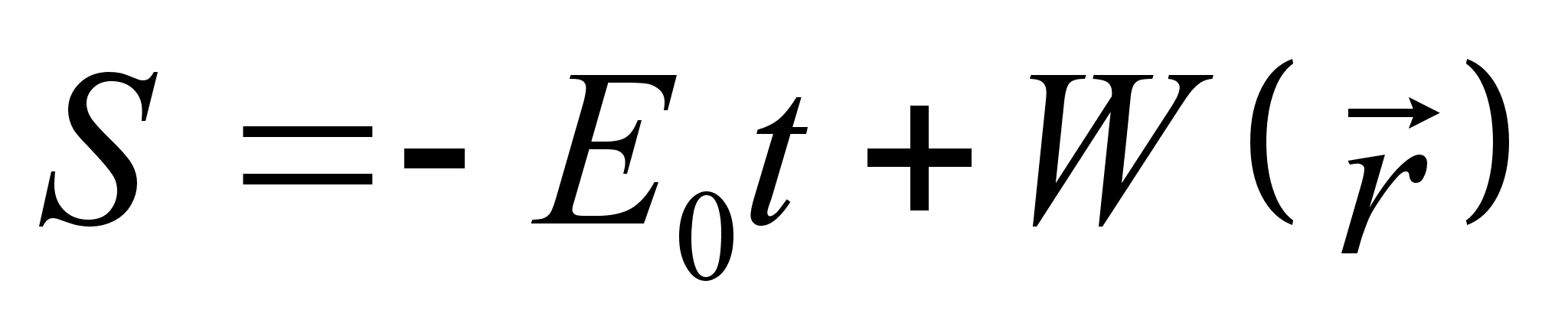
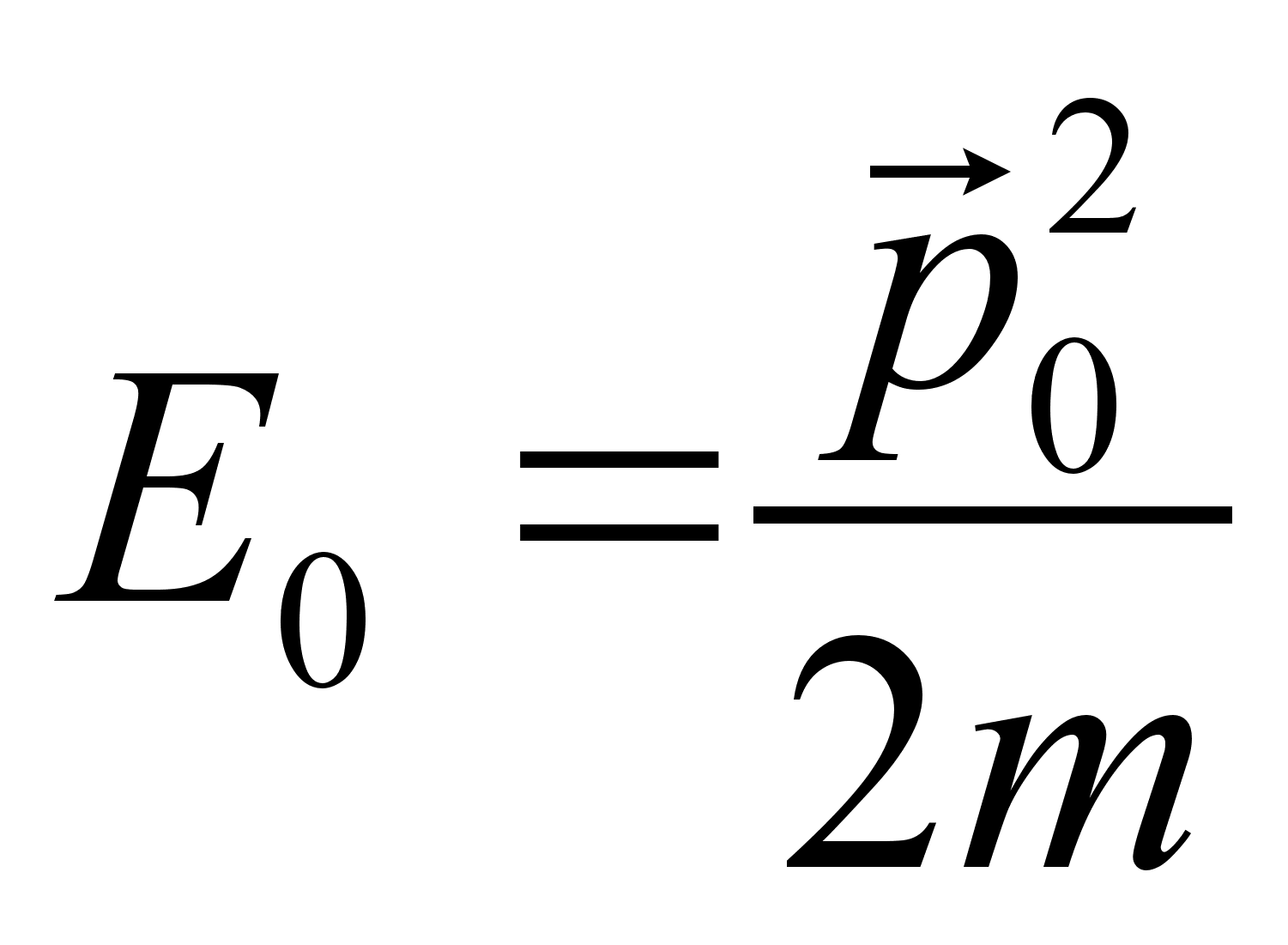
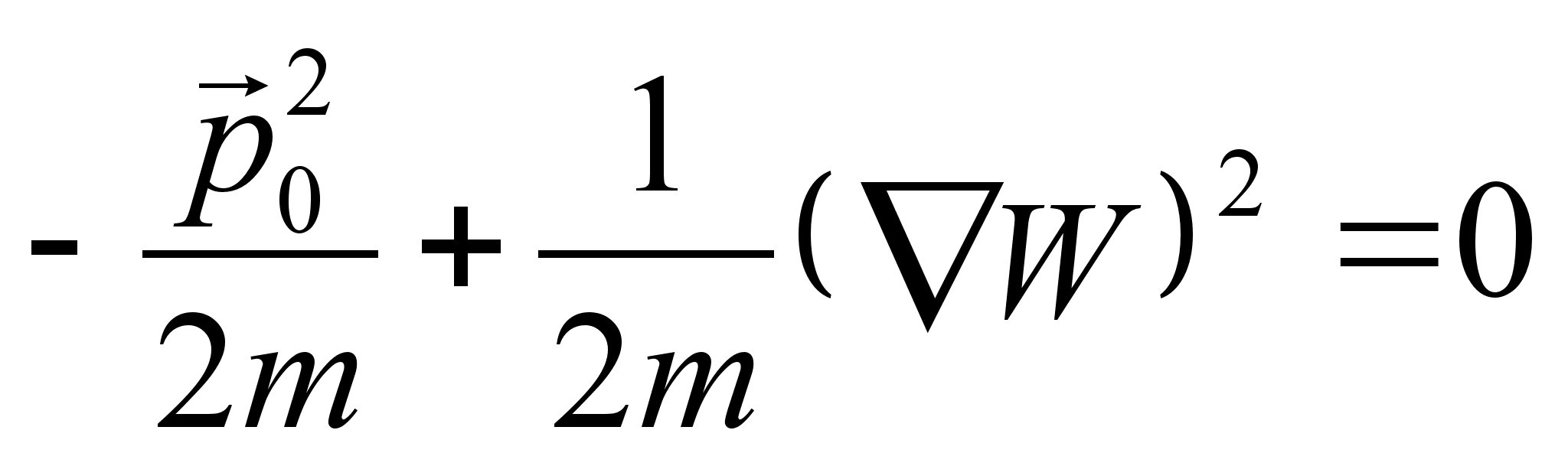
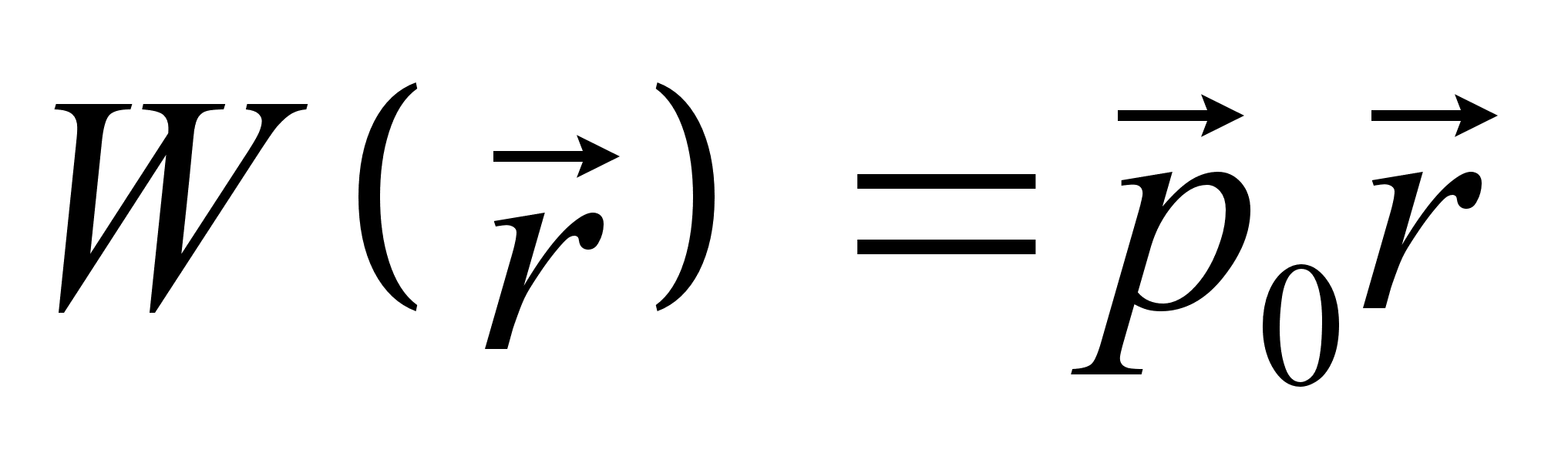
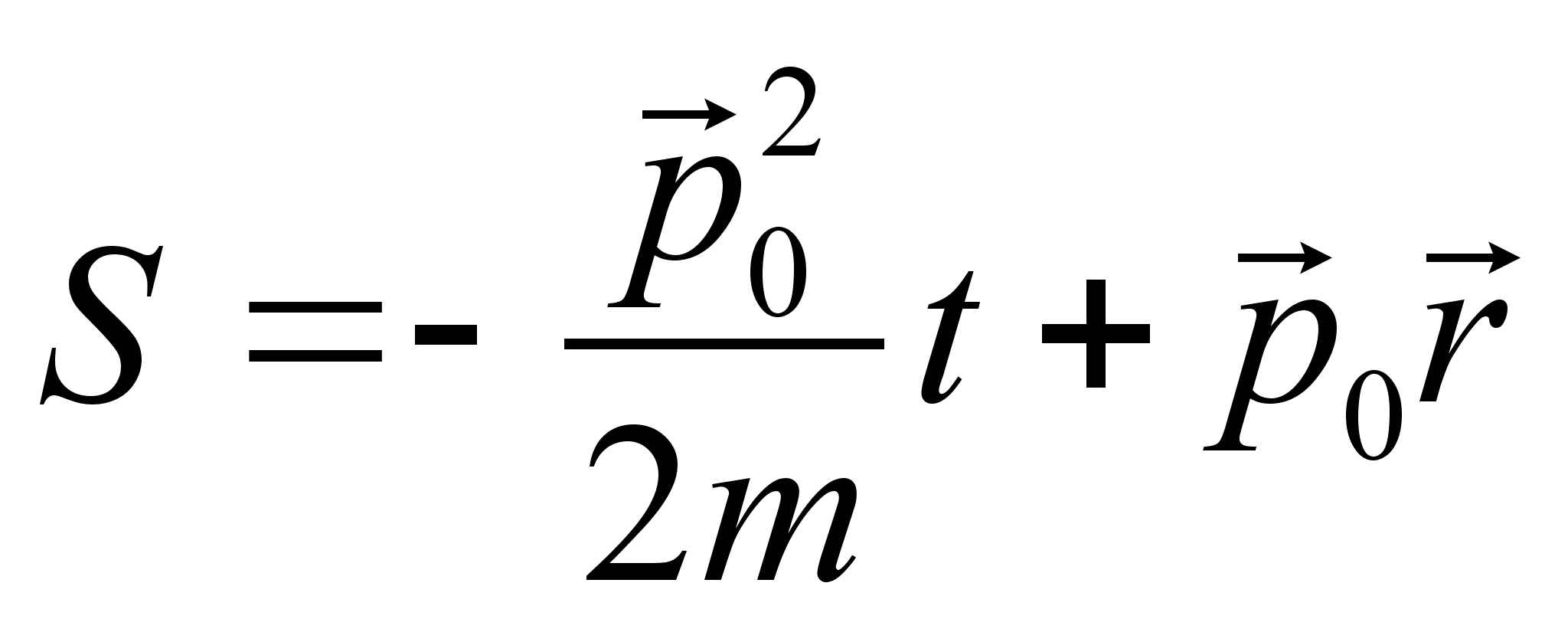
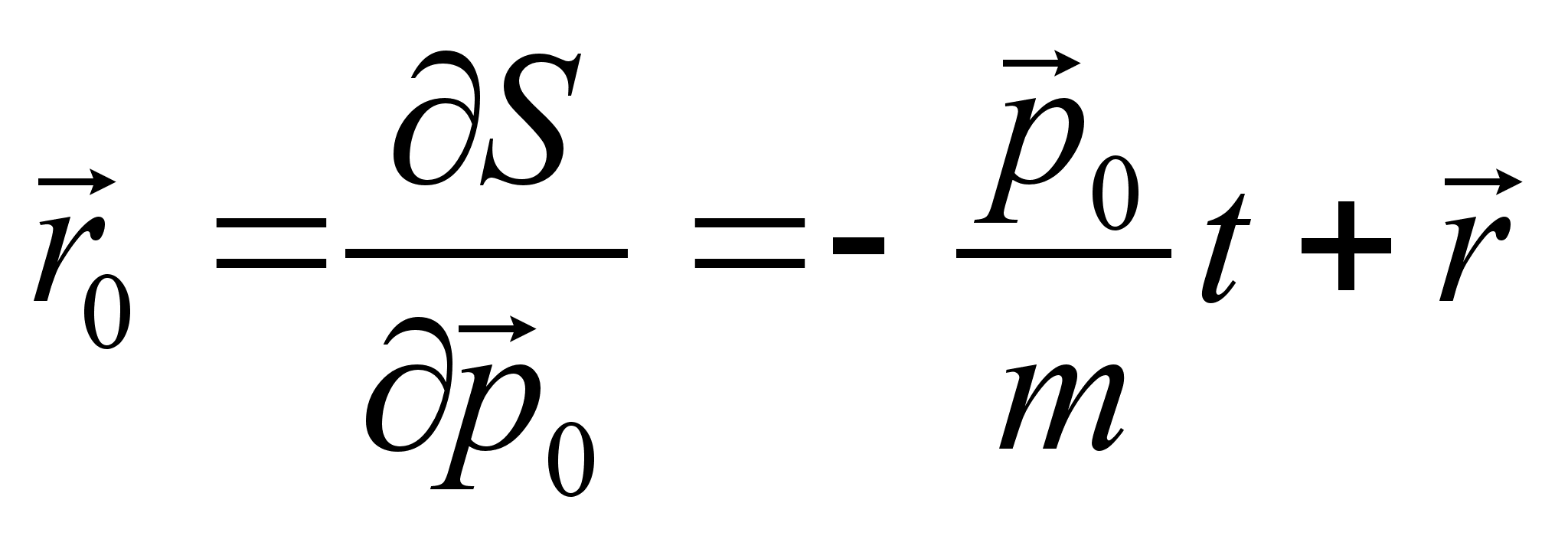
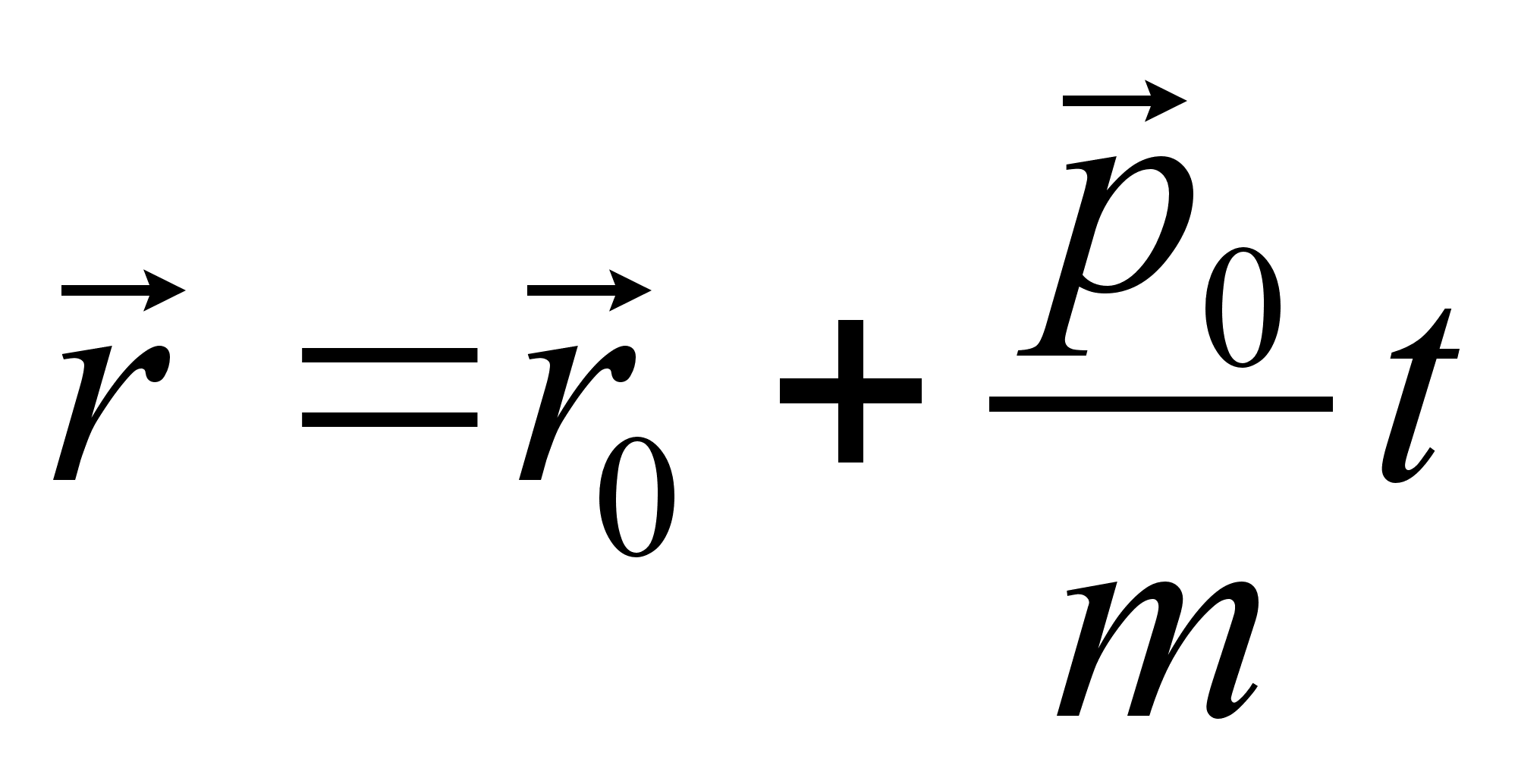
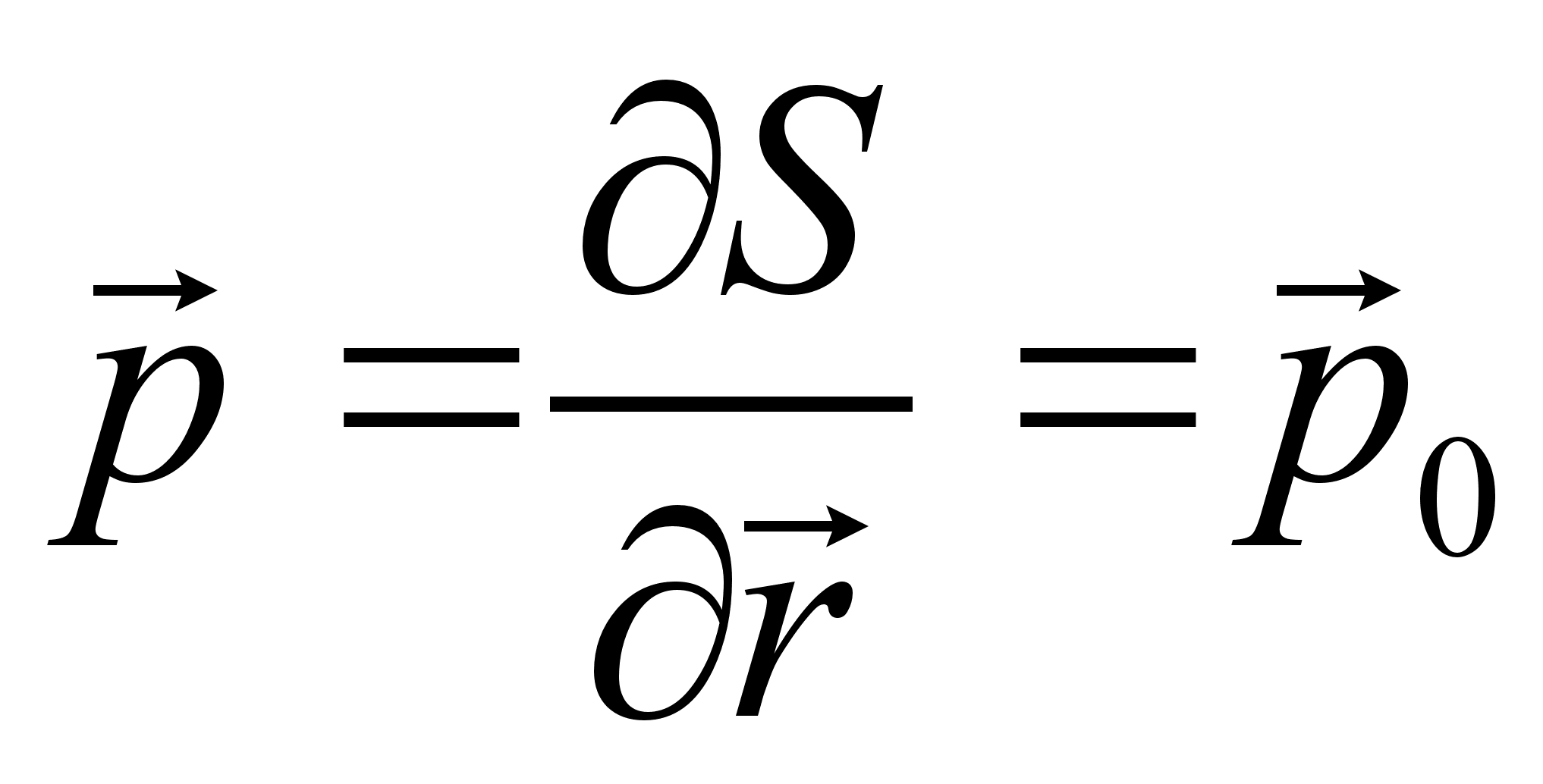
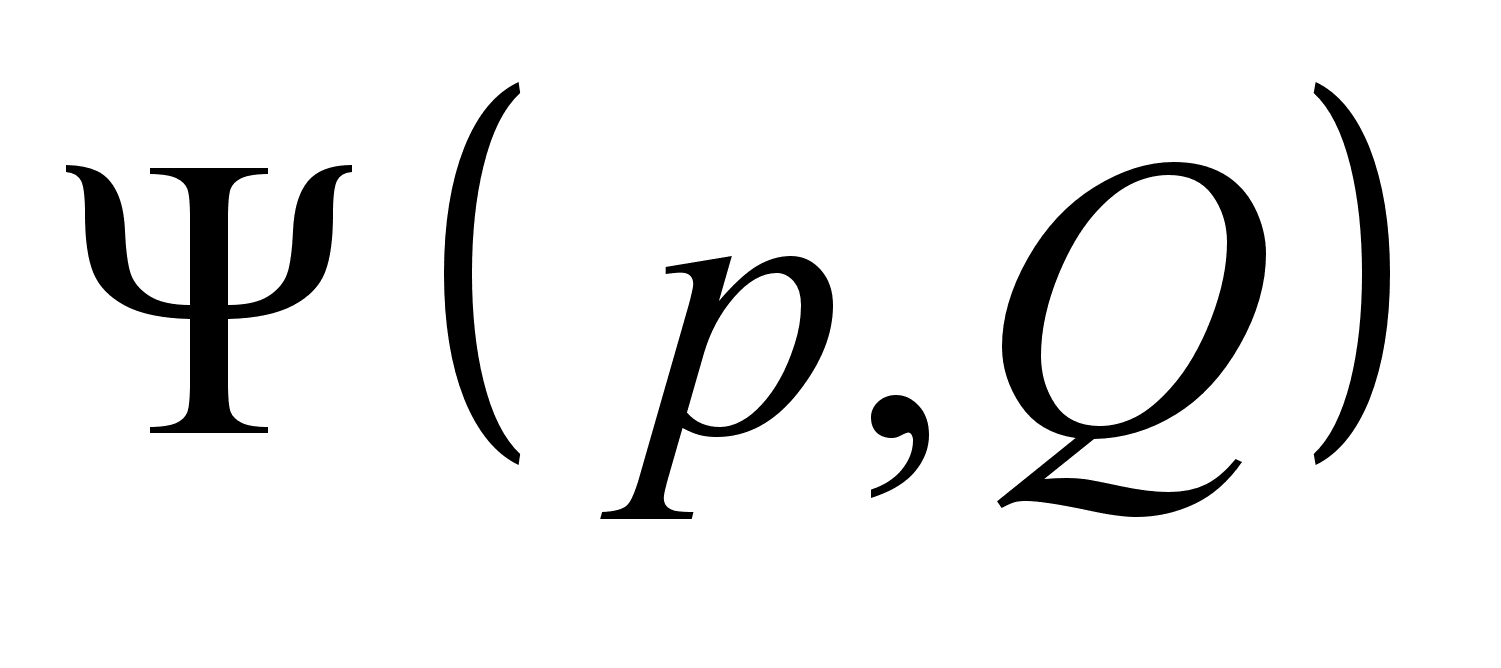 , приводящую к тому же каноническому преобразованию, что и
, приводящую к тому же каноническому преобразованию, что и 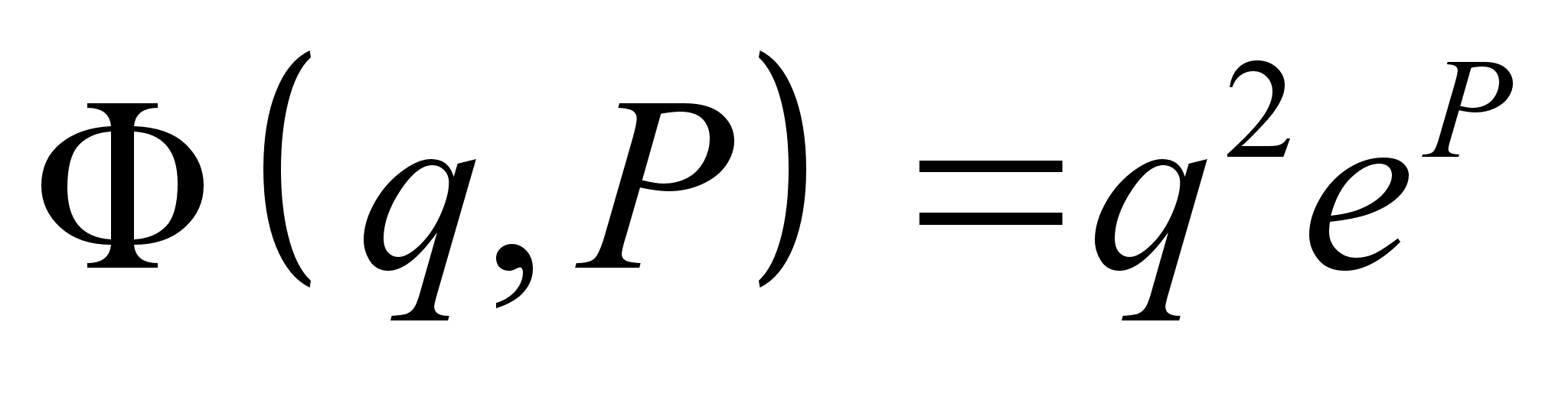 .
.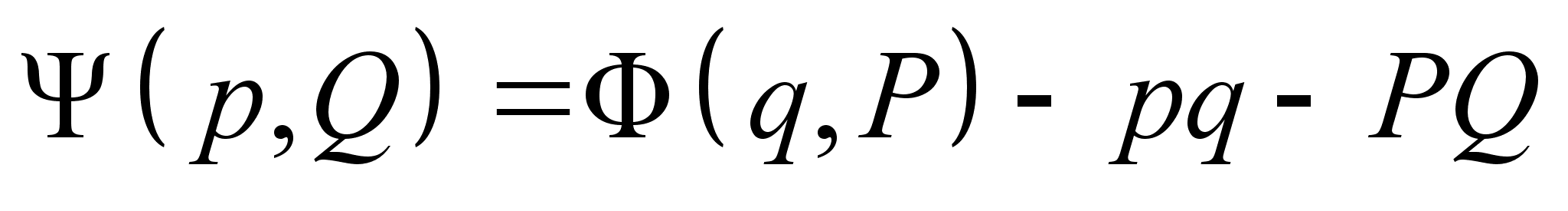
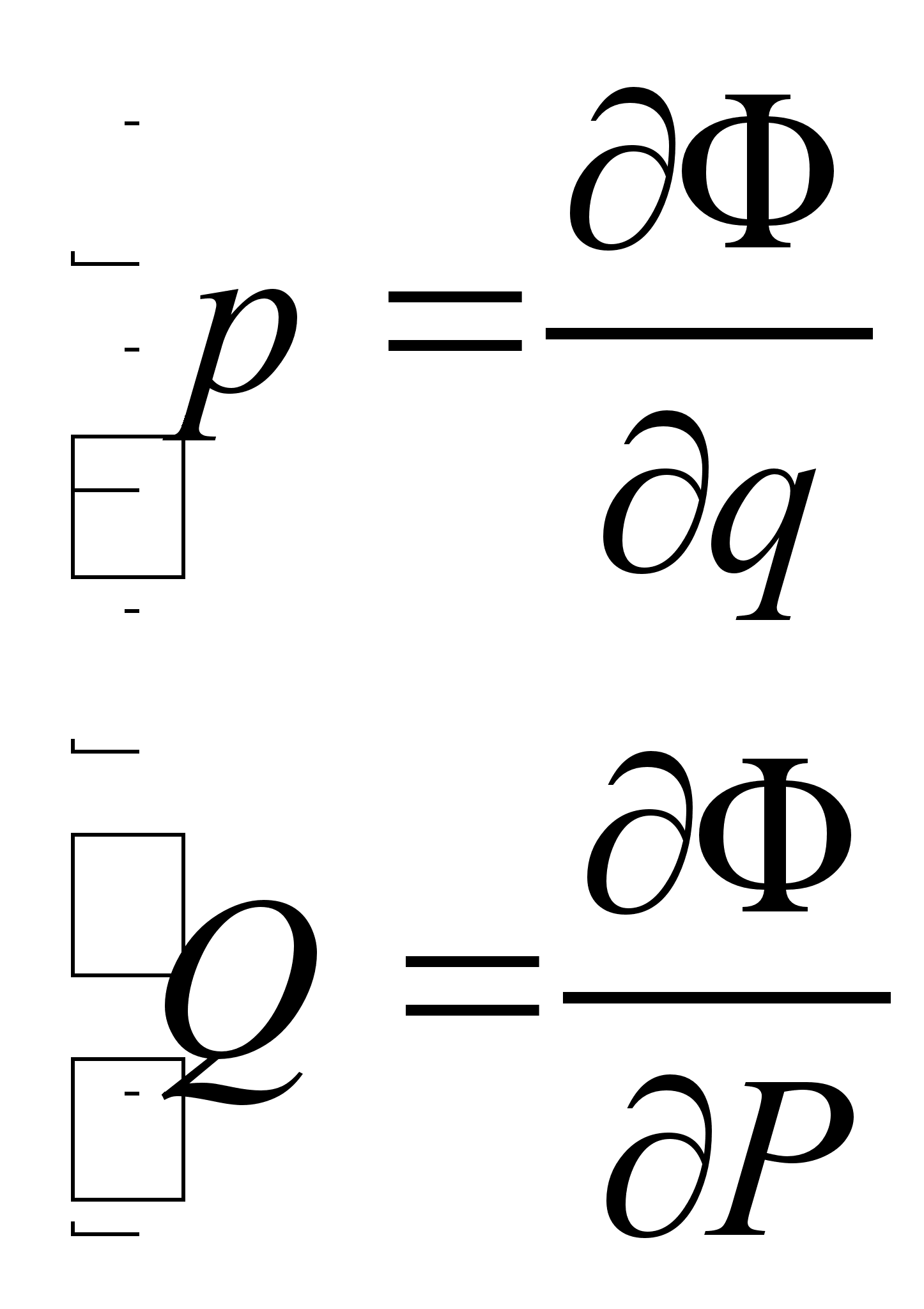
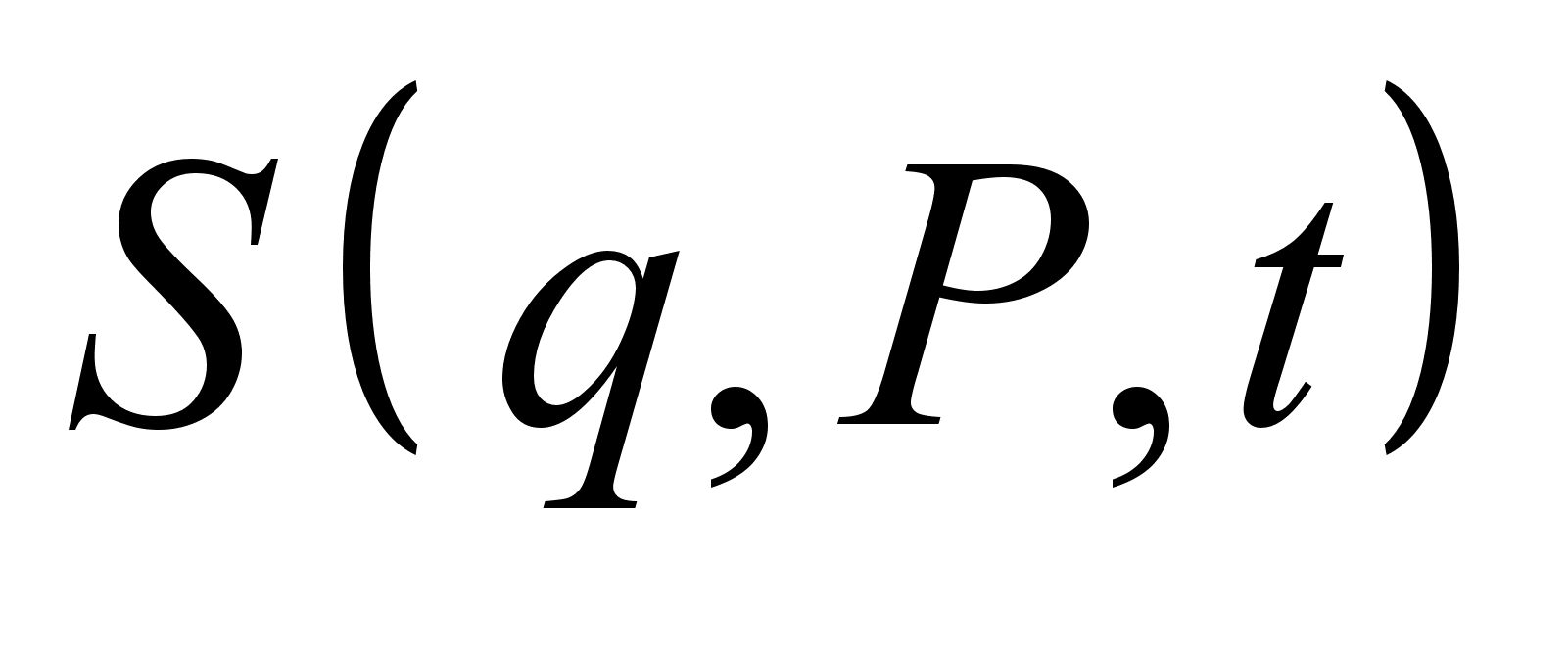 , порождающая каноническое преобразование к постоянным импульсам и координатам.
, порождающая каноническое преобразование к постоянным импульсам и координатам.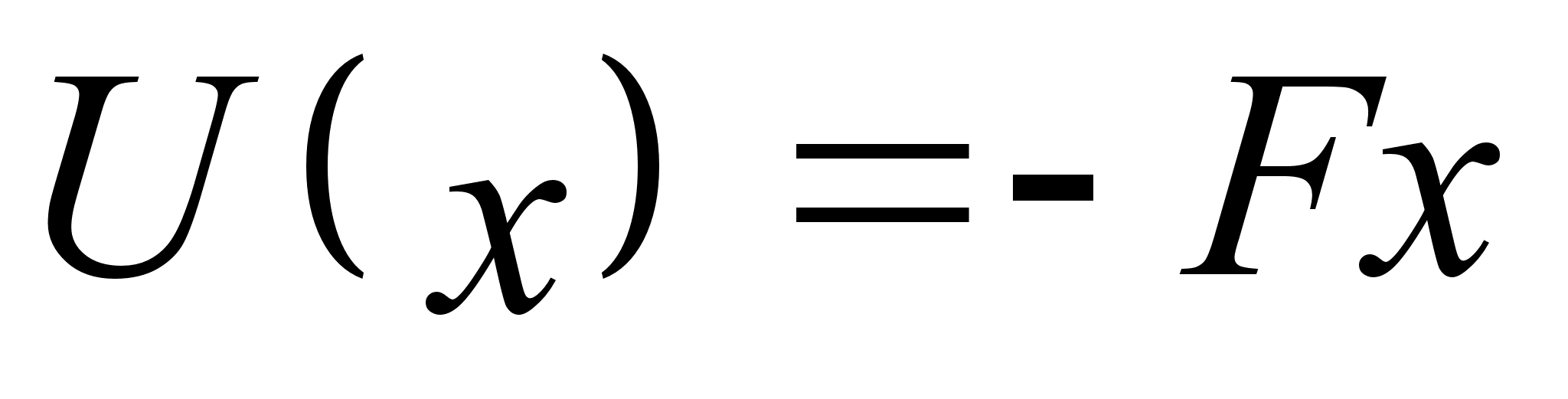
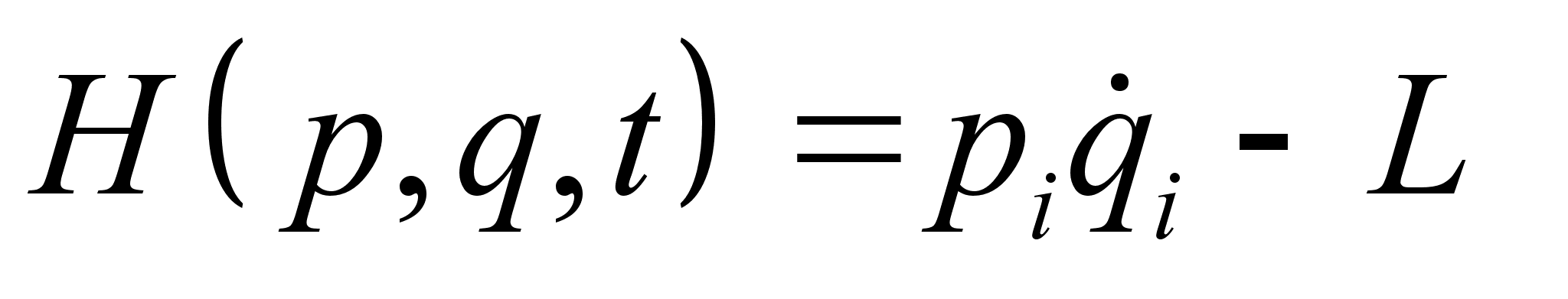
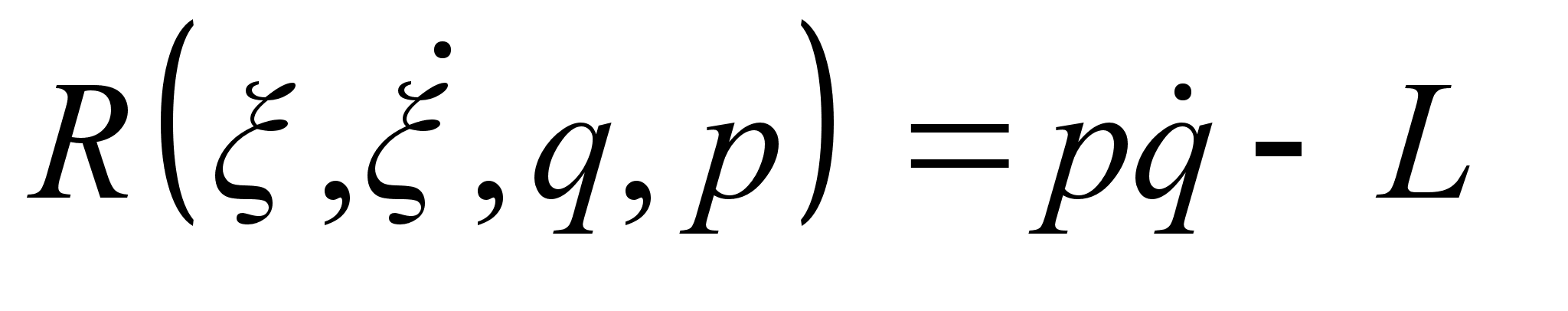
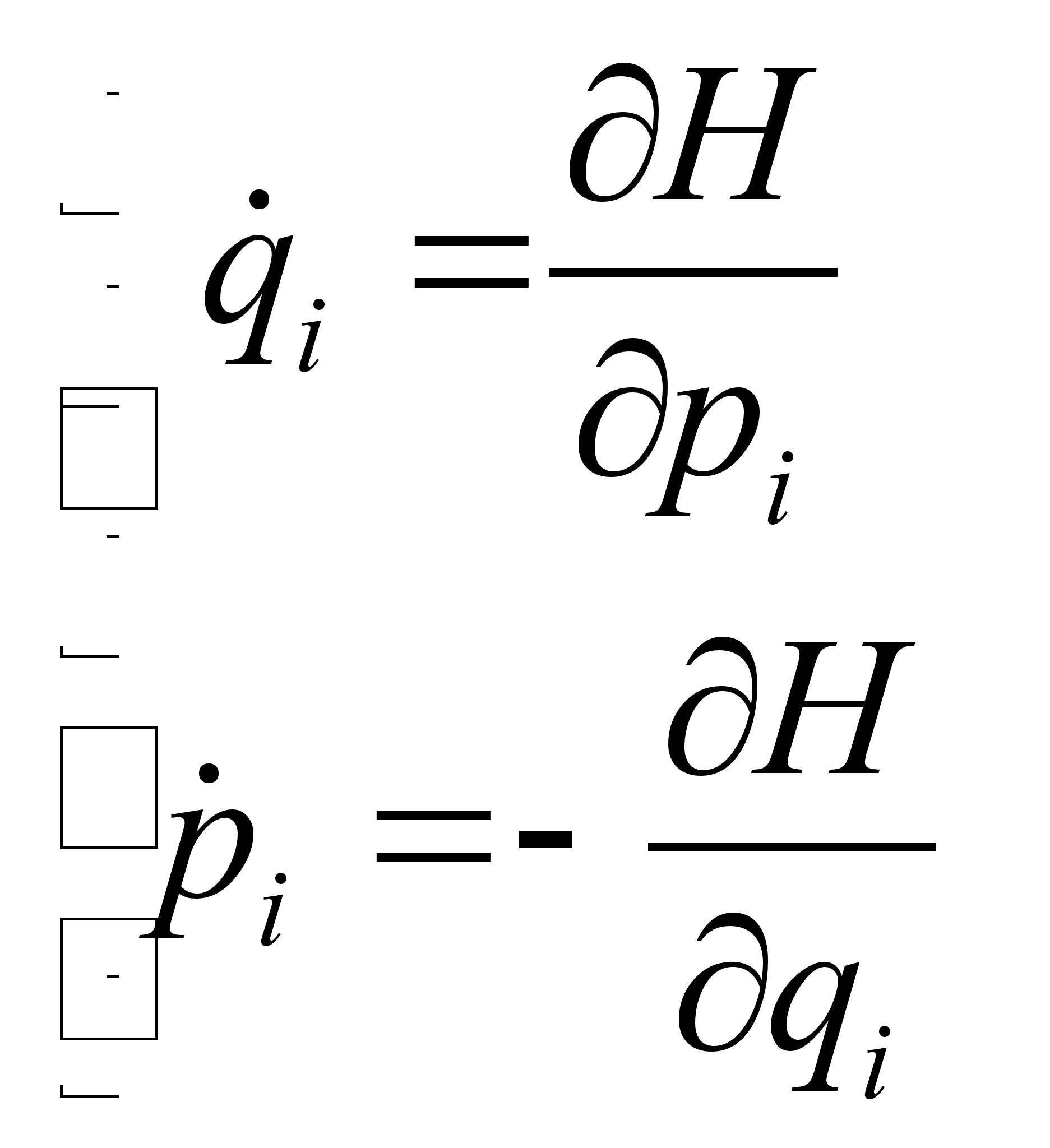
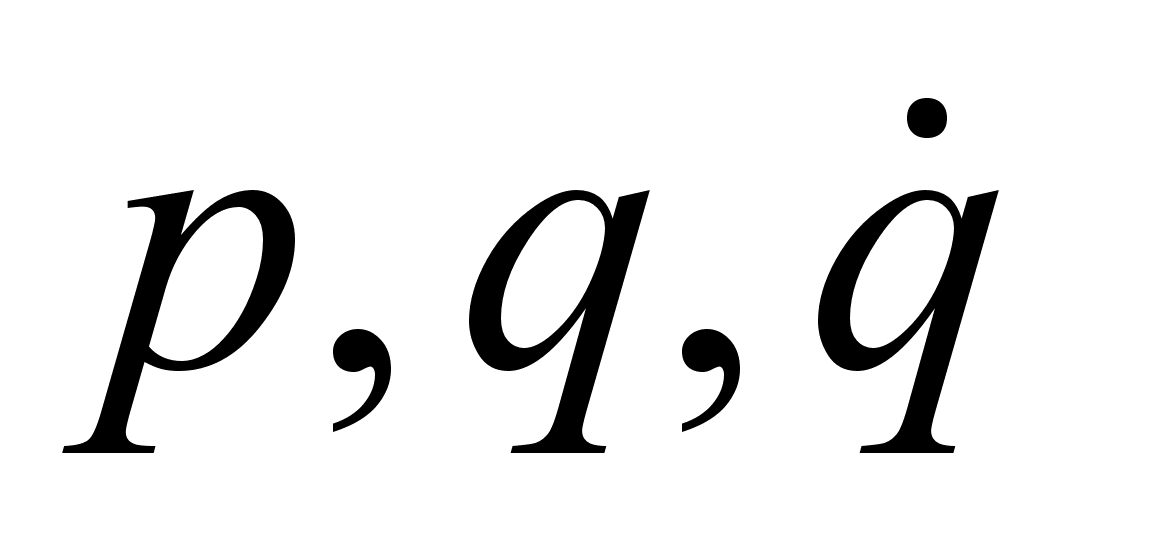 . А мы знаем, что функция Гамильтона
. А мы знаем, что функция Гамильтона 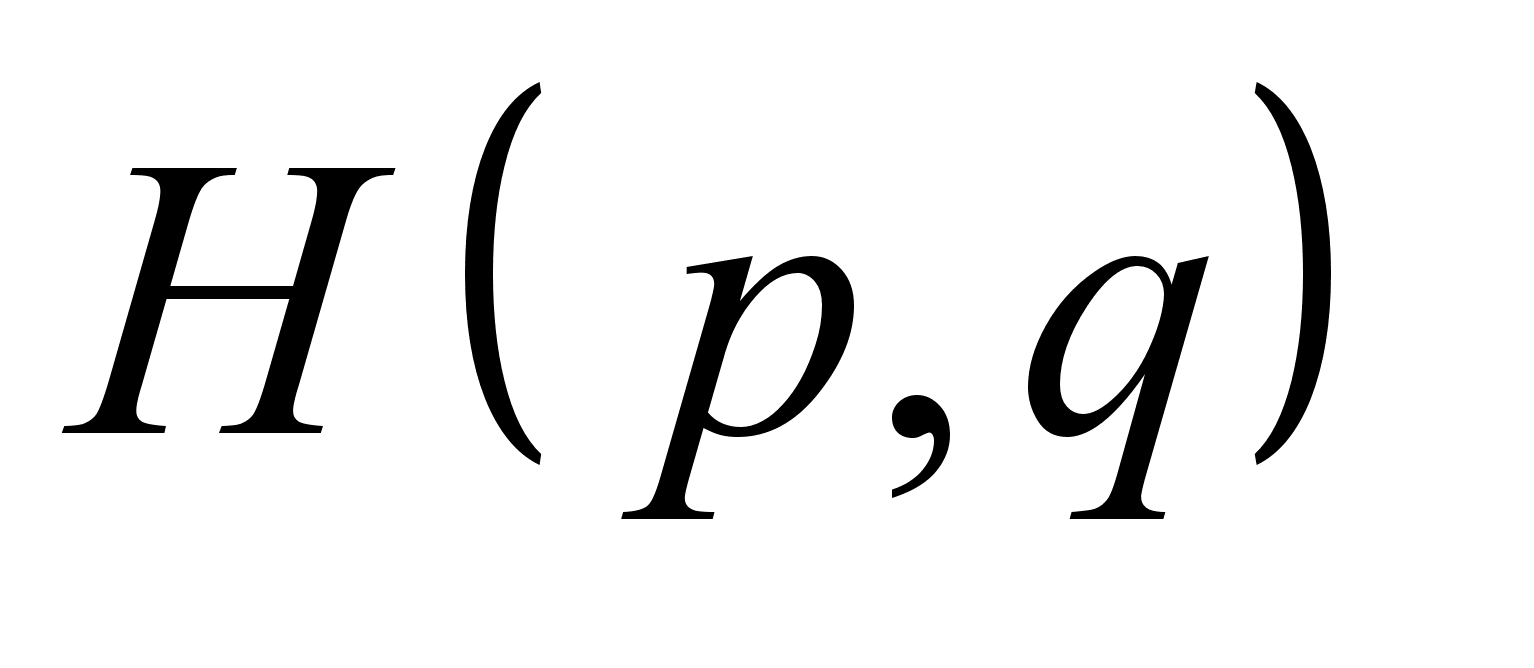 зависит только от
зависит только от 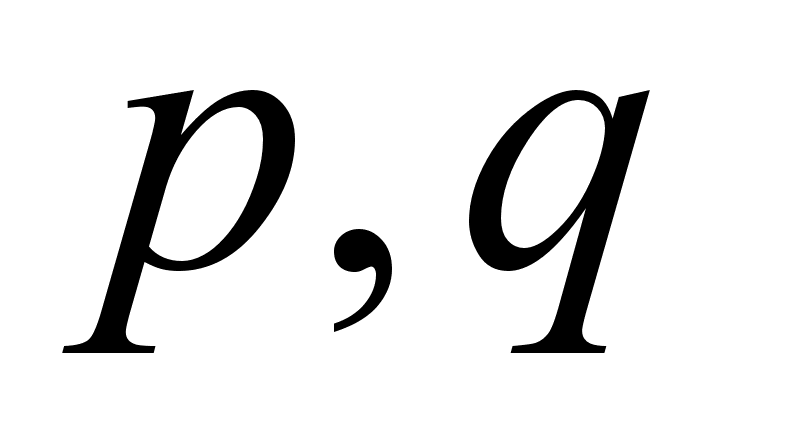 . Т.о. необходимо установить связь
. Т.о. необходимо установить связь 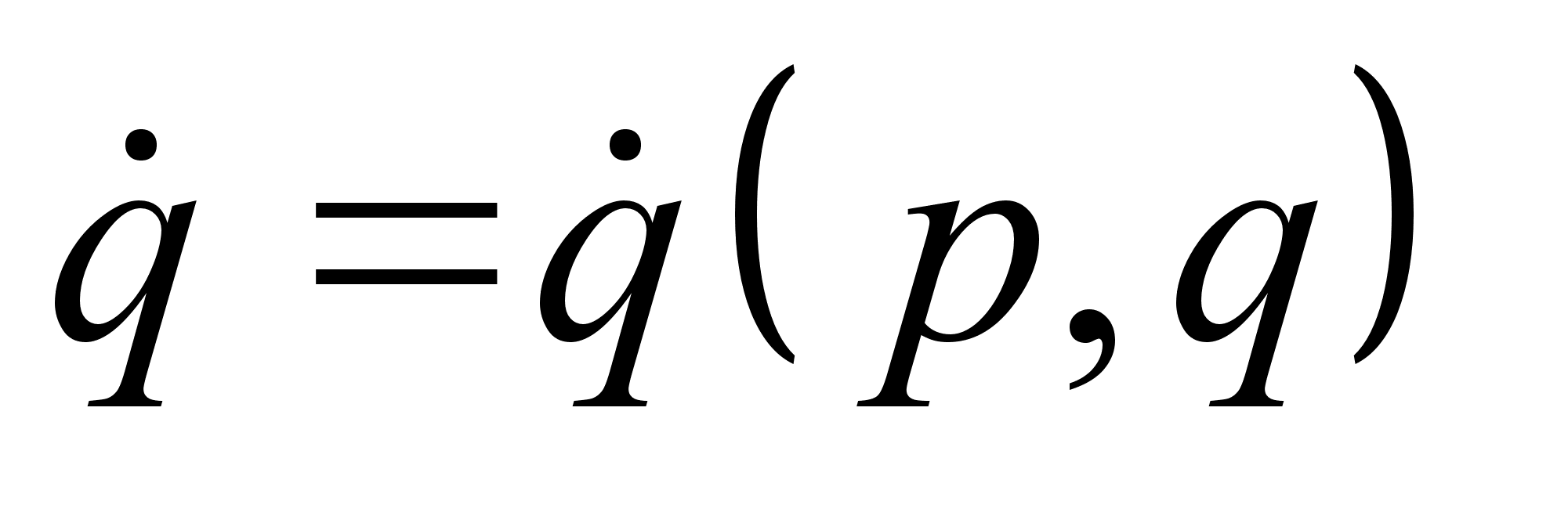 . Эту зависимость нам дает определение обобщенных импульсов:
. Эту зависимость нам дает определение обобщенных импульсов: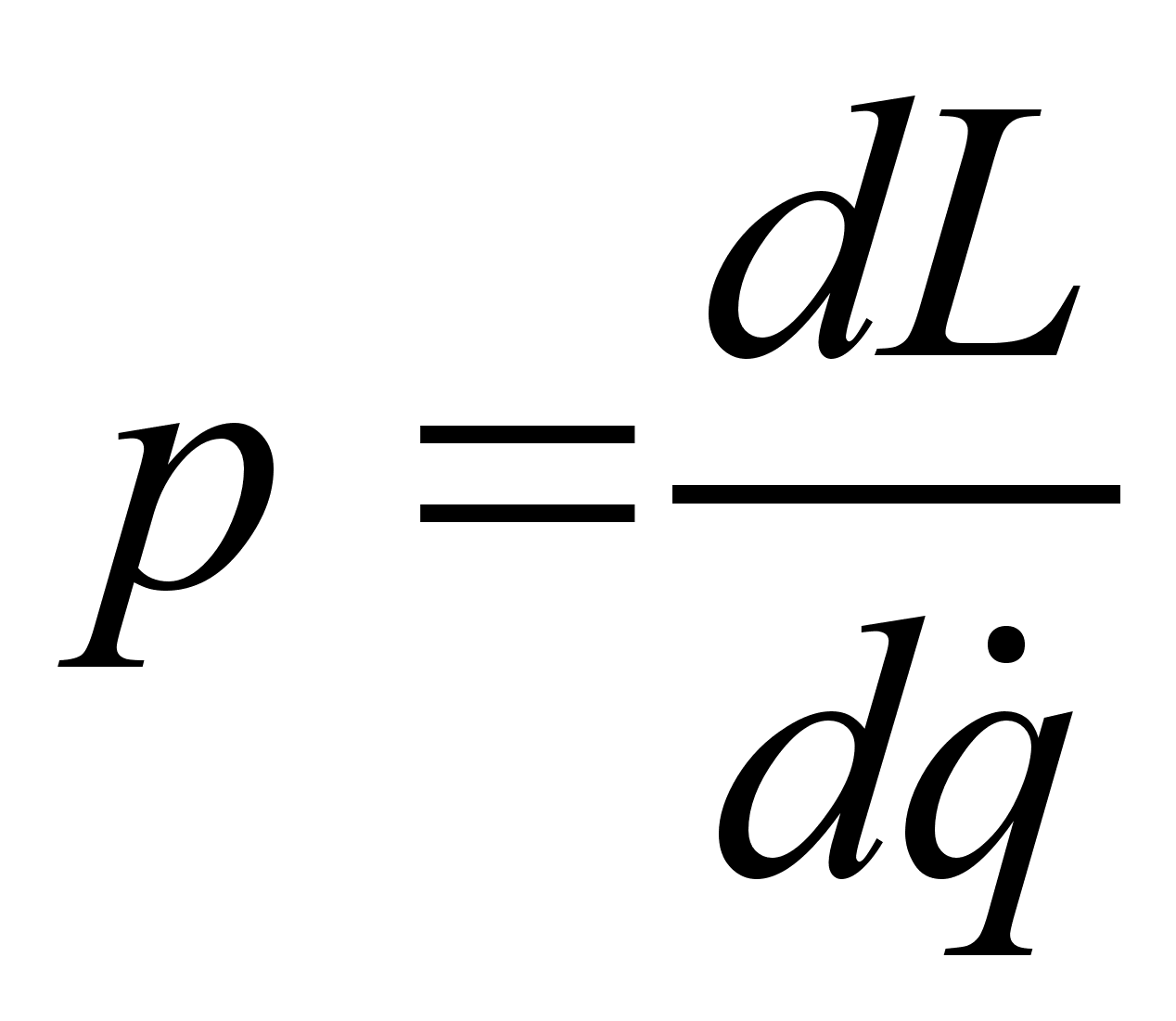
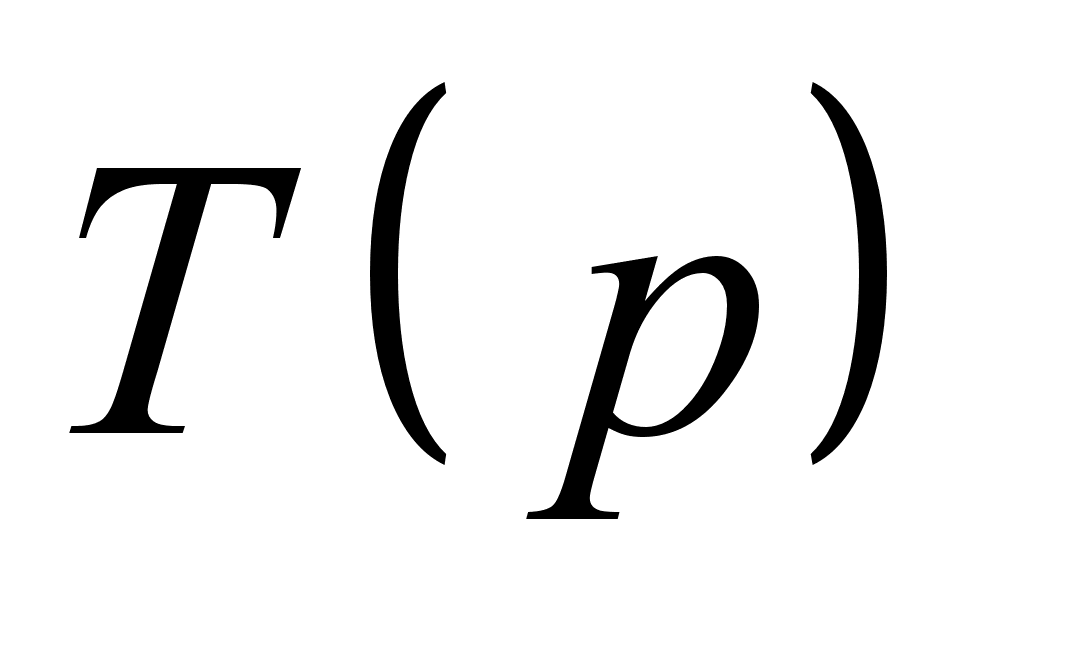 не известен, что является самым общим случаем, вид функции Гамильтона необходимо искать опираясь на ее определение. Т.е. через функцию Лагранжа. При этом нужно следовать следующей схеме:
не известен, что является самым общим случаем, вид функции Гамильтона необходимо искать опираясь на ее определение. Т.е. через функцию Лагранжа. При этом нужно следовать следующей схеме: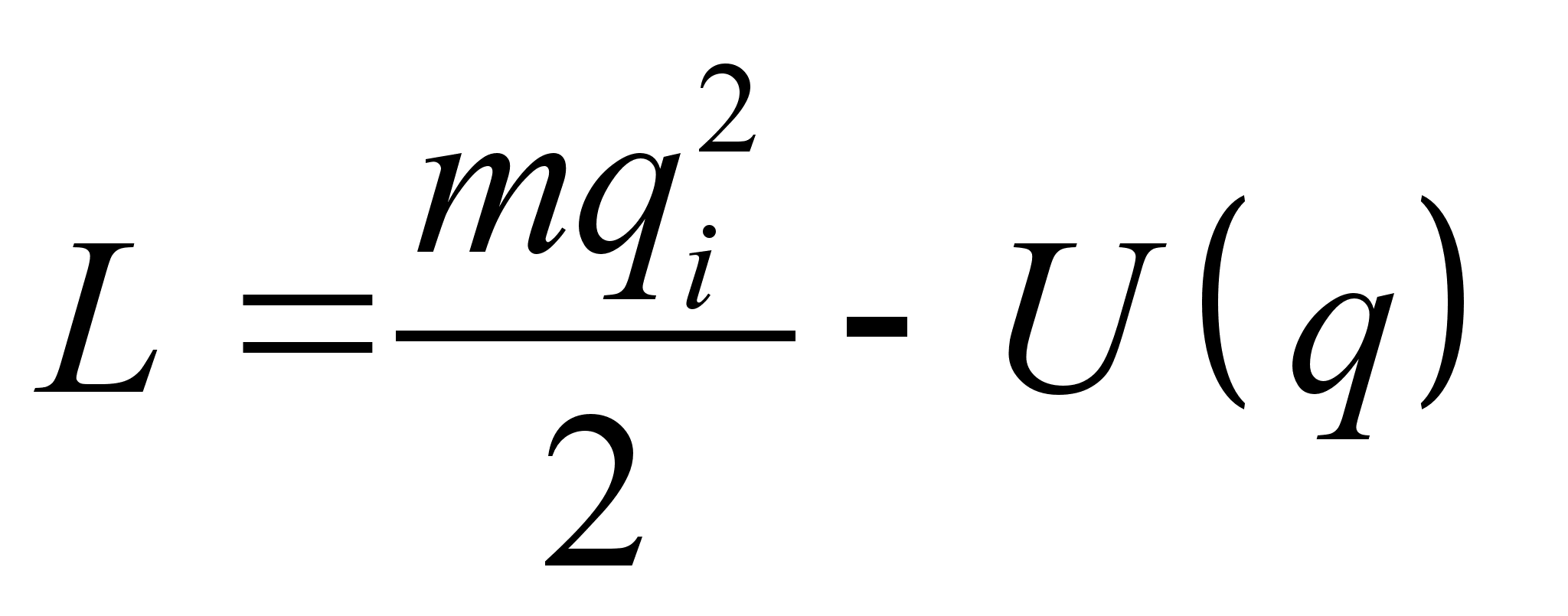
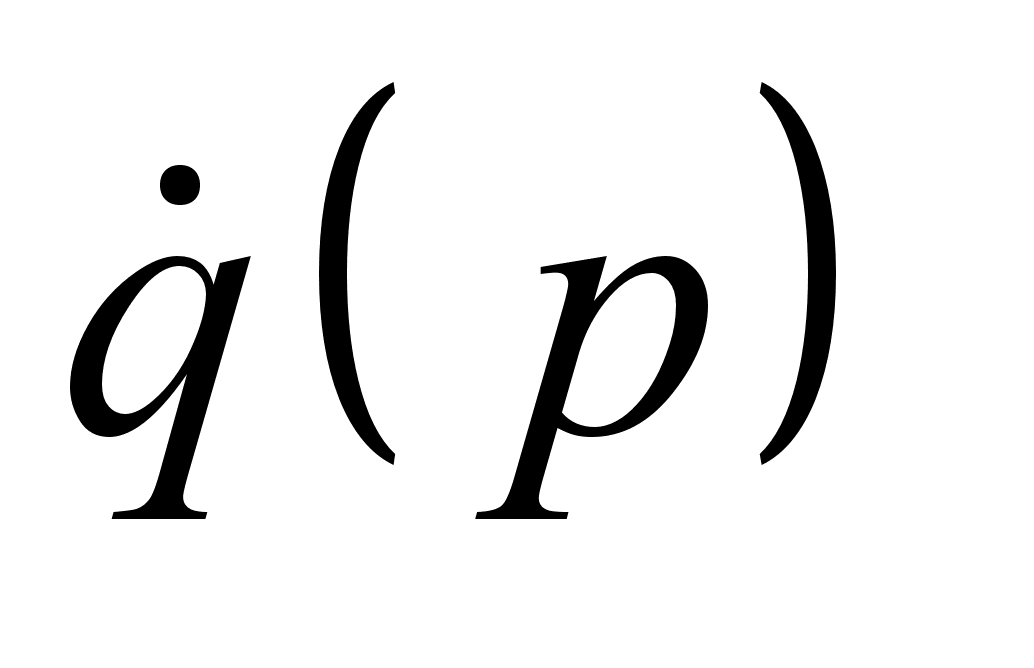
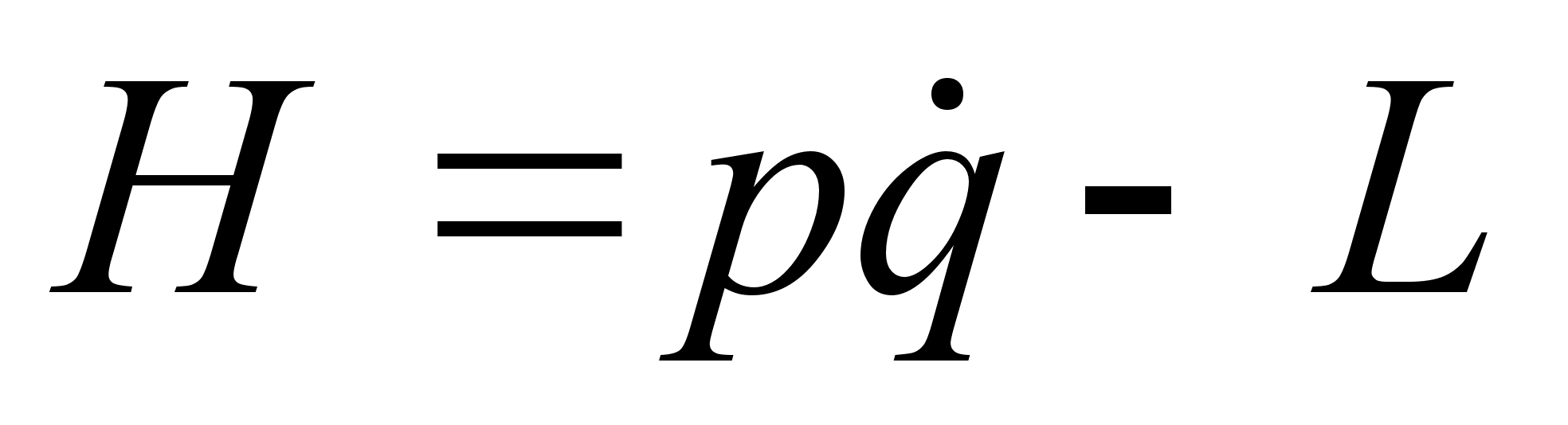
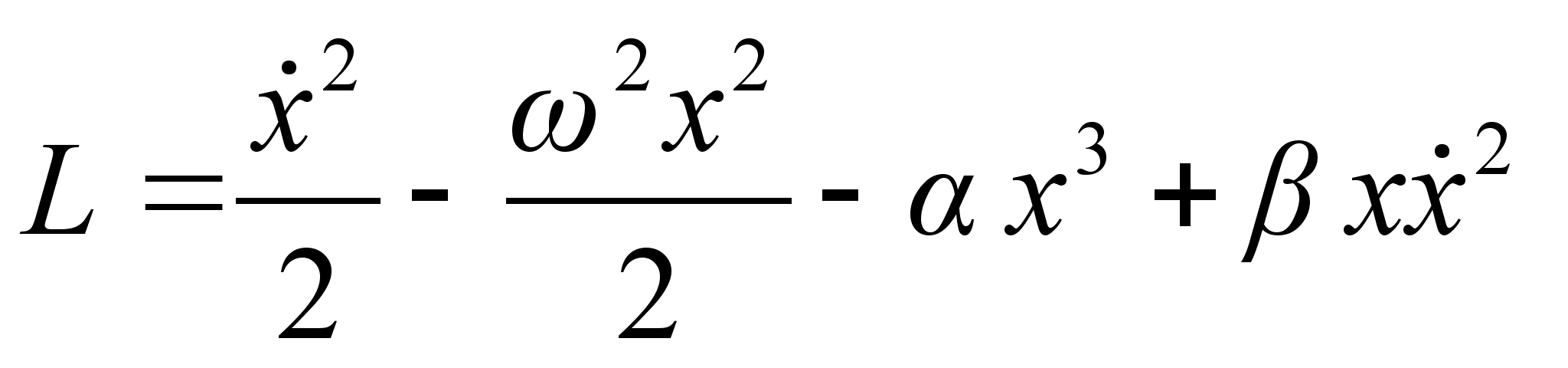
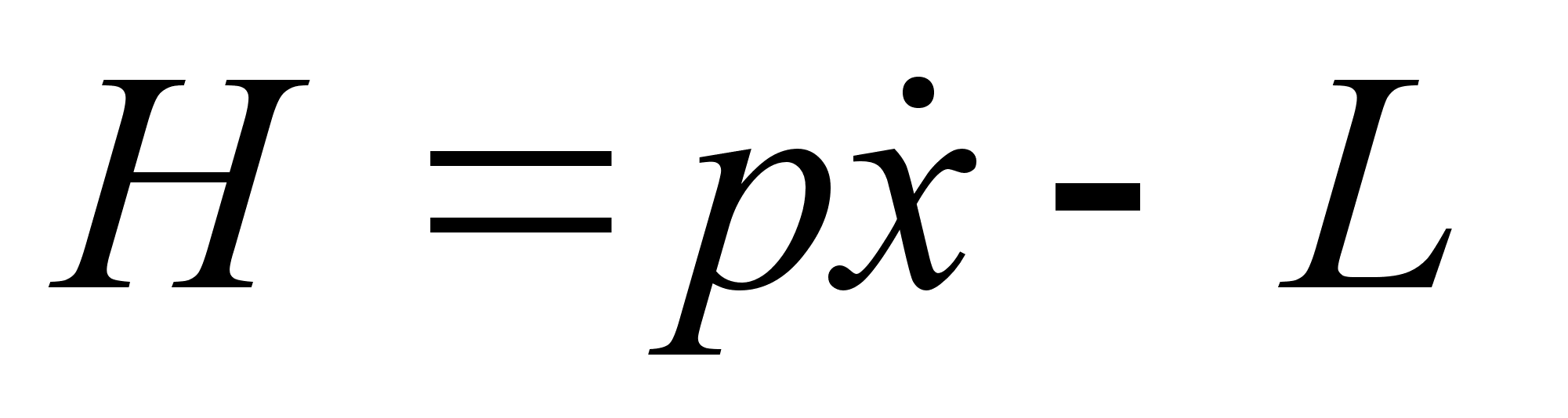
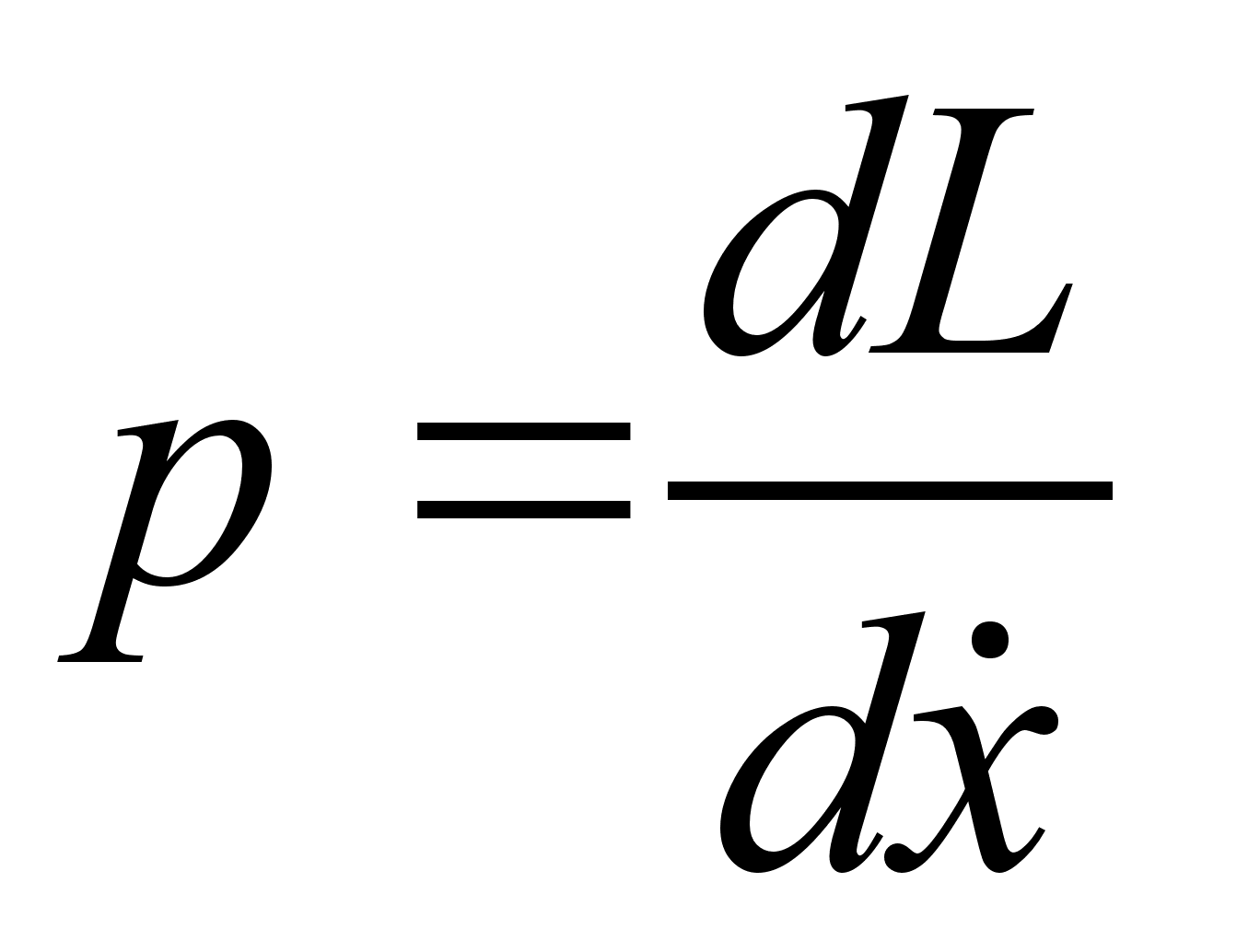
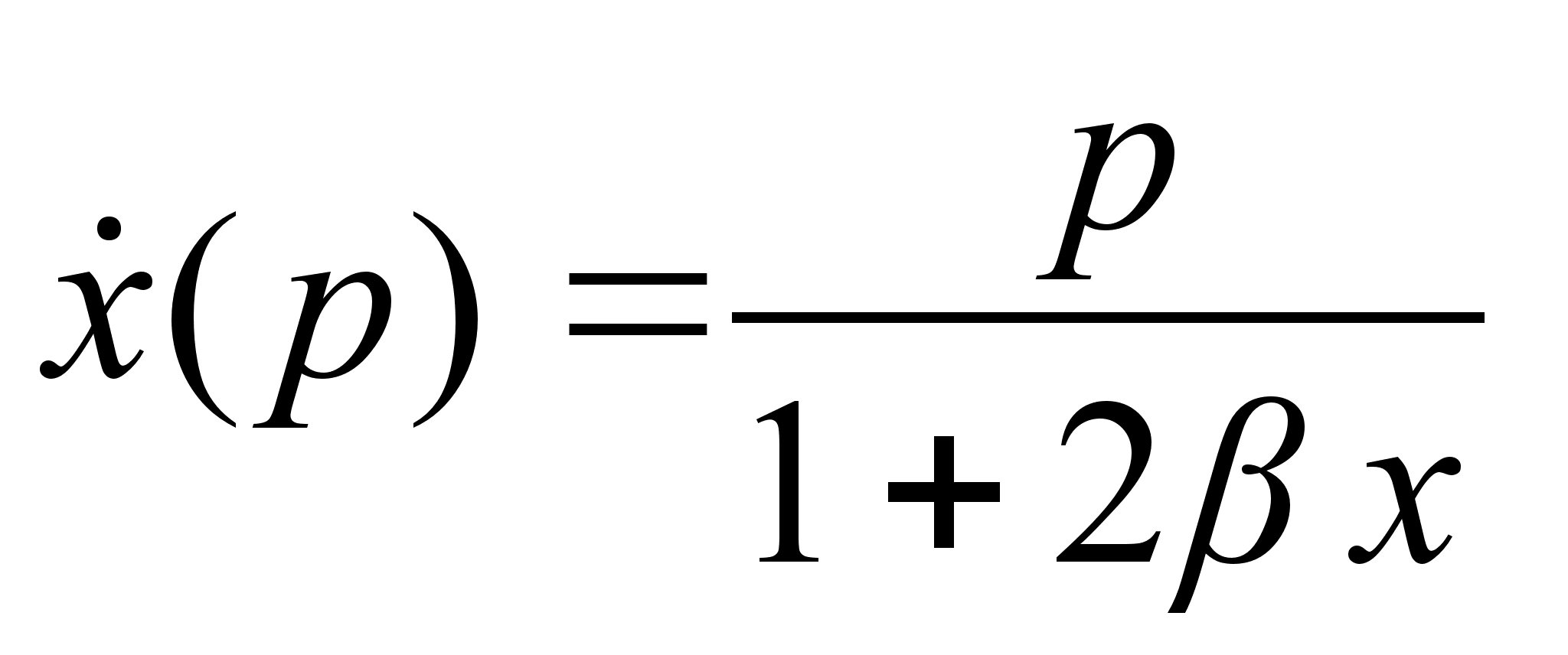
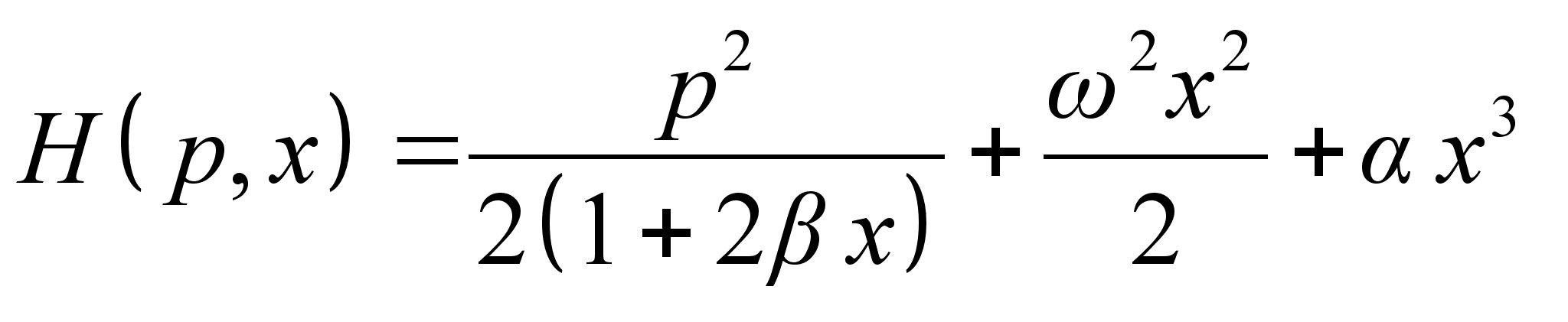
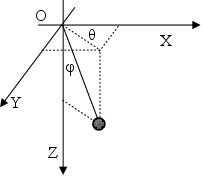 49.8 [] Материальная точка массы т подвешена с помощью стержня длины
49.8 [] Материальная точка массы т подвешена с помощью стержня длины 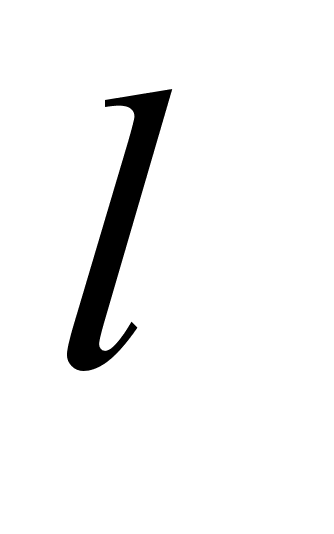 к плоскому шарниру, горизонтальная ось которого вращается вокруг вертикали с постоянной угловой скоростью
к плоскому шарниру, горизонтальная ось которого вращается вокруг вертикали с постоянной угловой скоростью 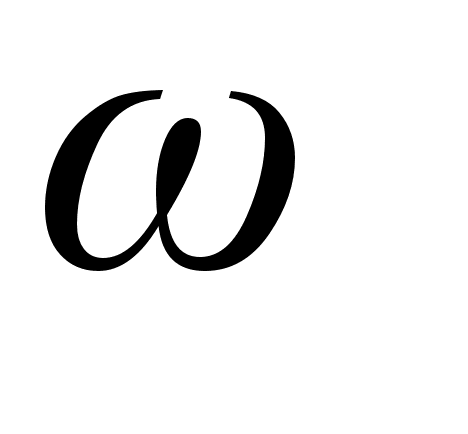 . Составить а) функцию Гамильтона и б) канонические уравнения движения. Массу стержня не учитывать.
. Составить а) функцию Гамильтона и б) канонические уравнения движения. Массу стержня не учитывать.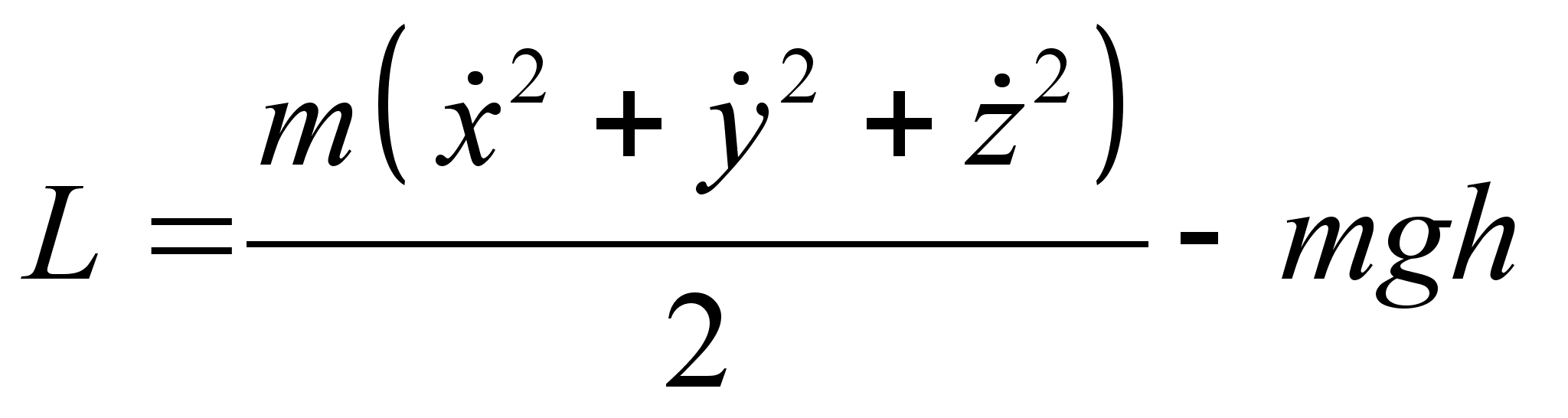
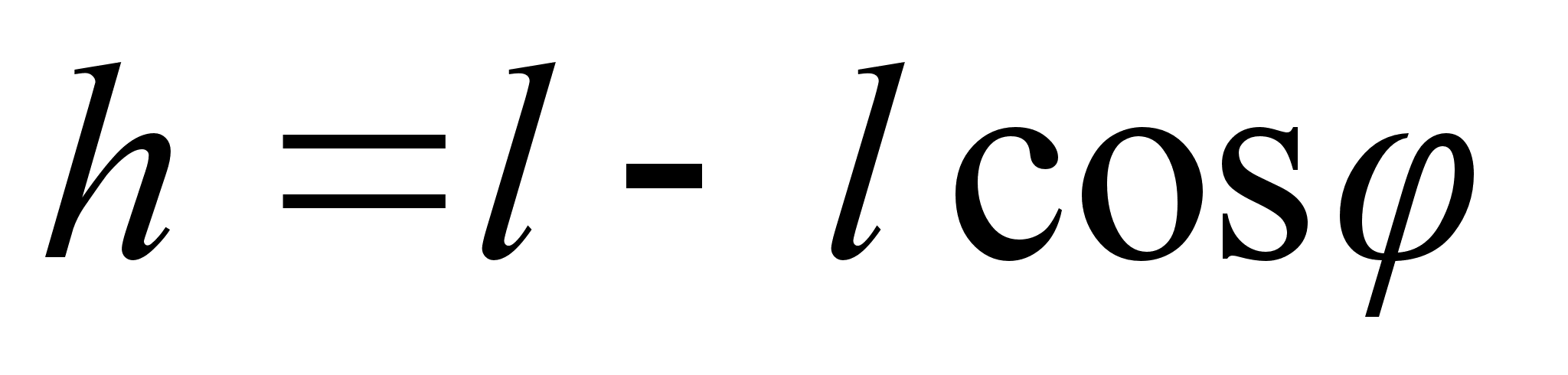 . Поскольку функция Лагранжа определена с точностью до аддитивной константы, либо постоянного множителя, перепишем в виде:
. Поскольку функция Лагранжа определена с точностью до аддитивной константы, либо постоянного множителя, перепишем в виде: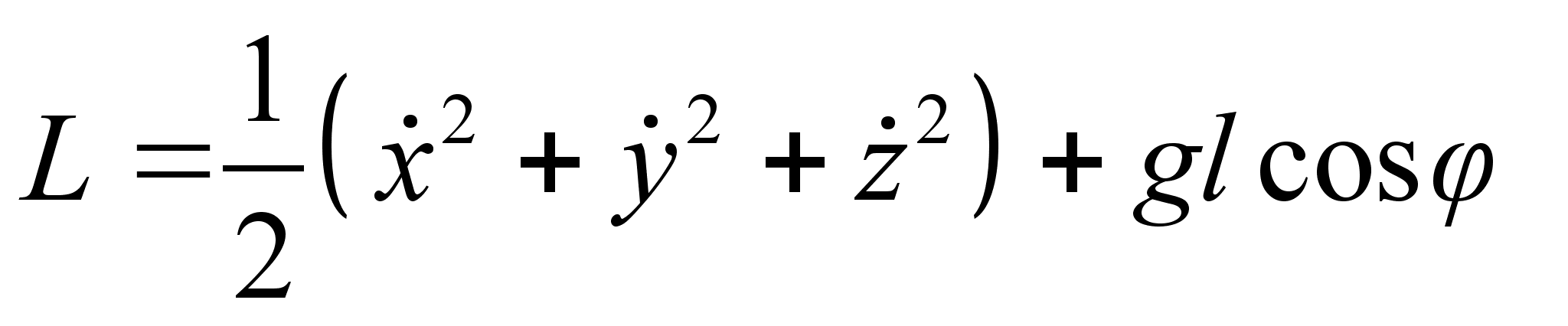
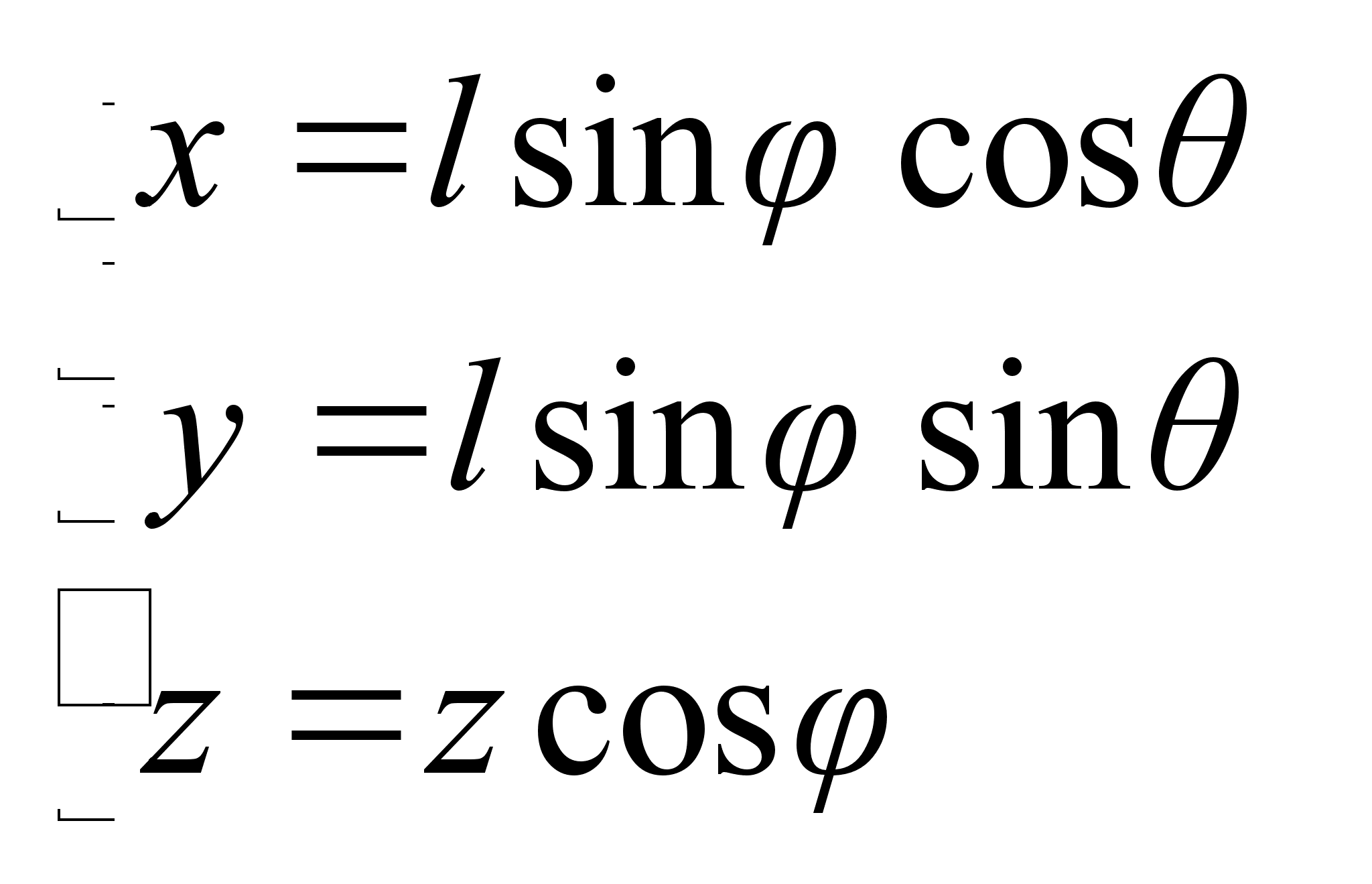
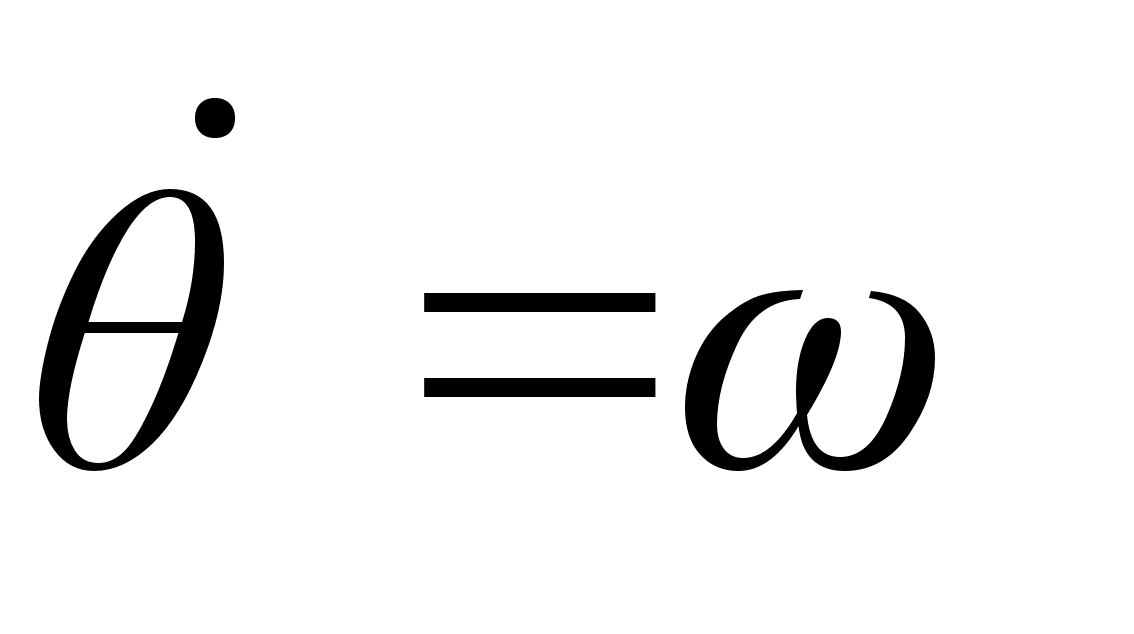 – по условию, получим выражение для функции Лагранжа с новой обобщенной координатой
– по условию, получим выражение для функции Лагранжа с новой обобщенной координатой  :
: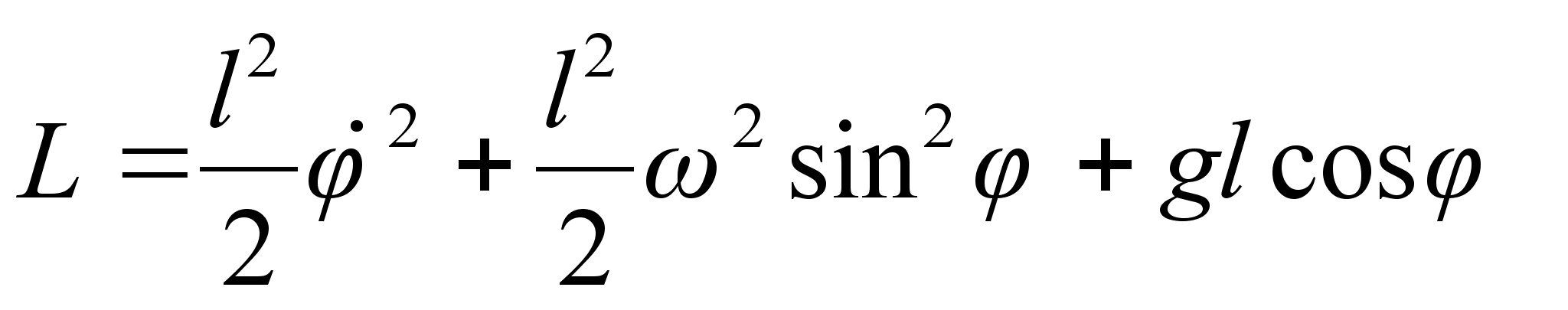
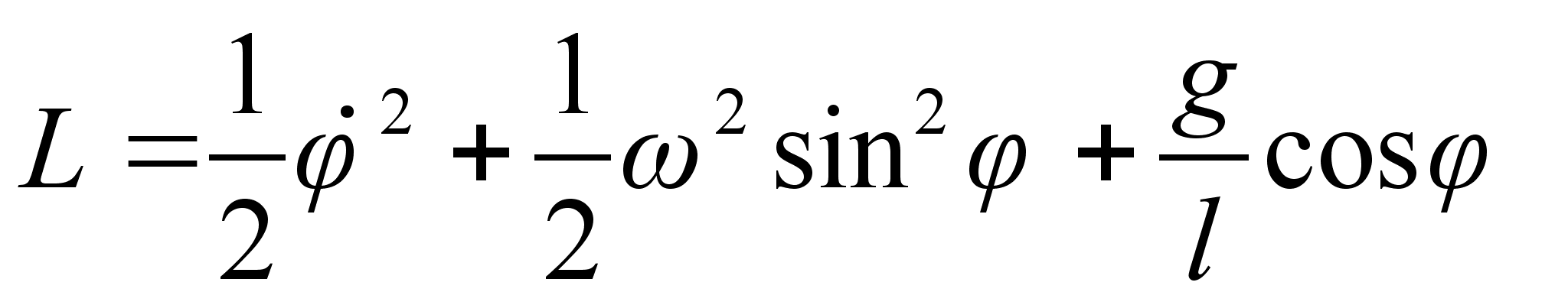
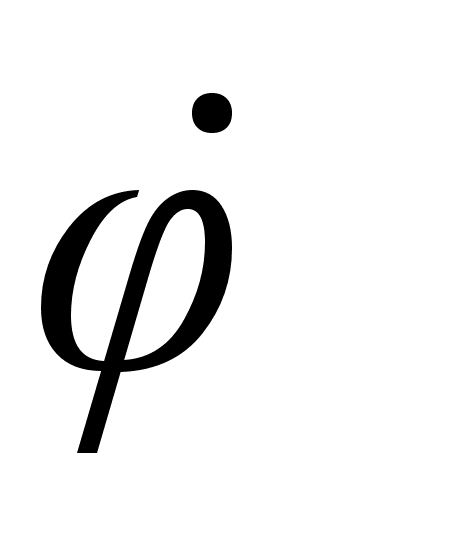 от обобщенного импульса системы. По определению обобщенных импульсов:
от обобщенного импульса системы. По определению обобщенных импульсов: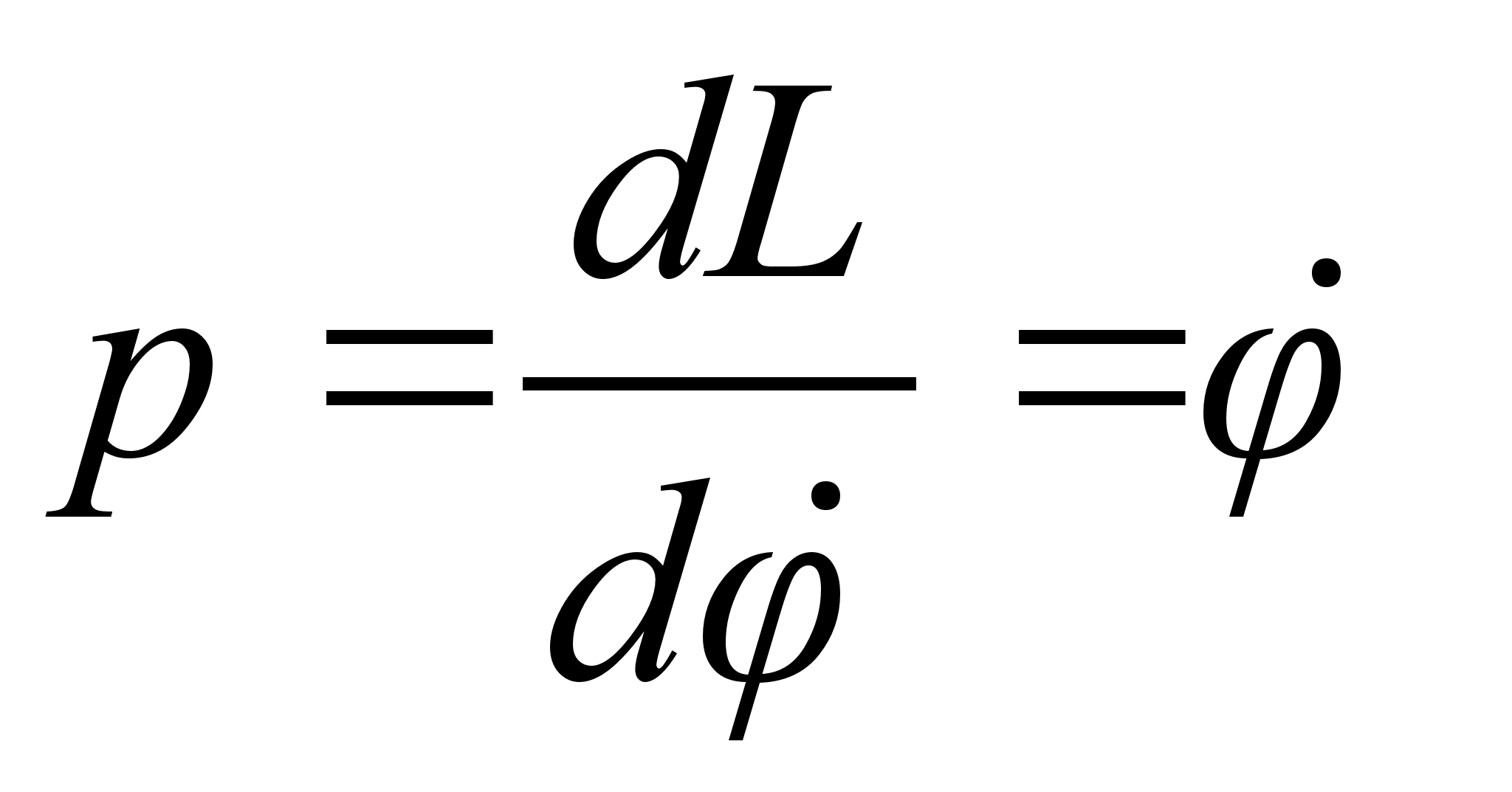
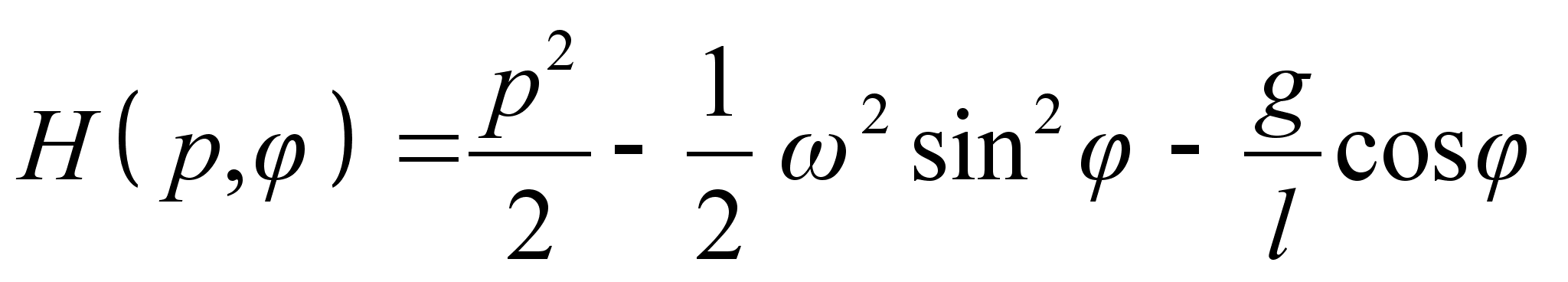
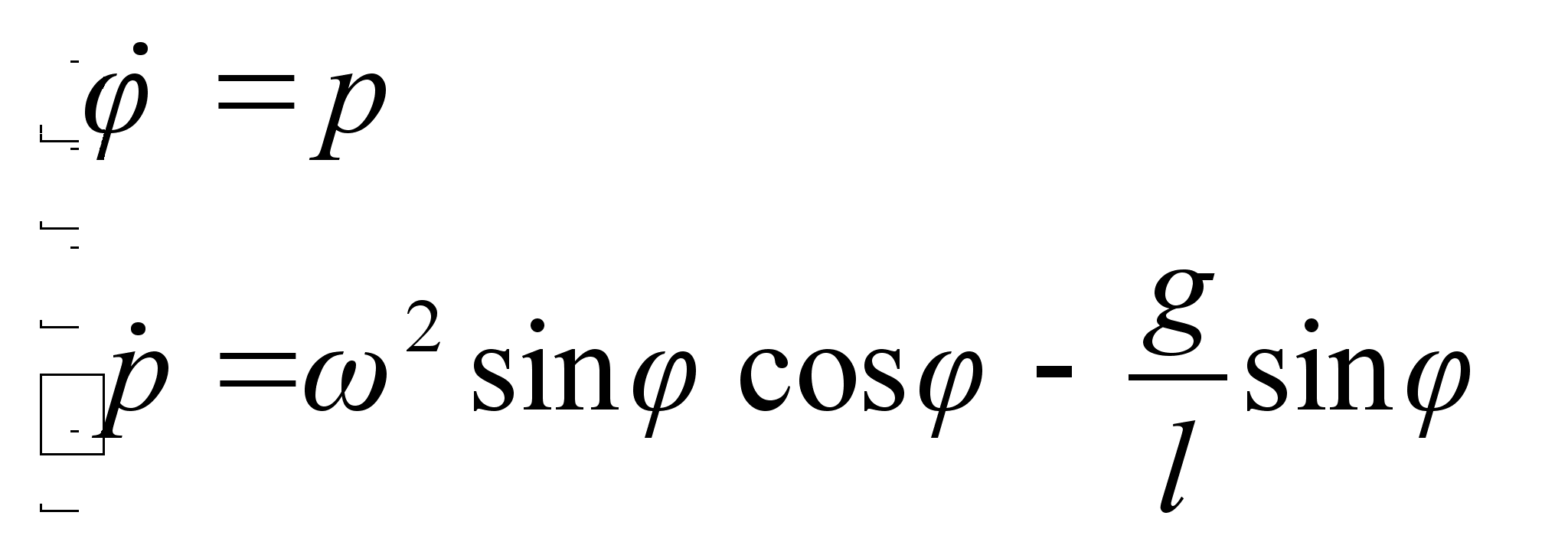
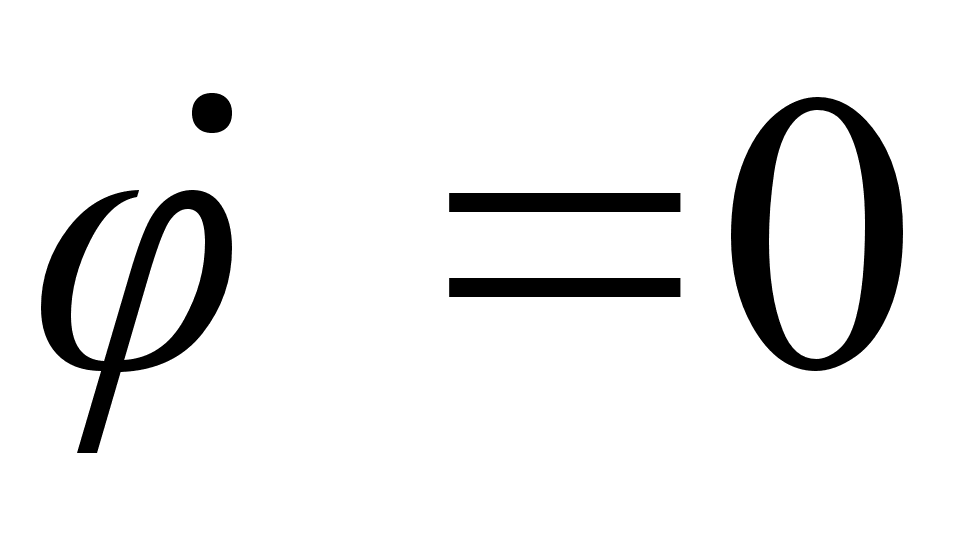 , т.е. шарик движется в горизонтальной плоскости, описывая окружность. Логично предположить, что такое движение будет выполняться лишь при некотором фиксированном угле
, т.е. шарик движется в горизонтальной плоскости, описывая окружность. Логично предположить, что такое движение будет выполняться лишь при некотором фиксированном угле 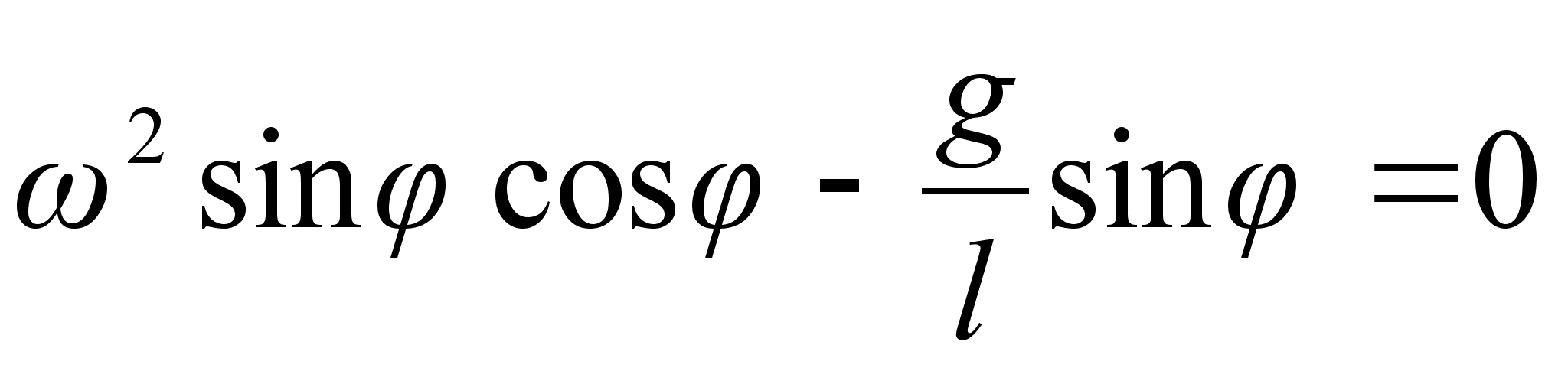
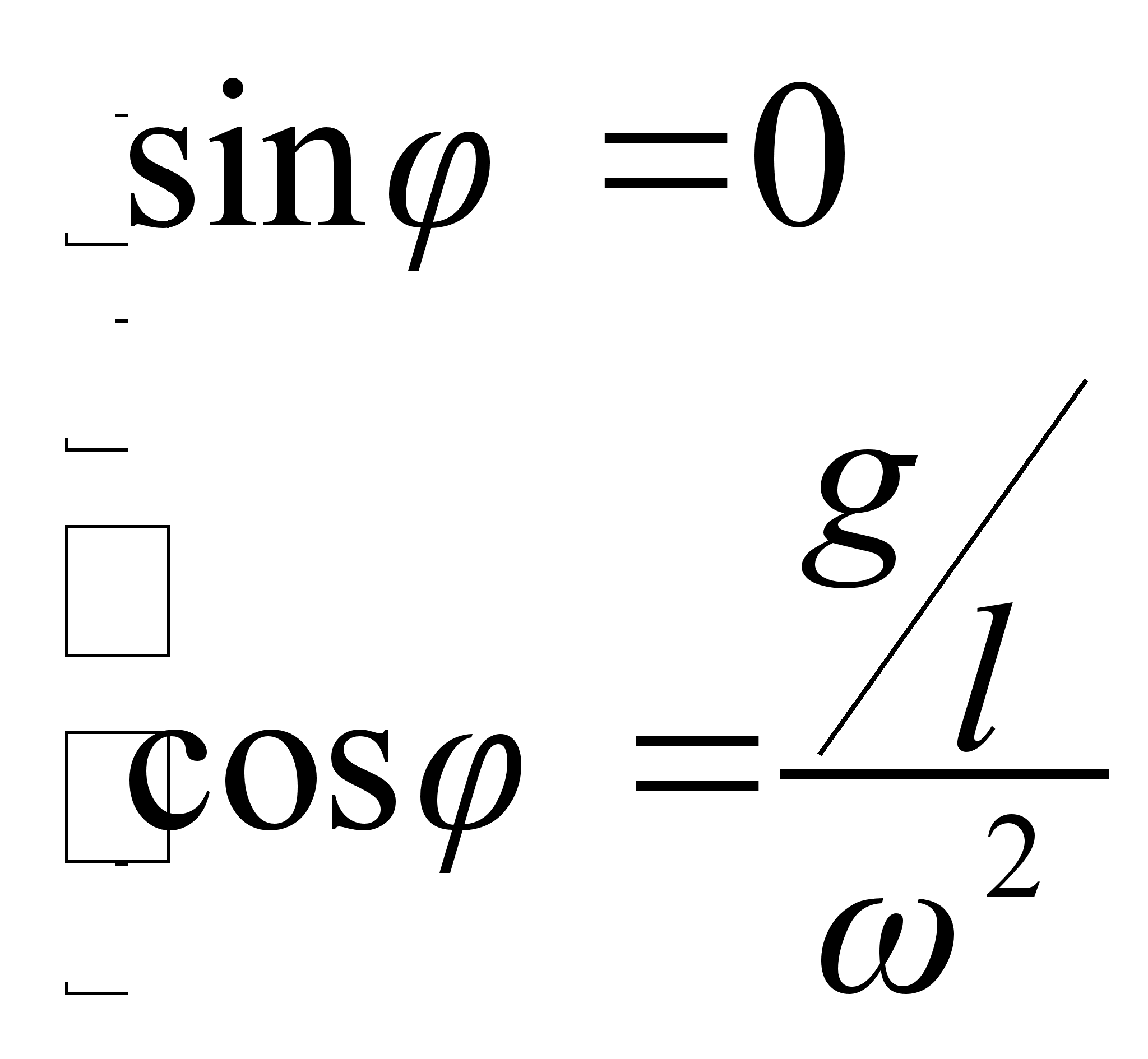
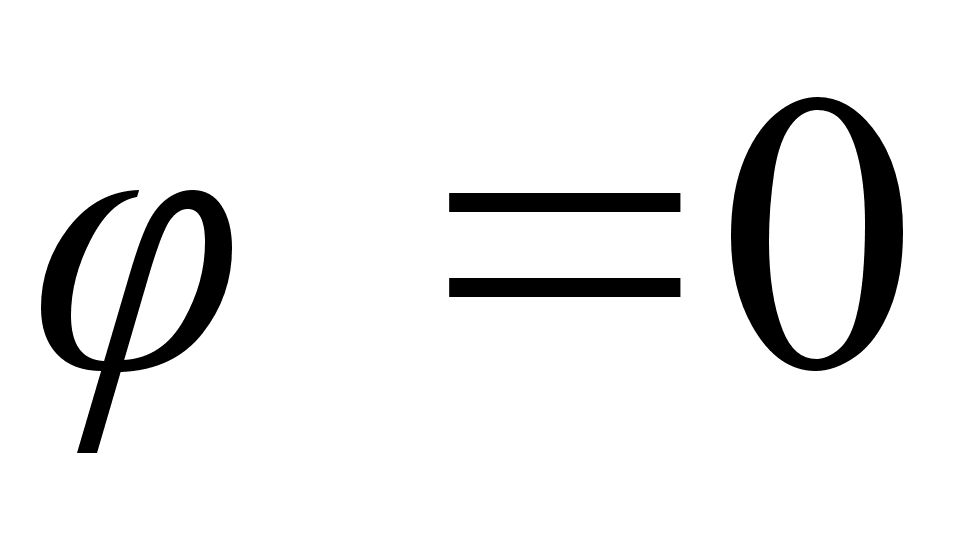 , что соответствует просто провисанию шарика — материальной точки. Т.о. условие движения маятника в плоскости есть:
, что соответствует просто провисанию шарика — материальной точки. Т.о. условие движения маятника в плоскости есть: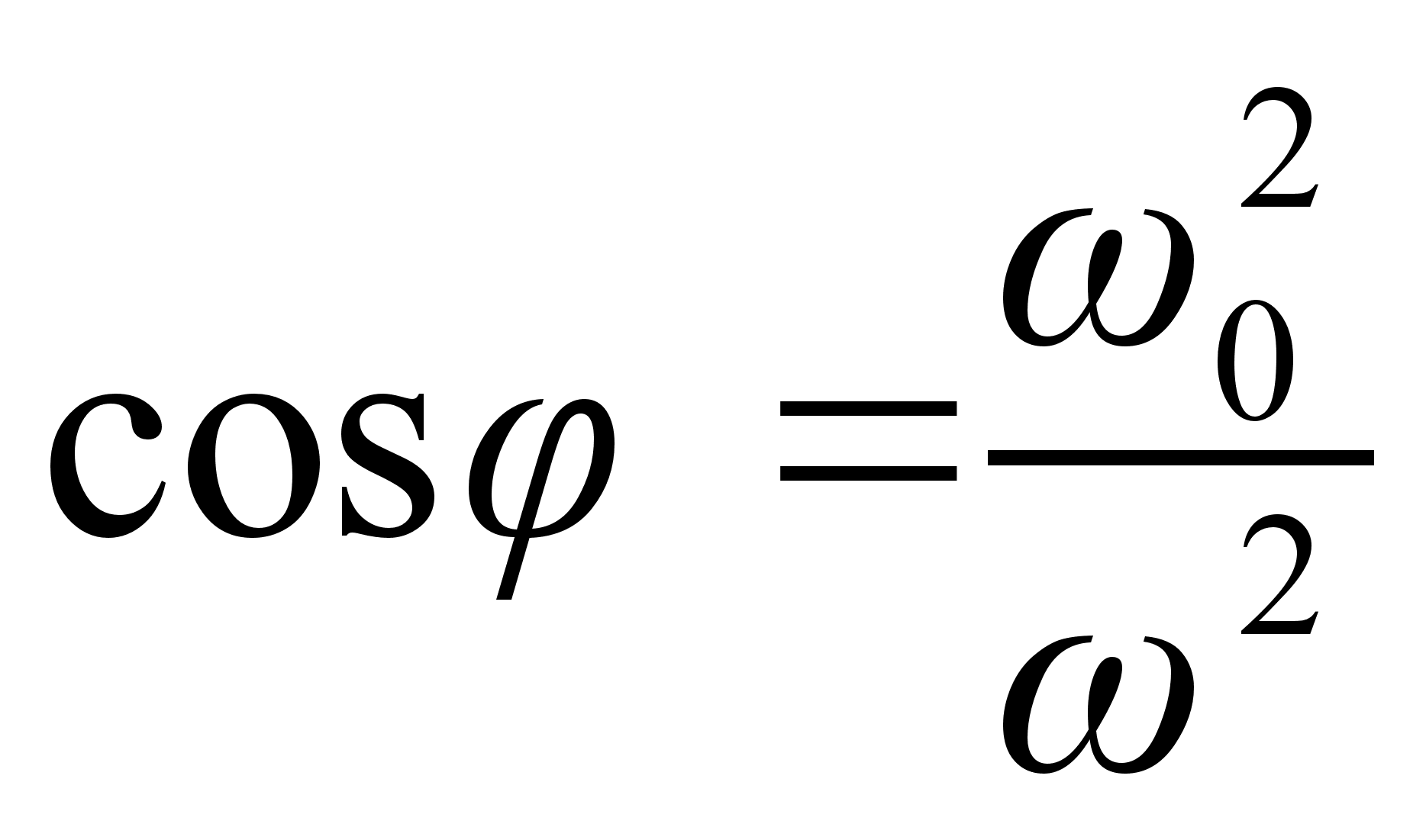
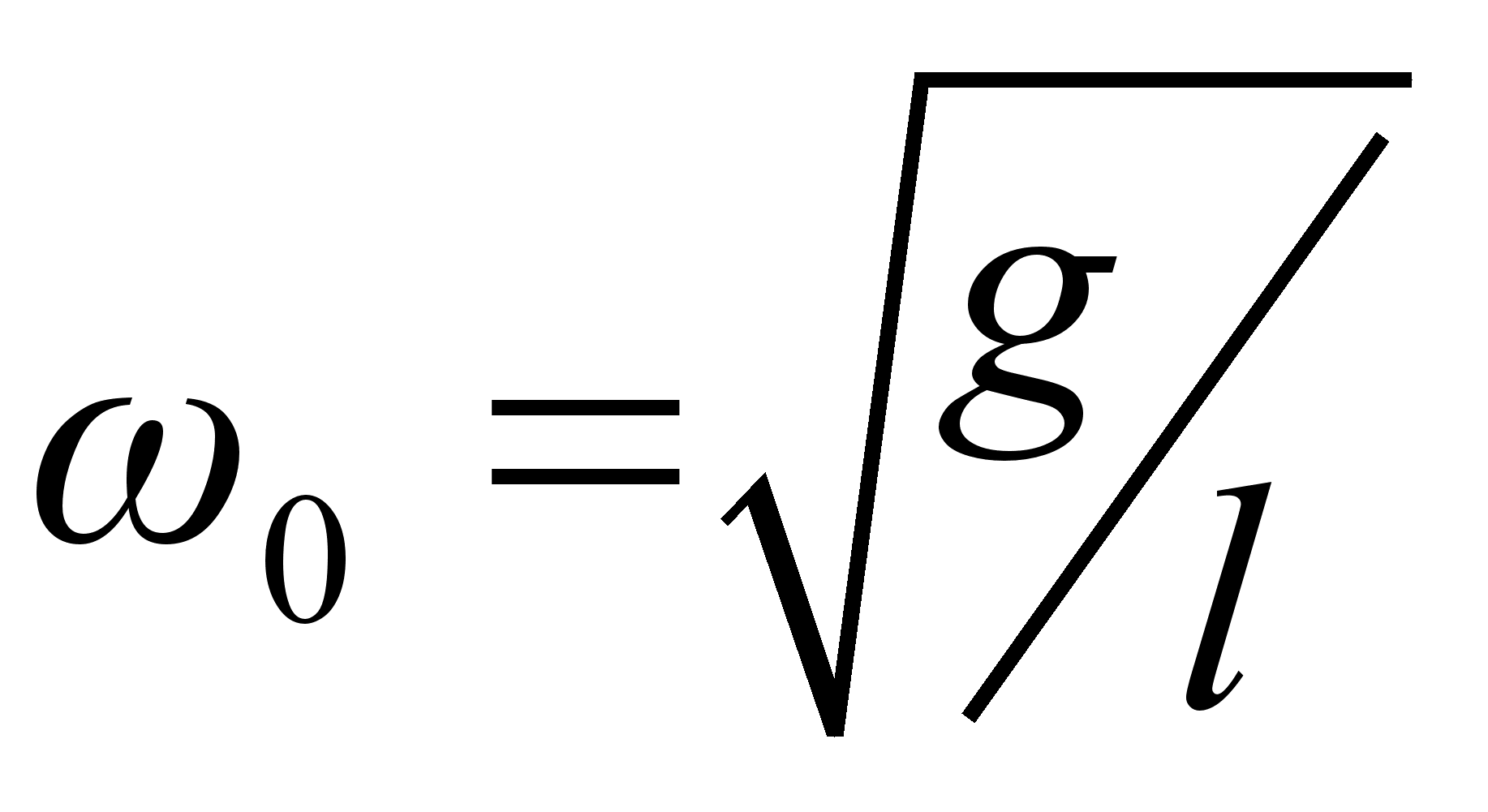 – собственная частота колебаний маятника. Более того, выражение дает зависимость угла отклонения, обуславливающего движение в плоскости, от частоты вращения вертикальной оси, и собственной частоты маятника. Т.о., чтобы добиться устойчивого вращения в плоскости при желаемом угле отклонения, необходимо подбирать отношение между собственной частотой (которая определяется длинной стержня) и частотой вращения оси. Заметим также, что значение угла
– собственная частота колебаний маятника. Более того, выражение дает зависимость угла отклонения, обуславливающего движение в плоскости, от частоты вращения вертикальной оси, и собственной частоты маятника. Т.о., чтобы добиться устойчивого вращения в плоскости при желаемом угле отклонения, необходимо подбирать отношение между собственной частотой (которая определяется длинной стержня) и частотой вращения оси. Заметим также, что значение угла 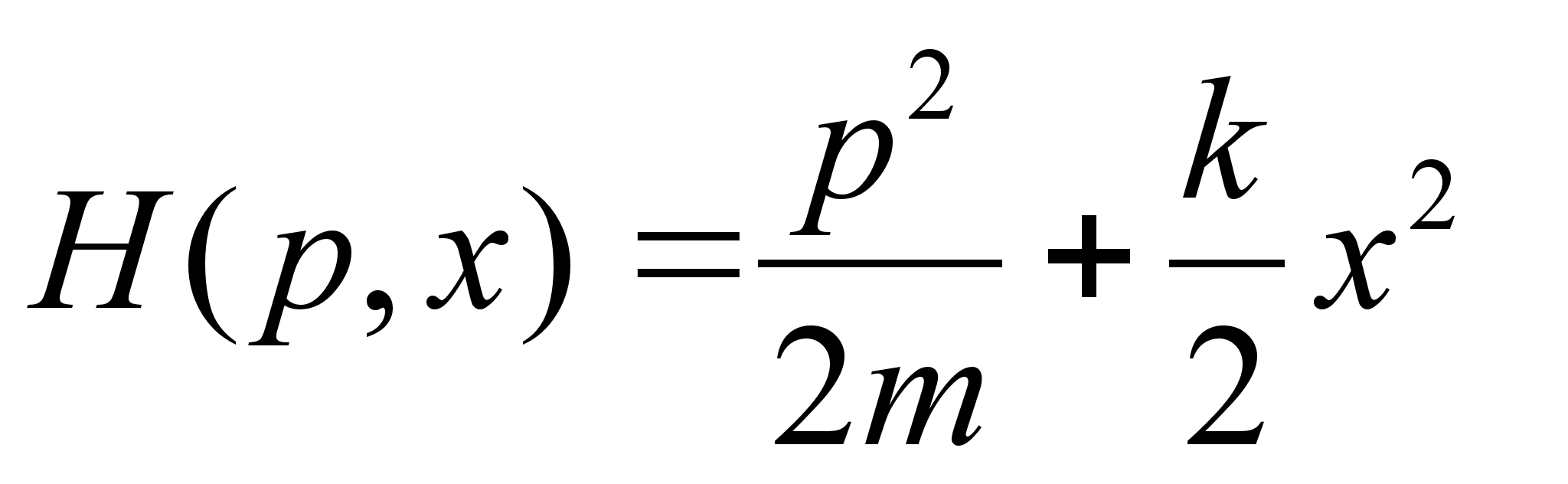
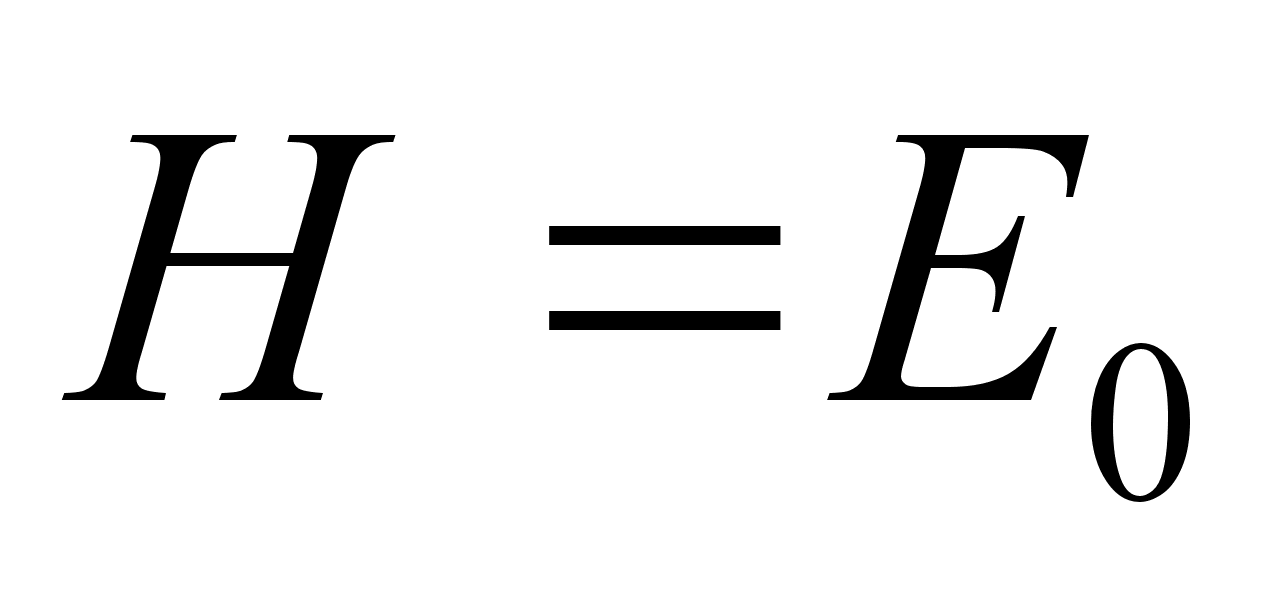 получим уравнение фазовой траектории гармонического осциллятора:
получим уравнение фазовой траектории гармонического осциллятора: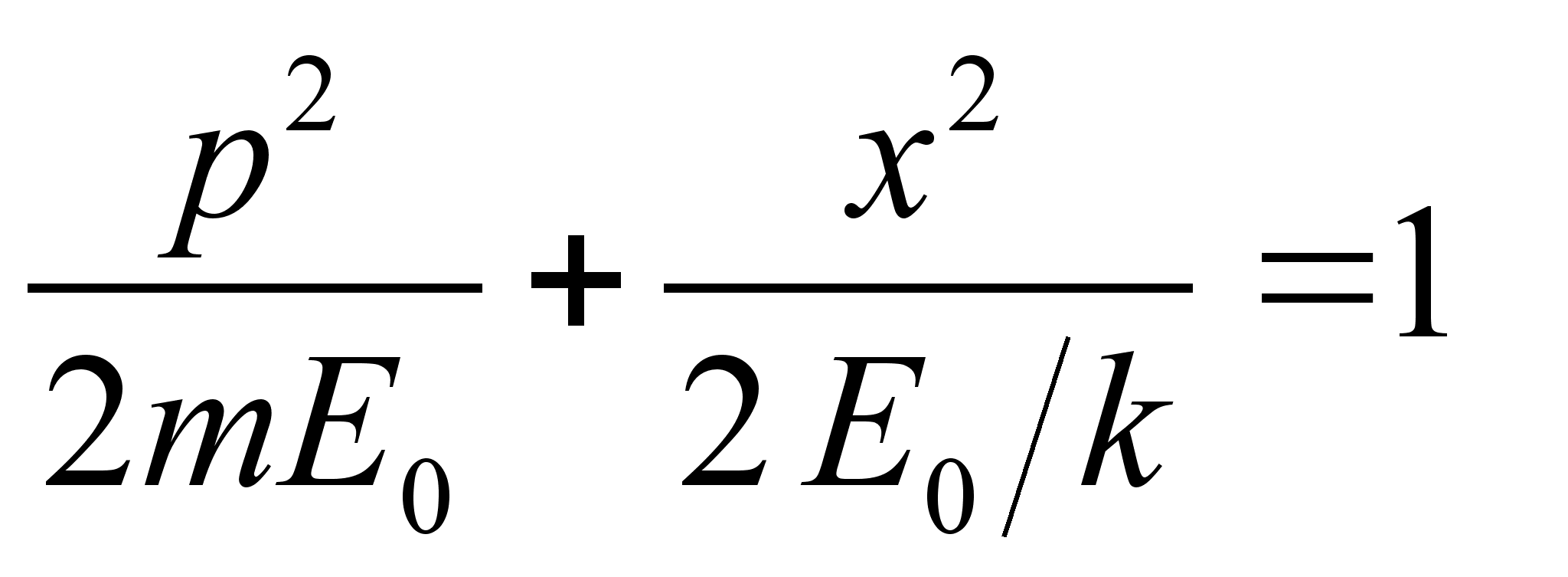
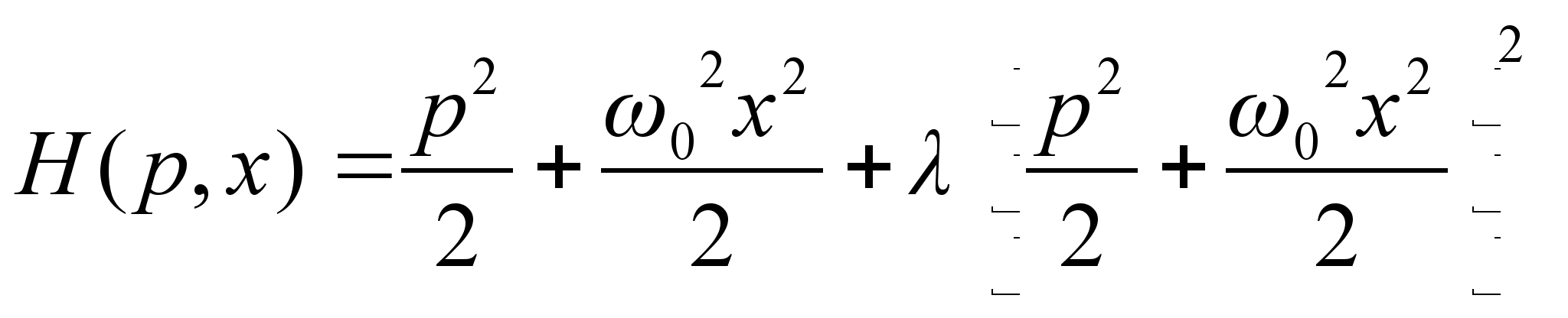
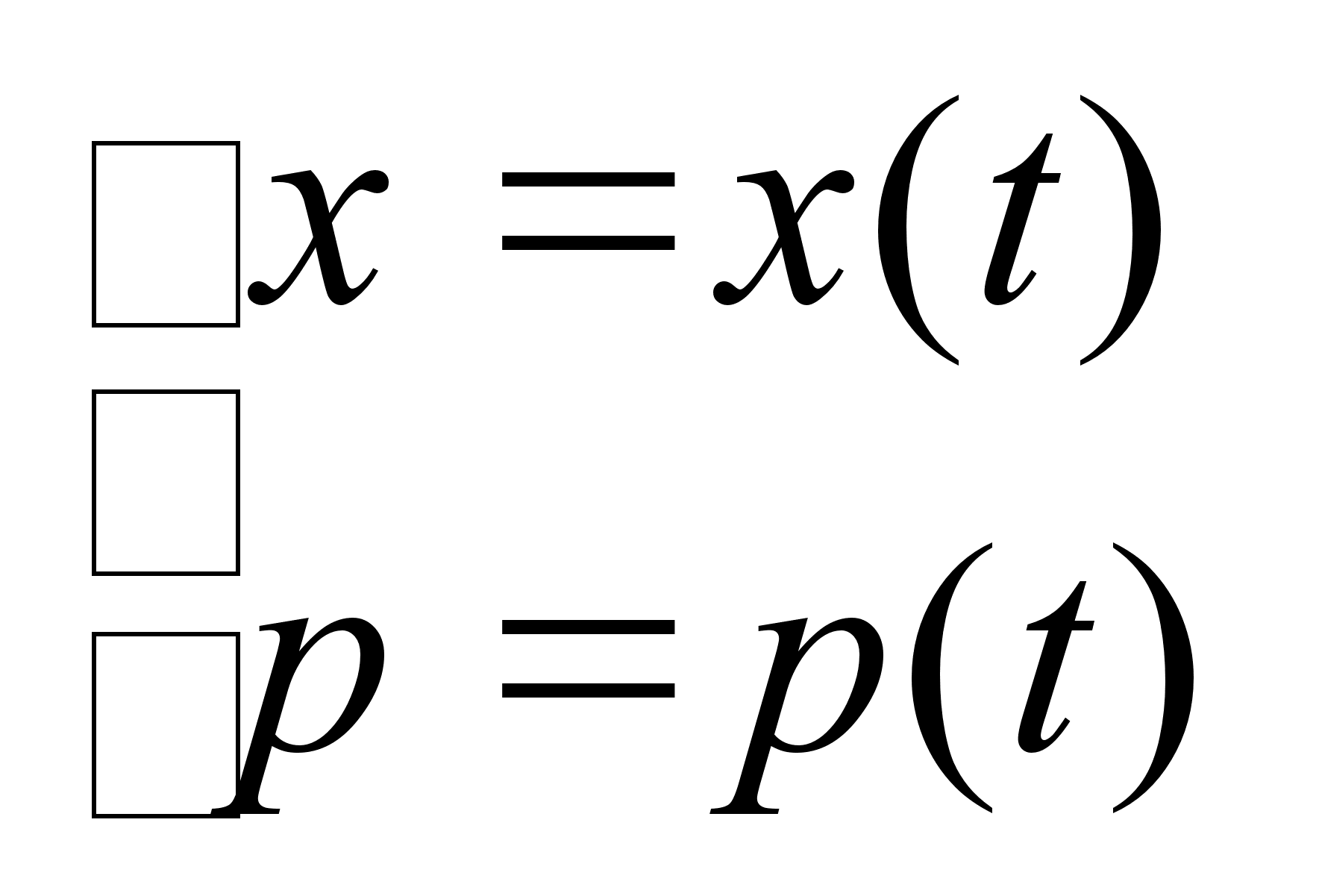 ,
,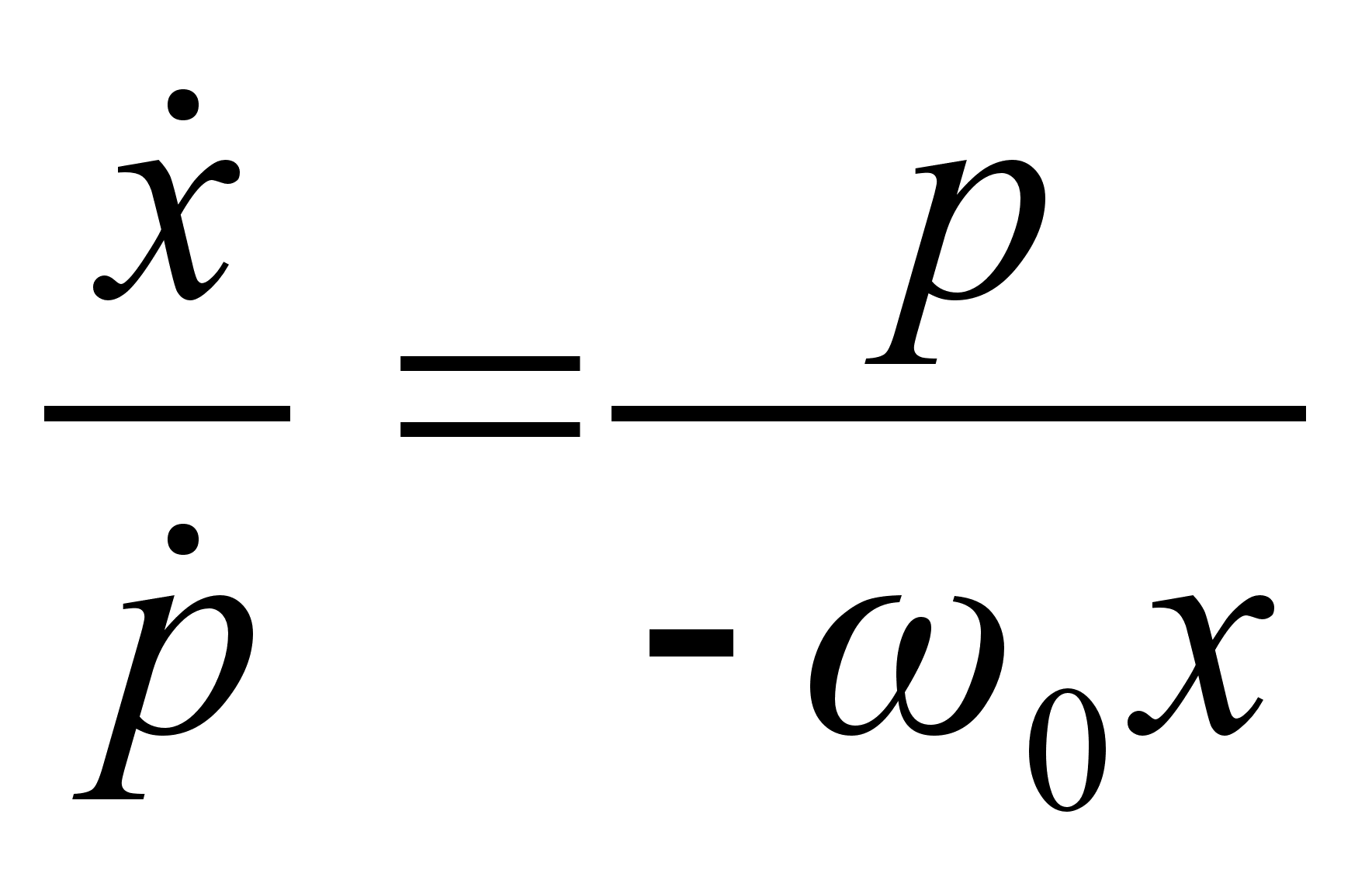 ,
,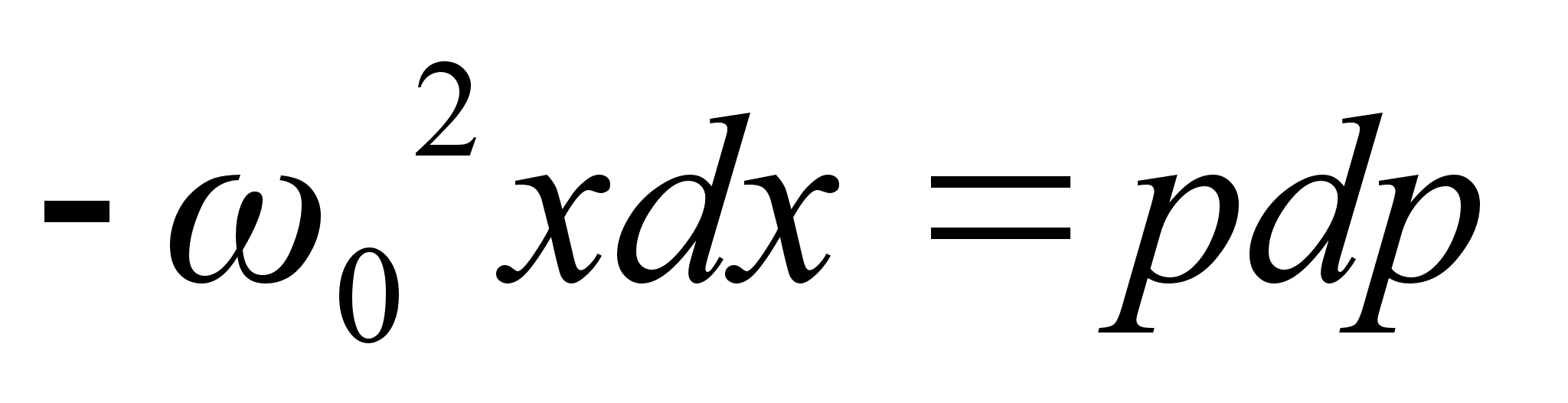
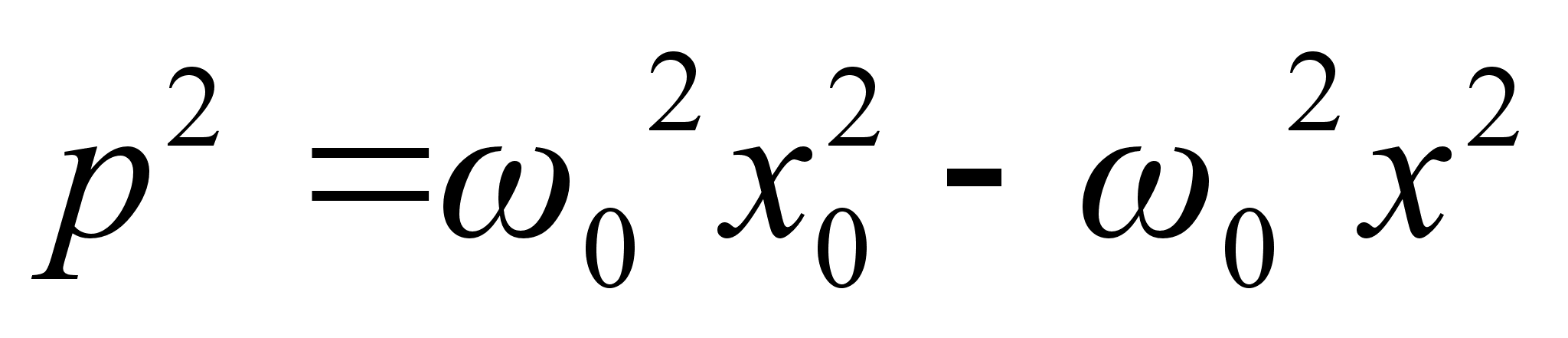
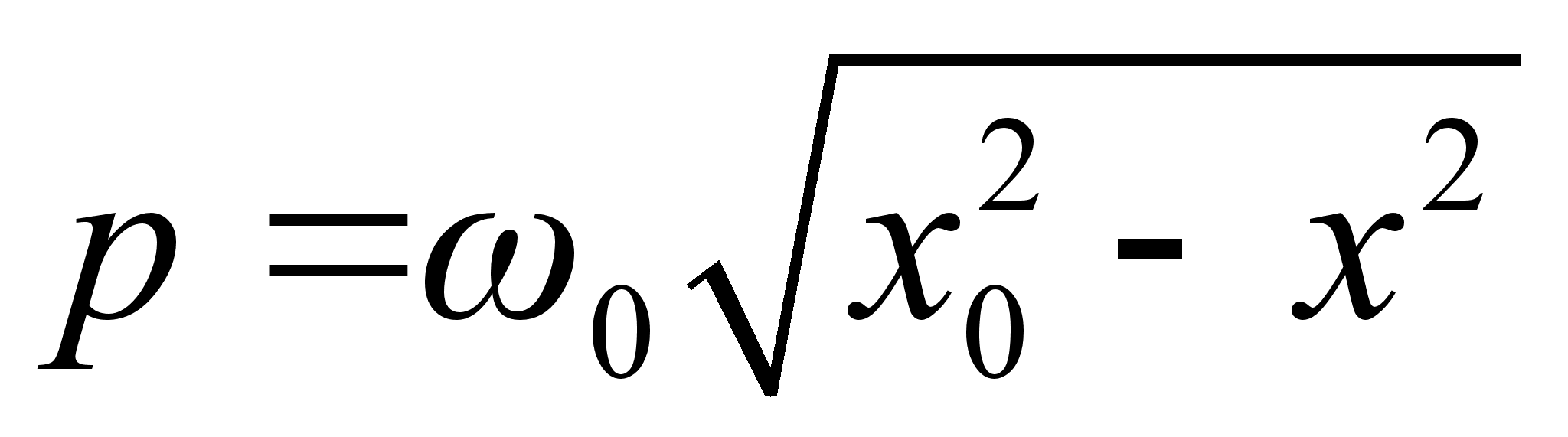
 и приравнивая его к значению
и приравнивая его к значению 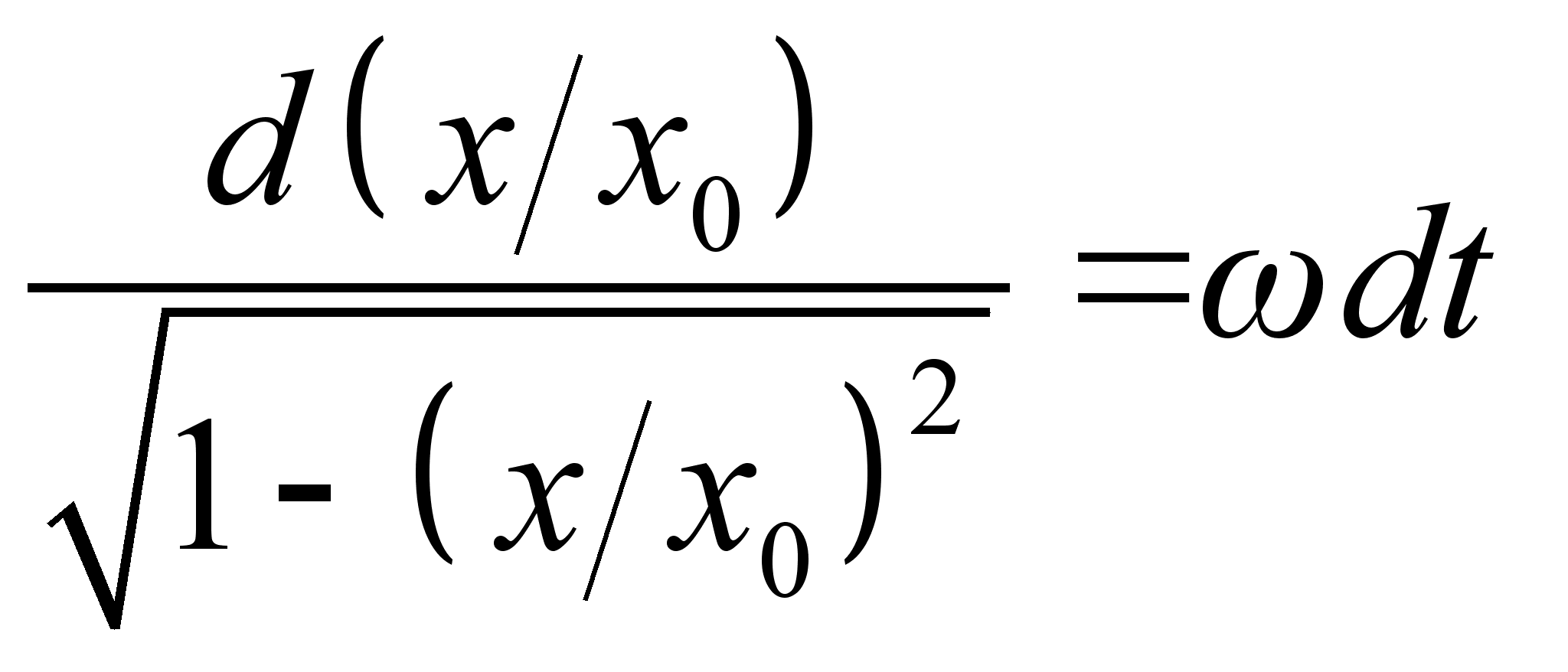 ,
,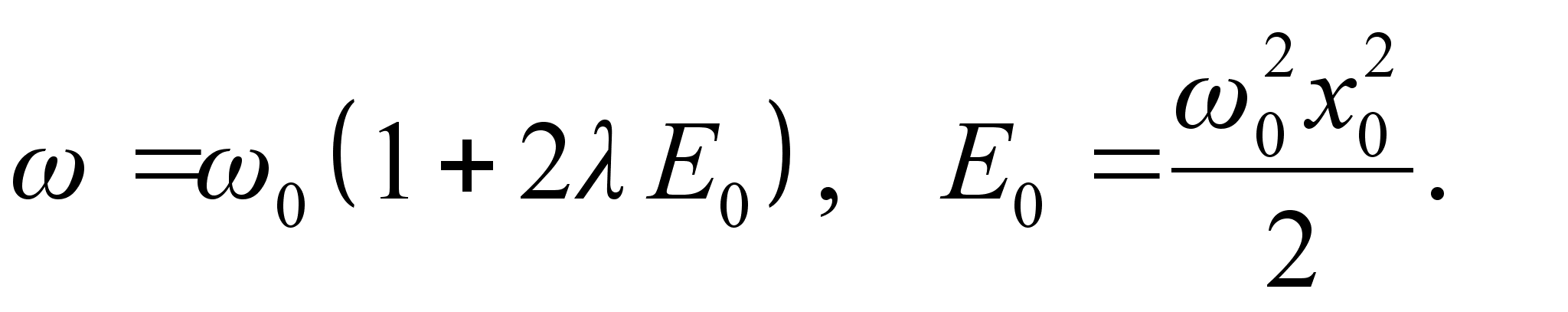
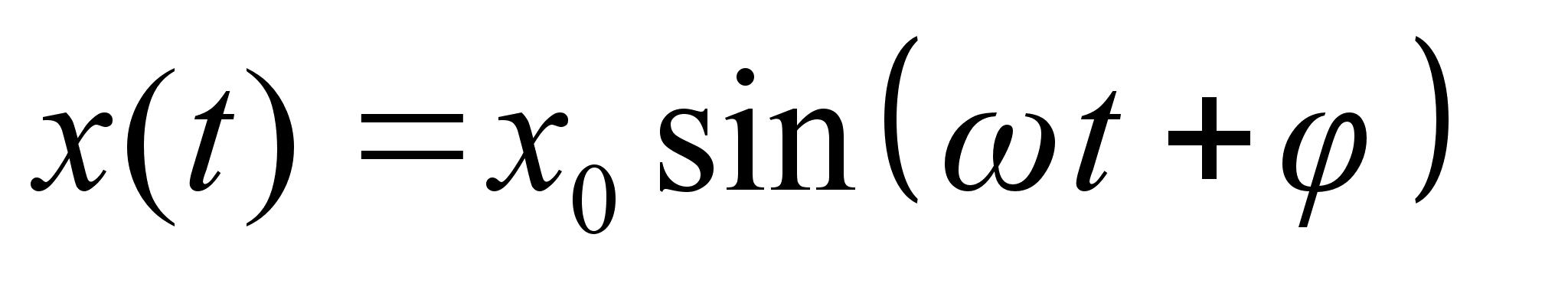
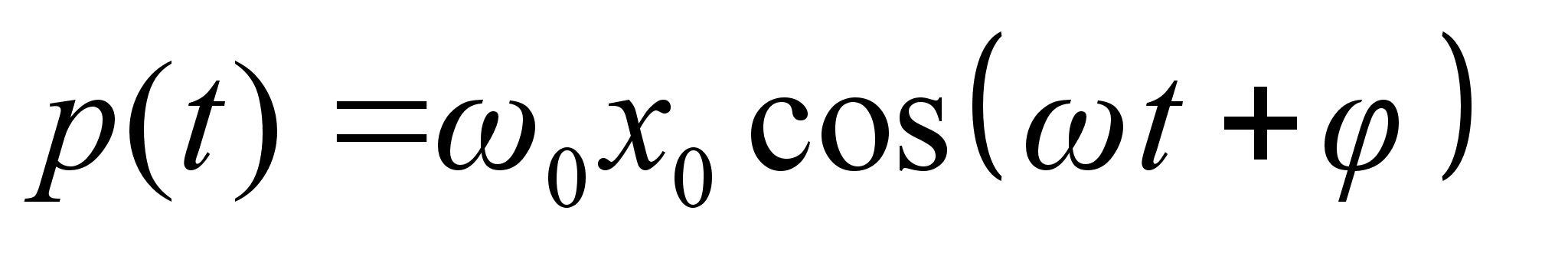
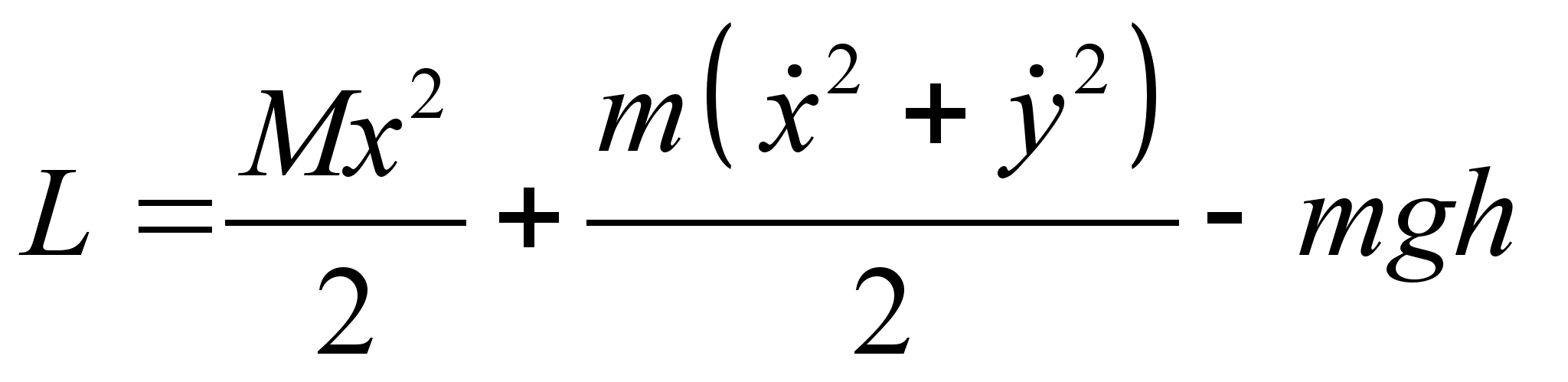
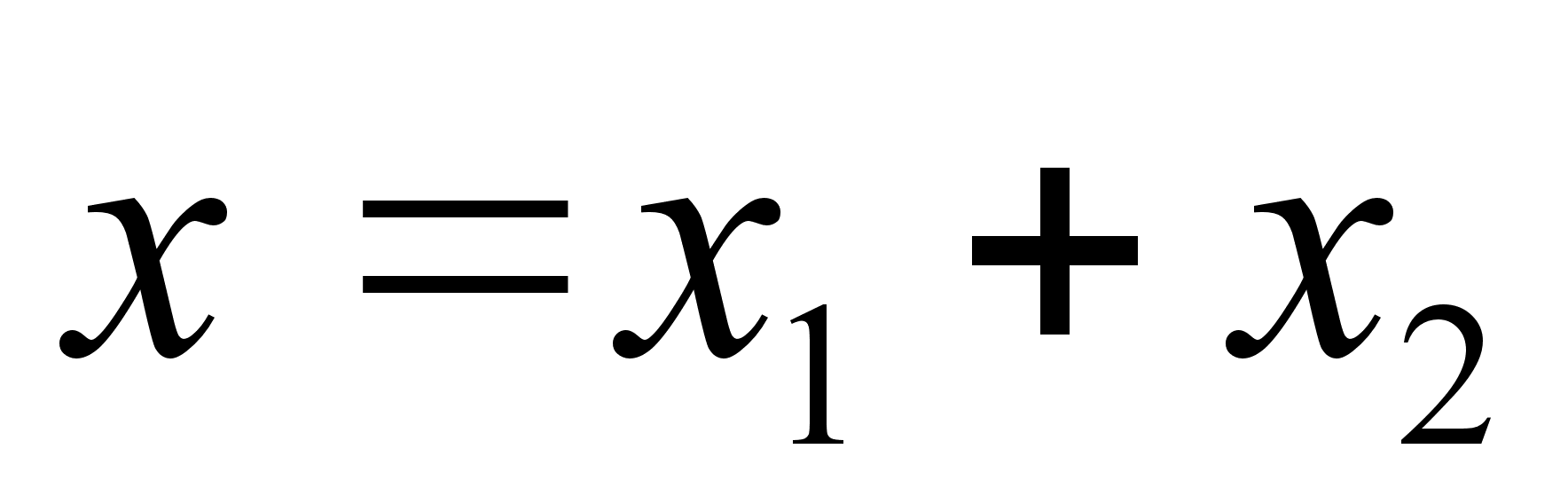
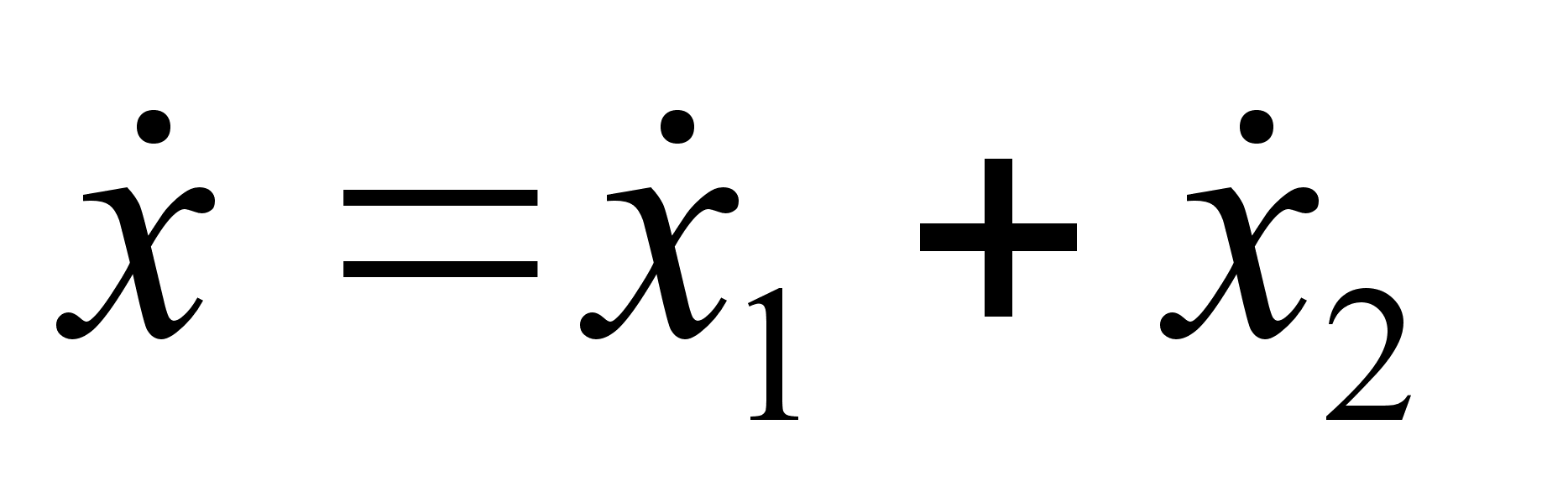
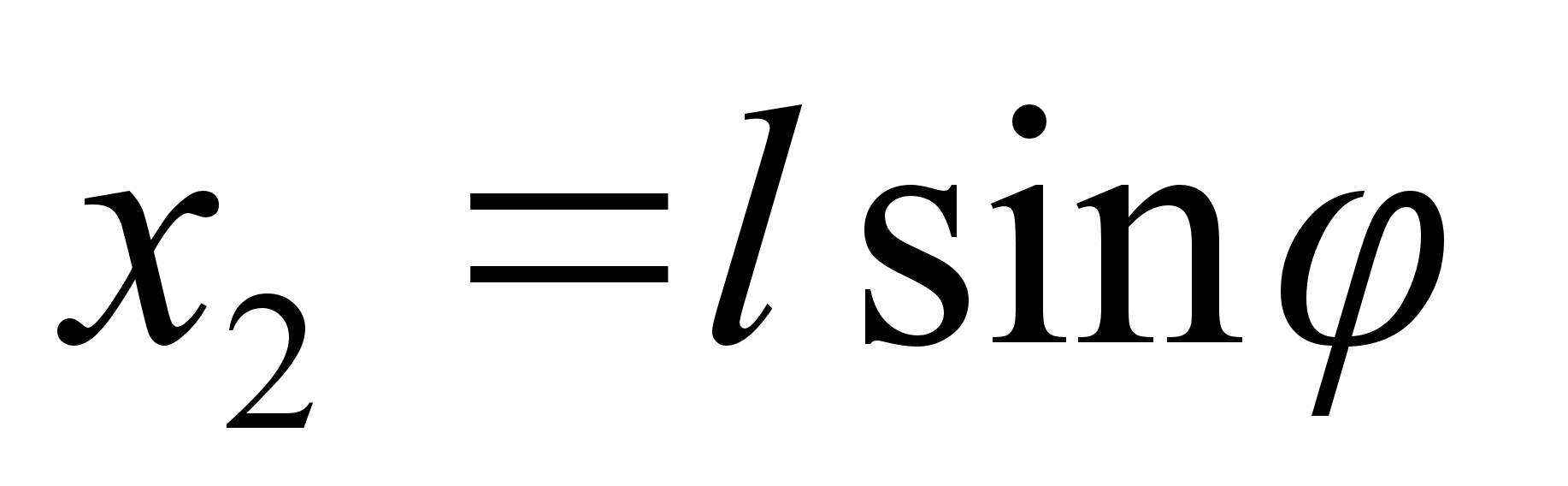
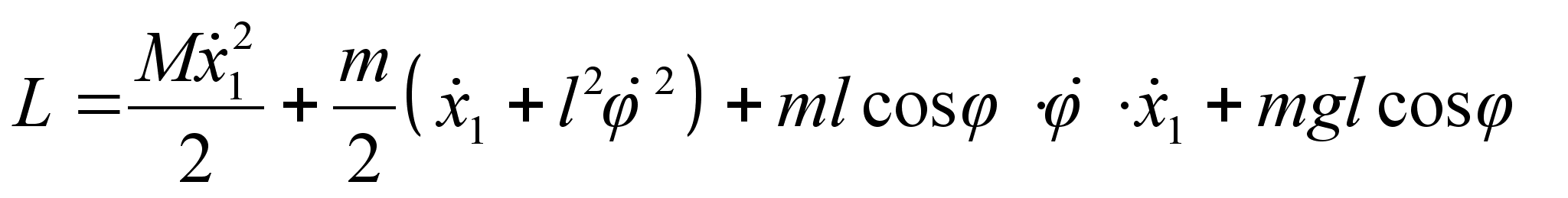
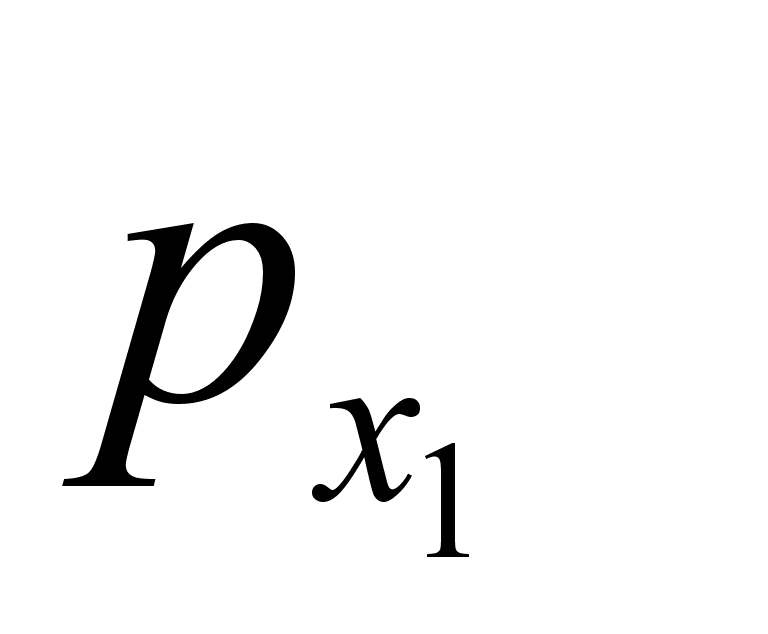 :
: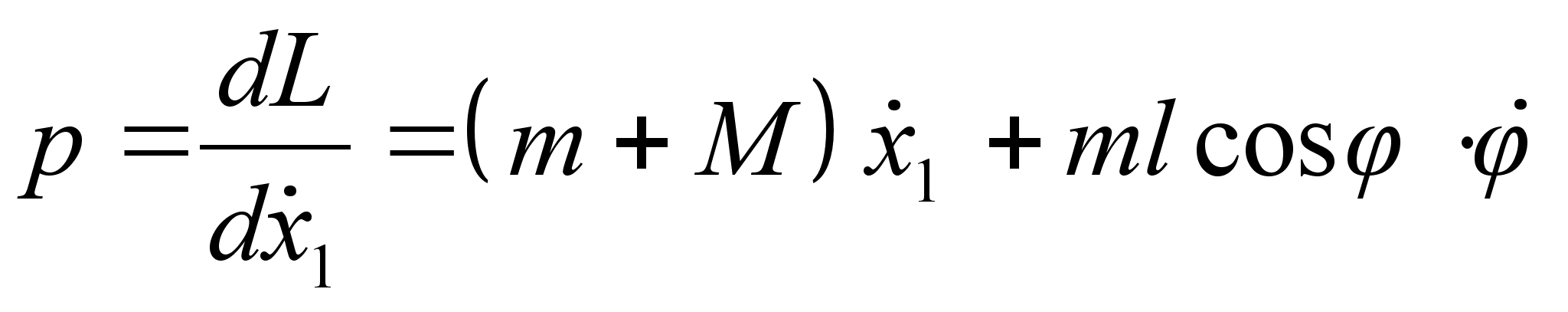

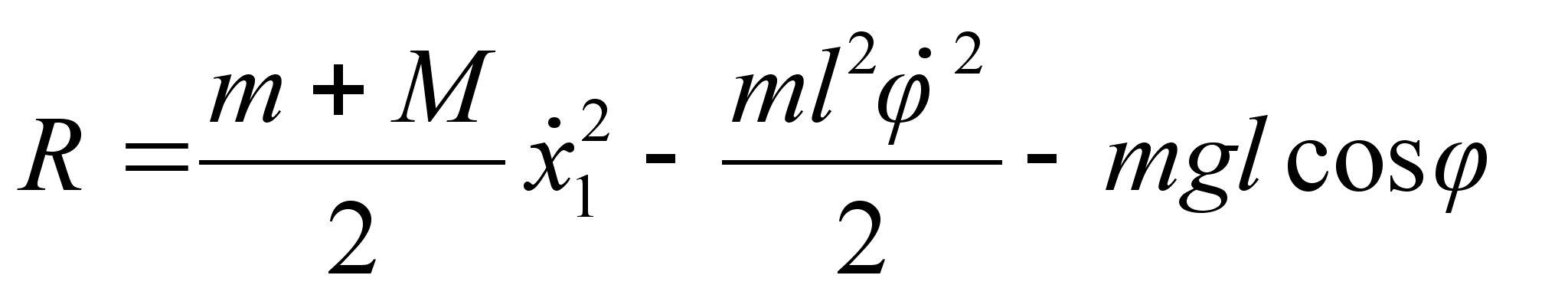
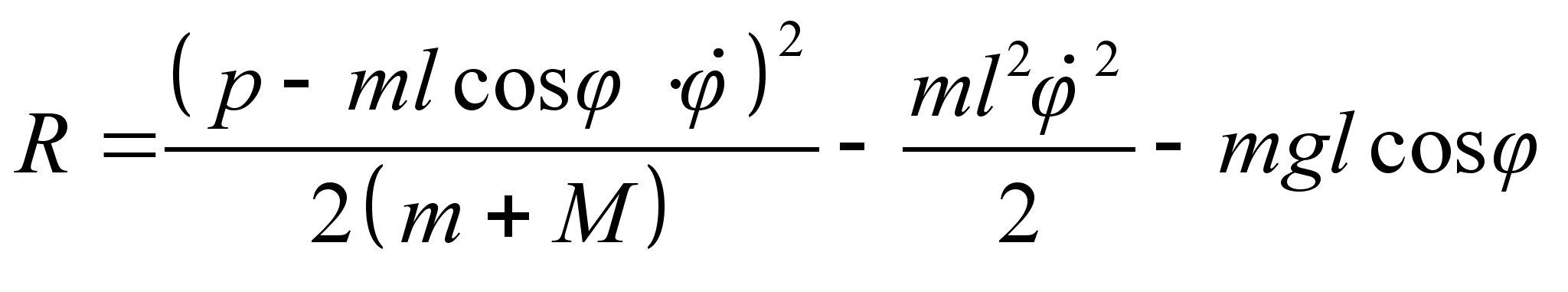
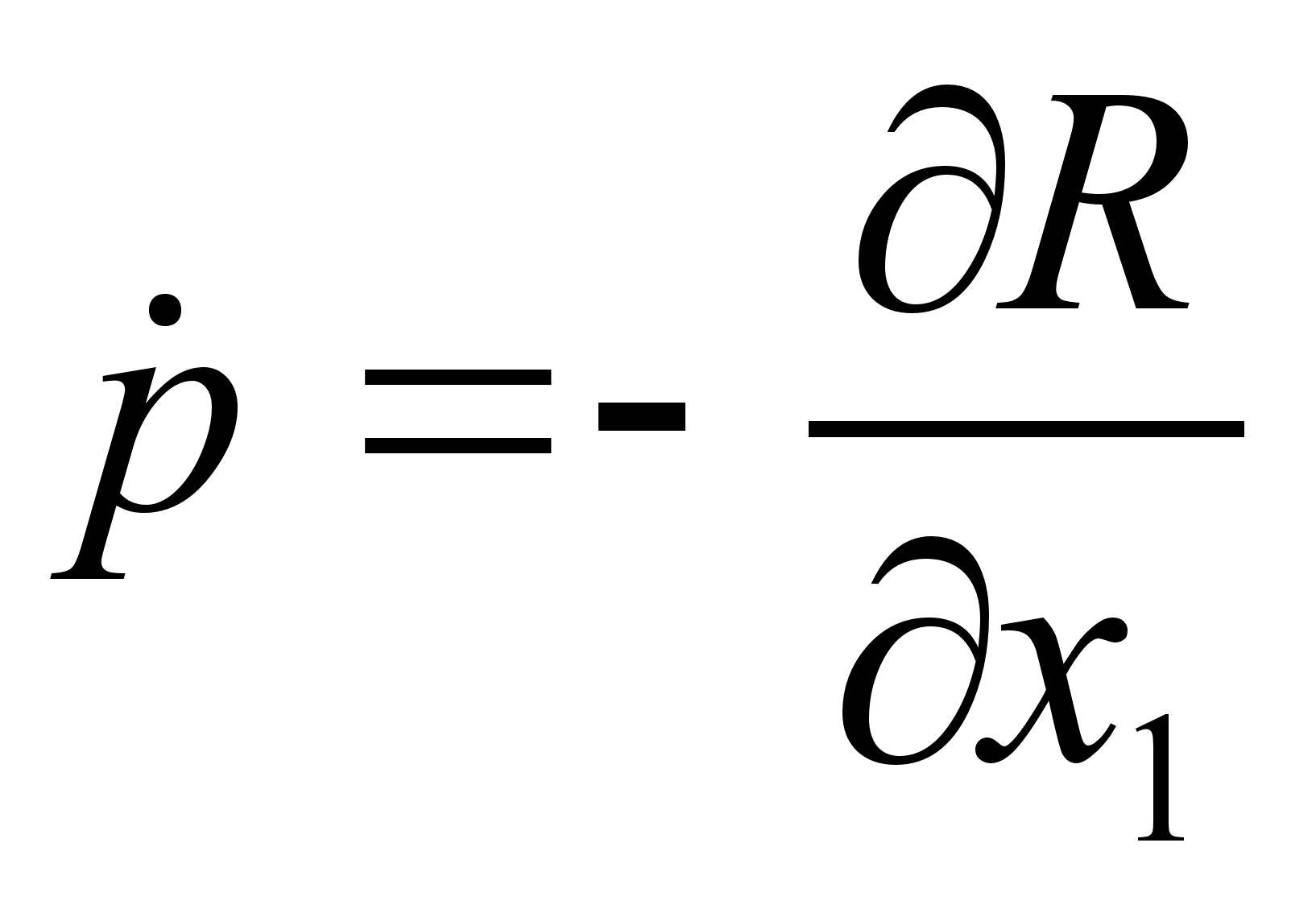
 .
.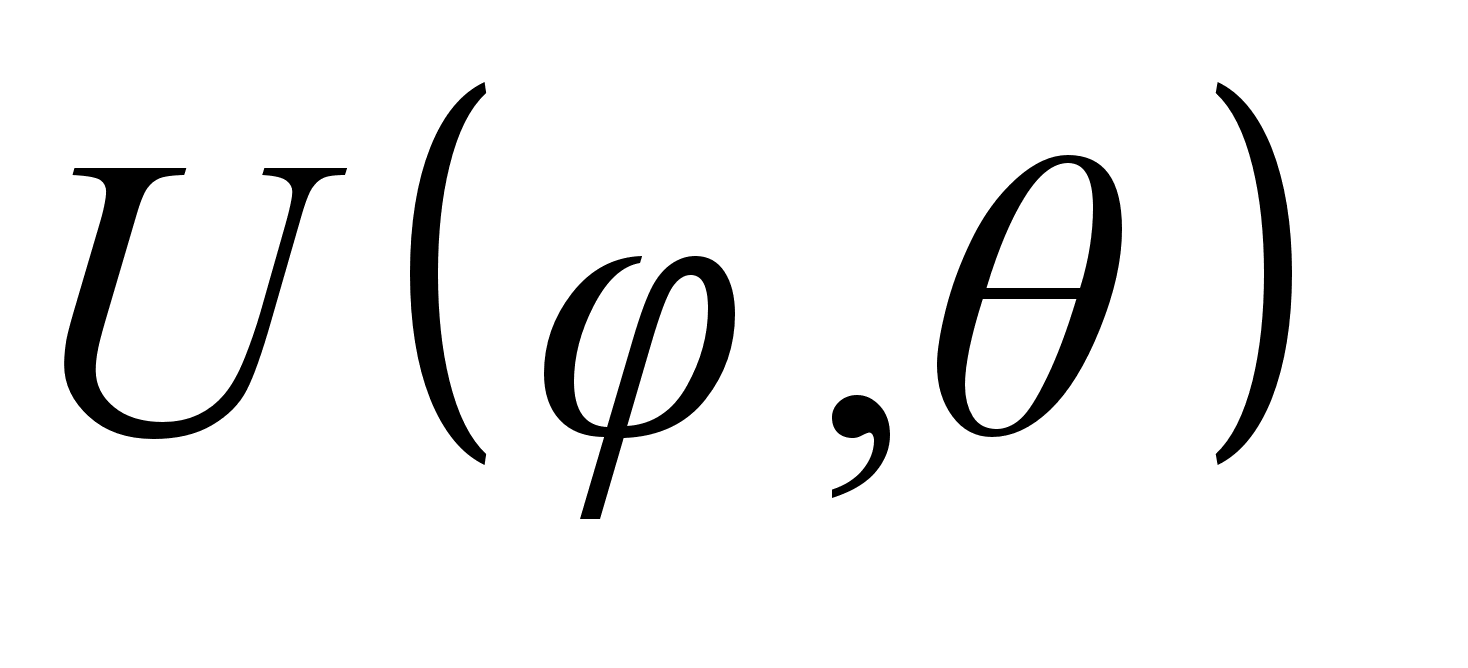 .
.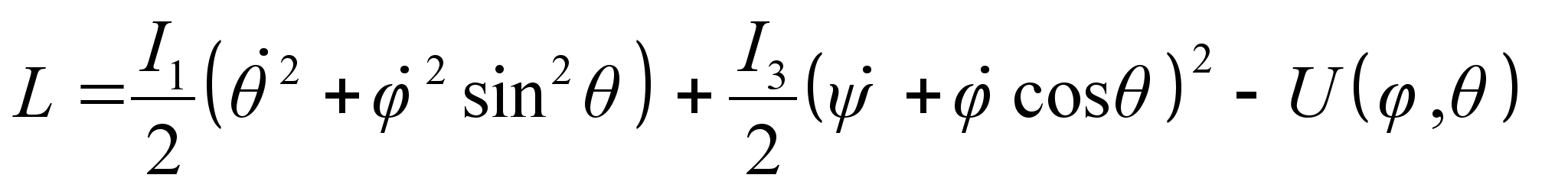
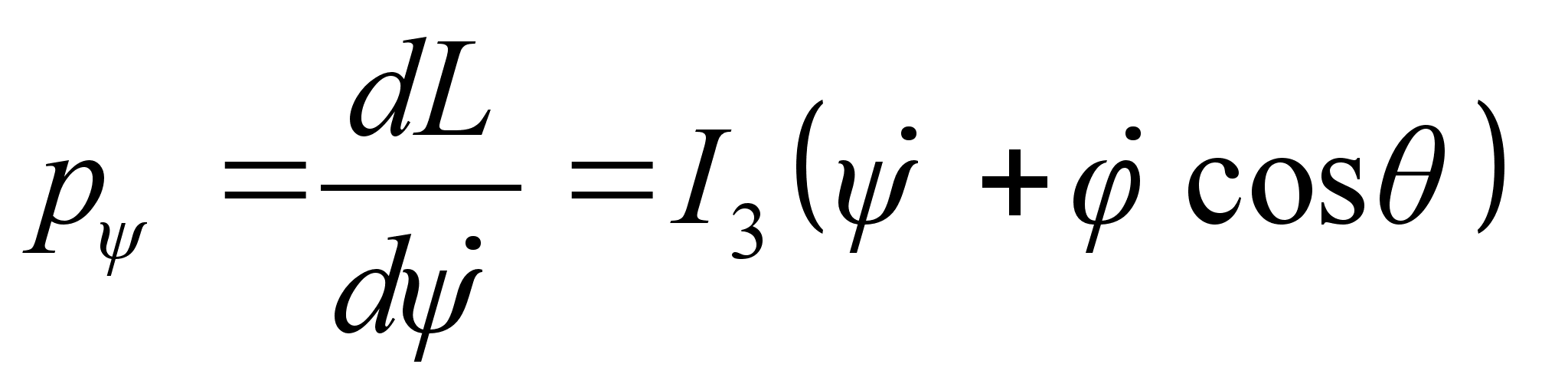
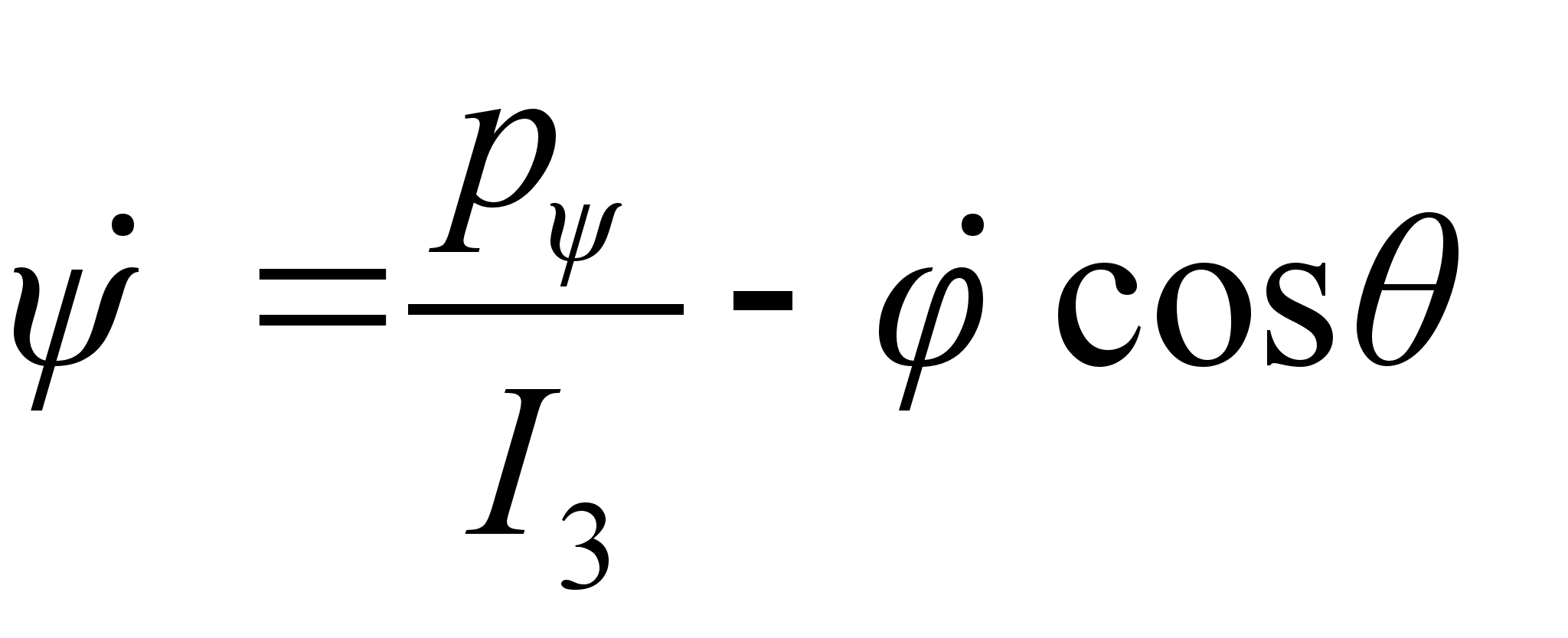
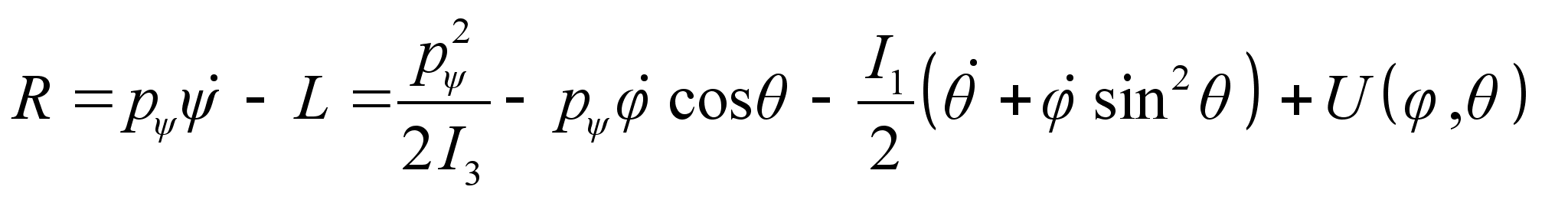
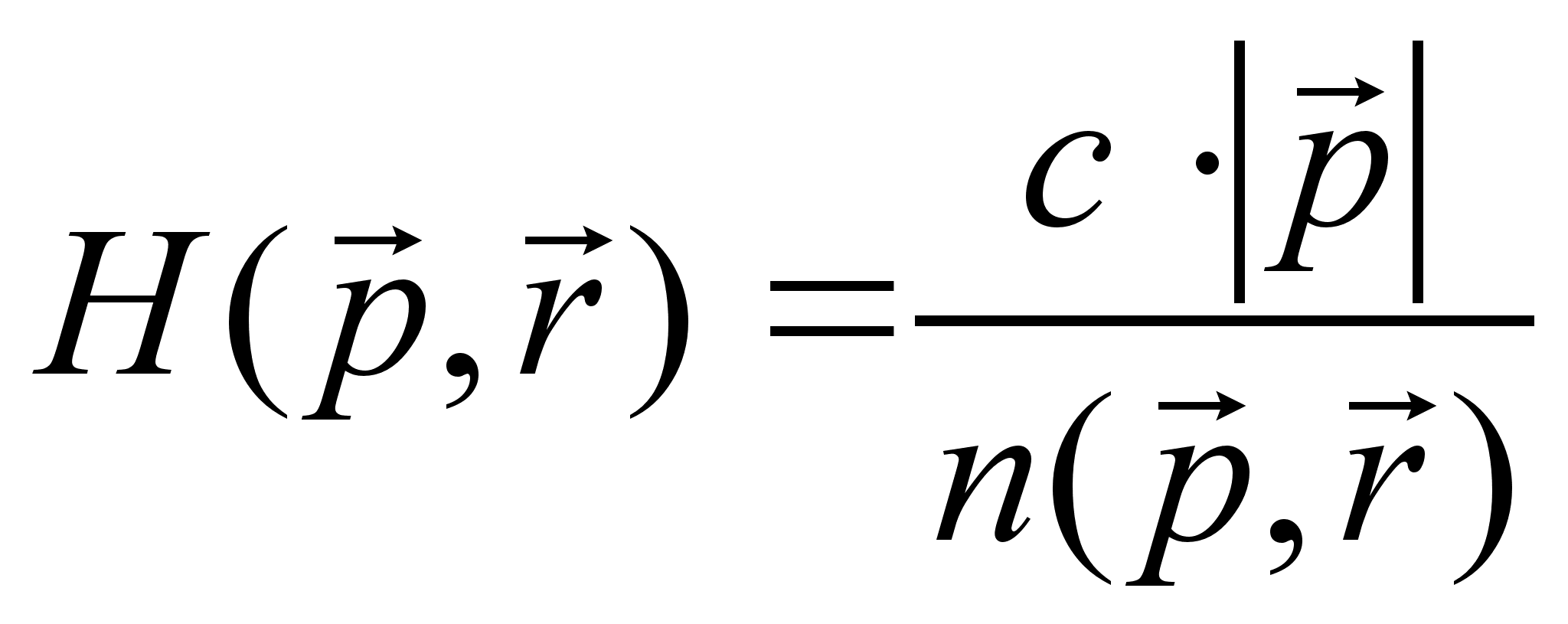 .
.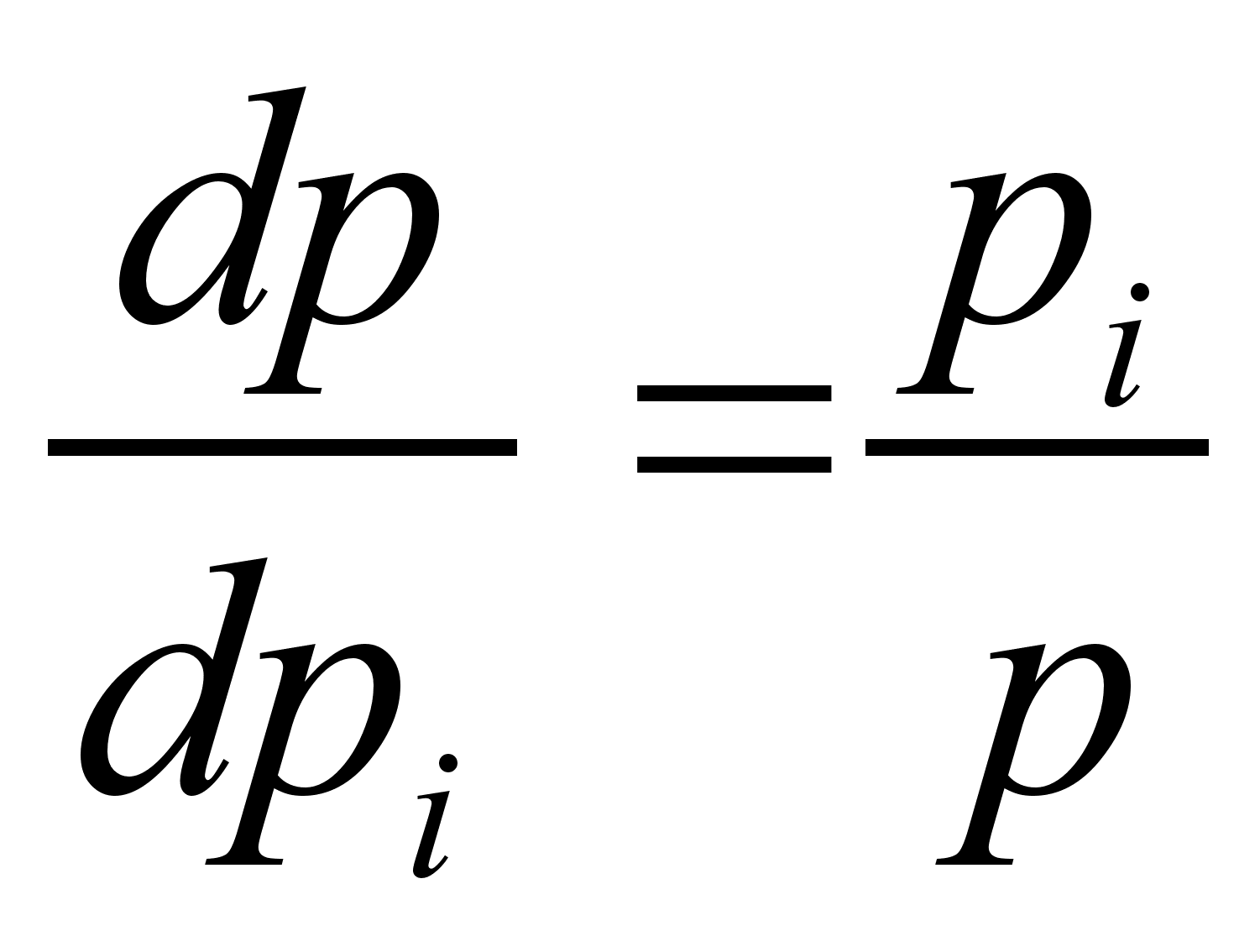 .
.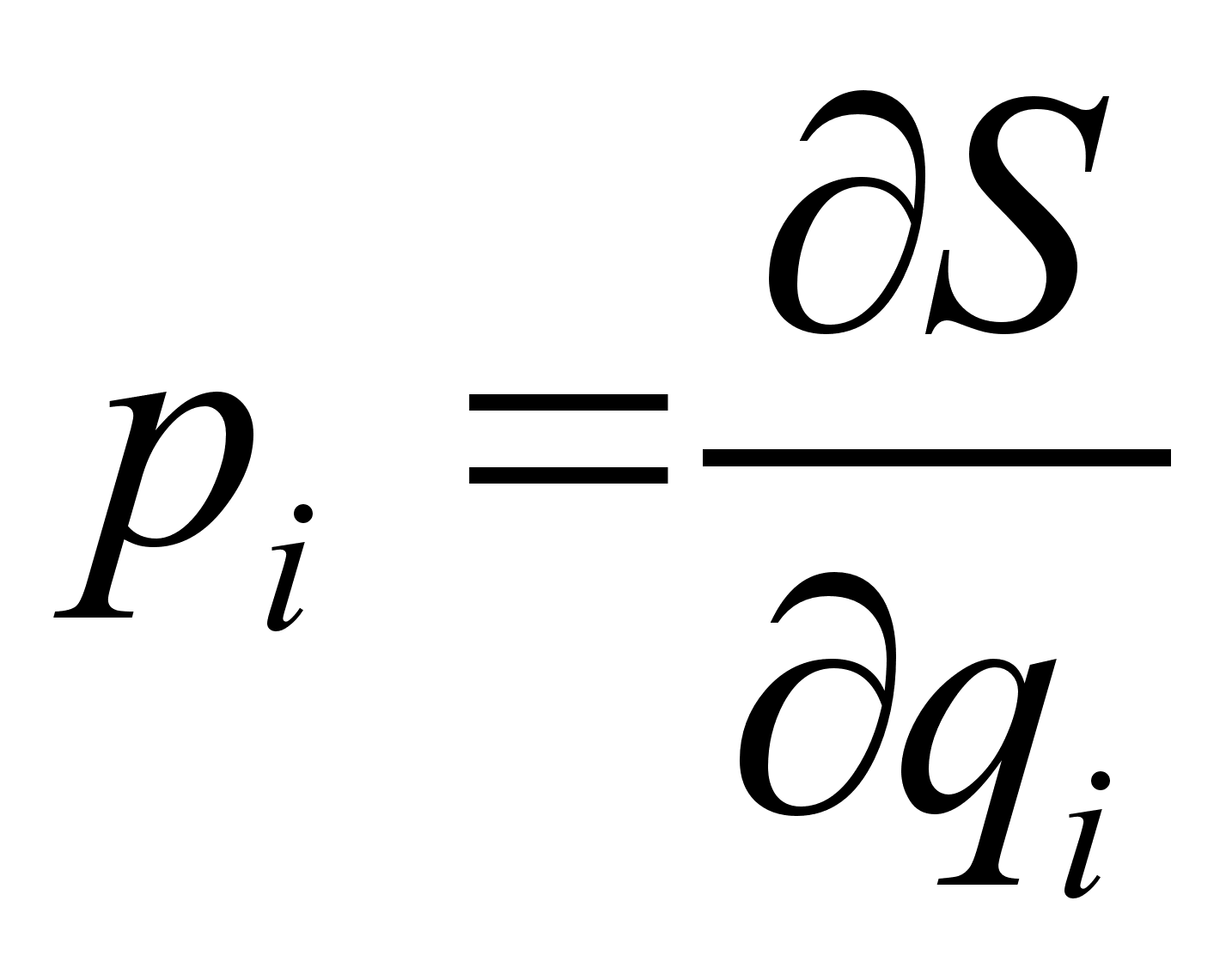
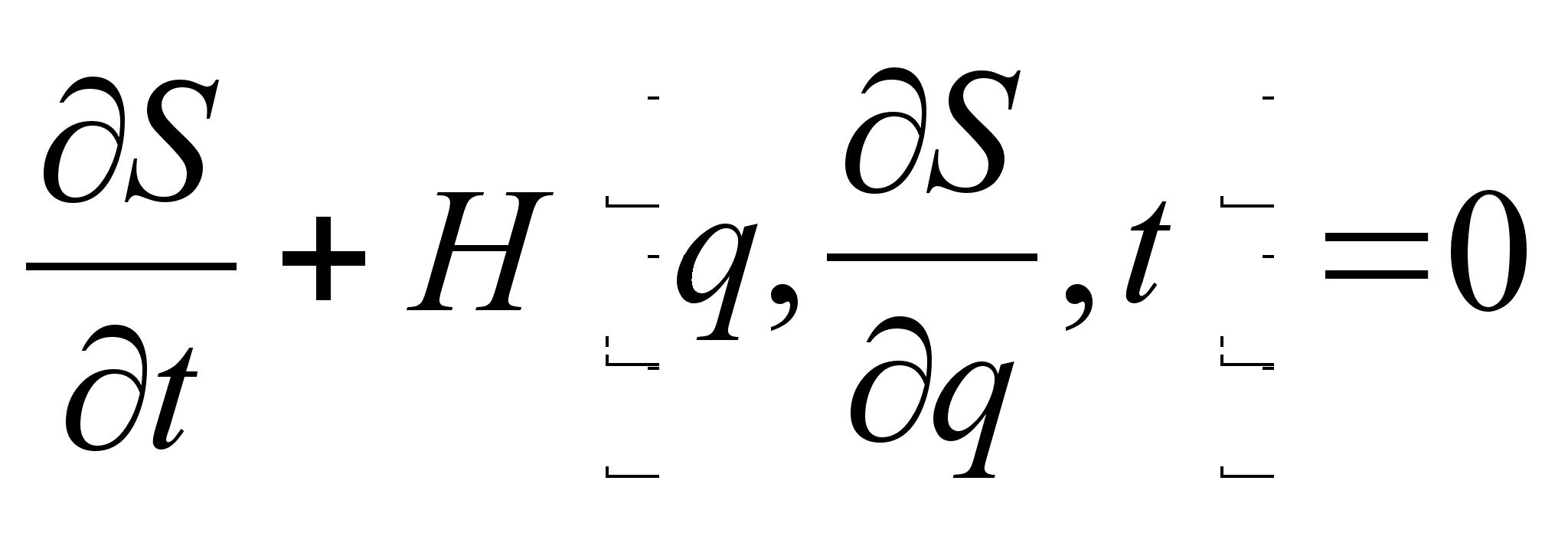
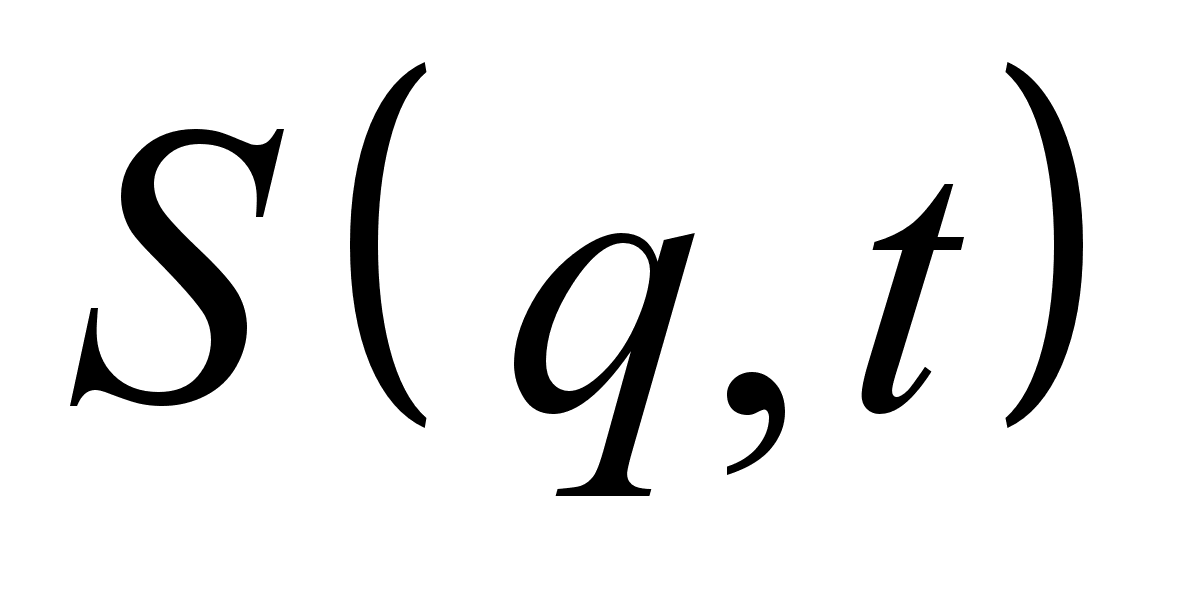 .
.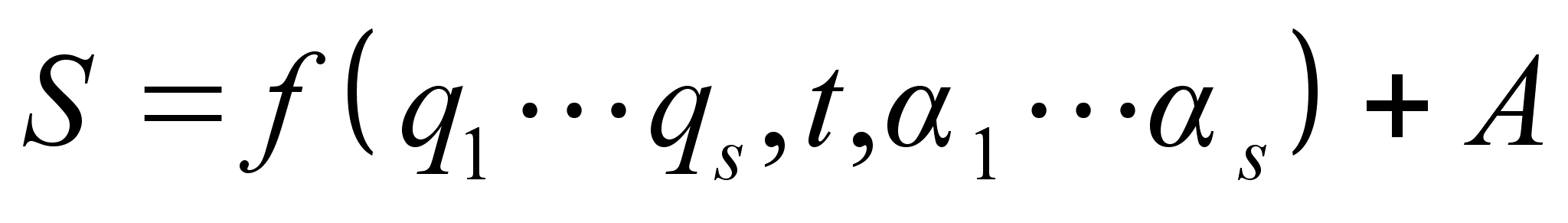
 будут выступать в качестве новых импульсов. Тогда новые координаты
будут выступать в качестве новых импульсов. Тогда новые координаты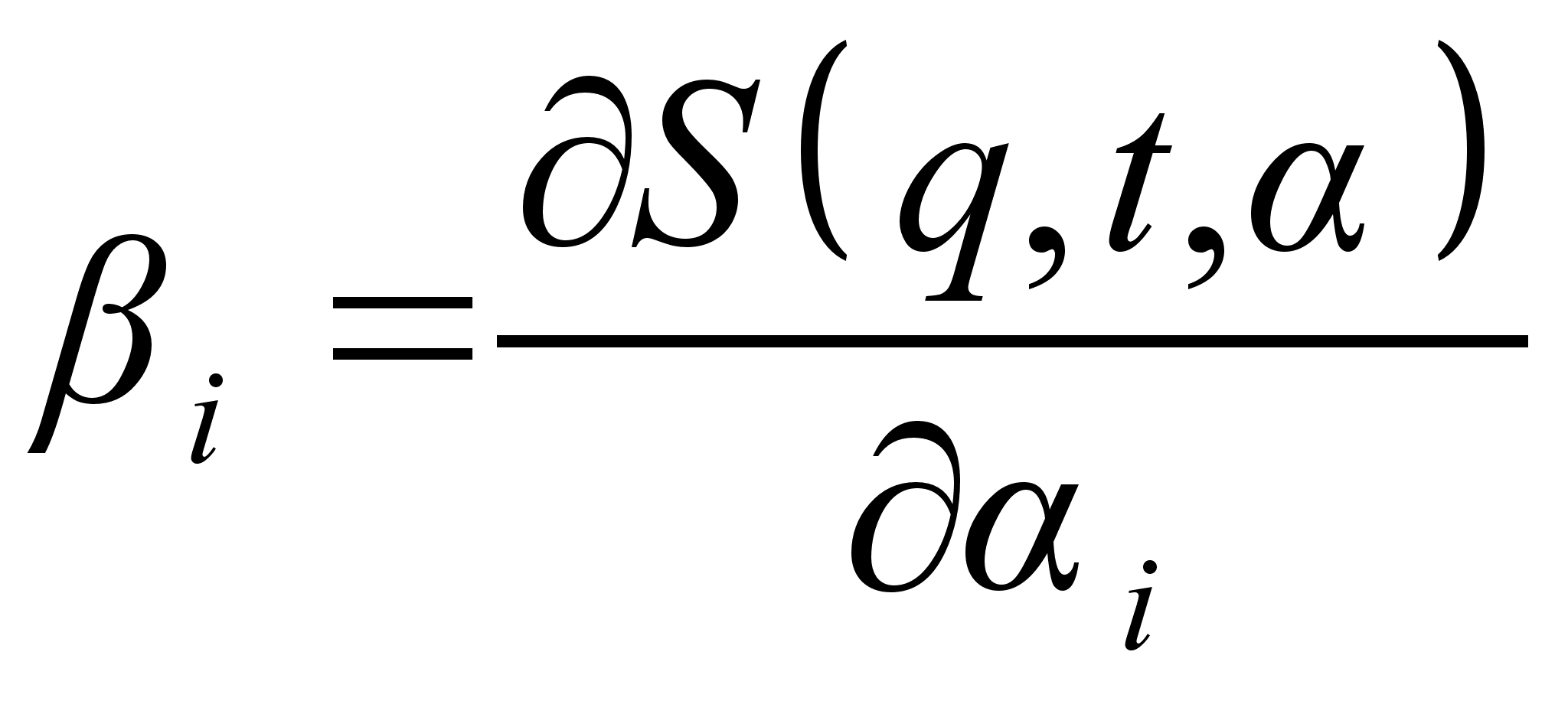
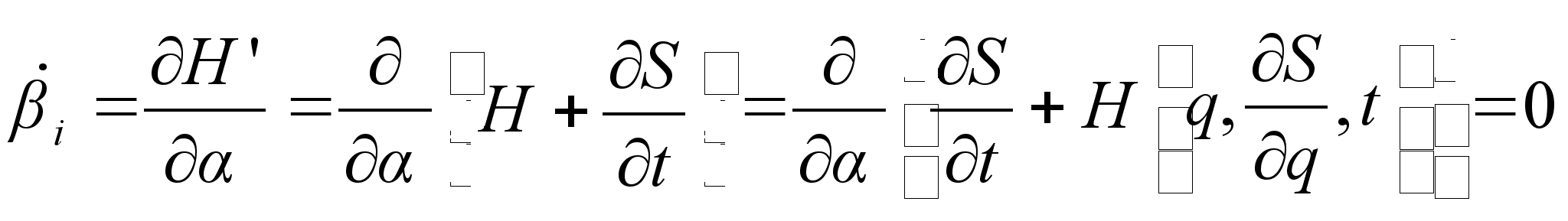
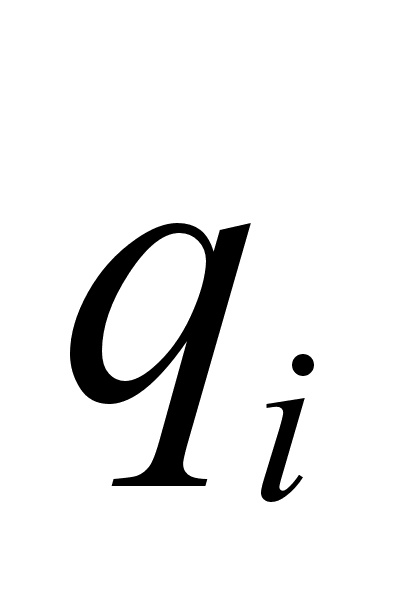 в виде функций от
в виде функций от  , мы и получим закон движения:
, мы и получим закон движения: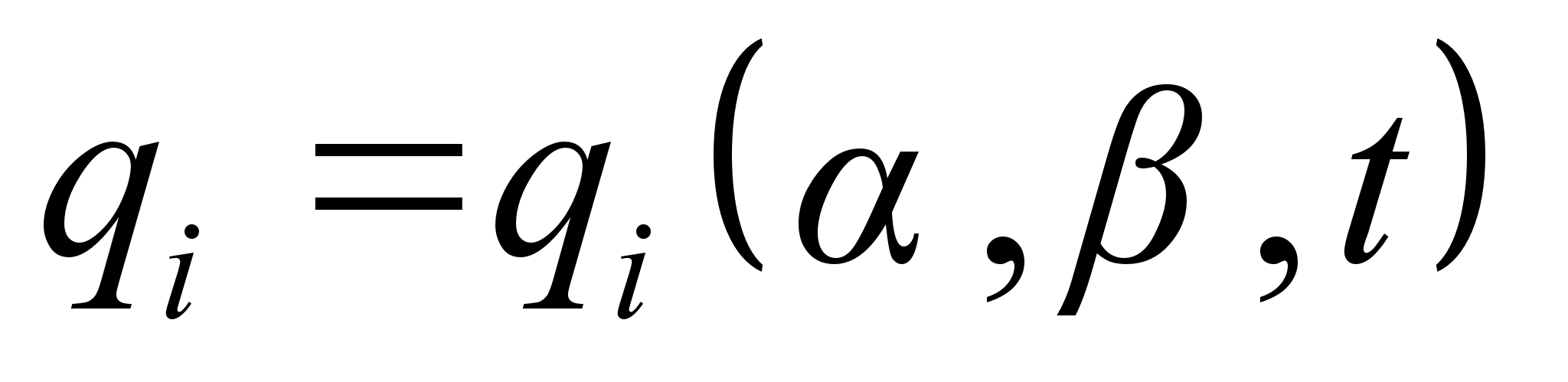
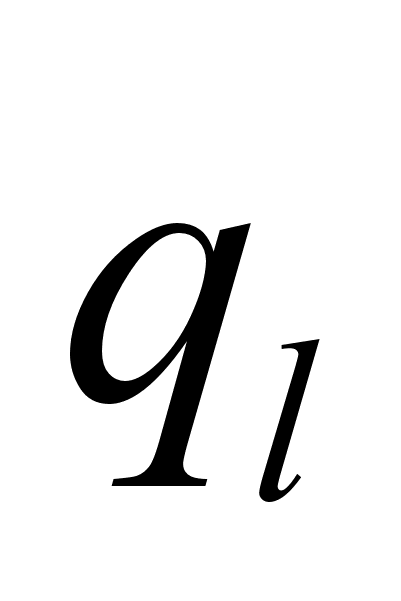 может быть связана лишь с соответствующим ей импульсом
может быть связана лишь с соответствующим ей импульсом 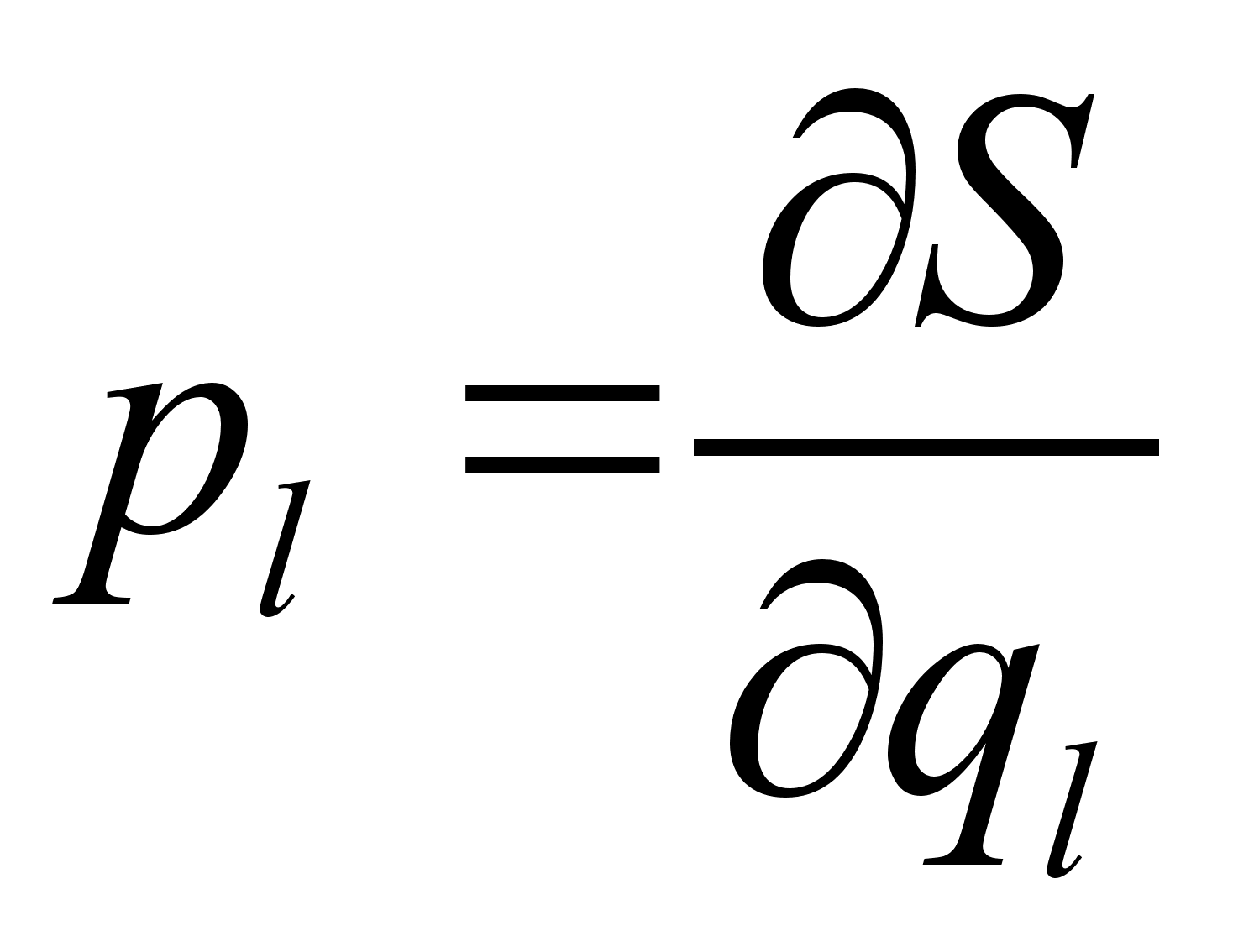 и не связана ни с какими другими импульсами или координатами, входящими уравнение Г.-Я. В частности это условие выполняется для циклических переменных.
и не связана ни с какими другими импульсами или координатами, входящими уравнение Г.-Я. В частности это условие выполняется для циклических переменных.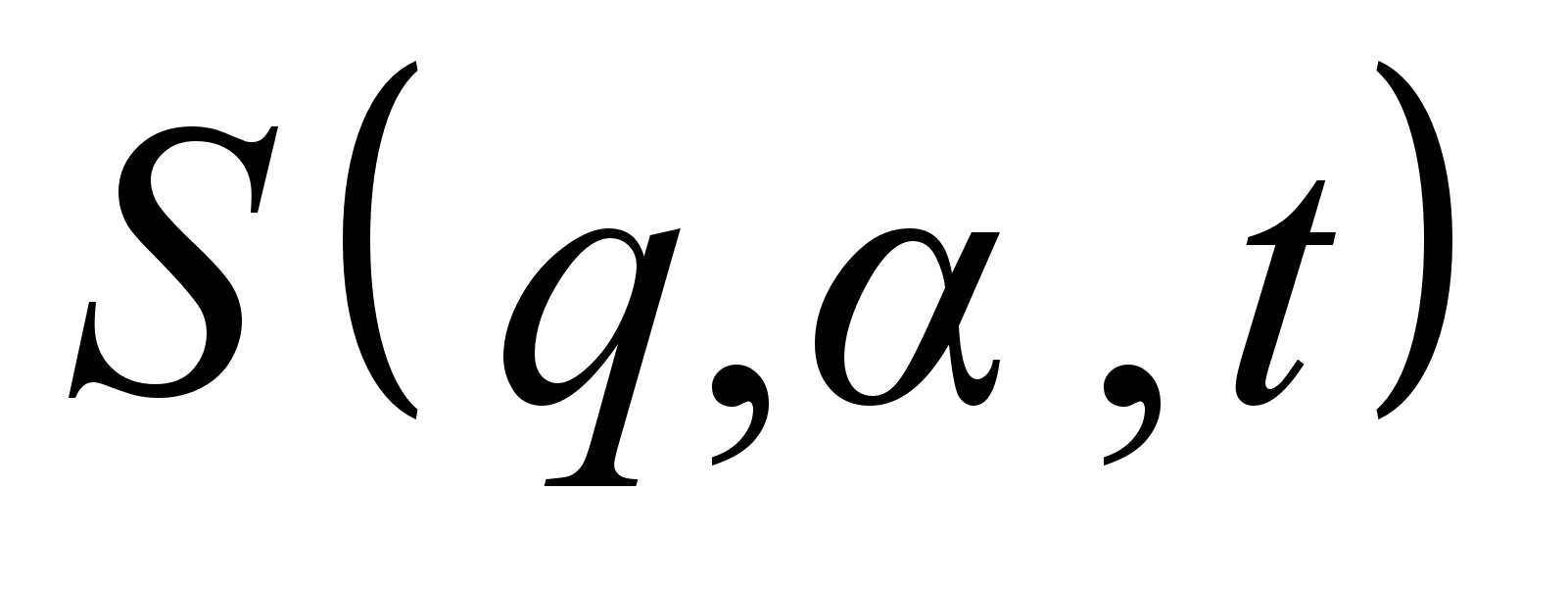 ;
;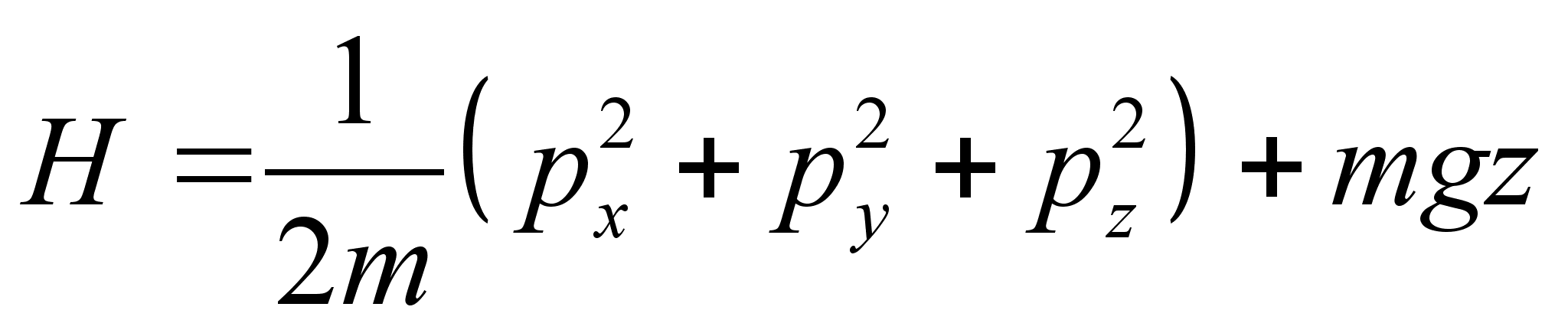
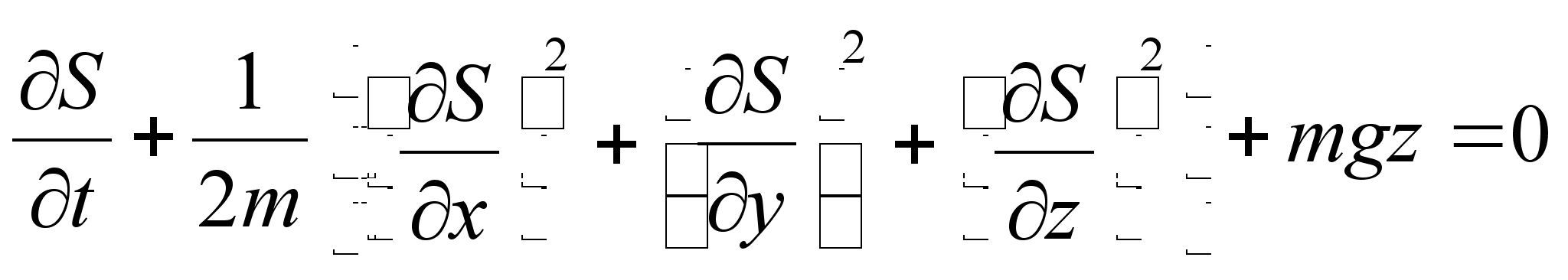
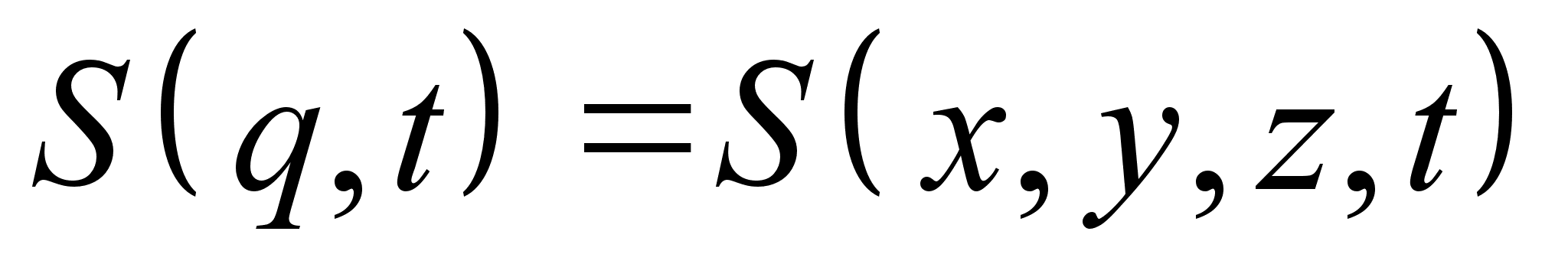 . Разделение переменных позволяет нам представить действие в виде суммы:
. Разделение переменных позволяет нам представить действие в виде суммы: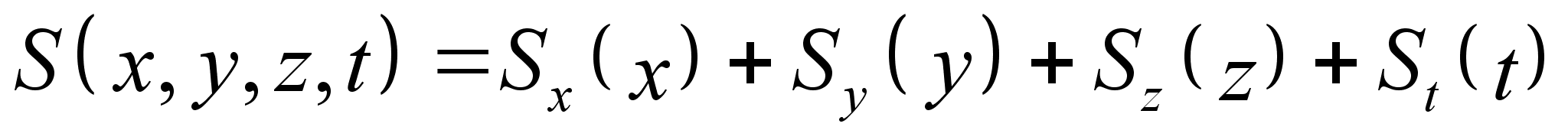
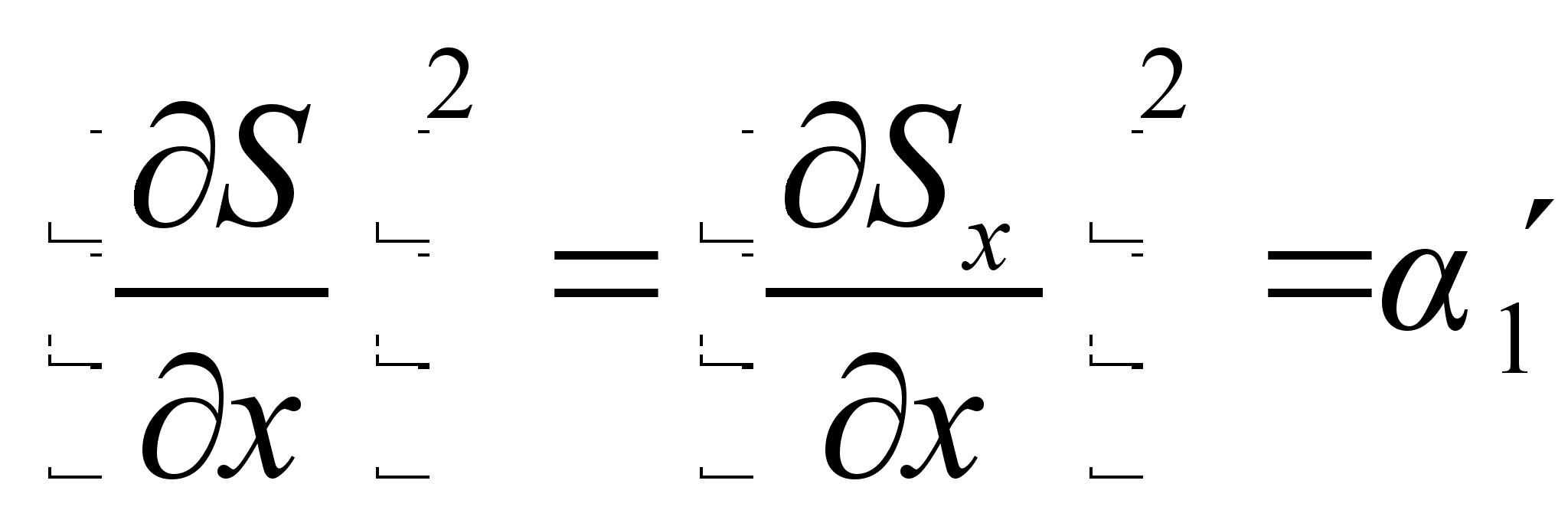
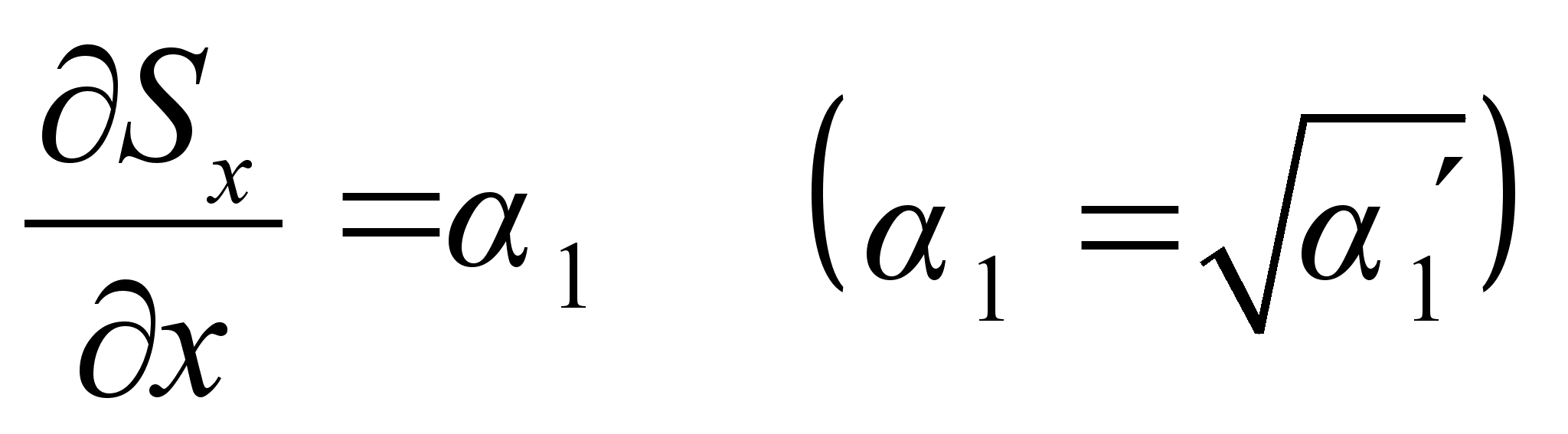
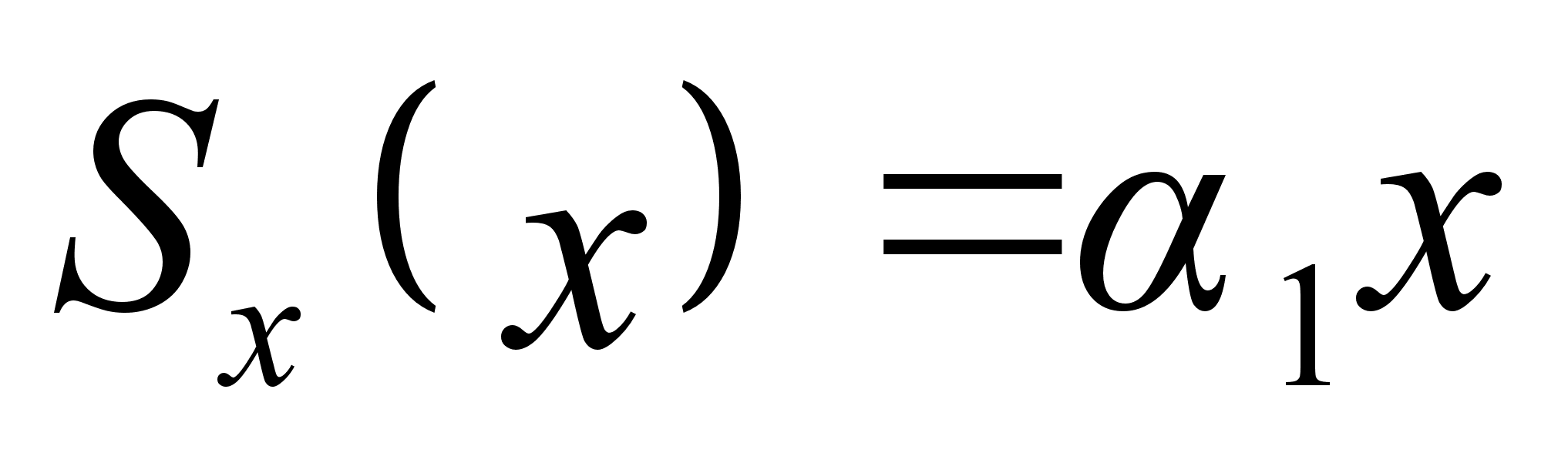
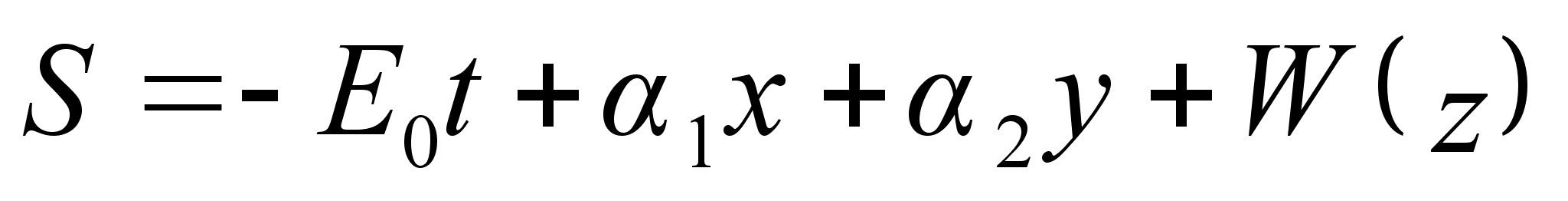
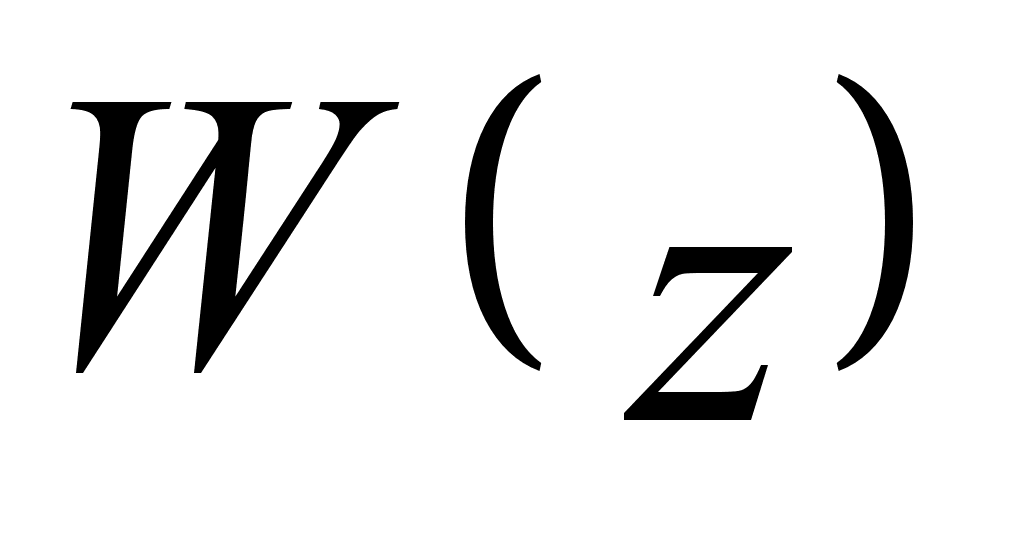 не должна содержать более констант. Полученная при интегрировании этой части действия константа будет выражаться через уже имеющиеся три. Поэтому вид функции
не должна содержать более констант. Полученная при интегрировании этой части действия константа будет выражаться через уже имеющиеся три. Поэтому вид функции 

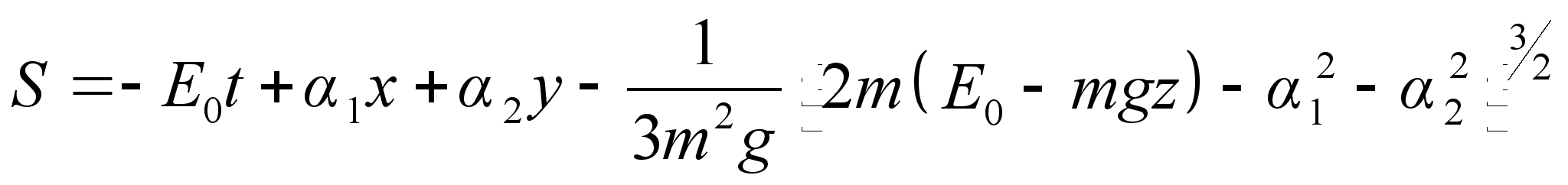
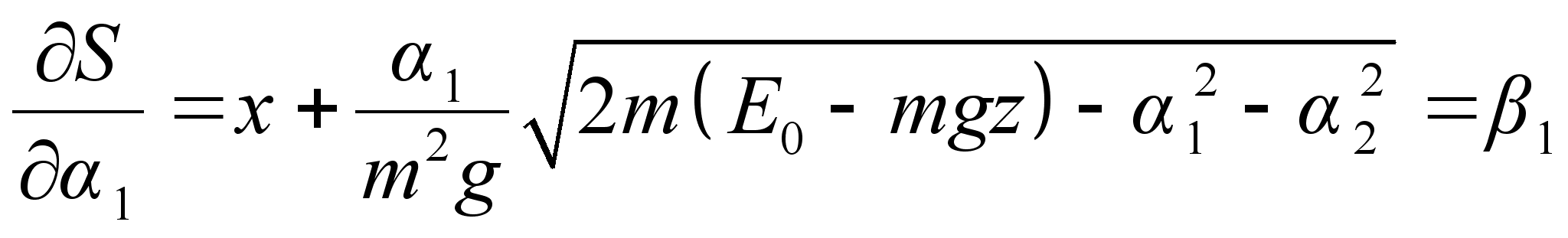
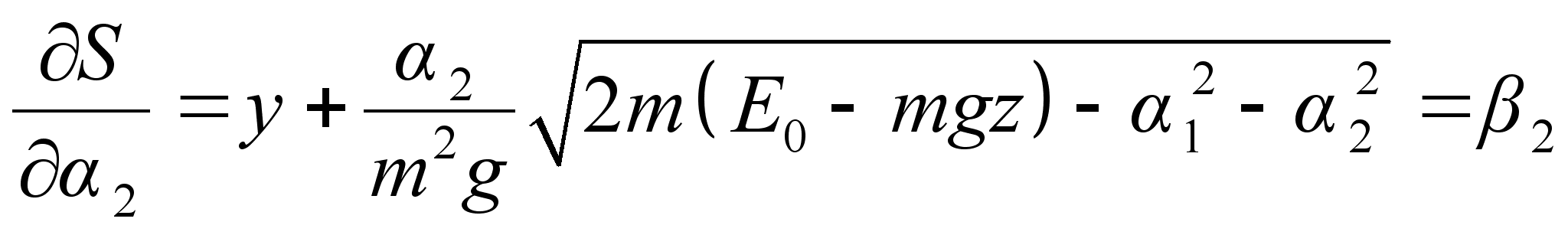
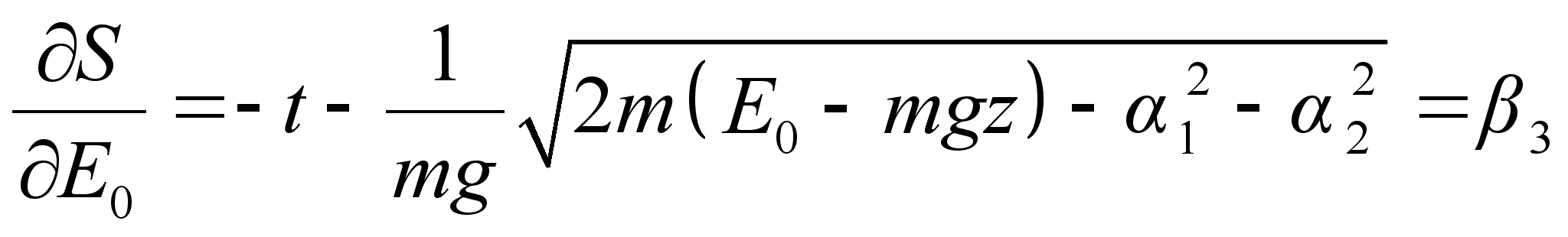
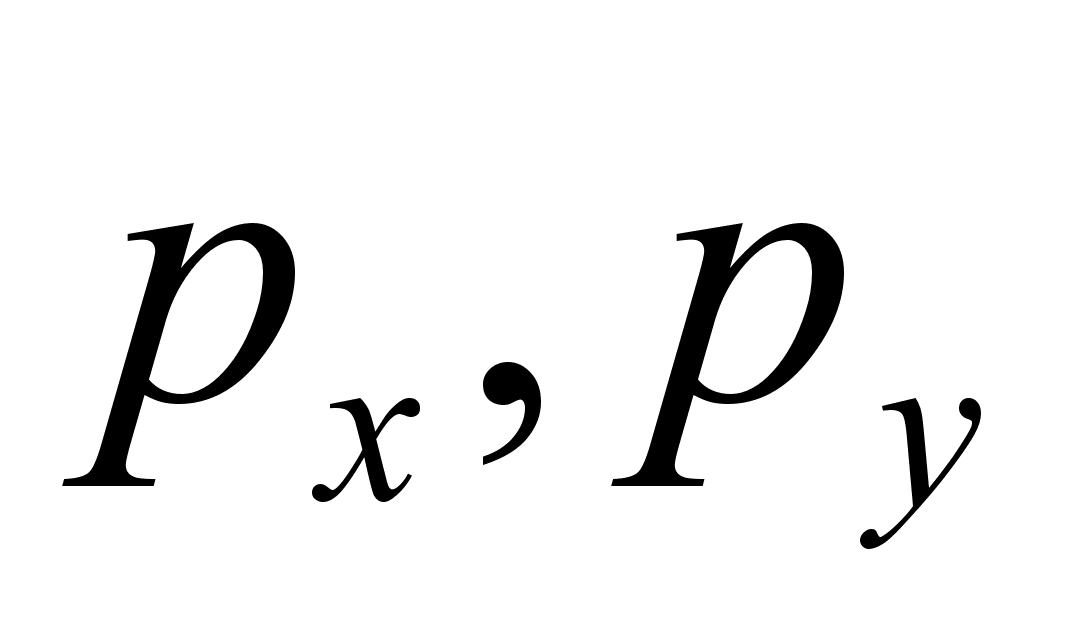 – сохраняются:
– сохраняются: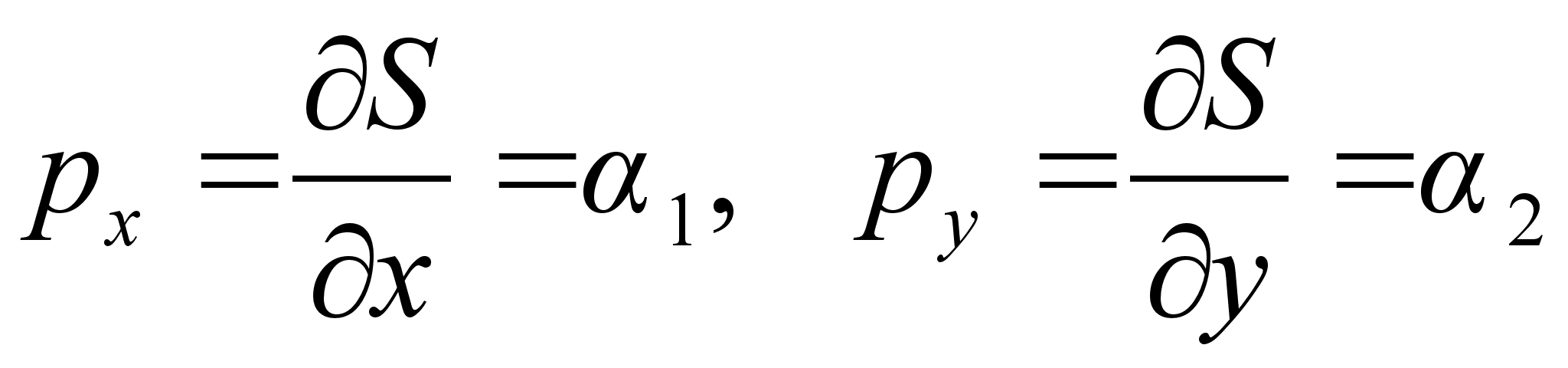
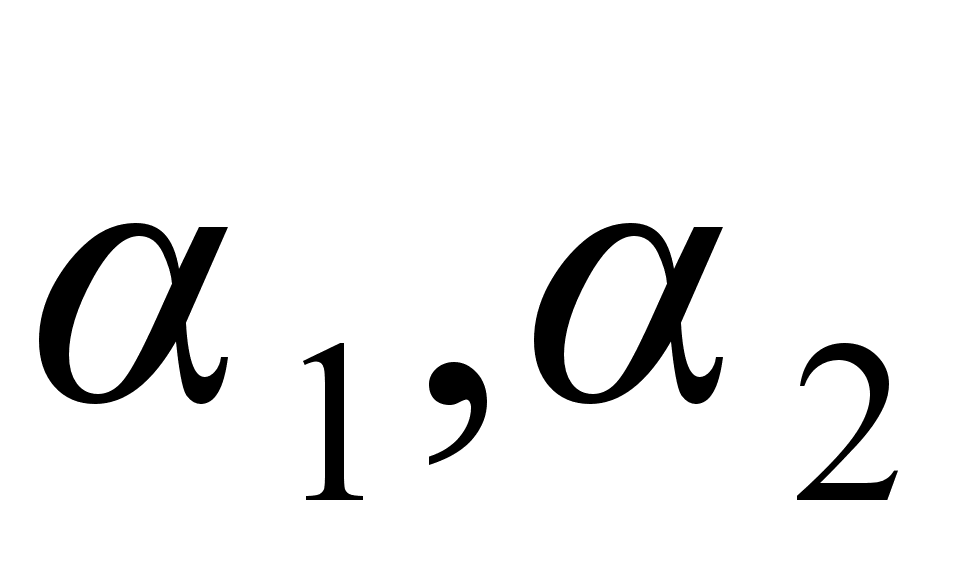 движение происходит по прямой вдоль оси Oz .
движение происходит по прямой вдоль оси Oz . , как функцию координат:
, как функцию координат: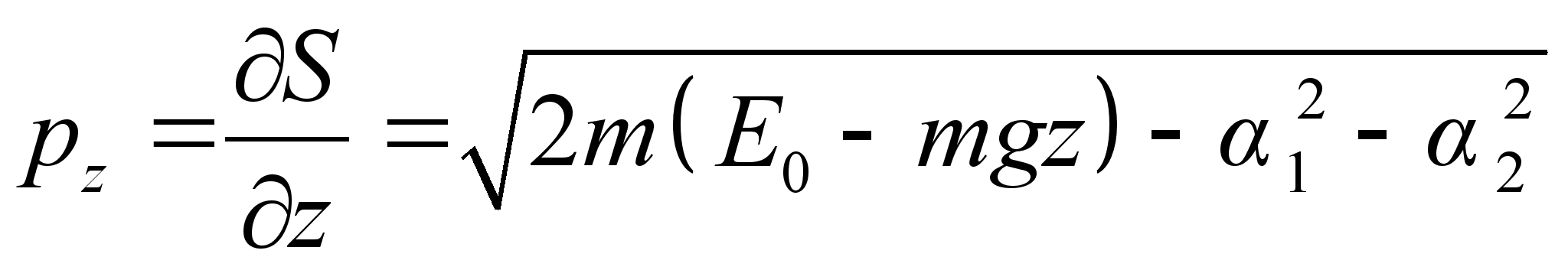
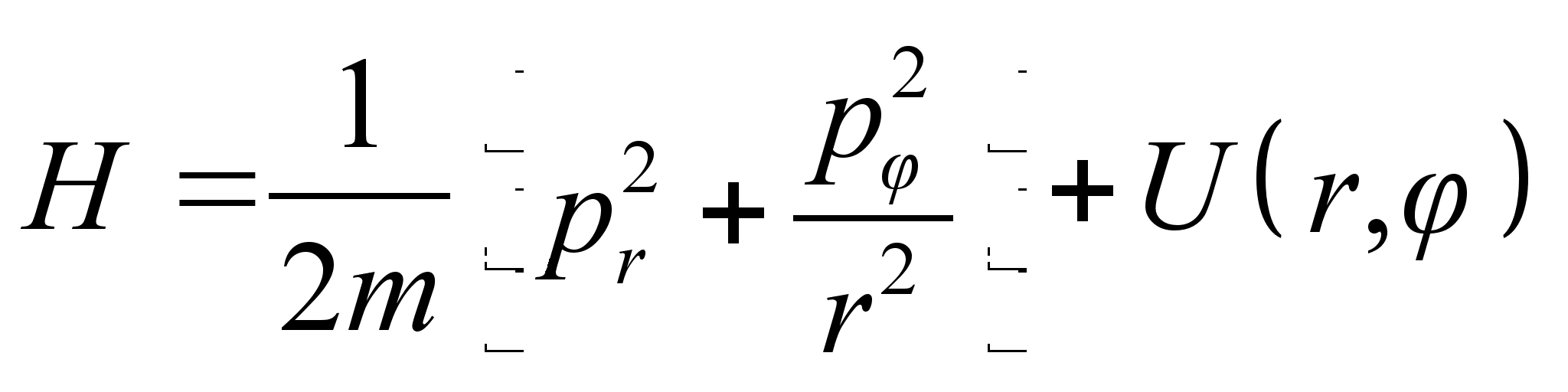
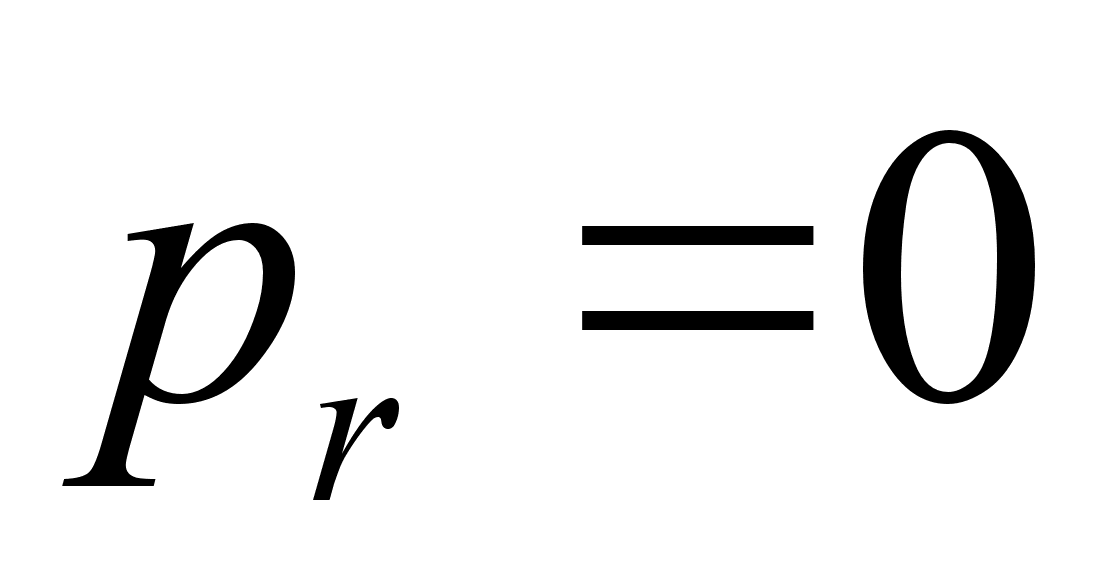 , а функция Гамильтона примет вид:
, а функция Гамильтона примет вид: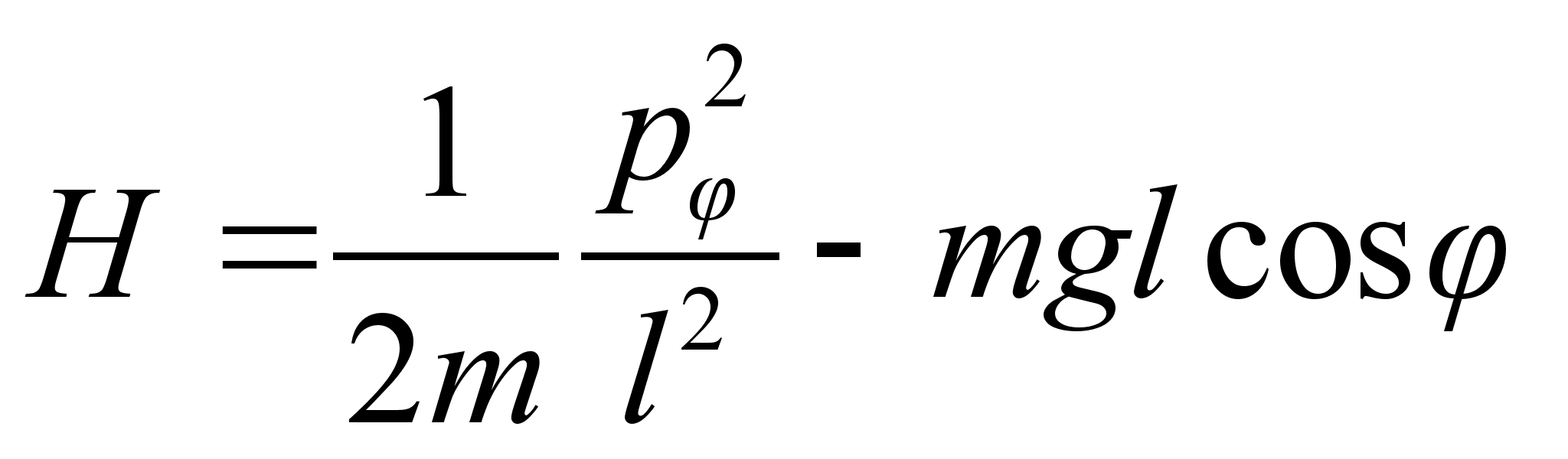


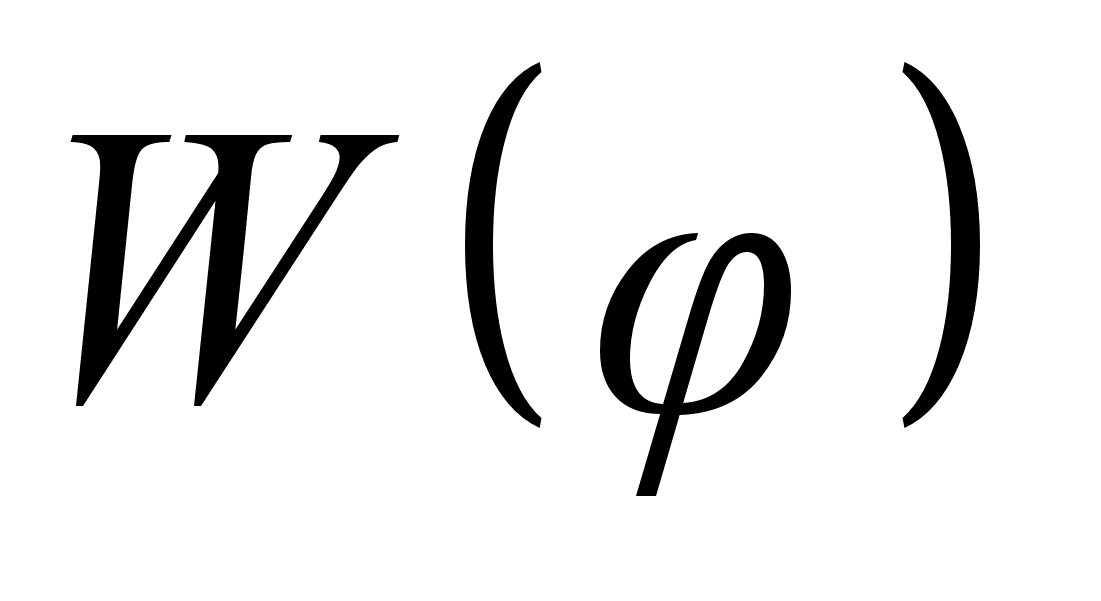 :
: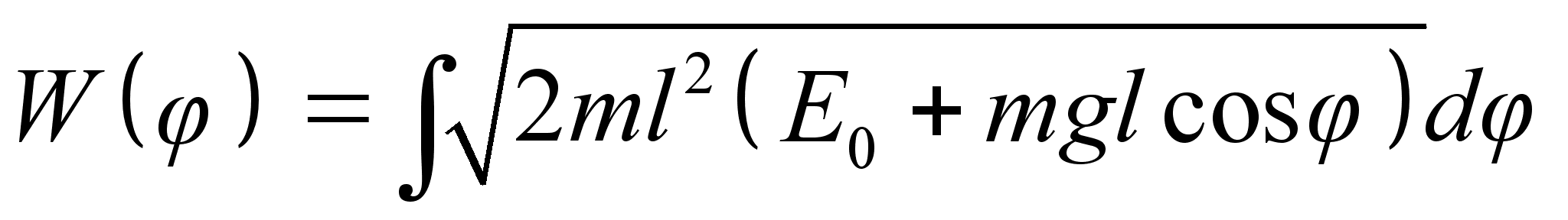
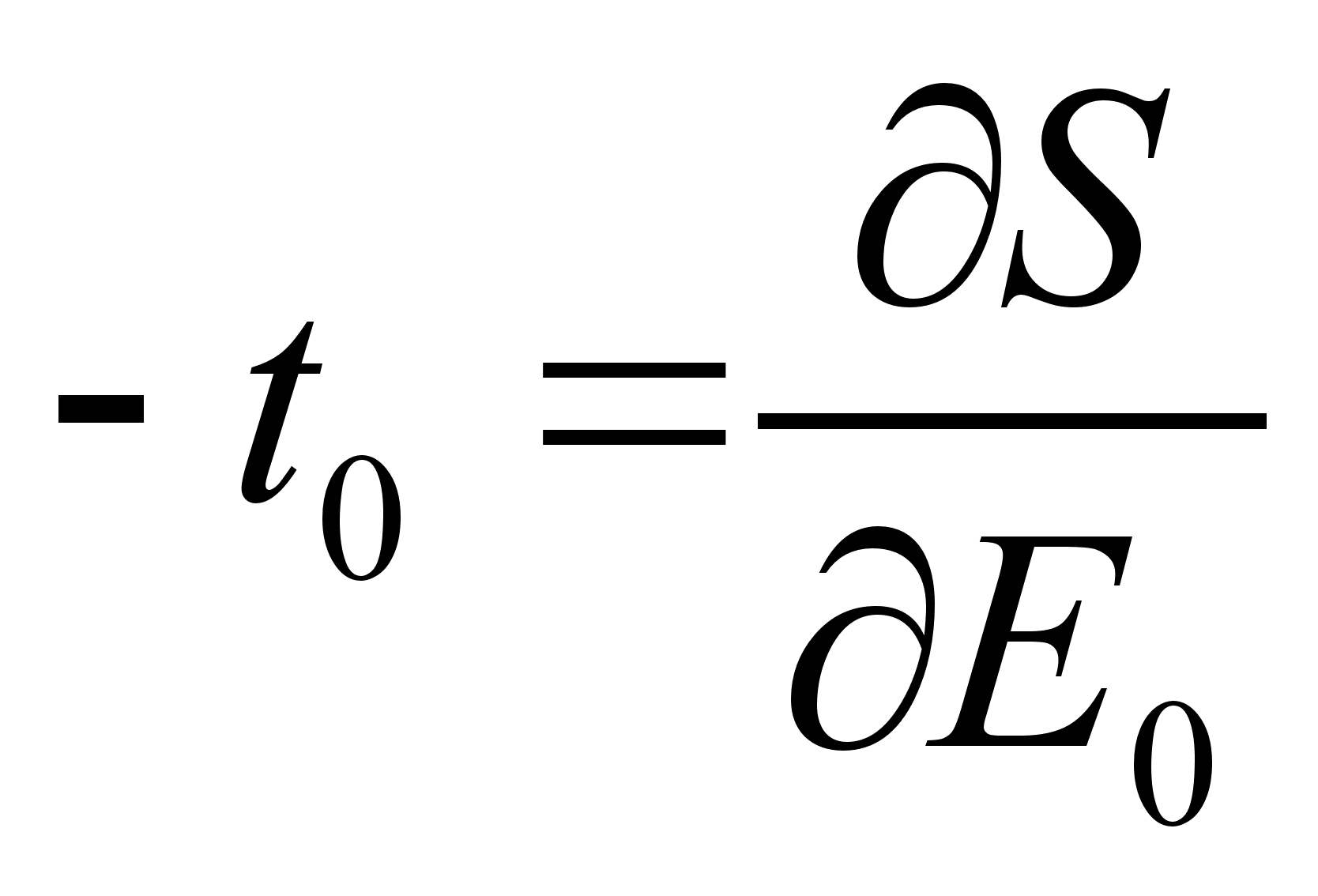
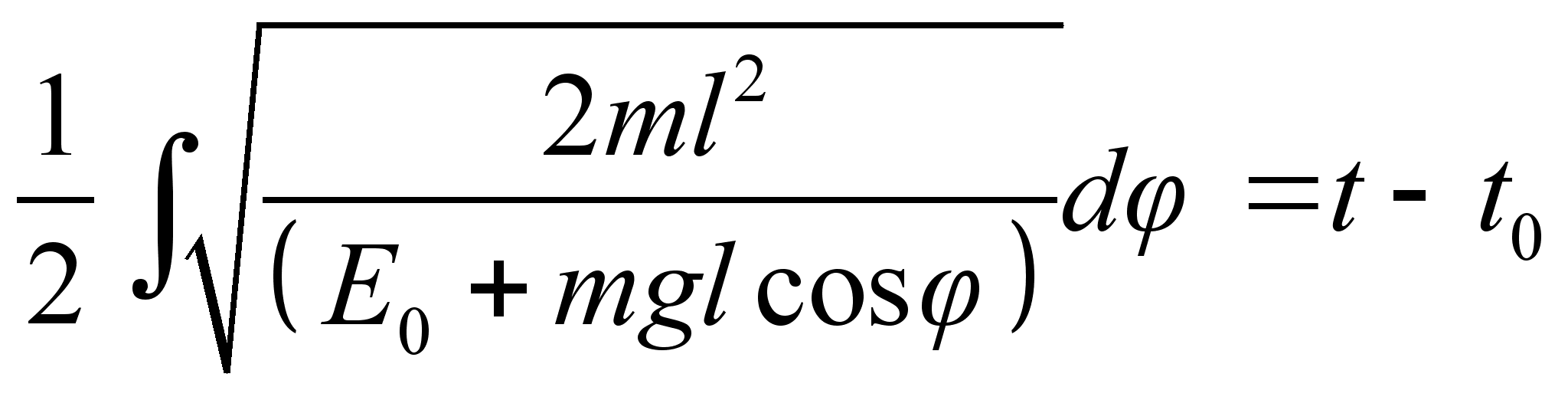


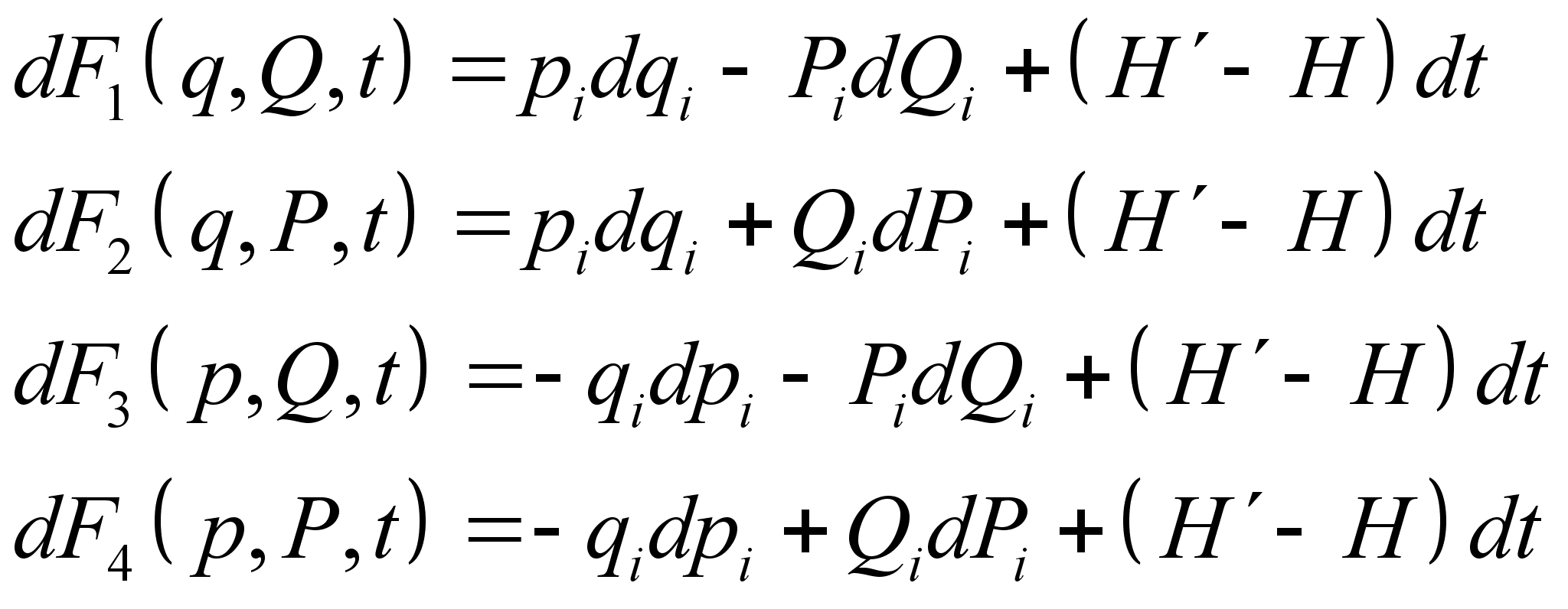
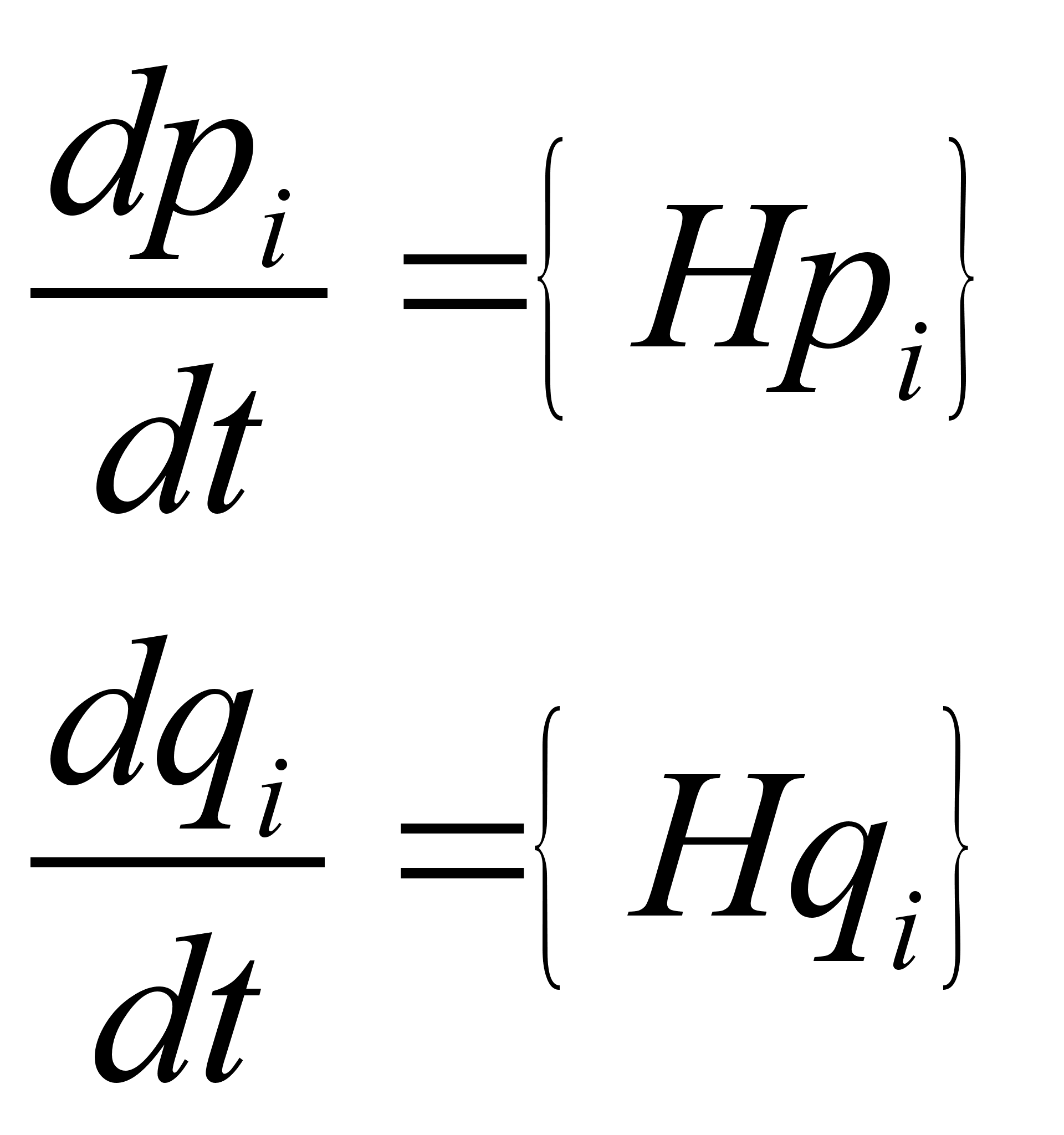
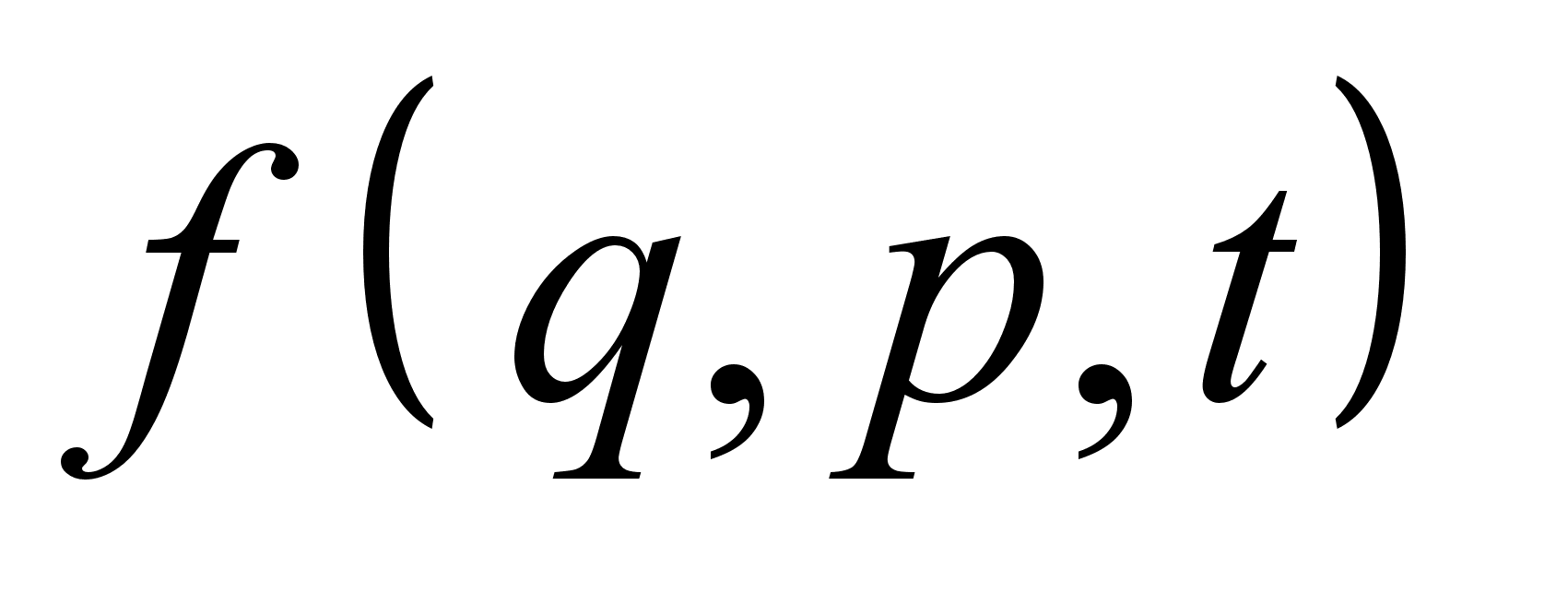 канонических переменных имеют место соотношения:
канонических переменных имеют место соотношения: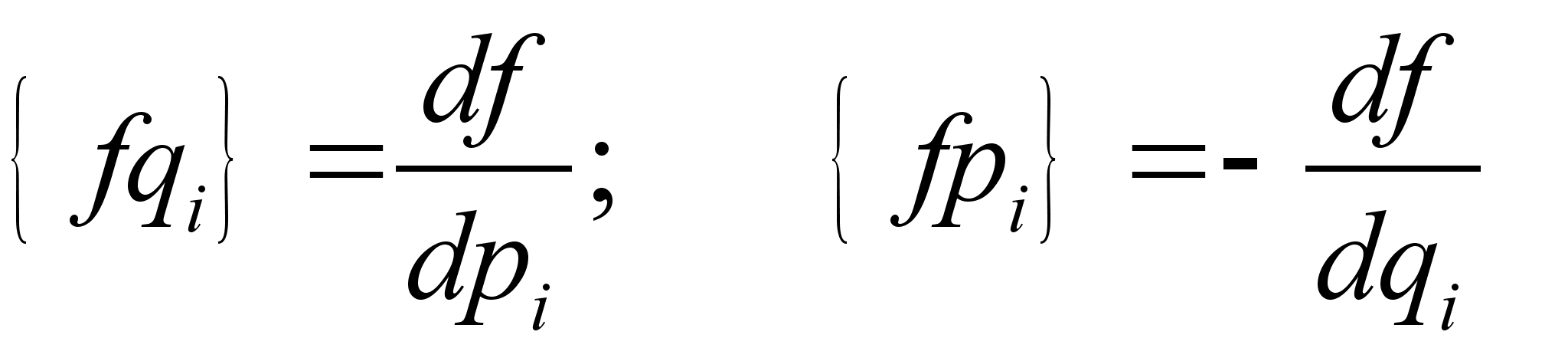
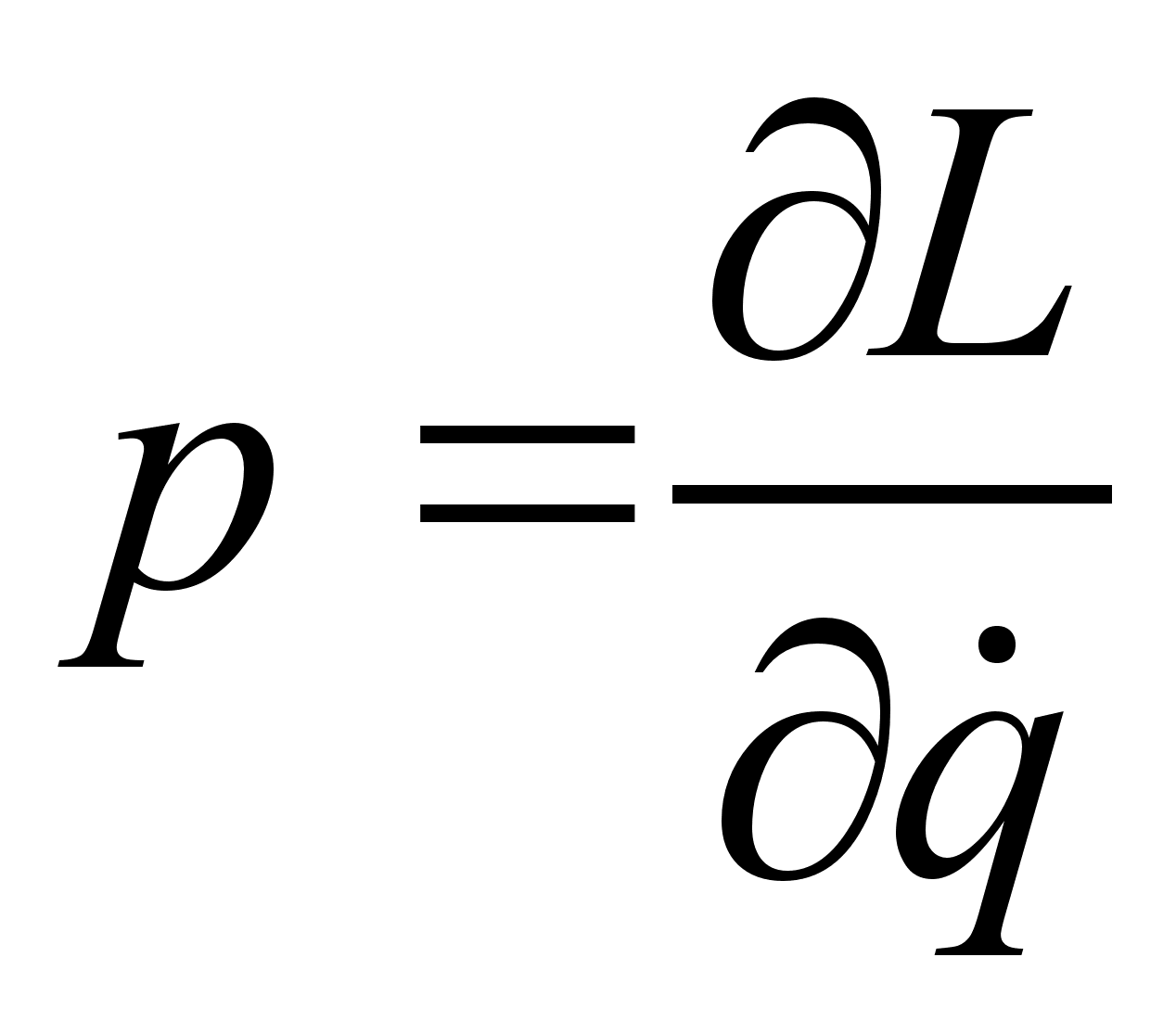
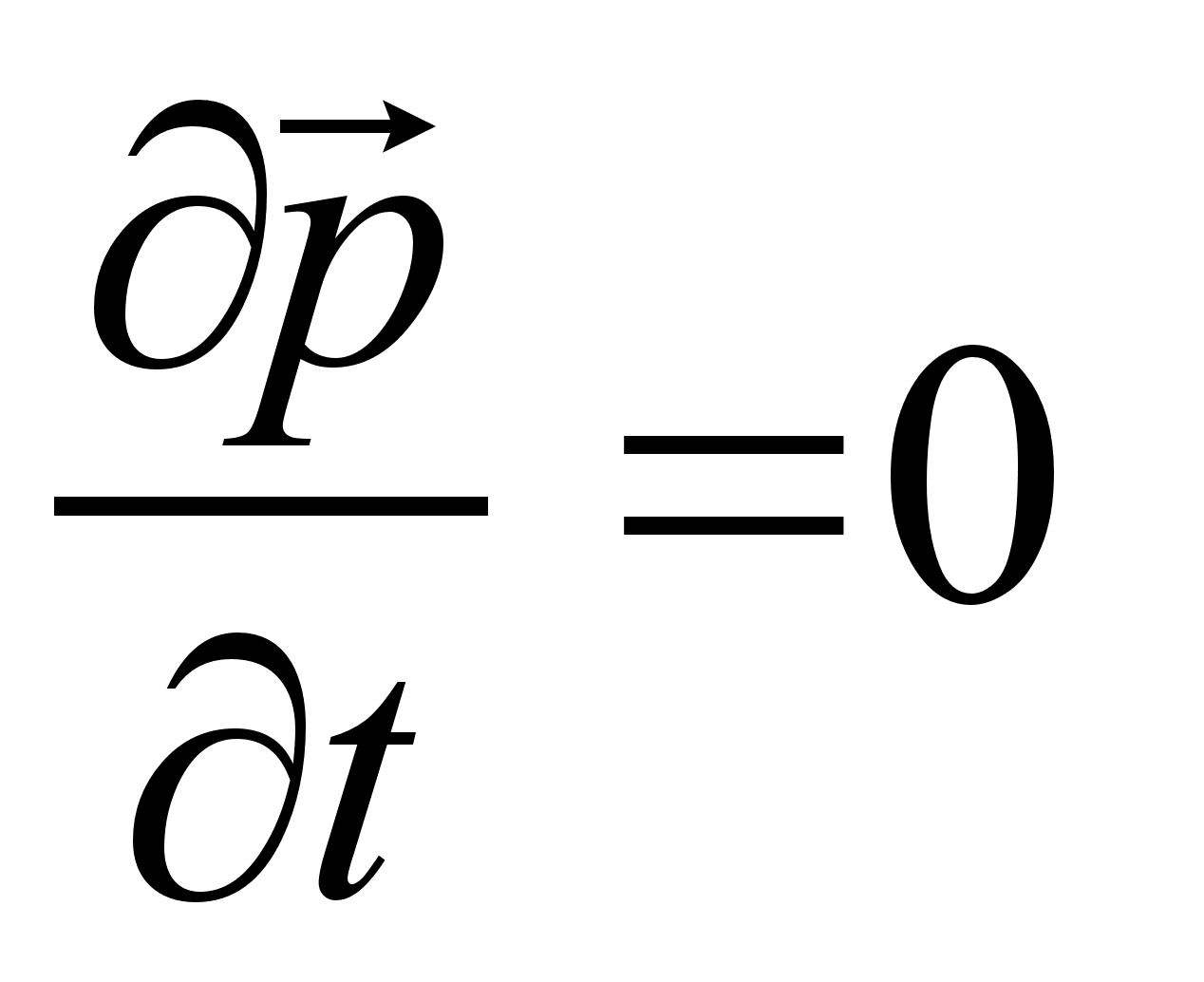
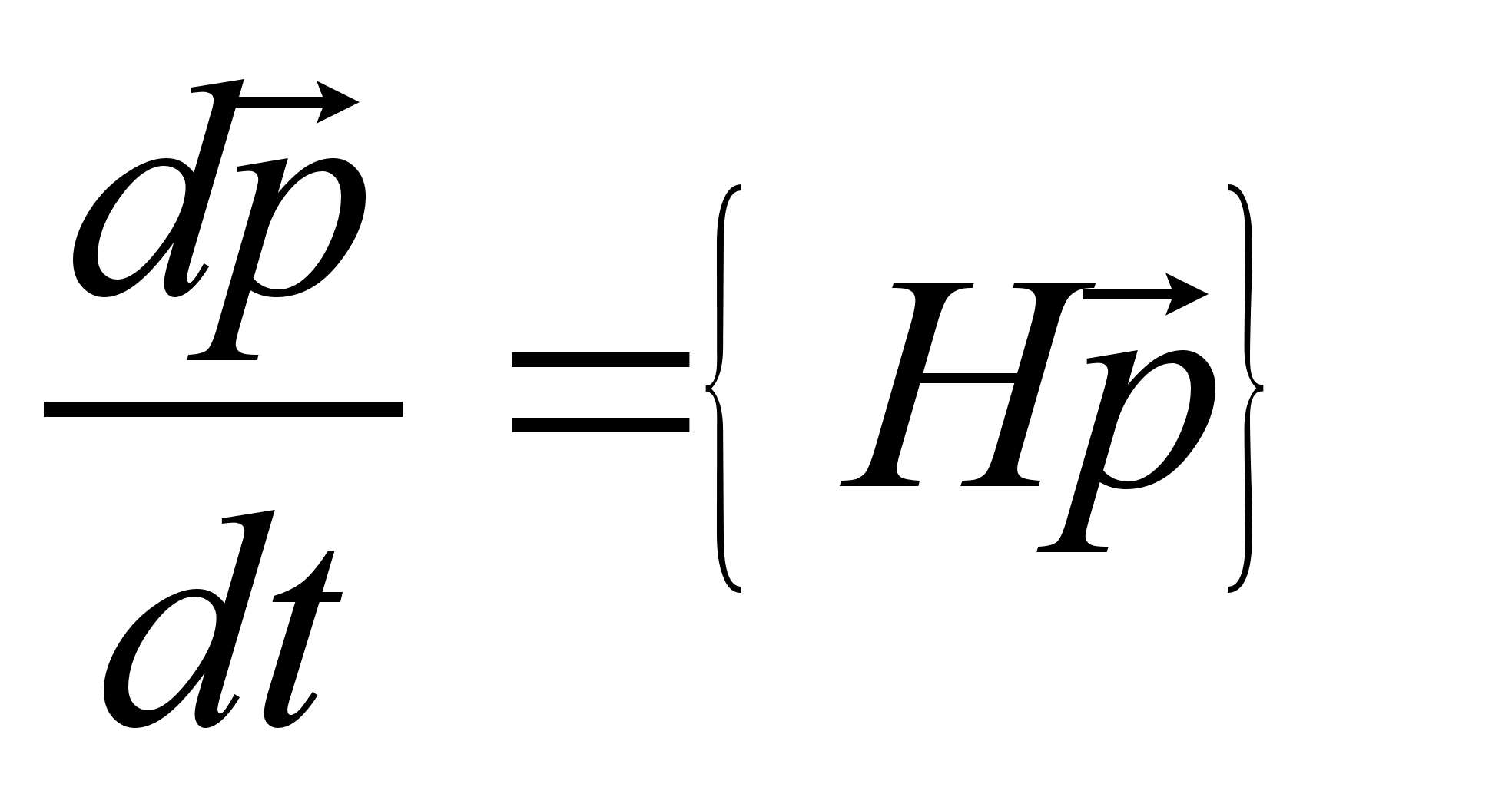
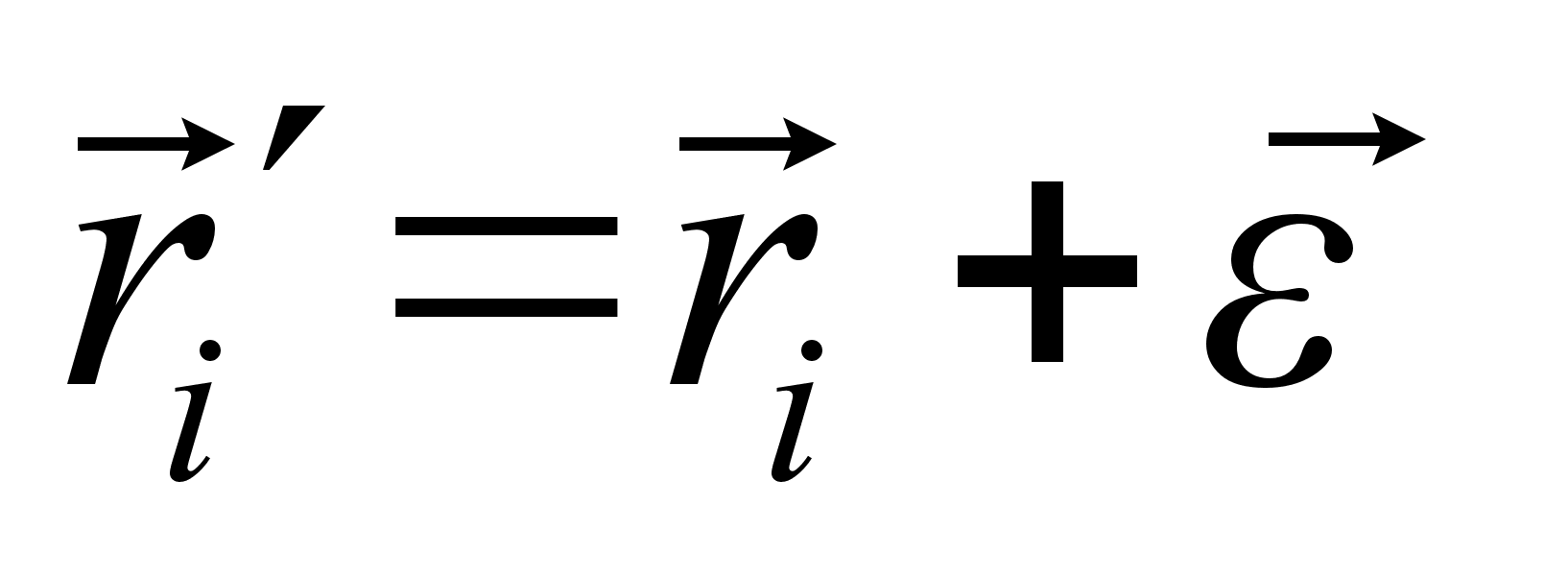
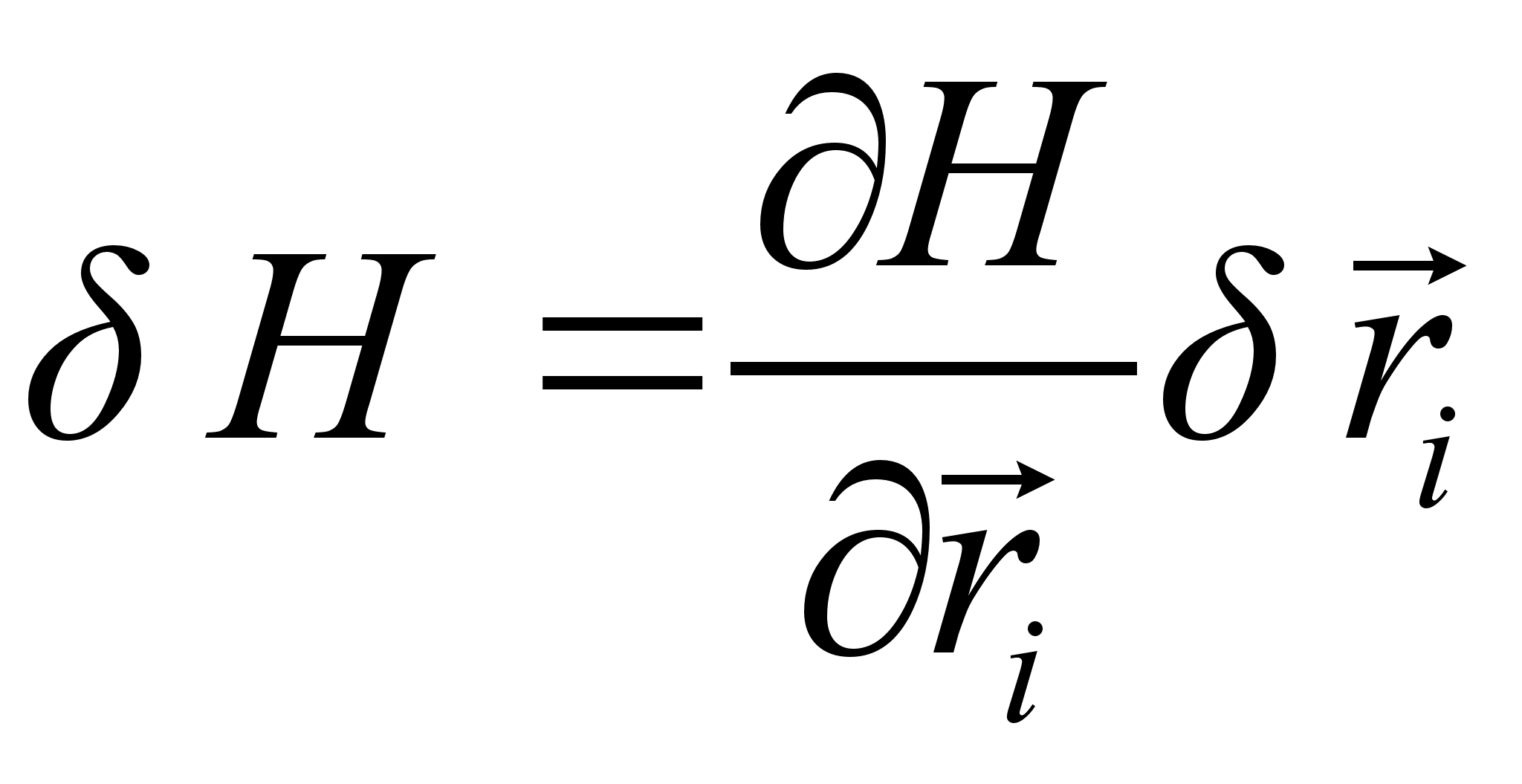
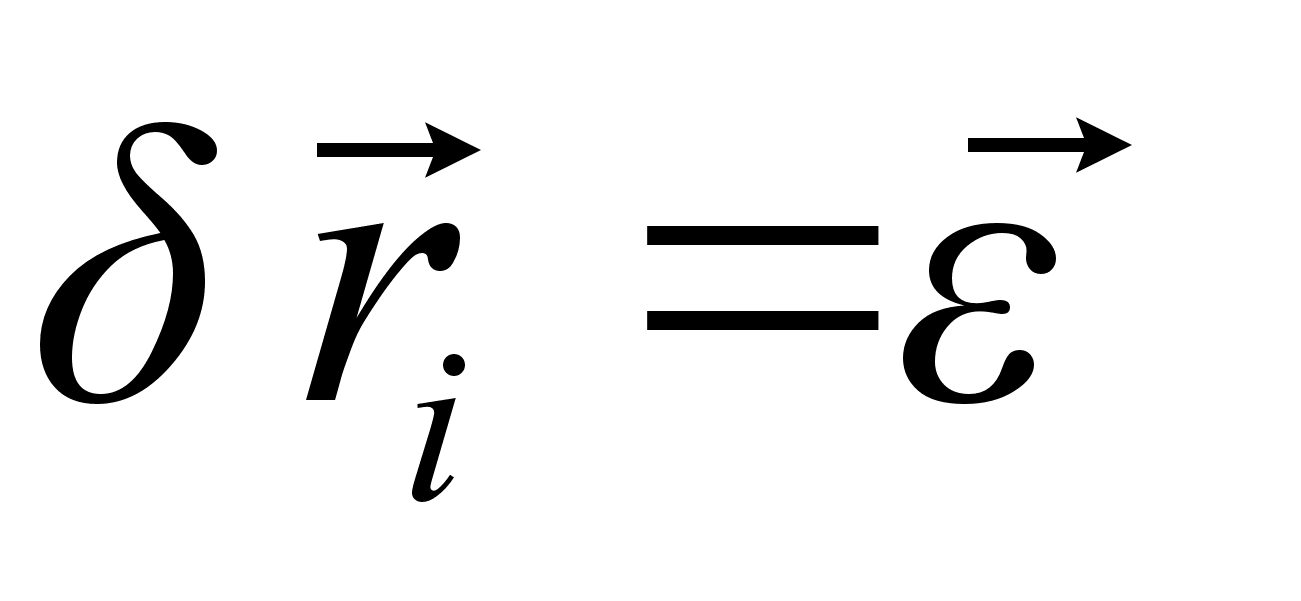 , можем вынести его за знак суммы. Принимая во внимание, что
, можем вынести его за знак суммы. Принимая во внимание, что 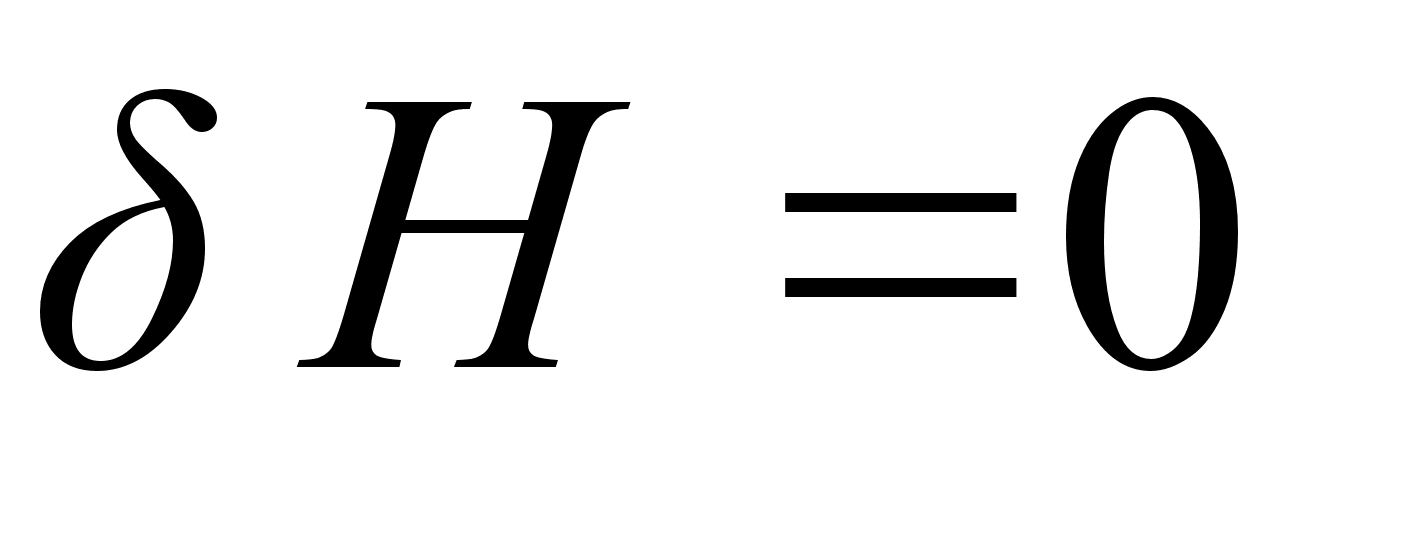 , получим:
, получим: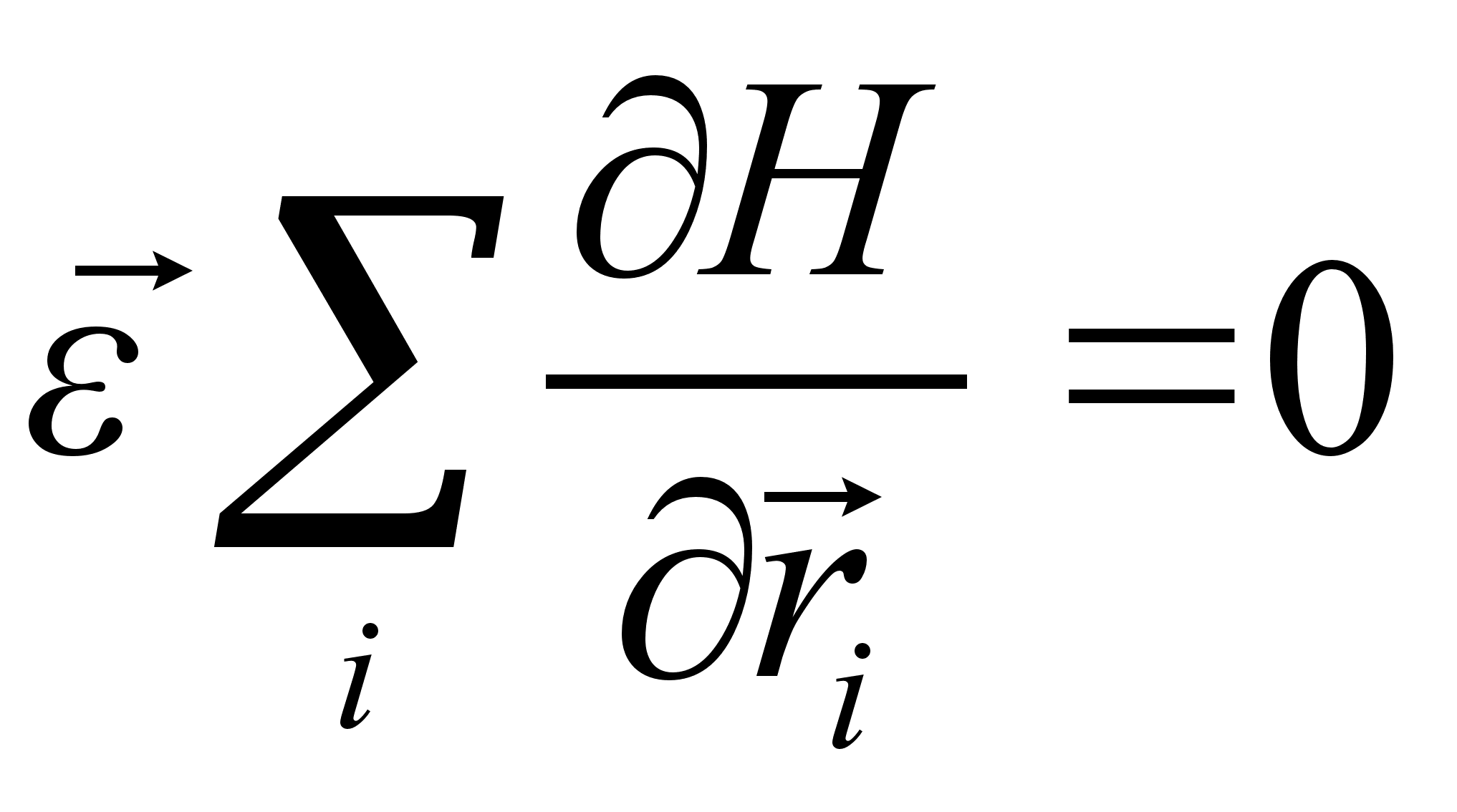
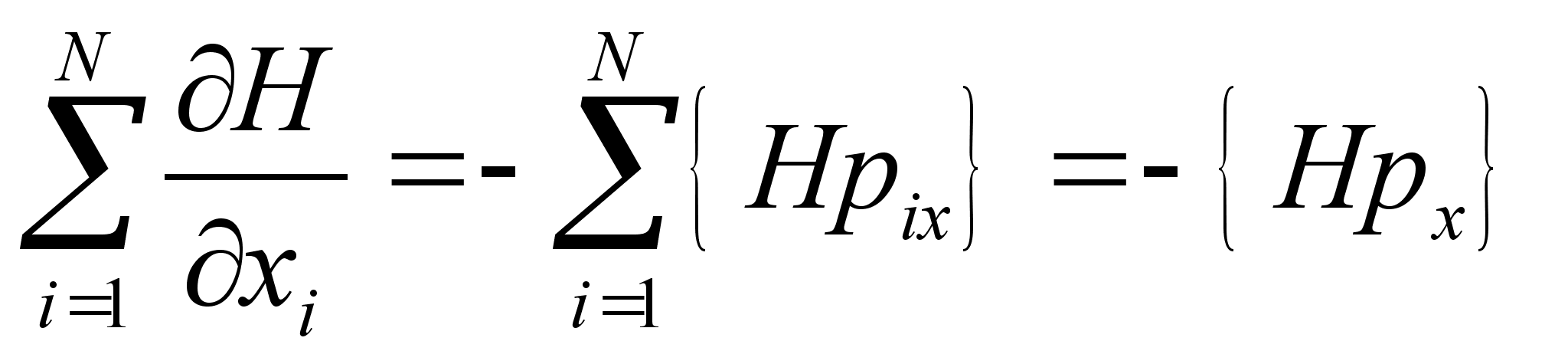
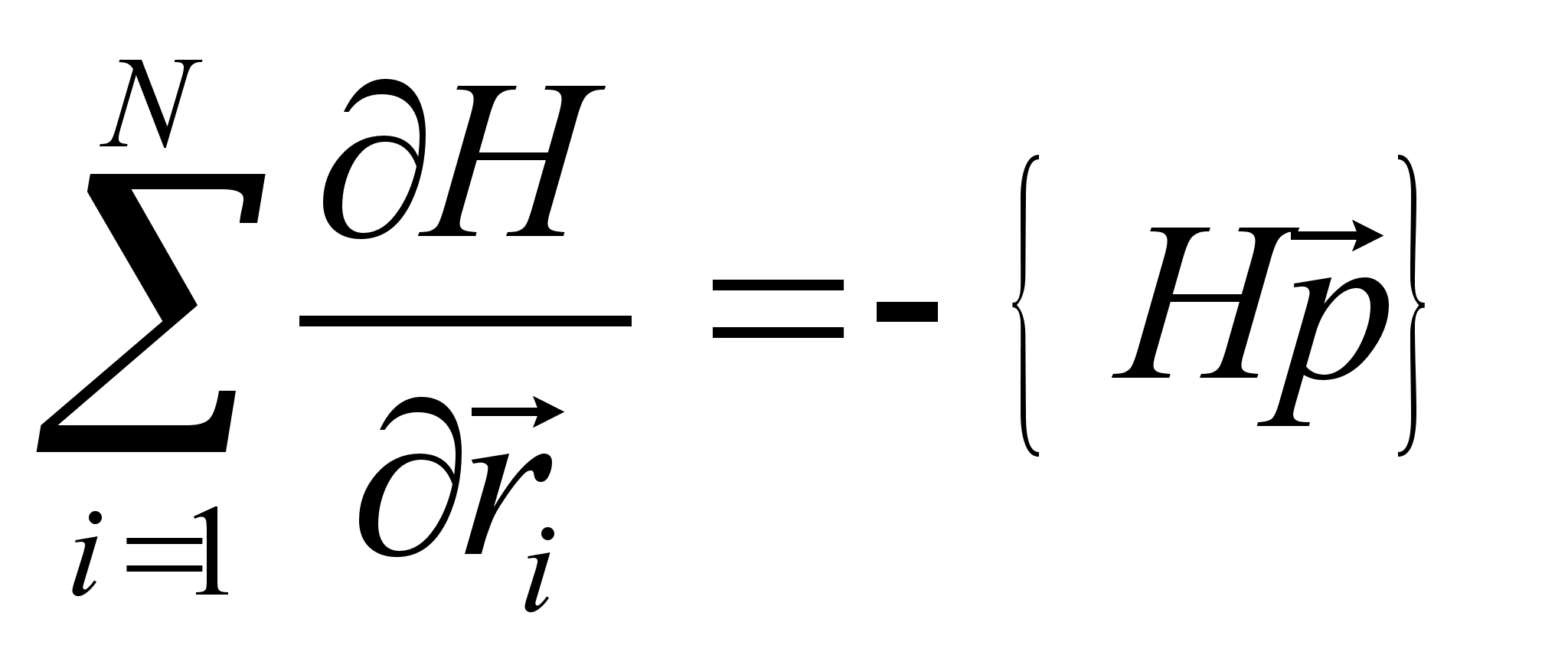
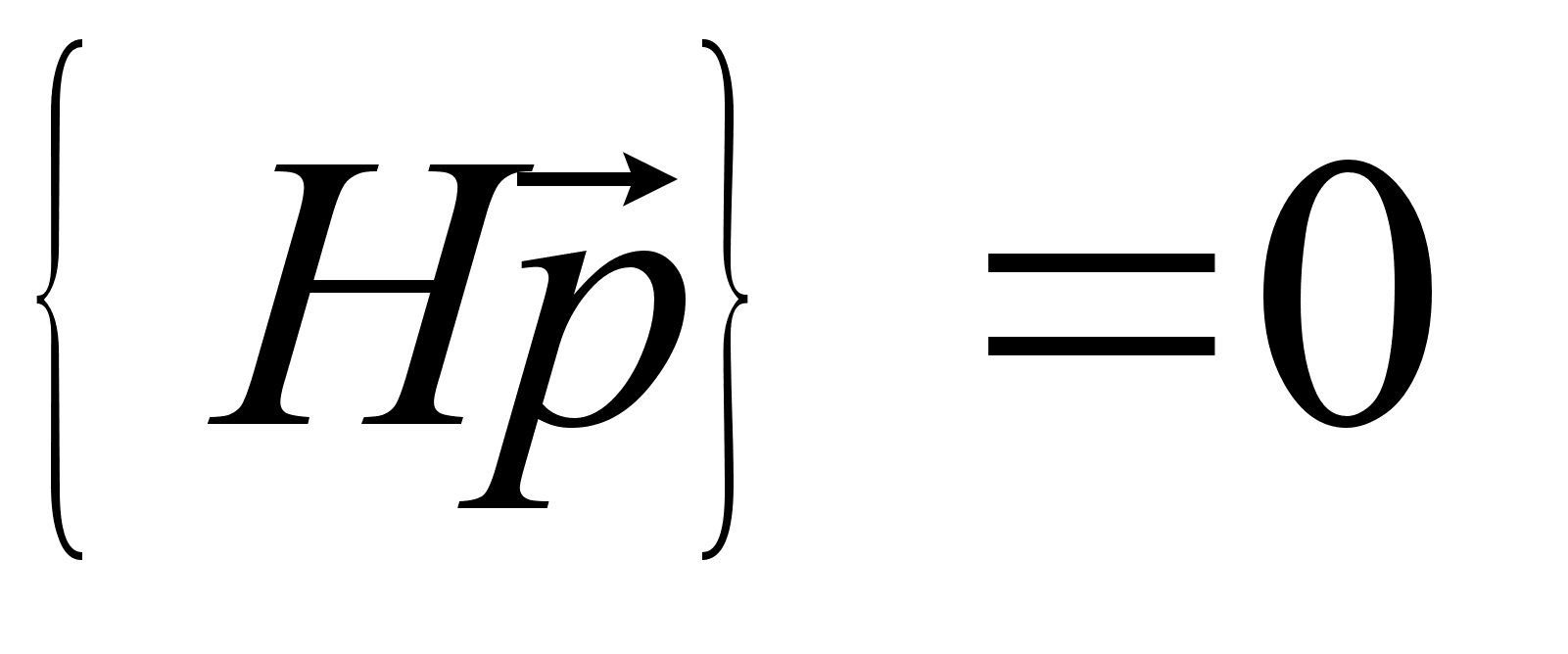
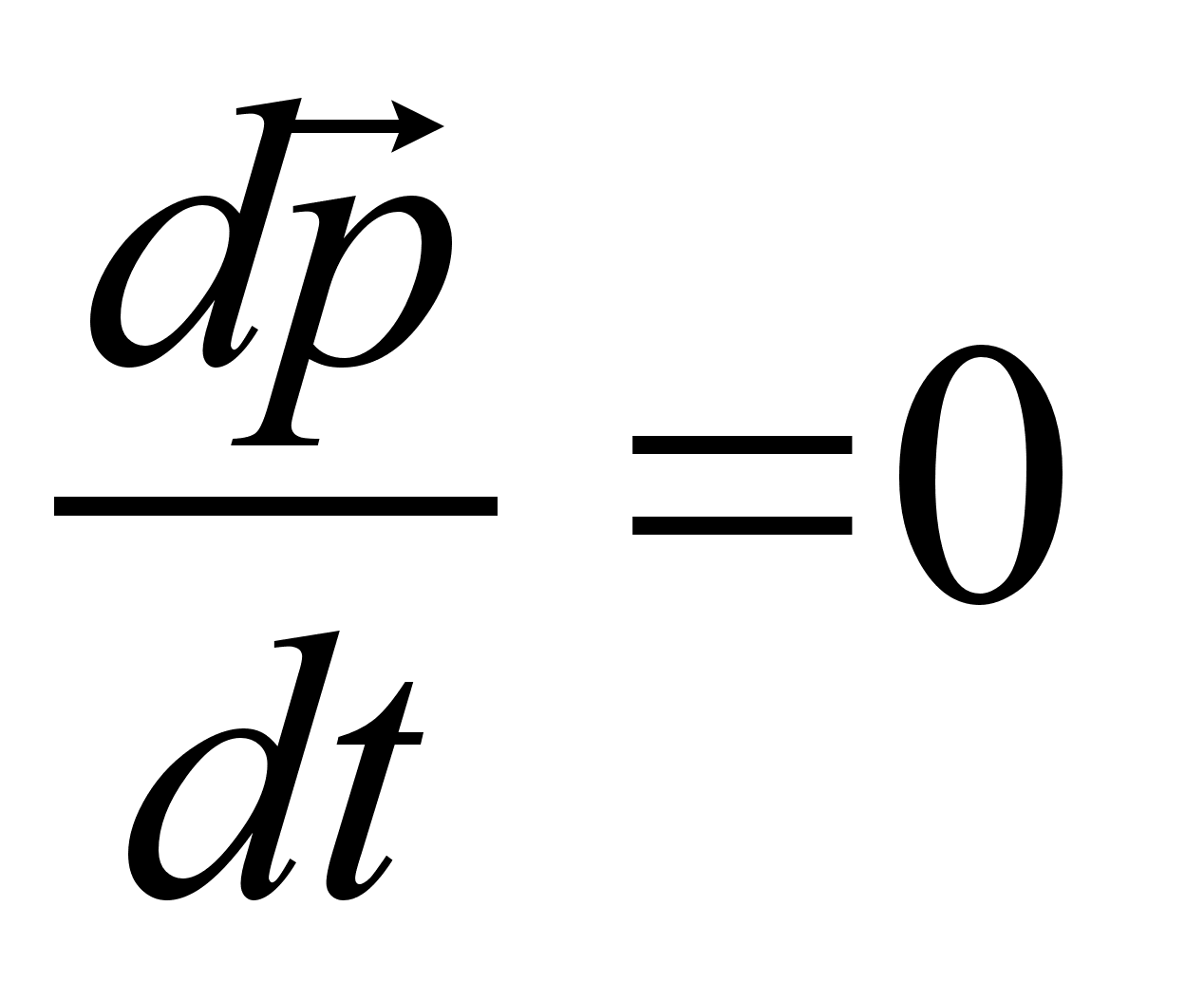
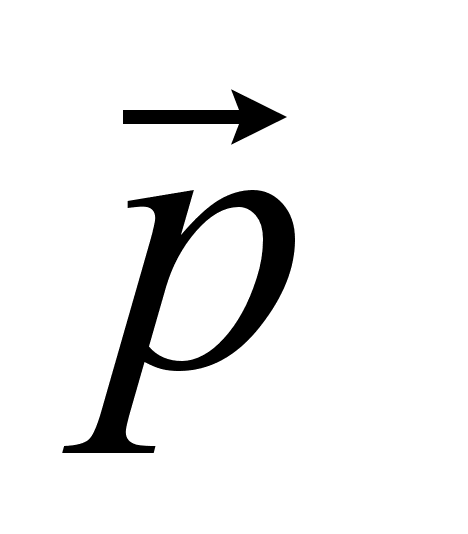 является интегралом движения.
является интегралом движения.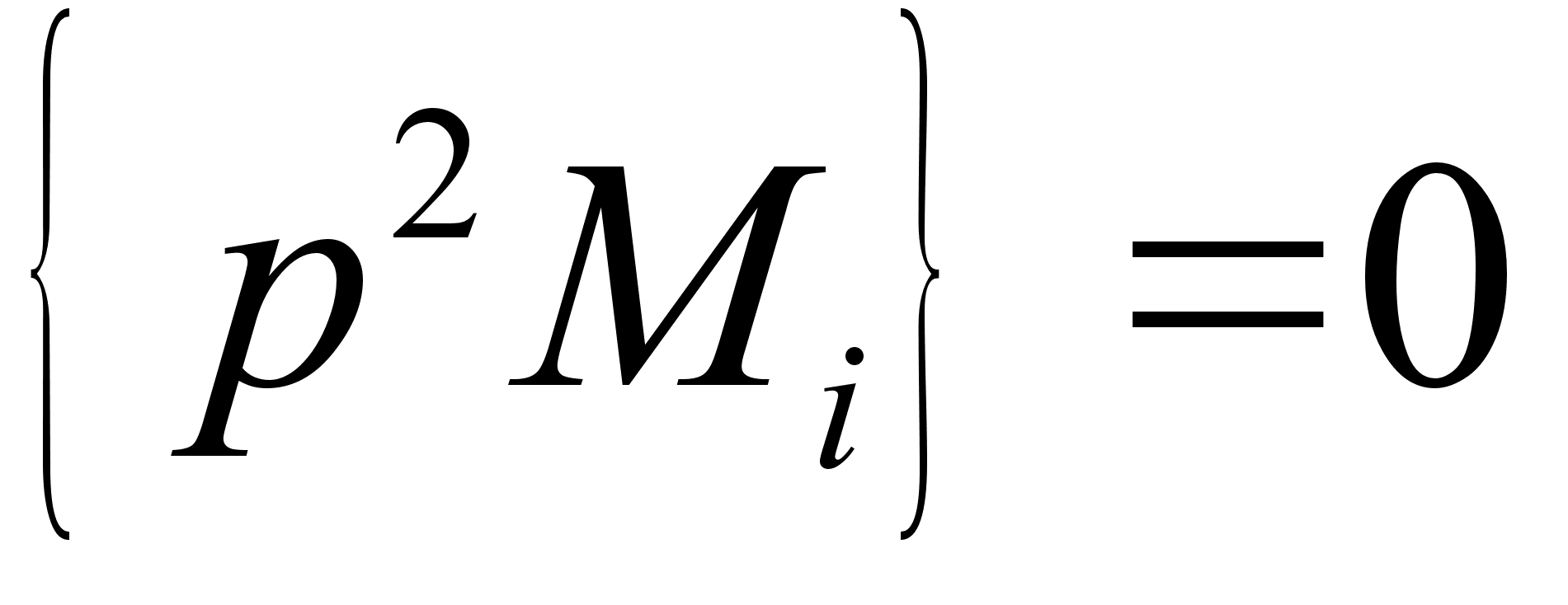 .
.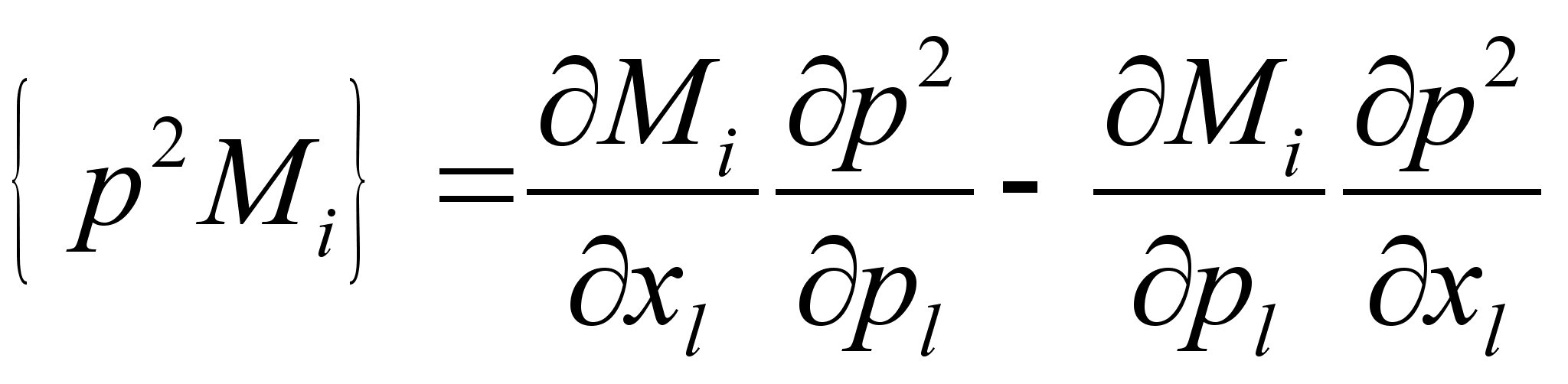
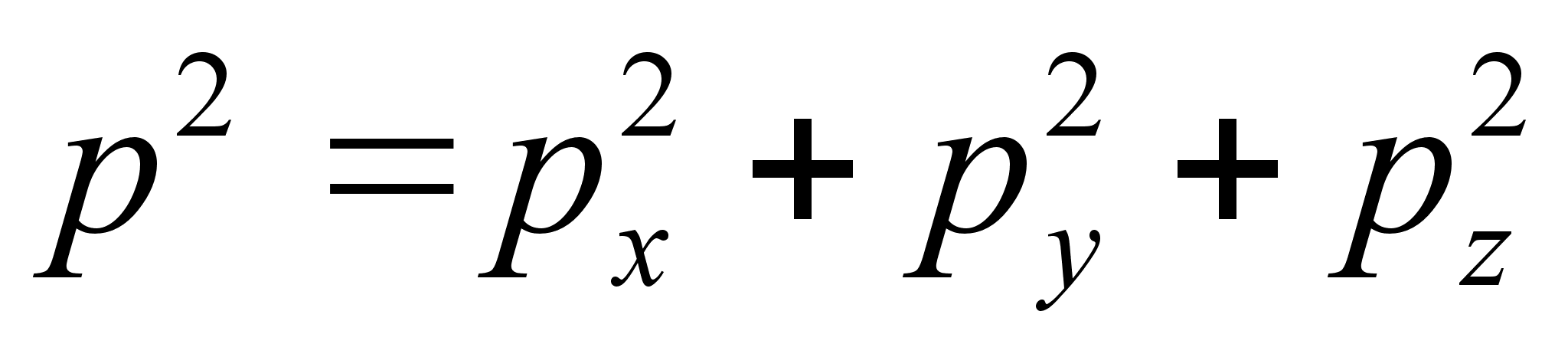 , и что импульсы и координаты являются независимыми переменными, получим:
, и что импульсы и координаты являются независимыми переменными, получим: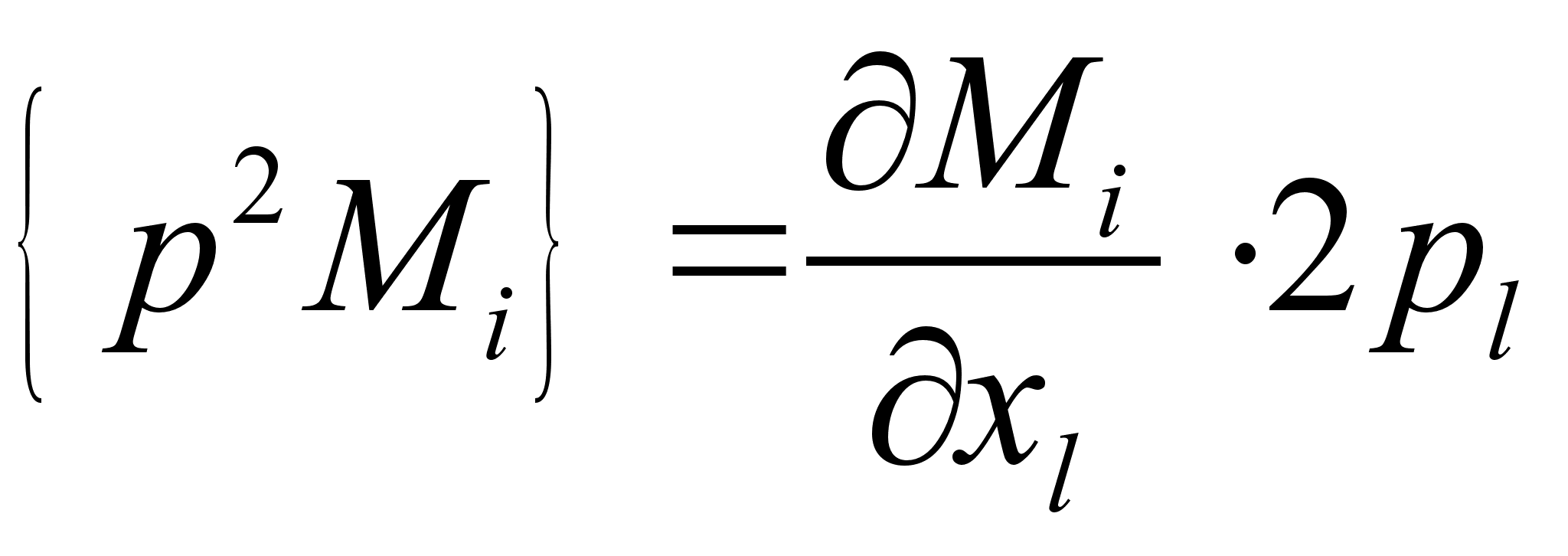
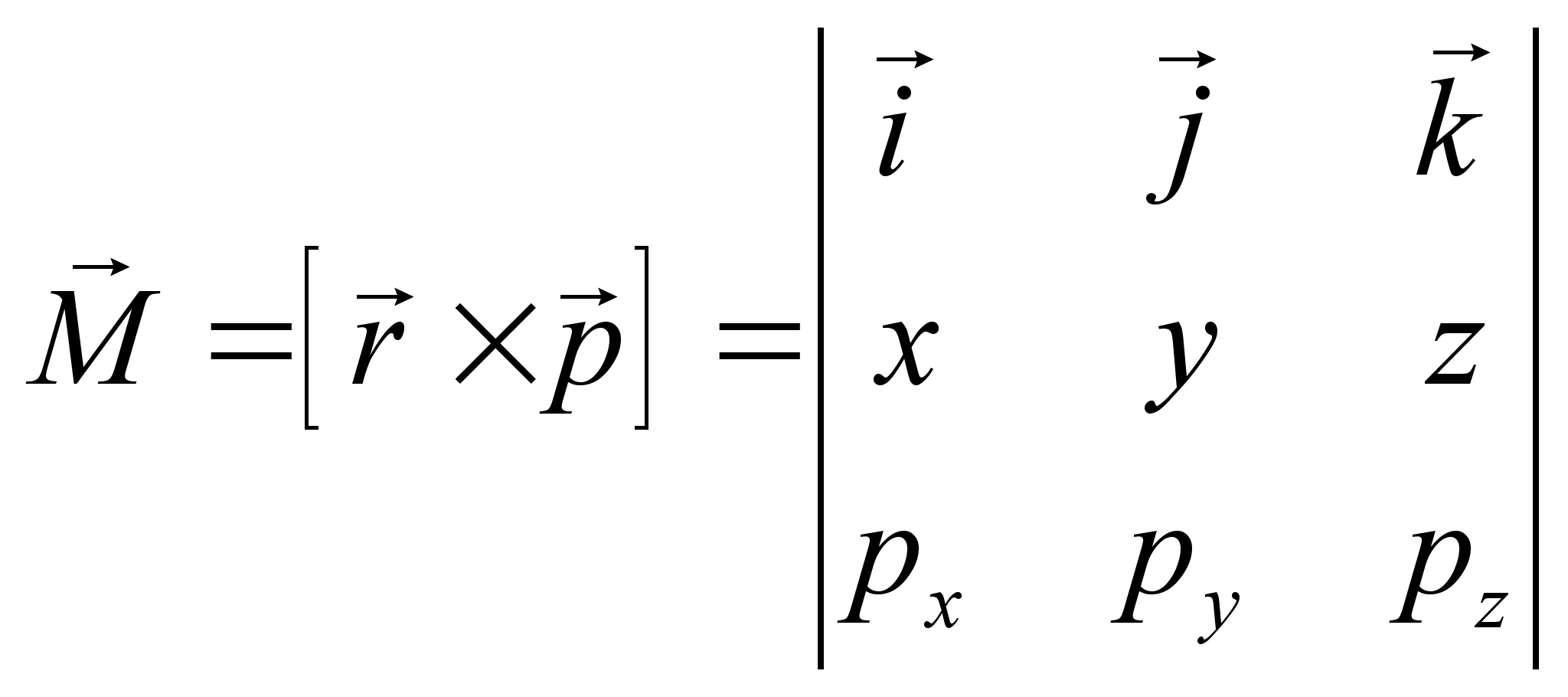
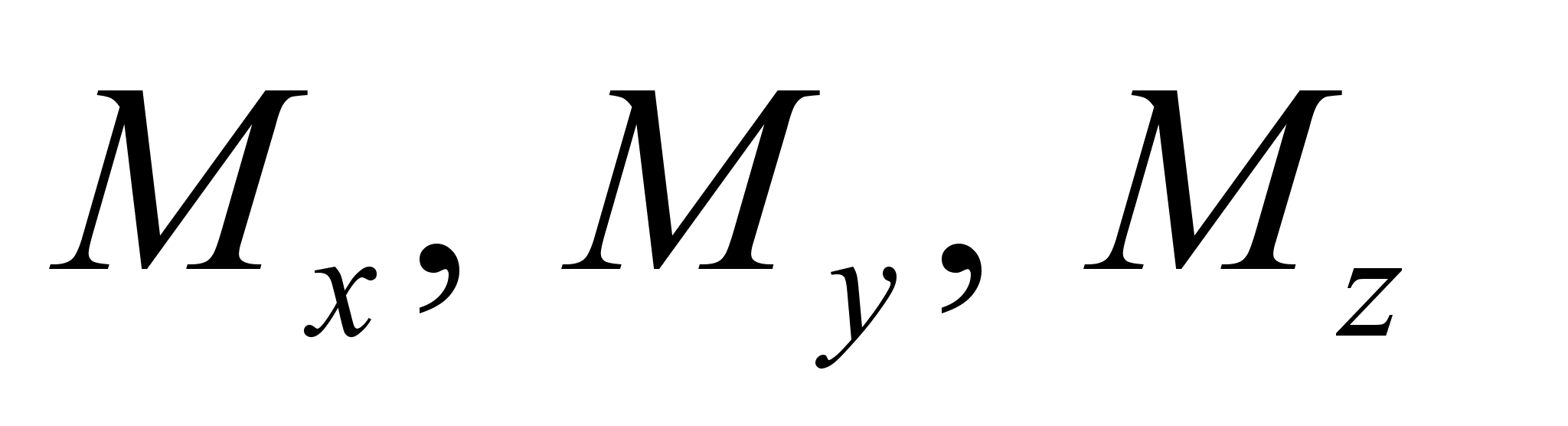 поочередно убеждаемся в тождественности последнего.
поочередно убеждаемся в тождественности последнего.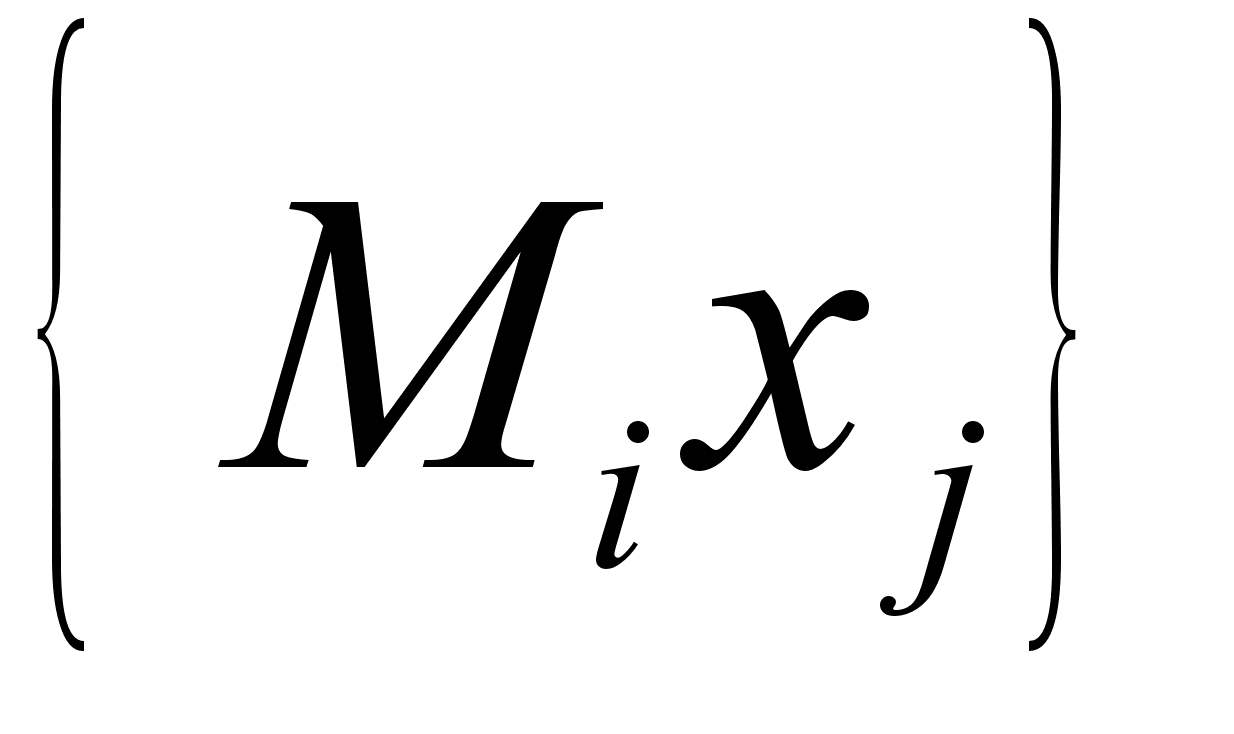 .
.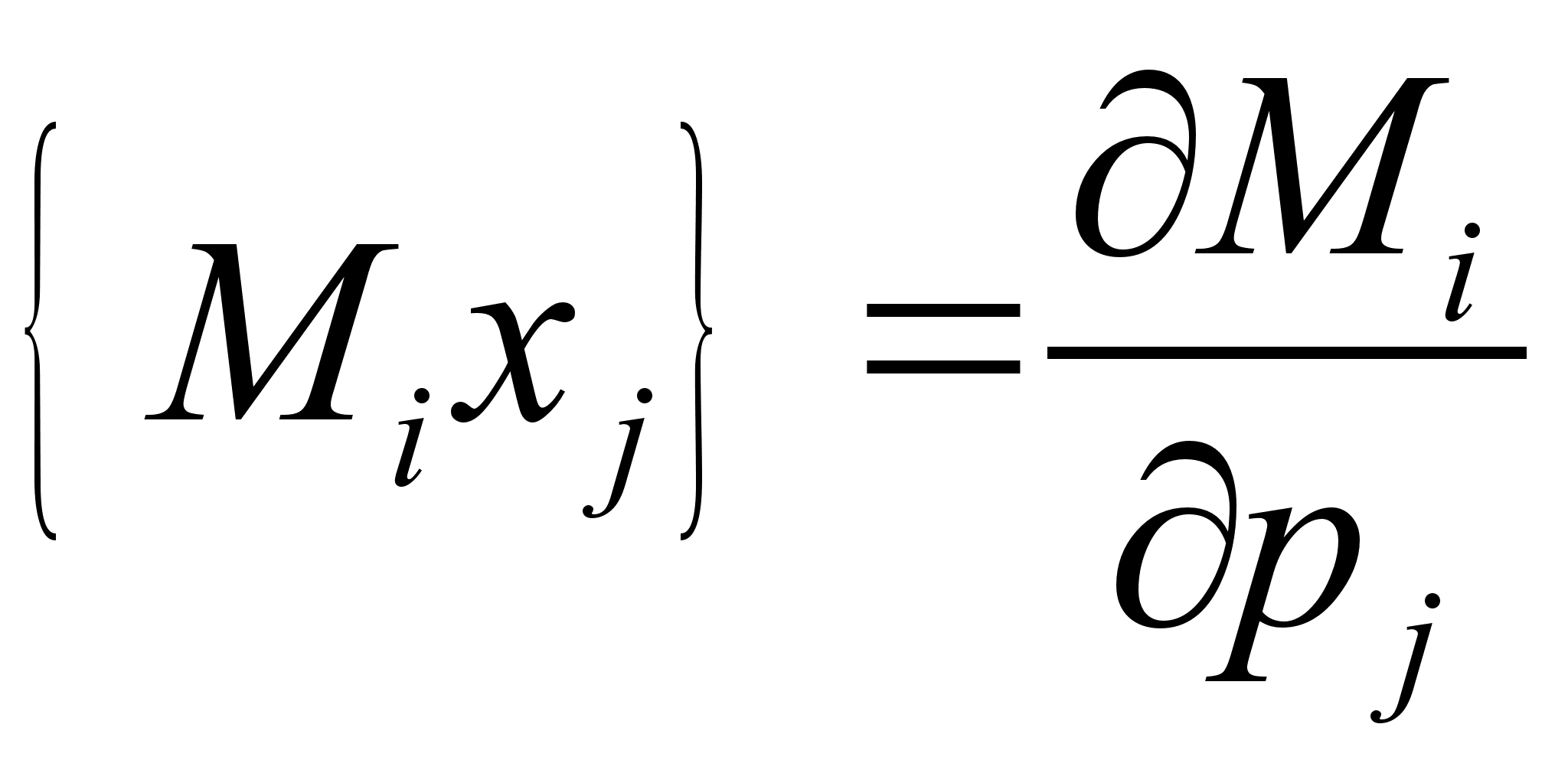
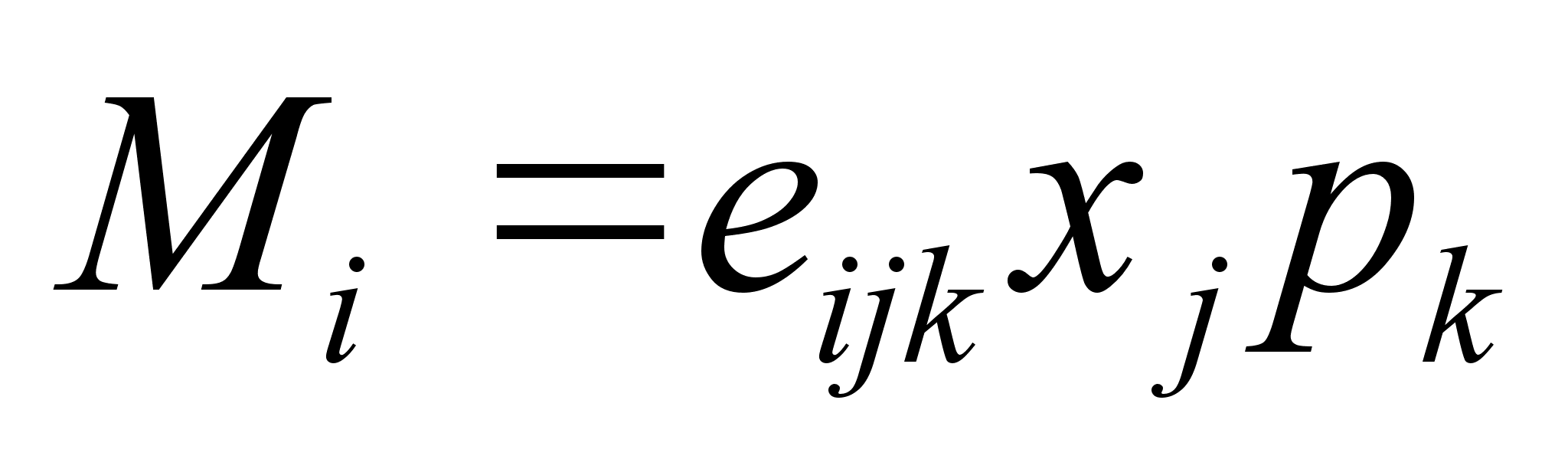 ,
, – полностью антисимметричный тензор, причем
– полностью антисимметричный тензор, причем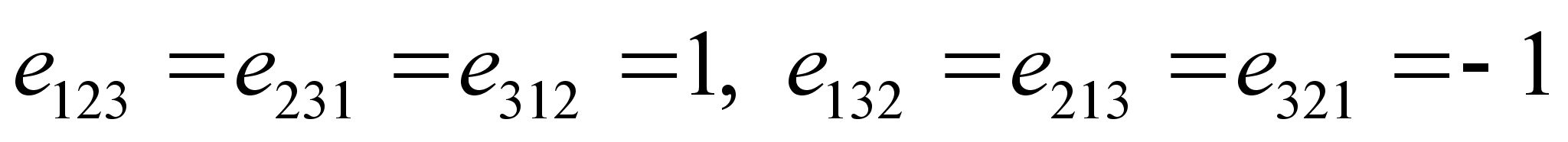 ,
,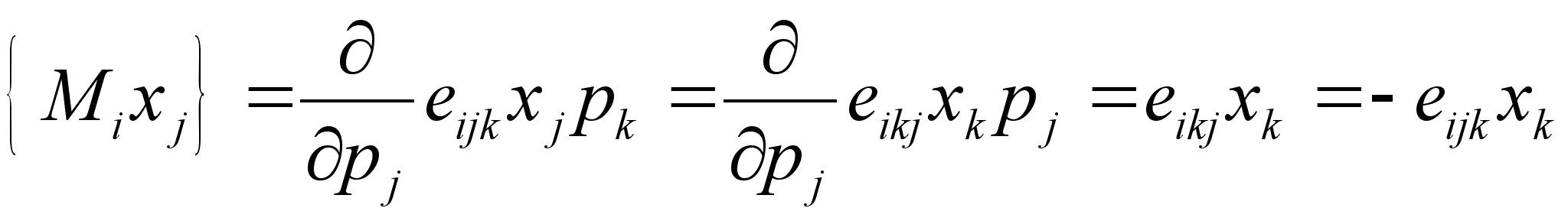
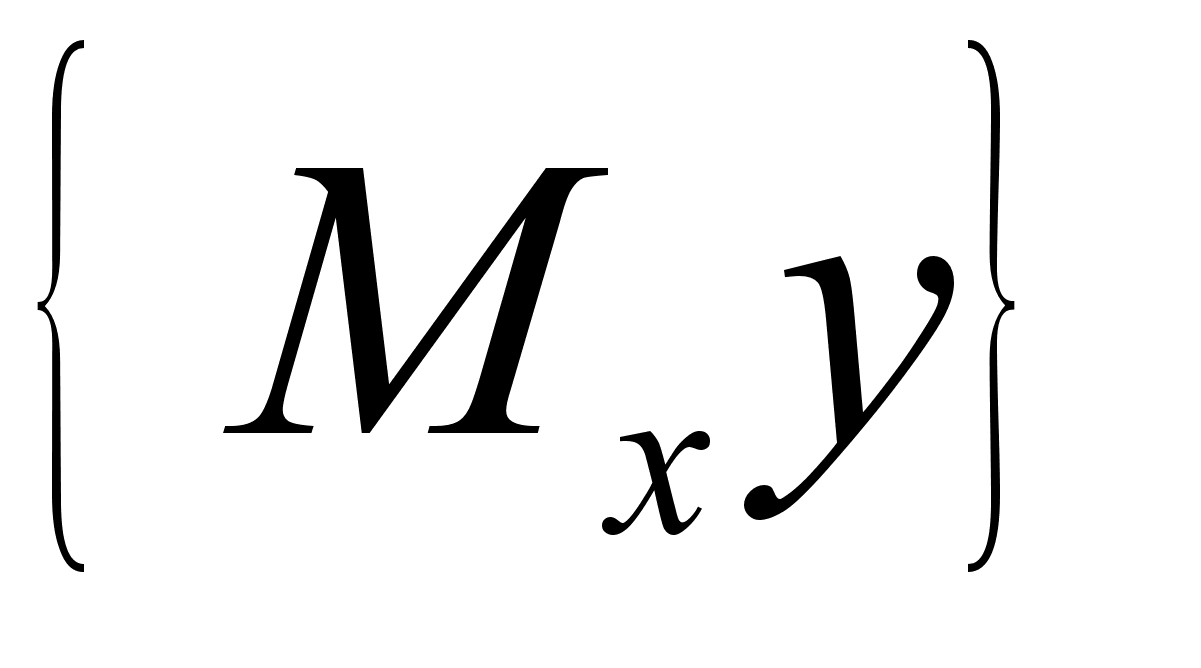 :
: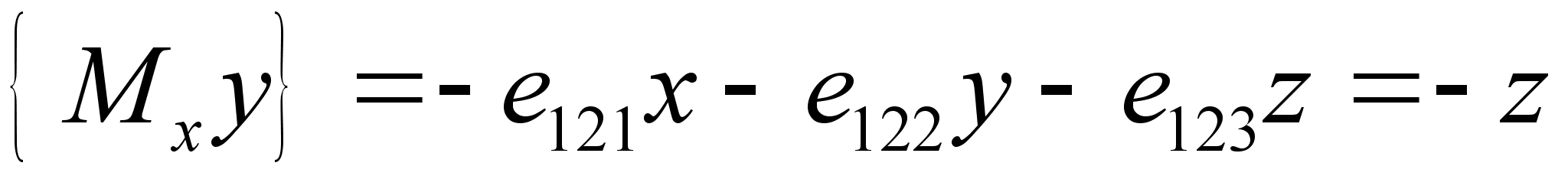
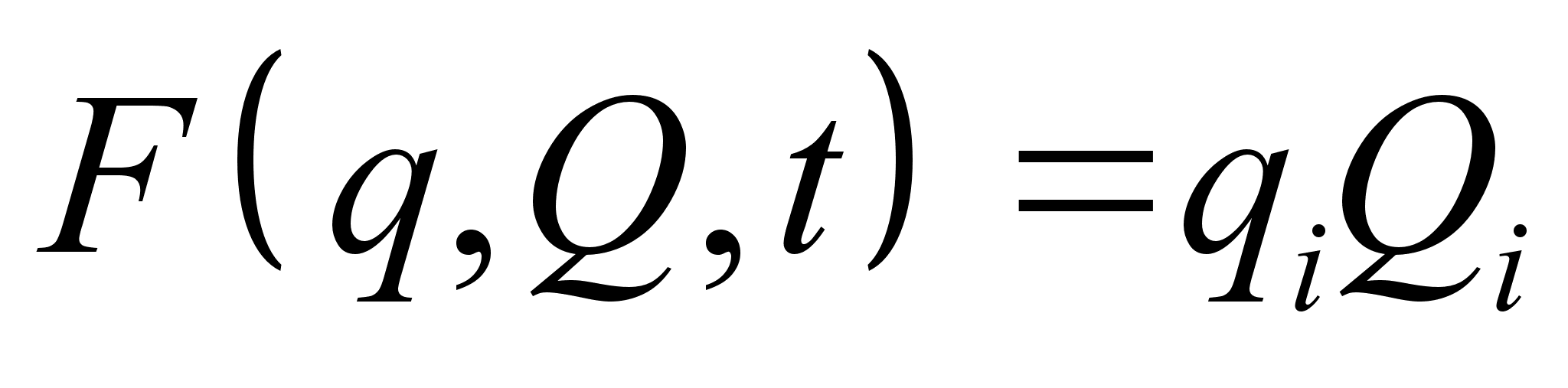 .
.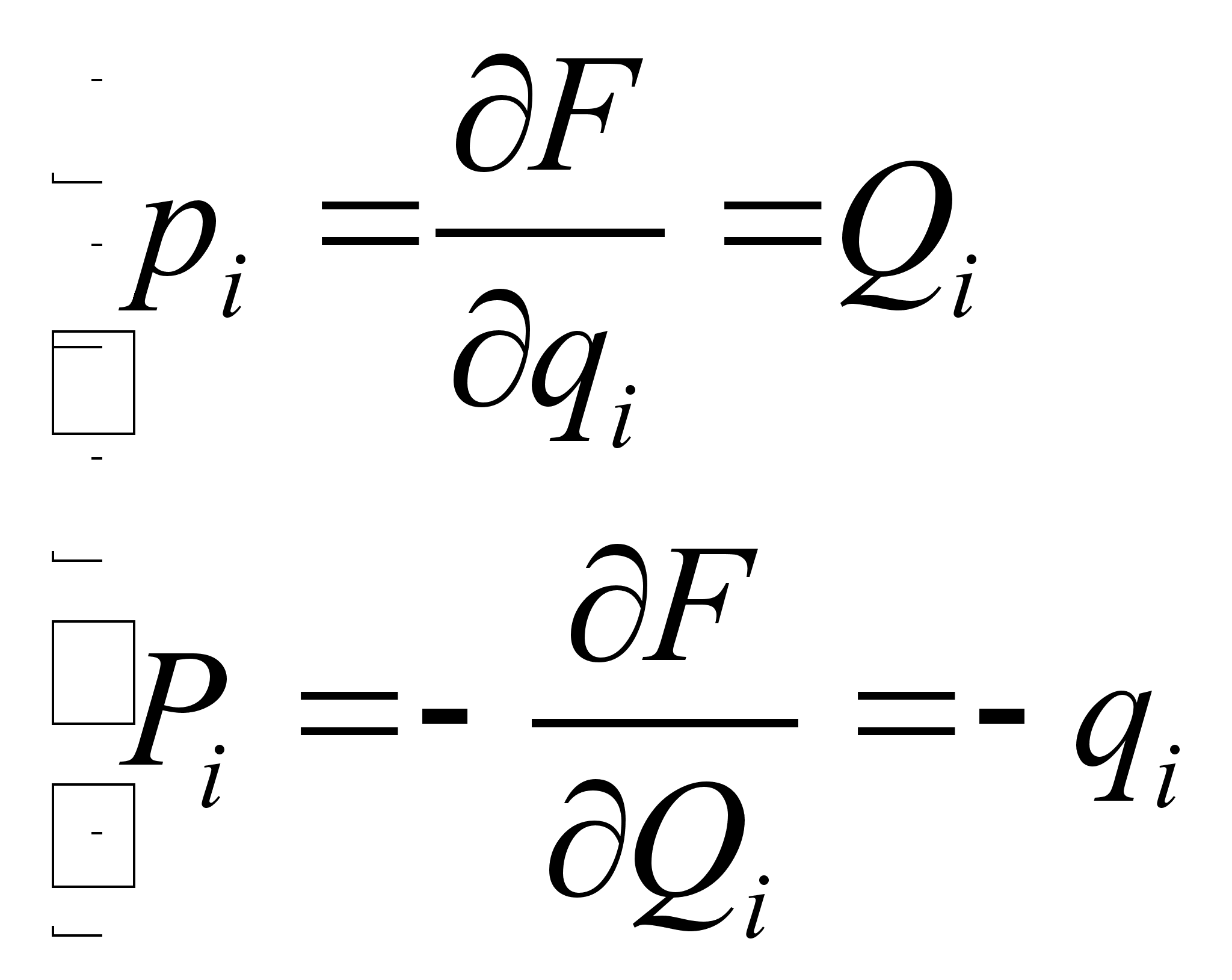
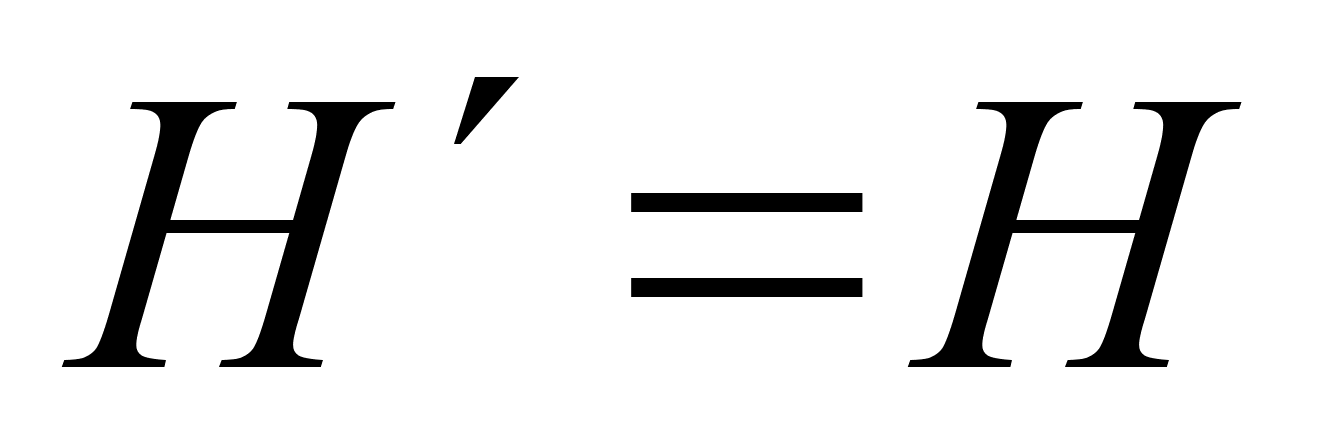 .
.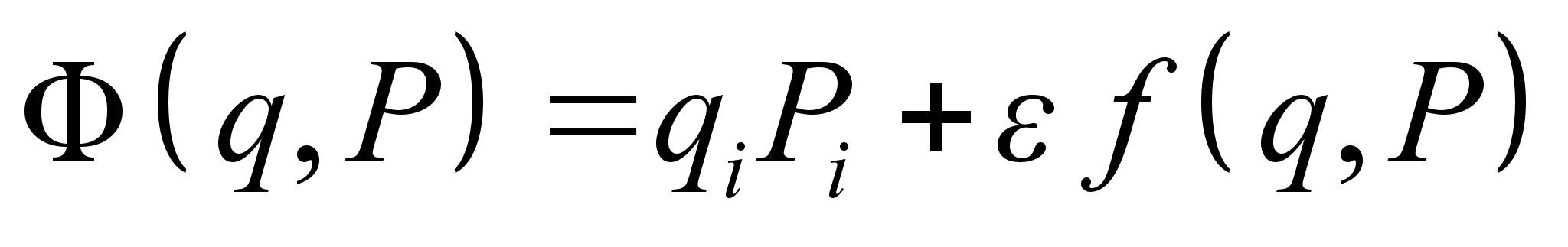 ,
,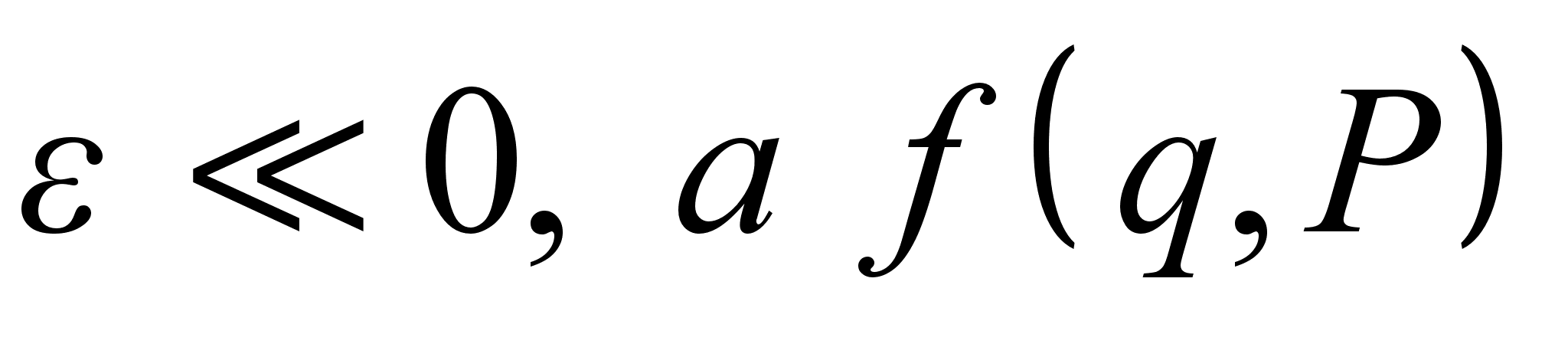 – интеграл движения.
– интеграл движения.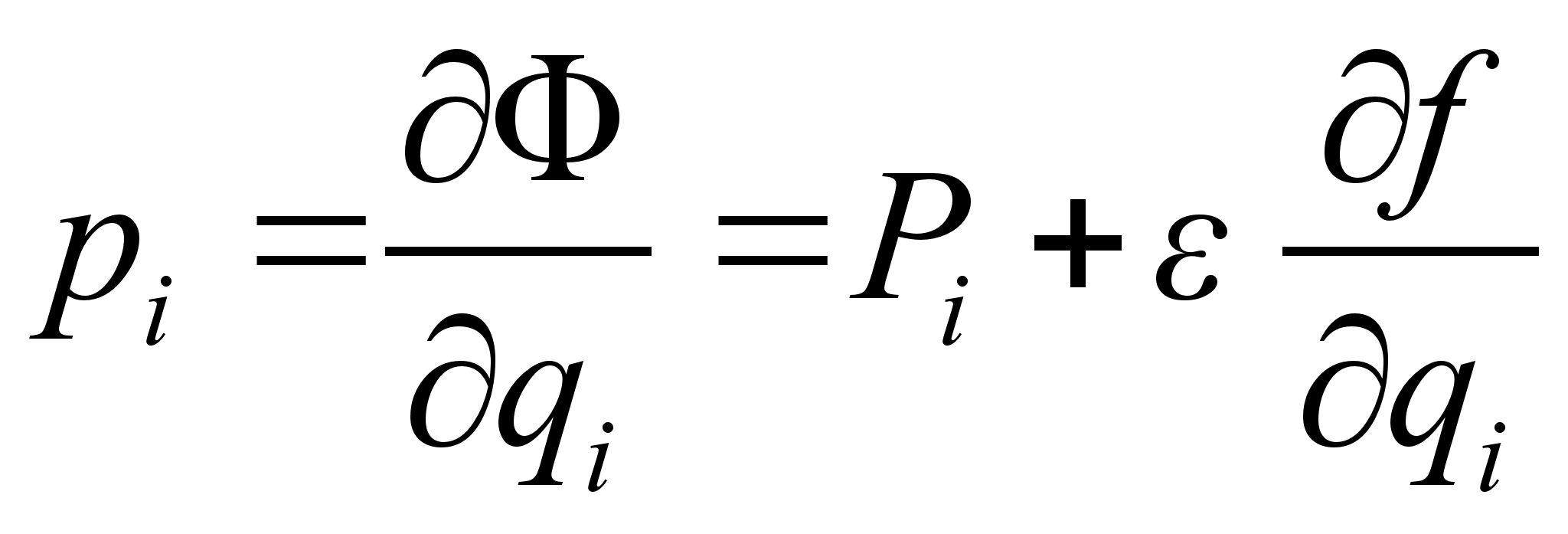
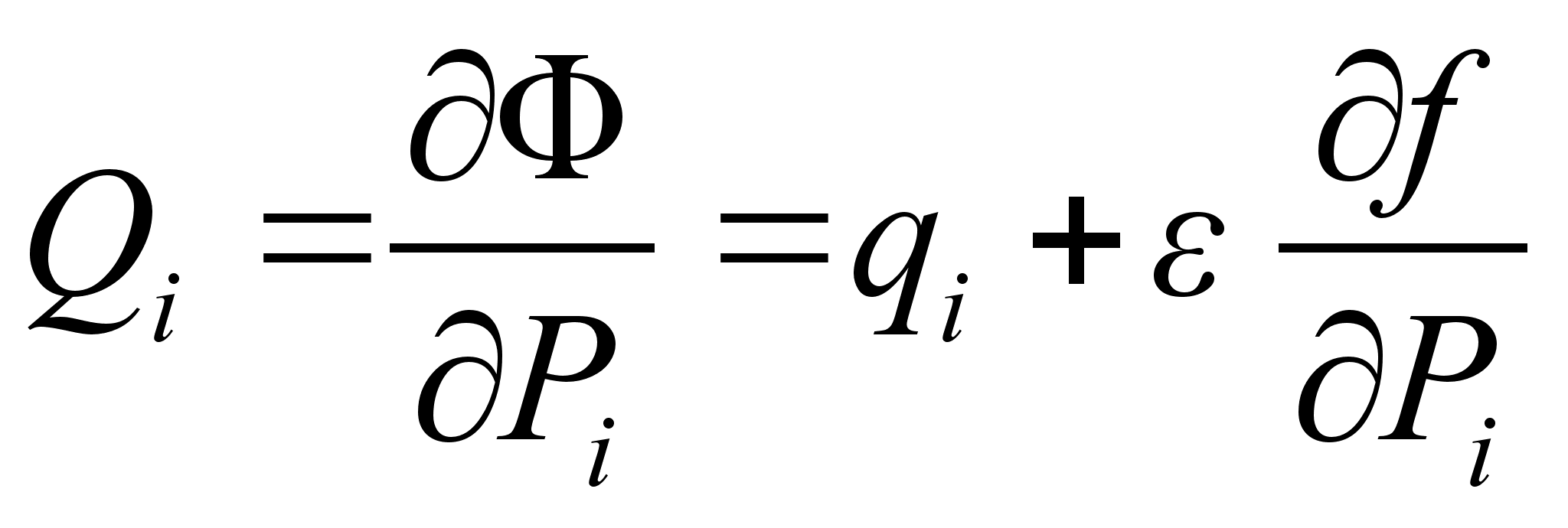
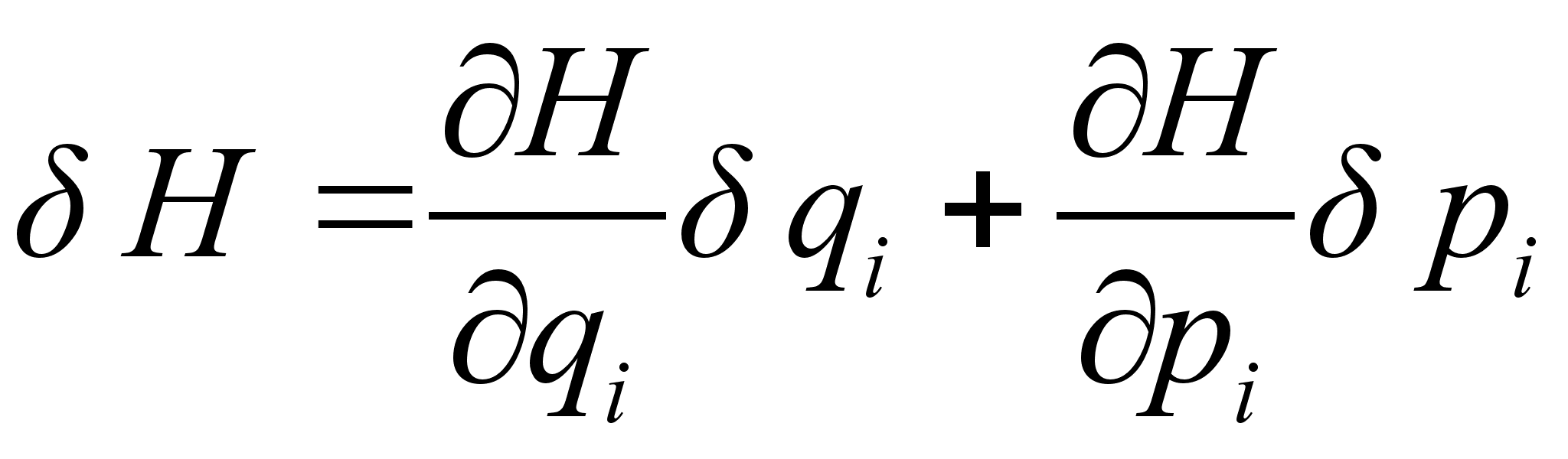
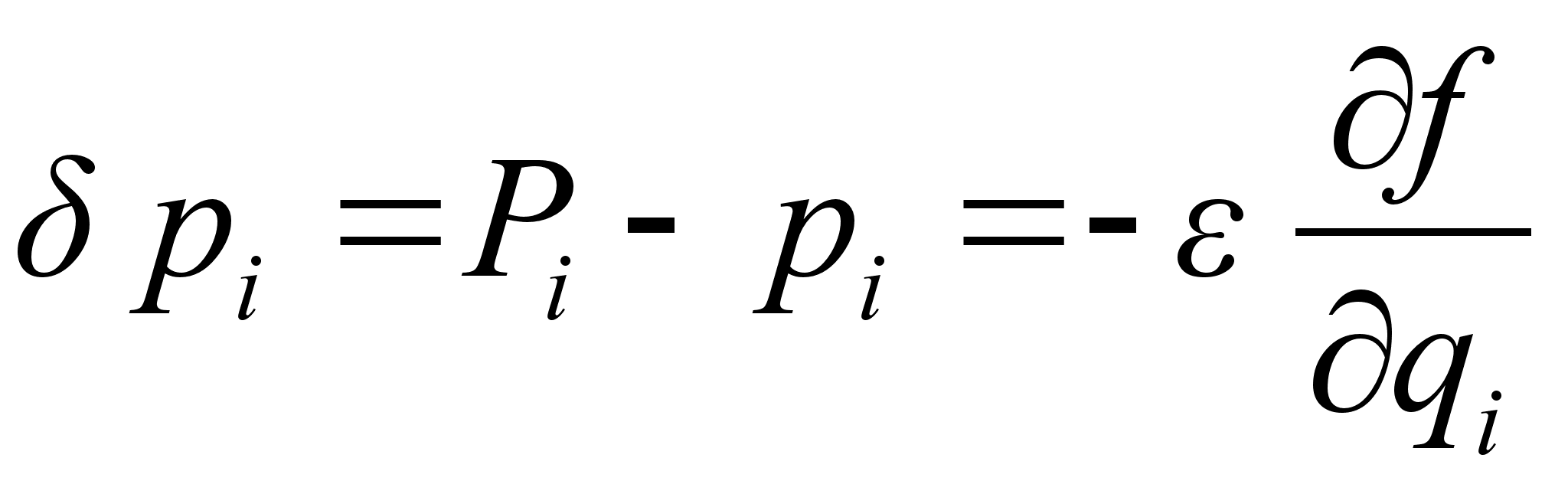
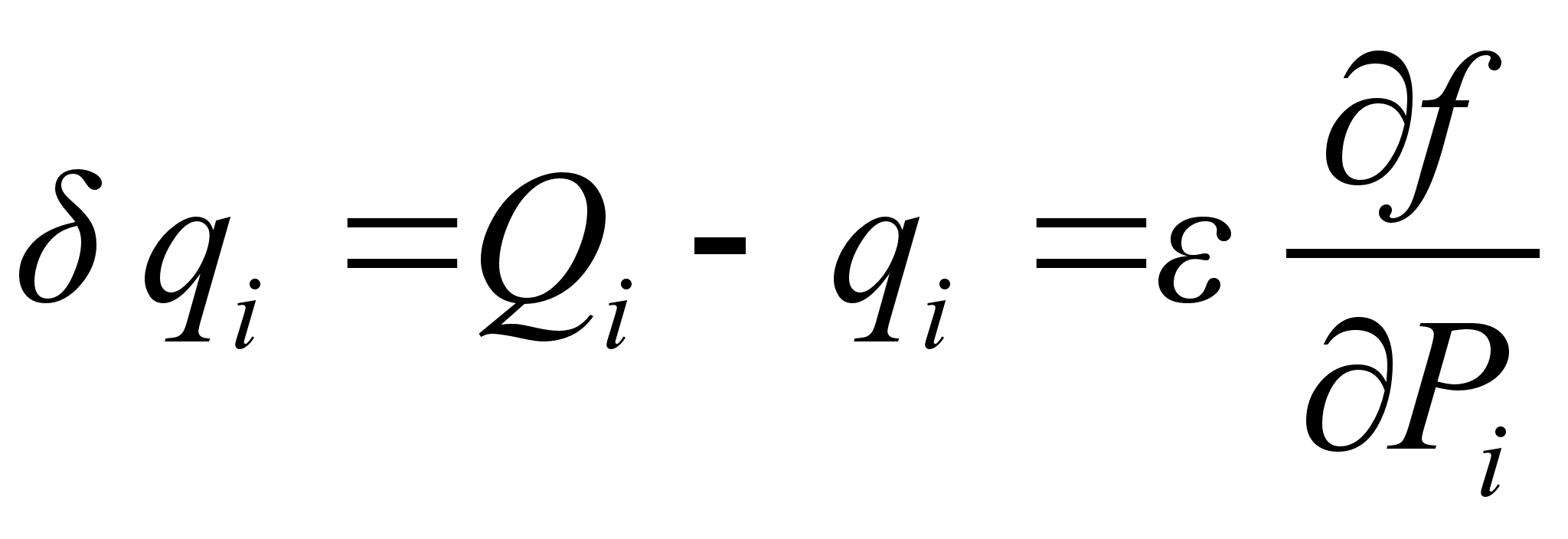
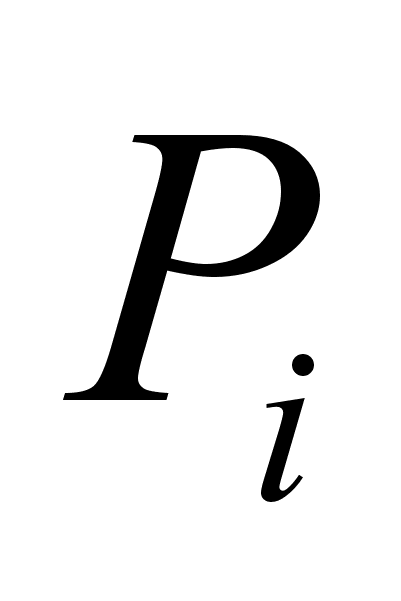 из уравнения и подставляя его в уравнение , с точностью до членов первого порядка малости, получим:
из уравнения и подставляя его в уравнение , с точностью до членов первого порядка малости, получим: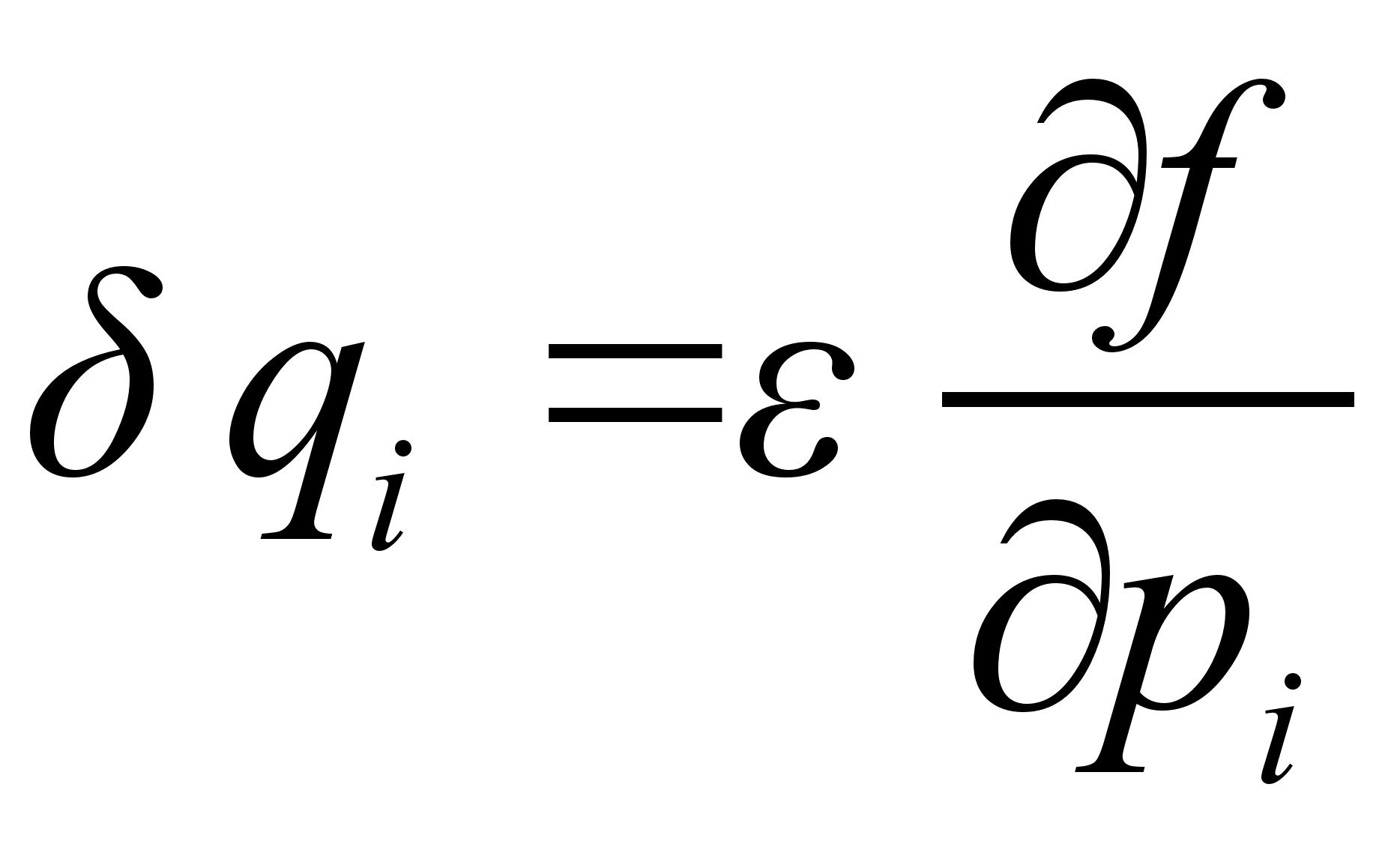
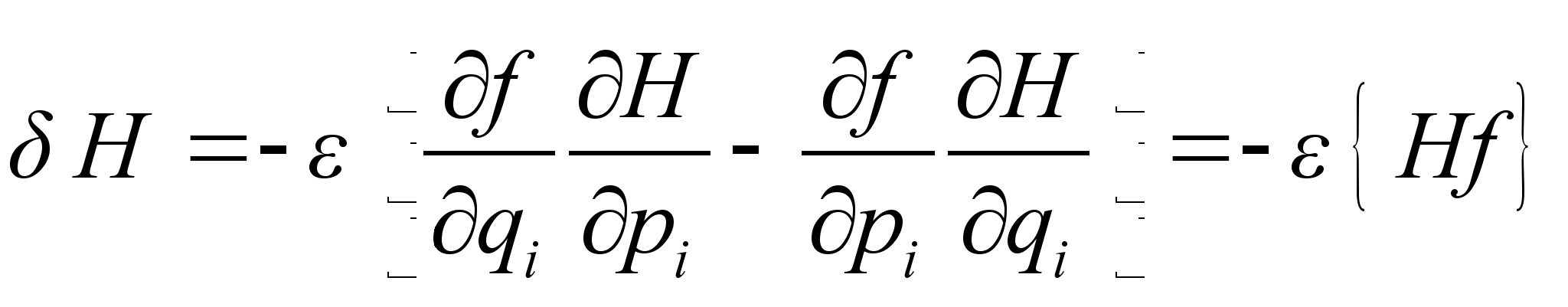
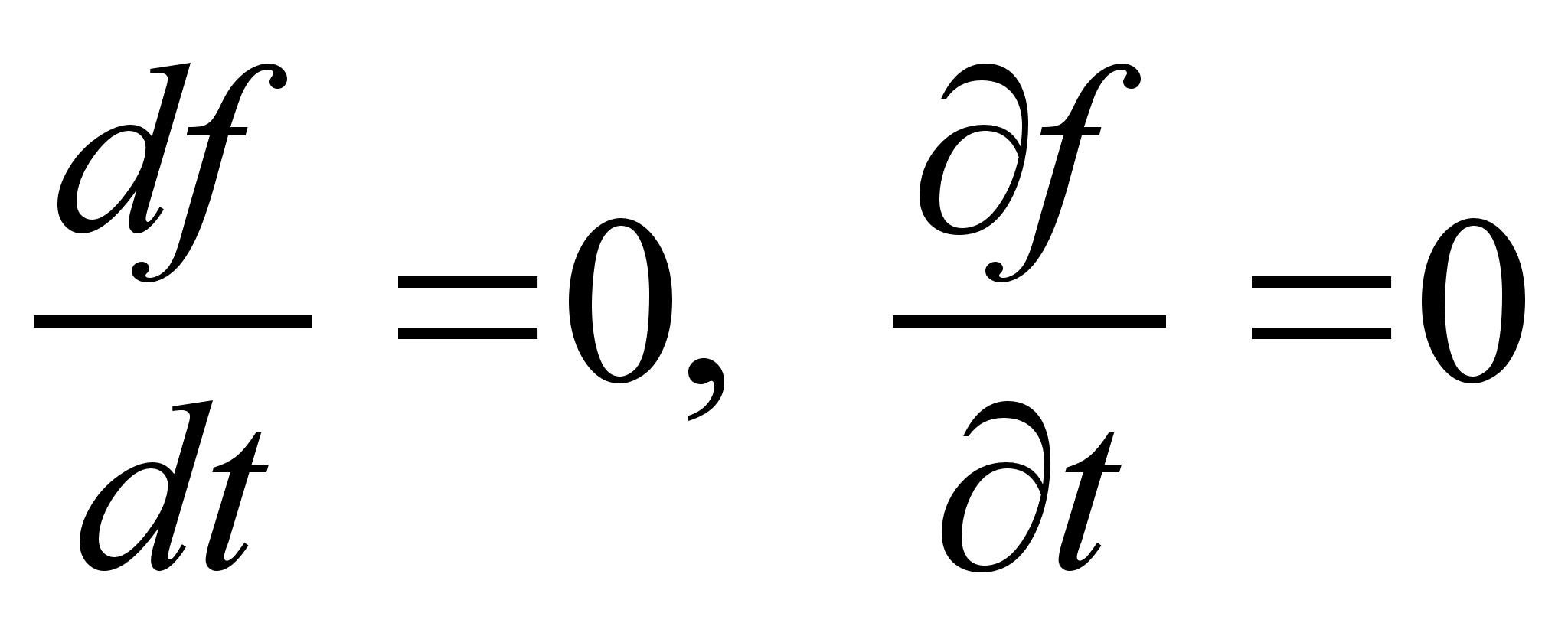
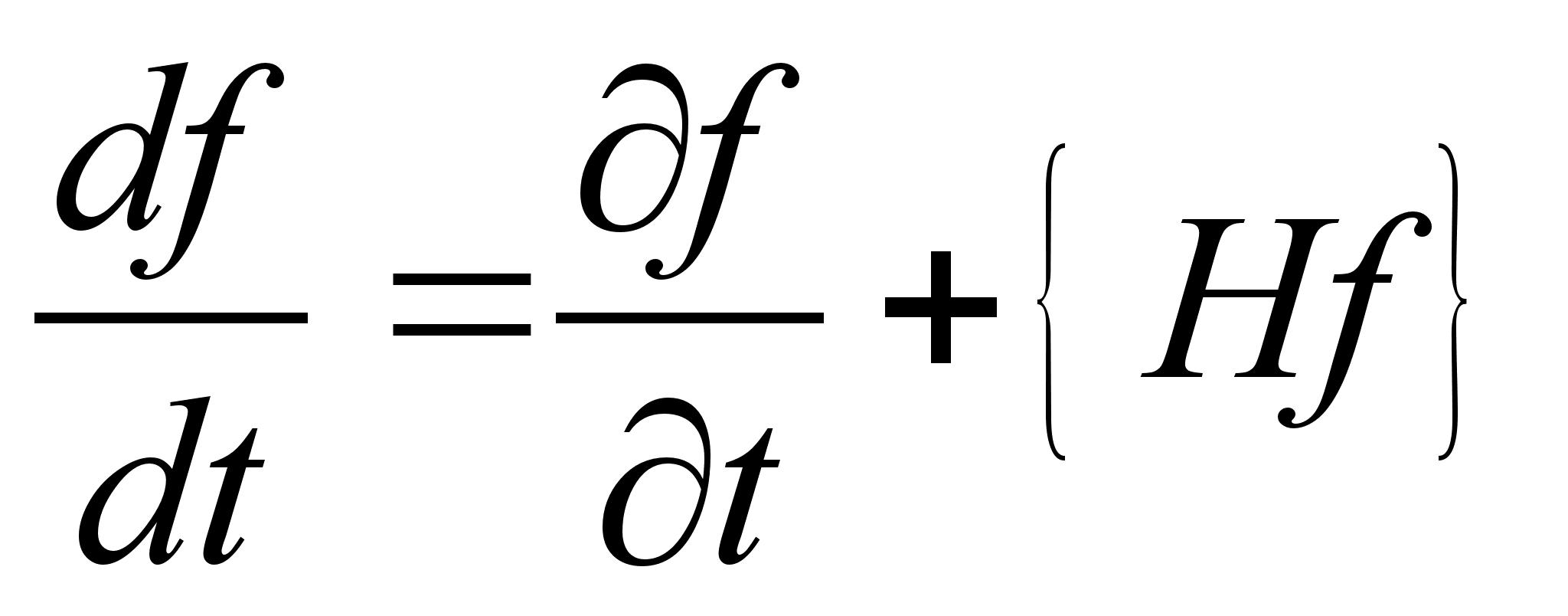
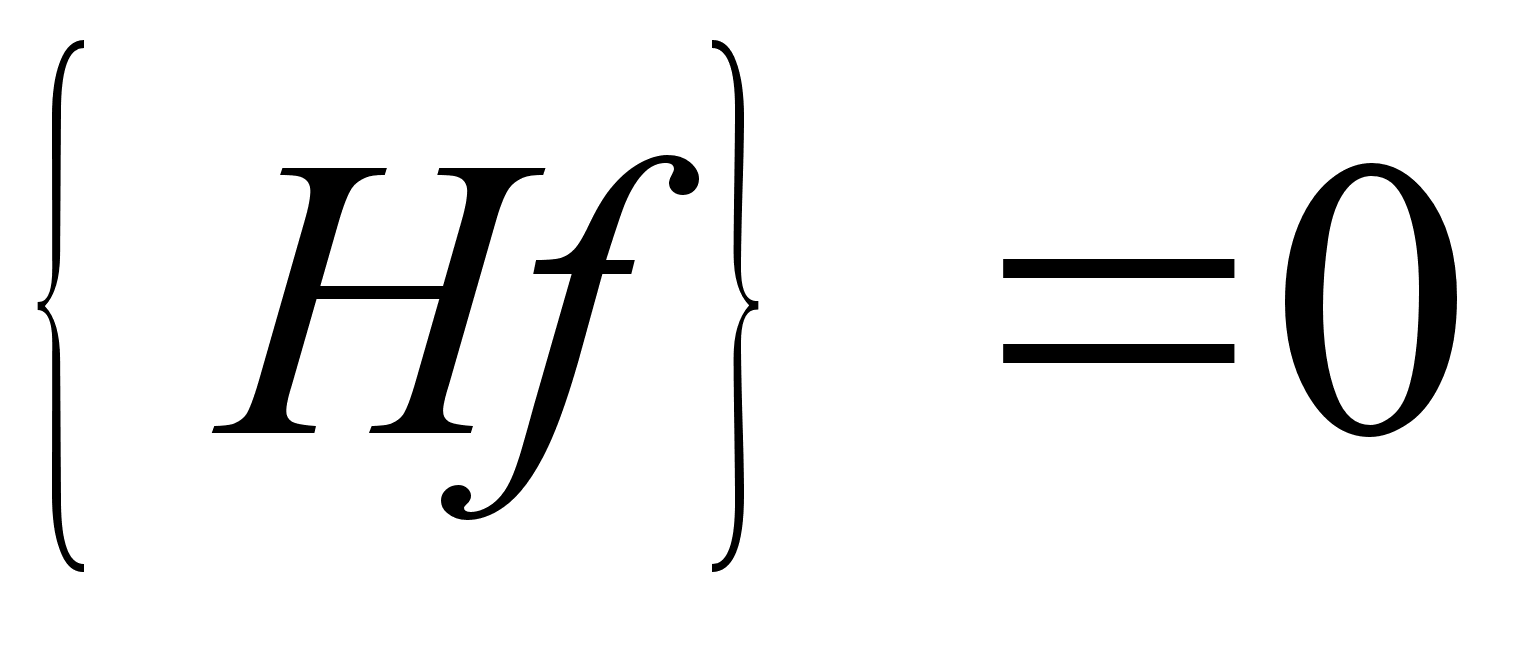
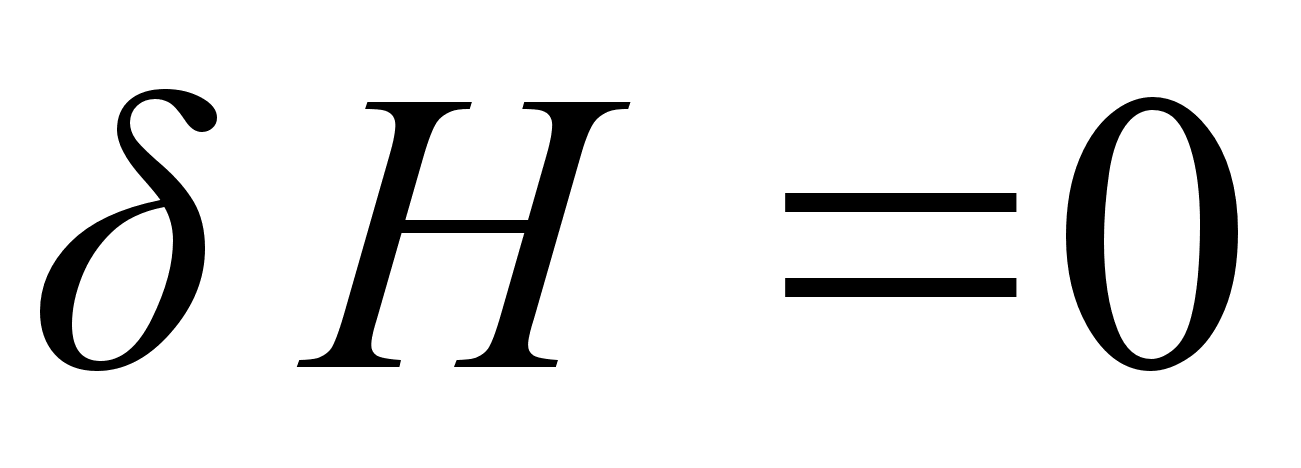 ,
, является интегралом движения свободной частицы в отсутствие внешних сил.
является интегралом движения свободной частицы в отсутствие внешних сил.
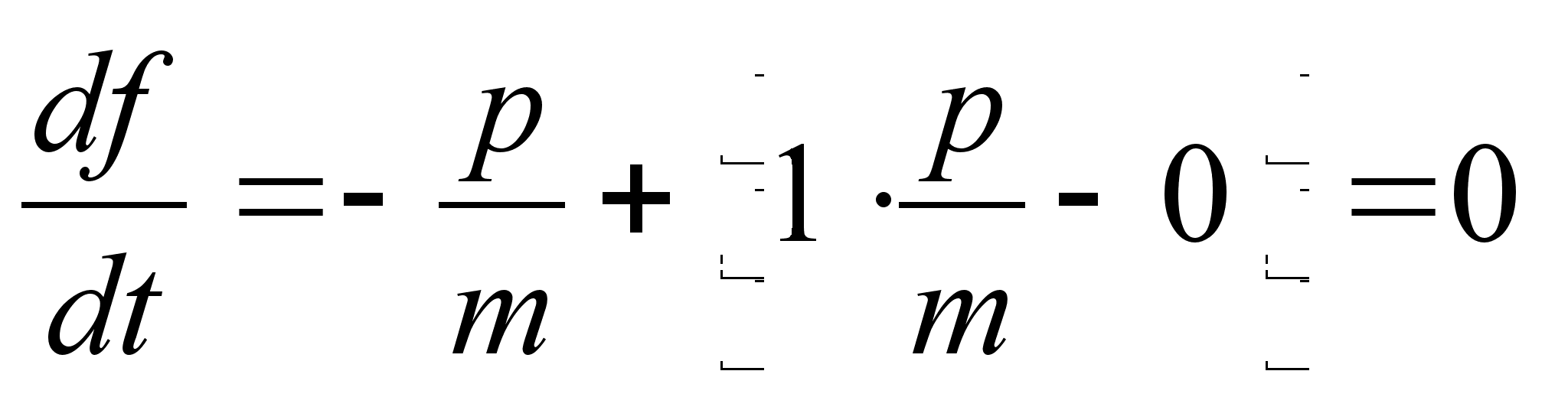
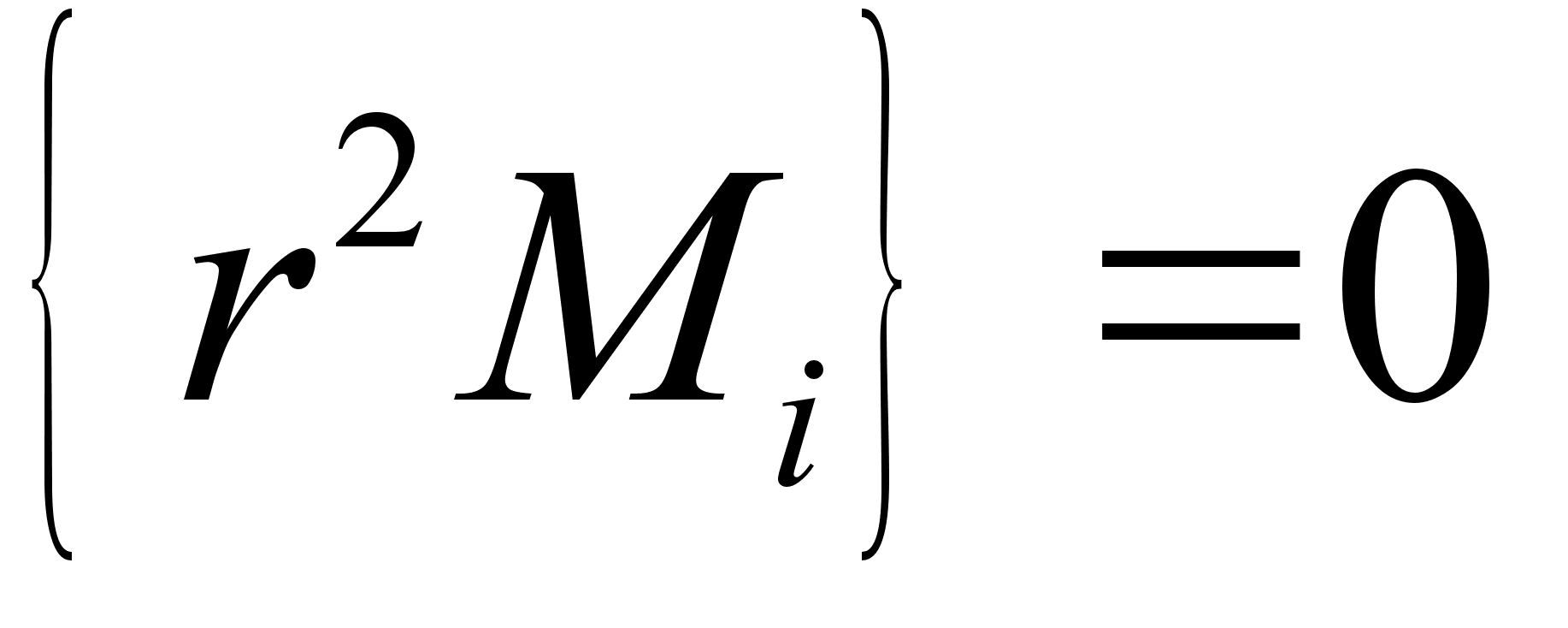 .
.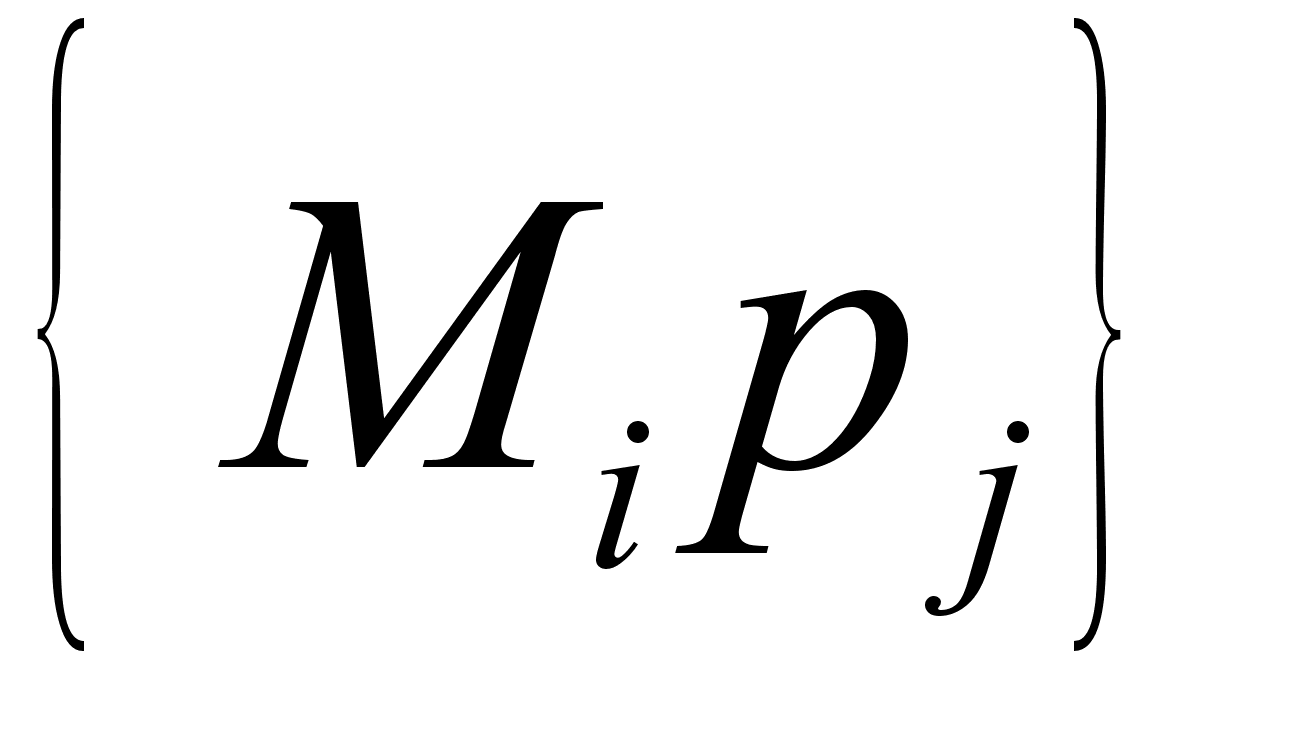 ,
, 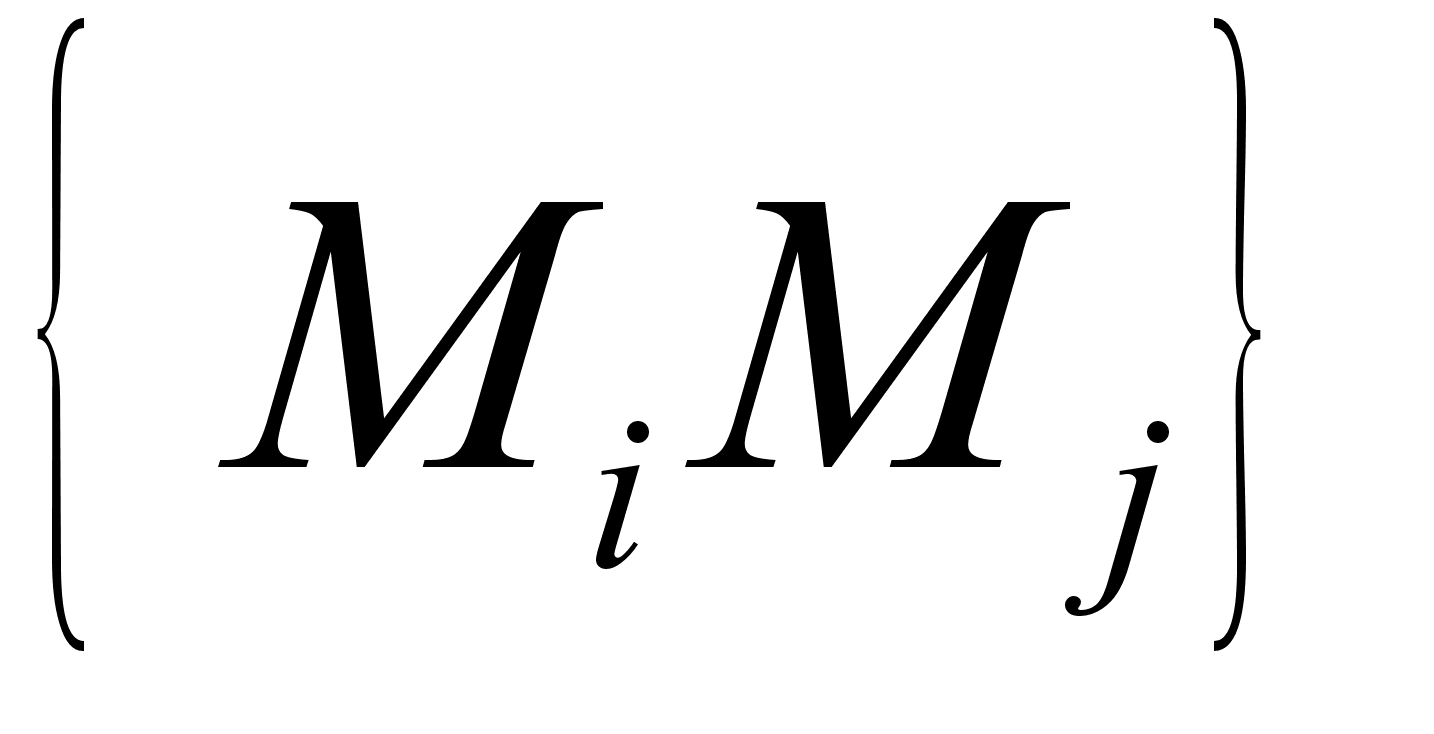 .
.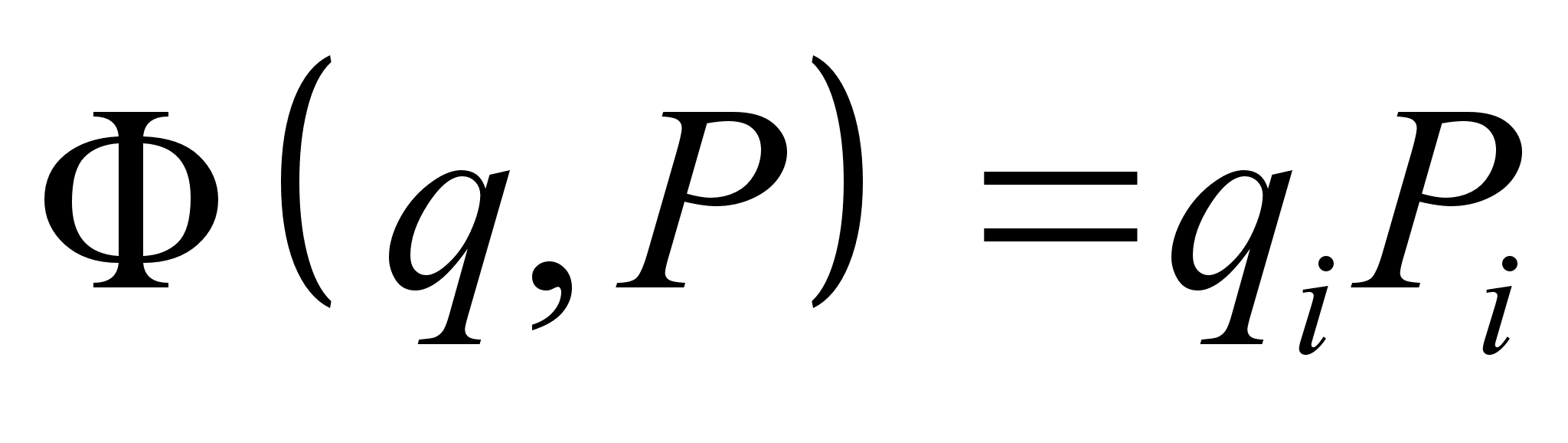 определяет тождественное каноническое преобразование.
определяет тождественное каноническое преобразование.