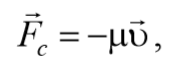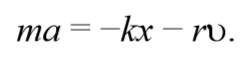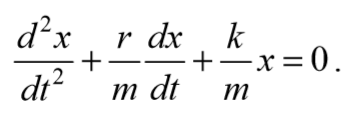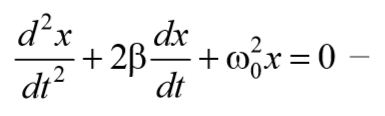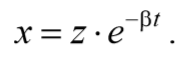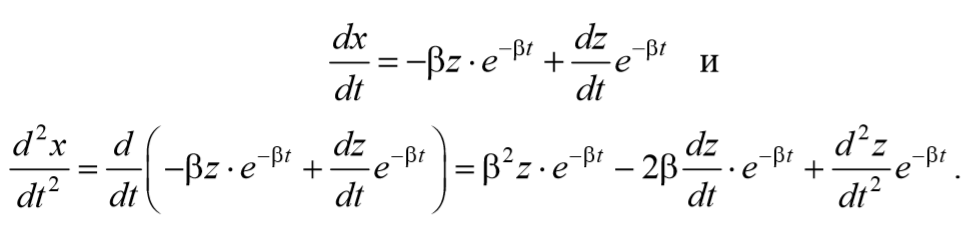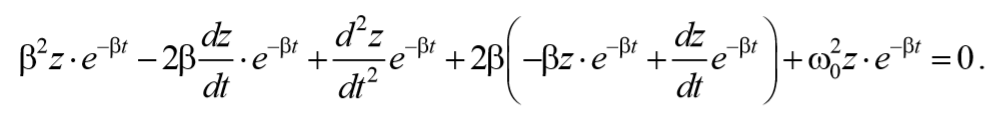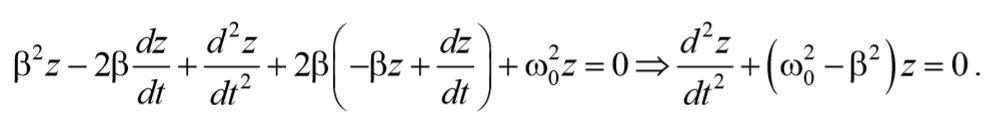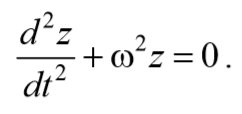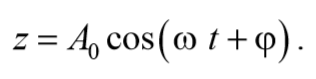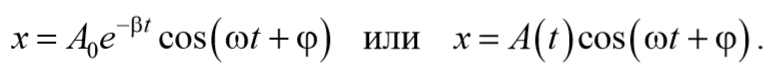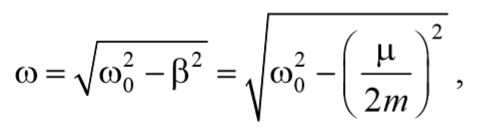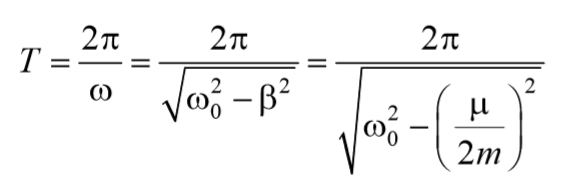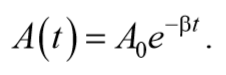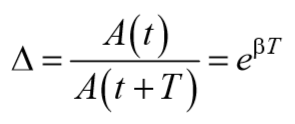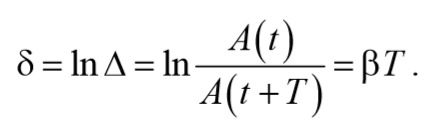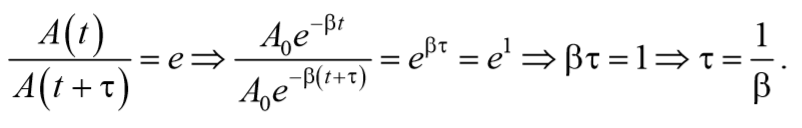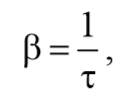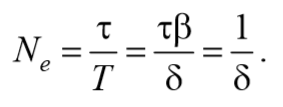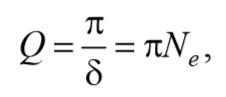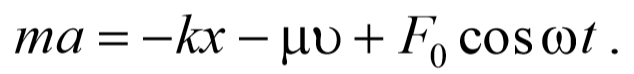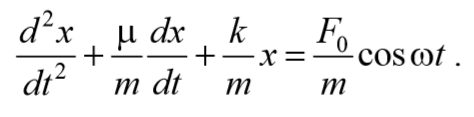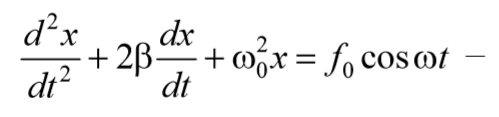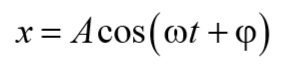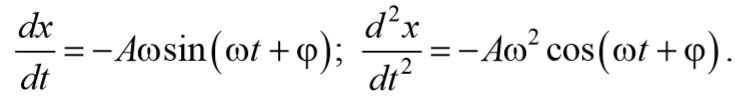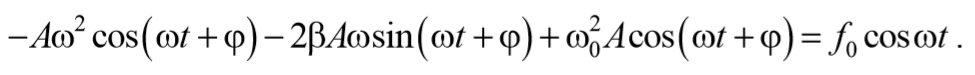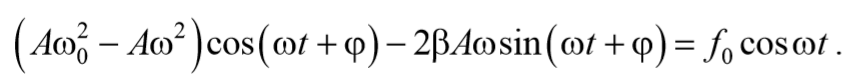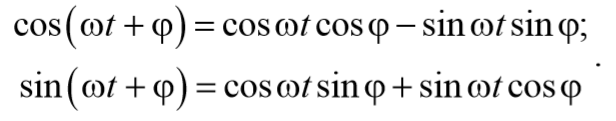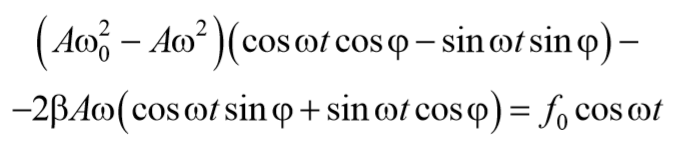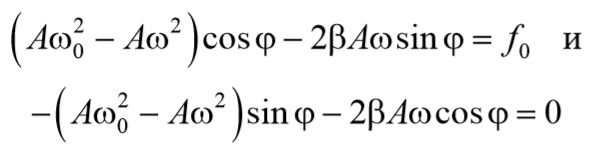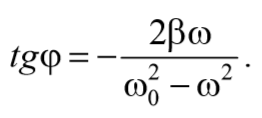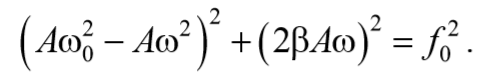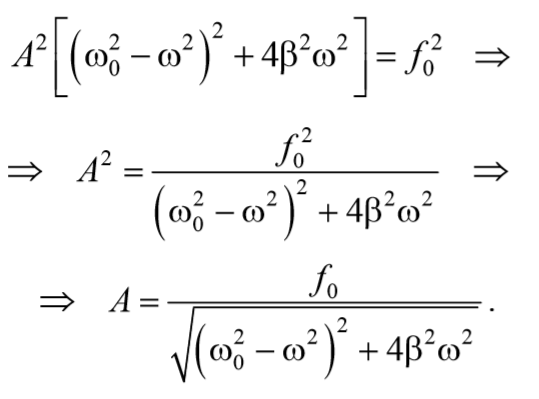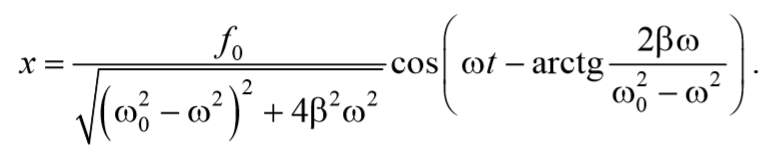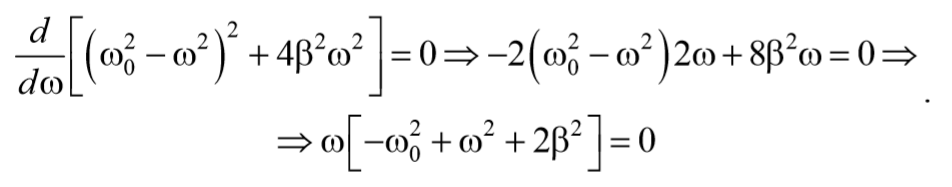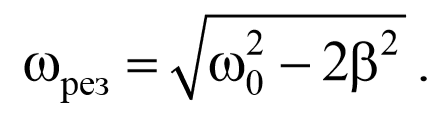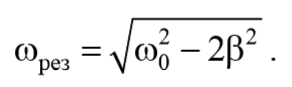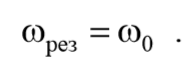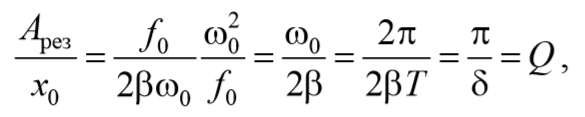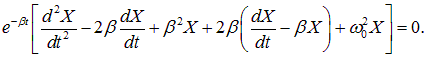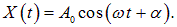Уравнение гармонических колебаний с затуханием

Лекция №8. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

5.6. Затухающие гармонические колебания.

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Затухающие колебания − это колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления, вызывающая затухание, зависит от скорости колебательного движения, т. е. ее можно считать прямо пропорциональной скорости

где μ − постоянная, называемая коэффициентом сопротивления.

Знак «минус» обусловлен тем, что сила и скорость имеют противоположные направления. Тогда второй закон Ньютона для гармонических колебаний при наличии сил сопротивления имеет вид

Учитывая , что a= $$d^2x\over dt^2$$ , а υ= $$dx\over dt$$ и разделив на массу m , получим

Применив обозначения $$ = ω_0<^2>$$ , $$ <μ\over m>= 2β$$ и $$ = f_0$$ получим

дифференциальное уравнение затухающих колебаний . Отметим, что ω₀ представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды. Эта частота называется собственной частотой .

Для решения уравнения (5.6.4) сделаем подстановку

Проведем замену переменных

Подставим (5.6.5 и 5.6.6) в выражение (5.6.4)

Преобразуем , сократив на e -βt

Рассмотрим случай, когда сопротивление среды настолько мало, что ω₀ 2 -β 2 >0 есть величина положи мы можем ввести тельная, и обозначение ω₀ 2 -β 2 =ω 2 , после чего уравнение (5.6.8) примает вид

В случае большого сопротивления среды ω₀ 2 -β 2 , движение становится непериодическим.

Решение уравнения (5.6.8) можно записать в виде

Окончательно, подставляя последнее уравнение в выражение (5.6.5), получаем общее решение дифференциального уравнения затухающих колебаний (5.6.4)

В соответствии с видом полученной функции движение можно рассматривать как гармоническое колебание с частотой

и амплитудой, изменяющейся по закону

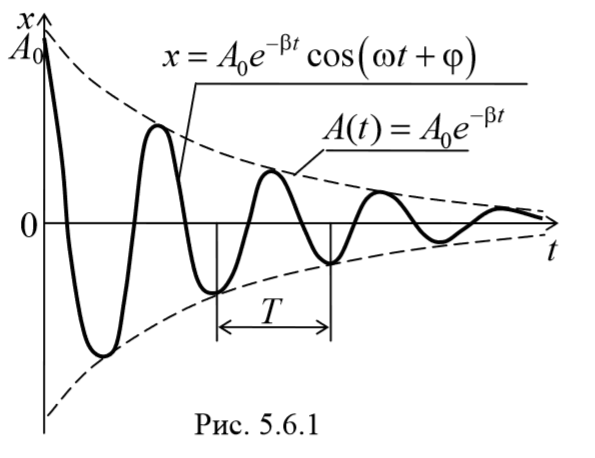
На рисунке показан график данной функции. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Верхняя из пунктирных кривых дает график функции A(t) , причем величина A₀ представляет собой амплитуду в начальный момент времени. Начальное смещение зависит от A₀ и также от начальной фазы φ , т.е. x₀=A₀cosφ .

5.7. Коэффициент затухания и логарифмический декремент затухания.

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно

и называется декрементом затухания .

Для характеристики системы обычно используется колебательной логарифмический декремент затухания , т.е. логарифм декремента затухания

Скорость затухания колебаний определяется величиной называем коэффициентом затухания $$β=<μ\over 2m>$$ .

Найдем время, называемое временем релаксации τ , за которое амплитуда уменьшается в e раз

т. е. коэффициент затухания обратен по величине промежутку времени, за который амплитуда колебаний уменьшается в e раз.

За время релаксации τ система успевает совершить $$N_e=<τ\over T>$$ колебаний

Следовательно, $$δ=<1\over N_e>$$ логарифмический декремент затухания обратно пропорционален по величине числу колебаний, за которые амплитуда колебаний уменьшается в e раз.

Для характеристики колебательной системы используется величина

которая называется добротностью колебательной системы.

Величина Q , пропорциональная числу колебаний, совершаемых системой за время, в течение которого амплитуда колебаний уменьшается в e раз.

5.8. Вынужденные колебания.

До сих пор мы рассматривали свободные колебания, когда выведенная из положения равновесия система совершает колебания будучи предоставленной самой себе. Рассмотрим колебательную систему, которая подвергается действию внешней силы, изменяющейся по гармоническому закону F=F₀cosωt . Колебания, возникающие под действием внешней периодически изменяющейся силы, называются вынужденными колебаниями . В этом случае уравнение второго закона Ньютона имеет вид

Учитывая , что a= $$d^2x\over dt^2$$ , а υ= $$dx\over dt$$ и разделив на массу m , получим

Применив обозначения $$ = ω_0<^2>$$ , $$ <μ\over m>= 2β$$ и $$ = f_0$$ получим

дифференциальное уравнение вынужденных колебаний.

Будем искать решение уравнения (5.8.3) в виде

предполагая, что результирующее колебание будет совершаться с частотой внешней вынуждающей силы.

Подставим (5.8.4) и (5.8.5) в уравнение (5.8.3)

Чтобы уравнение (69) обратилось в тождество необходимо, чтобы коэффициенты при cosωt и sinωt были равны нулю.

Из выражения (71) получаем

Возведем в квадрат уравнения (70) и сложим

Подставив полученные выражения (71) и (73) в выражение (64) получим уравнение вынужденных колебаний

5.9. Резонанс.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой частоте амплитуда колебаний достигает максимального значения.

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой собственной частоте колебательной системы называется резонансом , а соответствующая частота − резонансной частотой.

Найдем резонансную частоту. Амплитуда вынужденных колебаний будет max, когда выражение $$(ω_0<^2>-ω^2)^2 + 4β^2ω^2$$ в уравнении $$A=-ω^2)^2 + 4β^2ω^2>>$$ (5.8.13) будет минимальным.

Продифференцируем это выражение по ω и приравняем к нулю

Полученное уравнение имеет три решения: ω=0 и ω=± $$\sqrt <ω_0<^2>-2β^2>$$ . 2 . Первое решение соответствует максимуму знаменателя. Из остальных двух решений отрицательное не имеет физического смысла (частота не может быть отрицательной). Таким образом, резонансная циклическая частота

Подставив это значение в выражение для амплитуды (5.8.13), получим выражение для амплитуды при резонансе

Из последнего уравнения (5.9.3) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность, а резонансная частота, согласно (5.9.2), при тех же условиях (при β=0 ), совпадала бы с собственной частотой колебаний системы ω₀

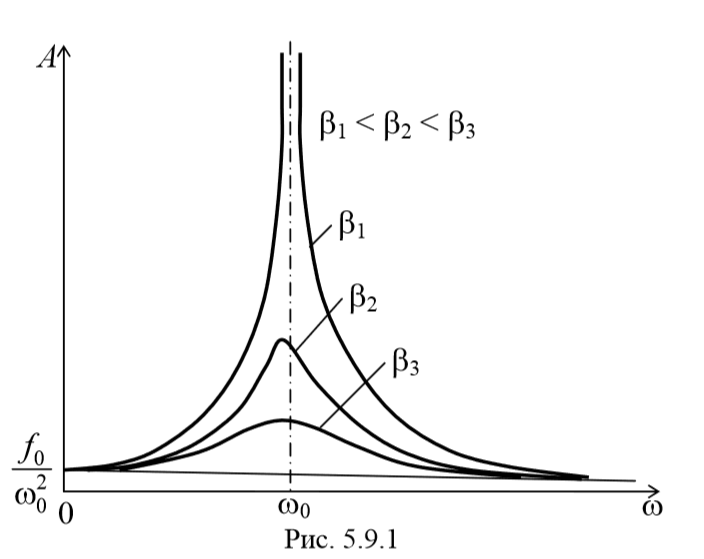
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы показана графически на рис. 5.9.1. В соответствии с (5.9.2) и (5.9.3), чем меньше параметр β , тем выше и правее лежит максимум данной кривой. Изображенная на рис. 5.9.1 совокупность графиков функций (5.8.13), соответствующих различным значениям параметра β , называется резонансными кривыми .

При стремлении ω к нулю все кривые приходят к одному и тому же, отличному от нуля, предельному значению, равному f₀ω₀ 2 . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы величины F₀

При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.

Наконец, отметим, что чем меньше β , тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» получается максимум. При малом затухании (т. е. β ) амплитуда при резонансе приближенно равна A_pes≈f₀/2βω₀ . Разделим это выражение на смещение x₀ из положения равновесия под действием постоянной силы F₀ , равное x₀=f₀/ω_p 2 . В результате получим

где δ = βТ – логарифмический декремент затухания (5.7.2); Q – добротность колебательной системы (5.7.6).

Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы. Следует отметить, что это справедливо лишь при небольшом затухании.

1.6. Свободные затухающие колебания

Гармонические колебания, существующие вечно, являются одной из физических абстракций. В реальных системах колебания по прошествии некоторого времени затухают из-за диссипации энергии. Таким образом, представлением о гармонических колебаниях можно пользоваться лишь для времен, малых по сравнению с характерным временем затухания. Затухание колебаний всегда будет наблюдаться в системах с трением.

Уравнение затухающих колебаний

Рассмотрим в качестве примера пружинный маятник, помещенный в вязкую среду. Помимо силы упругости на тело будет действовать сила сопротивления, пропорциональная скорости

где r — соответствующий коэффициент, зависящий от вязкости среды, размеров и формы тела. Поэтому уравнение движения примет вид:

Здесь новый, дополнительный параметр системы, называемый коэффициентом затухания. Колебания незатухающие, если .

Другой пример — электромагнитный контур. Если помимо конденсатора С и индуктивности L в контуре имеется еще и активное сопротивление R, то ЭДС самоиндукции равна сумме напряжения на конденсаторе и падения напряжения на сопротивлении. Поэтому уравнения (1.15) примут теперь вид:

Подставляем первое уравнение во второе:

Напомним, что комбинация L/R уже встречалась нам в теории электромагнетизма, где она характеризовала характерное время затухания (появления) экстратоков замыкания-размыкания. Таким образом, величина b имеет размерность обратного времени, совпадающую с размерностью циклической частоты.

Анализ решений

Итак, в обоих рассмотренных случаях дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид:

Дифференцируя функцию x(t), получаем:

Подставляем эти выражения в (1.67):

Выражение в квадратных скобках должно быть равно нулю. Замечаем, что в этом выражении сокращаются члены с первой производной . Получаем в итоге дифференциальное уравнение для функции X(t):

Здесь возможны два случая. Пусть сначала . Тогда можно ввести параметр

так что уравнение (1.71) примет вид:

Но это — стандартное уравнение гармонических колебаний, общее решение которого мы знаем:

Значит, мы нашли общее решение уравнения затухающих колебаний (1.67):

Во многих системах коэффициент затухания мал по сравнению с собственной частотой колебаний: . Тогда движение системы можно рассматривать как почти гармоническое колебание с частотой и с амплитудой, изменяющейся по закону (рис. 1.22)

Рис. 1.22. Свободные затухающие колебания

Коэффициент затухания определяет скорость уменьшения амплитуды колебаний: он обратен по величине промежутку времени, за который амплитуда уменьшается в e раз.

Период затухающих колебаний равен:

Пусть первое наибольшее положительное отклонение достигается в момент времени . Последующие наибольшие отклонения того же знака (A’, A», A»’ и т.д. — см. рис. 1.22) образуют геометрическую прогрессию:

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:

Это соотношение называется декрементом затухания. Логарифм этого отношения называется логарифмическим декрементом затухания:

Определим количество колебаний, которое совершит система за время . За это время амплитуда уменьшается в е раз, а число колебаний равно:

Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.

Для характеристики колебательной системы часто употребляется величина, называемая добротностью:

которая пропорциональна числу колебаний N_е, совершаемых системой за то время , за которое амплитуда колебаний уменьшается в е раз. Например, для электромагнитного контура при находим:

Мы видели, что полная энергия в колеблющейся системе пропорциональна квадрату амплитуды. При малом затухании (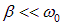) имеем:

где E₀ — значение полной энергии колеблющейся системы в начальный момент времени. Можно определить убыль энергии за период Т:

то есть при слабом затухании добротность, с точностью до множителя , равна отношению полной энергии, запасенной в колебательной системе в данный момент времени, к убыли энергии за один период колебаний.

При увеличении затухания частота колебаний

стремится к нулю, а период колебаний растет. В предельном случае

период обращается в бесконечность, то есть движение перестает быть периодическим. Соответствующий математический анализ показывает, что при движение носит апериодический характер — выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.

ЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ

Колебаниями называется вид движения физических тел или такие процессы, для которых характерна та или иная степень повторяемости во времени. Например, принципом повторяемости обладают: движения маятника и гитарной струны, голосовых связок и барабанной перепонки уха, колебания температуры воздуха и напряжения в электросети, изменение освещенности на улице в связи со сменой дня и ночи и т.д. Как видно из приведенных примеров, колебания имеют различное происхождение, иначе говоря, разную физическую природу: колебания механические, тепловые, электрические, электромагнитные, оптические и др.

Если повторяемость состояний колеблющейся системы имеет произвольный характер, то такие колебания называются апериодическими или непериодическими. Колебания, для которых последовательность состояний системы повторяется через равные промежутки времени, называются периодическими. В дальнейшем мы будем рассматривать в основном периодические колебания.

В зависимости от характера воздействия, оказываемого на колебательную систему извне, различают: свободные (или собственные) колебания и колебания вынужденные. По этому признаку различают еще автоколебания и параметрические колебания.

Свободными называются колебания, которые совершаются за счет внутренних сил системы, предоставленной самой себе после того, как ей был сообщён внешний первоначальный толчок, породивший эти колебания. Например, шарик на нити.

Вынужденными называются колебания, которые совершаются под постоянным воздействием внешней переменной силы. Например, колебания моста, когда по нему идут пешеходы.

Если с течением времени запас энергии колебательной системы не меняется, то такое колебание называется незатухающим. Если же эта энергия уменьшается, то – затухающим.

Независимо от природы, все виды колебательного движения имеют общие закономерности, т.е. протекают по одним и тем же законам и характеризуются одними и теми же параметрами: периодом Т, частотой ν, амплитудой А и фазой φ.

Закон колебательного движения – это уравнение, которое показывает, как с течением времени изменяются параметры, описывающие состояния колеблющегося тела. Простейшими являются гармонические колебания, для которых изменение величин, описывающих состояние системы, происходит по закону синуса или косинуса. Этот вид колебаний особенно важен, т.к. в природе и в практической сфере колебания очень часто имеют характер близкий к гармоническому или могут быть представлены как сумма нескольких простых гармонических колебаний.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Получим закон гармонических колебаний на примере механического движения механических колебаний. Это вид колебаний, при котором тело поочерёдно и многократно совершает отклонения от своего положения равновесия в одну и другую сторону.

Рассмотрим колебания пружинного маятника вдоль горизонтальной оси при отсутствии силы сопротивления. Пружинный маятник представляет собой массивный шарик массой m, прикрепленный к пружине с ничтожно малой массой и жесткостью k. Другой конец пружины закреплен неподвижно. Если вывести шарик из равновесия и отпустить, то под воздействием силы упругости деформированной пружины система пружина–шарик придет в колебательное движение. Положение шарика на оси будем определять смещением s, т.е. расстоянием от положения равновесия до шарика (рис.1). Наша цель решить основную задачу механики – найти ответ на вопрос: где будет находиться тело в произвольный момент времени t, т.е. найти вид функции s = f(t)?

Примем за начало отсчета точку 0, в которой находится центр шарика в равновесном состоянии системы, т.е. при отсутствии деформации в пружине. Пусть в момент времени t шарик находится на расстоянии s от положения равновесия. Характер движения в данный момент времени определяется равнодействующей приложенных к шарику сил: . Т.к. трение по условию отсутствует, а сила тяжести перпендикулярна стержню, то характер движения будет определяться только силой упругости деформированной пружины:

. (1)

В соответствии со 2-ым законом Ньютона эта сила сообщает шарику ускорение , тогда в скалярном виде (1) можно записать:

, (2)

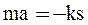
но т.к. a = d 2 s /dt 2 , то

. (3)

Разделим правую и левую часть (3) на m и обозначим k/m = . Сгруппировав все члены в левой части равенства, получим дифференциальное уравнение гармонических колебаний.

или . (4)

Это дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение: к 2 + = 0, корни которого к_1,2 = ±iω₀ – мнимые числа. Тогда общим решением (4) будет:

Для любых С₁ и С₂ всегда можно подобрать другие произвольные постоянные А и φ₀ такие, что С₁ = Аsin φ_0,1 а С₂ = Аcosφ_0,1, Тогда общее решение (5) примет вид:

Если выражения для С₁ и C₂ поменять местами (С₁ = Аcosφ_0,2 а С₂ = Аsin φ_0,2), то общее решение будет иметь вид:

Данные функции (6) и (7) и есть искомые кинематические уравнения гармонического колебания. Аргумент этой функции (w₀t + φ₀) называется фазой колебания; j₀ – постоянная составляющая фазы называется начальной фазой; – собственная циклическая (круговая) частота колебаний данного пружинного маятника ( , , тогда ); А – амплитуда колебаний, в данном случае максимальное значение смещения s. В общем случае, амплитуда А – это наибольшее значение величины, изменение которой с течением времени выбрали для описания изучаемых колебаний. Графики гармонического колебания представляют собой синусоиды (рис.2):

Получим уравнения, описывающие изменения скорости и ускорения тела, совершающего гармонические колебания. Пусть s = Аcos(ω₀t + φ₀), тогда:

, (8)

. (9)

Как видно, скорость и ускорение тоже изменяются по гармоническим законам, но скорость опережает по фазе смещение на p/2, а ускорение на p (рис.3), т.е. ускорение находится в противофазе со смещением. В целом, тела, на которые действуют равнодейству-ющие вида F = -ks (такие силы называются квазиупругими), будут совершать гармонические колебания.

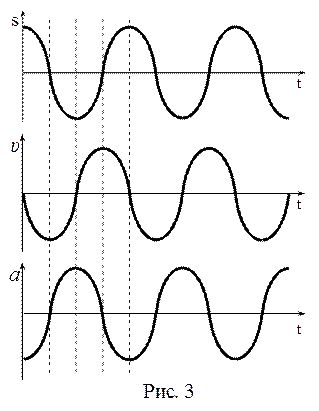
Рассмотрим процесс колебательного движения с энергетической точки зрения. Смещая тело из положения равновесия, мы деформируем пружину, сообщая тем самым системе запас потенциальной энергии. Отпустив тело, мы даем ему возможность двигаться к положению равновесия. При этом потенциальная энергия системы превращается в кинетическую. В момент прохождения положения равновесия потенциальная энергия полностью превращается в кинетическую. Продолжая движение по инерции, тело опять деформирует пружину, т.е. кинетическая энергия начинает превращаться в потенциальную. В момент, когда кинетическая энергия полностью превра тится в потенциальную, смещение достигнет амплитудного значения, тело остановится и начнет двигаться обратно. Опять потенциальная энергия будет превращаться в кинетическую и т.д. (рис.4). Т.о., с точки зрения энергетической, механическое колебание – это процесс многократных, последовательных превращений потенциальной энергии в кинетическую и обратно.

, (10)

, (11)

, (12)

т.е. полная энергия системы величина постоянная.

ЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

В реальных условиях, кроме возвращающей силы в колебательной системе обязательно будет действовать и сила сопротивления. Будем считать, что скорости движения при колебаниях будут небольшими, тогда сила сопротивления прямо пропорциональна скорости:

, (13)

где r –коэффициент сопротивления. Учитывая только силу сопротивления (13) и силу упругости (1) согласно II закону Ньютона для уравнения движения получим:

, (14)

. (15)

Разделив правую и левую часть (15) на m и обозначив k/m = , а r/m = 2β, получим:

или . (16).

Это однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение:

к 2 + 2b·к + w = 0 имеет корни . (17)

Из (17) видно, что движение будет колебательным, только если b 2 — β t (С₁cosωt + C₂sinωt).

Заменяя С₁ и С₂ через другие постоянные А₀ и φ₀ такие, что С₁ = А₀cosφ₀, а С₂ = А₀sinφ₀ окончательно получим:

Это уравнение свободных затухающих колебаний, график которых представлен на рис.5. Как видно амплитуда свободных затухающих колебаний убывает по экспоненциальному закону:

(рис.5, пунктирная линия). Круговая частота этого колебания w = , а период Т = 2π / . Как видно, ни частота, ни период затухающих колебаний не равны соответствующим параметрам собственных колебаний системы.

Для описания быстроты затухания колебаний используют три взаимосвязанные величины: коэффициент затухания – β, декремент затухания – δ и логарифмический декремент затухания – λ. Коэффициент затухания b = , [b] = 1/с. Декремент затухания –

(20)

и логарифмический декремент затухания

l = ℓnd = ℓnе βТ = βТ. (21)

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

Свободные колебания в силу наличия трения всегда будут затухающими. Чтобы колебания были незатухающими необходимо компенсировать потери энергии. Если рассматривать механические колебания, то роль фактора восполняющего эти потери может играть внешняя переменная сила, которую называют вынуждающей.