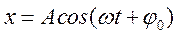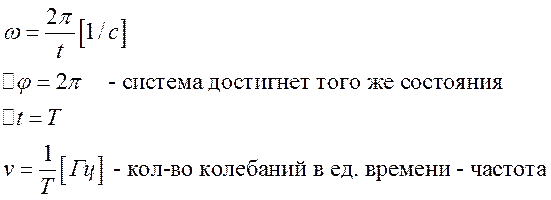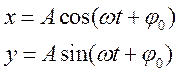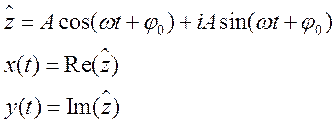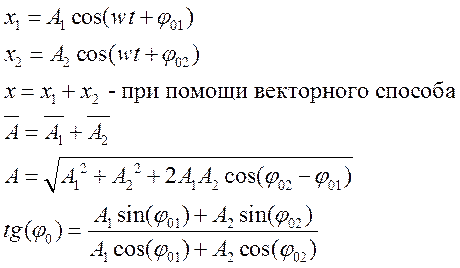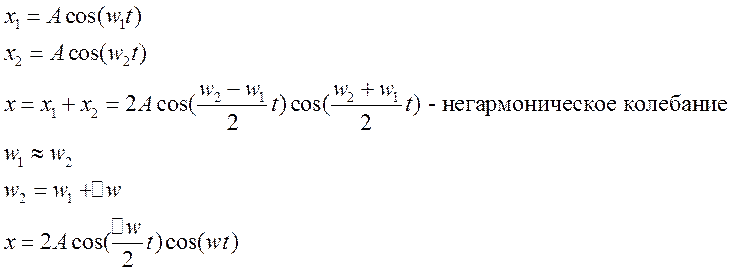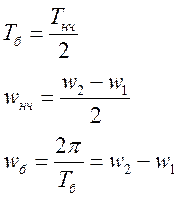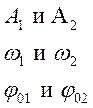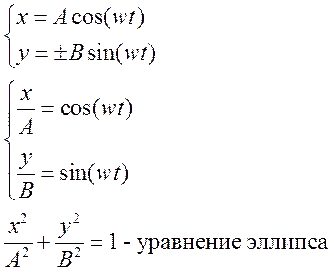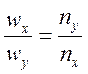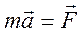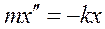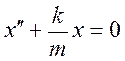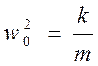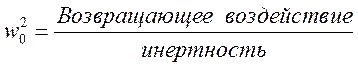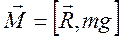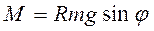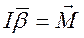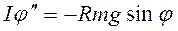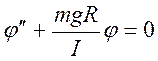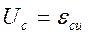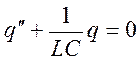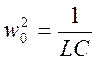Уравнение гармонического осциллятора энергия гармонического осциллятора

ЭНЕРГИЯ ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА

СОДЕРЖАНИЕ

5.1.МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

1.1. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ

1.2. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

1.3. ЭНЕРГИЯ ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА

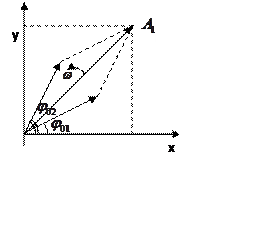
1.4. ВЕКТОРНАЯ ДИАГРАММА И СЛОЖЕНИЕ КОЛЕБАНИЙ

1.5. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

1.6. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

1.9. ОБРАЗОВАНИЕ ВОЛН

1.10. УРАВНЕНИЕ ПЛОСКОЙ УПРУГОЙ ВОЛНЫ

1.11.ЭНЕРГИЯ, ПЕРЕНОСИМАЯ УПРУГОЙ ВОЛНОЙ

1.12. ЭФФЕКТЫ СЛОЖЕНИЯ ВОЛН. СТОЯЧИЕ УПРУГИЕ ВОЛНЫ

1.13. ЗВУКОВЫЕ ВОЛНЫ

5.2 ЭЛКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ

2.1.Плоские электромагнитные волны и их свойства

Опыт Герца

Энергия электромагнитных волн

Излучение диполя

Световое давление

Шкала электромагнитных вол

5. 1 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ

Колебаниями в физике не только называют периодические или почти периодические движения тел, когда колеблющееся тело многократно повторяет одно и то же движение туда и обратно около определенного положения, а придают этому понятию более широкий смысл. Под колебаниями понимают всякий периодический или приблизительно периодический процесс, в котором значение той или иной физической величины повторяется точно или приблизительно точно через равные или приблизительно равные промежутки времени.

Колебаться, или осциллировать, может груз на конце пружины, маятник, струны гитары или фортепиано, напряжение между обкладками конденсатора в контуре радиоприемника; колеблются атомы в молекулах, в твердом теле атомы совершают колебания относительно своих фиксированных положений в кристаллической решетке. Пауки обнаруживают попавшую в их сети добычу по дрожанию паутины, дома и мосты дрожат при проезде тяжелых грузовиков. Почти все материальные предметы колеблются после того, как на них подействует импульс силы.

В зависимости от характера воздействия на колеблющуюся систему различают свободные колебания, вынужденные колебания, автоколебания, параметрические колебания. Свободными, или собственными, называются такие колебания, которые совершает выведенная из положения равновесия или получившая толчок система, будучи предоставлена самой себе. Если колеблющаяся система подвергается в процессе колебаний воздействию внешней периодически меняющейся силы, то она совершает колебания, называемые вынужденными.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Говоря о колебаниях тела в механике, мы подразумеваем повторяющееся движение по одной и той же траектории. Простейшим примером периодического движения служат колебания груза на конце пружины (пружинный маятник) (рис. 7.1).

Если сдвинуть груз вправо, растягивая пружину, или влево, сжимая ее, то пружина действует на груз с силой, которая стремится вернуть его в положение равновесия; такую силу называют возвращающей. Для нашей системы возвращающая сила прямо пропорциональна расстоянию х, на которое сжимается или растягивается пружина ( ). Эта сила сообщает грузу ускорение, и груз приходит в положение равновесия. В положении равновесия сила, действующая на груз, уменьшается до нуля, а скорость его в этой точке максимальна. Возвратившись в устойчивое состояние, колебательная система не может сразу остановиться. В механических колебательных системах этому мешает инертность колеблющегося тела. Поэтому груз пройдет положение равновесия и будет двигаться далее, что приведет к сжатию пружины. Сила со стороны пружины в результате ее сжатия замедляет движение груза, и в некоторой точке его скорость будет равна нулю. Затем груз начинает двигаться в противоположном направлении и приходит в точку, откуда он начал движение. Затем весь этот процесс повторяется. Пружина, груз – пример колебательной системы. Расстояние х груза от положения равновесия до точки, в которой в данный момент времени находится груз, называют смещением.

Любая колебательная система, в которой возвращающая сила прямо пропорциональна смещению, взятому с противоположным знаком (например, упругая сила ), совершает гармонические колебания. Такую силу называют квазиупругой, а саму систему часто называют гармоническим осциллятором.

Рассмотрим уравнение, описывающее колебания, совершаемые системой в направлении оси X в отсутствие сил трения. Для этого воспользуемся вторым законом Ньютона . Ускорение , а так как , то ускорение можно получить, если два раза взять производную от координаты по времени. Тогда . Так в математике обозначается вторая производная. Теперь уравнение движения осциллятора можно записать в виде:

.

Введем обозначение , тогда уравнение запишется в следующем виде:

,

здесь – ускорение движущейся точки.

Поскольку , – величина, зависящая от свойств системы, совершающей колебания. Решение этого уравнения имеет вид:

(7.1)

где и – произвольные постоянные, которые определяются из начальных условий. В качестве таковых можно, например, взять значение отклонения и скорости в момент времени . В справедливости (7.1) можно убедиться на простом опыте. Если к колеблющемуся грузу прикрепить карандаш и протягивать под ним с постоянной скоростью лист бумаги, то карандаш вычертит синусоиду.

Таким образом, смещение изменяется со временем по закону косинуса или синуса. Движение механической системы, находящейся под действием квазиупругой силы, представляет собой гармоническое движение.

На рис. 7.2 приведен график зависимости смещения частицы от времени. По горизонтальной оси отложено время , по вертикальной – смещение x. Так как косинус изменяется от -1 до +1, значения лежат в пределах от до . Величина наибольшего отклонения системы от положения равновесия называется амплитудой колебания. Амплитуда – постоянная положительная величина. Величина , стоящая под знаком косинуса, называется фазой колебания. Постоянная представляет собой значение фазы в момент и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета времени.

Поскольку косинус – периодическая функция с периодом , различные состояния частицы, совершающей гармонические колебания, повторяются через такой промежуток времени T, за который фаза колебания получает приращение . Этот промежуток времени называется периодом колебания. Его можно определить из условия:

,

.

Число колебаний в единицу времени называется частотой колебаний. Очевидно, что частота связана с периодом колебаний соотношением

.

Из определения периода следует, что . Величину называют круговой или циклической частотой. Так как она зависит от свойств самой колеблющейся системы, то ее часто называют собственной частотой колебаний системы.

Примером системы, совершающей гармонические колебания, является математический маятник. Математический маятник – это тело, подвешенное на невесомой и нерастяжимой нити, находящееся в поле тяжести Земли. Математический маятник представляет идеализированную модель, правильно описывающую реальный маятник лишь при определенных условиях. Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного на ней тела, масса нити ничтожна мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь.

Колебательную систему в данном случае образуют нить, присоединенное к ней тело и Земля, без которой эта система не могла бы служить маятником. При колебаниях математического маятника периодически изменяется угол отклонения маятника от положения равновесия. Период свободных гармонических колебаний математического маятника равен

,

где – длина нити, g – ускорение свободного падения. Таким образом, период свободных колебаний математического маятника не зависит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник.

ЭНЕРГИЯ ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА

Во время колебательных процессов происходит периодическое превращение потенциальной энергии системы в кинетическую. Например, отклонив математический маятник в сторону и, следовательно, подняв его на высоту h, ему сообщают потенциальную энергию . Она полностью переходит в кинетическую энергию движения , когда груз проходит положение равновесия и скорость его максимальна. При колебаниях пружинного маятника кинетическая энергия движения груза переходит в потенциальную энергию деформированной системы. Величина полной энергии колеблющейся системы в любой момент времени равна сумме ее кинетической и потенциальной энергии:

.

(7.2)

Поскольку скорость – это первая производная от координаты по времени, то

.

Учитывая, что и подставив выражения для и , получим:

.

То есть полная энергия системы, совершающей колебания, пропорциональна ее массе, квадрату амплитуды и квадрату собственной частоты. Так как силы, действующие на колеблющуюся частицу, являются консервативными, то ее механическая энергия остается постоянной. В процессе же колебаний происходит превращение кинетической энергии в потенциальную и обратно.

На рис. 7.3 приведен график зависимости потенциальной энергии от координаты частицы. С ростом x уменьшается кинетическая энергия и увеличивается потенциальная. Максимального значение потенциальная энергия достигает в поворотных точках , при этом кинетическая энергия равна нулю. Среднее за период значение кинетической энергии равно среднему за период значению потенциальной энергии.

Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа

Страницы работы

Содержание работы

1.Гармонические колебания. Характеристики и формы представления.

В общем случае состояние системы изменяется. Если в изменение обнаруживается повторяемость, то в системе происходят колебания. Если колебания повторяются через строго определенный промежуток времени, то такое колебание периодическое, а сам промежуток – это период Т. Колебания, происходящие по закону Sin или Cos называются гармоническими.

Причины гармонических колебаний:

1. Многие колебания во многих системах близки к гармоническим.
2. Любое произвольное колебание можно представить в виде суммы гармонических колебаний.

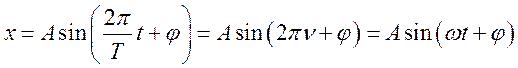
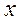
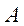
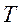
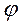
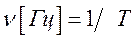
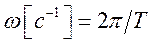
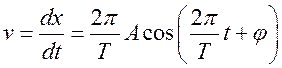
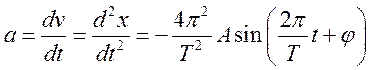
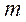
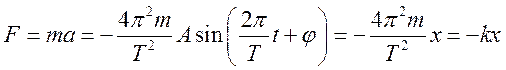
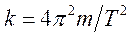
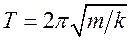
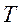
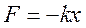
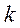
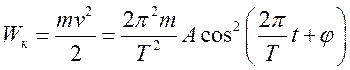
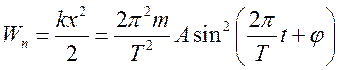
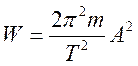
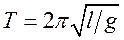
Уравнение гармонического колебательного движения имеет вид , где — смещение точки от положения равновесия, разное для разных моментов времени, — амплитуда, — период, — начальная фаза, — частота колебаний, — круговая частота. Скорость и ускорение точки, совершающей колебание, определяются соотношениями , . Сила, под действием которой точка массой совершает гармоническое колебание, , где , т.е. . Здесь — период колебаний точки, совершающей колебания под действием силы , где — жесткость пружины, численно равная силе, вызывающей смещение, равное единице. Кинетическая и потенциальная энергии колеблющейся точки имеют вид , . Полная энергия . Примером гармонических колебательных движений могут служить малые колебания маятника. Период колебаний математического маятника .

Характеристики и способы представления гармонических колебаний

x – смещение;

A — амплитуда (максимальное значение x);

— фаза;

— начальная фаза, при t = 0, зависит от состояния система и времени;

— скорость изменения фазы с течением времени, циклическая частота;

Применяется для сложных колебаний. Угловая скорость – циклическая частота.

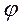
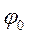
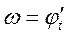
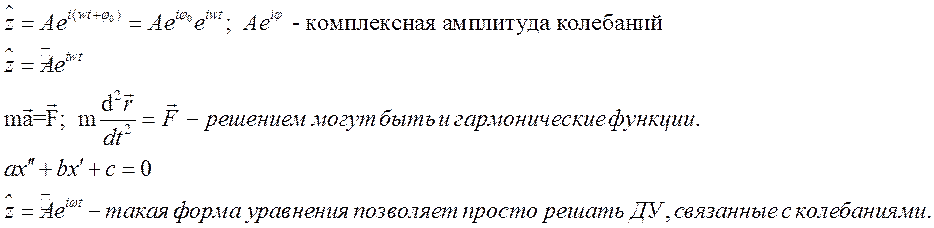
2.Сложение однонаправленных колебаний. Векторные диаграммы. Биения.

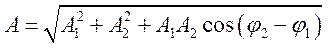
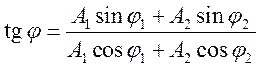
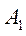
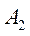
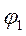
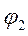
При сложении двух одинаково направленных гармонических колебаний одинакового периода получается гармоническое колебание того же периода с амплитудой и с начальной фазой, определяемой из уравнения , где и — амплитуды слагаемых колебаний, и — их начальные фазы.

1. Сложение однонаправленных колебаний с одинаковыми частотами:

Пусть система принимает участие в двух однонаправленных колебаниях с одной .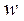

Сколько бы гармонических колебаний ни складывалось, получаем гармоническое колебание с такой же частотой, но у него своя амплитуда, которая зависит от амплитуды складываемых колебаний и от начальных фаз.

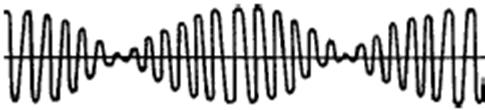
2. Сложение однонаправленных колебаний с разными частотами. Биения.

Результирующее x – это быстрое колебание с медленно изменяющейся амплитудой.

Если амплитуды разные, то нулевой амплитуды не получится. Если складываются колебания с разными частотами, то получаются не гармонические колебания.

3.Сложение перпендикулярных колебаний. Фигуры Лиссажу.

При сложении двух взаимно перпендикулярных колебаний одинакового периода уравнение траектории результирующего движения имеет вид .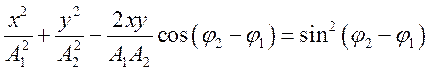

Сложение взаимно перпендикулярных колебаний

Разные

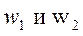
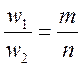
Результирующее движение в общем случае сложное. Траектория может получиться не замкнутой. Замкнутая, если — кратны друг другу или частоты относятся, как целые числа, , тогда получится фигура Лиссажу.

В общем случае фигура Лиссажу пересекает целое число раз каждую ось. Тогда частоты колебаний относятся между собой так, как относятся обратные числа:

4.Гармонические осцилляторы. Дифференциальное уравнение гармонического осциллятора. Собственные колебания и энергия осциллятора.

Среди любых систем можно выделить колебательную систему или осциллятор.

Такая система может совершать колебания сама по себе, те за счет внутренних причин, если у нее есть энергия. Если собственные колебания системы являются гармоническими то система- осциллятор.

Динамика гармонических колебаний описывается дифуром:

(1)

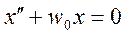
Если для системы получается уравнение (1) то система – гармонический осциллятор.

— собственная частота.

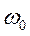
Дифференциальное уравнение гармонического осциллятора.

=> — решение этого уравнения есть функции вида

, .

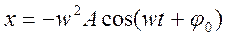
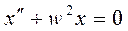
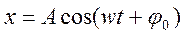
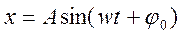
Пример 1 (Пружинный маятник.)

— дифференциальное уравнение гармонического осциллятора.

Решением дифференциального уравнения будет.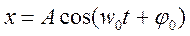

Величина собственной частоты зависит от свойств системы.

Причин колебаний 2:

3 свойства осциллятора:

1. Начальное положение.

2. Возвращающая сила.

Пример 2 (Физический маятник).

Равновесие когда

Если угол мал то:

— собственная частота.

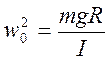
Пример 3 (Колебательный контур)

Сообщение заряда колебательному контуру выводит систему из положения равновесия.

— закон Кирхгофа.

=>

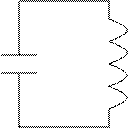
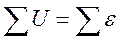
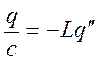
Возвращающие воздействие связанно с зарядом.

Энергия гармонического осциллятора.

Рассмотренные в примерах осцилляторы являются консервативными системами. Энергия с течением времени не меняется.

Квантовый гармонический осциллятор

Конспект лекции (с демонстрациями)

Аннотация: изучение качественной стороны решения уравнения Шредингера для гармонического осциллятора, выяснение отличий получаемых результатов от выводов классической механики. (Традиционное изложение темы, дополненное демонстрациями на компьютерных моделях.)

Одна из важных задач о движении микрочастиц – это задача о движении гармонического осциллятора — системе, способной совершать гармонические колебания. История квантовой теории реально начинается с Макса Планка, который в 1900 г. получил формулу для правильного описания спектрального распределения теплового излучения. Планк пришел к выводу, что не может обеспечить вывод своей магической формулы для распределения излучения, если только не сделать предположения, которое с философской точки зрения он считал почти неприемлемым. Это предположение заключалось в том, что рассматриваемые им в качестве излучателей гармонические осцилляторы должны обладать энергиями, не распределенными как непрерывные переменные (чего следовало бы ожидать), а принимающими дискретные и регулярным образом расположенные значения. Осцилляторы с частотой υ должны были обладать значениями энергии, которые были бы кратны, т.е. n раз умножены (где n = 0,1, 2,3. ) на нечто, названное им квантом энергии hυ.

Рассмотрим одномерный случай. (Трехмерные задачи сложны в математическом отношении, а практически все принципиальные особенности движения микрочастиц можно выявить и на одномерных задачах.) Изменение потенциальной энергии по оси x описывается формулой

Какие примеры движения окружающего мира хотя бы приближенно описываются такой потенциальной функцией?

• Колебания маятника с малой амплитудой.
• Другой пример – вертикальные колебания грузика, подвешенного на пружине.

В мире микрочастиц примерами могут быть колебания двухатомной молекулы или колебания атомов в кристаллах. Существенным для всех примеров является ограничение движения некоторой областью значений x. Частица не может покинуть параболическую потенциальную яму, края которой уходят на бесконечность.

Из классической механики известно, что проекция движения частицы на ось x представляет собой синусоидальное колебание около положения равновесия x = 0 с частотой:

Точки a₀ и -a₀, в которых полная энергия частицы E равна потенциальной энергии, являются для частицы точками поворота. Плотность вероятности обнаружения колеблющейся частицы в различных точках оси x описывается формулой

Минимальна вероятность найти частицу около положения равновесия, где она движется с максимальной скоростью. Вблизи точек поворота частица как бы «зависает», и там вероятность обнаружения максимальна.

Оценка минимальной энергии осциллятора

Посмотрим, к каким выводам о характере движения приводит квантовая механика. Начнем с простой оценки минимального значения энергии осциллятора E. Полная энергия осциллятора E складывается из кинетической и потенциальной энергий:

Используя соотношение неопределенности Гейзенберга, в качестве оценки значения импульса p возьмем p

Для малых значений x кинетическая энергия превышает потенциальную, тогда как при больших значениях x имеет место обратное соотношение между ними. Для основного состояния, где энергия минимальна, найдем минимум функции (2). Значение переменной x_min, соответствующее минимуму, равно:

а соответствующее значение энергии E имеет порядок

Заметим, что оценка энергии основного состояния дает ненулевое(!) значение. Уже простые вычисления приводят к нетривиальному результату.

Решения уравнения Шредингера

Нахождение точного решения требует решения уравнения Шредингера с потенциальной энергией (1), которое имеет вид

Трудности решения связаны со слагаемым, содержащим x 2 . Приведем здесь только результаты вычислений. Анализ показывает, что, как и в случае с прямоугольной потенциальной ямой, волновые функции, являющиеся решением этого уравнения, будут непрерывными и конечными не при всех значениях энергии E, а лишь при дискретном наборе значений:

где n принимает значения 0, 1, 2, . . Отметим, что энергетические уровни гармонического осциллятора в отличие от случая прямоугольной потенциальной ямы расположены на одинаковом энергетическом расстоянии друг от друга ΔE = hυ.

Важной особенностью решения является наличие так называемых нулевых колебаний — колебаний с энергией, соответствующих значению квантового числа n = 0. Отличие от нуля минимальной энергии осциллятора характерно для всех квантовых систем и является следствием соотношения неопределенностей (см. оценку выше). В реальных квантовых системах, например, кристаллах, эти колебания сохраняются, как показывает опыт, даже при температурах, близких к абсолютному нулю, когда, казалось бы, все тепловое движение должно прекратиться. Опыты по рассеянию света кристаллами при низких температурах это подтверждают. Велика роль нулевых колебаний и в объяснении природы сил молекулярных взаимодействий (пример ниже) и других молекулярных явлений.

Первые три волновых функции гармонического осциллятора выглядят так:

Здесь введено обозначение x₀ 2 = h/(4π 2 mυ).

Графики этих волновых функций представлены на рисунке ниже.

Пунктиром показаны границы, между которыми совершала бы колебания классическая частица. Значения a₀ отличаются для разных n, так как от n зависит энергия Е (

E 1/2 ). Очевидно, что при малых значениях квантового числа n плотность вероятности нахождения частицы, определяемая квадратом модуля волновой функции ψ₀(x) 2 , кардинальным образом отличается от плотности вероятности обнаружения классического осциллятора: в основном состоянии максимальное значение вероятности приходится на центр, модуль волновой функции для всех квантовых чисел n имеет наибольшие значения между классическими точками поворота и экспоненциально убывающие «хвосты» вне этих точек.

Определим для основного состояния, как велика вероятность P обнаружения частицы вне пределов классической области, т.е. вне области -a₀ Компьютерная модель

Компьютерная модель поможет Вам в исследовании квантового осциллятора. Ее возможности: после того, как Вы зададите порядковый номер атомов Z, из которых состоит молекула (по умолчанию Z=8), компьютер проведет необходимые расчеты и будет готов показать разрешенные значения энергии, соответствующие им волновые функции и распределения плотности вероятности нахождения частицы по координате. Двигайте указатель вдоль оси энергий (мышкой или клавишами со стрелками) и наблюдайте.

• как плотность уровней зависит от массы атомов;
• как энергия частицы зависит от квантового числа n;
• как вероятность обнаружить частицу зависит от x; убедитесь в том, что амплитуда колебаний частицы увеличивается с ростом ее энергии;
• как вероятность обнаружения частицы вне классической области зависит от квантового числа n. Для этого на нижнем графике установите крестик в начало области интегрирования, нажмите клавишу «Enter» и передвиньте крестик в конечную точку. Компьютер рассчитает площадь под кривой, равную вероятности обнаружить частицу в выбранном Вами диапазоне координат;

Смешение состояний (принцип суперпозиции)

Реальные объекты (атомы в молекуле, кристалле. ) редко находятся в основном состоянии. За счет, например, теплового возбуждения реальны состояния с квантовым числом n > 0. Одно из важнейших положений квантовой механики — принцип суперпозиции. Он гласит: если квантовая частица может находиться в состояниях, описываемых функциями Ψ₁, Ψ₂, . Ψ_n, то линейная комбинация (суперпозиция) волновых функций Ψ_i

где с_i — произвольные постоянные, также является волновой функцией, описывающей одно из возможных состояний частицы. Коэффициенты с_i изменяются во времени. Принцип неопределенности ΔtΔE>h/2π не позволяет определить зависимость от времени этих коэффициентов для конкретного осциллятора (можно, однако, получить средние значения для большого количества осцилляторов).

Для гармонического осциллятора интересен набор состояний, который минимизирует соотношение неопределенности «координата — импульс», т.е. произведение ΔpΔx=h/2π. Впервые он был построен Шредингером в 1926 г. Волновая функция Ψ(x,t) может быть разложена по волновым функциям стационарных состояний осциллятора

Коэффициенты этого разложения

Вероятность осциллятору находиться в состоянии с квантовым числом n равна

т.е. дается распределением Пуассона. Волновая функция Ψ(x,t) представляет нерасплывающийся волновой пакет. Центр пакета движется по классическому закону, ширина пакета не зависит от времени.

Эти состояния называют когерентными, так как они используются для описания когерентных свойств электромагнитного излучения в квантовой теории поля (R. Glauber, Нобелевская премия 2005 года; текст нобелевской лекции, 269 кб). Можно показать, что свободное электромагнитное поле эквивалентно бесконечному набору независимых гармонических осцилляторов.

Со свойствами когерентных состояния гармонического осциллятора можно познакомиться поближе с помощью компьютерной модели (автор L. Kocbach).

Вычисление средних значений

С помощью волновых функций можно найти среднее значение любой величины (если ее можно в принципе измерить экспериментально). Величина |ψ(x)| 2 dx — вероятность нахождения частицы в интервале dx. В случае многократных наблюдений за частицей |ψ(x)| 2 dx — доля частиц, которые находились в этом интервале, т.е. |ψ(x)| 2 является функцией распределения по координате. С ее помощью найдем, что среднее значение координаты

Аналогичным образом находится среднее значение любой функции координаты, например, для потенциальной энергии имеем

В этих формулах, чтобы вычислить среднее значение, мы умножаем значение функции в точке x на вероятность нахождения частицы около x и суммируем по всем возможным значениям x. В качестве примера найдем эти величины для основного состояния гармонического осциллятора

т.к. под интегралом нечетная функция, и

Среднее значение потенциальной энергии равно половине полной энергии этого состояния.

Правило для вычисления средней кинетической энергии отличается от приведенного, т.к. кинетическая энергия является функцией импульса p, а не координаты x:

Для основного состояния гармонического осциллятора

т.е. мы показали, что для основного состояния гармонического осциллятора средние значения потенциальной энергии и кинетической энергии равны между собой и составляют половину полной энергии осциллятора. Можно показать, что это утверждение будет справедливым и для любого другого состояния квантового гармонического осциллятора. Среднее значение потенциальной энергии увеличивается с ростом n, так как при больших значениях n функция ψ(x) заметно отлична от нуля в тех областях оси х, где потенциал U(x) увеличивается. Обратите на это внимание при экспериментах с компьютерной моделью .

Энергия излучения при переходе из одного состояния в другое равна

Набор равноотстоящих энергетических уровней гармонического осциллятора (3) на первый взгляд означает, что осциллятор может поглощать и испускать излучение с частотой, кратной υ, т.е. kυ , где k — разность квантовых чисел начального и конечного уровней осциллятора. Однако, на самом деле это не так. Точный анализ показывает, что если

где n и m квантовые числа начального и конечного состояний, среднее значение координаты не меняется во времени, и такие переходы запрещены.

Проверим выполнение этого условия для гармонического осциллятора. Пусть n=1, а m=0. Опуская постоянные, для интеграла получим выражение

т.к. под интегралом четная функция. Если положить n=2, m=1,

по той же причине. Переходы между соседними уровнями 0↔1 и 1↔2 являются разрешенными. Рассмотрим теперь переход между состояниями n=0 и m=2. Соответствующий интеграл имеет вид

поскольку функция под интегралом нечетная, а пределы симметричны относительно x=0. Следовательно, переходы 0↔2 запрещены. Особенности испускания и поглощения электромагнитного излучения гармоническим осциллятором таковы, что возможны переходы только между соседними уровнями Δn = ± 1. Это правило отбора для гармонического осциллятора.

Трехмерный гармонический осциллятор

В общем случае потенциальная энергия выражается суммой

Уравнение Шредингера допускает разделение переменных. Если решение искать в виде ψ(x,y,z)=X(x)Y(y)Z(z), получается три дифференциальных уравнения, совпадающих по виду с одномерным. Для изотропного случая (k_x =k_y =k_z = k) значения энергии таковы

где квантовые числа n₁, n₂ и n₃ пробегают значения от 0 до бесконечности. Как и в одномерной задаче, налицо дискретность значений энергии, не равная нулю нулевая энергия. Но в трехмерном случае решение определяется тремя квантовыми числами. И особенность: одно и то же значение энергии могут иметь различные состояния, для которых выполнено условие n₁+n₂+n₃ = const. Такие состояния называют вырожденными.

Взаимодействие двух осцилляторов

Существование нулевой энергии (формула (3) при n = 0) сыграло важную роль для объяснения такого загадочного явления, как межатомное взаимодействие у благородных газов. Так как это взаимодействие проявляется в уравнении состояния Ван-дер-Ваальса для реальных газов

оно названо ван-дер-ваальсовским. Если молекулы (атомы) обладают дипольным моментом, то их притяжение обусловлено взаимодействием диполей (качественно и количественно исследованный факт). Но нейтральные молекулы с симметричным в состоянии покоя распределением заряда могут взаимодействовать только при смещении зарядов, вызывающем появление дипольного момента. Такое смещение возникает при не исчезающих ни при каких условиях нулевых колебаний с энергией hυ/2. Появление дипольного момента у одной молекулы индуцирует дипольный момент в другой. Взаимодействие этих быстро меняющихся моментов и обуславливает притяжение.

В качестве простой модели рассмотрим два линейных осциллятора, расположенных на расстоянии R друг от друга и колеблющихся вдоль соединяющей их прямой. Положительные заряды будем считать неподвижными, x₁ и x₂ — смещение отрицательных частиц (электронов) от положения равновесия.

В отсутствии второго (или при очень большом R) потенциальная энергия каждого осциллятора может быть рассчитана по формуле (1), а частоту колебаний обозначим через υ₀

Энергия взаимодействия двух диполей по закону Кулона равна

Первые два слагаемых описывают отталкивание одноименных зарядов разных диполей, а вторые два — притяжение. Всегда R >> x₁ и R >> x₂. Поэтому разложим дроби в ряды и, удерживая по три члена разложения, получим

Полная энергия двух взаимодействующих осцилляторов равна (здесь p — импульс электрона)

выражение для полной энергии приводится к виду

представляющему сумму энергий двух независимых осцилляторов с несколько отличающимися частотами

Как мы видели, энергия этих осцилляторов имеет квантованные значения (см. (3) выше) и, следовательно, полная энергия нашей системы будет

а для основного состояния (n₁ = 0 и n₂ = 0)

Теперь надо учесть, что вторые слагаемые под корнями много меньше первых (связь электрона со своим ядром гораздо сильнее связи осцилляторов). Корни квадратные разложим в степенные ряды и ограничимся тремя членами в разложении. Это даст

Последнее выражение равно удвоенной энергии изолированного осциллятора минус небольшая энергия. Поскольку добавка отрицательна, полная энергия взаимодействующих осцилляторов меньше энергии изолированных, для разрыва связи нужно энергию затратить! И, заметим, энергия связи очень быстро убывает с расстоянием

Не было бы нулевых колебаний (чисто квантового эффекта), не существовало бы и связи молекул в основном состоянии.

Ангармонический осциллятор

Гармонический осциллятор — идеализация. Реальные зависимости U(x) выглядят как на рисунке справа. Парабола (штриховая кривая) является хорошим приближением только для малых колебаний вблизи положения равновесия. Для колебаний большой амплитуды формула (3) непригодна, интервалы между верхними уровнями энергии и нижними не одинаковы. Для верхних уровней энергии E_n потенциальная яма шире параболы, и поэтому интервалы между этими уровнями меньше интервалов между нижними уровнями.

Подведем итоги:

• энергия основного состояния частицы не равна нулю;
• энергия частицы квантована, и значение ее растет линейно с n;
• вероятность обнаружить частицу меняется от точки к точке;
• в трехмерном случае различным состояниям может соответствовать одно и то же значение энергии (вырождение);
• нулевые колебания объясняют происхождение сил притяжения между атомами инертных газов;
• для ангармонического осциллятора уровни не эквидистантны и правило отбора Δn = ± 1 нарушается;
• если значение квантового числа n устремить к бесконечности, решение переходит в классическое.

Если возникли какие-либо вопросы, напишите мне.