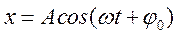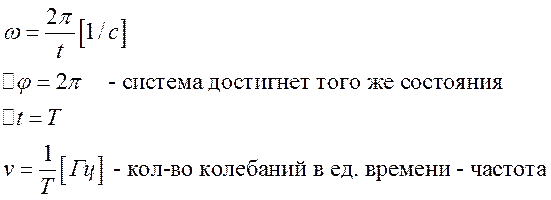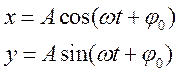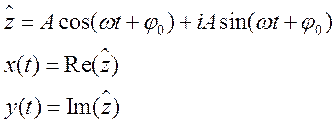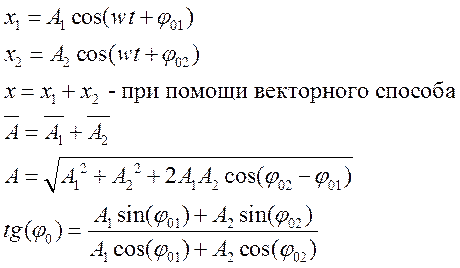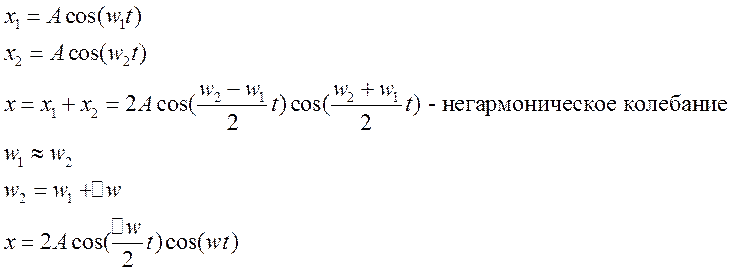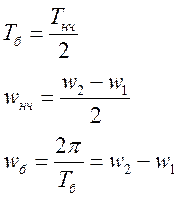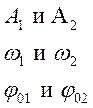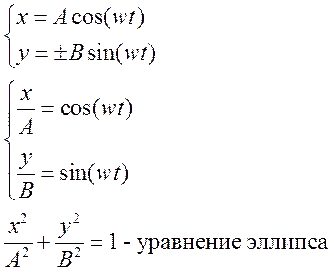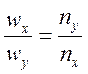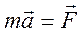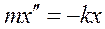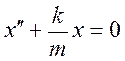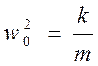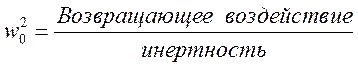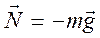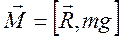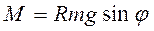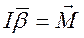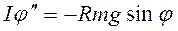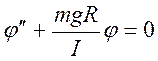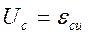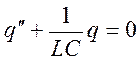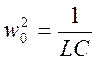Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа
Страницы работы
Содержание работы
1.Гармонические колебания. Характеристики и формы представления.
В общем случае состояние системы изменяется. Если в изменение обнаруживается повторяемость, то в системе происходят колебания. Если колебания повторяются через строго определенный промежуток времени, то такое колебание периодическое, а сам промежуток – это период Т. Колебания, происходящие по закону Sin или Cos называются гармоническими.
Причины гармонических колебаний:
- Многие колебания во многих системах близки к гармоническим.
- Любое произвольное колебание можно представить в виде суммы гармонических колебаний.
Уравнение гармонического колебательного движения имеет вид 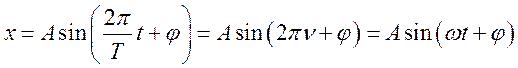
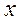
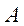
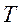
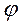
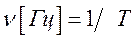
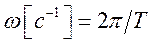
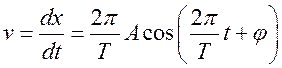
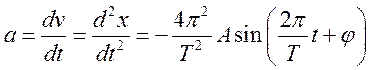
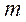
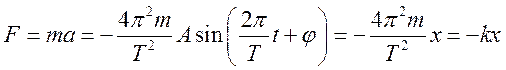
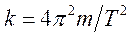
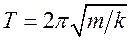
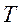
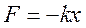
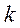
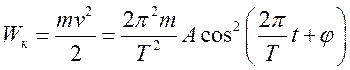
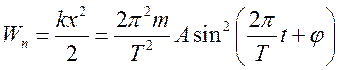
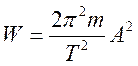
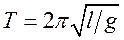
Характеристики и способы представления гармонических колебаний

A — амплитуда (максимальное значение x);
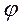
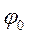
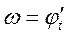

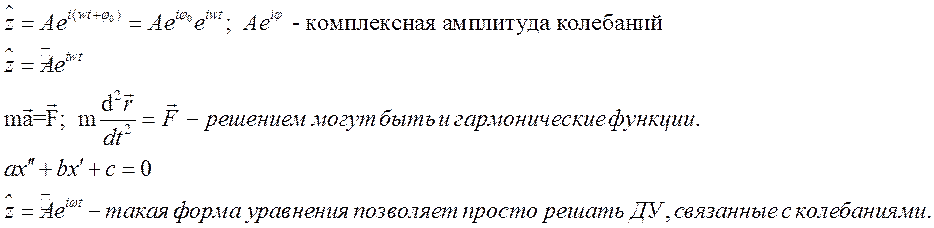
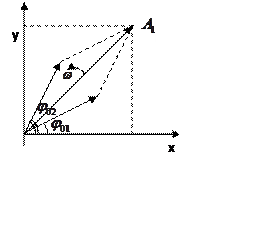
2.Сложение однонаправленных колебаний. Векторные диаграммы. Биения.
При сложении двух одинаково направленных гармонических колебаний одинакового периода получается гармоническое колебание того же периода с амплитудой 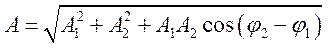
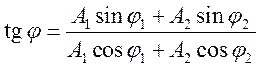
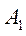
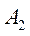
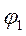
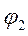
1. Сложение однонаправленных колебаний с одинаковыми частотами:
Пусть система принимает участие в двух однонаправленных колебаниях с одной 
Сколько бы гармонических колебаний ни складывалось, получаем гармоническое колебание с такой же частотой, но у него своя амплитуда, которая зависит от амплитуды складываемых колебаний и от начальных фаз.
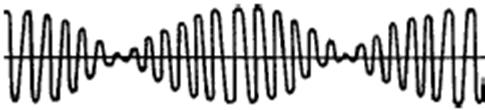
2. Сложение однонаправленных колебаний с разными частотами. Биения.
Результирующее x – это быстрое колебание с медленно изменяющейся амплитудой.
Если амплитуды разные, то нулевой амплитуды не получится. Если складываются колебания с разными частотами, то получаются не гармонические колебания.
3.Сложение перпендикулярных колебаний. Фигуры Лиссажу.
При сложении двух взаимно перпендикулярных колебаний одинакового периода уравнение траектории результирующего движения имеет вид 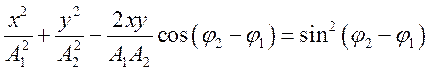
Сложение взаимно перпендикулярных колебаний
Разные
Результирующее движение в общем случае сложное. Траектория может получиться не замкнутой. Замкнутая, если 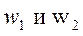
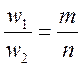
В общем случае фигура Лиссажу пересекает целое число раз каждую ось. Тогда частоты колебаний относятся между собой так, как относятся обратные числа:
4.Гармонические осцилляторы. Дифференциальное уравнение гармонического осциллятора. Собственные колебания и энергия осциллятора.
Среди любых систем можно выделить колебательную систему или осциллятор.
Такая система может совершать колебания сама по себе, те за счет внутренних причин, если у нее есть энергия. Если собственные колебания системы являются гармоническими то система- осциллятор.
Динамика гармонических колебаний описывается дифуром:
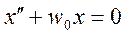
Если для системы получается уравнение (1) то система – гармонический осциллятор.
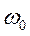
Дифференциальное уравнение гармонического осциллятора.
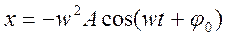
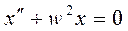
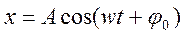
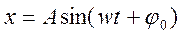
Пример 1 (Пружинный маятник.)

Решением дифференциального уравнения будет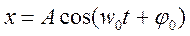
Величина собственной частоты зависит от свойств системы.
Причин колебаний 2:
3 свойства осциллятора:
1. Начальное положение.
2. Возвращающая сила.
Пример 2 (Физический маятник).

Если угол мал то:
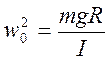
Пример 3 (Колебательный контур)
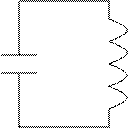
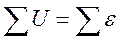
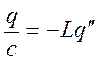
Возвращающие воздействие связанно с зарядом.
Энергия гармонического осциллятора.
Рассмотренные в примерах осцилляторы являются консервативными системами. Энергия с течением времени не меняется.