Уравнение гаусса в дифференциальной форме

Теорема Гаусса в присутствии диэлектриков

Влияние диэлектриков на электрическое поле сводится к ответному действию возникающих в поле поляризационных зарядов. Теорема Остроградского-Гауса для тел в вакууме электростатического поля может быть трансформирована с помощью добавления к свободным зарядам поляризационных для получения теоремы с диэлектриками. В этом случае она запишется как:

Со значением q j s υ в качестве связанных зарядов, q i — свободных зарядов, Φ E — потока вектора напряженности электрического поля.

Теорема Остроградского-Гаусса

Если использовать вектор электрического смещения D → , то это заметно облегчает анализ поля при наличии диэлектрика. Теорему Остроградского-Гаусса при наличии диэлектрика можно записать в интегральном виде:

∮ S D → · d S → = ∑ i = 1 N q i = Q , где Q является суммарным свободным зарядом, находящийся внутри объема, который ограничен поверхностью S .

Поток вектора D → через замкнутую поверхность может быть определен только с помощью свободных зарядов. В вакууме векторы D → и E → совпадающие.

Дифференциальная форма теоремы Гаусса выражения ∮ S D → · d S → = ∑ i = 1 N q i = Q изображается как:

d i v D → = ρ с ρ , являющейся объемной плотностью свободных зарядов.

Теорема Остроградского-Гаусса вида ∮ S D → · d S → = ∑ i = 1 N q i = Q и d i v D → = ρ справедлива только в электростатике и выполняется для переменных полей. Ее относят к составной части системы уравнений Максвелла.

Теорема Остроградского-Гаусса в дифференциальной форме

Напомним формулу вектора электрической индукции:

D → = ε 0 E → + P → со значением ε 0 в качестве электрической постоянной, E → — вектора напряженности, P → — вектора поляризации.

Произведем подстановку формулы D → = ε 0 E → + P → в d i v D → = ρ :

d i v D → = d i v ε 0 E → + P → = ε 0 d i v E → + d i v P → .

При использовании теоремы Остроградского-Гаусса дифференциального вида, получим:

d i v E → = 1 ε 0 ρ — d i v P → .

Для вектора напряженности вышеуказанная формула примет вид в присутствии диэлектрика:

d i v E → = 1 ε 0 ρ + ρ s v с ρ s v , являющейся плотностью заряда. В этом случае необходимо применить d i v E → = 1 ε 0 ρ + ρ s v и d i v E → = 1 ε 0 ρ — d i v P → :

d i v P → = — 1 ε 0 c s v .

Теорема Остроградского-Гаусса для диэлектриков

Теорема Остроградского-Гаусса для вектора электрического смещения в диэлектрике выглядит также, как и для напряженности поля в вакууме. Отсюда следует, что математические соотношения, получившиеся для E → поля в вакууме, аналогичны записям для однородного диэлектрика при замене напряженности электрического поля на вектор D → .

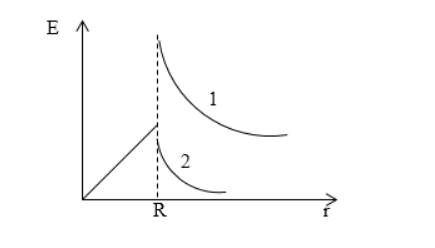
Дан диэлектрический шар, имеющий диэлектрическую проницаемость ε 1 , равномерно заряжен по объему с постоянной плотностью заряда ρ . Его нахождение в среде обусловлено наличием диэлектрической проницаемости ε 2 . Изобразить график напряженности поля шара от расстояния до его центра.

Решение

Поле, создаваемое шаром по заданным условиям, имеет сферическую симметрию. Необходимо рассмотреть его внутри шара r ≤ R . Для нахождения E ( r ) выбирается сферическая поверхность с радиусом меньше сферы. По теореме Остроградского-Гаусса:

E · S = q ε 1 ε 0 , где S — площадь поверхности сферы, которая была выделена. Отсюда следует:

Заряд, находящийся внутри сферы, ищем из формулы:

q = ρ V = ρ 4 3 π r 3 .

Очевидно, что будут происходить изменения напряженности поля внутри шара r ≤ R , согласно выражениям:

E · 4 π r 2 = ρ 4 3 π r 3 ε 1 ε 0 ,

E = ρ r 3 ε 1 ε 0 .

Перейдем к рассмотрению поля вне шара r ≥ R . Для нахождения E ( r ) выбираем сферическую поверхность с радиусом больше радиуса сферы. По теореме Остроградского-Гаусса получим:

E · S = q ε 2 ε 0 , где S обозначает площадь поверхности выделенной сферы. Отсюда следует:

Формула S = 4 π r 2 имеет r ≥ R . Поэтому находящийся внутри заряд выделенной сферы находится из:

q = ρ V = ρ 4 3 π R 3 .

Далее следует подставить площадь из S = 4 π r 2 , заряд из q = ρ V = ρ 4 3 π R 3 , подставив в E · S = q ε 2 ε 0 :

E · 4 πr 2 = ρ 4 3 πR 3 ε 2 ε 0 .

E = ρ R 3 3 ε 2 ε 0 r 2 .

В результате запишем:

E = ρ r 3 ε 1 ε 0 п р и r ≤ R , E = ρ R 3 3 ε 2 ε 0 r 2 п р и r ≥ R .

Ответ: графики показаны на рисунке 1 . Внутри шара напряженность увеличивается прямо пропорционально расстоянию от центра шара. Вне шара она равняется E

1 r 2 . На границе диэлектриков происходит разрыв. Кривая под номером 1 соответствует условию ε 1 > ε 2 .

Предположим, что имеется воображаемая сфера, в центре которой находится точечный заряд. Будет ли изменяться поток вектора напряженности через эту поверхность, если: 1 ) все пространство будет заполнено однородным и изотопным диэлектриком, 2 ) произвести замену сферической поверхности на кубическую?

Решение

1. По теореме Остроградского-Гаусса поток вектора напряженности через поверхность сферы в пространстве с диэлектриком будет равняться:

Φ E = ∮ S E → d S → = 1 ε 0 q + ∑ j = 1 K q j s v , со значением q j s v в качестве связанных зарядов, которые вызваны поляризацией диэлектрика полем одиночного заряда, q в качестве свободного заряда, находящегося в центре сферы.

Учитывая теорему Остроградского-Гаусса, формула потока вектора напряженности через поверхность сферы в пространстве без диэлектрика примет вид:

Φ E = ∮ S E → d S → = 1 ε 0 q .

1. Поле было создано при помощи точечного свободного заряда, то при замене формы поверхности потока вектор напряженности не будет изменяться, потому как равняется аналогичным значению заряда, находящегося на поверхности.

Теорема Остроградского — Гаусса

Вы будете перенаправлены на Автор24

Поток вектора напряженности поля точечного заряда

Рассмотрим поле точечного заряда $q$, найдем поток вектора напряжённости ($\overrightarrow$) через замкнутую поверхность $S$. Будем считать, что заряд находится внутри поверхности. Поток вектора напряженности через любую поверхность равен количеству линий вектора напряженности, которые выходят наружу (начинаются на заряде, если $q>0$) или количеству линий $\overrightarrow$входящих внутрь, если $q \[Ф_E=\frac<<\varepsilon >_0>\ \left(1\right),\]

где знак потока совпадает со знаком заряда.

Теорема Остроградского — Гаусса в интегральной форме

Допустим, что внутри поверхности S находится N точечных зарядов, величины $q_1,q_2,\dots q_N.$ Из принципа суперпозиции мы знаем, что результирующая напряженность поля всех N зарядов может быть найдена как сумма напряженностей полей, которые создаются каждым из зарядов, то есть:

Следовательно, для потока системы точечных зарядов можно записать:

Используем формулу (1), получаем, что:

Уравнение (4) значит, что поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, которые находятся внутри данной поверхности, деленой на электрическую постоянную. Это теорема Остроградского — Гаусса в интегральной форме. Данная теорема является следствием закона Кулона. Значение данной теоремы заключается в том, что она позволяет довольно просто вычислять электрические поля при различных распределениях зарядов.

Как следствие теоремы Остроградского — Гаусса надо сказать, что поток вектора напряженности ($Ф_E$) через замкнутую поверхность в случае при котором заряды находятся вне данной поверхности, равен нулю.

В том случае, когда можно не учитывать дискретность зарядов используют понятие объемной плотности заряда ($\rho $), если заряд распределен по объему. Она определена как:

где $dq$ — заряд, который можно считать точечным, $dV$ — малый объем. (Относительно $dV$ необходимо сделать следующее замечание. Данный объем мал настолько, чтобы плотность заряда в нем можно было считать постоянной, но достаточно велик, чтобы не начала проявляться дискретность заряда). Суммарный заряд, который находится в полости, можно найти как:

В таком случае формулу (4) перепишем в виде:

Теорема Остроградского — Гаусса в дифференциальной форме

Используя формулу Остроградского — Гаусса для любого поля векторной природы, с помощью которой осуществляется переход от интегрирования по замкнутой поверхности к интегрированию по объему:

Равенства в уравнении (9) выполняются для любого объема, а это осуществимо только, если функции, которые находятся в подынтегральных выражениях, равны в каждой токе пространства, то есть мы можем записать, что:

Готовые работы на аналогичную тему

Выражение (10) — теорема Остроградского — Гаусса в дифференциальной форме. Трактовка ее такова: заряды являются источниками электрического поля. Если $div\overrightarrow>0$, то в этих точках поля (заряды положительные) мы имеем источники поля, если $div\overrightarrow

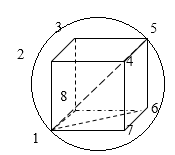
Задание: Заряд равномерно распределен по объему, в этом объеме выделена кубическая поверхность, со стороной b. Она вписана в сферу. Найдите отношение потоков вектора напряженности сквозь эти поверхности.

Согласно теореме Гаусса поток ($Ф_E$) вектора напряженности $\overrightarrow$ через замкнутую поверхность при равномерном распределении заряда по объему равен:

Следовательно, нам необходимо определить объемы куба и шара, если шар описать вокруг этого куба. Для начала, объем куба ($V_k$) если сторона его b равен:

Найдем объем шара ($V_$) по формуле:

где $D$ — диаметр шара и (так как шар описан вокруг куба), главная диагональ куба. Следовательно, нам необходимо выразить диагональ куба через его сторону. Это легко сделать, если использовать теорему Пифагора. Для вычисления диагонали куба, например, (1,5) нам сначала необходимо найти диагональ квадрата (нижнего основания куба) (1,6). Длина диагонали (1,6) равна:

В таком случает длина диагонали (1,5) равна:

Подставим в (1.3) найденный диаметр шара, получим:

Теперь мы можем найти потоки вектора напряженности через поверхность куба, она равна:

через поверхность шара:

Ответ: Поток через поверхность шара в 2,7 раза больше.

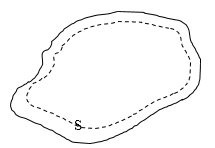
Задание: Докажите, что заряд проводника располагается на его поверхности.

Используем для доказательства теорему Гаусса. Выделим в проводнике замкнутую поверхность произвольной формы около поверхности проводника (рис.2).

Допустим, что заряды внутри проводника есть, запишем с теорему Остроградского — Гаусса для дивергенции поля имеем для любой точки поверхности S:

где $\rho -плотность\ $внутреннего заряда. Однако поля внутри проводника нет, то есть $\overrightarrow=0$, следовательно, $div\overrightarrow=0\to \rho =0$. Теорема Остроградского — Гаусса в дифференциальной форме локальна, то есть, она записана для точки поля, мы специальным образом точку не выбирали, следовательно, плотность заряда равна нулю в любой точке поля внутри проводника.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 03 12 2021

Электростатическая теорема Гаусса в дифференциальной форме. Дивергенция

Уравнение, связывающее поток вектора напряженности поля через замкнутую поверхность и заряд, помещенный внутри этой поверхности, представлено в интегральной форме:

Устремляя к нулю объем, ограниченный поверхностью интегрирования, вокруг какой-то точки и предполагая, что плотность электрического заряда это непрерывная функция координат, можно легко перейти к дифференциальной формулировке того же закона:

В данном уравнении ρ – плотность заряда в точке, вокруг которой стягивается замкнутая поверхность (стягивается так, что любой линейный размер ограничиваемого ею объема стремится к нулю).

Указанное требование предельного перехода (V→0) физически не осуществимо, так как оно равносильно требованию непрерывности ρ как функции координат.

И правда, когда объем V становится настолько мал, что внутри него оказывается небольшое число электронов или атомов, макроскопическое понятие средней плотности заряда теряет смысл. Стремление линейных размеров и объема к нулю понимается здесь, как и во всей макроскопической динамике, в том смысле, что рассматриваемые малые расстояния и объемы могут с точки зрения математического описания поля считаться ничтожными, вместе с тем они должны оставаться еще настолько большими, чтобы не теряли смысла понятия макроскопической физики, рассматривающей вещество как сплошную среду.

Отношение в левой стороне выражения (1) носит название расхождение или дивергенция вектора Е:

Из самого определения выступает физический смысл дивергенции какого-либо физического вектора. В самом деле поток, исходящий из объема, ограниченного данной поверхностью, указывает на существование источников этого потока внутри поверхности и количественно выражает их «мощность» (силу, интенсивность). Отношение полного исходящего потока к объему, который ограничивает поверхность, характеризует объемную плотность источников потока.

Давайте разберем небольшой пример, демонстрирующий наглядное представление о дивергенции.

Представим себе в комнате трубку с разреженным газом, светящимся при электрическом разряде (в нем возникает световой поток) или зажженную свечу. В комнате воздух прозрачен, а снаружи пропитан туманом и дымом (световой поток поглощается). Внутри газоразрядной трубки или пламени свечи дивергенция вектора плотности светового потока положительна, в комнатном воздухе дивергенция равна нулю, а за окном дивергенция отрицательна.

Выбрав ту или иную систему координат, можно записать дифференциальную операцию div E непосредственно из ее определения (2). В декартовой системе координат дивергенция будет иметь вид:

По самому определению дивергенция это скаляр, а сама дифференциальная операция применяется к вектору. Можно заметить, что формально результат, приведенный в формуле (3) можно представить как скалярное произведение векторов набла и Е:

Электростатическая теорема Гаусса в дифференциальной форме формулируется как:

Вывод следует из формул (1) и (2).

Пример 1

Напряженность поля изменяется по закону E_x = E₀(α/x), E_y = 0, E_z = 0 при α

Это поле плоского конденсатора с отрицательным объемным зарядом, поэтому напряженность поля убывает по мере удаления от положительной пластины (в направлении Е_Х).

Пример 2

Условия те же, что и в предыдущем примере, но напряженность поля изменяется по закону:

Решение

Непосредственно дифференцируя, находим:

Данное поле совпадает с полем заряженного цилиндра (r_ц Posted in Основы электричества

Добавить комментарий Отменить ответ

• Автоматизация технологических процессов (183)
• Альтернативная энергетика (34)
• Интернет вещей (IoT) (135)
• Микроконтроллеры (33)
• Моделирование электромеханических систем (22)
• Новости партнеров (1)
• Новости электроники (223)
• Основы электричества (44)
• Реактивная мощность (13)
• Робототехника (54)
• Станки с ЧПУ (46)
• Схемотехника (135)
• Теория автоматического управления (17)
• Электрика в быту (61)
• Электрические машины и аппараты. Трансформаторы (82)
• Электропривод (131)
• Электроснабжение (95)
• Электротехника (144)
• Энергосбережение (106)

• Магнитные пускатели — 144 660
• Логические элементы и их схемная реализация — 117 808
• В чем разница между NPN и PNP транзисторами? — 109 478
• Что такое активная, реактивная и полная мощность — 96 853
• Ввод и распределение электроэнергии в многоквартирном доме — 91 360
• Соотношение между фазными и линейными напряжениями. Номинальные напряжения — 89 958
• Что такое категории надежности электроснабжения? — 84 783
• 11 мифов о Bluetooth 5.0 — 80 653
• Мощность трехфазной сети — 73 477
• Что такое цветовая маркировка шин и проводов и зачем она нужна — 69 844