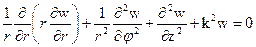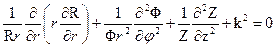Решение однородного уравнения Гельмгольца методом разделения переменных в цилиндрической системе координат
В цилиндрической системе координат (r,φ,z) однородное уравнение Гельмгольца примет вид
Будем искать решение этого уравнения в виде произведения трех функций
где R(r) – функция только координаты r, Φ(φ) – функция только координаты φ, Z(z) – функция только координаты z. В результате подстановки в исходное уравнение и деления на w=R . Φ . Z получаем:
Поступая аналогично случаю решения в декартовой системе координат, получаем систему следующих обыкновенных дифференциальных уравнений, эквивалентную уравнению Гельмгольца:
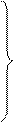
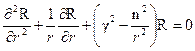
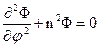
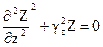
Общие решения этих уравнений известны, причем каждое можно записать в двух формах: с использованием функций Бесселя и Неймана или Ханкеля для первого уравнения и с использованием тригонометрических или экспоненциальных – для двух последних уравнений. Таким образом, находим следующее выражение w=R . Φ . Z
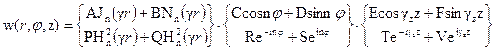
Форма записи имеет тот же смысл, что и для декартовой системы; аналогично также значение входящих в выражение постоянных.
[1] Подробно уравнения Максвелла рассматриваются в курсе «Электромагнитные поля и волны».
* Говоря точнее колебания синфазны в каждой области постоянного знака w = 2Pcoskz, а при изменении знака w имеет место скачок фазы на 180 0
Дата добавления: 2016-03-27 ; просмотров: 1351 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
РЕШЕНИЯ УРАВНЕНИЙ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
Дата добавления: 2014-10-13 ; просмотров: 1852 ; Нарушение авторских прав
6.1. Цилиндрические функции
В дальнейшем нам понадобится решать уравнение Гельмгольца в цилиндрических координатах. В результате разделения переменных появится обыкновенное дифференциальное уравнение:
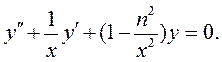 | (6.1) |
Оно называется уравнением цилиндрических функций, или уравнением Бесселя порядка n. Общее решение уравнения (6.1) записывают в следующей форме:
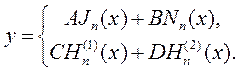 | (6.2) |
Оба варианта решений эквивалентны. Здесь:
· Jп(х) — функции Бесселя порядка п,
· Nn(x) — функции Неймана порядка п,
· Н (1) n(х) — функции Ханкеля (Ганкеля) первого рода порядка п,
· Н (2) n(х) — функции Ханкеля второго рода порядка п.
Это различные виды цилиндрических функций.
Функции Бесселя, Неймана и Ханкеля связаны соотношением:
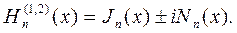 | (6.3) |
Цилиндрические функции не являются периодическими, но они «осциллируют». Функции Бесселя и Неймана с ростом х принимают значения, колеблющиеся около нуля с монотонно убывающей амплитудой и приближающиеся к тригонометрическим при х → ∞. Существенно то, что J0(0) = 1, а Jn(0) = 0 при n ≠ 0 и Nn(0) = -∞. Графики цилиндрических функций приведены на рис. 6.1.
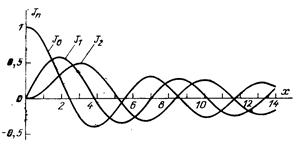 | 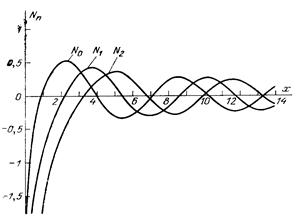 |
| Рис. 6.1. Графики цилиндрических функций |
В справочной литературе имеются таблицы цилиндрических функций. Программы для их расчета включены в библиотеки языков программирования с физико-техническим уклоном, например, в СИ++.
Нам понадобятся значения аргументов х, при которых функции Бесселя и их первые производные обращаются в нуль, т. е. корни х = υnm уравнения Jn(x) = 0 и корни х = μnm уравнения J’n (х) = 0. Они приведены в таблицах 6.1 и 6.2.
| Таблица 6.1 | Таблица 6.2 | ||||||
| Корни υmn уравнения Jn(x) = 0 | Корни μmn уравнения J’n(x) = 0 | ||||||
| n | m | n | m | ||||
| 2.405 | 5.520 | 8.654 | 11.792 | 3.832 | 7.016 | 10.173 | 13.324 |
| 3.832 | 7.016 | 10.173 | 13.324 | 1.841 | 5.331 | 8.536 | 11.706 |
| 5.136 | 8.417 | 11.620 | 14.796 | 3.054 | 6.706 | 7.969 | 13.170 |
| 6.380 | 7.761 | 13.016 | 16.223 | 4.201 | 8.015 | 11.346 | 14.586 |
Ниже приведены некоторые формулы, часто используемые при операциях с цилиндрическими функциями. Цилиндрические функции обозначены Zn(x). При этом подразумеваются функция Бесселя, Неймана или Ханкеля целого порядка.
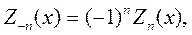 | (6.4) |
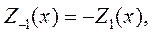 | (6.5) |
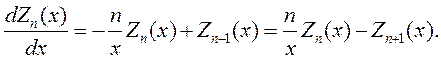 | (6.6) |
Далее из (6.6) следует:
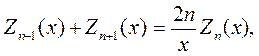 | (6.7) |
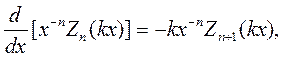 | (6.8) |
 | (6.9) |
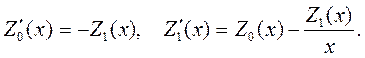 | (6.10) |
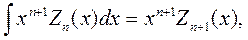 | (6.11) |
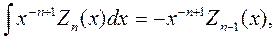 | (6.12) |
 | (6.13) |
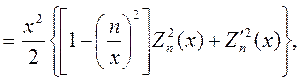 | |
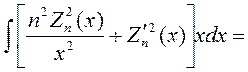 | (6.14) |
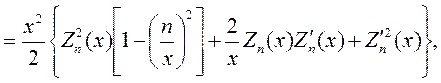 | |
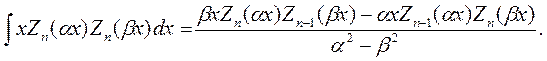  | (6.15) |
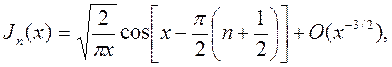 | (6.16) |
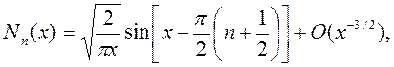 | (6.17) |
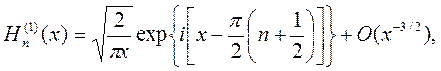 | (6.18) |
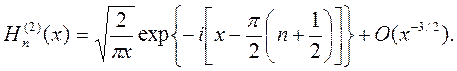 | (6.19) |
Запишем степенной ряд:
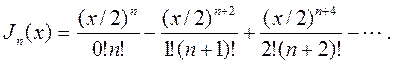 | (6.20) |
6.2. Задачи в цилиндрических координатах
Двумерное уравнение Гельмгольца в цилиндрических координатах имеет следующий вид:
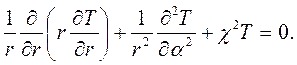 | (6.24) |
Решение этого уравнения будем искать как произведения T(r,α) = R(r)A(α).
Рядом не слишком сложных и логичных операций соотношение (6.24) можно разбить на два отдельных уравнения:
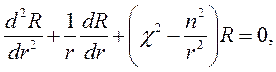 | (6.25) |
 | (6.26) |
Первое уравнение (6.25) — это уравнение Бесселя при у = R, х = χr. Его общее решение запишем в следующей форме:
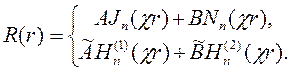 | (6.27) |
Решение второго уравнения, (6.26), также известно:
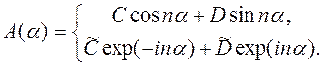 | (6.28) |
Таким образом, найден общий вид решения Т = RA уравнения в цилиндрических координатах, содержащий ряд неопределенных констант.
Для анализа распространения поля в круглом волноводе необходимо решить две краевые задачи (5.8) и (5.9) в цилиндрических координатах для кругового контура диаметром R. Собственные функции и собственные значения решения первой краевой задачи (5.8) имеют следующий вид:
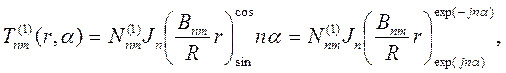 | (6.29) |
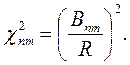 |
Решения второй краевой задачи (5.9) записываются так:
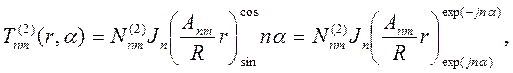 | (6.30) |
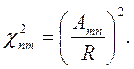 |
В заключение рассмотрим кольцевую область. Она имеет два контура в виде окружности на расстоянии R1 и R2 от центра.
Начнем с решения первой краевой задачи (5.8). Уравнение для собственных значений запишем в следующем виде:
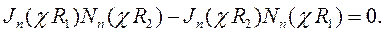 | (6.31) |
Для получения полных собственных функций воспользуемся следующим выражением:
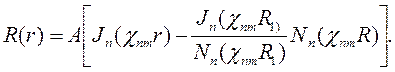 | (6.32) |
Его надо подставить в первую строчку (6.29) вместо 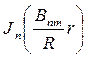
Уравнение относительно χ во второй краевой задаче (5.9) для той же кольцевой области записывается в виде:
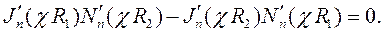 | (6.33) |
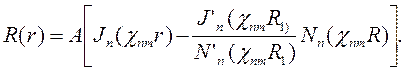 | (6.34) |
где χnm — корни (6.33); они приводятся в справочниках.
Для получения полных собственных функций надо внести R(r) (6.34) вместо 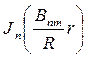
| | | следующая лекция ==> | |
| МАТЕМАТИЧЕСКИЙ АППАРАТ АНАЛИЗА ПРОДОЛЬНО-ОДНОРОДНЫХ СТРУКТУР | | | МАТЕМАТИЧЕСКИЙ АППАРАТ ИЗЛУЧЕНИЯ РАДИОВОЛН |
Не нашли то, что искали? Google вам в помощь!
Алгоритм решения уравнения Гельмгольца в цилиндрической области с импедансными граничными условиями Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Моденов В.П., Иванов С.А.
Построена и математически обоснована схема неполного метода Галеркина, предназначенная для исследования распространения аксиально-симметричных электромагнитных волн в цилиндрической области с граничными условиями 3-го рода с малым по модулю комплексным импедансом.
Похожие темы научных работ по математике , автор научной работы — Моденов В.П., Иванов С.А.
Текст научной работы на тему «Алгоритм решения уравнения Гельмгольца в цилиндрической области с импедансными граничными условиями»
АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА В ЦИЛИНДРИЧЕСКОЙ ОБЛАСТИ С ИМПЕДАНСНЫМИ ГРАНИЧНЫМИ УСЛОВИЯМИ
В. П. Моденов, С. А. Иванов
Построена и математически обоснована схема неполного метода Галеркина, предназначенная для исследования распространения аксиально-симметричных электромагнитных волн в цилиндрической области с граничными условиями 3-го рода с малым по модулю комплексным импедансом.
При расчете базовых элементов электродинамических многофункциональных систем сверхбыстрой обработки информации, использующих ОИС СВЧ, КВЧ и оптического диапазона частот, достаточно эффективна так называемая импедансная модель. Эта модель основана на применении эквивалентных граничных условий. К ним относятся импедане-ные условия Щукина-Леонтовича, двухсторонние импеданеные условия, импеданеные анизотропные граничные условия, граничные условия Вайнштейна и др. 1.
Цель данной работы — сформулировать и математически обосновать алгоритм решения уравнения Гельмгольца, аналогичный описанным в работах 6, для цилиндрической области на примере решения задачи дифракции оеееимметричных поперечно-электрических и поперечно-магнитных волн круглого волновода с поверхностным импедансом на конечном участке длины волновода.
Математическая постановка задачи заключается в решении уравнения Гельмгольца
в цилиндрической области О = <(г,г): 0 1
и (г, г) = ^2Бп(г)срп(г).
Существование и единственность решения задачи
Вначале заметим, что из (5), (8) следуют парциальные условия излучения вида
+ Лп$п(г) = 2лпА5п,п0 ехрСгЬ^), г 1. (9)
Применяя вторую формулу Грина в цилиндрической области О для точного решения задачи (1)-(8) и функции, комплексно сопряженной с ним, получим энергетические соотношения
(А) 1тк2 $г\и\2 йгйг +К$1та о о
= Ке 7„о |7п0-4|2 II ‘РпО II2 + Ке 7т0 ЬтоВ |21| 1рт01
(Б) 1шк2 ¡г\и\2йгйг^я>1шк\и\2\ йг
1 0 (1тН „(г)> — полная на отрезке [0, Щ система собственных функций соответствующей задачи (7). Потребуем, чтобы для приближенного решения 17м выполнялись условия непрерывности потока энергии (4) в сечениях г = 0 и г = 1 и приведенные выше парциальные условия излучения (9), которые запишем в виде
ск(+ ЛпСп(г) = 2^пА6п,п0 ехр(мпг), г 1. (12)
Применяя вторую формулу Грина для приближенного решения 17м и функции, комплексно сопряженной с ним, и учитывая, что функции Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Таким образом, приближенное решение задачи (1)-(8), построенное согласно (5), (11), (12), (14), (15), существует и единственно. Рассматривая функцию SN = U — UN и сводя соответствующую ей задачу к аналогичному энергетическому соотношению, можно показать сходимость в L2 приближенного решения к точному при N ^ оо, как это сделано в работе [5].
Для нахождения коэффициентов отражения и прохождения нормальных волн Rn и Тп при известных амплитудах падающих нормальных волн А и В требуется решить краевую задачу с граничными условиями (12) для системы обыкновенных дифференциальных уравнений 2-го порядка, получаемой из (14)—(15) относительно функций C’n(z). После чего по найденным коэффициентам С„(0) и Сп<1) определяются искомые коэффициенты Rn и Тп.
В настоящей работе решена краевая задача для уравнения Гельмгольца в цилиндрической области с импеданеными (в общем случае несамосопряженными) граничными условиями. Доказано существование и единственность решения этой задачи. Изложен алгоритм построения приближенного решения и доказана сходимость приближенного решения к точному. Построенное приближенное решение удовлетворяет условию непрерывности потока энергии и условию Мейкснера в особых точках. Результаты данной работы могут найти применение в задачах волноводной электродинамики с импеданеными граничными условиями при математическом моделировании на основе импедансной модели.
1. Pelozi G., Ufimtsev P.Ya. 11 IEEE Trans. AP. 1996. 38, N 1. P. 31.
2. Ильинский A.C., Слепян Г.Я. Колебания и волны в электродинамических системах с потерями. М., 1983.
3. Кравченко В.Ф., Казаров A.B. // Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. 1997. № И. С. 59.
4. Свешников А.Г., Ильинский A.C. // Вычислительные методы и программирование. 1969. № 13. С. 27.
5. Конюшенко В.В., Моденов В.П. // Электродинамика и техника СВЧ, КВЧ и оптического диапазона. 2002. №1. С. 21.
6. Свешников А.Г. // ЖВМ и МФ. 1963. 3, №1. С. 170.
7. Моденов В.П. // Радиотехника и электроника. 2005. 50, №2. С. 1.
http://life-prog.ru/1_38096_resheniya-uravneniy-v-tsilindricheskih-koordinatah.html
http://cyberleninka.ru/article/n/algoritm-resheniya-uravneniya-gelmgoltsa-v-tsilindricheskoy-oblasti-s-impedansnymi-granichnymi-usloviyami