Уравнение геометрического места точек удаленных от прямой

Составить уравнение геометрического места точек одинаково удаленных

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему нахождения геометрического места точек (ГМТ) по определенным условиям: удаленности от начала координат или произвольных точек, удаленности от кривых и прямых и т.п.

Геометрическое место точек: решения онлайн

Задача 1. Написать уравнение геометрического места точек, удаленных от прямой $х + 2у – 5 = 0$ на расстояние $sqrt $.

Задача 2. Составить уравнение линии, расстояние каждой точки которой от начала координат и от точки $(5;0)$ относятся как $2:1$.

Задача 3. Составить уравнение множества точек, для каждой из которых выполняется следующее условие: квадрат расстояния до точки $A(2,0)$ на 16 больше квадрата расстояния до оси ординат.

Задача 4. Составить уравнение линии, для каждой точки которой расстояние от точки $A(0,1)$ вдвое меньше расстояния от прямой $y=4$.

Задача 5. Составить уравнение геометрического места точек, сумма квадратов расстояний которых до точек $A(-3,0)$ и $B(0,3)$ равна 26. Построить эту линию.

Задача 6. Составить уравнение геометрического места точек, отношение расстояний которых до данной точки $A(2;0)$ и до данной прямой $x=4,5$ равно числу $2/3$. Полученное уравнение привести к простейшему виду и затем построить кривую.

Составить каноническое уравнение параболы, вершина которой лежит в начале координат и которая проходит через точку F(2;-4); ox– ось симметрии.

Ответ: .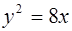

Задача 67.

Составить уравнение геометрического места точек, одинаково удаленных от точки F(2;0) и от прямой .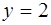

Ответ: .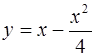

Задача 68.

Составить каноническое уравнение параболы, если ее фокус находится в точке пересечения прямой 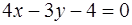с осью 0х.

Ответ: .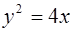

Задача 69.

На параболе 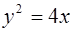найти точку, фокальный радиус которой равен 4.

Ответ: , .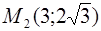

Задача 70.

Написать уравнение окружности, проходящей через начало координат и точки пересечения параболы 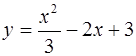с осями координат.

Ответ: .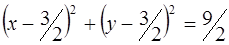

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8921 – | 7229 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Составить уравнение геометрического места точек, одинаково удаленных от точки F(0,2) и от прямой y=4. Найти точки пересечения этой кривой с осями координат и построить её

задан 23 Дек ’13 19:51

Надо приравнять квадраты расстояний от точки то точки, то есть $%x^2+(y-2)^2$%, и от точки до прямой, то есть $%(y-4)^2$%. После упрощений получится уравнение параболы. Остальное просто.

Здравствуйте

Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

Геометрические места точек

Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.

Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.

Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .

Уравнение геометрического места точек удаленных от прямой

§ 23. Метод геометрических мест точек в задачах на построение

Известно, что если смешать синий и жёлтый цвета, то получим зелёный.

Пусть на плоскости надо найти точки, обладающие какими-то двумя свойствами одновременно. Если синим цветом покрасить точки, обладающие первым свойством, а жёлтым — обладающие вторым свойством, то понятно, что зелёные точки будут обладать сразу двумя свойствами. В этом и состоит идея метода ГМТ, которую проиллюстрируем следующими задачами.

Задача 1. Постройте треугольник по трём данным его сторонам.

Решение. Пусть даны три отрезка, длины которых равны a , b , c (рис. 327). Надо построить треугольник ABC , в котором AB = c , AC = b , BC = a .

Проведём произвольную прямую. С помощью циркуля отложим на ней отрезок CB , равный a (рис. 328). Понятно, что задача свелась к построению третьей вершины треугольника, точки A .

Воспользуемся тем, что точка A обладает сразу двумя свойствами:

1) принадлежит геометрическому месту точек, удалённых от точки B на расстояние c , т. е. окружности с центром в точке B радиуса с (см. рис. 328);

2) принадлежит геометрическому месту точек, равноудалённых от точки C на расстояние b , т. е. окружности с центром в точке С радиуса b (см. рис. 328).

В качестве точки A можно выбрать любую из двух образовавшихся зелёных точек.

Полученный треугольник ABC является искомым, так как в нём AB = c , AC = b , BC = a .

Из описанного построения следует, что если каждый из трёх данных отрезков меньше суммы двух других, то эти отрезки могут служить сторонами треугольника.

Задача 2. Постройте фигуру, все точки которой принадлежат данному углу, равноудалены от его сторон и находятся на заданном расстоянии a от его вершины.

Решение. Искомые точки принадлежат сразу двум геометрическим местам точек: биссектрисе данного угла и окружности с центром в его вершине и радиусом, равным a .

Построим биссектрису угла и указанную окружность (рис. 329). Их пересечением является искомая точка X .

Задача 3. Постройте центр окружности радиуса R , проходящей через данную точку M и касающуюся данной прямой a .

Решение. Поскольку окружность касается прямой a , то её центр находится на расстоянии R от этой прямой. Геометрическим местом точек, удалённых от данной прямой на данное расстояние, являются две параллельные прямые (см. упражнение 498). Следовательно, центр окружности находится на прямой b или на прямой с (рис. 330).

Геометрическое место точек, являющихся центрами окружностей радиуса R , проходящих через точку M , — это окружность данного радиуса с центром в точке M . Поэтому в качестве центра искомой окружности можно выбрать любую из точек пересечения окружности с одной из прямых b или с (рис. 331).

Построение для случая, когда данная точка принадлежит данной прямой, рассмотрите самостоятельно.

Задача 4. Постройте треугольник по стороне, медиане, проведённой к этой стороне, и радиусу описанной окружности.

Решение. Построим окружность данного радиуса и проведём хорду AB , равную стороне искомого треугольника. Тогда концы хорды являются двумя вершинами искомого треугольника. Понятно, что третья вершина принадлежит одновременно построенной окружности и окружности с центром в точке O , являющейся серединой хорды AB , и радиусом, равным данной медиане. Каждый из треугольников ABС 1 и ABС 2 (рис. 332) является искомым. Поскольку эти треугольники равны, то задача имеет единственное решение.

622. Даны прямая m и точки A и B вне её (рис. 333). Постройте на прямой m точку, равноудалённую от точек A и B .

623. Точки A и B принадлежат прямой m . Постройте точку, удалённую от прямой m на расстояние a и равноудалённую от точек A и B . Сколько решений имеет задача?

624. Точки B и C принадлежат разным сторонам угла A , причём АВ ≠ АС . Постройте точку M , принадлежащую углу, равноудалённую от его сторон и такую, что MB = MC .

625. Точки B и C принадлежат разным сторонам угла A . Постройте точку D , принадлежащую углу, равноудалённую от его сторон и такую, что DC = BC . Сколько решений может иметь задача?

626. Постройте равнобедренный треугольник по основанию и боковой стороне.

627. Для данной окружности постройте точку, являющуюся её центром.

628. Постройте окружность данного радиуса, проходящую через данную точку, центр которой принадлежит данной прямой.

629. Постройте окружность данного радиуса, проходящую через две данные точки.

630. Найдите все точки, принадлежащие данной окружности и равноудалённые от концов данного отрезка. Сколько решений может иметь задача?

631. Даны две пересекающиеся прямые m и n и отрезок AB . Постройте на прямой m точку, удалённую от прямой n на расстояние AB . Сколько решений имеет задача?

632. В треугольнике ABC известно, что ∠ C = 90°. На катете AC постройте точку D , удалённую от прямой AB на расстояние CD .

633. Постройте равнобедренный треугольник по основанию и радиусу описанной окружности. Сколько решений может иметь задача?

634. Постройте треугольник по двум сторонам и медиане, проведённой к одной из данных сторон.

635. Постройте равнобедренный треугольник по боковой стороне и медиане, проведённой к боковой стороне.

636. На данной окружности постройте точку, находящуюся на данном расстоянии от данной прямой. Сколько решений может иметь задача?

637. На данной окружности постройте точку, равноудалённую от двух данных пересекающихся прямых. Сколько решений может иметь задача?

638. Между двумя параллельными прямыми дана точка. Постройте окружность, проходящую через эту точку и касающуюся данных прямых. Сколько решений имеет задача?

639. Постройте окружность, проходящую через данную точку A и касающуюся данной прямой m в данной точке B .

640. Даны две параллельные прямые и секущая. Постройте окружность, касающуюся этих трёх прямых.

641. Постройте треугольник по двум сторонам и радиусу описанной окружности. Сколько решений может иметь задача?

642. Постройте треугольник по стороне, высоте, проведённой к этой стороне, и радиусу описанной окружности. Сколько решений может иметь задача?

643. Постройте равносторонний треугольник по радиусу описанной окружности.

644. Три прямые попарно пересекаются и не проходят через одну точку. Постройте точку, равноудалённую от всех трёх прямых. Сколько решений имеет задача?

645. Постройте прямоугольный треугольник по катету и сумме гипотенузы и другого катета.

646. Постройте прямоугольный треугольник по гипотенузе и сумме катетов.

647. Постройте прямоугольный треугольник по гипотенузе и разности катетов.

648. Постройте прямоугольный треугольник по катету и разности гипотенузы и другого катета.

649. Постройте равнобедренный треугольник по основанию и разности боковой стороны и высоты, опущенной на основание.

650. Постройте треугольник по стороне, прилежащему к ней углу и сумме двух других сторон.

651. Постройте треугольник по стороне, прилежащему к ней углу и разности двух других сторон.

652. Постройте треугольник по стороне, противолежащему ей углу и разности двух других сторон.

653. Постройте треугольник по стороне, противолежащему ей углу и сумме двух других сторон.

654. Постройте треугольник по стороне, разности углов, прилежащих к этой стороне, и сумме двух других сторон.

655. Постройте треугольник по периметру и двум углам.

656. Постройте остроугольный треугольник по периметру, одному из углов и высоте, проведённой из вершины другого угла.

657. Постройте треугольник по высоте и медиане, проведённым из одной вершины, и радиусу описанной окружности.

658. Постройте треугольник по двум сторонам и медиане, проведённой к третьей стороне.

659. Постройте треугольник по стороне, высоте, проведённой к этой стороне, и медиане, проведённой к одной из двух других сторон.

Упражнения для повторения

660. На рисунке 334 ∠ A = 46°, ∠ ACB = 68°, ∠ DEC = 120°. Найдите углы треугольников EFC и DBE .

661. Через середину O стороны MK треугольника MKN провели прямую, перпендикулярную стороне MK и пересекающую сторону MN в точке C . Известно, что MC = KN , ∠ N = 50°. Найдите угол MCO .

662. В треугольнике ABC из вершины прямого угла C провели высоту CH и биссектрису CM . Длина отрезка HM в 2 раза меньше длины отрезка CM . Найдите острые углы треугольника ABC .

663. На рисунке 335 BD = DC , DN ⊥ BC , ∠ BDM = ∠ MDA . Найдите сумму углов MBN и BMD .

Наблюдайте, рисуйте, конструируйте, фантазируйте

664. Разрежьте фигуру, изображённую на рисунке 336, на три части, не являющиеся квадратами, так, чтобы из этих частей можно было сложить квадрат.

Когда сделаны уроки

Из истории геометрических построений

Умение достигать результат, используя минимальные средства, всегда считалось признаком высокого мастерства. Видимо, поэтому в Древней Греции в значительной степени было развито искусство выполнять геометрические построения с помощью только двух инструментов: дощечки с ровным краем (линейки) и двух заострённых палочек, связанных на одном конце (циркуля). Такое ограничение в выборе инструментов историки связывают с древнегреческой традицией, считавшей прямую и окружность самыми гармоничными фигурами. Так, в своей книге «Начала» великий учёный Евклид описывал построения геометрических фигур, при которых использовались лишь циркуль и линейка.

Существует много задач на построение. С некоторыми из них вы уже успели познакомиться. Однако есть три задачи на построение, которые сыграли в развитии математики особую роль. Эти задачи стали знаменитыми.

Задача о квадратуре круга. Построить квадрат, площадь которого равна площади данного круга.

Задача о трисекции угла (от латинских tria — «три» и section — «разрезание») . Разделить угол на три равные части.

Задача об удвоении куба. Построить куб, объём которого в 2 раза больше объёма данного куба.

Эти задачи занимали умы людей на протяжении тысячелетий. Их пытались решить и такие выдающиеся учёные древности, как Гиппократ Хиосский, Евдокс Книдский, Евклид, Эратосфен, Аполлоний Пергский, Герон, Папп, Платон, Архимед, и гении Нового времени Рене Декарт, Франсуа Виет, Исаак Ньютон. И лишь в середине XIX века была доказана их неразрешимость, т. е. невозможность выполнить указанные построения с использованием лишь циркуля и линейки. Этот результат был получен средствами не геометрии, а алгебры, благодаря переводу этих задач на язык уравнений.

Когда вы решали задачи на построение, особенно те, которые отмечены знаком , вы, по-видимому, испытали сложности, связанные с ограниченностью набора инструментов. Поэтому предложение ещё больше сузить возможности применяемых приборов может показаться вам по меньшей мере неожиданным. Однако ещё в Х веке персидский математик Мохаммед Абу-ль-Вефа описал решение целого ряда задач на построение с помощью линейки и циркуля, раствор которого нельзя было менять. Совсем удивительной является теорема, опубликованная в 1797 году итальянским математиком Лоренцо Маскерони (1750–1800): всякое построение, выполнимое циркулем и линейкой, можно проделать одним циркулем. При этом Маскерони обусловливал следующее: поскольку одним циркулем провести прямую нельзя, то прямая считается построенной, если построены какие-нибудь две её точки.

В ХХ веке была обнаружена книга датского учёного Георга Мора (1640–1697), в которой он также описал построения одним циркулем. Поэтому сформулированную выше теорему называют теоремой Мора — Маскерони.