Уравнение гиперболы вывод исследование формы

Задачи контрольных, курсовых, дипломных работ

Карта

Услуги токарных работ metallnk.ru. . Детальное описание Лестницы Уфа на нашем сайте.

Аналитическая геометрия

Гипербола

Каноническое уравнение гиперболы

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Обозначим фокусы через и ,

расстояние между ними через 2с, а модуль разности расстоя­ний от каждой точки гиперболы до фокусов через 2а. По определению 2а

Вывод канонического уравнения гиперболы.

Дата добавления: 2015-08-31 ; просмотров: 15770 ; Нарушение авторских прав

ГИПЕРБОЛА

Определение. Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух данных точек плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Вывод канонического уравнения гиперболы.

F₁F₂=2с (фокусное расстояние), причем по определению 2а 2 –а 2 ), получим: .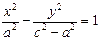

По условию а 2 –а 2 есть положительная величина, ее принято обозначать b 2 , т.е. b 2 =с 2 –а 2 (3). Тогда

(4),

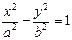
Это каноническое уравнение гиперболы. Очевидно, что гипербола – линия второго порядка.

2. Покажем, что всякая точка, координаты которой удовлетворяют уравнению (4), принадлежит гиперболе (по определению).

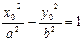
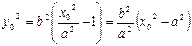
Пусть М₀(х₀; у₀) – точка, гиперболы, координаты которой удовлетворяют уравнению (4), т.е. . Отсюда . Найдем расстояния r₁=F₁М₀ и r₂=F₂М₀ (их называют левым и правым фокальными радиусами соответственно), применив формулу (3):

r₁= ,

аналогично r₂= , т.е.

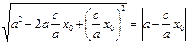
r₁= r₂= .

(Из условия (3): а 0, т.е. точка М₀ принадлежит гиперболе по определению.

Гипербола и её свойства

Гипербола и её форма.

Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
\frac>>-\frac>>=1.\label
$$

Из этого уравнения видно, что для всех точек гиперболы \(|x| \geq a\), то есть все точки гиперболы лежат вне вертикальной полосы ширины \(2a\) (рис. 8.6). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами \((a, 0)\) и \((-a, 0)\), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа \(a\) и \(b\) называются соответственно вещественной и мнимой полуосями гиперболы.

Рис. 8.6. Гипербола.

Для гиперболы оси канонической системы координат являются осями симметрии, а начало канонической системы — центром симметрии.

Доказательство аналогично доказательству соответствующего утверждения для эллипса.

Для исследования формы гиперболы найдем ее пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде \(y=kx\), поскольку мы уже знаем, что прямая \(x=0\) не пересекает гиперболу. Абсциссы точек перечения находятся из уравнения
$$
\frac>>-\fracx^<2>>>=1.
$$
Поэтому, если \(b^<2>-a^<2>k^ <2>> 0\), то
$$
x=\pm \frac<\sqrt-a^<2>k^<2>>>.
$$
Это позволяет указать координаты точек пересечения \((ab/v, abk/v)\) и \((-ab/v, -abk/v)\), где обозначено \(v=(b^<2>-a^<2>k^<2>)^<1/2>\). В силу симметрии достаточно проследить за движением первой из точек при изменении \(k\) (рис. 8.7).

Рис. 8.7. Пересечение прямой и гиперболы.

Числитель дроби \(ab/v\) постоянен, а знаменатель принимает наибольшее значение при \(k=0\). Следовательно, наименьшую абсциссу имеет вершина \((a, 0)\). С ростом \(k\) знаменатель убывает, и \(x\) растет, стремясь к бесконечности, когда \(k\) приближается к числу \(b/a\). Прямая \(y=bx/a\) с угловым коэффициентом \(b/a\) не пересекает гиперболу, и прямые с большими угловыми коэффициентами ее тем более не пересекают. Любая прямая с меньшим положительным угловым коэффициентом пересекает гиперболу.

Если мы будем поворачивать прямую от горизонтального положения по часовой стрелке, то \(k\) будет убывать, \(k^<2>\) расти, и прямая будет пересекать гиперболу во все удаляющихся точках, пока не займет положения с угловым коэффициентом \(-b/a\).

К прямой \(y=-bx/a\) относится все, что было сказано о \(y=bx/a\): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из приведенных рассуждений вытекает, что гипербола имеет вид, изображенный на рис. 8.7.

Прямые с уравнениями \(y=bx/a\) и \(y=-bx/a\) в канонической системе координат называются асимптотами гиперболы.