Уравнение главной нормали к кривой

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $\gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

\begin \vec=\vec(t_0), \quad x_0=x(t_0),\, y_0=y(t_0), \, z_0=z(t_0). \end

Пусть в точке $M$ $ \vec(t_0)\neq\vec<0>$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $\vec(t_0)$.

Пусть $\vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $\lambda\in(-\infty,+\infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $\lambda$ будут соответствовать разные значения $\vec$).

Если $\vec=\$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

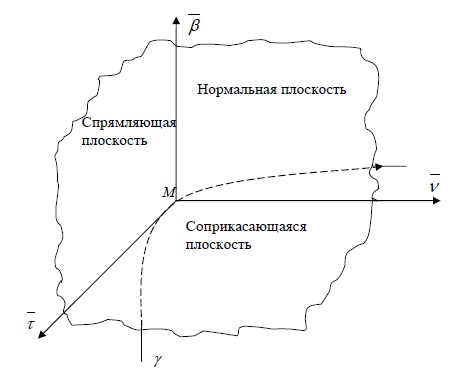
Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $\gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $\vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $\vec-\vec(t_0)$ и $\vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

\begin x'(t_0)\cdot(X-x(t_0))+y'(t_0)\cdot(Y-y(t_0))+z'(t_0)\cdot(Z-z(t_0))=0. \end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $\gamma$ параллельно векторам $\vec(t_0)$, $\vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $\vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $\vec-\vec(t_0)$, $\vec(t_0)$, $\vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

\begin \left| \begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \\ x'(t_0) & y'(t_0) & z'(t_0)\\ x»(t_0) & y»(t_0) & z»(t_0) \\ \end \right|=0 \end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $\gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ \vec(t_0)\times\vec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $\vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $\vec(t_0) \times\left[\vec(t_0),\vec(t_0)\right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $\gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $\vec-\vec(t_0)$, $\vec(t_0)$, $\vec(t_0)\times\vec(t_0)$: \begin \left(\vec-\vec(t_0),\, \vec(t_0),\, \vec(t_0)\times\vec(t_0)\right)=0. \end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ \vec<\tau>=\frac<\vec(t_0)><|\vec(t_0)|>. $$ Орт бинормали: $$ \vec<\beta>=\frac<\vec(t_0)\times\vec(t_0)><|\vec(t_0)\times\vec(t_0)|>. $$ Орт главной нормали: $$ \vec<\nu>=\frac<\vec(t_0) \times[\vec(t_0),\,\vec(t_0)]><|\vec(t_0) \times [\vec(t_0),\,\vec(t_0)]|>. $$

Правая тройка векторов $\vec<\tau>$, $\vec<\nu>$, $\vec<\beta>$ называется репером Френе.

Решение задач

Задача 1

Кривая $\gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

\begin 1\cdot X+0\cdot Y+1\cdot (Z-1)=0\,\,\ \Rightarrow \,\, X+Z=1. \end

\begin \left| \begin X-0 & Y-0 & Z-1 \\ 1 & 0 & 1\\ 0 & 2 & 1 \\ \end \right|=0 \end Раскрываем определитель, получаем уравнение: \begin -2X-Y+2Z-2=0 \end

\begin 1\cdot X-4\cdot Y-1\cdot (Z-1)=0\,\,\ \Rightarrow \,\, X-4Y-Z+1=0. \end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $\vec<\tau>$, $\vec<\nu>$, $\vec<\beta>$ не будет правой (по определению векторного произведения вектор $\vec<\tau>\times\vec<\beta>$ направлен так, что тройка векторов $\vec<\tau>$, $\vec<\beta>$, $\vec<\nu>=\vec<\tau>\times\vec<\beta>$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $\vec<\tau>$, $\vec<\nu>$, $\vec<\tilde<\beta>>$ образует репер Френе для кривой $\gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,\,\, y=\frac<2>,\,\, z=\frac<3>, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $\gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)\in\gamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $\vec(t_0)$, $\vec(t_0)$, поэтому записываем определитель \begin \left| \begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \\ &&\\ 1 & t_0 & t^2_0 \\ &&\\ 0 & 1 & 2t_0 \end \right|=0 \quad \Rightarrow \end

\begin (X-t_0)\cdot t_0^2 — (Y-t_0^2/2)\cdot 2t_0 + (Z-t_0^3/3)=0. \end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: \begin 9-t_0^3/3=0 \quad \Rightarrow \quad t_0=3. \end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $P\left(-\frac45,1,2\right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,\,\, y=1+t,\,\, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $\vec(t_0)$ и $\vec(t_0)\times\vec(t_0)$.

Записываем уравнение спрямляющей плоскости: \begin \left| \begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \\ 2t_0 & 1 & 2\\ 0 & 4 & -2 \end \right|= 0 \end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: \begin 5t_0^2-8t_0-4=0 \,\, \Rightarrow \,\, t_<01>=2,\, t_<02>=-\frac25. \end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: \begin & 5X-4Y-8Z+24=0,\\ & 25X+4Y+8Z=0. \end

Нормальная плоскость и главная нормаль кривой

Нормальная плоскость.

Плоскость \(\mathcal

\), проходящую через точку \(M_<0>\) кривой \(\Gamma\) и перпендикулярную касательной к этой кривой в точке \(M_<0>\), называют нормальной плоскостью кривой \(\Gamma\) в точке \(M_<0>\).

Рис. 22.5

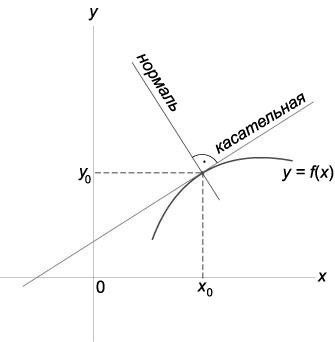
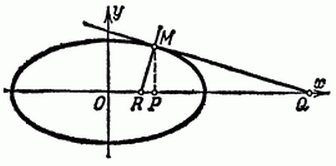
Если кривая \(\Gamma\) задана уравнением в векторной форме
$$
\Gamma=<\textbf=\textbf(t),\ \alpha\leq t\leq\beta>,\label
$$
где
$$
\textbf=(x,y,z),\quad \textbf(t)=(x(t),y(t),z(t)),\nonumber
$$
\(t_<0>\in[\alpha,\beta]\), \(\overrightarrow=\textbf(t_0)\) и \(\textbf‘(t_0)\neq 0\), то вектор \(\textbf‘(t_0)\) параллелен касательной к кривой \(\Gamma\) в точке \(M_<0>\). Пусть \(M\) — произвольная точка нормальной плоскости \(\mathcal

\) (рис. 22.5), \(\overrightarrow=\textbf\). Тогда вектор \(\overrightarrow_<0>=\textbf-\textbf(t_0)\) перпендикулярен вектору \(\textbf‘(t_<0>)\), и поэтому уравнение нормальной плоскости \(\mathcal

\) к кривой \(\Gamma\) в точке \(M_<0>\) можно записать в виде
$$
(\textbf-\textbf(t_<0>),\textbf‘(t_<0>))=0\nonumber
$$
или
$$
(x-x(t_<0>))x'(t_0)+(y-y(t_<0>))y'(t_<0>)+(z-z(t_0))z'(t_0)=0.\nonumber
$$

Главная нормаль.

Любую прямую, лежащую в нормальной плоскости \(\mathcal

\) к кривой \(\Gamma\) в точке \(M_<0>\), называют нормалью кривой \(\Gamma\) в точке \(M_<0>\). Среди всех нормалей выделяют одну — главную нормаль.

Понятие главной нормали требует введения дополнительных ограничений на вектор-функции, с помощью которых записываются уравнения кривых. Пусть \(\Gamma\) — гладкая кривая, заданная уравнением \eqref, причем для всех \(t\in[\alpha,\beta]\) существует \(\textbf″(t)\). В этом случае говорят, \(\Gamma\) — дважды дифференцируемая кривая без особых точек.

Если \(\Gamma\) — дважды дифференцируемая кривая без особых точек, заданная уравнением \eqref, \(s\) — переменная длина дуги кривой \(\Gamma\), то существуют \(\displaystyle \frac>\) и \(\displaystyle \frac\textbf>>\) и справедливы равенства
$$
\frac>=\frac<\textbf‘(t)>,\label
$$
$$
\fracr\textbf<>>>=\frac″(t)-s″(t)\textbf‘(t)><(s(t))^<3>>.\label
$$

\(\circ\) Применяя правило дифференцирования вектор-функции при замене переменного, получаем формулу \eqref:
$$
\frac>=\frac>