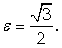Уравнение х2 у2 х у задает

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение показательных уравнений.

Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное уравнение
Решить уравнение

Немного теории.

Показательная функция, её свойства и график

Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) a n a m = a n+m

4) (ab) n = a n b n

7) a n > 1, если a > 1, n > 0

8) a n m , если a > 1, n n > a m , если 0 x , где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \( a \neq 1\)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leqslant 0\), и имеет корень при любом b > 0.

3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \( a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны тогда и только тогда, когда равны их показатели.

Решить уравнение 2 3x • 3 x = 576
Так как 2 3x = (2 3 ) x = 8 x , 576 = 24 2 , то уравнение можно записать в виде 8 x • 3 x = 24 2 , или в виде 24 x = 24 2 , откуда х = 2.
Ответ х = 2

Решить уравнение 3 х + 1 — 2 • 3 x — 2 = 25
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 (3 3 — 2) = 25, 3 х — 2 • 25 = 25,
откуда 3 х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2

Решить уравнение 3 х = 7 х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac<3^x> <7^x>= 1 \), откуда \( \left( \frac<3> <7>\right) ^x = 1 \), х = 0
Ответ х = 0

Решить уравнение 9 х — 4 • 3 х — 45 = 0
Заменой 3 х = t данное уравнение сводится к квадратному уравнению t 2 — 4t — 45 = 0. Решая это уравнение, находим его корни: t₁ = 9, t₂ = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень х = 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2

Решить уравнение 3 • 2 х + 1 + 2 • 5 x — 2 = 5 х + 2 х — 2
Запишем уравнение в виде
3 • 2 х + 1 — 2 x — 2 = 5 х — 2 • 5 х — 2 , откуда
2 х — 2 (3 • 2 3 — 1) = 5 х — 2 ( 5 2 — 2 )
2 х — 2 • 23 = 5 х — 2 • 23
\( \left( \frac<2> <5>\right) ^ = 1 \)
x — 2 = 0
Ответ х = 2

Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

Тема урока: «Уравнение с двумя переменными и его график»

Разделы: Математика

ЦЕЛЬ:1) Познакомить учащихся с понятием «уравнение с двумя переменными»;

2) Научить определять степень уравнения с двумя переменными;

3) Научить определять по заданной функции, какая фигура является графиком

4) Рассмотреть преобразования графиков с двумя переменными;

5) Учить учащихся «читать» графики и выполнять построение графиков по

заданному уравнению с двумя переменными, используя программу Agrapher ;

6) Развивать логическое мышление учащихся.

I.Новый материал — объяснительная лекция с элементами беседы.

(лекция проводится с использованием авторских слайдов; построение графиков выполнено в программе Agrapher)

У: При изучении линий возникают две задачи:

По геометрическим свойствам данной линии найти её уравнение;

Обратная задача: по заданному уравнению линии исследовать её геометрические свойства.

Первую задачу мы рассматривали в курсе геометрии применительно к окружности и прямой.

Сегодня мы будем рассматривать обратную задачу.

Рассмотрим уравнения вида:

– это примеры уравнений с двумя переменными.

Уравнения с двумя переменными х и у имеет вид f(x,y)= (x,y), где f и – выражения с переменными х и у.

Если в уравнении х(х-у)=4 подставить вместо переменной х её значение -1, а вместо у – значение 3, то получится верное равенство: 1*(-1-3)=4,

Пара (-1; 3) значений переменных х и у является решением уравнения х(х-у)=4.

То есть решением уравнения с двумя переменными называют множество упорядоченных пар значений переменных, образующих это уравнение в верное равенство.

Уравнения с двумя переменными имеет, как правило, бесконечно много решений. Исключения составляют, например, такие уравнения, как х 2 +( у 2 — 4 ) 2 = 0 или

Первое из них имеет два решения (0; -2) и (0; 2), второе – одно решение (0;0).

Уравнение х 4 + у 4 +3 = 0 вообще не имеет решений. Представляет интерес, когда значениями переменных в уравнении служат целые числа. Решая такие уравнения с двумя переменными, находят пары целых чисел. В таких случаях говорят, что уравнения решено в целых числах.

Два уравнения, имеющие одно и тоже множество решений, называют равносильными уравнениями. Например, уравнение х(х + у 2 ) = х + 1 есть уравнение третьей степени, так как его можно преобразовать в уравнение ху 2 + х 2 — х-1 = 0, правая часть которого – многочлен стандартного вида третьей степени.

Степенью уравнения с двумя переменными, представленного в виде F(х, у) = 0, где F(х,у)-многочлен стандартного вида, называют степень многочлена F(х, у).

Если все решения уравнения с двумя переменными изобразить точками в координатной плоскости, то получится график уравнения с двумя переменными.

Графиком уравнения с двумя переменными называется множество точек, координаты которых служат решениями этого уравнения.

Так, график уравнения ax + by + c = 0 представляет собой прямую, если хотя бы один из коэффициентов a или b не равен нулю(рис.1). Если a = b = c = 0, то графиком этого уравнения является координатная плоскость(рис.2), если же a = b = 0, а c0, то графиком является пустое множество(рис.3).

График уравнения y = a х 2 + by + c представляет собой параболу(рис.4), график уравнения xy=k (k0 ) – гиперболу(рис.5). Графиком уравнения х 2 + у 2 = r, где x и y – переменные, r – положительное число, является окружность с центром в начале координат и радиусом равным r(рис.6). Графиком уравнения является эллипс, где a и b – большая и малая полуоси эллипса (рис.7).

Построение графиков некоторых уравнений облегчается использованием их преобразований. Рассмотрим преобразования графиков уравнений с двумя переменными и сформулируем правила, по которым выполняются простейшие преобразования графиков уравнений

1) График уравнения F (-x, y) = 0 получается из графика уравнения F (x, y) = 0 с помощью симметрии относительно оси у.

2) График уравнения F (x, -y) = 0 получается из графика уравнения F (x, y) = 0 с помощью симметрии относительно оси х.

3) График уравнения F (-x, -y) = 0 получается из графика уравнения F (x, y) = 0 с помощью центральной симметрии относительно начала координат.

4) График уравнения F (x-а, y) = 0 получается из графика уравнения F (x, y) = 0 с помощью перемещения параллельно оси х на |a| единиц (вправо, если a > 0, и влево, если а 0, и вниз, если b 1, и с помощью растяжения от оси у в раз, если 0 1, и с помощью растяжения от оси x в раз, если 0 0 и 45 0 .

8) График уравнения F (x, y) = 0 в результате поворота около начала координат на угол 90 0 по часовой стрелке переходит в график уравнения F (-y, x) = 0, а против часовой стрелки – в график уравнения F (y, -x) = 0.

9) График уравнения F (x, y) = 0 в результате поворота около начала координат на угол 45 0 по часовой стрелке переходит в график уравнения F = 0, а против часовой стрелки – в график уравнения F = 0.

Из рассмотренных нами правил преобразования графиков уравнений с двумя переменными легко получаются правила преобразования графиков функций.

Пример 1. Покажем, что графиком уравнения х 2 + у 2 + 2х – 8у + 8 = 0 является окружность (рис.17).

Преобразуем уравнение следующим образом:

1) сгруппируем слагаемые, содержащие переменную х и содержащие переменную у, и представим каждую группу слагаемых в виде полного квадрата трехчлена: (х 2 + 2х + 1) + (у 2 -2*4*у + 16) + 8 – 1 – 16 = 0;

2) запишем в виде квадрата суммы (разности) двух выражений полученные трехчлены: (х + 1) 2 + (у – 4) 2 — 9 = 0;

3) проанализируем, согласно правилам преобразования графиков уравнений с двумя переменными, уравнение (х + 1) 2 + (у – 4) 2 = 3 2 : графиком данного уравнения является окружность с центром в точке (-1; 4) и радиусом 3 единицы.

Пример 2. Построим график уравнения х 2 + 4у 2 = 9.

Представим 4у 2 в виде (2у) 2 , получим уравнение х 2 + (2у) 2 = 9, график которого можно получить из окружности х 2 + у 2 = 9 сжатием к оси х в 2 раза.

Начертим окружность с центром в начале координат и радиусом 3 единицы.

Уменьшим в 2 раза расстояние каждой её точки от оси Х, получим график уравнения

Мы получили фигуру с помощью сжатия окружности к одному из её диаметров(к диаметру, который лежит на на оси Х). Такую фигуру называют эллипсом (рис.18).

Пример 3. Выясним, что представляет собой график уравнения х 2 — у 2 = 8.

Воспользуемся формулой F= 0.

Подставим в данное уравнение вместо Х и вместо У, получим:

У: Что представляет собой график уравнения у = ?

Д: Графиком уравнения у = является гипербола.

У: Мы преобразовали уравнение вида х 2 — у 2 = 8 в уравнение у = .

Какая линия будет являться графиком данного уравнения?

Д: Значит, и графиком уравнения х 2 — у 2 = 8 является гипербола.

У: Какие прямые являются асимптотами гиперболы у = .

Д: Асимптотами гиперболы у = являются прямые у = 0 и х = 0.

У: При выполненном повороте эти прямые перейдут в прямые = 0 и =0, т.е в прямые у = х и у = — х. (рис.19).

Пример 4 : Выясним, какой вид примет уравнение у = х 2 параболы при повороте около начала координат на угол 90 0 по часовой стрелке.

Используя формулу F (-у; х) = 0, заменим в уравнении у = х 2 переменную х на – у, а переменную у на х. Получим уравнение х = (-у) 2 , т. е. х = у 2 (рис.20).

Мы рассмотрели примеры графиков уравнений второй степени с двумя переменными и выяснили, что графиками таких уравнений могут быть парабола, гипербола, эллипс (в частности окружность). Кроме того, графиком уравнения второй степени может являться пара прямых (пересекающихся или параллельных).Это так называемый вырожденный случай. Так графиком уравнения х 2 — у 2 = 0 является пара пересекающихся прямых (рис.21а), а графиком уравнения х 2 — 5х + 6 + 0у = 0- параллельных прямых.

(учащимся выдаются «Карточки-инструкции» по выполнению построений графиков уравнений с двумя переменными в программе Agrapher (Приложение 2) и карточки «Практическое задание» (Приложение 3) с формулировкой заданий 1-8 Графики уравнений к заданиям 4-5 учитель демонстрирует на слайдах).

Задание1. Какие из пар (5;4), (1;0), (-5;-4) и (-1; —) являются решениями уравнения:

а) х 2 — у 2 = 0, б) х 3 — 1 = х 2 у + 6у ?

Подставив в заданное уравнение, поочерёдно координаты данных точек убеждаемся, что ни одна данная пара не является решением уравнения х 2 — у 2 = 0, а решениями уравнения х 3 — 1 = х 2 у + 6у являются пары (5;4), (1;0) и (-1; —).

Ответ:

125 — 1 = 100 + 24 (И)

-125 – 1 =-100 – 24 (Л)

-1 – 1 = — — (И)

Ответ: а); б) (5;4), (1; 0), (-1; —).

Задание 2. Найдите такие решения уравнения ху 2 — х 2 у = 12, в которых значение х равно 3.

Решение: 1)Подставим вместо Х в заданное уравнение значение 3.

2)Получим квадратное уравнение относительно переменной У, имеющее вид:

4) Решим это уравнение:

3у 2 — 9у – 12 = 0

Д = 81 + 144 = 225

Ответ: пары (3;4) и (3;-1) являются решениями уравнения ху 2 — х 2 у = 12

Задание3. Определите степень уравнения:

а) 2у 2 — 3х 3 + 4х = 2; в) (3 х 2 + х)(4х — у 2 ) = х;

б) 5у 2 — 3у 2 х 2 + 2х 3 = 0; г) (2у — х 2 ) 2 = х(х 2 + 4ху + 1).

Ответ: а) 3; б) 5; в) 4; г) 4.

Задание4. Какая фигура является графиком уравнения:

а) 2х = 5 + 3у; б) 6 х 2 — 5х = у – 1; в) 2(х + 1) = х 2 — у;

г) (х — 1,5)(х – 4) = 0; д) ху – 1,2 = 0; е) х 2 + у 2 = 9.

Ответ: а) прямая (рис.23а); б) парабола, ветви которой направлены вверх (рис.23б); в) парабола, ветви которой направлены вверх (рис.23в), г) две параллельные прямые х = 1,5 и х = 4 (рис.23г); д) гипербола (рис.23д); е) окружность, с центром в начале координат, радиусом равным 3 (рис.23е).

Задание5. Напишите уравнение, график которого симметричен графику уравнения х 2 — ху + 3 = 0 (рис.24) относительно: а) оси х; б) оси у; в)прямой у = х; г) прямой у = -х.

Проверьте с помощью программы Agrapher правильность выполнения задания.

Ответ: а) х 3 + ху + 3 = 0 (рис.24а); б) — х 3 + ху + 3 = 0 (рис.24б); в) у 3 — ух + 3 = 0 (рис.24в); г) (-у 3 ) + ух +3 = 0 (рис.24г).

Задание6. Составьте уравнение, график которого получается растяжением графика уравнения у= х 2 -3 (рис.25):

а) от оси х в 2 раза; б) от оси у в 3 раза.

Проверьте с помощью программы Agrapher правильность выполнения задания.

Ответ: а)у — х 2 + 3 = 0 (рис.25а); б) у-(x) 2 + 3 = 0 (рис.25б).

Задание7. На рисунке (рис.29) изображен график уравнения с двумя переменными. Найдите по графику (приближенно) два решения:

а) с одинаковыми значениями х: х = 1; -2;

б) с противоположными значениями у: у = 1, 2

Ответ: а) если х = 1, то у = -2,5 или у = 2,5, если х = -2, то у = -3,5 или у = -3,5;

б если у = 2,то х = 2,если у =-2, то х =-2; если у = 1, то х = 3,5, если у = -1, то х=-3,5

Задание8. Сравните взаимное расположение данных прямых и определите, каким преобразованием плоскости график первой прямой переводится в график второй прямой.

а) 3х-7у = 5 и 3(х-1)-7у = 5

б) 3х-7у = 5 и 3(х-1)-7(у+3) =5

в) 3х-7у = 5 и 3х + 7у = 5

г) 3х-7у = 5 и -3х-7у = 5

д) 3х-7у = 5 и 3х-7у = -5

е) 3х-7у = 5 и 7х-3у = 5

Ответ: а) прямые параллельны, перемещение параллельно оси х на 1 единицу вправо (рис.26а);

б) прямые параллельны, перемещение параллельно оси х на 1 единицу вправо и параллельно оси у на 3 единицы вниз (рис.26б);

в) прямые пересекаются, симметричное отображение относительно оси х (рис.26в);

г) прямые пересекаются, симметричное отображение относительно оси у (рис.26г);

д) прямые параллельны, симметричное отображение относительно начала координат (рис.26д);

е) прямые пересекаются, поворот около начала координат на 90по часовой стрелке и симметричное отображение относительно оси х (рис.26е).

III. Самостоятельная работа обучающего характера.

(учащимся выдаются карточки «Самостоятельная работа» и «Отчётная таблица результатов самостоятельной работы», в которую учащиеся записывают свои ответы и после самопроверки, по предложенной схеме оценивают работу) Приложение 4..

1.Определите степень уравнения:

а) 5х 3 -3х 2 у 2 + 8 = 0; б) (х + у + 1) 2 -(х-у) 2 = 2(х+у).

2. Является ли пара чисел (-2;3) решением уравнения:

а) х 3 + у 3 -5х 2 = 0; б) х 4 +4х 3 у +6х 2 у 2 + 4ху 3 + у 4 = 1.

3. Найдите множество решений уравнения:

х 4 + у 4 -8х 2 + 16 = 0.

4. Какой кривой (гиперболой, окружностью, параболой) является множество точек, если уравнение этой кривой имеет вид:

а) (х + 1) 2 + (у-1) 2 = 4;

(проверьте с помощью программы Agrapher правильность выполнения задания)

5. Постройте, используя программуAgrapher, график уравнения:

х 2 — 2х + у 2 — 4у = 20.

Укажите координаты центра окружности и её радиус.

6. Как следует на координатной плоскости переместить гиперболу у = , чтобы её уравнение приняло вид х 2 — у 2 = 16 ?

Проверьте свой ответ, выполнив графическое построение, используя программу Agrapher.

7.Как следует на координатной плоскости переместить параболу у = х 2 , чтобы её уравнение приняло вид х = у 2 — 1

1.Определите степень уравнения:

а)3ху = (у-х 3 )(х 2 +у); б) 2у 3 +5х 2 у 2 — 7 = 0.

2. Является ли пара чисел (-2;3) решением уравнения:

а) х 2 -у 2 -3х = 1; б) 8х 3 + 12х 2 у + 6ху 2 +у 3 =-1.

3. Найдите множество решений уравнения:

х 2 + у 2 -2х – 8у + 17 = 0.

4. Какой кривой (гиперболой, окружностью, параболой) является множество точек, если уравнение этой кривой имеет вид:

а) (х-2) 2 + (у + 2) 2 =9

(проверьте с помощью программы Agrapher правильность выполнения задания)

5. Постройте, используя программуAgrapher, график уравнения:

х 2 + у 2 — 6х + 10у = 2.

6.Как следует на координатной плоскости переместить гиперболу у = , чтобы её уравнение приняло вид х 2 — у 2 = 28 ?

7.Как следует на координатной плоскости переместить параболу у = х 2 , чтобы её уравнение приняло вид х = у 2 + 9.

5.2.8. Примеры решения задач по теме «Кривые 2-го порядка»

Определить тип уравнения кривой 2-го порядка:

Если L1·L2 > 0, то уравнение эллиптического типа;

Если L1·L2 0, следовательно, перед нами уравнение эллиптического типа.

В уравнении отсутствует произведение Ху, следовательно, квадратичная форма его старших членов имеет канонический вид; поэтому коэффициенты при Х2 и У2 являются собственными числами матрицы квадратичной формы. Итак, L1 = 4, L2 = 9, L1·L2 > 0, следовательно, перед нами уравнение эллиптического типа.

Геометрические образы, определяемые уравнением эллиптического типа:

— пустое множество («мнимый эллипс»).

Для приведения уравнения к каноническому виду нужно исключить из него слагаемые. Содержащие первые степени переменных. Для этого преобразуем левую часть:

Зададим параллельный перенос осей координат:

Тогда в новых координатах уравнение примет вид:

Каноническое уравнение эллипса.

Ответ: уравнение эллипса, канонический вид .

Привести уравнение к каноническому виду и указать геометрический образ, который оно определяет:

Собственные числа имеют разные знаки, значит, тип уравнения – гиперболический.

Геометрические образы, определяемые уравнением гиперболического типа:

— пара пересекающихся прямых.

Собственные числа имеют разные знаки, значит, тип уравнения – гиперболический.

Геометрические образы, определяемые уравнением гиперболического типа:

— пара пересекающихся прямых.

Заметим, что для данного уравнения нет необходимости искать явный вид преобразования координат, приводящего квадратичную форму к каноническому виду. Это связано с тем, что уравнение не содержит линейных членов, а его свободный член не изменится при преобразовании вида

Найденные собственные числа будут коэффициентами при Х2 и У2 для канонического вида квадратичной формы. Следовательно, в соответствующей координатной системе уравнение примет вид:

Каноническое уравнение гиперболы.

Ответ: уравнение гиперболического типа, канонический вид

.

Привести уравнение к каноническому виду и указать геометрический образ, который оно определяет:

Перед нами полное уравнение 2-го порядка, и для приведения его к каноническому виду потребуется провести оба преобразования координатных осей: поворот на такой угол, чтобы новые оси стали параллельными собственным векторам матрицы квадратичной формы (это преобразование квадратичной формы к каноническому виду), и параллельный перенос.

Перед нами полное уравнение 2-го порядка, и для приведения его к каноническому виду потребуется провести оба преобразования координатных осей: поворот на такой угол, чтобы новые оси стали параллельными собственным векторам матрицы квадратичной формы (это преобразование квадратичной формы к каноническому виду), и параллельный перенос.

Итак, тип уравнения – гиперболический.

Матрица перехода к новому базису:

.

Собственные векторы следует выбирать так, чтобы определитель матрицы перехода равнялся +1 – при этом не нарушается взаимное расположение координатных осей.

Запишем исходное уравнение в новых координатах:

2) Параллельный перенос:

В новых координатах получаем уравнение

Пара пересекающихся прямых.

Ответ: уравнение гиперболического типа, определяет пару пересекающихся прямых, канонический вид: У″ = ± 2Х″.

Не проводя преобразования координат, установить, что уравнение

Определяет прямую, и найти уравнение этой прямой.

Обратите внимание на то, что квадратичная форма, образованная старшими членами уравнения, является полным квадратом.

Иногда привести уравнение к простому виду удается с помощью алгебраических приемов. Представим левую часть уравнения в виде:

Ответ: уравнение определяет прямую Х – 3У + 2 = 0.

Эллипс, симметричный относительно осей координат, проходит через точки

Найти его эксцентриситет.

По условию задачи оси координат являются осями симметрии эллипса, поэтому, во-первых, его уравнение имеет канонический вид, а во-вторых, полуось А равна абсциссе точки А.

По условию задачи оси координат являются осями симметрии эллипса, поэтому, во-первых, его уравнение имеет канонический вид:

А во-вторых, полуось А равна абсциссе точки А, т. е. А = 6. Найдем B, подставив в уравнение эллипса координаты точки М:

Итак, уравнение эллипса:

Тогда расстояние от фокуса до начала координат

Вычислим эксцентриситет эллипса:

Ответ: эксцентриситет

Составить уравнение эллипса, фокусы которого лежат на прямой У + 6 = 0, эксцентриситет равен , а точка М(3; -1) является концом малой полуоси.

Найдите расстояние от точки М до прямой У + 6 = 0, т. е. длину малой полуоси эллипса. Центром симметрии эллипса будет точка О пересечения прямых F1F2 (Y + 6 = 0) и МО, проходящей через точку М перпендикулярно F1F2.

Найдем расстояние от точки М до прямой У + 6 = 0, т. е. длину малой полуоси эллипса. Нормальный вид уравнения данной прямой: -у – 6 = 0, тогда

Центром симметрии эллипса будет точка О пересечения прямых F1F2 (Y + 6 = 0) и МО, проходящей через точку М перпендикулярно F1F2.

Поскольку прямая F1F2 параллельна оси абсцисс, прямая МО параллельна оси ординат; следовательно, ее уравнение: Х = 3. Тогда координаты точки О:

С учетом расположения осей эллипса можно утверждать, что в системе координат, полученной параллельным переносом начала координат в точку

О(3; -6), то есть заданной преобразованием

Уравнение эллипса имеет канонический вид:

Найдем А из условия, что

Подставим найденные значения А и B в уравнение эллипса:

Ответ: уравнение эллипса: Х2 + 2У2 – 6Х + 24У + 31 = 0.

Составить уравнения директрис гиперболы.

Приведите уравнение гиперболы к каноническому виду и составьте уравнения директрис в виде

Приведем уравнение гиперболы к каноническому виду:

Осями симметрии являются координатные оси, А = 3, B = 4. Тогда

Ответ: уравнения директрис:

Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса

Найдите вначале координаты вершин и фокусов эллипса, а затем определите коэффициенты А и B в каноническом уравнении гиперболы.

Координаты вершин гиперболы: (А; 0) и (-А; 0), координаты фокусов: (С; 0) и (–С; 0). Соответственно координаты вершин эллипса: (А1; 0) и (-А1; 0), координаты фокусов: (С1; 0) и (-С1; 0). У данного эллипса А1 = 5,

Тогда для гиперболы А = 4, С = 5, откуда

,

И уравнение гиперболы:

Ответ:

Составить уравнение касательной к гиперболе

В ее точке М=<15; 4>.

Найдите вначале координаты нормали к гиперболе в точке М (если кривая задана уравнением F(X,Y) = 0, То нормаль к ней в точке М0=<Х0;у0>

Имеет координаты: П = (F′X(X0;Y0);F′Y(X0;Y0))), а затем составьте уравнение прямой, проходящей через точку М=<15; 4> перпендикулярно

Найдем координаты нормали к гиперболе в точке М.

Уравнение прямой, проходящей через точку М0(х0;у0) перпендикулярно вектору П = <A, B>, имеет вид:

А(х – х0) + В(у – у0) = 0.

Запишем уравнение касательной:

Ответ: Уравнение касательной:

Составить уравнение параболы, если даны ее фокус F(2; -1) и директриса

Используйте определение параболы: параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.

Используем определение параболы:

Параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.

Пусть точка М(Х, У) лежит на параболе. Тогда ее расстояние до фокуса

Выразим через Х и У расстояние от точки М до директрисы.

Нормальное уравнение директрисы:

Из определения параболы DM = MF,

Ответ: уравнение параболы: Х2 + 2Ху + У2 – 6Х + 2У + 9 = 0.

Составить уравнение параболы с вершиной в начале координат, если известно, что парабола симметрична относительно оси Ох и проходит через точку А=<9; 6>. Найти координаты ее фокуса.

Из условий задачи следует, что данная парабола задается каноническим уравнением

Подставьте в это уравнение координаты точки А и найдите значение параметра Р параболы.

Из условий задачи следует, что данная парабола задается каноническим уравнением

Подставим в это уравнение координаты точки А: 36 = 2Р·9, откуда Р = 2.

Следовательно, уравнение параболы имеет вид: У2 = 4Х.

Координаты фокуса параболы задаются формулой: F=<0,5P; 0>, то есть F=<1; 0>.

Ответ: уравнение параболы: У2 = 4Х; фокус F=<1; 0>.